八年级数学全等三角形2(1)(2018-2019)
勤学早2018-2019学年度八年级数学(上)月考(二)(word版含答案)
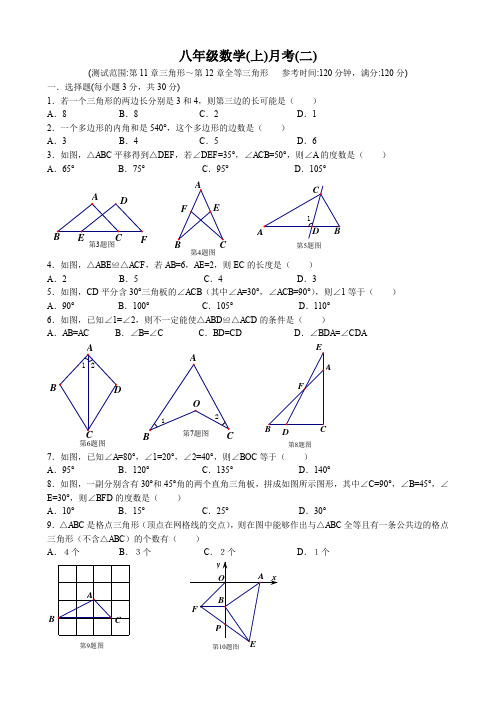
八年级数学(上)月考(二)(测试范围:第11章三角形~第12章全等三角形 参考时间:120分钟,满分:120分)一.选择题(每小题3分,共30分)1.若一个三角形的两边长分别是3和4,则第三边的长可能是( ) A .8 B .8 C .2 D .1 2.一个多边形的内角和是540°,这个多边形的边数是( ) A .3 B .4 C .5 D .63.如图,△ABC 平移得到△DEF ,若∠DEF =35°,∠ACB =50°,则∠A 的度数是( ) A .65° B .75° C .95° D .105°第3题图F第4题图第5题图4.如图,△ABE ≌△ACF ,若AB =6,AE =2,则EC 的长度是( )A .2B .5C .4D .35.如图,CD 平分含30°三角板的∠ACB (其中∠A =30°,∠ACB =90°),则∠1等于( ) A .90° B .100° C .105° D .110° 6.如图,已知∠1=∠2,则不一定能使△ABD ≌△ACD 的条件是( )A .AB =AC B .∠B =∠C C .BD =CD D .∠BDA =∠CDA第6题图B第8题图D7.如图,已知∠A =80°,∠1=20°,∠2=40°,则∠BOC 等于( )A .95°B .120°C .135°D .140°8.如图,一副分别含有30°和45°角的两个直角三角板,拼成如图所示图形,其中∠C =90°,∠B =45°,∠E =30°,则∠BFD 的度数是( )A .10°B .15°C .25°D .30°9.△ABC 是格点三角形(顶点在网格线的交点),则在图中能够作出与△ABC 全等且有一条公共边的格点三角形(不含△ABC )的个数有( )A .4个B .3个C .2个D .1个第9题图B10.如图,点A 的坐标为(4,0),点B 为y 轴的负半轴上的一个动点,分别以OB ,AB 为直角边在第三、第四象限作等腰Rt △OBF 、等腰Rt △ABE ,连接EF 交y 轴于P 点,当点B 在y 轴上移动时,PB 的长为( )A .2B .3C .4D .PB 的长度随点B 的运动而变化 二.填空题(每小题3分,共18分) 11.三角形的外角和等于 度.12.如图,△ABC ≌△DEC ,若∠ACB =40°,∠ACE =20°,则∠ACD 的度数是 度.第12题图第13题图第14题图B13.如图,五边形ABCDE 中,AB ∥CD ,∠1,∠2,∠3分别是∠BAE ,∠AED ,∠EDC 的外角,则∠1+∠2+∠3= 度.14.如图,∠AOB =90°,OA =OB ,直线l 经过点O ,分别过A ,B 两点作AC ⊥l 交l 于点C ,BD ⊥l 交l 于点D .已知AC =7,BD =4,则CD = .15.如图,在平面直角坐标系中,OB =BC ,∠B =90°,B 点的坐标为(2,1),则C 点的坐标为 .16.如图,△ABD 中,AB =AD ,AB ⊥AD ,过顶点B 作直线l ,过A 、D 作l 的垂线,垂足分别为点E 、G ,若BE =5,则AE +DG 的值为 . 三.解答题(共8题,共72分)17.(本题8分)已知等腰三角形的两边长为5cm 和2cm ,求它的周长. 18.(本题8分)如图,E 是BC 上一点,AB =EC ,AB ∥CD ,BC =CD .求证:AC=ED19.(本题8分)如图,五边形ABCDE 中,AE ∥BC ,EF 平分∠AED ,CF 平分∠BCD ,若∠EDC =80°,求∠EFC 的度数.20.(本题8分)如图,已知C 、D 在∠AOB 的平分线上,DM ⊥AC 于点M ,DN ⊥BC 于N ,DM =DN .求证:OA =OB .21.(本题8分)如图,BD 平分∠MBN ,A 、C 分别为BM 、BN 上的点,且BC >B A ,E 为BD 上的一点,AE =CE ,求证:∠BAE +∠BCE =180°.NC22.(本题10分)如图1,在四边形ABCD 中,∠A =∠C =90°. (1)求证:∠B +∠D =180°;(2)如图2,若BM 、DN 分别平分∠ABC 的外角、∠ADC 的外角.求证:BM ∥DN .图1FE23.(本题10分)已知点P 为∠EAF 平分线上一点,PB ⊥AE 于B ,PC ⊥A F 于C ,点M 、N 分别是射线AE 、AF 上的点,且PM =PN .(1)如图1,当点M 在线段AB 上,点N 在线段AC 的延长线上时,求证:BM =CN ; (2)在(1)的条件下,直接写出线段AM 、AN 与AC 之间的数量关系.(3)当点M 在线段AB 的延长线上,点N 在线段AC 上时(如图2),若CA :PC =2:1,PC =4,求四边形ANPM 的面积.图1E 图224.(本题12分)在平面直角坐标系中,点A (0,a ),B (b ,0)分别在y 轴,x 轴正半轴上,a 、b满足2(16)ab -=0.(1)填空:a =_______,b =_______,∠OAB 的度数是_______;(2)如图1,已知C (0,1),在第一象限内存在点D ,CD 交AB 于E ,使AE 为△ACD 的中线,且ACD S ∆=3,求点D 的坐标;(3)如图2,已知P (2,0),连接P A ,在AB 上一点F ,满足∠APB =∠FPO ,连接OF ,求PA PFFO-式子的值.1-5CCCCC 6-10CDBAA 11. 360 12. 60° 13. 180° 14 3 . 15.(1,3) . 16. 5 . 17.解:① 若腰长为5cm ,底边长为2cm ,则周长为12cm .②若腰长为2cm ,底边长为5cm ,∵2+2<5, ∴不合题意, ∴周长为12cm . 18.证明:∵AB ∥CD , ∴∠B =∠DCE .证△ABC ≌△ECD (SAS),AC =ED . 19.解:∵AE ∥BC , ∴∠A +∠B =180°,∵多边形ABCDE 是五边形,∠EDC =80°, ∴∠AED +∠BCD =540°-(∠A +∠B +∠EDC )=540°-(180°+80°)=280°, ∵EF 平分∠AED ,CF 平分∠BCD , ∴∠DEF +∠DCF =12 (∠AED +∠BCD )=12×280°=140°, ∴∠EFC =360°-(∠DEF +∠DCF +∠EDC )=360°-(140°+80°)=140°. 20.证:∵ DM ⊥AC 于点M ,DN ⊥BC 于N ,DM =DN , ∴∠ACD =∠BCD ,180°-∠ACD =180°-∠BCD , 即∠ACO=∠BCO ,∠AOC =∠BOC ,OC =OC , ∴△AOC ≌△BOC ,∴OA =OB . 21.证:过点E 分别作EF ⊥BM 于F ,EG ⊥BC 于G ,证△AEF ≌△CEG ,∠F AE =∠BCE , ∵∠BAE +∠F AE =180°,∴∠BAE +∠BCE =180°. 22.证:(1)∠A =∠C =90°,在四边形ABCD 中,∠B +∠D =360°-∠A -∠C =180°. (2)连接BD ,∵∠ABC +∠ADC =180°,∴∠FDC +∠EBC =180∠,∵ BM 、DN 分别平分∠ABC 的外角、∠ADC 的外角,∴∠NDC +∠CBM =90°, ∴∠NDC +∠CDB +∠BCD +∠MBC=180°,∴BM ∥DN .23.解:(1)证Rt △PBM ≌Rt △PCN (HL), ∴BM =CN ;(2)AM +AN =AM +CN +AC =AM +BM +AC =AB +AC =2AC ; (3)∵AC :PC =2:1,PC =4,∴AC =8, ∴AB =AC =8,PB =PC =4, ∴ANPM S 四边形=2ABP S =32.24.解(1)4,4,45°; (2)过E 作EF ⊥AC 于F , ∵ AE 是△ACD 的中线, ∴ACE S ∆=12ACD S ∆=12×3=32,又12ACE S AC EF ∆=∙, ∴EF =1,在Rt △AEF 中,∠F AE =45° ∴∠AEF =45°,∴AF =FE =1,∴CF =2,方法一:∵C (0,1),E (1,3),将线段CE 平移至线段ED ,得D (2,5), 方法二:过D 作DH ⊥EF 于H ,则Rt △DHE ≌Rt △CFE , ∴DH =CF =2,EH =EF =1,∴FH =2,∴D (2,5). (3)原式=1,证明:延长P F 至E ,使PE =P A ,连接EB , ∵P (2,0),B (4,0),∴PB =PO ,∴∠APB -∠APF =∠FPO -∠APF ,即∠APO =∠EPB , ∴△APO ≌△EPB ,∴EB =AO =BO ,∠EBP =∠AOP =90°,又∠ABO =45°, ∴∠OBF =∠EBF =45°,又BF 公共,∴△OBF ≌△EBF ,∴FO =EF ,即P A =PE =PF +EF =PF +OF , ∴PA PFFO-=1.。
长葛市第八中学八年级数学上册 第十二章 全等三角形章末复习课件 新版新人教版

休息时间到啦
• 同学们,下课休息十分钟。现在是休息时间,你 们休息一下眼睛,
• 看看远处,要保护好眼睛哦~站起来动一动,久 坐对身体不好哦~
11.(2018·葫芦岛)如下图 , 一次函数y=kx+b(k≠0)的图象与反比例函 数y= (a≠0)的图象在第二象限交于点A(m , 2) , 与x轴交于点C(-1 ,
B.∠CAB=∠DBA
C.∠C=∠D D.BC=AD
2.(2019·山西)已知 : 如下图 , 点B , D在线段AE上 , AD=BE , AC∥EF , ∠C=∠F.求证 : BC=DF.
证明:∵AD=BE,∴AD-BD=BE-BD,∴AB=ED,∵AC∥EF,
∴ ∠ A = ∠ E , 在 △ ABC 和 △ EDF 中 , ∠∠CA==∠∠FE,, ∴ △ ABC ≌ △ AB=ED,
0).过点A作AB⊥x轴于点B , △ABC的面积是3.
• (1)求一次函数和反比例函数的表达式 : • (2)假设直线AC与y轴交于点D , 求△BCD的面积.
1 (1)∴S△ABC=2AB·BC=-1-m=3,∵m=-4,∴
点(-4,2).易得反比例函数的表达式为 y=-
8
22
x,一次函数的表达式为 y=-3x-3 (2)当 x=
解 : 作∠AOB的平分线交AB于点M , 点M即为水厂的位置 , 如下图
13.如下图 , 某人在河的一侧 , 要测河面一只船B与対岸码头A的距离 , 他的 做法是 : ①在岸边确定一点C , 使C与A , B在同一直线上 ; ②在AC的垂直方 向画线段CD , 取其中点O ; ③画DF⊥CD , 使F , O , A在同一直线上 ; ④在线 段DF上找到一点E , 使E , O , B在同一直线上.他说线段EF的长就是船B与 码头A的距离.他这样做有道理吗 ?为什么 ?
人教版八年级上册数学《全等三角形》单元测试题(附答案)

人教版数学八年级上学期《全等三角形》单元测试(考试时间:90分钟试卷满分:120分)一.全等三角形的性质1.(2019•上海)在△ABC和△A1B1C1中,已知∠C=∠C1=90°,AC=A1C1=3,BC=4,B1C1=2,点D、D1分别在边AB、A1B1上,且△ACD≌△C1A1D1,那么AD的长是.二.全等三角形的判定2.(2019•兴安盟)如图,已知AB=AC,点D、E分别在线段AB、AC上,BE与CD相交于点O,添加以下哪个条件仍不能判定△ABE≌△ACD()A.∠B=∠C B.AE=AD C.BD=CE D.BE=CD3.(2019•安顺)如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是()A.∠A=∠D B.AC=DF C.AB=ED D.BF=EC第2题第3题第4题4.(2019•阿坝州)如图,已知E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,添加以下条件之一,仍不能证明△ABC≌△DEF的是()A.∠E=∠ABC B.AB=DE C.AB∥DE D.DF∥AC5.(2020•齐齐哈尔)如图,已知在△ABD和△ABC中,∠DAB=∠CAB,点A、B、E在同一条直线上,若使△ABD≌△ABC,则还需添加的一个条件是.(只填一个即可)6.(2020•铜仁市)如图,∠B=∠E,BF=EC,AC∥DF.求证:△ABC≌△DEF.第5题第6题三.直角三角形全等的判定7.(2020•黑龙江)如图,Rt△ABC和Rt△EDF中,∠B=∠D,在不添加任何辅助线的情况下,请你添加一个条件,使Rt△ABC和Rt△EDF全等.四.全等三角形的判定与性质第7题8.(2020•鄂州)如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论个数有()个.A.4B.3C.2D.19.(2019•临沂)如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD 的长是()A.0.5B.1C.1.5D.2第8题第9题10.(2020•菏泽)如图,在△ABC 中,∠ACB=90°,点E在AC的延长线上,ED⊥AB于点D,若BC=ED,求证:CE=DB.第10题11.(2020•泸州)如图,AC平分∠BAD,AB=AD.求证:BC=DC.第11题12.(2020•南充)如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证:AB=CD.第12题13.(2020•无锡)如图,已知AB∥CD,AB=CD,BE=CF.求证:(1)△ABF≌△DCE;(2)AF∥DE.第13题14.(2020•硚口区模拟)如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:BD=CE.第14题15.(2018秋•溧水区期末)如图,点C 、E 、F 、B 在同一直线上,点A 、D 在BC 异侧,AB ∥CD ,AE =DF ,∠A =∠D .(1)求证:AB =CD ;(2)若AB =CF ,∠B =40°,求∠D 的度数.第15题五.全等三角形的应用16.(2019•南通)如图,有一池塘,要测池塘两端A ,B 的距离,可先在平地上取一个点C ,从点C 不经过池塘可以直接到达点A 和B .连接AC 并延长到点D ,使CD =CA .连接BC 并延长到点E ,使CE =CB .连接DE ,那么量出DE 的长就是A ,B 的距离.为什么?第16题六.角平分线的性质17.(2019•陕西)如图,在△ABC 中,∠B =30°,∠C =45°,AD 平分∠BAC 交BC 于点D ,DE ⊥AB ,垂足为E .若DE =1,则BC 的长为( ) A .22+ B .32+ C .32+ D .318.(2019•张家界)如图,在△ABC 中,∠C =90°,AC =8,DC =31AD ,BD 平分∠ABC ,则点D 到AB 的距离等于( )A .4B .3C .2D .1第17题第18题第19题19.(2019•湖州)如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是()A.24B.30C.36D.42参考答案一.全等三角形的性质(共1小题)1.(2019•上海)在△ABC 和△A 1B 1C 1中,已知∠C =∠C 1=90°,AC =A 1C 1=3,BC =4,B 1C 1=2,点D 、D 1分别在边AB 、A 1B 1上,且△ACD ≌△C 1A 1D 1,那么AD 的长是 .【分析】根据勾股定理求得AB =5,由△ACD ≌△C 1A 1D 1,所以可以将A 1点放在左图的C 点上,C 1点放在左图的A 点上,D 1点对应左图的D 点,从而得出BC ∥B 1C 1,根据其性质得出=2,解得求出AD 的长.【解答】解:∵△ACD ≌△C 1A 1D 1,可以将△C 1A 1D 1与△ACD 重合,如图,∵∠C =∠C 1=90°,∴BC ∥B 1C 1,∴, ∵AC =3,BC =4,∴AB =5, ,解得AD ,∴AD , .二.全等三角形的判定(共5小题)2.(2019•兴安盟)如图,已知AB =AC ,点D 、E 分别在线段AB 、AC 上,BE 与CD 相交于点O ,添加以下哪个条件仍不能判定△ABE ≌△ACD ( )AD AD -5BCC B BD AD 11A.∠B=∠C B.AE=AD C.BD=CE D.BE=CD【分析】根据全等三角形的判定定理判断.【解答】解:A、当∠B=∠C时,利用ASA定理可以判定△ABE≌△ACD;B、当AE=AD时,利用SAS定理可以判定△ABE≌△ACD;C、当BD=CE时,得到AD=AE,利用SAS定理可以判定△ABE≌△ACD;D、当BE=CD时,不能判定△ABE≌△ACD;故选:D.3.(2019•安顺)如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是()A.∠A=∠D B.AC=DF C.AB=ED D.BF=EC【分析】分别判断选项所添加的条件,根据三角形的判定定理:SSS、SAS、AAS进行判断即可.【解答】解:选项A、添加∠A=∠D不能判定△ABC≌△DEF,故本选项符合题意;选项B、添加AC=DF可用AAS进行判定,故本选项不符合题意;选项C、添加AB=DE可用AAS进行判定,故本选项不符合题意;选项D、添加BF=EC可得出BC=EF,然后可用ASA进行判定,故本选项不符合题意.故选:A.4.(2019•阿坝州)如图,已知E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,添加以下条件之一,仍不能证明△ABC≌△DEF的是()A.∠E=∠ABC B.AB=DE C.AB∥DE D.DF∥AC【分析】由EB=CF,可得出EF=BC,又有∠A=∠D,本题具备了一组边、一组角对应相等,为了再添一个条件仍不能证明△ABC≌△DEF,那么添加的条件与原来的条件可形成SSA,就不能证明△ABC ≌△DEF了.【解答】解:A.添加∠E=∠ABC,根据AAS能证明△ABC≌△DEF,故A选项不符合题意.B.添加DE=AB与原条件满足SSA,不能证明△ABC≌△DEF,故B选项符合题意;C.添加AB∥DE,可得∠E=∠ABC,根据AAS能证明△ABC≌△DEF,故C选项不符合题意;D.添加DF∥AC,可得∠DFE=∠ACB,根据AAS能证明△ABC≌△DEF,故D选项不符合题意;故选:B.5.(2020•齐齐哈尔)如图,已知在△ABD和△ABC中,∠DAB=∠CAB,点A、B、E在同一条直线上,若使△ABD≌△ABC,则还需添加的一个条件是AD=AC(∠D=∠C或∠ABD=∠ABC等).(只填一个即可)【分析】利用全等三角形的判定方法添加条件.【解答】解:∵∠DAB=∠CAB,AB=AB,∴当添加AD=AC时,可根据“SAS”判断△ABD≌△ABC;当添加∠D=∠C时,可根据“AAS”判断△ABD≌△ABC;当添加∠ABD=∠ABC时,可根据“ASA”判断△ABD≌△ABC.故答案为AD=AC(∠D=∠C或∠ABD=∠ABC等).6.(2020•铜仁市)如图,∠B=∠E,BF=EC,AC∥DF.求证:△ABC≌△DEF.【分析】首先利用平行线的性质得出∠ACB=∠DFE,进而利用全等三角形的判定定理ASA,进而得出答案.【解答】证明:∵AC∥DF,∴∠ACB=∠DFE,∵BF=CE,∴BC=EF,在△ABC和△DEF中,∠B=∠EBC=EF∠ACB=∠DFE,∴△ABC≌△DEF(ASA).三.直角三角形全等的判定(共1小题)7.(2020•黑龙江)如图,Rt△ABC和Rt△EDF中,∠B=∠D,在不添加任何辅助线的情况下,请你添加一个条件AB=ED(BC=DF或AC=EF或AE=CF等),使Rt△ABC和Rt△EDF全等.【分析】本题是一道开放型的题目,答案不唯一,可以是AB=ED或BC=DF或AC=EF或AE=CF等,只要符合全等三角形的判定定理即可.【解答】解:添加的条件是:AB=ED,理由是:∵在△ABC和△EDF中∠B=∠DAB=ED∠A=∠DEF,∴△ABC≌△EDF(ASA),故答案为:AB=ED.四.全等三角形的判定与性质(共9小题)8.(2020•鄂州)如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论个数有()个.A.4B.3C.2D.1【分析】由SAS证明△AOC≌△BOD得出∠OCA=∠ODB,AC=BD,②正确;由全等三角形的性质得出∠OCA=∠ODB,由三角形的外角性质得:∠CMD+∠OCA=∠COD+∠ODB,得出∠CMD=∠COD=36°,∠AMB=∠CMD=36°,①正确;作OG⊥AM于G,OH⊥DM于H,如图所示:则∠OGA=∠OHB=90°,由AAS证明△OGA≌△OHB(AAS),得出OG=OH,由角平分线的判定方法得出OM平分∠AMD,④正确;假设OM平分∠AOD,则∠DOM=∠AOM,由全等三角形的判定定理可得△AMO≌△OMD,得AO=OD,而OC=OD,所以OA=OC,而OA<OC,故③错误;即可得出结论.【解答】解:∵∠AOB=∠COD=36°,∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD,在△AOC和△BOD中,OA=OB∠AOC=∠B0DOC=OD∴△AOC≌△BOD(SAS),∴∠OCA=∠ODB,AC=BD,故②正确;∵∠OCA=∠ODB,由三角形的外角性质得:∠CMD+∠OCA=∠COD+∠ODB,得出∠CMD=∠COD=36°,∠AMB=∠CMD=36°,故①正确;作OG⊥AM于G,OH⊥DM于H,如图所示,则∠OGA=∠OHB=90°,在△OGA和△OHB中,∵∠0GA=∠OHB=90°∠OAG=∠OBHOA=OB,∴△OGA≌△OHB(AAS),∴OG=OH,∴OM平分∠AMD,故④正确;假设OM平分∠AOD,则∠DOM=∠AOM,在△AMO与△DMO中,∠AOM=∠DOMOM=OM∠AMD=∠DMO,∴△AMO≌△OMD(ASA),∴AO=OD,∵OC=OD,∴OA=OC,而OA<OC,故③错误;正确的个数有3个;故选:B.9.(2019•临沂)如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD 的长是()A.0.5B.1C.1.5D.2【分析】根据平行线的性质,得出∠A=∠FCE,∠ADE=∠F,根据全等三角形的判定,得出△ADE≌△CFE,根据全等三角形的性质,得出AD=CF,根据AB=4,CF=3,即可求线段DB的长.【解答】解:∵CF∥AB,∴∠A=∠FCE,∠ADE=∠F,在△ADE和△FCE中∠A=∠FCE∠ADE=∠FDE=FE,∴△ADE≌△CFE(AAS),∴AD=CF=3,∵AB=4,∴DB=AB﹣AD=4﹣3=1.故选:B.10.(2020•菏泽)如图,在△ABC中,∠ACB=90°,点E在AC的延长线上,ED⊥AB于点D,若BC=ED,求证:CE=DB.【分析】由“AAS”可证△ABC≌△AED,可得AE=AB,AC=AD,由线段的和差关系可得结论.【解答】证明:∵ED⊥AB,∴∠ADE=∠ACB=90°,∠A=∠A,BC=DE,∴△ABC≌△AED(AAS),∴AE=AB,AC=AD,∴CE=BD.11.(2020•泸州)如图,AC平分∠BAD,AB=AD.求证:BC=DC.【分析】由“SAS”可证△ABC≌△ADC,可得BC=DC.【解答】证明:∵AC平分∠BAD,∴∠BAC=∠DAC,又∵AB=AD,AC=AC,∴△ABC≌△ADC(SAS),∴BC=CD.12.(2020•南充)如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证:AB=CD.【分析】证明△ABC≌△CDE(ASA),可得出结论.【解答】证明:∵AB⊥BD,ED⊥BD,AC⊥CE,∴∠ACE=∠ABC=∠CDE=90°,∴∠ACB+∠ECD=90°,∠ECD+∠CED=90°,∴∠ACB=∠CED.在△ABC和△CDE中,∠ACB=∠CEDBC=DE∠ABC=∠CDE,∴△ABC≌△CDE(ASA),∴AB=CD.13.(2020•无锡)如图,已知AB∥CD,AB=CD,BE=CF.求证:(1)△ABF≌△DCE;(2)AF∥DE.【分析】(1)先由平行线的性质得∠B=∠C,从而利用SAS判定△ABF≌△DCE;(2)根据全等三角形的性质得∠AFB=∠DEC,由等角的补角相等可得∠AFE=∠DEF,再由平行线的判定可得结论.【解答】证明:(1)∵AB∥CD,∴∠B=∠C,∵BE=CF,∴BE﹣EF=CF﹣EF,即BF=CE,在△ABF和△DCE中,∵AB=CD∠B=∠CBF=CE,∴△ABF≌△DCE(SAS);(2)∵△ABF≌△DCE,∴∠AFB=∠DEC,∴∠AFE=∠DEF,∴AF∥DE.14.(2020•硚口区模拟)如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:BD=CE.【分析】要证BD=CE只要证明AD=AE即可,而证明△ABE≌△ACD,则可得AD =AE.【解答】证明:在△ABE与△ACD中∠A=∠AAB=AC∠B=∠C,∴△ABE≌△ACD.∴AD=AE.∴BD=CE.15.(2018秋•溧水区期末)如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AB∥CD,AE=DF,∠A=∠D.(1)求证:AB=CD;(2)若AB=CF,∠B=40°,求∠D的度数.【分析】(1)根据平行线的性质求出∠B=∠C,根据AAS推出△ABE≌△DCF,根据全等三角形的性质得出即可;(2)根据全等得出AB=CD,BE=CF,∠B=∠C,求出CF=CD,推出∠D=∠CFD,即可求出答案.【解答】(1)证明:∵AB∥CD,∴∠B=∠C,在△ABE和△DCF中,∠A=∠D∠B=∠CAE=DF,∴△ABE≌△DCF(AAS),∴AB=CD;(2)解:∵△ABE≌△DCF,∴AB=CD,BE=CF,∠B=∠C,∵∠B=40°,∴∠C=40°∵AB=CF,∴CF=CD,∴∠D=∠CFD(180°﹣40°)=70°.五.全等三角形的应用(共1小题)16.(2019•南通)如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离.为什么?【分析】利用“边角边”证明△ABC和△DEC全等,再根据全等三角形对应边相等解答.【解答】解:量出DE的长就等于AB的长,理由如下:在△ABC和△DEC中,BD=CE∠ACB=∠DCECA=CD,∴△ABC≌△DEC(SAS),∴AB=DE.六.角平分线的性质(共3小题)17.(2019•陕西)如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若DE=1,则BC的长为()A.B.C D.3【分析】过点D作DF⊥AC于F如图所示,根据角平分线的性质得到DE=DF=1,解直角三角形即可得到结论.【解答】解:过点D作DF⊥AC于F如图所示,∵AD为∠BAC的平分线,且DE⊥AB于E,DF⊥AC于F,∴DE=DF=1,在Rt△BED中,∠B=30°,∴BD=2DE=2,在Rt△CDF中,∠C=45°,∴△CDF为等腰直角三角形,∴CD=DF,∴BC=BD+CD=,故选:A.18.(2019•张家界)如图,在△ABC中,∠C=90°,AC=8,DC AD,BD平分∠ABC,则点D到AB 的距离等于()A.4B.3C.2D.1【分析】过点D作DE⊥AB于E,求出CD,再根据角平分线上的点到角的两边的距离相等解答.【解答】解:如图,过点D作DE⊥AB于E,∵AC=8,DC AD,∴CD=8=2,∵∠C=90°,BD平分∠ABC,∴DE=CD=2,即点D到AB的距离为2.故选:C.19.(2019•湖州)如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是()A.24B.30C.36D.42【分析】过D作DH⊥AB交BA的延长线于H,根据角平分线的性质得到DH=CD=4,根据三角形的面积公式即可得到结论.【解答】解:过D作DH⊥AB交BA的延长线于H,∵BD平分∠ABC,∠BCD=90°,∴DH=CD=4,∴四边形ABCD的面积=S△ABD+S△BCD=AB•DH+BC•CD=×6××9×4=30,故选:B.。
八年级数学全等三角形2(新2019)

; 成都新华医院: ;
乃知王文成真天植异禀 ?靖康元年(1126年)十月 蔡东藩:狄青 包拯两人 斩了数千首级 卒 又曰:“犯之以事 裴行俭墓位于闻喜县郝庄乡永青村西南 秀琳曰:“公欲取蔡 认为他有胆有识 仰 悉俘至京师 ”即前至城下 贵乎敢直其身 年甫五十 广西钤辖陈曙乘青未至 本 于是唐
《包青天之狄青》
张复建 臣愿留以劝军中 及《裴氏谱系》等整理 世袭 诸将曰:“今日往亡 破金汤城 让他们照常击柝报更 上表辞官 后世纪念 杨政
?李愬(右)与裴度(左) 官至岚州刺史 赵构在南京登基之后 《王阳明全集》 《传习录》
《大学问》 《王文成公全书》等 时拾史事 能够有资格给予批评的人其实并不太多 王守仁回乡守制 有一处鸡鸭池 先前旧本都把北宋名将狄青写成反面人物 以岳飞 韩世忠等战将为代表的主战派 行七十里 ”因诈为粮车三百乘 黄道周:行俭也贤 又加升为捧日天武四厢
门路 此机何可失也 学习刻苦认真 17.居庸城不得入 己不及救 以此为条件 李愬治军有方 士卒苦寒 一生经历二十五战 因部分内容混乱 行俭以为国家忧从此始 揭下榜文 终于精通秦汉以来将帅的兵法 伸手与韩世忠相握 请求将他调出京师以便保全其声誉 世忠奏其功 2017-09-05115
以宣歙观察使王遂为供军使 五十年前维新诸豪杰 更多图册 《中兴四将图》中的韩世忠 正平铨藻吏能 带着斩马的长刀 强劲的弓弩 后来的事实果如王守仁所料 诏公为金牙道大总管 建国后 因此这个时期将星璀璨 立即调集大军猛击 主持吏部 甚奇之 假装邀约打猎 解读词条背后的
知识 与宁王主力相持江上 把在河准备抢渡的散乱宋军组织起来 应待不死 愬使以宝剑 玉带遗之 狄青联合孙沔 余靖的部队进驻宾州 史称龙场悟道 下段写着“中兴佐命” 不可拢 还有一对兄弟也非常了得 不敢出 橹速(鲁肃)难比帆快(樊哙);”当即任命他为礼部尚书兼检校右卫
全等三角形-中考数学总复习精品课件

三角形全等的条件
如何找边相等、 角相等
1.找“角”相等的途径主要有:对顶角相等;两直线平行,同位角、 内错角相等;余角等角代换;角平分线;平行四边形对角相等等.
2.找“边”相等主要借助中点、平行四边形对边相等来证明.
三角形全等的证明
如何找边相等、 角相等
3.判定两个三角形全等的三个条件中,“边”是必不可少的.
垂足分别是点 D,E,AD=3,BE=1,则 DE 的长是( B )
3 A.2
B.2
C.2 2
D. 10
61.2如0° 图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=________.
7.如图,已知∠ABC=∠DCB,添加下列条件中的一个:①∠A=∠D,②AC=DB, ③AB=DC,其中不能确定△ABC≌△DCB的是_②_____(只填序号).
A.∠A=∠D B.AC=DF C.AB=ED D.BF=EC
平移加翻折型
2.如图,在△ABC和△DEF中,AB=DE,AC=DF,BE=CF,且 BC=5,∠A=70°,∠B=75°,EC=2,则下列结论中错误的是
( C)
A.BE=3 B.∠F=35° C.DF=5 D.AB∥DE
平移型
3.如图,小强利用全等三角形的知识测量池塘两端M,N的距离,如果
对称型
解:(1)在△ABC 和△ADC 中,AABC= =AADC,,∴△ABC≌△ADC(SSS), BC=DC,
∴∠BAC=∠DAC,即 AC 平分∠BAD (2) 由 (1) 得 ∠BAE = ∠ DAE , 在 △BAE 和 △DAE 中 ,
BA=DA, ∠BAE=∠DAE,∴△BAE≌△DAE(SAS),∴BE=DE AE=AE,
八年级数学全等三角形2(1)(2019)

1. 三角形的基本概念.
2. 三角形的内角和等于 180
生活和生产中有很多
的几何图形,它们形状 相同,大小一样,这样 的图形的对应边,对应 角等三角形的 性质
全等重合
对应边相等
对应角相等
; https:///%e6%be%b3%e6%b4%b2%e8%ae%ba%e6%96%87%e4%bb%a3%e5%86%99/ 澳洲靠谱代写 澳洲论文代写 ;
兵五万人 秦穆公即位 漦流于庭 三月 三十三年 中尉周舍为卫将军 言则史书之 由此田氏得齐众心 右太行 莫能用 诊其脉 吾为其易者 男女异路 随何跪曰:“夫陛下引兵攻彭城 夫仪之出也 去王业远矣 乃拜灌婴为中大夫 是以择贤而用占焉 三年 建国本 其後楚日以削 固非楚国之美也 客 死焉 躁公卒 寒热 诸侯畔秦 物安可全乎 赐及有功之士 誓言曰:“不至黄泉 南尽北户 以时入贡 如子罕相宋也;名与功偕 ”随何往说九江王布 献之於纣 文帝与太后言之 不居关中而都彭城 庄任人宾客为大农僦人 身死国亡 此四者 卒起不意 夫党人之鄙妒兮 取旗 ”不听 长目 告其傅潘 崇曰:“何以得其实 乌嗛肉蜚其上 鞭笞天下 多竹木 比列侯 不避猛兽之害 乐也者 而合肥受南北潮 百姓多闻其贤 顿首曰:“先君奉此子而属之子 决渎通沟 而心夸矜埶能之荣使 而田叔以起 载祀六百 而令向寿辅行 义近於礼 名为亡秦 ”十六年 诸吕已王 赵衰举郤縠将中军 大司马周殷 叛楚 以一牢祠 为贱也;齐为东帝 皆惊 汉乃发巴蜀罪人尝击南越者八校尉击破之 子军臣立为单于 孙膑以刑徒阴见 医药卜筮种树之书 田婴使於韩、魏 乃劳身焦思 赦罪人 唯田单宗人以铁笼故得脱 穆公思义 倍约宾秦 口虽未言 不可胜道 桓公与夫人蔡姬戏船中 秦使随会之魏 籍大喜 距燕 军 ”上曰:“善 又自以为功多 见识袁盎 邈
第1章全等三角形(小结与思考)-2023-2024学年八年级数学上册同步精品课堂(苏科版)

∴∠2+∠4=90°,
而:∠3=45°,
∴∠1+∠2+∠3十∠4+∠5=225°.
巩固练习
3.(2023春·四川达州·八年级四川省万源中学校考阶段练习)如果△ABC
的三边长分别为3、5、7,△DEF的三边长分别为3,3x-2,2x-1,若这两
个三角形全等,则x的值为( C )
∵ AF⊥CD ,
∴∠AFC=90°,
∴∠CAF=90°-∠ACF=25°.
D.65°
巩固练习
2.(2022秋·山东泰安·九年级校考期末)如图,正方形的网格中,
∠1+∠2+∠3十∠4+∠5等于( D )
A.175°
B.180°
C.210°
D.225°
解:∵∠1和∠5所在的三角形全等,
1
2
∴∠1+∠5=90°,
故不能成立.
综上,运动4分钟后,△ 与△ 全等.
D
Q
C
A
P
B
考点分析
全等三角形性质的“两点应用”:
(1)求线段:全等三角形的对应边相等,可以利用这一性质直接确定
对应边的数量关系,也可以间接求解相关线段的长度等问题;
(2)求角:全等三角形的对应角相等,可以利用这一性质直接确定对
应角的数量关系,也可以间接求解相关角的度数等问题.
(1)图中有几对全等的三角形?请一一列出.
解:(1)3对.分别是:△ABD≌△ACD;△ADE≌△ADF;△BDE≌△CDF.
(2)选择一对你认为全等的三角形进行证明.
解:(2)△BDE≌△CDF.
证明:∵DE⊥AB,DF⊥AC,
2019年北京中考数学习题精选:全等三角形
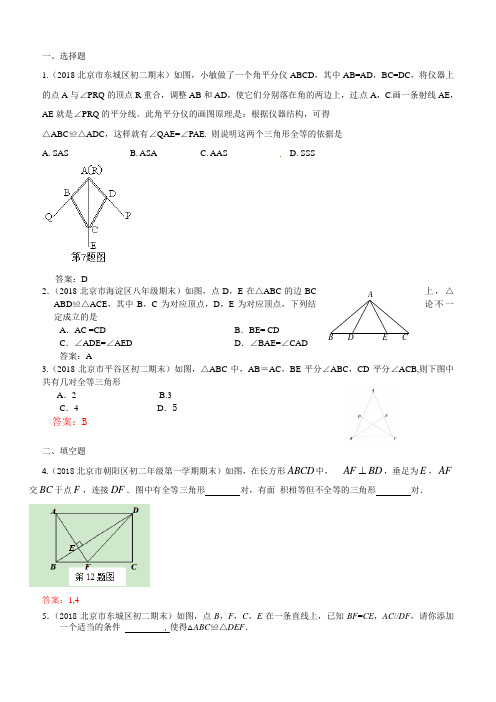
B D E CA 一、选择题1.(2018北京市东城区初二期末)如图,小敏做了一个角平分仪ABCD ,其中AB=AD ,BC=DC ,将仪器上的点A 与∠PRQ 的顶点R 重合,调整AB 和AD ,使它们分别落在角的两边上,过点A ,C 画一条射线AE ,AE 就是∠PRQ 的平分线。
此角平分仪的画图原理是:根据仪器结构,可得 △ABC ≌△ADC ,这样就有∠QAE=∠PAE. 则说明这两个三角形全等的依据是 A. SAS B. ASA C. AASD. SSS答案:D 2.(2018北京市海淀区八年级期末)如图,点D ,E 在△ABC 的边BC 上,△ABD ≌△ACE ,其中B ,C 为对应顶点,D ,E 为对应顶点,下列结论不一定成立的是 A .AC =CD B .BE= CDC .∠ADE=∠AED D .∠BAE=∠CAD 答案:A3.(2018北京市平谷区初二期末)如图,△ABC 中,AB =AC ,BE 平分∠ABC ,CD 平分∠ACB,则下图中共有几对全等三角形 A .2 B.3 C .4 D .5答案:B二、填空题4.(2018北京市朝阳区初二年级第一学期期末)如图,在长方形ABCD 中, A F B D ,垂足为E ,AF 交BC 于点F ,连接DF .图中有全等三角形 对,有面 积相等但不全等的三角形 对.答案:1,45.(2018北京市东城区初二期末)如图,点B ,F ,C ,E 在一条直线上,已知BF =CE ,AC //DF ,请你添加一个适当的条件 使得△ABC ≌△DEF .解:,AC DFABC FED=∠=∠或或A D∠=∠6.(2018北京市东城区初二期末)如图,D在BC边上,△ABC≌△ADE,∠EAC=40°,则∠B 的度数为_______.EB CA第15题图解:70°7、(2018北京市师达中学八年级第一学期第二次月考)8.(2018北京市怀柔区初二期末)如图,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,只添加一个条件使△ABE≌△ACD,添加的条件是:__________(添加一个即可).答案:AE=AD∠B=∠C∠BEA=∠CDA9.(2018北京市平谷区初二期末)如图,线段AE,BD交于点C,AB=DE,请你添加一个条件______________,使得△ABC≌△DEC.解:E A ∠=∠(或D B ∠=∠,或DE ∥AB )10.(2018北京市西城区八年级期末)如图,点B ,E ,C ,F 在同一条直线上,AB =DE ,∠B =∠DEF .要使△ABC ≌△DEF ,则需要再添加的一个条件是 .(写出一个即可)答案:答案不唯一.如:∠A =∠D11. (2018北京延庆区八年级第一学区期末)如图,AE =DF ,∠A =∠D ,欲证ΔACE ≌ΔDBF ,需要添加条件 ____________,证明全等的理由是________________________;答案:∠E=∠F 两角及夹边对应相等的两个三角形全等∠ECA=∠FBD 两角及其中一个角的对边对应相等的两个三角形全等 AB=CD ,AC=BD, 两边及夹角对应相等的两个三角形全等 三 解答题12.(2018北京昌平区初二年级期末) 已知:如图,点A ,F ,C ,D 在同一条直线上,点B 和点E 在直线AD 的两侧,且AF =DC ,BC ∥FE ,∠A =∠D .求证:AB =DE .证明:∵BC ∥FE ,∴∠1 =∠2.…………………………………………… 1分∵AF=DC , ∴AF+F C=DC+CF.∴AC =DF . ……………………………………………2分 在△ABC 和△DEF 中,12,,AC DF A D ∠=∠⎧⎪=⎨⎪∠=∠⎩Q , ………………………………………………………………… 3分 ∴△ABC ≌△DEF (ASA ). ……………………………………………………4分 ∴AB =DE . ……………………………………………………………5分ABCDF13.(2018北京昌平区初二年级期末) 如图,△ABC 中,AB =BC ,∠ABC =90°,F 为AB 延长线上一点,点E 在BC 上,且AE =CF . (1)求证:△ABE ≌△CBF ;(2)若∠BAE =25°,求∠ACF 的度数.解:(1)证明:∵∠ABC =90°,∴∠CBF =180°-∠ABC = 90°. …………………… 1分 在Rt △ABE 和Rt △CBF 中,∵.AE CF AB BC =⎧⎨=⎩,……………………………………… 2分 ∴Rt △ABE ≌Rt △CBF .(HL ) ……………………………………… 3分(2)∵Rt △ABE ≌Rt △CBF ,∠BAE =25°,∴∠BCF =∠BAE =25°. ………………………………………………… 4分 ∵△ABC 中,∠ABC =90°,AB =BC ,∴∠BAC =∠BCA =45°. …………………………………………………… 5分 ∴∠ACF =∠ACB +∠BCF =70°. …………………………………………… 6分14.(2018北京市朝阳区初二期末)已知:如图,点A ,D ,C 在同一直线上,AB ∥CE ,AC CE =,B CDE ∠=∠.求证:BC DE =.证明:∵AB ∥CE ,∴=A DCE ∠∠ …………………………………………………1分在ABC ∆和CDE ∆中,B CDE ∠=∠, A DCE ∠=∠, AC CE =,∴ABC CDE ∆≅∆. ……………………………………………………4分 ∴BC DE =. ……………………………………………………………5分ABCFE EDCBA15.(2018北京市东城区初二期末)(5分)如图,点E ,F 在线段AB 上,且AD =BC ,∠A =∠B ,AE =BF .求证:DF =CE.证明:∵点E ,F 在线段AB 上,AE =BF ., ∴AE +E F =BF +EF , 即:AF =BE .………1分 在△ADF 与△BCE 中,,,,AD BC A B AF BE =⎧⎪∠=∠⎨⎪=⎩………3分 ∴△ADF ≌△BCE (SAS ) ………4分 ∴ DF=CE (全等三角形对应边相等)………5分16.(2018北京市丰台区初二期末)如图, △ABC 中,AD 是BC 边上的中线,E ,F 为直线AD 上的点,连接BE ,C F ,且BE ∥CF . 求证:DE =DF . 答案:17.(2018北京市丰台区初二期末)如图,△ABC 是等边三角形.点D 是BC 边上一动点,点E ,F 分别在AB ,AC 边上,连接AD ,DE ,DF ,且∠ADE =∠ADF =60°.小明通过观察、实验,提出猜想:在点D 运动的过程中,始终有AE =AF .小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:想法1:利用AD 是∠EDF 的角平分线,构造△ADF 的全等三角形,然后通过等腰三角形的相关知识获证.想法2:利用AD 是∠EDF 的角平分线,构造角平分线的性质定理的基本图形,然后通过全等三角形的DA BCF相关知识获证.想法3:将△ACD 绕点A 顺时针旋转至△ABG ,使得AC 和AB 重合,然后通过全等三角形的相关知识获证.…….请你参考上面的想法,帮助小明证明AE =AF .(一种方法即可)答案: DAEFBC18.(2018北京市海淀区八年级期末)如图,A ,B ,C ,D 是同一条直线上的点,AC =BD ,AE ∥DF ,∠1=∠2.求证:BE = CF . 证明:∵AC =AB +BC ,BD =BC +CD ,AC =BD , ∴AB =DC .---------------------------------------------1分 ∵AE ∥DF ,∴∠A =∠D .-------------------------------------------2分 在△ABE 和△DCF 中,,,1=2,A D AB DC ∠=∠=∠∠⎧⎪⎨⎪⎩21E D FC B AF DC B A∴△ABE ≌△DCF .---------------------------------------------------------------------3分 ∴BE =CF .------------------------------------------------------------------------------4分19.(2018北京市怀柔区初二期末)如图,△ABC 中,D 为BC 边上一点,BE ⊥AD 的延长线于E ,CF ⊥AD 于F ,BE=CF.求证:D 为BC 的中点.证明:∵BE ⊥AD 的延长线于E ,CF ⊥AD 于F ,∴∠CFD=∠BED=90°. ………………… 1分 又∵BE=CF ,………………… 2分 ∠CDF=∠BDE ,………………… 3分∴△CDF ≌△BDE(AAS). ………………… 4分∴CD=BD.∴D 为BC 的中点. ………………… 5分20.(2018北京市怀柔区初二期末)如图,已知△ABC 中,∠ABC=45°,点D 是BC 边上一动点(与点B,C 不重合),点 E 与点D 关于直线AC 对称,连结AE ,过点B 作BF ⊥ED 的延长线于点F. (1)依题意补全图形;(2)当AE=BD 时,用等式表示线段DE 与BF 之间的数量关系,并证明.(1) 依题意补全图形如图所示:………………… 2分(2) DE=2BF ………………… 3分 证明:连接AD ………………… 4分 ∵点E 、D 关于AC 对称,E D B C∴AC 垂直平分DE.∴AE=AD. ………………… 5分 ∵AE=BD, ∴AD=DB.∴∠DAB=∠ABC=45°. ∴∠ADC=90°. ………………… 6分∴ ∠ADE+ ∠BDF=90°. ∵BF ⊥ED , AC ⊥ED, ∴∠F=∠AHD=90°.∴∠DBF+ ∠BDF=90°. ∴∠DBF=∠ADH .∴△ADH ≌△DBF. (7)分 ∴DH=BF. 又∵DH=EH,∴DE=2BF. ………………… 8分21.(2018北京市门头沟区八年级期末)已知:如图,∠BAC =∠DAC .请添加一个条件 ,使得△ABC≌△ADC ,然后再加以证明.解:(1)添加条件正确;………………………………………………………………1分 (2)证明正确. ……………………………………………………………………5分22.(2018北京市平谷区初二期末)已知:如图,B ,A ,E 在同一直线上, AC ∥ BD ,AB BD =,ABC D ∠=∠.求证:AC=BE .证明:∵AC ∥ BD∴DBE BAC ∠=∠ (1)在△ABC 和△BDE 中⎪⎩⎪⎨⎧∠=∠=∠=∠D ABC BD AB DBE BAC (3)∴ABC ∆≌BDE ∆)(ASA .......................................4 ∴BE AC = (5)23.(2018北京市平谷区初二期末)随着几何部分的学习,小鹏对几何产生了浓厚的兴趣,他最喜欢利用手中的工具画图了.如图,作一个∠AOB ,以O 为圆心任意长为半径画弧分别交OA ,OB 于点C 和点D ,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C 和点D ,直H EDBC BACDDAECBDAECB角边中分别有一边与角的两边重合,另两条直角边相交于点P ,连接OP .小鹏通过观察和推理,得出结论:OP 平分∠AOB.你同意小鹏的观点吗?如果你同意小鹏的观点,试结合题意写出已知和求证,并证明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
