化工热力学-GG-第2章 流体的PVT关系-陕西理工学院-冯新-148
合集下载
化工热力学2流体的P-V-T关系
进行计算。
（2）为判断真实气体状态方程的正确程度提供了
一个标准：当P
0或 V
∞时，任何状态方程都
还原为理想气体方程。
肇庆学院
《化工热力学》
流体的P-V-T关系
2.2.2 立方型状态方程
立方型状态方程可以展开成为V的三次方形式。
范德华（Van der Waals）方程是第一个适用真实气
体的立方型方程，其形式为：
(1)SRK方程 300 Tr 0.7351 408.1
T 1 0.48 1.574 0.176 0.176 0.176 1 0.7351
2 0.5
2
1.2259
8.3142 408.12 a 0.42748 1.2259 1653.7kPa m6 / kmol 2 3648
流体的P-V-T关系
R 2Tc 2.5 (8.314) 2 (126.2) 2.5 6 0.5 -2 a 0.42748 0.42748 1.5588(Pa m K mol ) 6 pc 3.394 10 b 0.08664 RTc 8.314 126.2 5 3 -1 b 0.08664 2.6802 10 (m mol ) 6 pc 3.394 10
（1）理想气体状态方程
RT 8.314 273.15 7 p 4.8987 10 Pa 5 V 4.636 10 4.8987 107 -101.33 106 p 51.7% 6 101.33 10
与实验值相比，误差为51.7%
肇庆学院 《化工热力学》 （2）RK方程 将Tc、pc值代入式(2-13)和式(2-14)
（a）三次方程求根公式； （b）迭代法。 直接求解较困难，一般使用迭代法。
化工热力学-GG-第2章 流体的PVT关系-144
9
§2.1.1 T –V 图
在常压下加热水
T 5
2 1
3 4
10
v
11
§2.1.1 T -V图
12
§2.1.2 P-V图
P 0.2Mpa P 1Mpa T =150 C
o
P 0.4762Mpa T =150o C
P 0.4762Mpa T =150 C
o
P 0.4762Mpa T =150o C
1400℃， 5-10万atm
3
火灾中的液化气罐之所以会发生爆炸， 是由于温度升高使液化气由液体变成 气体，继而内部压力急剧升高，使液 化气罐超压爆炸；
T↑→P↑
4
化工生产恰恰就是巧妙利用物质随T 、 p变 化，状态和性质大幅度变化的特点，依据热 力学原理来实现物质的低成本大规模生产。
例如，先进的超临界萃取技术，就是物质在利用
第6章化工过 程能量分析 (H,S, W，Ex ) 第7章 压缩、膨 胀、动力循环与 制冷循环( H, S, Q, W, η )
第4章流体混合物的热力 学性质
给出能量 有效 利用 极限
化 工 热 力 学 的 任 务
ˆ ˆ ( , M i , Gi f i , i , ai , i )
6
p-V-T关系的用途
恒温线
14
临界点—p-V-T中最重要的性质
1）Tc、pc 是纯物质能够呈现汽液平衡时的最高温度 和最高压力。 要使气体液化温度绝对不能超过Tc 。 气体“液化”的先决条件是T<Tc，否则无论施加多大 的压力都不可能使之液化。 2）临界等温的数学特征：等于临界温度的等温线在 临界点出现水平拐点。 P V TC 0 在C点 重要！ 15 2 P V 2 TC 0 在C点
§2.1.1 T –V 图
在常压下加热水
T 5
2 1
3 4
10
v
11
§2.1.1 T -V图
12
§2.1.2 P-V图
P 0.2Mpa P 1Mpa T =150 C
o
P 0.4762Mpa T =150o C
P 0.4762Mpa T =150 C
o
P 0.4762Mpa T =150o C
1400℃， 5-10万atm
3
火灾中的液化气罐之所以会发生爆炸， 是由于温度升高使液化气由液体变成 气体，继而内部压力急剧升高，使液 化气罐超压爆炸；
T↑→P↑
4
化工生产恰恰就是巧妙利用物质随T 、 p变 化，状态和性质大幅度变化的特点，依据热 力学原理来实现物质的低成本大规模生产。
例如，先进的超临界萃取技术，就是物质在利用
第6章化工过 程能量分析 (H,S, W，Ex ) 第7章 压缩、膨 胀、动力循环与 制冷循环( H, S, Q, W, η )
第4章流体混合物的热力 学性质
给出能量 有效 利用 极限
化 工 热 力 学 的 任 务
ˆ ˆ ( , M i , Gi f i , i , ai , i )
6
p-V-T关系的用途
恒温线
14
临界点—p-V-T中最重要的性质
1）Tc、pc 是纯物质能够呈现汽液平衡时的最高温度 和最高压力。 要使气体液化温度绝对不能超过Tc 。 气体“液化”的先决条件是T<Tc，否则无论施加多大 的压力都不可能使之液化。 2）临界等温的数学特征：等于临界温度的等温线在 临界点出现水平拐点。 P V TC 0 在C点 重要！ 15 2 P V 2 TC 0 在C点
化工热力学第2章 流体的PVT关系和状态方程
P
RT V b
V
a
V
b
a
ac
T
0.42748
R 2Tc2 Pc
T
b 0.08664 RTc Pc
T
1
0.48
1.574
0.176
2
1
T 0.5 r
2
在临界点: T 1
优点
➢ 与RK方程相比，SRK方程大大提高了表达纯物质汽液平 衡的能力，使之能用于混合物的汽液平衡计算，故在工 业上获得了广泛的应用。
6.734m3
/ kmol
V1
6.814
4.2486.734 6.7346.734
0.08058 0.08058
6.198
V2
6.814
4.2486.198 6.1986.198
0.08058 0.08058
6.146
V3 6.141 V4 6.140 V 6.140m3 / kmol
( 2 ) SRK方程
Thiesen, 1885年提出 Onnes, 1901年改进
pV a(1 b' p c' p2 d ' p3 .....) 原型 p 0 理想气体
Z pV 1 Bp Cp2 Dp3 RT
Z pV 1 B C D
RT
V V2 V3
B B RT
C C B2 R2T 2
8.3142 408.12.5
a 0.42768 3.648 103
2.725104 kPa m6 K 0.5 / kmol2
b 0.08664 8.314 408.1 0.08058m3 / kmol 3.648 103
RT
a
P V b T1/2V V b
化工热力学 第二章 流体的压力,体积,温度的关系：状态方程式
5
m 3 kmol
1 3
0.08664 a PC 2 b 0.42748 R
a 0.08664 1 TC b 0.42748 R
2 3
VC 3.847 b
化工热力学
第二章
流体的PVT关系
化工热力学
第二章
流体的PVT关系C 6a 4 3 VC b VC
两式相比得:
2
2a VC b TC 3 R VC
2
2 VC b VC 3
VC 3b
27 R 2TC a 64 PC
2
2a 4b 8a TC 3 R 27b 27bR
化工热力学
第二章
流体的PVT关系
(a)、求蒸汽的摩尔体积 将RK方程两端乘
V b 整理成：
P
aV b T PV V b
1 2
RT V b P
写成迭代形式：
RT Vi 1 b P
aVi b T PVi Vi b
1 2
化工热力学
化工热力学
3
第二章
2
流体的PVT关系
0 .5
PVi RTVi ab / T Vi 1 2 0.5 Pb bRT a / T
如令： b 2 C
3
bRT a ，则上式写成： 1 P PT 2
取初值：
RT 2 ab CVi 1 Vi Vi 1 P PT 2
2P 0 V 2 T Tc
27 R T a 64 PC
2
2 C
RTC b 8PC
化工热力学
第二章
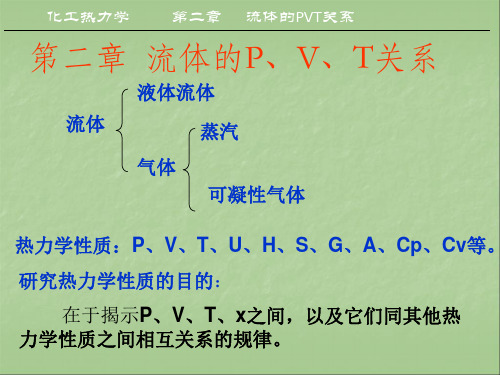
m 3 kmol
1 3
0.08664 a PC 2 b 0.42748 R
a 0.08664 1 TC b 0.42748 R
2 3
VC 3.847 b
化工热力学
第二章
流体的PVT关系
化工热力学
第二章
流体的PVT关系C 6a 4 3 VC b VC
两式相比得:
2
2a VC b TC 3 R VC
2
2 VC b VC 3
VC 3b
27 R 2TC a 64 PC
2
2a 4b 8a TC 3 R 27b 27bR
化工热力学
第二章
流体的PVT关系
(a)、求蒸汽的摩尔体积 将RK方程两端乘
V b 整理成：
P
aV b T PV V b
1 2
RT V b P
写成迭代形式：
RT Vi 1 b P
aVi b T PVi Vi b
1 2
化工热力学
化工热力学
3
第二章
2
流体的PVT关系
0 .5
PVi RTVi ab / T Vi 1 2 0.5 Pb bRT a / T
如令： b 2 C
3
bRT a ，则上式写成： 1 P PT 2
取初值：
RT 2 ab CVi 1 Vi Vi 1 P PT 2
2P 0 V 2 T Tc
27 R T a 64 PC
2
2 C
RTC b 8PC
化工热力学
第二章
化工热力学第2章流体的PVT关系
时，这种流体就处于对比状态。
例如：H2 和N2这两种流体
对于H2
状态点记为1，P1 V1 T1
Tr1 =T1/TcH2
Pr1=P1/PcH2
对于N2
状态点记为2，P2 V2 T2
Tr2 =T2/TcN2
Pr2=P2/PcN2
当Tr1=Tr2 ，Pr1=Pr2 时，此时就称这两种流体处
一.P-T图
P
Pc
3液
相
固
相
2
1
密 流 区 C
气相
Tc T
1-2线 汽固平衡线（升华线）
2-c线 汽液平衡线（汽化线） 2-3线 液固平衡线（熔化线） C点临界点，2点三相点 P<Pc,T<Tc的区域，属汽体 P<Pc,T>Tc的区域，属气体 P＝Pc,T＝Tc的区域，两相 性质相同
P>Pc,T>Tc的区域，密流区
压缩因 子，方 程的计 算值和 实测值 的符合 程度是 判断方 程的优 劣标志 之一。
2. R-K Equation (1949年，Redlich and Kwong)
(1) R-K Eq的一般形式：
P
RT V-b
-
a T0.5V(V
b)
(2-11)
① R-K Equation中常数值不同于范德华方程中的a、b值， 不能将二者混淆。 在范德华方程中，修正项为a/V2，没有考虑温度的影响 在R-K方程中，修正项为，考虑了温度的影响。 ② R-K Equation中常数a、b值是物性常数，具有单位。
为表征物质分子的偏心度，既非球型分子偏离球对称的 程度，简单流体为0
R-K Eq经过修改后，应用范围扩宽。 SRK Eq：可用于两相PVT性质的计算，对烃类计算，其 精确度很高。
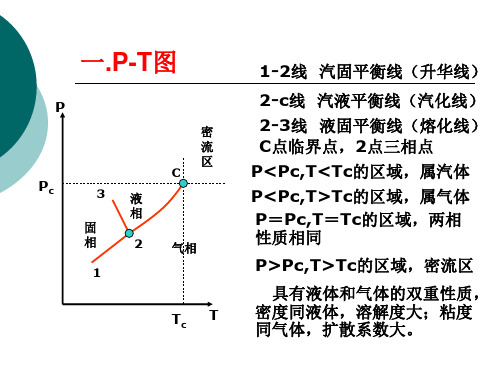
例如：H2 和N2这两种流体
对于H2
状态点记为1，P1 V1 T1
Tr1 =T1/TcH2
Pr1=P1/PcH2
对于N2
状态点记为2，P2 V2 T2
Tr2 =T2/TcN2
Pr2=P2/PcN2
当Tr1=Tr2 ，Pr1=Pr2 时，此时就称这两种流体处
一.P-T图
P
Pc
3液
相
固
相
2
1
密 流 区 C
气相
Tc T
1-2线 汽固平衡线（升华线）
2-c线 汽液平衡线（汽化线） 2-3线 液固平衡线（熔化线） C点临界点，2点三相点 P<Pc,T<Tc的区域，属汽体 P<Pc,T>Tc的区域，属气体 P＝Pc,T＝Tc的区域，两相 性质相同
P>Pc,T>Tc的区域，密流区
压缩因 子，方 程的计 算值和 实测值 的符合 程度是 判断方 程的优 劣标志 之一。
2. R-K Equation (1949年，Redlich and Kwong)
(1) R-K Eq的一般形式：
P
RT V-b
-
a T0.5V(V
b)
(2-11)
① R-K Equation中常数值不同于范德华方程中的a、b值， 不能将二者混淆。 在范德华方程中，修正项为a/V2，没有考虑温度的影响 在R-K方程中，修正项为，考虑了温度的影响。 ② R-K Equation中常数a、b值是物性常数，具有单位。
为表征物质分子的偏心度，既非球型分子偏离球对称的 程度，简单流体为0
R-K Eq经过修改后，应用范围扩宽。 SRK Eq：可用于两相PVT性质的计算，对烃类计算，其 精确度很高。
化工热力学 冯新 答案
第二章习题解答一、问答题：2-1【参考答案】：流体p-V-T 关系是化工热力学的基石，是化工过程开发和设计、安全操作和科学研究必不可少的基础数据。
（1）流体的PVT 关系可以直接用于设计。
（2）利用可测的热力学性质（T ，P ，V 等）计算不可测的热力学性质（H ，S ，G ，等）。
只要有了p-V-T 关系加上理想气体的id p C ，可以解决化工热力学的大多数问题。
2-2【参考答案】：1）超临界流体区的特征是：T >T c 、p >p c 。
2）临界点C 的数学特征：3）饱和液相线是不同压力下产生第一个气泡的那个点的连线；4）饱和汽相线是不同压力下产生第一个液滴点（或露点）那个点的连线。
5）过冷液体区的特征：给定压力下液体的温度低于该压力下的泡点温度。
6）过热蒸气区的特征：给定压力下蒸气的温度高于该压力下的露点温度。
7）汽液共存区：在此区域温度压力保持不变，只有体积在变化。
2-3【参考答案】：气体只有在低于T c 条件下才能被液化。
2-4【参考答案】：不同。
真实气体偏离理想气体程度不仅与T 、p 有关，而且与每个气体的临界特性有关，即最本质的因素是对比温度、对比压力以及偏心因子r T ，r P 和ω。
2-5【参考答案】：偏心因子ω为两个分子间的相互作用力偏离分子中心之间的作用力的程度。
其物理意义为：一般流体与球形非极性简单流体（氩，氪、氙）在形状和极性方面的偏心度。
为了提高计算复杂分子压缩因子的准确度。
偏心因子不可以直接测量。
偏心因子ω的定义为：000.1)p lg(7.0T s r r--==ω ， ω由测定的对比温度为0.7时的对比饱和压力的数据计算而得，并不能直接测量。
2-6 【参考答案】：所谓状态方程的普遍化方法是指方程中不含有物性常数a ，b ，而是以对比参()()()()点在点在C V P C V PTT 0022==∂∂∂数作为独立变量；普遍化状态方程可用于任何流体、任意条件下的PVT 性质的计算。
化工热力学第二章 流体的pVT关系
化工热力学
第二章 流体的PVT关系
第2章 流体的p-V-T关系
流体指除固体以外的流动相的总称。均 匀流体一般分为液体和气体两类。
南阳理工学院 生化学院
化工热力学
第二章 流体的PVT关系
重点内容
纯物质的p-V-T关系
状态方程 立方型状态方程 多参数状态方程 对应态原理及其应用 流体的蒸气压、蒸发焓和蒸发熵
方程形式： p RT a(T )
V b V (V b)
Soave 是把R-K 方程中的常数a 看作是温度的函数，在SRK 方程中，a 不仅是物性的函数，而且还是温度的函数，只有在特 定的温度下，对于某一物质而言， a 才能为定值。
方程常数：
a(T
)
ac
(Tr
,)
0.42748
混合规则与混合物的p-V-T关系 液体的p-V-T关系
南阳理工学院 生化学院
化工热力学
第二章 流体的PVT关系
本章要求：
1.了解纯物质的P-T图和P-V图 2.正确、熟练地应用R-K方程、两项维里方程计 算单组分气体的P-V-T关系 3.正确、熟练地应用三参数普遍化方法计算单组 分气体的P-V-T关系 4.了解计算真实气体混合物P-V-T关系的方法， 并会进行计算。
化工热力学
第二章 流体的PVT关系
V T
p
V
V V p T
dV dT dp V
对于液体，由于其具有不可压缩性，体积膨胀系数和等温 压缩系数是温度和压力的弱函数，其数值可以从文献或工具书 中查到。因此，在液体的温度和压力变化不大时，可以将体积 膨胀系数和等温压缩系数当作常数，则
第二章 流体的PVT关系
第2章 流体的p-V-T关系
流体指除固体以外的流动相的总称。均 匀流体一般分为液体和气体两类。
南阳理工学院 生化学院
化工热力学
第二章 流体的PVT关系
重点内容
纯物质的p-V-T关系
状态方程 立方型状态方程 多参数状态方程 对应态原理及其应用 流体的蒸气压、蒸发焓和蒸发熵
方程形式： p RT a(T )
V b V (V b)
Soave 是把R-K 方程中的常数a 看作是温度的函数，在SRK 方程中，a 不仅是物性的函数，而且还是温度的函数，只有在特 定的温度下，对于某一物质而言， a 才能为定值。
方程常数：
a(T
)
ac
(Tr
,)
0.42748
混合规则与混合物的p-V-T关系 液体的p-V-T关系
南阳理工学院 生化学院
化工热力学
第二章 流体的PVT关系
本章要求：
1.了解纯物质的P-T图和P-V图 2.正确、熟练地应用R-K方程、两项维里方程计 算单组分气体的P-V-T关系 3.正确、熟练地应用三参数普遍化方法计算单组 分气体的P-V-T关系 4.了解计算真实气体混合物P-V-T关系的方法， 并会进行计算。
化工热力学
第二章 流体的PVT关系
V T
p
V
V V p T
dV dT dp V
对于液体，由于其具有不可压缩性，体积膨胀系数和等温 压缩系数是温度和压力的弱函数，其数值可以从文献或工具书 中查到。因此，在液体的温度和压力变化不大时，可以将体积 膨胀系数和等温压缩系数当作常数，则
化工热力学2流体的P-V-T关系
2P V 2
T Tc
0
肇庆学院
《化工热力学》 流体的P-V-T关系
2.2 气体的状态方程（Equation of state）
纯流体的状态方程（EOS）是描述流体P-V-T 性质的关系式。由相律可知，对纯流体有：
f(P,V,T)=0
混合物的状态方程中还包括混合物的组成（通 常是摩尔分数）
Tc T
超临界流体既不同于液体，又不同于气体，密度可以接近 液体，但又具有气体的体积可变性和传递性质，可以作为特殊 的萃取溶剂和反应介质。
肇庆学院
《化工热力学》 流体的P-V-T关系
图2.3 纯物质的P-V图
肇庆学院
《化工热力学》 流体的P-V-T关系
特性：高于Tc的的等温线光滑，无转折点。
T2 T1
2.2.1 理想气体方程（Ideal Gas EOS）
pV=RT
Z=PV/RT=1
p为气体压力；V为摩尔体积； T为绝对温度；R为通用气体常数
R=8.314 (m3·Pa)/(mol·K)
肇庆学院
《化工热力学》 流体的P-V-T关系
2.2.1 理想气体方程 理想气体方程的应用： （1）在较低压力和较高温度下可用理想气体方程 进行计算。 （2）为判断真实气体状态方程的正确程度提供了 一个标准：当P 0或V ∞时，任何状态方程都 还原为理想气体方程。
流体的P-V-T关系
（1）用一个状态方程即可精确地代表相当广泛范围 内的P、V、T实验数据，借此可精确地计算所需的P、
V、T数据， 从而大大减少实验测定的工作量。
（2）用状态方程可计算不能直接从实验测定的其他
热力学性质。
（3）用状态方程可进行相平衡计算
肇庆学院
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
溶液+萃取质A 原料A+B 萃取质A
萃取
萃取残质B
循环萃取剂
分离
新鲜萃取剂
38
利用超临界CO2流体技术从植物/动物中提 取纯天然的高附加值的物质
高附加值的天然产品 （从樱桃核中提取）
O CH
苯甲酮
OH CH2
苯甲醇
有樱桃味 US$120/Ib 无樱桃味 US$14/Ib
US$140/Ib US$14/Ib
48.1
49.7 71.7 41.9 37.5 37.5
32.2
9.2 36.5 96.6 196.6 135.0
0.203
0.218 0.450 0.217 0.232 0.228
36
超临界流体萃取过程简介
将萃取原料装入萃取釜。采用CO2为超临界溶剂。 CO2气体经热交换器冷凝成液体； 用加压泵把压力提升到工艺过程所需的压力(应高于CO2的 pc)，同时调节温度 ，使其成为超临界CO2流体。 CO2流体作为溶剂从萃取釜底部进入，与被萃取物料充分接 触，选择性溶解出所需的化学成分。 含溶解萃取物的高压CO2流体经节流阀降压到低于CO2的pc 以下进入分离釜，由于CO2溶解度急剧下降而析出溶质，自 动分离成溶质和CO2气体二部分，前者为过程产品，定期从 分离釜底部放出，后者为循环CO2气体，经过热交换器冷凝 成CO2液体再循环使用。 整个分离过程是利用CO2流体在超临界状态下对有机物有极 高的溶解度，而低于临界状态下对有机物基本不溶解的特性， 将CO2流体不断在萃取釜和分离釜间循环，从而有效地将需 37 要分离提取的组分从原料中分离出来。
第4章 流体混合物的热力学 性质
第7章压缩、膨胀、动 力循环与制冷循环 ( H, S, Q, W, η )
给出能量 有效 利用 极限
化 工 热 力 学 的 任 务
ˆ ˆ ( , M i , Gi f i , i , ai , i )
2
引言
万事万物状态、性质的变化绝大多 数是由于物质T，p变化引起的。 自然界最软的石墨在1400℃，510万atm的高温高压下，能变成最 硬的金刚石； 1atm下，-191℃下的空气会变成 液体，-213℃则变成了坚硬的固体。
第二章 流体的 PVT关系
1
各章之间的联系
第2章 流体的PVT关系 ( p-V-T, EOS) 第5章 相平衡
ˆ pyi p i xi
V i s i s i
给出物质 有效 利用 极限
第3章 纯流体的热力学 性质(H,S,U，难测； 由EOS+Cp得到）
第6章 化工过程能量分 析(H,S, W，Ex )
35
各种溶剂的临界特性
流体名称 分子式 临界压力 (bar) 临界温度 (℃) 临界密度 (g/cm3)
二氧化碳
水 氨
CO2
H2 O NH3
72.9
217.6 112.5
31.2
374.2 132.4
0.433
0.332 0.235
乙烷
乙烯 氧化二氮 丙烷 戊烷 丁烷
C2H6
C 2 H4 N2O C 3 H8 C5H12 C4H10
39
§2.2 状态方程
从§2.1可知，流体的p-V-T数据是多么的重要。 毫无疑问，流体的p-V-T数据是可以直接测定的。现已 积累了大量水、空气、氨和氟里昂等的 p-V-T数据。 但测定数据费时耗资，而且测定所有流体的所有p-V-T 数据是不现实的，特别是高温高压下的p-V-T数据测定 不但技术上相当困难而且非常危险。 仅从有限的p-V-T测定数据不可能全面地了解流体的pV-T行为。 流体的p-V-T数据更重要作用是通过它推算内能、焓、 熵等信息。 需要P-V-T关系的解析形式！——状态方程！
表1 各种气体的Tc、pc以及正常沸点Tb
物质 Tc ， ℃ pc ，atm Tb ， ℃ 燃烧值，kJ/g
甲烷 乙烷 丙烷 正丁烷 正戊烷 正己烷
-82.62 32.18 96.59 151.9 196.46 234.4
45.36 48.08 41.98 37.43 33.32 29.80
-161.45 -88.65 -42.15 -0.5 36.05 68.75
P 0.4762Mpa T =150 C
o
P 0.4762Mpa T =150o C
T =150o C
Ps (T1 ) P s (T2 )
T Tc Tc T1 Tc T2 Tc
12
§2.1.2 P-V图
临界点
在C点 1点、2线、 4区 2 P V 2 T 0 在C点
④
P
V T 0
超临界流体区 （T>Tc和P>Pc）
①过冷液体区L
③汽液两相平衡区 F=C-P+2=1
②过热蒸汽区
什么是正 常沸点？
①饱和液相线
（泡点线）
②饱和汽相线 （露点线 ）
恒温线
13
临界点—p-V-T中最重要的性质
1）Tc、pc 是纯物质能够呈现汽液平衡时的最高温度 和最高压力。 要使气体液化温度绝对不能超过Tc 。 气体“液化”的先决条件是T<Tc，否则无论施加多大 的压力都不可能使之液化。 2）临界等温的数学特征：等于临界温度的等温线在 临界点出现水平拐点。 P V TC 0 在C点 重要！ 14 2 P V 2 TC 0 在C点
1)临界温度要高，否则在常温或普通低温范 围内不能被液化； 2) 在冷凝温度下的蒸汽压也不宜过高； 3)为了使蒸发压力高于大气压力。
制冷剂的选择离不开p-V-T数据。
29
3.液化气成分的选择 【例2-4】液化气是理想的气体燃料。对家庭用液化气 的要求是加压后变成液体储于高压钢瓶里，打开减压阀 后即汽化，以便燃烧。请你根据对液化气储存和使用的 要求来选择液化气成分。
6
第二章 内容
§2.1 纯流体的p-V-T相图 §2.2 气体状态方程（EOS） §2.3 对应态原理和普遍化关联式 §2.4 液体的p-V-T性质 §2.5 真实气体混合物p-V-T关系
§2.6 状态方程的比较和选用
7
§2.1 纯流体的p-V-T相图
§2.1.1 T –V 图 §2.1.2 p-V 图 §2.1.3 p-T 图 §2.1.4 p-V-T 立体相图 §2.1.5 纯流体p-V-T关系的应用及思考
甲烷：Tc= -82.62℃，pc=4.536 MPa, 。
问：室温下能否通过加压使天然气变成LNG ？ 气体“液化”的先决条件是物质T<Tc。
27
临界点——最重要的性质
28
2. 制冷剂的选择
在选择氟里昂替代品时，离不开p-V-T数 据。 制冷剂工作特点:低压饱和蒸汽室温下饱 和液体交替变化。 对制冷剂的要求：
1）由于刚性容器体积保持不变， 因此加热过程在等容线上变化，到 达B1时，汽液共存相变为液相单相； 继续加热，当T>Tc，则最终单相为 超临界流体，即C1点。
2）当水慢慢加热后，则状态从位 于汽液共存区的A2，变为汽相单相 B2，继续加热，当T>Tc，则最终
25
单相为临界流体C2。
§2.1 纯流体的P-V-T相图
§2.1.1 T -V图 §2.1.2 P-V图 §2.1.3 P-T图 §2.1.4 P-V-T立体相图 §2.1.5 纯流体P-V-T关系的应用
26
§2.1.5 纯流体p-V-T关系的应用
1.气体液化和低温技术 流体p-V-T关系的最大应用就是气体的液化。 如空气液化、天然气液化。 为了便于储运，一般需将天然气制成液化天然气 （LNG）。
55.6 52.0 50.5 49.6 49.1 48.4
30
P-T图
液相区
8atm下变成液体
气相区
1atm下变成气体
31
液化气的p-T 图
-82.62 ℃
室温10~40℃
乙烯、丙烯、 丁烯能做液化 气吗？
96.59℃
TC = 196.46 Tb =36.05 ℃
物质
√ 正丁烷 √
正戊烷 Ⅹ 正己烷 Ⅹ
汽化曲线、熔化曲线、升华曲线
三相点(Tt,Pt)和临界点(Tc,Pc,Vc) 等容线
临界等容线V=Vc、V>Vc、V<Vc
17
§2.1.4 P-V-T立体相图
P-V-T立体相图
18
§2.1.4 P-V-T立体相图
水的P-V-T立体相图
19
【例2-1】 将下列纯物质经历的过程表 示在p-V图上：
5
P-V-T关系的用途
1.流体的p-V-T关系可直接用于设计，如： 1) 输送管道直径的选取。 2）储罐的体积、承受压力。
2.利用可测的热力学性质（T，P，V，CP）计算不 可测的热力学性质（H，S，G，f，φ，α，γ）。 而2点的意义比1点要大得多。（将在第3、4章介 绍）
有了p-V-T关系，热力学的大多数问题均可得到解 决。
V
【例2-2】
： 现有一过程，从pV 图的状态点 a( 过 热蒸气 ) 出发，到达 状态点d（过冷液 体）可以有两种途 径：①均相途径 (a→b→c→d) ； ② 非 均 相 途 径 (a→b’→ c’→d) 。 请在 p-T 图上画出 对应的路径。
22
A
B
C
D
23
【例2-2】
24Biblioteka 【例2-3】 在4L的刚性容器中装有50℃、2kg水的饱和 汽液混合物，已知50℃水的饱和液相体积Vsl=1.0121 ， 饱和汽相体积Vsv=12032；水的临界体积Vc=3.111 。现 在将水慢慢加热，使得饱和汽液混合物变成了单相，问： 此单相是什么相？ 如果将容器换为400L，最终答案是 什么？