学考传奇(济南专版)2016届中考数学第3章第4节二次解读
《学考传奇16年》综合检测题(三)

姓 名 准考证号学 校 班 级 座 号————————————密——————————————封——————————————线———————————————济南市2016年初三年级学业水平考试综合检测题(三)一、(15分)1.下列词语中加点字的读音完全正确的一项是( )(3分) A.滑稽.(j ī) 啜.泣(chu î) 砭.骨(bi ān) 气冲斗.牛(d îu) B.寒噤.(j ìn ) 尴尬.(ɡà) 扶掖.(y è) 龙吟凤哕.(su ì) C.媲.美(b ì) 诘.责(ji é) 酝.酿(y ùn ) 鳞次栉.比(ji ē) D.哂.笑(sh ěn ) 恻.隐(c è) 汲.取(j í) 万恶不赦.(sh è) 2.下列词语中没有错别字.....的一项是( )(3分) A.慰藉 莹火虫 豁然开朗 转瞬即逝 B.阴晦 文曲星 孜孜不倦 怒不可遏 C.惘然 儒子牛 一张一弛 沧海桑田 D.肯切 度假村 门庭若市 隐天蔽日 3.下列句子中加点成语使用恰当....的一项是( )(3分) A .法国大昆虫家法布尔,把科学和文学巧妙地结合起来,用富有诗意的笔触描绘了一个绚丽多姿、光怪陆离....的昆虫世界。
B .他在人声鼎沸的赛场上能做到充耳不闻....、心静如水,而一旦发力,就令对手不寒而栗。
C .田先生生气了,涨红了脸说道:“你们说的都是杯弓蛇影....,纯属无中生有,完全不符合事实。
”D .字义丰富是汉字的一大特点,掌握了常用字的字义有利于理解词语,汉语中很多词可以望文生义,望文知义....。
4.下列句子没有语病....的一项是( )(3分) A.我们必须及时纠正并随时发现学习过程中的缺点。
B.这场比赛的胜利,将决定我们能否顺利进入决赛阶段。
C.“低头族”是指在社交场合不关注身边的人,跟人聊天时老忍不住看手机。
学考传奇(济南专版)中考数学 第4章 几何初步与三角形 第1节 几何初步与相交线 平行线考点实训-人

第1节几何初步与相交线平行线1.(2015·某某某某)若∠A=34°,则∠A的补角为( )A.56°B.146°C.156°D.166°2.(2015·某某)如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )→C→D→→C→F→B→C→E→F→→C→M→B3.(2015·某某黔东南)如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=( )A.70°B.80°C.110°D.100°4.(2015·某某某某)将一副三角尺按如图方式进行摆放,∠1,∠2不一定互补的是( )5.(2015·某某凉山)如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )A.52°B.38°C.42°D.60°6.(2015·某某)如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )A.122°B.151°C.116°D.97°7.计算:(1)33°52′+21°54′=;(2)36°27′×3=.8.(2015·某某永州)如图,∠1=∠2,∠A=60°,则∠ADC=_______度.9.(2015·某某某某)将一副三角尺按如图所示的方式放置,使含30°角的三角尺的短直角边和45°角的三角尺的一条直角边重合,则∠1的度数是________°.10.(2015·某某某某)如图,点A,C,F,B在同一条直线上,CD平分∠ECB,FG∥∠ECA为α度,则∠GFB为______度(用关于α的代数式表示).参考答案7.(1)55°46′ (2)109°21′2。
学考传奇(济南专版)中考数学第4章几何初步与三角形第1
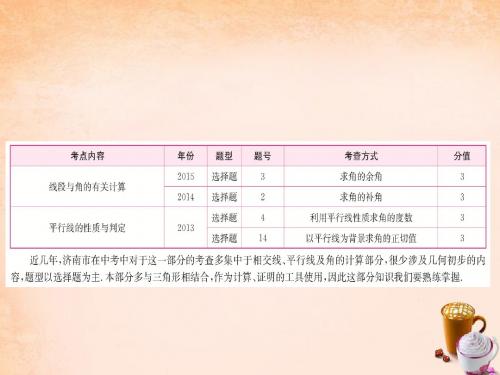
3.垂直性质: (1)在同一平面内,过直线外一点__有__且__只__有__一条直线与 已知直线垂直. (2)直线外一点与直线上各点连线的所有线段中,垂__线__段_ 最短. (3)点到直线的距离:直线外一点到这条直线的垂线段的 长度,叫作点到直线的距离.
知识点5 平行线
1.平行公理: (1)经过直线外一点,__有__且__只__有____一条直线与这条直线 平行. (2)若两直线都与第三条直线平行,那么这两条直线 _______.
平行
2.性质与判定:
(1)同位角____相__等____ 两直线平行.
(2)内错角相等 两直线_____平__行______.
(3)同旁内角____互__补____ 两直线平行.
知识点6 命题与定理
1.命题:一般地,对某件事情做出判断的语句(陈述句) 叫作命题.命题有___题__设___和__结__论__1_两部分组成,常写成 “如果……,那么……”的形式.按照命题是否成立,分为 真命题和假命题. 2.定理:经过推理,证明为真的命题叫作定理.
3.余角、补角:
(1)余角:如果两个角的和等于__9_0_°__,那么这两个角互 为余角.即若α +β =90°,则α ,β 互为余角.同角或等角的 余角___相__等_____. (2)补角:如果两个角的和等于___1_8_0_°__,那么这两个角 互为补角.即α +β =___1_8_0_°___,则α ,β 互为补角.同角或等 角的补角____相__等_____.
1.角的定义: (1)有公共端点的_两__条__射__线__组成的图形叫作角.这个公共 端点叫作角的___顶__点____,这两条射线叫作角的边. (2)一条射线绕着它的端点旋转而形成的图形叫作角.
山东省济南市2016年中考数学试题含答案解析

B.30°
第 3 题图 【答案】B 【解析】∵△ABC 是等腰直角,∠ACB=90°,∴∠CAB=45°. ∵∠1=15°,∴∠3=∠CAB-∠1=45°-15°=30°. ∵l1∥l2,∴∠2=∠3=30°. 故答案选 B.
第 3 题答案图 4.如图,以下给出的几何体中,其主视图是矩形,俯视图是三角形的是(
3 2
)
B.x>3
C.x<
3 2
D.x<3
第 9 题图 【答案】C 【解析】把点 A(0,3)代入 y=-2x+b,得 3=0+b.∴b=3. 一次函数解析式为 y=-2x+3. 由-2x+3> 0,得 x<
3 . 2
故答案选 C. 10.某学校在八年级开设了数学史、诗词赏析、陶艺三门校本课程,若小波和小睿两名同学每人随机选择其中 一门课程,则小波和和小睿选到同一课程的概率是( )
2
第 8 题图 【答案】B 【解析】图①中的点 A 和图②中的点 A′是一对对应点,将点 A 先向右平移 1 个单位,再向下平移 3 个单位就 得到点 A′,所以 B 选项正确. 故答案选 B.
第 8 题答案图 9.如图,若一次函数 y=-2x+b 的图像交 y 轴于点 A(0,3),则不等式-2x+b>0 的解集为( A. x >
第 21 题图 1 5 【答案】 3 6
第 21 题图 2
第 21 题图 3
【解析】在图 2 中,设 DM=x,则 AM=EM=10-x. 1 ∵点 E 是 CD 的中点,AB=CD=8 3,∴DE=CE= CD=4 3. 2 在 Rt△DEM 中,∵DE2+DM2=EM2,∴(4 3)2+x2=(10-x)2.解得 x=2.6. ∴DM=2.6,AM=EM=10-2.6=7.4. 过点 N 作 NF⊥CD 于点 F(如答案图 1),则△DEM∽△FNE. ∴ DE EM 4 3 7.4 37 37 3.∴AN=EN= 3. = .∴ = . 解得 EN= FN EN 10 EN 6 6
学考传奇(济南专版)2016中考数学 题型突破专题5 动手操.

(2015·济宁)将一副三角尺(在Rt△ABC中, ∠ACB=90°,∠B=60°;在Rt△EDF中,∠EDF=90°, ∠E=45°)如图摆放,点D为AB的中点,DE交AC于点P,DF
经过点C.将△EDF绕点D顺时针方向旋转角α (0°<α <60°)
,DE′交AC于点M,DF′交BC于点N,则 的值为( )
操作类问题是指应用所学知识对可实施性、操作性问题, 进行动手测量、作图(象)、取值、计算等实验,猜想获得 数学结论的探索研究性活动.考查学生的动手能力、实践能力、 分析和解决问题的能力.
解决该问题的基本思路是:“操作→分析问题→解决问题.”
一、图形变换操作 此类操作题常与轴对称、平移、旋转、相似或位似等 变换有关,掌握图形变换的性质是解决这类题目的关键.
角相等、对应点到旋转中心的距离相等的性质解答.
(2014·珠海)如图,在Rt△ABC中,∠BAC=90°,
AB=4,AC=3,线段AB为半圆O的直径,将Rt△ABC沿射线AB
方向平移,使斜边与半圆O相切于点G,得△DEF,DF与BC交 于点H. (1)求BE的长; (2)求Rt△ABC与△DEF重叠 (阴影)部分的面积.
3.(2015·甘肃武威)如图①所示,将直尺摆放在三角板ABC上,使直
尺与三角板的边分别交于点D,E,F,G,量得∠CGD=42°.
(1)求∠CEF的度数; (2)将直尺向下平移,使直尺的边缘 通过三角板的顶点B,交AC边于点H,如 图②所示,点H,B在直尺上的读数分别 为4,13.4,求BC的长(结果保留两位小 数). (参考数据:sin 42°≈0.67,cos 42°≈0.74,tan 42°≈0.90)
PM CN
3 3 1 A. 3B. C. D. 2 3 2
山东省济南市2016届九年级中考三模数学试题解析(解析版)

一、选择题(本大题共15小题,每小题3分,满分45分,在每小题给出的四个选项中,只有一个是符合题意的)1.2的倒数是()A.2 B.-2 C.12D.-12【答案】C. 【解析】试题解析:∵2×12=1,∴2的倒数是12.故选C.考点:倒数.2.将数字86400用科学记数法表示为()A.8.64×105B.8.64×104C.86.4×103D.864×102【答案】B.【解析】试题解析:86400=8.64×104,故选B.考点:科学记数法----表示较大的数.3.如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是()【答案】B.【解析】试题解析:从左面看易得第一层有2个正方形,第二层最左边有一个正方形.故选B.考点:简单几何体的三视图.4.如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于()A.60° B.50° C.45° D.40°【答案】D.【解析】试题解析:∵∠C=80°,∠CAD=60°,∴∠D=180°-80°-60°=40°,∵AB∥CD,∴∠BAD=∠D=40°.故选D.考点:平行线的性质.5.为了解某班学生每周做家务劳动的时间,某综合实践活动小组对该班9名学生进行了调查,有关数据如下表.则这9名学生每周做家务劳动的时间的众数及中位数分别是()每周做家务的时间(小时)0 1 2 3 4人数(人) 2 2 3 1 1A.3,2.5 B.1,2 C.3,3 D.2,2【答案】D.【解析】试题解析:表中数据为从小到大排列.数据2小时出现了三次最多为众数;2处在第5位为中位数.所以本题这组数据的中位数是2,众数是2.故选D.考点:1.众数;2.中位数.6.下列计算正确的是()A.-x3+3x3=2x3B.x+x=x2C.x3+2x5=3x3D.x5-x4=x【答案】A.【解析】试题解析:A.-x3+3x3=(-1+3)x3=2x3,所以此选项正确;B.x+x=2x,所以此选项错误;C.x3与2x5不是同类项,所以不能合并,所以此选项错误;D.x5与x4不是同类项,所以不能合并,所以此选项错误;故选A.考点:整式的运算.7.三角形的两边长分别是3和6,第三边是方程x2-6x+8=0的解,则这个三角形的周长是()A.11 B.13 C.11或13 D.11和13【答案】B.考点:1.一元二次方程的解;2.三角形的周长.8.如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于()A D.2 3【答案】B.【解析】试题解析:由格点可得∠ABC所在的直角三角形的两条直角边为2,4,==故选B.考点:解直角三角形.9.若反比例函数1yx=的图象上有两点P1(1,y1)和P2(2,y2),那么()A.y1>y2>0 B.y2>y1>0 C.y1<y2<0 D.y2<y1<0【答案】A.【解析】试题解析:∵点P1(1,y1)和P2(2,y2)在反比例函数1yx=的图象上,∴y1=1,y2=12,∴y1>y2>0.故选A.考点:反比例函数的图象与性质.10.不等式组840312xx-⎩≤-⎧⎨>的解集在数轴上表示为()【答案】A.【解析】试题解析:340128xx-⎧⎨≤-⎩>①②,由①得,x>1,由②得,x≥2,故此不等式组得解集为:x≥2.在数轴上表示为:.故选A.考点:1.解一元一次不等式组;2.在数轴上表示不等式组的解集.11.如图Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为()A...+2 D.+2【答案】C.【解析】试题解析:过点B作BO⊥AC于O,延长BO到B′,使OB′=OB,连接DB′,交AC于E,此时DB′=DE+EB′=DE+BE的值最小.连接CB′,易证CB′⊥BC,根据勾股定理可得=,则△BDE周长的最小值为.故选C.考点:1.轴对称-最短路线问题;2.勾股定理.12.如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B′处,AB′与y轴交于点D,则点D的坐标为()A.(0,-92) B.(0,-94) C.(0,-72) D.(0,-74)【答案】D.【解析】试题解析:由折叠的性质可知,∠B′AC=∠BAC,∵四边形OABC为矩形,∴OC∥AB,∴∠BAC=∠DCA,∴∠B′AC=∠DCA,∴AD=CD,设OD=x,则DC=6-x,在Rt△AOD中,由勾股定理得,OA2+OD2=AD2,即9+x2=(6-x)2,解得:x=94,∴点D的坐标为:(0,-94),故选B.考点:1.矩形的性质;2.坐标与图形性质;3.翻折变换(折叠问题).13.如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O-C-D-O路线作匀速运动,设运动时间为t(s).∠APB=y(°),则下列图象中表示y与t之间函数关系最恰当的是()【答案】C.【解析】试题解析:当动点P在OC上运动时,∠APB逐渐减小;当P在 CD上运动时,∠APB不变;当P在DO上运动时,∠APB逐渐增大.故选C.考点:动点函数图象的问题.14.如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍.如果搭建正三角形和正六边形共用了2016根火柴棍,并且正三角形的个数比正六边形的个数多6个,那么能连续搭建正三角形的个数是()A.222 B.280 C.286 D.292【答案】D.【解析】试题解析:设连续搭建三角形x个,连续搭建正六边形y个.由题意得,215120166x yx y+++=⎧⎨-=⎩,解得:292286 xy=⎧⎨=⎩.故选D.考点:二元一次方程组的应用.15.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b2-4ac>0;③方程ax2+bx+c=0的另一个根在2和3之间;④2c<3b;⑤a十b>m(am+b),(m≠1的实数)其中正确的结论有()A .1个B .2个C .3个D .4个 【答案】D. 【解析】试题解析:∵抛物线开口向下, ∴a<0,∵对称轴为直线x=-2ba=1,即b=-2a , ∴b>0,∵抛物线与y 轴的交点在x 轴上方, ∴c>0,∴abc<0,所以①错误; ∵抛物线与x 轴有两个交点, ∴b 2-4ac >0,所以②正确;∵抛物线与x 轴的一个交点在点(-1,0)和原点之间,而对称轴为直线x=1, ∴抛物线与x 轴的另一个交点在点(2,0)和点(3,0)之间, ∴方程ax 2+bx+c=0的另一个根在2和3之间,所以③正确; ∵x=-1时,y <0, ∴a -b+c <0,而a=-12b , ∴2c<3b ,所以④正确;∵x=1时,函数值最大,最大值为a+b+c ,∴a+b+c>am 2+mb+c (m≠1),即a 十b >m (am+b ),所以⑤正确. 故选D .考点:二次函数的图象与性质.二、填空题(本大题共6小题,每小题3分,满分18分,把答案填在题中横线上)16.分解因式:2x 2+4x+2= . 【答案】2(x+1)2. 【解析】试题解析:原式=2(x 2+2x+1)=2(x+1)2. 考点:提公因式法与公式法的综合运用.17.当x 时,【答案】≤2.【解析】试题解析:2-x≥0,解得:x≤2.考点:二次根式有意义的条件.18.袋中装有除颜色外其余都相同的红球和黄球共25个,小明通过多次模拟实验后,发现摸到的红球、黄球的概率分别是25和35,则袋中黄球有个.【答案】15. 【解析】试题解析:∵摸到黄球的概率是35,∴袋中黄球有袋中黄球有35×25=15个.考点:概率的意义.19.如图,△ABC内接于⊙O,∠C=45°,AB=2,则⊙O的半径为.【解析】试题解析:连接OA,OB,∵∠C=45°,∴∠AOB=2∠C=90°,∵OA=OB,∴△OAB是等腰直角三角形,.考点:1.圆周角定理;2.等腰直角三角形.20.如图,△AOB和△ACD均为正三角形,顶点B、D在双曲线y=4x(x>0)上,则S△OBP= .【答案】4.【解析】试题解析:过A作AF⊥OB,作P作PG⊥OB,∵△OAB与△ADC都为等边三角形,∴∠BOA=∠DAC=60°,∴AD∥OB,∴AF=PG(平行线间的距离处处相等),∵OB为△OBA和△OBP的底,∴12OBAF=12OBPG,即S△OBP=S△OAB(同底等高的三角形面积相等),过B作BE⊥x轴,交x轴于点E,可得S△OBE =S△ABE=12S△OBA,∵顶点B在双曲线y=4x(x>0)上,即k=4,∴S△OBE =|k|42 22==,则S△OBP =S△OBA=2S△OBE=4,考点:1.反比例函数系数k的几何意义;2.等边三角形的性质.21.如图,正方形ABCD的边长为4,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为.【解析】试题解析:连接OC,∵O为正方形ABCD的中心,∴∠DCO=∠BCO,又∵CF与CE都为圆O的切线,∴CO平分∠ECF,即∠FCO=∠ECO,∴∠DCO-∠FCO=∠BCO-∠ECO,即∠DCF=∠BCE,又∵△BCE沿着CE折叠至△FCE,∴∠BCE=∠ECF,∴∠BCE=∠ECF=∠DCF=13∠BCD=30°,在Rt△BCE中,设BE=x,则CE=2x,又BC=4,根据勾股定理得:CE2=BC2+BE2,即4x2=x2+42,解得:考点:1.切线的性质; 2.正方形的性质;3.翻折变换(折叠问题).三、解答题(本大题共7个小题,共57分.解答时写出必要的文字说明、证明过程或演算步骤)222cos30°.【答案】4.【解析】试题分析:原式利用二次根式除法,绝对值的代数意义,以及特殊角的三角函数值计算即可得到结果.试题解析:原式42-=4.考点:实数的混合运算.23.解方程:2131 x x=--.【答案】x=-1.【解析】试题分析:分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.试题解析:去分母得:2x-2=x-3,解得:x=-1,检验x=-1是分式方程的解.考点:解分式方程.24.如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.【答案】证明见解析.【解析】考点:1.全等三角形的判定与性质;2.平行线的判定..25.某路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°,求路况显示牌BC的长度.(结果保留根号)【答案】()米.【解析】试题分析:在Rt△ABD中,知道了已知角的对边,可用正切函数求出邻边AD的长;同理在Rt△ABC中,知道了已知角的邻边,用正切值即可求出对边AC的长;进而由BC=AC-AB得解.试题解析:∵在Rt△ADB中,∠BDA=45°,AB=3m,∴DA=3m,在Rt△ADC中,∠CDA=60°,∴tan60°=CA AD,∴CA=∴BC=CA-BA=()米.考点:解直角三角形的应用—俯角仰角问题.26.某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:利润=售价-进价)甲乙进价(元/件)15 35售价(元/件)20 45若商店计划销售完这批商品后能使利润达到1100元,问甲、乙两种商品应分别购进多少件?【答案】100件;60件.【解析】考点:二元一次方程组的应用.27.在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.(1)写出点M坐标的所有可能的结果;(2)求点M的横坐标与纵坐标之和是偶数的概率.【答案】(1)所有可能结果见解析;(2)59.【解析】试题分析:(1)列表得出所有等可能的情况结果即可;(2)列表得出点M的横坐标与纵坐标之和是偶数的情况数,即可求出所求的概率.试题解析:(1)列表如下:1 2 31 (1,1)(2,1)(3,1)2(1,2) (2,2) (3,2) 3 (1,3) (2,3) (3,3)则点M 坐标的所有可能的结果有9个:(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(2,3)、(3,1)、(3,2)、(3,3);(2)求出横纵坐标之和,如图所示:1 2 3 12 3 4 23 4 5 3 4 5 6得到之和为偶数的情况有5种,故P (点M 的横坐标与纵坐标之和是偶数)=59. 考点:列表法与树状图法.28.如图,在平面直角坐标系xOy 中,矩形OBCD 的顶点B ,D 的坐标分别为(8,0),(0,4).若反比例函数y=1k x(x >0)的图象经过对角线OC 的中点A ,分别交DC 边于点E ,交BC 边于点F .设直线EF 的函数表达式为y=k 2x+b .(1)反比例函数的表达式是 ;(2)求直线EF 的函数表达式,并结合图象直接写出不等式k 2x+b <1k x的解集; (3)若点P 在直线BC 上,将△CEP 沿着EP 折叠,当点C 恰好落在x 轴上时,点P 的坐标是 .【答案】(1)y=8x ,(2)y=-12x+5,x <2或x >8.(3)(8,-5)或(8,). 【解析】 试题分析:(1)求出点A 坐标代入y=1k x 即可解决. (2)根据一次函数的图象在反比例函数图象的下面,即可写出不等式的解集.(3)如图作EM⊥OB 于M ,利用翻折不变性,设设PC=PN=x ,利用△EMN∽△NBP 得PN PB EN MN =,求出x 即可解决问题.试题解析:(1)∵四边形OBCD 是矩形,∴OD=BC=4,OB=CD=8,∵OA=OC,∴点A 坐标(4,2),∵点A 在反比例函数y=1k x 上, ∴k 1=8,∴反比例函数为y=8x, (2)∵点E 、F 在反比例函数图象上,∴点E 坐标(2,4),点F 坐标(8,1),设直线EF 为y=kx+b ,则2481k b k b +=⎧⎨+=⎩, 解得125k b ⎧=-⎪⎨⎪=⎩,∴直线EF 为y=-12x+5, 于图象可知不等式k 2x+b <1k x 的解集为x <2或x >8. (3)如图作EM⊥OB 于M ,∵∠DOM=∠EMO=∠EDO=90°,∴四边形DEMO 是矩形,∴EM=DO=4,∵△EPN 是由△EPC 翻折得到,∴EC=EN=6,PC=PN ,∠ECP=∠ENP=90°,设PC=PN=x ,=∵∠ENM+∠PNB=90°,∠PNB+∠NPB=90°,∴∠ENM=∠NPB,∵∠EMN=∠PBN,∴△EMN∽△NBP, ∴PN PB EN MN=, ∴6x =∴x=9∴PB=BC -PC=4-(-5.当点P′在CB 延长线上时,由△EMN′∽△N′BP′,设P′B=x, ∵P N P B EN MN '''='', ∴46x +=,+5,此时点P 坐标(8,)故答案为(8,-5)或(8,)考点:反比例函数综合题.29.如图,在矩形ABCD 中,AD=4,M 是AD 的中点,点E 是线段AB 上一动点,连接EM 并延长交线段CD 的延长线于点F .(1)如图1,求证:AE=DF ;(2)如图2,若AB=2,过点M 作MG⊥EF 交线段BC 于点G ,判断△GEF 的形状,并说明理由;(3)如图3,若AB=M 作MG⊥EF 交线段BC 的延长线于点G .①直接写出线段AE 长度的取值范围;②判断△GEF 的形状,并说明理由.【答案】(1)证明见解析;(2)△GEF 是等腰直角三角形.理由见解析;(3.△GEF 是等边三角形.【解析】 试题分析:(1)由条件可以得出AM=DM ,∠A=∠ADF=90°,∠AME=∠DMF,可以证明△AEM≌△DFM,就可以得出结论.(2)过点G 作GH⊥AD 于H ,通过条件可以证明△AEM≌△HMG,得出ME=MG ,进而得出∠EGM=45°,再由(1)的结论可以得出∠EGF=90°,从而得出结论.(3)①当点G 、C 重合时利用三角形相似就可以求出AE 的值,从而求出AE 的取值范围.②过点G 作GH⊥AD 交AD 延长线于点H ,证明△AEM∽△HMG,可以得出EM AM MG GH,从而求出,就可以求出∠MEG=60°,就可以得出结论.试题解析:(1)如图1,证明:在矩形ABCD 中,∠EAM=∠FDM=90°,∠AME=∠FMD.∵AM=DM,∴△AEM≌△DFM.∴AE=DF.(2)答:△GEF 是等腰直角三角形.证明:过点G 作GH⊥AD 于H ,如图2,∵∠A=∠B=∠AHG=90°,∴四边形ABGH是矩形.∴GH=AB=2.∵MG⊥EF,∴∠GME=90°.∴∠AME+∠GMH=90°.∵∠AME+∠AEM=90°,∴∠AEM=∠GMH.∴△AEM≌△HMG.∴ME=MG.∴∠EGM=45°.由(1)得△AEM≌△DFM,∴ME=MF.∵MG⊥EF,∴GE=GF.∴∠EGF=2∠EGM=90°.∴△GEF是等腰直角三角形.(3)①当C、G重合时,如图4,∵四边形ABCD 是矩形,∴∠A=∠ADC=90°,∴∠AME+∠AEM=90°.∵MG⊥EF,∴∠EMG=90°.∴∠AME+∠DMC=90°,∴∠AEM=∠DMC,∴△AEM∽△DMC ∴AE AM MD CD=, ∴2AE =②△GEF 是等边三角形.证明:过点G 作GH⊥AD 交AD 延长线于点H ,如图3,∵∠A=∠B=∠AHG=90°,∴四边形ABGH 是矩形.∴GH=AB=∵MG⊥EF,∴∠GME=90°.∴∠AME+∠GMH=90°.∵∠AME+∠AEM=90°,∴∠AEM=∠GMH.又∵∠A=∠GHM=90°,∴△AEM∽△HMG. ∴EM AM MG GH=. 在Rt△GME 中,∴tan∠MEG=MG GH EM AM==. ∴∠MEG=60°.由(1)得△AEM≌△DFM.∴ME=MF.∵MG⊥EF,∴GE=GF.∴△GEF 是等边三角形.考点:相似形综合题30.已知抛物线C 1:y=ax 2+bx+32(a≠0)经过点A (-1,0)和B (3,0). (1)求抛物线C 1的解析式,并写出其顶点C 的坐标;(2)如图1,把抛物线C 1沿着直线AC 方向平移到某处时得到抛物线C 2,此时点A ,C 分别平移到点D ,E 处.设点F 在抛物线C 1上且在x 轴的下方,若△DEF 是以EF 为底的等腰直角三角形,求点F 的坐标;(3)如图2,在(2)的条件下,设点M 是线段BC 上一动点,EN⊥EM 交直线BF 于点N ,点P 为线段MN 的中点,当点M 从点B 向点C 运动时:①tan∠ENM 的值如何变化?请说明理由;②点M 到达点C 时,直接写出点P 经过的路线长.【答案】(1) y=-12x2+x+32;顶点C的坐标为(1,2);(2) F(-3,-6);(3) ①tan∠ENM的值为定值,【解析】试题分析:(1)根据待定系数法即可求得解析式,把解析式化成顶点式即可求得顶点坐标;(2)根据A、C的坐标求得直线AC的解析式为y=x+1,根据题意求得EF=4,求得EF∥y轴,设F(m,-12m2+m+32),则E(m,m+1),从而得出(m+1)-(-12m2+m+32)=4,解方程即可求得F的坐标;(3)①先求得四边形DFBC是矩形,作EG⊥AC,交BF于G,然后根据△EGN∽△EMC,对应边成比例即可求得tan∠ENM=EMEN=2;②根据勾股定理和三角形相似求得试题解析:(1)∵抛物线C1:y=ax2+bx+32(a≠0)经过点A(-1,0)和B(3,0),∴3239302a ba b⎧-+=⎪⎪⎨⎪++=⎪⎩解得121ab⎧=-⎪⎨⎪=⎩,∴抛物线C1的解析式为y=-12x2+x+32,∵y=-12x2+x+32=-12(x-1)2+2,∴顶点C的坐标为(1,2);(2)如图1,作CH⊥x轴于H,∵A(-1,0),C(1,2),∴AH=CH=2,∴∠CAB=∠ACH=45°,∴直线AC的解析式为y=x+1,∵△DEF是以EF为底的等腰直角三角形,∴∠DEF=45°,∴∠DEF=∠ACH,∴EF∥y轴,∵DE=AC,∴EF=4,设F(m,-12m2+m+32),则E(m,m+1),∴(m+1)-(-12m2+m+32)=4,解得m=3(舍)或m=-3,∴F(-3,-6);(3)①tan∠ENM的值为定值,不发生变化;如图2,∵DF⊥AC,BC⊥AC ,∴DF∥BC,∵DF=BC=AC,∴四边形DFBC 是矩形,作EG⊥AC,交BF 于G ,,∵EN⊥EM,∴∠MEN=90°,∵∠CEG=90°,∴∠CEM=∠NEG,∴△ENG∽△EMC, ∴EM EC EN EG=, ∵F(-3,-6),EF=4,∴E(-3,-2),∵C(1,2),,∴EM EN =, ∴tan∠ENM=EM EN =2; ∵tan∠ENM 的值为定值,不发生变化; ②点P 经过的路径是线段P 1P 2,如图3,∵四边形BCEG是矩形,GP2=CP2,∴EP2=BP2,∵△EGN∽△ECB,∴EN EGEB EC=,,,=,∵P1P2是△BEN的中位线,∴P1P2=12∴点M到达点C时,点P.考点:二次函数综合题.。
学考传奇(济南专版)2016中考数学 题型突破专题1 探索规.

一、数列规律 这类问题通常是先给出一组数,通过观察、归纳这组 数的共性规律,写出一个一般性的结论.解决这类题目的关 键是找出题目中的规律,分清不变量和变化量,寻求变化
部分与序号间的关系.
【分析】观察不难发现,被开方数是从1开始的连续自然数, 每一行的数据的个数是从2开始的连续偶数,求出n-1行的数 据的个数,再加上n-2得到所求数的被开方数,然后写出算术
得x2=(x-a1)2+a1,即
1 x (a1 1) . ∵x为整数点,∴ a1=1, 2
∴M1 (1,1).
2a1x a12 a1,
M2(a2,a2)是抛物线y2=(x-a2)2+a2=x2-2a2x+a22+a2顶点, 抛物线y=x2与y2相交于A2,
x 2 x 2 2a 2 x a 2 2 a 2,
A 2 D2
A 2 D3 2
解得x=3.
同理可求
3 2. x2 x
9 27 81 由此规律可得 A3C3 ,A 4C4 ,A5C5 , , 2 4 8
∴
n 1 3 【答案】 38 A n Cn . n 2 A 9 C9 7 . 2 8 32 27
即正方形A9C9C10D10的边长是
左边=右边.
∴(2n+1)2-4n2=2(2n+1)-1. 【点评】此题考查数字的变化规律,找出数字之间的运算 规律,利用规律解决问题.
102016
-2520
三、图形规律
这类题目通常是给出一组图形的排列(或通过操作得到
一系列的图形),探求图形的变化规律,以图形为载体考查 图形所蕴含的数量关系.解决此类问题时应先观察图形的变化 趋势,是增加还是减少,然后从第一个图形进行分析,运用 从特殊到一般的探索方式,分析归纳找出增加或减少的变化
2016山东省济南市中考数学试卷(含答案解析)
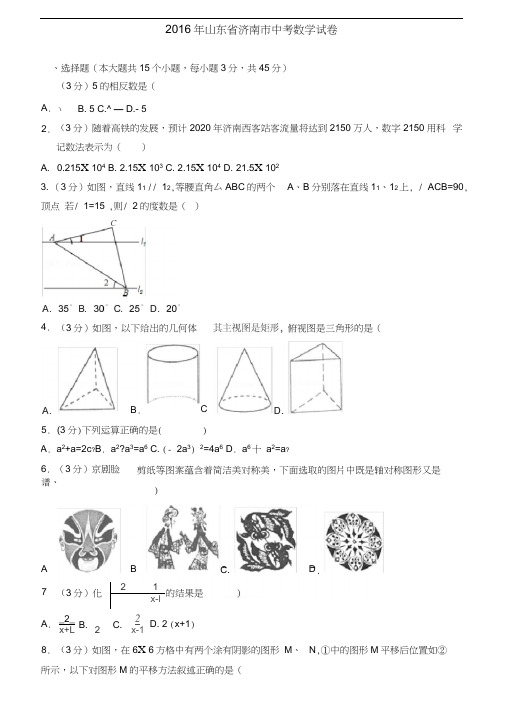
22016年山东省济南市中考数学试卷、选择题(本大题共15个小题,每小题3分,共45分) (3分)随着高铁的发展,预计2020年济南西客站客流量将达到2150万人,数字2150用科 学记数法表示为()A. 0.215X 104B. 2.15X 103C. 2.15X 104 D . 21.5X 102 3. (3分)如图,直线11 // 12,等腰直角厶ABC 的两个顶点 若/ 1=15°,则/ 2的度数是( )A . (3分)5的相反数是() B. 5 C.^ — D.- 52. A 、B 分别落在直线11、12上, / ACB=90,(3分)下列运算正确的是( )A . a 2+a=2c ?B . a 2?a 3=a 6 C. (- 2a 3) 2=4a 6 D . a 6十 a 2=a ? 6. (3分)京剧脸谱、剪纸等图案蕴含着简洁美对称美,下面选取的图片中既是轴对称图形又是21x-lA . _2_ x+L B.2 x-1D. 2 (x+1) (3分)如图,在6X 6方格中有两个涂有阴影的图形 M 、 所示,以下对图形M 的平移方法叙述正确的是(8. N ,①中的图形M 平移后位置如② C4. C . (3分)如图,以下给出的几何体中,B .5. 俯视图是三角形的是()C.A .B. D .(3分)化简7. C.的结果是9. (3分)如图,若一次函数y=-2x+b 的图象交y 轴于点A (0, 3),则不等式-2x+b > 0的解10. (3分)某学校在八年级开设了数学史、诗词赏析、陶艺三门校本课程,若小波和小睿两名 同学每人随机选择其中一门课程,则小波和小睿选到同一课程的概率是(11.(3分)若关于x 的一元二次方程x 2- 2x+k=0有两个不相等的实数根,则k 的取值范围是( )A . k v 1B . k < 1C. k >— 1D. k > 112. (3分)济南大明湖畔的 超然楼”被称作 江北第一楼”某校数学社团的同学对超然楼的高 度进行了测量,如图,他们在 A 处仰望塔顶,测得仰角为30。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 NB MB, 2
【解答】(1)将点A,B的坐标代入抛物线的表达式 得 a b 4 1,
5b 4 1. 解得 a=1 , b=-6. 25a
∴抛物线的表达式为y=x2-6x+4.
OQ OG 2 QG 2 n 2 4.
设⊙Q与直线AC相切于点E,则QE=OQ= 在Rt△AGF与Rt△QEF中, ∵∠AGF=∠QEF=90°,∠AFG=∠QFE, ∴Rt△AGF∽Rt△QEF, ∴
n 2 4.
AF AG 3 5 3 ,即 , 2 QF QE 6n n 4
3 b , 2 求得 c 0. 3 3 得y=x2 + 16 2
顶点B(4,3),
x.
S阴影=OC×CB=12.
(2)①如图,由(1)可知顶点B的坐标为(4,3), ∵BC垂直平分线段OA, ∴OP=2BC=6. ∴∠MNA为Rt△PMN的外角, ∴∠MNA一定为钝角,
若△MAN为等腰三角形时,
则∠NMA=∠NAM.
又∵∠OPM+∠OMP=90°,∠NMA+∠OMP=90°, ∴∠NMA=∠OPM,∠NAM=∠OPM, ∴△OPM∽△OAP,
PO MO ∴ , 即 6 t. AO PO 8 6 ∴t= 9 . 2 即当t= 9 时,△MAN是等腰三角形. 2
t t 2 ②由MN所在直线方程为y= 6 x- 6 , 3 与直线AB的解析式y=- x+6联立, 4 2 得点N的横坐标为xN= 72 2t , 9 2t 即t2-xNt+36- 9 xN=0, 2
解:(1)如答图1所示,过点D作DE⊥x轴于点E,则 DE=3,OE=2. ∵tan∠DBA=
DE 1 , BE 2
∴BE=6,
∴OB=BE-OE=4,
∴B(-4,0).
∵点B(-4,0),D(2,3)在抛物线y=ax2+bx-2(a≠0)上,
1 a , 16a 4b 2 0, 2 ∴ 解得 4a 2b 2 3, b 3 , 2 ∴抛物线的解析式为y= 1 x2+ 3 x-2. 2 2
17 解(1)由题知点B(0,4),C(3,2 )在抛物线上, c 4, b 2, 17 1 所以 9 3b c. 解得 c 4. 6 2 1 2 所以y=- x +2x+4. 6 所以当x=- b =6时,y最大=10. 2a
即拱顶D到地面OA的距离为10 m.
3 1 ∴BE= 2 a,AB= 2
a.
1 由题意,得2x+3a+2· a=80, 2 1 x. ∴a=202 ∴y=AB·BC= 3 ax= 3 (20- 1 x)x. 2 2 2 2 即y=- 3 x +30x(0<x<40). 4
(2)∵y=-
3 4
x2+30x
=-
3 (x-20)2+300, 4
∵点M(m,n)பைடு நூலகம்抛物线y=
1 2 3 ∴n= m + m-2,代入上式得 2 2
1 2
x2+
3 2 x-2上,
S四边形BMCA=-m2-4m+5=-(m+2)2+9, ∴当m=-2时,四边形BMCA面积有最大值,最大值为9.
(3)假设存在这样的⊙Q.如答图2所示,设直线x=-2与x轴 交于点G,与直线AC交于点F. 设直线AC的解析式为y=kx+b,
∴当x=20时,y有最大值,最大值是300平方米.
考点2
二次函数的综合应用
【名师指点】二次函数的综合应用常常与其他知识点综合
作为中考试题的压轴题,难度一般较大.二次函数与几何知
识结合,常常设置动点及存在性问题,解答此类问题一般
先设动点存在,选取某一时刻作为研究对象,然后根据题 意建立方程模型或者函数模型求解.
1 3 (2)抛物线的解析式为y= 2 x2+ 2 x-2,
令x=0,得y=-2,∴C(0,-2).
令y=0,得x=-4或1,∴A(1,0).
设点M坐标为(m,n)(m<0,n<0),
如答图1所示,过点M作MF⊥x轴于点F,则MF=-n,
OF=-m,BF=4+m.
S四边形BMCA =SBMF +S梯形MFOC +SAOC 1 1 1 = BF MF+ (MF+OC) OF+ OA OC 2 2 2 1 1 1 = (4+m) (-n)+ (-n+2) (-m)+ 1 2 2 2 2 =-2n-m+1.
(2)由题知车最外侧与地面OA的交点为(2,0).
22 当x=2时,y= 3 >6,所以可以通过. 1 (3)令y=8,即- x2+2x+4=8. 6
解得x1=6+2 x1-x2=4
3 ,x2=6-2 3
,
3
, m.
答:两排灯的水平距离最小是4
3
解:(1)设AE=a,由题意可得AE·AD=2BE·BC,AD=BC,
【分析】(1)将点A,B的坐标代入抛物线的解析式,得到关 于a,b的方程,从而可求得a,b的值; (2)设点P的坐标为P(m,m2-6m+4),由平行四边形的面积为 30可知S△CBP=15,由S△CBP=S梯形CEDP-S△CEB-S△PBD,得到关于
m的方程求得m的值,从而可求得点P的坐标;
将A(1,0),C(0,-2)代入得
k b 0, b 2, 解得k=2,b=-2,
∴直线AC解析式为y=2x-2,令x=-2,得y=-6,
∴F(-2,-6),GF=6.
在Rt△AGF中,由勾股定理得
AF AG 2 GF2 32 62 3 5.
设Q(-2,n),在Rt△AGF中,由勾股定理得
(2)根据“利润=单价×销售量”列出W关于x的二次函数表
达式即可; (3)利用二次函数的性质求出W的最大值,以及此时x的值即 可.
【解答】(1)设y与x的一次函数关系式为y=kx+b,
由题意,得 80 60k b,
100 50k b. 解得k=-2,b=200.
∴y与x的一次函数关系式为y=-2x+200(30≤x≤60).
9 4 36 x N x N 2 ≥0, 由判别式Δ=
2
得xN≥6或xN≤-14,又0<xN<8, ∴xN的最小值为6,此时t=3, 当t=3时,N的坐标为(6, 3 ),此时PN
2
取最小值为
15 . 2
考点1
二次函数的实际应用
【名师指点】二次函数的实际应用常考类型有求解面积问 题、物理运动问题、生活生产问题、利润问题等.解答时要
仔细分析题干中的变量之间的关系,合理设未知数,根据
题目所给条件,合理选取二次函数表达式进行解答.
(2015·湖北鄂州)鄂州市化工材料经销公司购进一
种化工原料若干千克,价格为每千克30元.物价部门规定其 销售单价不高于每千克60元,不低于每千克30元.经市场调 查发现:日销售量y(千克)是销售单价x(元)的一次函数, 且当x=60时,y=80;x=50时,y=100.在销售过程中,每天
(2)W=(x-30)(-2x+200)-450
=-2x2+260x-6 450
=-2(x-65)2+2 000.
(3)由(2)知W=-2(x-65)2+2 000. ∵-2<0, ∴当x<65时,W随x的增大而增大. 又∵30≤x≤60,
∴当x=60时,W有最大值,最大值为1 950.
答:当销售单价为60元时,该公司获利最大,最大利润为 1 950元.
还要支付其他费用450元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围; (2)求该公司销售原料日获利W(元)与销售单价x(元)之间的 函数关系式;
(3)当销售单价为多少元时,该公司日获利最大?最大获利
是多少元?
【分析】(1)根据y与x成一次函数关系,设y=kx+b,把x与y 的两对值代入求出k与b的值,确定出一次函数表达式,并 求出x的取值范围;
化简得n2-3n-4=0, 解得n=4或n=-1.
∴存在一个以Q点为圆心,OQ为半径且与直线AC
相切的圆,点Q的坐标为(-2,4)或(-2,-1).
解:(1)设平移后抛物线的解析式为
3 y=x2+bx+c, 16
将点A(8,0),O(0,0)代入,
得 c 0,
3 2 0 8 8b c, 16
