九年级数学平移与旋转
新人教版初中数学——图形的轴对称、平移与旋转-知识点归纳及中考典型题解析
新人教版初中数学——图形的轴对称、平移与旋转知识点归纳及中考典型题解析一、轴对称图形与轴对称轴对称图形轴对称图形定义如果一个图形沿着某条直线对折后，直线两旁的部分能够完全重合，那么这个图形就叫做轴对称图形，这条直线叫做对称轴如果两个图形对折后，这两个图形能够完全重合，那么我们就说这两个图形成轴对称，这条直线叫做对称轴性质对应线段相等AB=ACAB=A′B′，BC=B′C′，AC=A′C′对应角相等∠B=∠C∠A=∠A′，∠B=∠B′，∠C=∠C′对应点所连的线段被对称轴垂直平分区别(1)轴对称图形是一个具有特殊形状的图形，只对一个图形而言；(2)对称轴不一定只有一条(1)轴对称是指两个图形的位置关系，必须涉及两个图形；(2)只有一条对称轴关系(1)沿对称轴对折，两部分重合；(2)如果把轴对称图形沿对称轴分成“两个图形”，那么这“两个图形”就关于这条直线成轴对称(1)沿对称轴翻折，两个图形重合；(2)如果把两个成轴对称的图形拼在一起，看成一个整体，那么它就是一个轴对称图形1等腰三角形、矩形、菱形、正方形、圆．2．折叠的性质折叠的实质是轴对称，折叠前后的两图形全等，对应边和对应角相等．【注意】凡是在几何图形中出现“折叠”这个字眼时，第一反应即存在一组全等图形，其次找出与要求几何量相关的条件量．解决折叠问题时，首先清楚折叠和轴对称能够提供我们隐含的且可利用的条件，分析角之间、线段之间的关系，借助勾股定理建立关系式求出答案，所求问题具有不确定性时，常常采用分类讨论的数学思想方法．3．作某点关于某直线的对称点的一般步骤（1）过已知点作已知直线（对称轴）的垂线，标出垂足；（2）在这条直线另一侧从垂足除法截取与已知点到垂足的距离相等的线段，那么截点就是这点关于该直线的对称点．4．作已知图形关于某直线的对称图形的一般步骤（1）作出图形的关键点关于这条直线的对称点；（2）把这些对称点顺次连接起来，就形成了一个符合条件的对称图形．二、图形的平移1．定义在平面内，一个图形由一个位置沿某个方向移动到另一个位置，这样的图形运动叫做平移．平移不改变图形的形状和大小．2．三大要素一是平移的起点，二是平移的方向，三是平移的距离．3．性质（1）平移前后，对应线段平行且相等、对应角相等；（2）各对应点所连接的线段平行(或在同一条直线上)且相等；（3）平移前后的图形全等．4．作图步骤（1）根据题意，确定平移的方向和平移的距离；（2）找出原图形的关键点；（3）按平移方向和平移距离平移各个关键点，得到各关键点的对应点；（4）按原图形依次连接对应点，得到平移后的图形．三、图形的旋转1．定义在平面内，一个图形绕一个定点沿某个方向(顺时针或逆时针)转过一个角度，这样的图形运动叫旋转．这个定点叫做旋转中心，转过的这个角叫做旋转角．2．三大要素旋转中心、旋转方向和旋转角度．3．性质（1）对应点到旋转中心的距离相等；（2）每对对应点与旋转中心所连线段的夹角等于旋转角；（3）旋转前后的图形全等．4．作图步骤（1）根据题意，确定旋转中心、旋转方向及旋转角；（2）找出原图形的关键点；（3）连接关键点与旋转中心，按旋转方向与旋转角将它们旋转，得到各关键点的对应点；（4）按原图形依次连接对应点，得到旋转后的图形．【注意】旋转是一种全等变换，旋转改变的是图形的位置，图形的大小关系不发生改变，所以在解答有关旋转的问题时，要注意挖掘相等线段、角，因此特殊三角形性质的运用、锐角三角函数建立的边角关系起着关键的作用．四、中心对称图形与中心对称中心对称图形中心对称图形定义如果一个图形绕某一点旋转180°后能与它自身重合，我们就把这个图形叫做中心对称图形，这个点叫做它的对称中心如果一个图形绕某点旋转180°后与另一个图形重合，我们就把这两个图形叫做成中心对称性质对应点点A与点C，点B与点D点A与点A′，点B与点B′，点C与点C′对应线段AB=CD，AD=BCAB=A′B′，BC=B′C′，AC=A′C′对应角∠A=∠C∠B=∠D∠A=∠A′，∠B=∠B′，∠C=∠C′区别中心对称图形是指具有某种特性的一个图形中心对称是指两个图形的关系联系把中心对称图形的两个部分看成“两个图形”，则这“两个图形”成中心对称把成中心对称的两个图形看成一个“整体”，则“整体”成为中心对称图形平行四边形、矩形、菱形、正方形、正六边形、圆等．考向一轴对称轴对称图形与轴对称的区别与联系区别：轴对称图形是针对一个图形而言，它是指一个图形所具有的对称性质，而轴对称则是针对两个图形而言的，它描述的是两个图形的一种位置关系，轴对称图形沿对称轴对折后，其自身的一部分与另一部分重合，而成轴对称的两个图形沿对称轴对折后，一个图形与另一个图形重合.联系：把成轴对称的两个图形看成一个整体时，它就成了一个轴对称图形．典例1第24届冬季奥林匹克运动会，将于2022年02月04日～2022年02月20日在中华人民共和国北京市和张家口市联合举行，全国上下掀起喜迎冬奥热潮，下列四个汉字中是轴对称图形的是A．B．C．D．【答案】A【解析】A、是轴对称图形，故此选项正确；B、不是轴对称图形，故此选项错误；C、不是轴对称图形，故此选项错误；D、不是轴对称图形，故此选项错误．故选A．1．下列图形中不是轴对称图形的是A．B．C．D．考向二平移1．平移后，对应线段相等且平行，对应点所连的线段平行（或共线）且相等．2．平移后，对应角相等且对应角的两边分别平行或一条边共线，方向相同．3．平移不改变图形的形状和大小，只改变图形的位置，平移后新旧两图形全等．典例2下列运动中：①荡秋千；②钟摆的摆动；③拉抽屉时的抽屉；④工厂里的输送带上的物品，不属于平移的有A．4个B．3个C．2个D．1个【答案】C【解析】①荡秋千，是旋转，不是平移；②钟摆的摆动，是旋转，不是平移；③拉抽屉时抽屉的运动，是平移；④工厂里的输送带上的物品运动，是平移；故选C．2．下列四组图形都含有两个可以重合的三角形，其中可以通过平移其中一个三角形得到另一个三角形的是A．B．C．D．3．如图，两只蚂蚁以相同的速度沿两条不同的路径，同时从A出发爬到B，则A．乙比甲先到B．甲比乙先到C．甲和乙同时到D．无法确定考向三旋转通过旋转，图形中的每一点都绕着旋转中心沿相同的方向旋转了同样大小的角度，任意一对对应点与旋转中心的连线所成的角都是旋转角，对应点到旋转中心的距离相等，对应线段相等，对应角相等．在旋转过程中，图形的形状与大小都没有发生变化．典例3 如图，在ABC △中，65BAC ∠=︒，以点A 为旋转中心，将ABC △绕点A 逆时针旋转，得AB C ''△，连接BB '，若BB'AC ∥，则BAC '∠的大小是A ．15︒B ．25︒C ．35︒D ．45︒【答案】A【解析】∵△ABC 绕点A 逆时针旋转到△AB ′C ′的位置， ∴AB ′=AB ，∠B ′AC ′=∠BAC =65︒， ∴∠AB ′B =∠ABB ′， ∵BB ′∥AC ，∴∠ABB ′=∠CAB =65°， ∴∠AB ′B =∠ABB ′=65°， ∴∠BAB ′=180°–2×65°=50°，∴∠BAC ′=∠B ′AC ′–∠BAB ′=65°–50°=15°， 故选A ．4．五角星可以看成由一个四边形旋转若干次而生成的，则每次旋转的度数可以是A ．36°B ．60°C ．72°D ．90°5．如图将△ABC 绕点A 顺时针旋转90°得到△AED ，若点B 、D 、E 在同一条直线上，∠BAC =20°，则∠ADB的度数为A．55°B．60°C．65°D．70°考向四中心对称识别轴对称图形与中心对称图形：①识别轴对称图形：轴对称图形是一类具有特殊形状的图形，若把一个图形沿某条直线对称，直线两旁的部分能完全重合，则称该图形为轴对称图形．这条直线为它的一条对称轴．轴对称图形有一条或几条对称轴．②中心对称图形识别：看是否存在一点，把图形绕该点旋转180°后能与原图形重合．典例4下列图形中，既是中心对称图形，又是轴对称图形的是A．B．C．D．【答案】B【解析】A、不是中心对称图形，也不是轴对称图形，故此选项错误；B、是中心对称图形，又是轴对称图形，故此选项正确；C、不是中心对称图形，也不是轴对称图形，故此选项错误；D、不是中心对称图形，也不是轴对称图形，故此选项错误，故选B．6．下列图形中，△A′B′C′与△ABC成中心对称的是A．B．C．D．1．下列四个图形中，不是轴对称图形的是A．B．C．D．2．已知点A的坐标为（3，–2），则点A向右平移3个单位后的坐标为A．（0，–2）B．（6，–2）C．（3，1）D．（3，–5）3．下列说法中正确的有①旋转中心到对应点的距离相等；②对称中心是对称点所连线段的中点；③旋转后的两个图形的对应边所在直线的夹角等于旋转角；④任意一个等边三角形都是中心对称图形．A．1个B．2个C．3个D．4个4．如图，在方格纸中的△ABC经过变换得到△DEF，正确的变换是A．把△ABC向右平移6格B．把△ABC向右平移4格，再向上平移1格C．把△ABC绕着点A顺时针旋转90°，再向右平移6格D．把△ABC绕着点A逆时针旋转90°，再向右平移6格5．如图，已知菱形OABC的顶点O（0，0），B（–2，–2），若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D的坐标为A．（1，–1）B．（–1，–1）C．（1，1）D．（–1，1）6．在菱形ABCD中，AB=2，∠BAD=120°，点E，F分别是边AB，BC边上的动点，沿EF折叠△BEF，使点B的对应点B’始终落在边CD上，则A、E两点之间的最大距离为__________．7．将一张长方形纸条折成如图所示的形状，若∠1=110°，则∠2=__________°．8．如图所示，直线EF过平行四边形ABCD对角线的交点O，且分别交AD、BC于E、F，那么阴影部分的面积是平行四边形ABCD面积的____．9．如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α（0°<α<90°）．若∠1=112°，则∠α=__________°．10．△ABC 在平面直角坐标系xOy 中的位置如图所示．（1）若△A 1B 1C 1与△ABC 关于原点O 成中心对称，则点A 1的坐标为__________； （2）将△ABC 向右平移4个单位长度得到△A 2B 2C 2，则点B 2的坐标为__________； （3）画出△ABC 绕O 点顺时针方向旋转90°得到的△A 3B 3C 3，并求点C 走过的路径长．11．如图，在ABC △中，D 为BC 上任一点，DE AC ∥交AB 于点E DF AB ，∥交AC 于点F ，求证：点E F ，关于AD 的中点对称．12．在如图所示的正方形网格中，每个小正方形的边长都是1，△ABC的顶点都在正方形网格的格点（网格线的交点）上．（1）请在如图所示的网格平面内作出平面直角坐标系，使点A坐标为（1，3），点B坐标为（2，1）；（2）请作出△ABC关于y轴对称的△A'B'C'，并写出点C'的坐标；（3）判断△ABC的形状．并说明理由．13．如图，已知∠BAC=40°，把△ABC绕着点A顺时针旋转，使得点B与CA的延长线上的点D重合，连接CE．（1）△ABC旋转了多少度？（2）连接CE，试判断△AEC的形状．（3）若∠ACE=20°，求∠AEC的度数．1．下列四个图形中，可以由下图通过平移得到的是A．B．C．D．2．在平面直角坐标系中，将点（2，1）向右平移3个单位长度，则所得的点的坐标是A．（0，5）B．（5，1）C．（2，4）D．（4，2）3．如图，在平面直角坐标系中，已知点A（2，1），点B（3，–1），平移线段AB，使点A落在点A1（–2，2）处，则点B的对应点B1的坐标为A．（–1，–1）B．（1，0）C．（–1，0）D．（3，0）4．把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合，则这个旋转角度至少为A．30°B．90°C．120°D．180°5．如图，在ABCD中，将△ADC沿AC折叠后，点D恰好落在DC的延长线上的点E处．若∠B=60°，AB=3，则△ADE的周长为A．12 B．15 C．18 D．216．如图，将△ABC沿BC边上的中线AD平移到△A′B′C′的位置．已知△ABC的面积为16，阴影部分三角形的面积9．若AA′=1，则A′D等于A．2 B．3 C．4 D．3 27．如图，点E是正方形ABCD的边DC上一点，把△ADE绕点A顺时针旋转90°到△ABF的位置．若四边形AECF的面积为20，DE=2，则AE的长为A．4 B．25C．6 D．268．如图，将等边△AOB放在平面直角坐标系中，点A的坐标为（4，0），点B在第一象限，将等边△AOB 绕点O顺时针旋转180°得到△A′OB′，则点B′的坐标是__________．9．如图，在△ABC中，∠BAC=90°，AB=AC=10 cm，点D为△ABC内一点，∠BAD=15°，AD=6 cm，连接BD，将△ABD绕点A按逆时针方向旋转，使AB与AC重合，点D的对应点为点E，连接DE，DE交AC于点F，则CF的长为__________cm．10．如图，在△ABC中，AB=AC=4，将△ABC绕点A顺时针旋转30°，得到△ACD，延长AD交BC的延长线于点E，则DE的长为__________．11．如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△OAB的三个顶点O（0，0）、A（4，1）、B（4，4）均在格点上．（1）画出△OAB关于y轴对称的△OA1B1，并写出点A1的坐标；（2）画出△OAB绕原点O顺时针旋转90°后得到的△OA2B2，并写出点A2的坐标；（3）在（2）的条件下，求线段OA在旋转过程中扫过的面积（结果保留π）．12．如图，在矩形ABCD中，对角线AC的中点为O，点G，H在对角线AC上，AG=CH，直线GH绕点O 逆时针旋转α角，与边AB、CD分别相交于点E、F（点E不与点A、B重合）．（1）求证：四边形EHFG是平行四边形；（2）若∠α=90°，AB=9，AD=3，求AE的长．13．在Rt△ABC中，∠ABC=90°，∠ACB=30°，将△ABC绕点A顺时针旋转一定的角度α得到△DEC，点A、B的对应点分别是D、E．（1）当点E恰好在AC上时，如图1，求∠ADE的大小；（2）若α=60°时，点F是边AC中点，如图2，求证：四边形BEDF是平行四边形．变式拓展1．【答案】A【解析】A．不是轴对称图形，故本选项符合题意；B．是轴对称图形，故本选项不符合题意；C．是轴对称图形，故本选项不符合题意；D．是轴对称图形，故本选项不符合题意．故选A．2．【答案】D【解析】A、可以通过轴对称得到，故此选项错误；B、可以通过旋转得到，故此选项错误；C、可以通过轴对称得到，故此选项错误；D、可通过平移得到，故此选项正确；故选D．3．【答案】C【解析】由平移的性质可知，甲、乙两只蚂蚁的行走的路程相同，且两只蚂蚁的速度相同，所以两只蚂蚁同时到达，故选C．4．【答案】C【解析】根据旋转的性质可知，每次旋转的度数可以是360°÷5=72°或72°的倍数．故选C．5．【答案】C【解析】∵将△ABC绕点A顺时针旋转90°得到△AED，∴∠BAC=∠DAE=20°，AB=AE，∠BAE=90°，∴∠BEA=45°，∵∠BDA=∠BEA+∠DAE=45°+20°，∴∠BDA=65°.故选C．6．【答案】A【解析】A、是中心对称图形，故本选项正确；B、是轴对称图形，故本选项错误；C、是旋转变换图形，故本选项错误；D、是旋转变换图形，故本选项错误．1．【答案】C【解析】A、是轴对称图形，故本选项不符合题意；B、是轴对称图形，故本选项不符合题意；C、不是轴对称图形，故本选项符合题意；D、是轴对称图形，故本选项不符合题意；故选C．2．【答案】B【解析】∵将点A（3，–2）向右平移3个单位所得点的坐标为（6，–2），∴正确答案是B选项.故选B．3．【答案】C【解析】①旋转中心到对应点的距离相等，正确；②对称中心是对称点所连线段的中点，正确；③旋转后的两个图形的对应边所在直线的夹角等于旋转角，正确；④任意一个等边三角形都是中心对称图形，错误．说法正确的有3个，故选C．4．【答案】D【解析】根据图象，△ABC 绕着点A 逆时针方向90°旋转与△DEF 形状相同，向右平移6格就可以与△DEF 重合．故选D ． 5．【答案】C【解析】菱形OABC 的顶点O （0，0），B （–2，–2）， 得D 点坐标为（022-，022-），即（–1，–1）． 每秒旋转45°，则第60秒时，得45°×60=2700°，2700°÷360°=7.5周， OD 旋转了7周半，菱形的对角线交点D 的坐标为（1，1）； 故选C ． 6．【答案】23-【解析】如图，作AH ⊥CD 于H ．∵四边形ABCD 是菱形，∠BAD =120°， ∴AB ∥CD ，∴∠D +∠BAD =180°， ∴∠D =60°， ∵AD =AB =2，∴AH =AD ·sin60°3= ∵B ，B ′关于EF 对称， ∴BE =EB ′，当BE 的值最小时，AE 的值最大，根据垂线段最短可知，当EB ′3AH ==时，BE 的值最小， ∴AE 的最大值=23， 故答案为：23． 7．【答案】55【解析】∵1110∠=︒，纸条的两边互相平行，∴3180118011070.∠=︒-∠=︒-︒=︒根据翻折的性质，()()1121803180705522∠=⨯︒-∠=⨯︒-︒=︒．故答案为：55． 8．【答案】14【解析】根据中心对称图形的性质，得AOE COF △≌△，则阴影部分的面积等于BOC △的面积，为平行四边形ABCD 面积的14．故答案为：14． 9．【答案】22【解析】如图，∵21112∠=∠=︒（对顶角相等），∴336090211268.∠=-⨯︒-=︒︒︒ ∴'906822BAB ∠=-=︒︒︒，∴旋转角'22.BAB α∠=∠=︒故答案为：22．10．【解析】（1）若△A 1B 1C 1与△ABC 关于原点O 成中心对称，则点A 1的坐标为（2，–3）．（2）将△ABC 向右平移4个单位长度得到△A 2B 2C 2，则点B 2的坐标为（3，1）． （3）将△ABC 绕O 点顺时针方向旋转90°，则点C 走过的路径长=90π2180=π．11．【解析】如图，连接EF 交AD 于点O ．DE AC ∥交AB 于E DF AB ，∥交AC 于F ，∴四边形AEDF 是平行四边形， ∴点E F ，关于AD 的中点对称．12．【解析】（1）如图所示：（2）如图所示：'''A B C △即为所求：C '的坐标为()55-，； （3）2221454162091625AB AC BC =+==+==+=，，，∴222AB AC BC +=， ∴ABC △是直角三角形．13．【解析】（1）∵∠BAC =40°，∴∠BAD =140°，∴△ABC 旋转了140°．（2）由旋转的性质可知AC =AE ，∴△AEC 是等腰三角形． （3）由旋转的性质可知，∠CAE =∠BAD =140°，又AC =AE ， ∴∠AEC =（180°–140°）÷2=20°．1．【答案】D【解析】∵只有D 的图形的形状和大小没有变化，符合平移的性质，属于平移得到； 故选D ． 2．【答案】B【解析】将点（2，1）向右平移3个单位长度，则所得的点的坐标横坐标增加3，即（5，1）．故选B ． 3．【答案】【解析】由点A （2，1）平移后所得的点A 1的坐标为（–2，2），可得坐标的变化规律是：左移4个单位，上移1个单位，∴点B 的对应点B 1的坐标为（–1，0）．故选C ． 4．【答案】C【解析】∵360°÷3=120°，∴旋转的角度是120°的整数倍，∴旋转的角度至少是120°．故选C ． 5．【答案】C【解析】由折叠可得，∠ACD =∠ACE =90°，∴∠BAC =90°， 又∵∠B =60°，∴∠ACB =30°，∴BC =2AB =6，∴AD =6，直通中考由折叠可得，∠E =∠D =∠B =60°，∴∠DAE =60°，∴△ADE 是等边三角形，∴△ADE 的周长为6×3=18，故选C ． 6．【答案】B【解析】∵S △ABC =16.S △A ′EF =9，且AD 为BC 边的中线，∴S △A ′DE =12S △A ′EF =92，S △ABD =12S △ABC =8， ∵将△ABC 沿BC 边上的中线AD 平移得到△A 'B 'C '，∴A ′E ∥AB ，∴△DA ′E ∽△DAB ， 则2()A'DE ABD S A'D AD S =△△，即299()1816A'D A'D ==+，解得A ′D =3或A ′D =﹣37（舍），故选B ． 7．【答案】D【解析】∵△ADE 绕点A 顺时针旋转90°到△ABF 的位置．∴四边形AECF 的面积等于正方形ABCD 的面积等于20，∴AD =DC =2，∵DE =2，∴Rt △ADE 中，AE =22AD DE +=26，故选D ．8．【答案】（﹣2，﹣23） 【解析】作BH ⊥y 轴于H ，如图，∵△OAB 为等边三角形，∴OH =AH =2，∠BOA =60°，∴BH =3OH =23，∴B 点坐标为（2，23）， ∵等边△AOB 绕点O 顺时针旋转180°得到△A ′OB ′， ∴点B ′的坐标是（﹣2，﹣23）． 故答案为：（﹣2，﹣23）． 9．【答案】10–26【解析】如图，过点A 作AG ⊥DE 于点G ，由旋转知：AD =AE ，∠DAE =90°，∠CAE =∠BAD =15°，∴∠AED =∠ADG =45°，在△AEF 中，∠AFD =∠AED +∠CAE =60°，在Rt △ADG 中，AG =DG =2AD =32， 在Rt △AFG 中，GF =3AG =6，AF =2FG =26，∴CF =AC –AF =10–26， 故答案为：10–26．10．【答案】23–2【解析】根据旋转过程可知：∠CAD =30°=∠CAB ，AC =AD =4．∴∠BCA =∠ACD =∠ADC =75°．∴∠ECD =180°–2×75°=30°．∴∠E =75°–30°=45°．过点C 作CH ⊥AE 于H 点，在Rt △ACH 中，CH =12AC =2，AH =23． ∴HD =AD –AH =4–23．在Rt △CHE 中，∵∠E =45°，∴EH =CH =2．∴DE =EH –HD =2–（4–23）=23–2．故答案为3–2．11．【解析】（1）如下图所示，点A 1的坐标是（–4，1）；（2）如下图所示，点A 2的坐标是（1，–4）；（3）∵点A （4，1），∴OA 221417+=∴线段OA 290(17)⨯π⨯=174π．12．【解析】（1）∵对角线AC的中点为O，∴AO=CO，且AG=CH，∴GO=HO，∵四边形ABCD是矩形，∴AD=BC，CD=AB，CD∥AB，∴∠DCA=∠CAB，且CO=AO，∠FOC=∠EOA，∴△COF≌△AOE（ASA），∴FO=EO，且GO=HO，∴四边形EHFG是平行四边形；（2）如图，连接CE，∵∠α=90°，∴EF⊥AC，且AO=CO，∴EF是AC的垂直平分线，∴AE=CE，在Rt△BCE中，CE2=BC2+BE2，∴AE2=（9–AE）2+9，∴AE=5．13．【解析】（1）如图1，∵△ABC绕点A顺时针旋转α得到△DEC，点E恰好在AC上，∴CA=CD，∠ECD=∠BCA=30°，∠DEC=∠ABC=90°，∵CA=CD，∴∠CAD=∠CDA=12（180°–30°）=75°，∴∠ADE=90°–75°=15°；（2）如图2，∵点F是边AC中点，∴BF=12 AC，∵∠ACB=30°，∴AB=12AC，∴BF=AB，∵△ABC绕点A顺时针旋转60得到△DEC，∴∠BCE=∠ACD=60°，CB=CE，DE=AB，∴DE=BF，△ACD和△BCE为等边三角形，∴BE=CB，∵点F为△ACD的边AC的中点，∴DF⊥AC，易证得△CFD≌△ABC，∴DF=BC，∴DF=BE，而BF=DE，∴四边形BEDF是平行四边形．。
平移和旋转的区别与联系(数学图形初中知识点总结)
平移和旋转的区别与联系（数学图形初中知识点总结）平移和旋转是数学图形初中数学的基础知识，也是我们在生活中常见的几何变换方式。
本文将围绕平移和旋转的区别与联系进行阐述。
一、平移平移在数学上的定义是指图形在平面内按照某个方向和距离进行移动。
可以理解为保持图形形状和大小不变，只是在平面上改变它的位置。
平移有以下几个基本要素：1. 平移向量：平移向量指平移前后的两个点之间的矢量，它的长度和方向表示了平移的大小和方向。
2. 平移距离：平移距离指平移向量的长度，表示了平移的距离。
3. 平移方向：平移方向指平移向量的方向，表示了平移的方向。
平移的特点是不改变图形的大小和形状，只是改变了它的位置。
因为平移不改变图形的性质，所以它被广泛应用于数学、几何、物理等领域中。
二、旋转旋转在数学上的定义是指围绕固定点或固定直线进行的旋转。
可以理解为图形保持大小不变，只是在平面上进行旋转。
旋转有以下几个基本要素：1. 旋转中心：旋转的中心点。
2. 旋转角度：旋转的角度，用度（°）表示。
3. 旋转方向：旋转的方向，可以是顺时针或逆时针。
与平移不同，旋转可以改变图形的方向和形状，但保持了它的大小不变。
三、平移与旋转的区别从定义上来看，平移和旋转的基本区别在于它们的操作对象和方式不同。
平移是通过改变图形的位置来实现变换，而旋转是通过改变图形的方向和形状来实现变换。
具体而言，平移的基本要素是向量，而旋转的基本要素是旋转中心、旋转角度和旋转方向。
其次，平移和旋转的性质也不同。
平移不改变图形的大小和形状，只是变其位置，而旋转则可以改变图形的方向和形状，但保持了它的大小不变。
最后，平移和旋转的应用场景也不同。
平移应用于地图制作、机器人控制、图像处理等领域，旋转则应用于建筑设计、物理学、电子工程等领域。
四、平移与旋转的联系虽然平移和旋转有着不同的操作对象、方式和性质，但它们也有着联系。
这里列举以下几点：1. 都是几何变换：平移和旋转都是几何变换的基本形式，是描述图形如何在平面上变换的数学工具。
第三单元《平移和旋转》教材分析（精选12篇）
第三单元《平移和旋转》教材分析（精选12篇）第三单元《平移和旋转》教材分析篇1平移和旋转是依据《全日制义务教育数学课程标准（实验稿）》（以下简称《标准》）的要求，在小学数学里新增加的教学内容。
平移和旋转是物体或图形在空间变化位置的方式，认识平移和旋转对发展空间观念有重要的作用。
本套教材两次教学平移和旋转，第一次安排在三年级（下册），第二次安排在第二学段。
本单元是第一次教学，在知识与技能方面的教学目标是：认识生活里常见的平移和旋转现象；能在方格纸上把简单的图形沿水平方向或竖直方向平移。
全单元教材安排了两道例题、一次“试一试”、一次“想想做做”。
第一道例题教学日常生活里的平移和旋转现象。
列举的火车、电梯、缆车的运动和风扇、螺旋桨、钟摆的运动都是学生比较熟悉的，他们能根据画面想像出实际状态。
教材通过这些物体的运动，让学生初步体会生活里的平移和旋转现象很普遍，具有对物体平移、旋转的感性认识。
平移和旋转教材没有下定义，也没有用语言描述，只要求学生有初步的认识。
教学时可以让学生说说这些运动有什么相同点，通过观察、想像、比较等学习活动初步感受平移和旋转。
“想想做做”第1题要求学生凭借初步的感受判断九幅图中各个物体的运动是平移还是旋转。
第2题到生活中去寻找平移和旋转。
这两道题既帮助学生充实感知材料，又引导学生从数学的角度观察生活现象。
第3题要求学生用手势表示平移或旋转，让他们用动作表达、交流自己对这两种运动的认识，也是对众多现实的平移、旋转现象的初步概括。
可见，教材在安排平移、旋转的教学活动时，充分考虑了小学生的年龄特点和认知发展水平，有层次地逐渐递进。
第二道例题及“试一试”有两个教学任务：一是认识平面图形的平移，二是学会在方格纸上平移简单的图形。
例题的重点是观察图形向什么方向平移了几格，用定性描述和定量刻画相结合的方式描述图形的平移。
“试一试”则按要求平移图形，体会图形的运动。
例题和“试一试”是连贯的，“试一试”比例题更有挑战性。
数学旋转和平移知识点总结
数学旋转和平移知识点总结一、旋转的基本概念1.1 旋转的概念所谓旋转，就是通过一个固定的点，将平面上的点或者图形绕着这个点进行转动的过程。
这个固定的点被称为旋转中心，转动的角度叫做旋转角。
在数学中，我们通常用一个坐标系来描述旋转的过程，通过将点或者图形绕着坐标系的原点旋转，来描述旋转的过程。
1.2 旋转的表示在数学中，我们可以通过旋转矩阵、三角函数等方式来表示旋转变换。
旋转矩阵是用来描述旋转变换的一个重要工具，它能够将点或者图形绕着旋转中心进行旋转，并将旋转后的点或者图形表示出来。
三角函数能够帮助我们计算旋转后的点的坐标，从而描述旋转的过程。
1.3 旋转的性质旋转具有一些重要的性质，例如角度不变性、共线性不变性、长度比例不变性等。
这些性质在实际问题中有着重要的应用，能够帮助我们更好地理解旋转变换。
1.4 旋转的定理在数学中，我们有着一些关于旋转的重要定理，例如旋转定理、旋转对称定理等。
这些定理能够帮助我们解决与旋转相关的各种问题，是数学中的重要内容。
1.5 旋转的应用旋转在实际生活和工程中有着广泛的应用，例如在建筑设计、机械加工、航天航空等领域。
旋转能够帮助我们更好地描述和分析各种物体的形状和结构，具有重要的工程应用价值。
二、平移的基本概念2.1 平移的概念平移是将平面上的点或者图形沿着某一方向进行平行移动的过程。
在数学中，我们通常用向量或者坐标变换来描述平移的过程，通过平移向量或者平移矩阵来表示平移变换。
2.2 平移的表示在数学中，平移变换可以通过向量加法或者矩阵相加来表示，从而描述平移的过程。
平移变换可以将点或者图形沿着某一方向进行平行移动，并得到平移后的点或者图形的位置。
2.3 平移的性质平移具有一些重要的性质，例如平移不改变长度、方向和大小等。
这些性质在实际问题中有着重要的应用，能够帮助我们更好地理解平移变换。
2.4 平移的定理在数学中，我们有着一些关于平移的重要定理，例如平移定理、平移对称定理等。
九年级数学中考知识点归纳复习 第24讲 平移、对称、旋转与位似 视图和投影
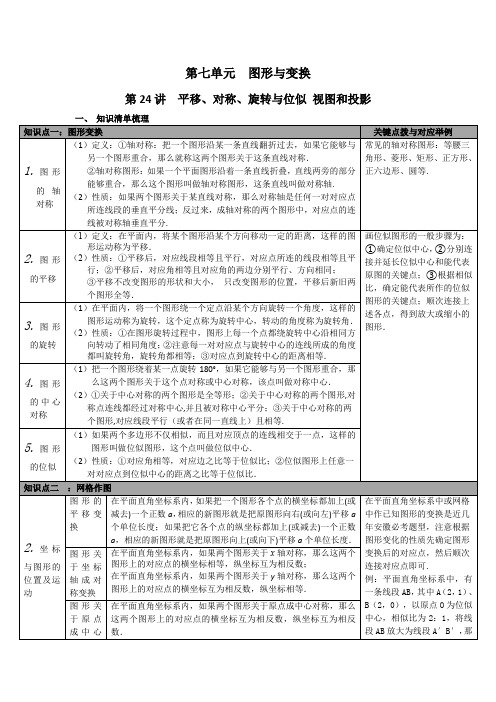
在平面直角坐标系内，如果两个图形的位似中心为原点，相似比为k，那么这两个位似图形对应点的坐标的比等于k或－k．
视图与投影
二、知识清单梳理
知识点一：三视图内容
关键点拨
1.三视图
主视图：从正面看到的图形.
俯视图：从上面看到的图形.
左视图：从左面看到的图形.
例：长方体的主视图与俯视图如图所示，则这个长方体的体积是36 .
4.图形的中心对称
（1）把一个图形绕着某一点旋转180°，如果它能够与另一个图形重合，那么这两个图形关于这个点对称或中心对称，该点叫做对称中心．
（2）①关于中心对称的两个图形是全等形；②关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分；③关于中心对称的两个图形,对应线段平行（或者在同一直线上）且相等.
2.三视图的对应关系
(1)长对正：主视图与俯视图的长相等，且相互对正；
(2)高平齐：主视图与左视图的高相等，且相互平齐；
(3)宽相等：俯视图与左视图的宽相等，且相互平行．
3.常见几何体的三视图常见几何体的三视图
正方体：正方体的三视图都是正方形.
圆柱：圆柱的三视图有两个是矩形，另一个是圆.
圆锥：圆锥的三视图中有两个是三角形，另一个是圆.
第七单元图形与变换
第24讲平移、对称、旋转与位似视图和投影
一、知识清单梳理
知ห้องสมุดไป่ตู้点一：图形变换
关键点拨与对应举例
1.图形的轴对称
（1）定义：①轴对称：把一个图形沿某一条直线翻折过去，如果它能够与另一个图形重合，那么就称这两个图形关于这条直线对称．
②轴对称图形：如果一个平面图形沿着一条直线折叠，直线两旁的部分能够重合，那么这个图形叫做轴对称图形，这条直线叫做对称轴.
数学平移与旋转
数学平移与旋转数学是一门精确而又抽象的学科，它以逻辑推理和符号运算为基础，探索着世界的奥秘。
在数学的世界里，平移和旋转是两个常见且重要的概念。
它们不仅在几何学中有着广泛的应用，还在其他学科中发挥着重要的作用。
本文将探讨数学中的平移与旋转，并探索它们的应用。
一、平移平移是指将一个图形沿着某个方向移动一定的距离，而不改变其形状和大小。
在平面几何中，平移是一种基本的变换方式，它可以通过向量来描述。
设有一个向量v=(a,b)，表示平移的方向和距离，那么对于平面上的任意点P(x,y)，它在平移后的位置P'(x',y')可以表示为P' = P + v。
这意味着P'的坐标是P的坐标加上向量v的坐标。
平移在几何学中有着广泛的应用。
例如，在地图上标注城市的位置时，我们常常需要将地图上的点进行平移，以便使得城市的位置更加清晰明了。
此外，在计算机图形学中，平移也是一种重要的变换方式。
通过平移，我们可以将图形在屏幕上进行移动，使其出现在我们希望的位置。
二、旋转旋转是指将一个图形绕着某个中心点旋转一定的角度，而不改变其形状和大小。
在几何学中，旋转是一种常见的变换方式，它可以通过矩阵运算来描述。
设有一个点P(x,y)，它在绕着原点逆时针旋转θ角度后的位置P'(x',y')可以表示为：x' = x*cosθ - y*sinθy' = x*sinθ + y*cosθ这里，θ表示旋转的角度。
旋转在几何学中有着广泛的应用。
例如，在建筑设计中，我们常常需要对建筑物进行旋转，以便使其朝向更加合适。
此外，在计算机图形学中，旋转也是一种重要的变换方式。
通过旋转，我们可以对图形进行倾斜、翻转等操作，使其呈现出我们想要的效果。
三、平移与旋转的应用平移和旋转不仅在几何学中有着广泛的应用，还在其他学科中发挥着重要的作用。
在物理学中，平移和旋转是描述物体运动的基本概念。
初中数学知识归纳平移旋转与对称变换的特点
初中数学知识归纳平移旋转与对称变换的特点初中数学知识归纳：平移、旋转与对称变换的特点在初中数学学习中，平移、旋转和对称变换是常见的几何变换形式。
它们在几何图形的变换和性质研究中起着重要的作用。
本文将对平移、旋转和对称变换的特点进行归纳总结。
一、平移的特点平移是指在平面上将一个图形沿着固定的方向和距离移动，使得图形的每一个点都按照相同的方式进行移动。
平移的特点可以归纳如下：1. 保持图形的大小和形状不变：平移只改变图形的位置，而不改变它的大小和形状。
2. 保持图形的内外角度不变：平移前后的图形内外角度是相等的。
3. 保持图形的对称性质：如果一个图形在平移前是对称的，那么它在平移后仍然是对称的。
二、旋转的特点旋转是指将一个图形绕着某一点旋转一定角度，使得图形相对于旋转中心发生变换。
旋转的特点可以归纳如下：1. 保持图形的大小和形状不变：旋转只改变图形的位置和方向，而不改变它的大小和形状。
2. 保持图形的对称性质：如果一个图形在旋转前是对称的，那么它在旋转后仍然是对称的。
3. 保持图形的内外角度不变：旋转前后的图形内外角度是相等的。
三、对称变换的特点对称变换是指将一个图形通过镜像等方式进行改变，使得图形的形状相对于某一条直线、某一点或某个轴对称。
对称变换的特点可以归纳如下：1. 保持图形的大小和形状不变：对称变换只改变图形的位置和方向，而不改变它的大小和形状。
2. 保持图形的内外角度不变：对称变换前后的图形内外角度是相等的。
3. 保持图形的对称性质：对称变换前后的图形仍然是对称的，对称轴或对称中心位置可能发生改变。
综上所述，平移、旋转和对称变换是初中数学中常见的几何变换形式。
它们在图形位置、形状和对称性质的研究中具有重要的作用。
通过对它们的特点进行归纳总结，我们可以更好地理解和应用这些数学概念。
当然，除了这几种几何变换外，还有其他形式的变换，如放缩变换、剪切变换等，它们在实际问题中也有广泛的应用。
通过学习和掌握这些变换的特点，我们可以更好地理解和分析几何图形的性质，并应用于解决实际问题。
2024年九年级数学中考专题：二次函数平移对称旋转 课件
(x,y +b)
(x,y -b)
口诀：上加下减，左减右加
坐
标
旋
转
变
换
一、坐标平移旋转对称
点(x,y) 绕着（m,n）旋转180° ，求旋转后的
点的坐标？
中点坐标公式：
A(1 , 1 ), B(2 , 2 ),
1 +2 1 +2
AB中点 (
,
)
2
2
旋转后的点的坐标( − ,2n-y)
中考专题：
二次函数平移旋转对称
目录
一
二
三
坐标平移旋
转对称
二次函数
表达式
例题讲解
四
方法归纳
五
学以致用
一、坐标平移
旋转对称
坐
标
平
移
变
换
一、坐标平移旋转对称
x轴 向左平移a个单位(x,y)
向右平移a个单位(x,y)
(x-a,y)
(x+a,y)
y轴 向上平移b个单位(x,y)
向下平移b个单位(x,y)
坐
标
对
称
变
换
一、坐标平移旋转对称
关于x轴对称 (x,y)
关于y轴对称 (x,y)
(x, -y)
(- x, y)
口诀:关于谁对称，谁不变，另一个互为相反数
关于原点O对称 (x,y部互为相反数
二 、二次函数
表达式
二、二次函数表达式
一般式：y = 2 + + ( ≠ 0, , 均为常数)
变式2
(3)抛物线2 与抛物线1 关于原点O对称，求抛物线 2 的表达
式
三、例题讲解
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
game456
[单选]总行程由()和空驶行程构成。A.重车公里B.载重行程C.平均车日行程D.有效行程 [单选]关于病原携带状态，下列不正确的是（）A.可以出现在显性感染后，也可出现在隐性感染后B.是许多传染病的重要传染源C.并非所有的传染病都有病原携带者D.并非所有的病原携带者都能排出病原体E.机体有免疫反应，但不足以清除病原体 [名词解释]免疫自稳(immunologichomeostasis) [单选]制订调查取证方案的主要目的是（）。A、明确调查程序B、确定调查人员、方法、手段和措施C、收集证据，查清案件事实D、以上都是 [单选]如果加入切换的影片入出点和入点没有可扩展区域，已经到头，那么（）A.系统会自动在出点和入点处根据切换的时间加入一段静止画面来过渡B.系统会自动在出点和入点处以入点为准根据切换的时间加入一段画面来过渡C.系统会自动在出点和入点处以出点为准根据切换的时间来加入一段 [单选]在我国，两个以上的人同日就同样的商标申请商标权的，商标权应授予（）的人。A.最先使用B.最先设计C.最先申请D.最先申请和使用 [单选]下列颅骨凹陷性骨折中，不宜采取手术治疗的是（）A.合并脑损伤或大面积骨折片陷入颅腔，引起颅内压增高者B.骨折片压迫重要部位引起神经功能障碍者C.非功能部位的大面积凹陷性骨折，凹陷深度超过1cm者D.位于大静脉窦处的凹陷性骨折，尚未引起颅内压增高者E.开放性颅骨骨折 [单选]女婴6个月，发热3天，T39～41℃，烦躁、拒食、吐奶伴腹泻，于12月20日入院。体检：T40℃，神清，烦躁不安，皮肤散在出血点，颈抵抗（－），布氏征（－），前囟突出。血WBC17．6×109／L，中性粒细胞87％，淋巴细胞13％。腰穿脑脊液检查：压力310mmH2O，WBC1360×109／L，多 [填空题]氨合成催化剂的毒物主要有（）、（）、（）。 [单选]风心病二尖瓣狭窄患者，随右心功能不全的加重，会减轻的临床表现是（）.A.肝大伴压痛B.心率增快C.急性肺水肿发作D.心尖区舒张期隆隆样杂音E.胃肠道淤血症状 [单选,A2型题,A1/A2型题]休克患者使用血管扩张药物，说法正确的是（）A.补充血容量同时即可使用B.血容量基本补足，但末梢血运未见好转时使用C.血压及中心静脉压完全恢复正常D.血容量恢复，毛细血管充盈后方可使用E.血容量完全补足时方可使用 [多选]行政补偿的内涵，随着行政管理实践的发展有一个演变、拓展的过程。理论上一般认为行政补偿包括的内涵为（）。A.追加补偿B.特别补偿C.征用补偿D.公务行为附随结果的补偿E.无因管理补偿 [单选]出生1分钟的新生儿，心率94次／分，无呼吸，四肢稍屈，无喉反射，口唇青紫全身苍白。Apgar评分为（）.A.5分B.4分C.3分D.2分E.1分 [问答题,简答题]冰机入口温度下降的原因及如何处理？ [单选]某进口设备采用运费在内价(CFR)形式，在该价格中包含的费用是()。A.出口国装运港至进口国目的港之间的运输保险费B.进口国国内运费、装卸费C.进口国国内运输保险费D.出口国装运港至进口国目的港之间的海运费 [填空题]苗圃中大苗的培育常需经过（）和（）过程。 [单选]当年播种，当年开花结果，然后死亡的植株是（）。A.一年生植物B.两年生植物C.多年生植物D.木本植物 [单选]以下有关混凝土的碳化说法错误的是（）。A.混凝土的碳化会减弱对钢筋的保护作用B.混凝土的碳化会增加混凝土的收缩C.混凝土的碳化会引起混凝土的微细裂缝D.混凝土的碳化有弊无利 [单选]煤的元素组成主要由（）六种组成。A、碳、氢、磷、氯、铅、锗B、氧、氮、氟、钒、硫、碳C、磷、硫、碳、氧、氢、氮 [多选]下列关于SC的叙述，哪一些是正确的()A．能抵抗蛋白酶对分泌型IgA的降解作用B．介导分泌型IgA的转运C．IgA缺陷者可合成SCD．由粘膜上皮细胞合成E．辅助分泌型IgA与特异性抗原结合 [填空题]历史数据采集可以对（）和（）两种格式进行存储。 [问答题,案例分析题]【病例摘要】王某，女，68岁，工人。于2011年9月15日就诊。患者于3年前出现颜面及双下肢水肿，时轻时重，伴血压升高，血压最高170/100mmHg，曾到多家医院检查尿常规：蛋白（++）～（+++），近一个月来水肿加重，而来就诊。现症见：颜面及双下肢水肿，乏力，纳 [单选]专一保险合同与重复保险合同的主要区别在于()。A.保险标的是否为特定物B.保险金额的确定方式C.保险人的数量D.保险人所负责任的次序 [单选,A1型题]下列不应选用青霉素G的情况是（）。A.梅毒B.伤寒C.鼠咬热D.气性坏疽E.钩端螺旋体病 [单选]良好的道德风气有助于遵纪守法，这是因为（）A.道德和法律在内容上相互重叠B.道德和法律之间有相互作用的系统C.有些法律规范就是道德习惯转化而来的D.依靠道德约束可以替代法律惩罚 [单选]二氧化碳放空阀的位号是（）。A.PV-0704B.PV-0705C.PV-0717BD.PV-0711B [判断题]出入境旅客携带物的检验检疫，以现场检疫为主，其他检疫手段为辅。（）A.正确B.错误 [单选]配备双向辅助导向轮，耙装机可在拐弯（）以内的巷道进行装载。A.30°B.60°C.90°D.120° [单选]电源频率增加一倍，变压器绕组感应电动势也（）。A、增加一倍B、不变C、减少一倍D、略有增加 [单选,A2型题,A1/A2型题]在《实验室认可管理办法》规定的认可原则中，未包含（）。A.自愿申请原则B.非歧视原则C.专家评审原则D.国家认可原则E.国家强制原则 [填空题]SAN粉料的堆积密度为（）。 [问答题,简答题]投资连结产品如何控制风险？ [单选]原油换热回收热量用Q1表示，冷却负荷用Q2表示，则热回收率η=（）×100％。A.Q1/Q2B.Q2/（Q1+Q2）C.Q1/（Q1+Q2）D.Q2/Q1 [单选]如果一份关于炮射的NOTAM的项中填入了“0800-1000”，则表示（）.A.炮射时间为项和项时间段内每天8时至10时以外的时间B.炮射时间为项和项时间段内每天8时至10时C.炮射时间为每天8时至10时，与项和无关 [单选]在25℃时，0.01mol∙kg糖水的渗透压为π1，0.01mol∙kg食盐水的渗透压为Π2，则两者的渗透压（）。A.无法比较B.Π1＞Π2C.Π1＝Π2D.Π1＜Π2 [填空题]国际单位制规定质量的单位是千克，符号为（）。 [单选]下列各项属于集体资产的是（）。A.农户承包经营的土地B.家庭生产资料C.农户家庭生活资料D.农户承包经营中除土地以外的其它生产资料 [单选]热痹的治法应为（）A.清利湿热，通络止痛B.清热通络，祛风除湿C.清热解毒，养阴止痛D.清热化湿，活血止痛E.清热化湿，凉血止痛 [单选]水力清淤时，应该注意（）。A、在用水季节施行B、按先下游后上游，分阶段进行C、引入含沙量较少的清水D、关闭一切闸门 [单选,A2型题,A1/A2型题]二尖瓣球囊成形术的适应证有（）A.心功能2～3级B.瓣口面积1.5～2.0cm2C.年龄65岁D.轻度二尖瓣狭窄E.近期有风湿活动