传输线分布参数、传输线方程及解
合集下载
第2章传输线理论

j z
1 2Z0
(U1
I1Z0 )e
j z
(2―2―14)
同样可以写成三角函数表达式
U (z)
U1 cos z
jZ0
sin z
I
(
z)
j
U1 Z0
sin
z
I1
cos
z
(2―2―15)
第2章 传输线理论
三、入射波和反射波的叠加 由式(2―2―5)和式(2―2―6)两式可以看出,传输线 上任意位置的复数电压和电流均有两部分组成,即有
U (z)
A1e j z
A2e j z
Ui(z) Ur(z)
I
(z)ຫໍສະໝຸດ 1 Z0A1e j z
1 Z0
A2e j z
Ii(z)
Ir(z)
(2―2―16)
第2章 传输线理论
根据复数值与瞬时值的关系,并假设A1、A2为实数, 则沿线电压的瞬时值为
u(z,t) Re[U (Z )e ji ] A1 cos(t z) A2 cos(t z)
式中v0为光速。由此可见,双线和同轴线上行波电
压和行波电流的相速度等于传输线周围介质中的光速,
它和频率无关,只决定周围介质特性参量ε,这种波称为
无色散波。
第2章 传输线理论
(三) 相波长λp
相波长λp是指同一个时刻传输线上电磁波的相位相 差2π的距离,即有
p
2
vp f
vpT
0 r
(2―3―5)
第2章 传输线理论
这种路的分析方法,又称为长线理论。事实上,“场” 的理论和“路”的理论既是紧密相关的,又是相互补充 的。有些传输线宜用“场”的理论去处理,而有些传输 线在满足一定条件下可以归结为“路”的问题来处理, 这样就可借用熟知的电路理论和现成方法,使问题的处 理大为简化。
第二章传输线理论

第一部分表示由信号源向负载方向传播的行波,称之为入射波。 第二部分表示由负载向信号源方向传播的行波,称之为反射波。
习题:
2-1
2-2
入射波和反射波沿线
2-4
的瞬时分布图如图
第二章 传输线理论
2-3 传输线的特性参量
传输线的特性参量主要包括:相位常数、特性阻抗、 相速和相波长、输入阻抗、反射系数、驻波比(行波系数) 和传输功率等。
jZ0tgβ
z
=
jZ0tg
2πz λ
=
沿线电压电流的瞬时分布和振幅分布,如上图 jXin
第二章 传输线理论
2. 终端开路
由于负载阻抗 ZL = ∞ 因而终端电流 I2 = 0
U (0) = A1 + A2 = Ui2 +Ur2 = 2Ui2 ⇒Ui2 = Ur2
第二章 传输线理论
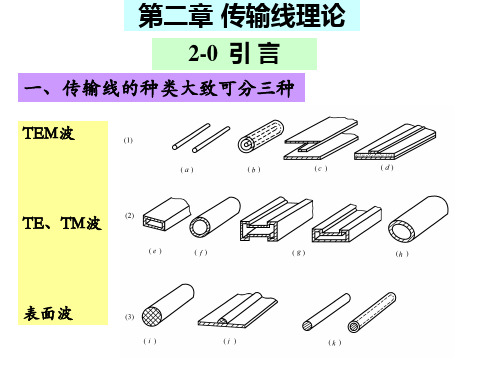
微波传输线大致可分三种类型
(1)TEM波 (2)TE、TM波 (3)表面波
第二章 传输线理论
二、分布参数及分布参数电路
传输线有长线和短线之分。所谓长线是指传输线的 几何长度与线上传输电磁波的波长比值(电长度)大于或 接近1,反之称为短线。
长线
分布参数电路
(Long Line)
考虑分布参数效应
u(z,t) = Re[U (z)e jωt ] = A1 cos(ω t + β z)+ A2 cos(ω t - β z) =ui (z,t ) + ur (z,t )
i(z,t) = Re[I (z)e jωt ]
=
A1 Z0
cos(ω
t+
β
z)-
A2 Z0
cos(ω
t-
第二章 传输线理论总结

当Z0为实数时,电压入射波与电流入射波的相位 相同;电压反射波与电流反射波相位相反。
三、 传输线的特性参数
1、特性阻抗Z0
将传输线上导行波的电压与电流之比定义为传输线的 特性阻抗, 用Z0来表示, 其倒数称为特性导纳, 用Y0来表
示。
由定义得 Z 0
R1 jL1 G1 jC1
可见特性阻抗Z0通常是个复数, 且与工作频率有关。 它由传输 线自身分布参数决定而与负载及信源无关, 故称为特性阻抗。
或者
二、传输线方程
2. 时谐均匀传输线方程
a. 时谐传输线方程
对于时谐电压和电流, 可用复振幅表示为 v(z, t)=Re[V(z)e jωt] i(z, t)=Re[I(z)e jωt] 将上式代入(2.1-1)式, 即得时谐传输线方程:
dV ( z ) ( R1 jL1 ) I ( z ) Z1 I ( z ) dz (2.1-3) dI ( z ) (G1 jC1 )V ( z ) Y1V ( z ) dz Z1 R1 jL1 传输线单位长度的串联阻抗 式中 传输线单位长度的并联导纳 Y1 G1 jC1
(2.1-11)
二、传输线方程
2. 时谐均匀传输线方程
c. 电压、电流的定解
V (d ) VL chd I L Z 0 shd VL I (d ) shd I L chd Z0
写成矩阵形式:
(2.1-12)
chd V (d ) I (d ) shd Z0
无耗线 j L1C1
低耗线
0, L1C1
(2.1-22)
R1 G1Z 0 c d 2Z 0 2
(2.1-23)
传输线方程及其解

它通常是个复数,且与工作频率 有关。特性阻抗由传输线自身分 布参数决定,而与负载及信号源 无关,故称为“特性阻抗”。
对于均匀无耗传输线 Z 0 L / C
当损耗很小时,即当 R L G C 时,特性阻抗为
Z 0 ( R jL) /(G jC ) L C (1 R / jL)1/ 2 (1 G / jC ) 1/ 2 L C (1 R / 2 jL)(1 G / 2 jC ) L C
第一章 均匀传输线理论之•均匀传输线方程及其解
第一章 均匀传输线理论
1.1节 1.2节 1.3节 1.4节 1.5节 1.6节 1.7节
微波工程基础
均匀传输线方程及其解 传输线的阻抗与状态参量 无耗传输线的状态分析 传输线的传输功率、效率与损耗 阻抗匹配 史密斯圆图及其应用 同轴线的特性阻抗
1
第一章 均匀传输线理论之•均匀传输线方程及其解
c d
微波工程基础
LC
16
第一章 均匀传输线理论之•均匀传输线方程及其解
(3) 相速与传输线波长(相波长) 相速(phase velocity) —传输线上行波等相位面沿传输 方向的传播速度。 其表达式为
vp
dz dt L C
不管是入射波还是反射波,它们都是行波。
z
行波在传播过程中其幅度按e 衰减,称 为衰减常数。而相位随z 连续滞后 z ,故称 为相位常数。
微波工程基础
14
第一章 均匀传输线理论之•均匀传输线方程及其解
6. 传输线的工作特性参数
(1)特性阻抗——传输线上行波的电压与电流的比值
R jL Z0 G jC
对于均匀无耗传输线 Z 0 L / C
当损耗很小时,即当 R L G C 时,特性阻抗为
Z 0 ( R jL) /(G jC ) L C (1 R / jL)1/ 2 (1 G / jC ) 1/ 2 L C (1 R / 2 jL)(1 G / 2 jC ) L C
第一章 均匀传输线理论之•均匀传输线方程及其解
第一章 均匀传输线理论
1.1节 1.2节 1.3节 1.4节 1.5节 1.6节 1.7节
微波工程基础
均匀传输线方程及其解 传输线的阻抗与状态参量 无耗传输线的状态分析 传输线的传输功率、效率与损耗 阻抗匹配 史密斯圆图及其应用 同轴线的特性阻抗
1
第一章 均匀传输线理论之•均匀传输线方程及其解
c d
微波工程基础
LC
16
第一章 均匀传输线理论之•均匀传输线方程及其解
(3) 相速与传输线波长(相波长) 相速(phase velocity) —传输线上行波等相位面沿传输 方向的传播速度。 其表达式为
vp
dz dt L C
不管是入射波还是反射波,它们都是行波。
z
行波在传播过程中其幅度按e 衰减,称 为衰减常数。而相位随z 连续滞后 z ,故称 为相位常数。
微波工程基础
14
第一章 均匀传输线理论之•均匀传输线方程及其解
6. 传输线的工作特性参数
(1)特性阻抗——传输线上行波的电压与电流的比值
R jL Z0 G jC
第五章 传输线理论

t2 0 t2 0
2019/2/4
由此可见:不管传输线的结构是什么,TEM波在 横截面内的场结构问题就是解二维拉普拉斯方 程,与静态场的解完全相同.
14
2Ht Et 2 ez ez jez H t 2 z z H t 2 ez ez H t 0 z 见书265 根据: A B C ( A C) B ( A B)C 面B2.2式 2 2 Ht Ht 2 (e z )e z (e z e z ) H t 0 2 2 z z 2 2 2 Ht 2 令 Ht 0 2 z 2 同理可得: Et 2 Et 0 2 2019/2/4 15 z
2019/2/4
Zl
z
z o
分布参数
3
集中(总)参数
一、分布参数: 电流流过传输线将使导体发热 电流流过导体其周围将有磁场
分布电阻。 分布电感。
导体间绝缘不完善而存在漏电流 分布电导。 导体间有电压,其间便有电场 分布电容。 二、均匀传输线的分布参数及其等效电路:
1、均匀传输线:
Zg
Eg ~
12
5.1.3 用场的概念分析传输线:
定性分析
ex e y ez t ez x y z z
2019/2/4
一、无耗、均匀、各向同性媒质中TEM波 时谐电磁场复数形式满足的麦氏方程组: Ht jEt H J j D Et jHt E j B Ht 0 B 0 D Et 0
(3)、已知电源电动势 Eg 和内阻 Zg 及负载阻抗 Zl 时的解: 将
2019/2/4
由此可见:不管传输线的结构是什么,TEM波在 横截面内的场结构问题就是解二维拉普拉斯方 程,与静态场的解完全相同.
14
2Ht Et 2 ez ez jez H t 2 z z H t 2 ez ez H t 0 z 见书265 根据: A B C ( A C) B ( A B)C 面B2.2式 2 2 Ht Ht 2 (e z )e z (e z e z ) H t 0 2 2 z z 2 2 2 Ht 2 令 Ht 0 2 z 2 同理可得: Et 2 Et 0 2 2019/2/4 15 z
2019/2/4
Zl
z
z o
分布参数
3
集中(总)参数
一、分布参数: 电流流过传输线将使导体发热 电流流过导体其周围将有磁场
分布电阻。 分布电感。
导体间绝缘不完善而存在漏电流 分布电导。 导体间有电压,其间便有电场 分布电容。 二、均匀传输线的分布参数及其等效电路:
1、均匀传输线:
Zg
Eg ~
12
5.1.3 用场的概念分析传输线:
定性分析
ex e y ez t ez x y z z
2019/2/4
一、无耗、均匀、各向同性媒质中TEM波 时谐电磁场复数形式满足的麦氏方程组: Ht jEt H J j D Et jHt E j B Ht 0 B 0 D Et 0
(3)、已知电源电动势 Eg 和内阻 Zg 及负载阻抗 Zl 时的解: 将
传输线方程
egz
V + = A1e-
gz
表示向+z方向传播的波,即自源到 1 + I = A e 1 负载方向的入射波,用V+或I +表示. Z0
V - = A2 e g z
gz
表示向-z方向传播的波,即自负载 到源方向的反射波,用V-或I -表示。 I - = - 1 A e g z 2 Z0 电压电流解为
j wt j y v ( z ) j wt 轾 v( z , t ) = V0 cos(wt + y v ( z )) = Re 轾 V e e = Re V ( z ) e 0 犏 犏 臌 臌 j wt j y I ( z ) j wt 轾 i ( z , t ) = I 0 cos(wt + y I ( z )) = Re 轾 I e e = Re I ( z ) e 0 犏 犏 臌 臌
③TEM波传输线的长度为10cm,当信号频率为 10GHz ( λ
=3cm)时。
l /λ ①短线(0.00167);②长线(3.33);③长线(3.33)。
2. 传输线的分布参数 (Distributed parameter)
低频传输线在低频电路中只起连接线的作用,因频率低, 其本身分布参数所引起的效应可以忽略不计,所以在低频电路 中只考虑时间因子而忽略空间效应,因而把传输线当作集总参 数电路来处理是允许的。 而对于微波传输线,因为频率很高,此时分布参数效应不 能再忽视了,传输线不能仅当作连接线,它将形成分布参数电 路,参与整个电路的工作。因而传输线在电路中所引起的效应 必须用传输线理论来研究。 亦即,在微波传输线上处处存在分布电阻、分布电感,线 间处处存在分布电容和漏电电导。用R1、L1、G1、C1分别表 示传输线单位长度的电阻、电感、电导和电容,它们的数值 与传输线截面尺寸、导体材料、填充介质以及工作频率有关。
V + = A1e-
gz
表示向+z方向传播的波,即自源到 1 + I = A e 1 负载方向的入射波,用V+或I +表示. Z0
V - = A2 e g z
gz
表示向-z方向传播的波,即自负载 到源方向的反射波,用V-或I -表示。 I - = - 1 A e g z 2 Z0 电压电流解为
j wt j y v ( z ) j wt 轾 v( z , t ) = V0 cos(wt + y v ( z )) = Re 轾 V e e = Re V ( z ) e 0 犏 犏 臌 臌 j wt j y I ( z ) j wt 轾 i ( z , t ) = I 0 cos(wt + y I ( z )) = Re 轾 I e e = Re I ( z ) e 0 犏 犏 臌 臌
③TEM波传输线的长度为10cm,当信号频率为 10GHz ( λ
=3cm)时。
l /λ ①短线(0.00167);②长线(3.33);③长线(3.33)。
2. 传输线的分布参数 (Distributed parameter)
低频传输线在低频电路中只起连接线的作用,因频率低, 其本身分布参数所引起的效应可以忽略不计,所以在低频电路 中只考虑时间因子而忽略空间效应,因而把传输线当作集总参 数电路来处理是允许的。 而对于微波传输线,因为频率很高,此时分布参数效应不 能再忽视了,传输线不能仅当作连接线,它将形成分布参数电 路,参与整个电路的工作。因而传输线在电路中所引起的效应 必须用传输线理论来研究。 亦即,在微波传输线上处处存在分布电阻、分布电感,线 间处处存在分布电容和漏电电导。用R1、L1、G1、C1分别表 示传输线单位长度的电阻、电感、电导和电容,它们的数值 与传输线截面尺寸、导体材料、填充介质以及工作频率有关。
电磁场与电磁波课件7.4传输线理论
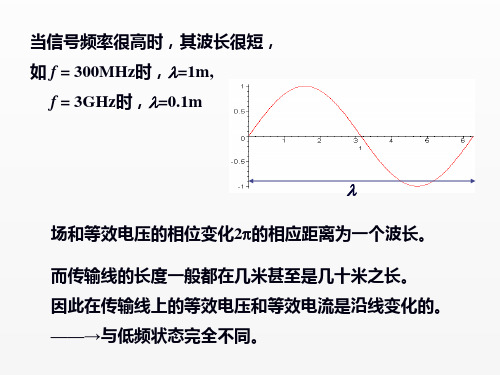
当信号频率很高时,其波长很短,
如 f = 300MHz时,l=1m, f = 3GHz时,l=0.1m
l
场和等效电压的相位变化2p的相应距离为一个波长。 而传输线的长度一般都在几米甚至是几十米之长。 因此在传输线上的等效电压和等效电流是沿线变化的。 ——→与低频状态完全不同。
传输线理论 长线理论
传输线是以TEM导模方式传 输电磁波能量。
W
ln d
d
2.传输线方程
传输线方程是研究传输线上电压、电流的变化规律及 其相互关系的方程。
1)一般传输方程
传输线上的电压和电流是 距离和时间的函数, 则线元 Dz<<l上电压和电流的差为
v(z z,t) v(z,t) v(z,t) z z
i(z z,t) i(z,t) i(z,t) z z
Dz传输线上的等效电路
ez , ez 分别表示向+z和-z方向传播的波。
用双曲函数来表示
V (d ) V0chd Z 0 I 0 shd
I (d)
V0 Z0
shd
I 0chd
写成矩阵形式:
V (d)
I
(d )
chd
shd
Z0
Z 0 shd chd
V0
I
0
③信号源和负载条件解
第二章 传输线理论
已知
v(z Dz,t) v(z,t) v(z,t) Dz z
应用基尔霍夫定律:
i(z Dz,t) i(z,t) i(z,t) Dz z
第二章 传输线理论
L上: v L di ,C上: i C dv
dt
dt
v(z,t) z
z i(z,t) z
z
Rl z i(z,t) Gl z v(z,t)
如 f = 300MHz时,l=1m, f = 3GHz时,l=0.1m
l
场和等效电压的相位变化2p的相应距离为一个波长。 而传输线的长度一般都在几米甚至是几十米之长。 因此在传输线上的等效电压和等效电流是沿线变化的。 ——→与低频状态完全不同。
传输线理论 长线理论
传输线是以TEM导模方式传 输电磁波能量。
W
ln d
d
2.传输线方程
传输线方程是研究传输线上电压、电流的变化规律及 其相互关系的方程。
1)一般传输方程
传输线上的电压和电流是 距离和时间的函数, 则线元 Dz<<l上电压和电流的差为
v(z z,t) v(z,t) v(z,t) z z
i(z z,t) i(z,t) i(z,t) z z
Dz传输线上的等效电路
ez , ez 分别表示向+z和-z方向传播的波。
用双曲函数来表示
V (d ) V0chd Z 0 I 0 shd
I (d)
V0 Z0
shd
I 0chd
写成矩阵形式:
V (d)
I
(d )
chd
shd
Z0
Z 0 shd chd
V0
I
0
③信号源和负载条件解
第二章 传输线理论
已知
v(z Dz,t) v(z,t) v(z,t) Dz z
应用基尔霍夫定律:
i(z Dz,t) i(z,t) i(z,t) Dz z
第二章 传输线理论
L上: v L di ,C上: i C dv
dt
dt
v(z,t) z
z i(z,t) z
z
Rl z i(z,t) Gl z v(z,t)
第3章传输线理论

U 0 I0 Zc U I0 Zc , I0 0 , 2Z c 2Z c
则分别是负载处的入射波电流和反射波电流。
3.1.3传输线的工作特性参数和工作状态参数 一.传输线的工作特性参数
(1)特性阻抗 Z c 传输线的特性阻抗是传输线上任意点处的入射波电压 与入射波电流之比,或反射波电压与反射波电流之比的负 值,即
3.1.2 传输线方程及其时谐稳态解
根据传输线等效电路和基尔霍夫定律,即可 导出传输线上电压、电流所满足的方程。
i i+di u+du R0dz L0dz G0dz C0dz
负载
~
u
z
i u (u du) R0 dz i L0 dz t
z+dz
z
传输线及其等效电路
u i (i di) G0 dz u C0 dz t
0 均匀平行双导线的任意横截面
x
二、传输线的分布参数
以平行双导线为例: 双导线间存在电压且均有电荷分布,因此双导线组成 了一个电容。 双导线在无限远处闭合形成回路,该回路电流产生的 磁力线与该回路自身相交链,必有自感。 双导线若非理想导体,则必表现出电阻性质。 双导线周围的媒质若非理想媒质,则双导线间存在漏 电导。 以上分析说明:平行双导线自身处处体现出电容、电 感、电阻、电导的效应,也就是说这些电路参数(电容、 电感、电阻、电导)是均匀分布在平行双导线自身上的, 因此称为分布参数。其他传输线也都具有这种分布参数。 一般给出单位长度的传输线上的分布参数,即:电容 (F/m)、电感(H/m)、电阻(Ω /m)、电导(S/m)。
是传输线上电压波和电流波的传播常数,它一般为复数,
其中 为衰减常数, 为相移常数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计及在微波波段中, 1/是a一阶小量,对于 1 /及a 2以上 量完全可以忽略。则
I2E0r0
而 R E0l l
I 2r0
.
一、低频传输线和微波传输线
和直流的同样情况比较
5.08107
0.066/ f , 若f=1010Hz, 0.66106
3.8310
1
R 2 2103 3.8310 2.07 / m
也即直径是d=6.06 m。这种情况,已不能称为微波 传输线,而应称之为微波传输“柱”比较合适,其 粗度超过人民大会堂的主柱。2米高的实心微波传输 铜柱约514吨重(铜比重是8.9T/m3),按我国古典名 著《西游记》记载:孙悟空所得的金箍棒是东海龙 王水晶宫的定海神针,重10万8千斤,即54吨。而 这里的微波柱是514吨,约9根金箍棒的重量,估计 孙悟空是无法拿动的!
集肤效应带来的第二个直接效果是:柱内部几乎 无物,并无能量传输。 .
一、低频传输线和微波传输线
看来,微波传输线必须走自己的路。每一种事物都 有自己独特的本质,硬把不适合的情况强加给它, 必然会出现荒唐的结论。刚才讨论的例子正是因为 我们硬设想把微波“关在”铜导线内传播,事实上 也不可能。“满圆春色关不住,一枝红杏出墙来” 微波功率应该(绝大部分)在导线之外的空间传输, 这便是结论。
低频电路有很多课程,唯独没有传输线课程。理由 很简单:只有两根线有什么理论可言?这里却要深 入研究这个问题。
1、低频传输线 在低频中,我们中要研究一条线(因为另一条线是作 为回路出现的)。电流几乎均匀地分布在导线内。电 流和电荷可等效地集中在轴线上,见图(2-1)。 由分析可知,Poynting矢量集中在导体内部传播,外 部极少。事实上,对于低频,我们只须用I,V和
J
传
H
输
D
S
空 间
E
d
J
图 2-4 双导. 线
二、传输线方程
传输线方程也称电报方程。在沟通大西洋电缆 (海底电缆)时,开尔芬首先发现了长线效应:电报 信号的反射、传输都与低频有很大的不同。经过仔 细研究,才知道当线长与波长可比拟或超过波长时, 我们必须计及其波动性,这时传输线也称长线。
为了研究无限长传输线的支配方程,定义电压u 和电流i均是距离和时间的函数,即
k2H 0
.
d 2U dz 2
2U
0
d 2I dz 2
2I
dz
dI (G jC)U YU
dz
.
(2-5)
三、无耗传输线方程
无耗传输线是我们所研究的最重要条件之一,可表
示为:R=0,G=0这时方程写出
dU j LI dz
dI j C U dz
二次求导的结果
dE j H dz
dH j E 2H dz 2
计及 JE
I JS Er02
同时考虑Ohm定律 V Edl
R0V IE E d rl02lr025.81071(2103)2
1.37103/m
代入铜材料 5.8107 .
一、低频传输线和微波传输线
2. 微波传输线 当频率升高出现的第一个问题是导体的集肤效应
(Skin Effect)。导体的电流、电荷和场都集中在导体 表面。
第2章
2.1 传输线方程
Transmission Line Equation
上面讨论了微波基本概念,并且指出了工程中所 关心的微波传输问题。微波传输的最明显特征是别 树一帜的微波传输线,例如,双导线、同轴线、带 线和微带等等。我们很容易提出一个问题:微波传 输线为什么不采用50Hz电明线呢?
.
一、低频传输线和微波传输线
[ 例 2 ] 研 究 f =10GHz=1010Hz、 l =3cm、
r0=2mm导线的线耗R
这种情况下, JJ0ea(r0r)
其中, J0是r的表r0 面电流密度,a是衰线常数。对于良
导体,由电磁场理论可知
1
2
— —称之为集肤深度。.
一、低频传输线和微波传输线
I Jds J0ea(r0r)ds E0 ea(r0r)rdrd I2E0ear0 0r0reardr2E0ear0a1 0r0rdear 2E0ear0 a1rear 0r0eardr2E0a1r0 a12 a12ear0
式(2-3)是均匀传输线方程或. 电报方程。
(2-2) (2-3)
二、传输线方程
如果我们着重研究时谐(正弦或余弦)的变化情况,有
u(z,t)Re U(z)ejt
i(z,t)Re
I(z)ejt
(2-4)
(2-4)式中,U(z)、I(z)只与z有关,表示在传输线z处
的电压或电流的有效复值。
du (R jL)I ZI
.
一、低频传输线和微波传输线
Ohm定律解决即可,无须用电磁理论。不论导线怎
样弯曲,能流都在导体内部和表面附近。(这是因为
场的平方反比定律)。
J ,
+£
E 2=
J S
V
Et
E1 H
-
图 2-1 .低频传输线
一、低频传输线和微波传输线
[例1]计算半径r0=2mm=2×10-3m的铜导线单 位长度的直流线耗R0
从直流到1010Hz,损耗要增加1500倍。
R r0 1.515103 R0 2
.
一、低频传输线和微波传输线
r0
r0
图2-2 直线电流均匀分布 图2-3 微波集肤效应
损耗是传输线的重要指标,如果要将 r0 ,r 使损耗与 直流保持相同,易算出
r 1 3.03 m
2R0.
一、低频传输线和微波传输线
u i
u((z2,-t1) ) i( z , t )
.
二、传输线方程
i(z) u(z)
z
i(z+ z)
u(z+ z)
z+ z
Lz
Rz
Cz
Gz
图 2-5 长线效应
.
二、传输线方程
利用基尔霍夫定律,有
u z
Ri
L
i t
i z
Gu
C
u t
当典型Δz→0时,有
u(zz,t)u(z,t)Ri(z,t)Li(zt,t)z i(zz,t)i(z,t)Gu(z,t)Cu(zt,t)z
最简单而实用的微波传输线是双导线,它们与低 频传输线有着本质的不同:功率是通过双导线之间 的空间传输的。
.
一、低频传输线和微波传输线
这时,使我们更加明确了Guide Line的含义,导线 只是起到引导的作用,而实际上传输的是周围空间 (Space)(但是,没有Guide Line又不行)。D和d是 特征尺寸,对于传输线性质十分重要。
I2E0r0
而 R E0l l
I 2r0
.
一、低频传输线和微波传输线
和直流的同样情况比较
5.08107
0.066/ f , 若f=1010Hz, 0.66106
3.8310
1
R 2 2103 3.8310 2.07 / m
也即直径是d=6.06 m。这种情况,已不能称为微波 传输线,而应称之为微波传输“柱”比较合适,其 粗度超过人民大会堂的主柱。2米高的实心微波传输 铜柱约514吨重(铜比重是8.9T/m3),按我国古典名 著《西游记》记载:孙悟空所得的金箍棒是东海龙 王水晶宫的定海神针,重10万8千斤,即54吨。而 这里的微波柱是514吨,约9根金箍棒的重量,估计 孙悟空是无法拿动的!
集肤效应带来的第二个直接效果是:柱内部几乎 无物,并无能量传输。 .
一、低频传输线和微波传输线
看来,微波传输线必须走自己的路。每一种事物都 有自己独特的本质,硬把不适合的情况强加给它, 必然会出现荒唐的结论。刚才讨论的例子正是因为 我们硬设想把微波“关在”铜导线内传播,事实上 也不可能。“满圆春色关不住,一枝红杏出墙来” 微波功率应该(绝大部分)在导线之外的空间传输, 这便是结论。
低频电路有很多课程,唯独没有传输线课程。理由 很简单:只有两根线有什么理论可言?这里却要深 入研究这个问题。
1、低频传输线 在低频中,我们中要研究一条线(因为另一条线是作 为回路出现的)。电流几乎均匀地分布在导线内。电 流和电荷可等效地集中在轴线上,见图(2-1)。 由分析可知,Poynting矢量集中在导体内部传播,外 部极少。事实上,对于低频,我们只须用I,V和
J
传
H
输
D
S
空 间
E
d
J
图 2-4 双导. 线
二、传输线方程
传输线方程也称电报方程。在沟通大西洋电缆 (海底电缆)时,开尔芬首先发现了长线效应:电报 信号的反射、传输都与低频有很大的不同。经过仔 细研究,才知道当线长与波长可比拟或超过波长时, 我们必须计及其波动性,这时传输线也称长线。
为了研究无限长传输线的支配方程,定义电压u 和电流i均是距离和时间的函数,即
k2H 0
.
d 2U dz 2
2U
0
d 2I dz 2
2I
dz
dI (G jC)U YU
dz
.
(2-5)
三、无耗传输线方程
无耗传输线是我们所研究的最重要条件之一,可表
示为:R=0,G=0这时方程写出
dU j LI dz
dI j C U dz
二次求导的结果
dE j H dz
dH j E 2H dz 2
计及 JE
I JS Er02
同时考虑Ohm定律 V Edl
R0V IE E d rl02lr025.81071(2103)2
1.37103/m
代入铜材料 5.8107 .
一、低频传输线和微波传输线
2. 微波传输线 当频率升高出现的第一个问题是导体的集肤效应
(Skin Effect)。导体的电流、电荷和场都集中在导体 表面。
第2章
2.1 传输线方程
Transmission Line Equation
上面讨论了微波基本概念,并且指出了工程中所 关心的微波传输问题。微波传输的最明显特征是别 树一帜的微波传输线,例如,双导线、同轴线、带 线和微带等等。我们很容易提出一个问题:微波传 输线为什么不采用50Hz电明线呢?
.
一、低频传输线和微波传输线
[ 例 2 ] 研 究 f =10GHz=1010Hz、 l =3cm、
r0=2mm导线的线耗R
这种情况下, JJ0ea(r0r)
其中, J0是r的表r0 面电流密度,a是衰线常数。对于良
导体,由电磁场理论可知
1
2
— —称之为集肤深度。.
一、低频传输线和微波传输线
I Jds J0ea(r0r)ds E0 ea(r0r)rdrd I2E0ear0 0r0reardr2E0ear0a1 0r0rdear 2E0ear0 a1rear 0r0eardr2E0a1r0 a12 a12ear0
式(2-3)是均匀传输线方程或. 电报方程。
(2-2) (2-3)
二、传输线方程
如果我们着重研究时谐(正弦或余弦)的变化情况,有
u(z,t)Re U(z)ejt
i(z,t)Re
I(z)ejt
(2-4)
(2-4)式中,U(z)、I(z)只与z有关,表示在传输线z处
的电压或电流的有效复值。
du (R jL)I ZI
.
一、低频传输线和微波传输线
Ohm定律解决即可,无须用电磁理论。不论导线怎
样弯曲,能流都在导体内部和表面附近。(这是因为
场的平方反比定律)。
J ,
+£
E 2=
J S
V
Et
E1 H
-
图 2-1 .低频传输线
一、低频传输线和微波传输线
[例1]计算半径r0=2mm=2×10-3m的铜导线单 位长度的直流线耗R0
从直流到1010Hz,损耗要增加1500倍。
R r0 1.515103 R0 2
.
一、低频传输线和微波传输线
r0
r0
图2-2 直线电流均匀分布 图2-3 微波集肤效应
损耗是传输线的重要指标,如果要将 r0 ,r 使损耗与 直流保持相同,易算出
r 1 3.03 m
2R0.
一、低频传输线和微波传输线
u i
u((z2,-t1) ) i( z , t )
.
二、传输线方程
i(z) u(z)
z
i(z+ z)
u(z+ z)
z+ z
Lz
Rz
Cz
Gz
图 2-5 长线效应
.
二、传输线方程
利用基尔霍夫定律,有
u z
Ri
L
i t
i z
Gu
C
u t
当典型Δz→0时,有
u(zz,t)u(z,t)Ri(z,t)Li(zt,t)z i(zz,t)i(z,t)Gu(z,t)Cu(zt,t)z
最简单而实用的微波传输线是双导线,它们与低 频传输线有着本质的不同:功率是通过双导线之间 的空间传输的。
.
一、低频传输线和微波传输线
这时,使我们更加明确了Guide Line的含义,导线 只是起到引导的作用,而实际上传输的是周围空间 (Space)(但是,没有Guide Line又不行)。D和d是 特征尺寸,对于传输线性质十分重要。
