SPSS主成分分析操作步骤,详细的很啊^_^==
主成分分析spss操作步骤
5.主成分表达式：将SPSS 软件中表“Component Matrix”中的第i列向量除以第 i个特征根的开根后就得到第i个主成分的变量系数向量（在“transform→compute”中进行计算），由此写出主成分表达式。
1.原始指标数据的标准化采集p维随机向量n个样品,，构造样本阵,对样本阵元进行标准化变换,得标准化阵Z。（一般由计算机自动完成）。
2.在“Analyze”菜单中选择“Data Reduction…factor”，把变量选入“variables”栏。
3.“Extraction”按钮：选择主成分法为系数矩阵计算方法，确定以相关系数阵（Correlation Matrix）为分析对象。
6.主成分命名，用 SPSS 软件中表“Component Matrix”中的第பைடு நூலகம்列中系数绝对值大的对应变量对命名。
7.主成分与综合主成分（评价）值。综合主成分（评价）公式：F 综合 = λ1F1+λ2F2+K+λkFkpΣi = 1λi其中 λipi = 1Σλi在SPSS 软件中表“ Total Variance Explained”下“ Initial Eig rnvalues（主成分方差）”栏的“% of Variance（方差率）”中。
如何利用SPSS进行主成分分析
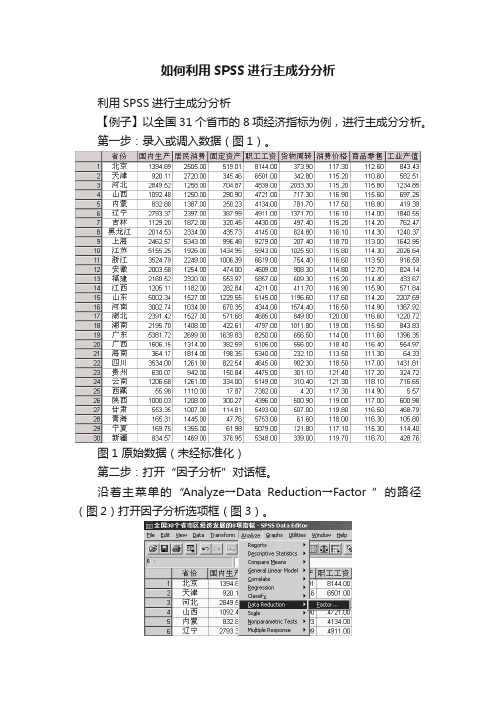
如何利用SPSS进行主成分分析利用SPSS进行主成分分析【例子】以全国31个省市的8项经济指标为例，进行主成分分析。
第一步：录入或调入数据（图1）。
图1 原始数据（未经标准化）第二步：打开“因子分析”对话框。
沿着主菜单的“Analyze→Data Reduction→Factor ”的路径（图2）打开因子分析选项框（图3）。
图2 打开因子分析对话框的路径图3 因子分析选项框第三步：选项设置。
首先，在源变量框中选中需要进行分析的变量，点击右边的箭头符号，将需要的变量调入变量（Variables）栏中（图3）。
在本例中，全部8个变量都要用上，故全部调入（图4）。
因无特殊需要，故不必理会“Value ”栏。
下面逐项设置。
图4 将变量移到变量栏以后⒈设置Descriptives选项。
单击Descriptives按钮（图4），弹出Descriptives对话框（图5）。
图5 描述选项框在Statistics 栏中选中Univariate descriptives 复选项，则输出结果中将会给出原始数据的抽样均值、方差和样本数目（这一栏结果可供检验参考）；选中Initial solution 复选项，则会给出主成分载荷的公因子方差（这一栏数据分析时有用）。
在Correlation Matrix 栏中，选中Coefficients 复选项，则会给出原始变量的相关系数矩阵（分析时可参考）；选中Determinant 复选项，则会给出相关系数矩阵的行列式，如果希望在Excel 中对某些计算过程进行了解，可选此项，否则用途不大。
其它复选项一般不用，但在特殊情况下可以用到（本例不选）。
设置完成以后，单击Continue 按钮完成设置（图5）。
⒉ 设置Extraction 选项。
打开Extraction 对话框（图6）。
因子提取方法主要有7种，在Method 栏中可以看到，系统默认的提取方法是主成分（∏ρινχιπαλ χομπονεντσ），因此对此栏不作变动，就是认可了主成分分析方法。
如何正确应用SPSS软件做主成分分析
精品文档供您编辑修改使用专业品质权威编制人：______________审核人：______________审批人：______________编制单位：____________编制时间：____________序言下载提示：该文档是本团队精心编制而成，希望大家下载或复制使用后，能够解决实际问题。
文档全文可编辑，以便您下载后可定制修改，请根据实际需要进行调整和使用，谢谢!同时，本团队为大家提供各种类型的经典资料，如办公资料、职场资料、生活资料、学习资料、课堂资料、阅读资料、知识资料、党建资料、教育资料、其他资料等等，想学习、参考、使用不同格式和写法的资料，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!And, this store provides various types of classic materials for everyone, such as office materials, workplace materials, lifestylematerials, learning materials, classroom materials, reading materials, knowledge materials, party building materials, educational materials, other materials, etc. If you want to learn about different data formats and writing methods, please pay attention!如何正确应用SPSS软件做主成分分析一、概述主成分分析（Principal Component Analysis, PCA）是一种常用的多变量分析方法，通过将原始变量进行线性组合，得到少数几个新的主成分，用于降低原始变量的维度，并揭示变量之间的结构干系。
用SPSS进行详细的主成分分析步骤
用SPSS进行详细的主成分分析步骤主成分分析是一种常用的多元统计分析方法，用于降低数据的维度从而简化数据集。
SPSS（统计软件）提供了强大的主成分分析功能，以下是详细的主成分分析步骤。
步骤1：打开数据集首先，打开SPSS软件并加载需要进行主成分分析的数据集。
选择“文件”>“打开”>“数据”，浏览并选择要进行主成分分析的数据文件，然后点击“打开”。
步骤2：选择变量在SPSS中，主成分分析可以应用于数值型变量。
在“数据视图”中，选择需要进行主成分分析的变量。
你可以按住Ctrl键选择多个变量，或者按住Shift键选择连续的变量。
步骤3：进行主成分分析在SPSS的主菜单中，选择“分析”>“降维”>“因子”（或者“主成分”）。
这将打开主成分分析的对话框。
步骤4：选择成分数量在主成分分析对话框中，选择“主成分”选项卡。
在该选项卡，你需要指定要提取的主成分数量。
通常，一个好的经验是提取具有特征值大于1的主成分。
步骤5：选择成分提取方法在同一选项卡，你可以选择主成分的计算方法。
最常用的方法是“主成分”和“因子”，但在大部分情况下，“主成分”方法效果更好。
步骤6：选择旋转方法在主成分分析对话框的“旋转”选项卡中，你可以选择使用特定的旋转方法。
主成分的旋转可以帮助解释和可解释性。
最常用的旋转方法是“变量最大化”（Varimax）或“正交旋转”。
步骤7：输出选项在主成分分析对话框的“输出”选项卡中，你可以选择需要输出的结果。
例如，你可以选择输出成分系数矩阵、方差解释和旋转后的成分矩阵等。
步骤8：点击运行完成以上设置后，点击“确定”按钮来运行主成分分析。
SPSS将执行主成分分析，并在输出窗口中显示结果。
步骤9：解释结果通过分析输出结果，你可以解释每个主成分的方差解释比例、因子载荷和特征值等。
方差解释比例表示每个主成分对总方差的贡献程度。
因子载荷表示每个变量对每个主成分的贡献程度。
步骤10：绘制因子图在SPSS中，你还可以绘制因子图来可视化主成分分析的结果。
SPSS主成分分析操作步骤-详细的很啊^-^==教案资料
SPSS主成分分析操作步骤，详细的很啊^_^SPSS在调用Factor Analyze过程进行分析时，SPSS会自动对原始数据进行标准化处理，所以在得到计算结果后指的变量都是指经过标准化处理后的变量，但SPSS不会直接给出标准化后的数据，如需要得到标准化数据，则需调用Descriptives过程进行计算。
图表 3 相关系数矩阵图表 4 方差分解主成分提取分析表主成分分析在SPSS中的操作应用(3) 图表 5 初始因子载荷矩阵从图表3可知GDP与工业增加值，第三产业增加值、固定资产投资、基本建设投资、社会消费品零售总额、地方财政收入这几个指标存在着极其显著的关系，与海关出口总额存在着显著关系。
可见许多变量之间直接的相关性比较强，证明他们存在信息上的重叠。
主成分个数提取原则为主成分对应的特征值大于1的前m个主成分。
注：特征值在某种程度上可以被看成是表示主成分影响力度大小的指标，如果特征值小于1，说明该主成分的解释力度还不如直接引入一个原变量的平均解释力度大，因此一般可以用特征值大于1作为纳入标准。
通过图表4（方差分解主成分提取分析）可知，提取2个主成分，即m=2，从图表5（初始因子载荷矩阵）可知GDP、工业增加值、第三产业增加值、固定资产投资、基本建设投资、社会消费品零售总额、海关出口总额、地方财政收入在第一主成分上有较高载荷，说明第一主成分基本反映了这些指标的信息；人均GDP和农业增加值指标在第二主成分上有较高载荷，说明第二主成分基本反映了人均GDP和农业增加值两个指标的信息。
所以提取两个主成分是可以基本反映全部指标的信息，所以决定用两个新变量来代替原来的十个变量。
但这两个新变量的表达还不能从输出窗口中直接得到，因为“Component Matrix”是指初始因子载荷矩阵，每一个载荷量表示主成分与对应变量的相关系数。
用图表5（主成分载荷矩阵）中的数据除以主成分相对应的特征值开平方根便得到两个主成分中每个指标所对应的系数[2]。
SPSS中主成分分析的基本操作
SPSS中主成分分析的基本操作第一步：打开数据文件在SPSS软件中，首先需要打开待分析的数据文件。
可以通过“文件”菜单中的“打开”选项或者快捷键Ctrl+O来打开数据文件。
第二步：选择主成分分析命令在SPSS的分析菜单中，找到主成分分析命令。
主成分分析命令通常位于“多元数据”选项下，可以选择“主成分分析”或者“因素分析”命令。
第三步：选择变量在主成分分析对话框中，需要选择待分析的变量。
可以通过将变量拖放到“变量”列表中，或者点击“变量”列表中的“向下”按钮来选择变量。
对于连续型变量，选择“尺度”选项为“刻度”。
如果只选择一个变量，则进行的是一元主成分分析；如果选择多个变量，则进行的是多元主成分分析。
第四步：设置选项在主成分分析对话框中的“选项”选项卡中，可以设置一些分析选项。
比如可以选择是否进行自动提取主成分、是否进行共同度估计和调整共同度、是否进行特征值和入因子选择等。
这些选项根据具体情况而定，可以根据需要进行设置。
通常，初次进行主成分分析时，可以使用默认设置。
第五步：运行主成分分析在主成分分析对话框中设置完成后，点击“确定”按钮即可运行主成分分析。
SPSS将会自动计算出特征值、特征向量、共同度、因子载荷等主成分分析相关结果。
第六步：结果解读主成分分析结果会显示在SPSS的主输出窗口中。
可以查看特征值表、因子载荷矩阵、方差贡献率等结果。
特征值表显示了每个主成分的特征值和解释的方差比例。
通常可以保留特征值大于1的主成分。
因子载荷矩阵显示了每个变量在主成分中的系数，可以用于解释变量之间的相关关系。
方差贡献率显示了每个主成分对总方差的贡献程度，可以用于选择保留的主成分个数。
需要注意的是，在进行主成分分析之前，需要对数据进行预处理。
通常需要进行数据标准化或者归一化，以保证变量之间的单位一致。
对于缺失值，可以通过删除或者插补的方法进行处理。
总结一下，在SPSS中进行主成分分析的基本操作包括打开数据文件、选择主成分分析命令、选择变量、设置选项、运行主成分分析和结果解读。
主成分分析SPSS操作步骤
主成分分析SPSS操作步骤主成分分析（PCA）是一种常用的多变量数据分析方法，用于识别数据集中的主要变量和模式。
SPSS是一种常用的统计软件，它提供了执行主成分分析的功能。
下面是主成分分析的SPSS操作步骤的完整版：1.打开SPSS软件并加载数据-启动SPSS软件并创建一个新的数据文件。
-保存数据文件。
2.选择主成分分析变量-在主菜单栏中，选择“分析”>“降维”>“主成分”。
-在弹出的对话框中，选择要用于主成分分析的变量。
-将变量添加到“变量”框中。
-点击“统计”按钮打开主成分分析统计选项。
-如果需要计算主成分的相关系数矩阵，选择“相关系数矩阵”。
-如果需要计算主成分的协方差矩阵，选择“协方差矩阵”。
-如果要进行奇异值分解（SVD）而不是特征值分解（EVD），选择“奇异值分解”。
3.设置提取主成分的条件-在主成分分析对话框中，点击“提取”按钮。
-在提取对话框中，设置提取主成分的条件。
-如果希望提取具有特征值大于1的主成分，选择“使用特征值大于1作为提取准则”。
-如果希望提取具有特征值大于指定值的主成分，选择“提取的特征值”并输入指定值。
-如果希望提取具有累积百分比大于指定值的主成分，选择“累积百分比”并输入指定值。
- 如果希望根据Kaiser准则提取主成分，选择“Kaiser准则”。
-点击“确定”关闭提取对话框。
4.设置旋转条件-在主成分分析对话框中，点击“旋转”按钮。
-在旋转对话框中，选择用于旋转主成分的方法。
-如果希望使用方差最大化法进行旋转，选择“方差最大化（方差交换法）”。
-如果希望使用极大似然法进行旋转，选择“极大似然法”。
-如果希望使用斜交旋转进行旋转，选择“斜交旋转”。
-点击“确定”关闭旋转对话框。
5.设置保存选项和结果-在主成分分析对话框中，点击“保存”按钮。
-在保存对话框中，选择是否保存所有结果或仅保存特定结果。
-如果要保存所有结果，选择“所有的主成分”。
-如果要保存仅选择的主成分，选择“仅选择的主成分”并点击“选择”按钮选择要保存的主成分。
SPSS进行主成分分析的步骤(图文)
SPSS进行主成分分析的步骤(图文) SPSS进行主成分分析的步骤主成分分析（Principal Component Analysis, PCA）是一种常用的多元统计分析方法，用于降低数据维度并探索数据之间的关系。
SPSS是一个功能强大的统计分析软件，本文将介绍使用SPSS进行主成分分析的步骤，以图文形式进行详细说明。
一、打开SPSS软件并导入数据1. 在SPSS软件中，点击菜单栏的 "File"，然后选择 "Open"。
2. 在打开的窗口中，找到并选择你要进行主成分分析的数据文件。
3. 点击 "Open"，将数据导入SPSS软件中。
二、准备数据1. 在SPSS软件的数据编辑视图中，确保你要进行主成分分析的变量都已经正确导入。
2. 如果有需要，可以对数据进行预处理（如去除离群值、标准化等），以符合主成分分析的要求。
三、进行主成分分析1. 在SPSS软件的菜单栏中，选择 "Analyze"，然后点击 "Dimension Reduction"，再选择 "Factor..."。
2. 在弹出的对话框中，将需要进行主成分分析的变量依次移至右侧的框中。
3. 点击 "Extraction" 选项卡，选择主成分提取方法（如常用的主成分法）并设置参数。
4. 点击 "Rotation" 选项卡，选择主成分旋转方法（如常用的方差最大旋转法）并设置参数。
5. 可以点击 "Descriptives" 选项卡，勾选 "Correlation matrix" 和"KMO and Bartlett's test" 以获取更详细的分析结果。
6. 点击 "OK" 开始进行主成分分析。
四、解读主成分分析结果1. SPSS将在输出窗口中显示主成分分析的结果，包括提取的成分个数、特征根、方差贡献率等。
(完整版)主成分分析SPSS操作步骤
主成分分析SPSS操作步骤以教材第五章习题8的数据为例，演示并说明主成分分析的详细步骤：一．原始数据的输入注意事项:关键注意设置好数据的类型（数值?字符串?等等）以及小数点后保留数字的个数即可。
二．选项操作1. 打开SPSS的“分析"→“降维”→“因子分析”，打开“因子分析"对话框（如下图）2. 把六个变量：食品、衣着、燃料、住房、交通和通讯、娱乐教育文化输入到右边的待分析变量框.3. 设置分析的统计量打开最右上角的“描述”对话框，选中“统计量"里面的“原始分析结果”和“相关矩阵”里面的“系数”。
（选中原始分析结果，SPSS自动把原始数据标准差标准化，但不显示出来;选中系数，会显示相关系数矩阵。
）。
然后点击“继续".打开第二个的“抽取”对话框：“方法”里选取“主成分”;“分析”、“输出"和“抽取”这三项都选中各自的第一个选项即可。
然后点击“继续”。
第三个的“旋转”对话框里,选取默认的也是第一个选项“无”。
第四个“得分”对话框中，选中“保存为变量"的“回归”；以及“显示因子得分系数矩阵”。
第五个“选项"对话框，默认即可.这时点击“确定”，进行主成分分析。
三．分析结果的解读按照SPSS输出结果的先后顺序逐个介绍1.相关系数矩阵：是6个变量两两之间相关系数大小的方阵。
2。
共同度：给出了这次主成分分析从原始变量中提取的信息，可以看出交通和通讯最多,而娱乐教育文化损失率最大。
CommunalitiesInitial Extraction食品 1.000.878衣着 1.000.825燃料1。
000.841住房 1.000.810交通和通讯 1.000。
919娱乐教育文化 1.000.5843.总方差的解释：系统默认方差大于1的为主成分，所以只取前两个,前两个主成分累加占到总方差的80。
939％。
并且第一主成分的方差是3。
568,第二主成分的方差是1.288。
SPSS进行主成分分析的步骤(图文)教程文件
S P S S进行主成分分析的步骤(图文)主成分分析的操作过程原始数据如下（部分）调用因子分析模块（Analyze―Dimension Reduction―Factor），将需要参与分析的各个原始变量放入变量框，如下图所示：单击Descriptives按钮，打开Descriptives次对话框，勾选KMO and Bartlett’s test of sphericity选项（Initial solution选项为系统默认勾选的，保持默认即可），如下图所示，然后点击Continue按钮，回到主对话框：其他的次对话框都保持不变（此时在Extract次对话框中，SPSS已经默认将提取公因子的方法设置为主成分分析法），在主对话框中点OK按钮，执行因子分析，得到的主要结果如下面几张表。
①KMO和Bartlett球形检验结果：KMO为0.635>0.6，说明数据适合做因子分析；Bartlett球形检验的显著性P值为0.000<0.05，亦说明数据适合做因子分析。
②公因子方差表，其展示了变量的共同度，Extraction下面各个共同度的值都大于0.5，说明提取的主成分对于原始变量的解释程度比较高。
本表在主成分分析中用处不大，此处列出来仅供参考。
③总方差分解表如下表。
由下表可以看出，提取了特征值大于1的两个主成分，两个主成分的方差贡献率分别是55.449%和29.771%，累积方差贡献率是85.220%；两个特征值分别是3.327和1.786。
④因子截荷矩阵如下：根据数理统计的相关知识，主成分分析的变换矩阵亦即主成分载荷矩阵U 与因子载荷矩阵A 以及特征值λ的数学关系如下面这个公式：λiiiAU=故可以由这二者通过计算变量来求得主成分载荷矩阵U 。
新建一个SPSS 数据文件，将因子载荷矩阵中的各个载荷值复制进去，如下图所示：计算变量（Transform-Compute Variables）的公式分别如下二张图所示：计算变量得到的两个特征向量U1和U2如下图所示（U1和U2合起来就是主成分载荷矩阵）：所以可以得到两个主成分Y1和Y2的表达式如下：Y1＝0.456X1+0.401X2+0.428X3+0.490X4+0.380X5+0.253X6Y2＝-0.367X1+0.322X2-0.323X3-0.303X4+0.453X5+0.602X6由上面两个表达式，可以通过计算变量来得到Y1、Y2的值。
用SPSS进行详细的主成分分析步骤
用SPSS进行详细的主成分分析步骤1.打开SPSS软件，并导入需要进行主成分分析的数据集。
选择“文件”-“打开”-“数据”，然后选择相应的数据文件。
2.在菜单栏上选择“分析”-“数据降维”-“主成分”，然后点击“主成分”。
3. 在主成分分析对话框中，将需要进行主成分分析的变量移动到“自变量”框中。
可以使用Shift键或Ctrl键进行多个变量的选择。
此外，还可以选择“统计量”以及“标准化”选项，根据实际需求进行配置。
4.点击“提取”选项卡，有两种提取方案可供选择：基于特征值和基于方差。
基于特征值的提取方案可根据特定的特征值进行选择，基于方差的提取方案则是根据解释的方差比例进行选择。
在这里，我们选择“基于方差”。
5.在“基于方差”选项中，可以通过观察累积解释方差贡献的曲线，选择合适的主成分数量。
通常选择解释方差贡献超过80%或90%的主成分。
6.点击“提取”按钮，将所选的主成分提取到右侧的框中。
7.在“得分”选项卡中，选择是否计算主成分得分。
得分即将原始变量映射到主成分空间中的值。
如果需要得分，可以选择“格式”以及“保存”选项。
选择“格式”可确定得分的输出格式，选择“保存”可将得分保存在结果中。
8.在“选项”选项卡中，可以选择是否进行标准化，以及其他附加选项。
9.点击“确定”按钮开始运行主成分分析。
SPSS将根据所选择的参数进行计算，并在输出窗口中显示结果。
10.在输出窗口中，可以查看主成分的方差解释比例、累积解释比例、特征向量（各个主成分的系数）等统计信息。
此外，还可以查看每个主成分的得分和载荷。
11.可以根据需要，导出主成分得分、载荷、特征值等结果，以供后续分析使用。
选择“文件”-“另存为”-“数据”或“导出”即可将结果保存为特定格式的文件。
以上就是使用SPSS进行主成分分析的详细步骤。
在进行主成分分析时，应根据研究目的和数据特点选择适当的参数，并结合统计结果进行解释和分析。
用SPSS进行详细的主成分分析步骤
怎样用SPSS进行主成分分析怎样用SPSS进行主成分分析一、基本概念与原理主成分分析（principal component analysis）将多个变量通过线性变换以选出较少个数重要变量的一种多元统计分析方法。
又称主分量分析。
在实际课题中，为了全面分析问题，往往提出很多与此有关的变量（或因素），因为每个变量都在不同程度上反映这个课题的某些信息。
但是，在用统计分析方法研究这个多变量的课题时，变量个数太多就会增加课题的复杂性。
人们自然希望变量个数较少而得到的信息较多。
在很多情形，变量之间是有一定的相关关系的，当两个变量之间有一定相关关系时，可以解释为这两个变量反映此课题的信息有一定的重叠。
主成分分析是对于原先提出的所有变量，建立尽可能少的新变量，使得这些新变量是两两不相关的，而且这些新变量在反映课题的信息方面尽可能保持原有的信息。
主成分分析首先是由K.皮尔森对非随机变量引入的，尔后H.霍特林将此方法推广到随机向量的情形。
信息的大小通常用离差平方和或方差来衡量。
（1）主成分分析的原理及基本思想。
原理：设法将原来变量重新组合成一组新的互相无关的几个综合变量，同时根据实际需要从中可以取出几个较少的总和变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析，也是数学上处理降维的一种方法。
基本思想：主成分分析是设法将原来众多具有一定相关性（比如P个指标），重新组合成一组新的互相无关的综合指标来代替原来的指标。
通常数学上的处理就是将原来P个指标作线性组合，作为新的综合指标。
最经典的做法就是用F1（选取的第一个线性组合，即第一个综合指标）的方差来表达，即Var(F1)越大，表示F1包含的信息越多。
因此在所有的线性组合中选取的F1应该是方差最大的，故称F1为第一主成分。
如果第一主成分不足以代表原来P个指标的信息，再考虑选取F2即选第二个线性组合，为了有效地反映原来信息，F1已有的信息就不需要再出现再F2中，用数学语言表达就是要求Cov(F1, F2)=0，则称F2为第二主成分，依此类推可以构造出第三、第四，……，第P个主成分。
利用SPSS进行主成分分析
利用SPSS进行主成分分析主成分分析是一种用于数据降维和探索关联性的统计方法。
它可以通过将一组相关变量转换成一组不相关的主成分，来帮助我们理解变量之间的关联关系。
利用SPSS进行主成分分析的步骤如下：1.打开SPSS软件，并导入要进行主成分分析的数据。
选择“文件”菜单下的“导入”选项，然后选择要导入的数据文件。
2.在数据文件导入成功后，点击“分析”菜单，然后选择“降维”子菜单中的“主成分”选项。
3.在弹出的“主成分”对话框中，将所有的变量移到右侧的“变量”框中。
这些变量将会是主成分分析的输入变量。
4. 可以选择“提取”选项卡来设置主成分的提取方法。
常用的方法有Kaiser准则和自由值大于1的原则。
选择适合自己数据的方法，并设置提取的主成分数目。
5.可以选择“旋转”选项卡来设置主成分的旋转方法。
常用的方法有旋转后的成分的内生性、方差最大化等。
同样，选择适合自己数据的方法，并设置旋转的方法。
6.设置好主成分分析的参数后，可以点击“统计”按钮来选择要计算的统计量，如特征值、方差解释比等。
7.设置完所有参数后，点击“确定”按钮开始进行主成分分析。
SPSS将会自动进行计算，并将结果显示在输出窗口中。
8.结果中会包含主成分的特征值、特征向量、方差解释比等信息。
通过分析这些信息，我们可以判断每个主成分的解释能力和重要性，进而得到主成分分析的结论。
需要注意的是，在进行主成分分析之前，需要对数据进行必要的预处理，如数据清洗、缺失值处理等。
此外，主成分分析的结果需要谨慎解释，因为主成分分析是一种线性降维方法，可能会损失一部分信息。
总之，SPSS是一种强大的统计软件，可以方便地进行主成分分析，并得到结果。
通过合理设置参数和分析结果，可以帮助我们更好地理解变量之间的关联关系，为进一步的数据分析提供依据。
主成分分析操作详细步骤
主成分分析操作详细步骤
1、打开SPSS统计软件，点击“文件”—“新建”，出现“数据文件”、“表格”、“报告”、“图形”等四个选项，其中“数据文件”是
一个空的数据文件，可以手动输入数据。
2、点击“数据”—“获取外部数据”—“从文本文件／框架文件／Excel文件中获取数据”，在“文件类型”框中选择要导入的文件类型，
点击“完成”，之后点击“浏览”，可以选择准备好的数据文件，导入到SPSS统计软件中。
3、点击“分析”—“统计分析”—“主成分分析”，出现“主成分
变量”框，可以选择要进行主成分分析的变量，这些变量可以是各种指标，选择完毕后，点击“确定”。
4、在“主成分变量”框下方出现“控制参数”，有四个选项：“去
除非对角线元素”、“解释剩余变量”、“解释变量模式”、“把因子得
分作为自变量”，其中“解释变量模式”用来控制主成分分析的输出，可
以设置要输出哪些统计量，一般设置为对变量进行“全部”的解释。
5、点击“保存”，“控制参数”框下方出现“文件”，可以选择要
将计算结果保存到何处，一般设置为“当前文件夹”即可。
6、点击“确定”，软件执行计算，完成后会出现分析结果的表格。
《SPSS数据分析教程》——主成分分析
《SPSS数据分析教程》——主成分分析主成分分析的原理是基于多元统计中的线性代数知识。
假设我们有一个包含p个变量的数据集，我们的目标是找到一组新的变量（即主成分），使得它们能够更好地解释原始数据的方差。
具体来说，主成分是原始变量的线性组合，通过计算协方差矩阵的特征值和特征向量来确定。
特征值表示方差的大小，特征向量表示主成分的方向。
主成分分析的步骤如下：1.数据准备：收集并导入数据到SPSS软件中，确保数据的格式正确，并删除缺失值。
2.变量标准化：主成分分析基于变量之间的协方差矩阵，为了消除不同变量之间的量纲差异，需要对数据进行标准化处理。
选择“数据”菜单下的“标准化”选项，在弹出的对话框中选择需要标准化的变量，并指定标准化的方法。
3.因子分析：选择“分析”菜单下的“降维”选项，再选择“主成分”。
在弹出的对话框中，将原始变量移入右侧的“因子”框中。
可以选择是否计算主成分得分和旋转主成分。
得分可以用于后续的回归分析或聚类分析，旋转可以使主成分更具解释性和可解释性。
4.结果解释：主成分分析后，SPSS会显示特征值和特征向量的汇总表。
特征值表示主成分解释的方差比例，特征向量表示主成分的权重。
通常，我们选择特征值大于1的主成分，因为它们能够解释原始数据的较大比例的方差。
通过观察特征向量，可以解释主成分的意义，比如一些主成分与一些变量之间的相关性。
5.结果可视化：为了更好地理解主成分分析的结果，可以使用散点图或其他图表进行可视化。
选择“图表”菜单下的“散点图”选项，将主成分得分画在散点图上，可以观察主成分之间的相关性和数据的集中程度。
上述是主成分分析的基本步骤和SPSS操作流程。
通过主成分分析，我们可以将复杂的高维数据转化为一组简单的主成分，方便我们对数据进行分析和解释。
同时，主成分分析也可以作为其他数据分析方法的前期处理步骤，如聚类分析、回归分析等。
如何利用SPSS进行主成分分析
利用SPSS进行主成分分析【例子】以全国31个省市的8项经济指标为例，进行主成分分析。
第一步：录入或调入数据（图1）。
图1 原始数据（未经标准化）第二步：打开“因子分析”对话框。
沿着主菜单的“Analyze→Data Reduction→Factor ”的路径（图2）打开因子分析选项框（图3）。
图2 打开因子分析对话框的路径图3 因子分析选项框第三步：选项设置。
首先，在源变量框中选中需要进行分析的变量，点击右边的箭头符号，将需要的变量调入变量（Variables）栏中（图3）。
在本例中，全部8个变量都要用上，故全部调入（图4）。
因无特殊需要，故不必理会“Value ”栏。
下面逐项设置。
图4 将变量移到变量栏以后⒈设置Descriptives选项。
单击Descriptives按钮（图4），弹出Descriptives对话框（图5）。
图5 描述选项框在Statistics 栏中选中Univariate descriptives 复选项，则输出结果中将会给出原始数据的抽样均值、方差和样本数目（这一栏结果可供检验参考）；选中Initial solution 复选项，则会给出主成分载荷的公因子方差（这一栏数据分析时有用）。
在Correlation Matrix 栏中，选中Coefficients 复选项，则会给出原始变量的相关系数矩阵（分析时可参考）；选中Determinant 复选项，则会给出相关系数矩阵的行列式，如果希望在Excel 中对某些计算过程进行了解，可选此项，否则用途不大。
其它复选项一般不用，但在特殊情况下可以用到（本例不选）。
设置完成以后，单击Continue 按钮完成设置（图5）。
⒉ 设置Extraction 选项。
打开Extraction 对话框（图6）。
因子提取方法主要有7种，在Method 栏中可以看到，系统默认的提取方法是主成分（∏ρινχιπαλ χομπονεντσ），因此对此栏不作变动，就是认可了主成分分析方法。
主成分分析SPSS操作步骤
主成分分析SPSS操作步骤步骤一：准备数据1.打开SPSS软件并导入需要进行主成分分析的数据文件。
可以通过点击“文件”->“打开”->“数据”来导入数据文件。
2.确保数据文件中的每个变量是数值型数据，并且不存在缺失值。
如果有缺失值，可以进行数据清洗或者填补缺失值。
步骤二：设置主成分分析选项1.在SPSS软件的“分析”菜单中选择“降维”->“主成分”->“因子”。
2.在弹出的“因子分析”对话框中，将需要进行主成分分析的变量移动到“因子分析变量”框中。
可以通过点击变量名称并使用“箭头”按钮来移动变量。
3.在“因子分析变量”框下方的“选项”按钮中，可以设置主成分分析方法、提取因子的标准和旋转方法。
一般情况下，可以保持默认设置。
4.点击“确定”开始进行主成分分析。
步骤三：查看分析结果1.主成分分析结果会在SPSS软件的输出窗口中显示。
可以查看提取的因子数量、因子的方差解释比例和特征根。
2.在“公共性”表中，可以查看变量对每个因子的贡献情况，公共性值越接近1表示变量对因子的贡献越大。
3.在“言语编码”表中，可以查看每个变量在各个因子上的系数，系数绝对值较大的变量与该因子的相关性较高。
4.在“旋转过的因子载荷矩阵”表中，可以查看经过旋转后每个变量与因子之间的相关系数。
步骤四：解释主成分分析结果1.根据主成分分析结果，可以选择提取前几个因子进行解释。
一般情况下，可以选择提取方差解释比例较高的因子。
2.根据每个变量在各个因子上的系数和旋转后的因子载荷矩阵，可以解释每个因子的含义和各个变量对因子的贡献。
3.将解释后的因子作为新的变量，可以用于后续的统计分析。
步骤五：进行因子旋转（可选）1.在主成分分析之后，可以对因子进行旋转，以使得因子与变量之间的相关性更为清晰和直观。
2.在“因子分析”对话框中的“选项”按钮中，可以选择旋转方法。
常用的旋转方法有正交旋转和斜交旋转。
3.点击“计算”开始进行因子旋转，旋转后的结果将显示在“旋转过的因子载荷矩阵”表中。
如何在SPSS数据分析报告中进行主成分分析？
如何在SPSS数据分析报告中进行主成分分析？关键信息项1、数据准备要求2、主成分分析步骤3、结果解读方法4、报告撰写要点1、数据准备要求11 数据质量检查确保数据的完整性，不存在缺失值。
若有缺失值，需采取适当的方法进行处理，如均值插补、回归插补等。
检查数据的准确性，避免错误的数据录入。
评估数据的分布特征，判断是否符合正态分布。
若不符合，可能需要进行数据转换。
12 变量选择选择具有相关性且能反映研究问题的变量。
避免包含过多无关或冗余的变量，以免增加分析的复杂性。
13 数据标准化对数据进行标准化处理，使不同变量具有相同的量纲和可比性。
2、主成分分析步骤21 打开 SPSS 软件并导入数据启动 SPSS 程序，通过“文件”菜单中的“打开”选项导入准备好的数据文件。
22 选择主成分分析方法在“分析”菜单中，选择“降维”子菜单中的“因子分析”。
23 设置分析参数将需要分析的变量选入“变量”框。
选择提取主成分的方法，如基于特征值大于 1 或指定提取的主成分个数。
24 输出结果选项设置根据需求选择输出相关的统计量和图表，如成分矩阵、碎石图等。
25 执行分析点击“确定”按钮，执行主成分分析。
3、结果解读方法31 成分矩阵解读观察成分矩阵中各变量在主成分上的载荷值，判断变量与主成分的相关性。
载荷值的绝对值越大，表明变量与主成分的相关性越强。
32 特征值和方差贡献率关注特征值，通常选择特征值大于 1 的主成分。
方差贡献率表示主成分解释原始变量变异的比例，累计方差贡献率反映了所选主成分对原始变量信息的综合解释程度。
33 碎石图分析通过碎石图直观判断主成分的重要性和提取的合理性。
34 成分得分计算如有需要，可计算成分得分，用于后续的进一步分析或建模。
4、报告撰写要点41 研究背景和目的阐述简要介绍研究的背景、问题以及进行主成分分析的目的。
42 数据来源和预处理说明描述数据的来源、样本量以及所进行的数据预处理步骤和方法。
SPSS进行主成分分析步骤(图文)
主成分分析的操作过程原始数据如下（部分）调用因子分析模块（Analyze―Dimension Reduction―Factor），将需要参与分析的各个原始变量放入变量框，如下图所示：单击Descriptives按钮，打开Descriptives次对话框，勾选KMO and Bartlett’s test of sphericity选项（Initial solution选项为系统默认勾选的，保持默认即可），如下图所示，然后点击Continue按钮，回到主对话框：其他的次对话框都保持不变（此时在Extract次对话框中，SPSS已经默认将提取公因子的方法设置为主成分分析法），在主对话框中点OK按钮，执行因子分析，得到的主要结果如下面几张表。
①KMO和Bartlett球形检验结果：KMO为0.635>0.6，说明数据适合做因子分析；Bartlett球形检验的显著性P值为0.000<0.05，亦说明数据适合做因子分析。
②公因子方差表，其展示了变量的共同度，Extraction下面各个共同度的值都大于0.5，说明提取的主成分对于原始变量的解释程度比较高。
本表在主成分分析中用处不大，此处列出来仅供参考。
③总方差分解表如下表。
由下表可以看出，提取了特征值大于1的两个主成分，两个主成分的方差贡献率分别是55.449%和29.771%，累积方差贡献率是85.220%；两个特征值分别是3.327和1.786。
④因子截荷矩阵如下：根据数理统计的相关知识，主成分分析的变换矩阵亦即主成分载荷矩阵U 与因子载荷矩阵A 以及特征值λ的数学关系如下面这个公式：λiiiAU=故可以由这二者通过计算变量来求得主成分载荷矩阵U 。
新建一个SPSS 数据文件，将因子载荷矩阵中的各个载荷值复制进去，如下图所示：计算变量（Transform-Compute Variables ）的公式分别如下二张图所示：计算变量得到的两个特征向量U1和U2如下图所示（U1和U2合起来就是主成分载荷矩阵）：所以可以得到两个主成分Y1和Y2的表达式如下：Y1＝0.456X1+0.401X2+0.428X3+0.490X4+0.380X5+0.253X6Y2＝-0.367X1+0.322X2-0.323X3-0.303X4+0.453X5+0.602X6由上面两个表达式，可以通过计算变量来得到Y1、Y2的值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
SPSS主成分分析操作步骤，详细的很啊^_^
SPSS在调用Factor Analyze过程进行分析时，SPSS会自动对原始数据进行标准化处理，所以在得到计算结果后指的变量都是指经过标准化处理后的变量，但SPSS不会直接给出标准化后的数据，如需要得到标准化数据，则需调用Descriptives过程进行计算。
图表 3 相关系数矩阵
图表 4 方差分解主成分提取分析表
主成分分析在SPSS中的操作应用(3) 图表 5 初始因子载荷矩阵
从图表3可知GDP与工业增加值，第三产业增加值、固定资产投资、基本建设投资、社会消费品零售总额、地方财政收入这几个指标存在着极其显著的关系，与海关出口总额存在着显著关系。
可见许多变量之间直接的相关性比较强，证明他们存在信息上的重叠。
主成分个数提取原则为主成分对应的特征值大于1的前m个主成分。
注：特征值在某种程度上可以被看成是表示主成分影响力度大小的指标，如果特征值小于1，说明该主成分的解释力度还不如直接引入一个原变量的平均解释力度大，因此一般可以用特征值大于1作为纳入标准。
通过图表4（方差分解主成分提取分析）可知，提取2个主成分，即m=2，从图表5（初始因子载荷矩阵）可知GDP、工业增加值、第三产业增加值、固定资产投资、基本建设投资、社会消费品零售总额、海关出口总额、地方财政收入在第一主成分上有较高载荷，说明第一主成分基本反映了这些指标的信息；人均GDP和农业增加值指标在第二主成分上有较高载荷，说明第二主成分基本反映了人均GDP和农业增加值两个指标的信息。
所以提取两个主成分是可以基本反映全部指标的信息，所以决定用两个新变量来代替原来的十个变量。
但这两个新变量的表达还不能从输出窗口中直接得到，因为“Component Matrix”是指初始因子载荷矩阵，每一个载荷量表示主成分与对应变量的相关系数。
用图表5（主成分载荷矩阵）中的数据除以主成分相对应的特征值开平方根便得到两个主成分中每个指标所对应的系数[2]。
将初始因子载荷矩阵中的两列数据输入（可用复制粘贴的方法）到数据编辑窗口（为变量B1、B2），然后利用“TransformàCompute Variable”，在Compute Variable对话框中输入“A1=B1/SQR(7.22)”
[注：第二主成分SQR后的括号中填1.235]，即可得到特征向量A1(见图表6)。
同理，可得到特征向量A2。
将得到的特征向量与标准化后的数据相乘，然后就可以得出主成分表达式[注：因本例只是为了说明如何在SPSS进行主成分分析，故在此不对提取的主成分进行命名，有兴趣的读者可自行命名]：
F 1=0.353ZX
1
+0.042ZX
2
-0.041ZX
3
+0.364ZX
4
+0.367ZX
5
+0.366ZX
6
+0.352ZX
7
+0.364ZX
8+0.298ZX
9
+0.355ZX
10
F 2=0.175ZX
1
-0.741ZX
2
+0.609ZX
3
-0.004ZX
4
+0.063ZX
5
-0.061ZX
6
-0.022ZX
7
+0.158ZX
8-0.046ZX
9
-0.115ZX
10
图表 6 Compute Variable对话框
前文提到SPSS会自动对数据进行标准化，但不会直接给出，需要我们自己另外算，我们可以通过AnalyzeàDescriptive Statisticsà Descriptives对话框来实现：弹出Descriptives对话框后，把X1～X10选入Variables框，在Save standardized values as variables前的方框打上钩，点击“OK”，经标准化的数据会自动填入数据窗口中，并以Z开头命名。
图表 7 Descriptives对话框
主成分分析在SPSS中的操作应用(4)
以每个主成分所对应的特征值占所提取主成分总的特征值之和的比例作为权重计算主成分综合模型：
即可得到主成分综合模型：
F=7.22/（7.22+1.225）*F1+1.225/(7.22+1.225)*F2
根据主成分综合模型即可计算综合主成分值，并对其按综合主成分值进行排序，即可对各地区进行综合评价比较，结果见图表8。
图表 8 综合主成分值
对得出的综合主成分(评价)值，我们可用实际结果、经验与原始数据做聚类分析进行检验，对有争议的结果，可用原始数据做判别分析解决争议，具体评价与检验本文不做论述，如读者有兴趣可自行进行检验论述。
四、小结
本文旨在阐述如何利用SPSS软件进行正确的主成分分析，使读者能正确使用SPSS进行主成分分析，以解决实际问题；避免出现读者因子分析与主成分分析混用的情况，并希望今后的相关教科书能够说明清楚主成分分析在SPSS中的操作。