可修复系统可靠性.ppt

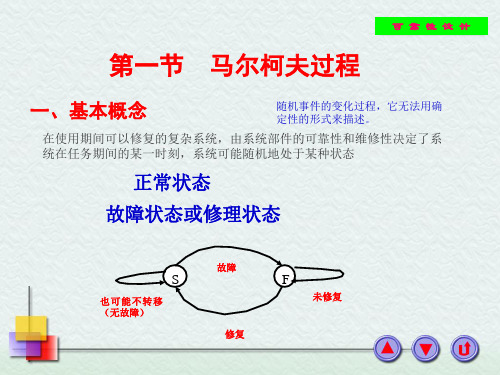
1．马尔柯夫性
设 {X (t),t T}是一个随机过程，如果{X(t),t T}
在时刻 t t0 所处的状态为已知时，它在t 时刻所处状态的条件分布与其在 t0之前所
0
处的状态无关，通俗地说，就是在知道随
机过程“现在”的条件下，其“将来”的
条件分布不依赖于“过去”{，X则(t)称,t T}
具有马尔柯夫性。
MTBF
MTBF MTTR
(6-11)
当且M可T靠B度F＝R（1 t，）M和T维TR修=度1M时（，t）有均为指数分布，
A＝
MTBF
MTBF MTTR
（6-12）
如上所述的瞬时、任务、稳态有效度之间的关系， 见图6-1。
图6-1 瞬时、任务、稳态有效度
（4）固有有效度（Inherent Availability）： 固有有效度可表示为（事后维修）
维修总台数
▪ 2．维修密度函数m（t）
如果维修度函数M（t）连续可导，则M（t） 的导数称为维修密度函数，记为m（t）。
m（t）＝ dM (t)
dt
(6-2)
若已知维修密度函数m（t），则
M（t）=
t
m(t )dt
0
▪ 3．修复率μ（t）
修复率指修理时间已达到某一时刻但尚未修复的
产品在该时刻后的单位时间内完成修理的概率，
A＝
工作时间 工作时间 实际不能工作时间
MTBF MTBF MADT
（6-13）
式中 MADT（Mean Active Down Time）——平均实际不能工作时间；
MTBF——平均无故障工作时间。
▪ 固有有效度也可表示为（预防性维修）
A（t1，t2）＝ MTBM MTBM M
(6-14)
式中 MTBM（Mean Time Between Maintenances）——两次维修间平均时间；
可表示为μ（t）。它是用单位时间修复发生故障
的产品的比例来度量维修性的一个尺度。
μ（t）= 1 dM (t) m(t)
1 M (t) dt 1 M (t)
（6-3）
若M（t）服从指数分布，即
M（t）＝1－e－μt
则修复率为常数μ。
(6-4)
▪ 4．平均修复时间MTTR
平均修复时间是指可修复的产品的平均修
▪ 2．马尔柯夫过程 设 {X (t),t T}的状态空间为S， 如果 n 2, t1 t2 tn T ，在条
第一节 维修及其数量指标
一、维修性特征量
1．维修度M（t）
▪ 维修度（Maintainability）是指在规定的条件下使 用的可维修产品，在规定的时间内，按规定的程序
和方法进行维修时，保持或恢复到能完成规定功能 的概率，记为M（t）。
M（t）＝P（Y≤t）
（6-1）
＝
t
0 m(t)dt
＝ t时刻内修复的台数
第六章
更多内容请关注 /study.asp?vip=8386126
可修复系统可靠性
第一节 维修及其数量指标 第二节 马尔柯夫过程 第三节 串联可修系统 第四节 并联可修系统 第五节 可修复系统 第六节 串并联可修系统 第七节 柔性连接系统可靠性 第八节 实例研究
是时间t→∞时瞬时有效度A（t）的极限，
即
A（∞）＝A＝ lim A(t) t
稳态有效度也可表示为
(6-9)
可工作时间
A＝ 可工作时间 不能工作时间
U U
D（6-10）
U——可维修的系统、机器、设备或部件等 产 品平均能正常工作的时间，单位为h
D——产品平均不能工作时间，单位为h。
或表达为
A＝
习题
维修性特征量和可靠性特征量的关系
▪ 1、 对应关系
▪ M（t）与F（t）、m（t）与f（t）、μ（t）与λ （t）、MTBF与MTTR是——对应的；
▪ 2、区别
▪ 可靠性指标依据的是从开始工作到故障发生的 时间（寿命）数据，而维修性指标依据的是发 生故障后进行维修所花费的时间——修复时间 数据。两者相比，维修时间数据比寿命数据要 小得多。另外，可靠性是由设计、制造、使用 等因素所决定的，而维修性是人为地排除故障， 使产品的功能恢复，因而人为因素影响更大。
▪ 试求：（1）160min的维修度；
▪ （2）MTTR；
▪ （3）120min时的修复率，Δt＝15min。
▪ 解（1）M (t) ＝
t时刻内修复的台数 维修总台数
＝0.65
各台修复时间的总和
▪ （2）MTTR＝ 维修总台数
▪ MTTR＝（48＋59＋68＋…＋198＋200）/20＝
133.55min
▪ ▪
μ（（132）0）μ=（t）12 2＝15＝1在.1时%间到区时间刻（t仍t，未t修好t的）台内数修复 的t 台数
于是
二、有效性特征量 1．有效度 （1）瞬时有效度（Instantaneous
Availability）：瞬时有效度指在某一特定 瞬时，可修产品保持正常工作使用状态或 功能的概率
——平均维修时间。
M
第二节 马尔柯夫过程
一、随机过程的概念
设E是随机试验， {}是它的样本空间，T
是一个参数集，若对于每一个 t T ,都有随
机变量X (t,), 与之对应，则称随机变 量族{x(t,),t T} 为随机过程或随机函数，通 常记作{X (t),t T} 或 X (t) 。
二、马尔柯夫过程的概念
（2）平均有效度（Mean Availability）： 可修产品在时间区间［0，t］内的平均有
效度，即瞬时有效度A（t）在［0，t］内 的平均值，记为（t）。
（3）稳态有效度（Steady Availability）：稳 态有效度或称为时间有效度（Time Availability），又叫可工作时间比UTR （Up Time Ratio），记为A（∞）或A。它
理时间，其估计值为修复时间总和与修复
次数之比，记作MTTR（Mean Time To
Repair）。
MTTR
=
E(Y
)=
0 tdM (t)
(6-5)
若修复时间服从指数分布，如式（6-4）所
示，则平均修复时间是修复率的倒数，即
MTTR = 1
(6-6)
▪ 例6-1 某电视机厂的维修站修理了该厂生产的20台 电视机，每台的修理时间（单位为min）如下：48， 59，68，86，90，105，110，120，126，128， 144，150，157，161，172，176，180，193， 198，200。