生物数学课程论文
探索数学在生物技术中的应用作文

探索数学在生物技术中的应用作文数学在生物技术中的应用生物技术是将生物学和相关科学的原理,以及工程技术的方法应用于生物体中的有关生产、科学研究和服务领域的一门学科。
而数学作为一门基础学科,在生物技术领域中也发挥着重要的作用。
本文将探索数学在生物技术中的应用。
一、基因组学中的数学基因组学是研究基因组的组成、功能以及相互关系的学科。
而基因组学的研究涉及到庞大的数据量,这就需要数学在数据分析和处理方面发挥作用。
例如,在测序技术中,每个碱基的信号会投影到图像上,而通过数学模型对图像进行分析,可以准确地确定碱基序列。
此外,通过数学模型和算法的帮助,可以对基因组进行高效的比对和比较。
通过比对,可以找到基因组中的共有基因,进一步研究它们的功能和相互作用。
数学在基因组学中的应用,可以提供更多的信息和理论支持,加速基因组学的发展。
二、蛋白质结构预测蛋白质是生物体内功能最为重要的分子之一。
而蛋白质的结构与其功能息息相关。
然而,实验测定蛋白质的结构非常耗时耗力,因此数学在预测蛋白质结构方面发挥了关键的作用。
通过建立数学模型和算法,可以预测蛋白质的二级结构和三级结构。
这些预测模型利用了蛋白质序列中的局部相似性和一些规则性的结构模式,并通过数学统计方法进行分析和预测。
这种方法可以为研究者提供蛋白质结构重要的参考信息,从而更好地研究蛋白质的功能和作用机制。
三、网络生物学中的数学建模网络生物学是通过构建生物体内分子之间的相互作用网络来研究生物系统的学科。
而网络生物学的研究需要对大量的生物分子进行分类、分析和模型构建。
在这个过程中,数学的方法发挥了重要作用。
通过数学建模和分析,可以将复杂的生物网络简化成数学模型,从而通过模拟和计算来预测生物系统的行为。
这种方法可以帮助研究者更好地理解生物系统的运作机制,并为生物技术的应用提供重要的理论基础。
四、生物信息学中的统计学应用生物信息学是将计算机科学、数学和统计学等方法应用于生物学研究的学科。
探索数学在生物学中的运用

探索数学在生物学中的运用数学和生物学是两个截然不同的学科,一个以数字和符号为基础,另一个则研究生命和生物体。
然而,在现代科学中,数学在生物学中的运用却变得越来越重要。
数学在生物学领域的应用不仅仅加深了我们对生命的理解,更帮助我们揭示了许多生物系统中的规律和模式。
本文将探索数学在生物学中的运用,并讨论数学对生物学的贡献和影响。
1. 数学在遗传学中的应用遗传学研究了基因的遗传规律和遗传变异。
数学的统计学方法在遗传学中扮演着重要角色。
通过数学模型和概率统计方法,我们能够预测不同基因型和表型的出现频率,解释遗传变异背后的规律。
同时,数学还能帮助我们分析基因的连锁和重组,揭示基因在染色体上的相对位置。
这些数学方法为遗传学研究提供了有力的工具,使我们能够更好地理解遗传背后的数学规律。
2. 数学在生态学中的应用生态学研究了生物体在自然环境中的相互作用和生态系统的结构和功能。
数学在生态学研究中的运用尤为突出。
数学模型能够模拟和预测物种的种群动态、物种相互作用和生态系统的稳定性。
举个例子,Lotka-Volterra模型可以描述食物链中捕食者和被捕食者的相互作用,预测它们的种群变动。
另外,数学在物种多样性的研究中也起到了重要作用。
通过数学模型,我们能够评估物种的丰富度、均匀度和多样性,并发现生态系统中的关键物种。
数学为生态学提供了一种定量化的方法,使我们能够更好地理解和保护自然生态系统。
3. 数学在分子生物学中的应用分子生物学研究了生物分子(如DNA和蛋白质)的结构、功能和相互作用。
数学在分子生物学中的应用主要集中在序列分析和蛋白质结构预测方面。
通过数学和计算机模型,我们可以分析DNA和蛋白质序列之间的相似性,推断它们之间的进化关系,发现基因和蛋白质功能上的相似性。
此外,数学模型还可以预测蛋白质的结构和折叠方式,揭示蛋白质的功能和相互作用机制。
这些数学方法为分子生物学研究提供了强大的工具,推动了生物分子领域的发展。
数学模型在高中生物新课程教学中应用论文

浅谈数学模型在高中生物新课程教学中的应用【摘要】数学模型是用来描述一个系统或它的性质的数学形式,是联系实际问题与数学的桥梁,具有解释、判断、预测等重要功能。
笔者就生物新课程教学中引入数学模型的意义、常用的数学模型种类及应用数学模型应注意的问题进行了深入探讨。
【关键词】生物;数学模型;种类;价值;应用生命科学是自然科学中的一个重要的分支。
高中生物新课程要求学生具备一定的科学素养和创新能力,因此在教学中,教师应注重思维方式的培养。
充分运用数学模型解决生物学问题,提高学生的逻辑思维能力,拓展学生思维空间,培养学生创造性地解决问题的能力。
1、生物新课程引入数学模型的意义1.1数学模型是指用字母、数字和其他数学符号构成的等式或不等式,或用图表、图像、框图、数理逻辑等来描述系统的特征及其内部联系或与外界联系的模型。
它是真实系统的一种抽象。
是联系实际问题与数学的桥梁,具有解释、判断、预测等重要功能。
在科学研究中,数学模型是发现问题和探索新规律的有效途径之一。
生物课程中应用数学模型,有利于培养学生透过现象揭示本质的洞察能力。
同时,通过生物科学与数学知识的整合,有利于培养学生简约、严密的思维品质。
1.2数学方法的介入,使我们对自然规律有了更多的认识,数学模型在生物学中越来越表现出强大的生命力,它通过建立可以表述生命系统发展状况等的数学系统,对生命现象进行量化,以数学关系描述生命现象,再运用逻辑推理、求解和运算等方法达到对生命现象进行研究的目的。
1.3数学模型的运用能很好地帮助学生解决一些生物学实际问题,深入理解生物学上的基本概念,提高逻辑思维能力和学习兴趣。
2、几种常见数学模型在生物新课程教学中的应用2.1集合图形首先,集合思想多运用于解决遗传问题的分类处理,例如某个体有两种基因型,可以分成两种情况分别处理然后再叠加;再如计算后代两种遗传病的患病概率时也可以用集合思想加以解决。
例:假如水稻高秆(d)对矮秆(d)为显性,抗稻瘟病(r)对易感稻瘟病(r)为显性,两对性状独立遗传,用一个纯合易感病的矮秆品种与一个纯合抗病高秆品种杂交,f2代中出现既抗病又抗倒伏类型的比例a.1/8b.1/16c.3/16d..3/8解题要点:先算出f2代中抗倒伏的概率为1/4,抗病的概率为3/4,然后利用集合思想计算,如图。
七年级生物数学论文

七年级生物数学论文
简介
本文旨在探讨生物学和数学之间的关系,并探索七年级生物学
和数学的一些应用。
生物学和数学的关系
生物学和数学之间存在密切的关联。
生物学依赖于数学的概率
和统计方法来分析和解释生物数据。
数学的建模方法也在生物学中
被广泛应用,用于研究生物系统及其复杂性。
七年级生物学应用
七年级的生物学主要包括生物多样性、细胞结构和功能、生物
进化等内容。
这些主题可以通过数学方法来深入理解和应用。
生物多样性的数学模型
生物多样性是指地球上不同物种的多样性和分布。
我们可以使
用数学模型来研究和预测物种多样性的变化。
例如,用于描述物种
丰富度和物种分布的数值指标,如生物多样性指数和物种面积曲线,可以帮助我们了解不同地区的生物多样性特征。
细胞结构和功能的数学分析
细胞是生物体的基本单位,其结构和功能对于生物学的理解至
关重要。
数学分析可以帮助我们理解细胞的构造和功能之间的关系。
例如,利用数学模型可以研究细胞的膜传递过程和酶催化反应的动
力学。
生物进化的数学建模
生物进化是生物学中的重要概念,数学建模可以帮助我们研究
和理解进化过程。
例如,使用数学模型可以推断物种的共同祖先,
预测群体的遗传变异以及预测物种适应环境变化的能力。
结论
生物学和数学之间的关系是密不可分的。
数学方法在生物学中
的应用有助于我们深入理解生物系统的复杂性和动态变化。
七年级
生物学的研究可以通过数学分析来加深对生物学概念的理解和应用。
生物数学课程论文
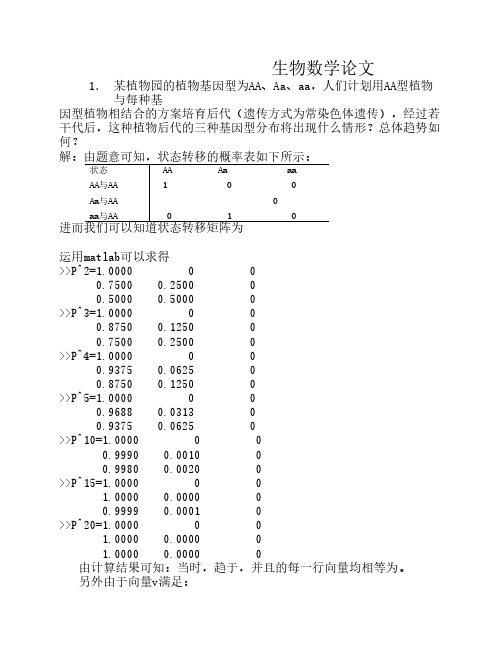
生物数学论文1. 某植物园的植物基因型为AA、Aa、aa,人们计划用AA型植物与每种基因型植物相结合的方案培育后代(遗传方式为常染色体遗传),经过若干代后,这种植物后代的三种基因型分布将出现什么情形?总体趋势如何?解:由题意可知,状态转移的概率表如下所示:状态AA Aa aaAA与AA 1 0 0Aa与AA 0aa与AA 0 1 0进而我们可以知道状态转移矩阵为运用matlab可以求得>>P^2=1.0000 0 00.7500 0.2500 00.5000 0.5000 0>>P^3=1.0000 0 00.8750 0.1250 00.7500 0.2500 0>>P^4=1.0000 0 00.9375 0.0625 00.8750 0.1250 0>>P^5=1.0000 0 00.9688 0.0313 00.9375 0.0625 0>>P^10=1.0000 0 00.9990 0.0010 00.9980 0.0020 0>>P^15=1.0000 0 01.0000 0.0000 00.9999 0.0001 0>>P^20=1.0000 0 01.0000 0.0000 01.0000 0.0000 0由计算结果可知:当时,趋于,并且的每一行向量均相等为。
另外由于向量v满足:列出求解向量的线性方程组解得:所以经过若干代后,这种植物后代的三种基因型AA、Aa 、aa分布为向量。
即将出现下列情形:即Aa 、aa类基因型将消失,所有的植物的基因型都为AA。
总体趋势为Aa和aa类基因型逐渐减少直至消失,而AA类基因型逐渐增加。
2、试建立人口Logistic(逻辑)模型,并说明模型中何参数为自然增长率,为什么?解:设人口净增长率与人口极限以及目前的人口都有关系。
设表示维持种群生存的最大数量,当前人口数为,种群未饱和程度用比值,为比例系数。
高中生物教材数学论文

高中生物教材数学论文人教版高中生物教材模块必修1《分子与细胞》将模型分为物理模型、概念模型和数学模型三种。
教材中对模型的定义是:模型是人们为了达到某种特定目的,对所认识的对象进行简化的、概括性的描述。
这种描述可以是定量的,也可以是定性的;可以借助具体的实际物体也可借助抽象手段。
教材中数学模型概念指的是数学模型是用来描述一个系统或它的性质的数学形式。
高中生物教材中的数学模型数量很多、种类有很多。
有数字模型、比例模型、方程式模型、公式模型、概率模型、集合模型、曲线模型、线段模型、表格模型、几何图模型等等。
1.数字模型生物教材中的概念繁多,很多概念、生理过程、化学组成等都与数字有关。
通过数字描述组成或过程而建立的模型叫数字模型。
数字有分数、百分数、数字的。
如:1)百分数模型:用无水乙醇提取绿叶中的色素,用体积分数为50%的酒精洗去花生子叶切片表面苏丹III或苏乃? IV染液的浮色,用体积分数70%酒精溶液进行消毒,用体积分数95%的酒精配制解离液;用质量分数为8%的盐酸改变细胞膜的通透性,使染色体的DNA和蛋白质分离;2)组合数字模型:ATP的123模型(一个腺苷,两个高能磷酸健,三个憐酸集团);DNA分子的12345模型(一个DNA分子,两条脱氧核苷酸链,磷酸集团、脱氧核糖、含氮碱基三个组成结构,四种碱基,五种组成元素)等。
2.比例模型在生物学习中还存在一些溶液配制、基因表达、遗传性状分离等过程中涉及比例关系,把这些通过比例关系构建的模型称为比例模型。
如:1)配制比例模型在必修1第六章第一节中《观察洋葱根尖分生区有丝分裂》实验,用质量分数为15%的盐酸与体积分数为95%的酒精1: 1混合配制解离液。
2)遗传性状分离比模型一对性状的杂交实验中,Fi代杂合子自交,子代基因型比例为显性纯合子:显性杂合子:隐性纯合子二1: 2: 1,表现型比例为显性性状:隐性性状=3: 1; Fi代杂合子测交,子代基因型为显性杂合子:隐性纯合子=1: 1,表现型为显性性状:隐性性状=1: 1。
数学在生物学研究中的应用实例探讨

数学在生物学研究中的应用实例探讨在当今科学领域,学科之间的交叉融合日益频繁,数学作为一门基础学科,在生物学研究中发挥着越来越重要的作用。
它为生物学家提供了强大的工具和方法,帮助他们更深入地理解生命现象、揭示生物规律。
接下来,让我们通过一些具体的实例,来探讨数学在生物学研究中的广泛应用。
在遗传学研究中,数学模型被广泛用于预测基因的遗传规律。
例如,孟德尔通过大量的豌豆杂交实验,运用统计学方法得出了基因的分离定律和自由组合定律。
他对实验数据的仔细分析和数学计算,为遗传学的发展奠定了基础。
如今,随着基因测序技术的飞速发展,生物学家可以获得大量的基因数据。
通过建立数学模型,如概率模型和统计模型,可以预测基因的突变率、基因在群体中的分布频率等,从而更好地理解基因的遗传和变异机制。
在生态学领域,数学同样有着不可或缺的地位。
生态学家常常利用数学模型来研究生物种群的动态变化。
例如,逻辑斯蒂增长模型可以描述在有限资源条件下种群数量的增长规律。
该模型表明,种群数量起初会呈指数增长,但随着资源的限制,增长速度逐渐减缓,最终达到环境所能容纳的最大容量,即所谓的“环境容纳量”。
通过对这个模型的分析和计算,生态学家可以预测种群的发展趋势,为保护濒危物种、控制有害生物的爆发等提供科学依据。
另外,数学中的微分方程在研究生态系统的稳定性方面也发挥着重要作用。
比如,洛特卡沃尔泰拉模型用于描述捕食者与被捕食者之间的相互关系。
通过求解微分方程,可以了解在不同条件下,捕食者和被捕食者种群数量的变化规律,以及生态系统的稳定性。
这有助于我们制定合理的生态保护策略,维护生态平衡。
在生物医学研究中,数学也大显身手。
药物动力学就是一个典型的例子。
药物在体内的吸收、分布、代谢和排泄过程可以用数学模型来描述。
通过建立房室模型,结合数学分析和计算,可以预测药物在体内的浓度变化,从而确定最佳的给药方案,提高药物治疗的效果,减少副作用。
在神经科学研究中,数学方法用于分析神经元的放电模式和神经网络的信息传递。
生物课堂教学数学模型论文:在生物课堂教学中构建数学模型

生物课堂教学数学模型论文:在生物课堂教学中构建数学模型摘要:模型方法是人们认识自然界的一种重要方式,也是理论思维发展的重要形式。
无论在生物科学研究还是在学习科学的过程中,模型和模型方法都起着十分重要的作用。
关键词:生物课堂教学数学模型构建模型方法是人们认识自然界的一种重要方式,也是理论思维发展的重要形式。
无论在生物科学研究还是在学习生物科学的过程中,模型和模型方法都起着十分重要的作用。
一、数学模型在生物学中的作用数学模型是联系实际问题与数学的桥梁,具有解释、判断、预测等重要功能。
引导学生构建数学模型,有利于培养学生透过现象解释本质的洞察能力。
同时,我们通过生物科学与数学的整合,有利于培养学生简约、严密的思维品质;让学生体验由具体到抽象的思维转化过程。
构建数学模型,能使学生的知识能力发生迁移,起到举一反三的效果。
二、数学模型构建的一般步骤(建立细菌增长的数学模型)三、生物课堂教学中数学模型构建举例1.种群增长模型的数学构建(1)“j”型增长模型:①条件:食物充足、空间充裕、气候适宜,没有天敌的条件下。
②此种情况下种群增长的数学公式:nt= n0mt。
③该种种群增长模型适于描述实验室中、外来物种入侵时等“理想条件”增长情况。
④研究该种种群增长模型的意义在于:引进外来物种时要慎重等。
(2)“s”型增长模型:①形成原因:自然资源和空间的有限性,种内斗争加剧,其捕食者数量增加。
②增长曲线:如图1③k值、1/2k的意义:有害动物的防治、野生生物资源的保护和利用,以及濒危动物种群的拯救和恢复。
【例题】在一个玻璃容器内,装入一定量的符合小球藻生活的营养液,接种少量的小球藻,每隔一段时间测定小球藻的个体数量,绘制成曲线,如图2所示:下列4图中能正确表示小球藻种群数量增长率随时间变化趋势的曲线分析:上述例题中小球藻的增长曲线是s型,其增长率在各个阶段是不同的。
当种群数量为k/2时,种群的增长率最高;种群数量为k值时,种群的出生率等于死亡率即种群的增长率为零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
生物数学论文1. 某植物园的植物基因型为AA、Aa、aa,人们计划用AA型植物与每种基
因型植物相结合的方案培育后代(遗传方式为常染色体遗传),经过若干代后,这种植物后代的三种基因型分布将出现什么情形?总体趋势如何?
解:由题意可知,状态转移的概率表如下所示:
状态AA Aa aa
AA与AA 1 0 0
Aa与AA 0
aa与AA 0 1 0
进而我们可以知道状态转移矩阵为
运用matlab可以求得
>>P^2=1.0000 0 0
0.7500 0.2500 0
0.5000 0.5000 0
>>P^3=1.0000 0 0
0.8750 0.1250 0
0.7500 0.2500 0
>>P^4=1.0000 0 0
0.9375 0.0625 0
0.8750 0.1250 0
>>P^5=1.0000 0 0
0.9688 0.0313 0
0.9375 0.0625 0
>>P^10=1.0000 0 0
0.9990 0.0010 0
0.9980 0.0020 0
>>P^15=1.0000 0 0
1.0000 0.0000 0
0.9999 0.0001 0
>>P^20=1.0000 0 0
1.0000 0.0000 0
1.0000 0.0000 0
由计算结果可知:当时,趋于,并且的每一行向量均相等为。
另外由于向量v满足:
列出求解向量的线性方程组
解得:
所以经过若干代后,这种植物后代的三种基因型AA、Aa 、aa分布为向量。
即将出现下列情形:即Aa 、aa类基因型将消失,所有的植物的基因型都为AA。
总体趋势为Aa和aa类基因型逐渐减少直至消失,而AA类基因型逐渐增加。
2、试建立人口Logistic(逻辑)模型,并说明模型中何参数为自然增长率,为什么?
解:设人口净增长率与人口极限以及目前的人口都有关系。
设表示维持种群生存的最大数量,当前人口数为,种群未饱和程度用比值,为比例系数。
我们建立人口Logistic(逻辑)模型:
由(1)式可得:
(3)
初始条件:当时,,即
(4)
由(3)-(4)得:
最后求解得到:
当时,,所以说明r即为自然增长率
3.1968年,介壳虫偶然从澳大利亚传入美国,威胁着美国的柠檬生产。
随后,美国又从澳大利亚引入了介壳虫的天然捕食者——澳洲瓢虫。
后来,DDT被普通使用来消灭害虫,柠檬园主想利用DDT进一步杀死介壳虫。
谁料,DDT同样杀死澳洲瓢虫。
结果,介壳虫增加起来,澳洲瓢虫反倒减少了。
试建立数学模型解释这个现象。
解:依据题意,捕食者为澳洲瓢虫,被捕食者为介壳虫。
设介壳虫的数量为,澳洲瓢虫的数量为。
考虑增长能力与本身增殖成正比,设比例系数为>0,即增长的数量为,死亡率与两个种群个体相遇的机率成正比,设比例系数为>0,即减少的数量为。
考虑增长能力与被捕食者的数量也有关系,比例系数为>0,即增长的数量为,死亡率考虑与自身成正比,设比例系数为>0,即减少的数量为。
建立数模方程组如下:
(1)
解方程组(1)得:
即得到:
所以: (2)
先从平衡点考虑:
(3)
由(3)可以求得
(4)
由此可知:为平衡点。
引入新的变量和,并且满足下列条件:
(5)
由(5)式可得:
(6)
由(1)和(6)可得:
(7)
即:
得到椭圆方程:
作变换利用极坐标:
(8)
将(8)代入(7)中得到:,即。
周期
一个周期之内种群的平均大小,的平均大小为:
可以得到:的平均值为0。
从而可得: 同理可得:
当利用DDT进一步杀死介壳虫时,设杀死率为c,则在原来的方程的基础上增加和两项,从而建立新的方程:
显然可以得到:
结果,介壳虫增加起来,澳洲瓢虫反倒减少了。
