2001年全国初中数学竞赛历年竞赛试题及参考答案
2001年全国初中数学竞赛历年竞赛试题及参考答案

2 001年TI 杯全国初中数学竞赛试题 一、 选择题(30分) 1. 化简)2(2)2(2234++-n n n ,得( )。
(A )8121-+n (B) 12+-n (C) 87 (D)47 答案:C 2. 如果c b a ,,是三个任意整数,那么2,2,2a c c b b a +++ ( )。
(A )都不是整数 (B )至少有两个整数(C )至少有一个整数 (D )都是整数答案:C3. 如果b a ,是质数,且,013,01322=+-=+-m b b m a a 那么b a a b +的值为( )。
(A )22123 (B )222125或 (C )22125 (D )222123或 答案:B4. 如图,若将正方形分成k 个全等的矩形,其中上、下各横排两个,中间竖排若干个,则k 的值为( ) ……(A )6 (B )8 (C )10 (D )12答案:B5. 如图,若PA=PB ,∠APB=2∠ACB ,AC 与PB 交于点D,且PB=4,PD=3,则AD ⨯DC等于( )。
(A )6 (B )7 (C )12 (D )16答案:B6. 若b a ,是正数,且满足)111)(111(12345b a -+=,则b a 和之间的大小关系是( )。
(A )b a > (B )b a = (C )b a < (D )不能确定答案:A二、 填空题(30分)7. 已知:2323,2323-+=+-=y x 。
那么=+22y x x y ____________。
答案:970 8. 若,28,1422=++=++x xy y y xy x 则y x +的值为____________。
答案:6或-79. 用长为1,4,4,5的线段为边作梯形,那么这个梯形的面积等于____________。
答案:36或1010. 销售某种商品,如果单价上涨m %,则售出的数量就将减少150m 。
2002~2013年全国初中数学竞赛试题及答案(完整版)

2002年全国初中数学竞赛试题一、选择题1.设a <b <0,a 2+b 2=4ab ,则ba ba -+的值为【 】 A 、3 B 、6 C 、2 D 、32.已知a =1999x +2000,b =1999x +2001,c =1999x +2002,则多项式a 2+b 2+c 2-ab -bc -ca 的值为【 】A 、0B 、1C 、2D 、33.如图,点E 、F 分别是矩形ABCD 的边AB 、BC 的中点,连AF 、CE 交于点G ,则ABCDAGCD S S 矩形四边形等于【 】A 、65 B 、54 C 、43 D 、32ABC DEF G4.设a 、b 、c 为实数,x =a 2-2b +3π,y =b 2-2c +3π,z =c 2-2a +3π,则x 、y 、z 中至少有一个值【 】A 、大于0B 、等于0C 、不大于0D 、小于0 5.设关于x 的方程ax 2+(a +2)x +9a =0,有两个不等的实数根x 1、x 2,且x 1<1<x 2,那么a 的取值范围是【 】A 、72-<a <52 B 、a >52 C 、a <72- D 、112-<a <06.A 1A 2A 3…A 9是一个正九边形,A 1A 2=a ,A 1A 3=b ,则A 1A 5等于【 】 A 、22b a + B 、22b ab a ++ C 、()b a +21D 、a +b 二、填空题7.设x 1、x 2是关于x 的一元二次方程x 2+ax +a =2的两个实数根,则(x 1-2x 2)(x 2-2x 1)的最大值为 。
8.已知a 、b 为抛物线y =(x -c)(x -c -d)-2与x 轴交点的横坐标,a <b ,则b c c a -+-的值为 。
9.如图,在△ABC 中,∠ABC =600,点P 是△ABC 内的一点,使得∠APB =∠BPC =∠CPA ,且PA =8,PC =6,则PB = 。
历届(第1-23届)希望杯数学竞赛初一七年级真题及答案

“希望杯”全国数学竞赛(第1-23届)初一年级/七年级第一/二试题目录1.希望杯第一届(1990年)初中一年级第一试试题......................003-0052.希望杯第一届(1990年)初中一年级第二试试题......................010-0123.希望杯第二届(1991年)初中一年级第一试试题...... 0错误!未定义书签。
-0204.希望杯第二届(1991年)初中一年级第二试试题...... 0错误!未定义书签。
-0265.希望杯第三届(1992年)初中一年级第一试试题...... 0错误!未定义书签。
-0326.希望杯第三届(1992年)初中一年级第二试试题...... 0错误!未定义书签。
-0407.希望杯第四届(1993年)初中一年级第一试试题...... 0错误!未定义书签。
-0508.希望杯第四届(1993年)初中一年级第二试试题...... 0错误!未定义书签。
-0589.希望杯第五届(1994年)初中一年级第一试试题...... 0错误!未定义书签。
-06610.希望杯第五届(1994年)初中一年级第二试试题..... 0错误!未定义书签。
-07311.希望杯第六届(1995年)初中一年级第一试试题..... 0错误!未定义书签。
-080 12希望杯第六届(1995年)初中一年级第二试试题..... 0错误!未定义书签。
-08713.希望杯第七届(1996年)初中一年级第一试试题..... 0错误!未定义书签。
-09814.希望杯第七届(1996年)初中一年级第二试试题....... 错误!未定义书签。
-10515.希望杯第八届(1997年)初中一年级第一试试题....... 错误!未定义书签。
-11316.希望杯第八届(1997年)初中一年级第二试试题....... 错误!未定义书签。
-12017.希望杯第九届(1998年)初中一年级第一试试题....... 错误!未定义书签。
2001年第16届江苏省初中数学竞赛试卷(初三C卷)

2001年第16届江苏省初中数学竞赛试卷(初三C卷)一、选择题(共6小题,每小题6分,满分36分)1.(2005•菏泽)已知,则的值为()A.5 B.6 C.3 D.42.若两个方程x2+ax+b=0和x2+bx+a=0只有一个公共根,则()A.a=b B.a+b=0 C.a+b=1 D.a+b=﹣13.下列给出的4个命题:命题1 若|a|=|b|,则a|a|=b|b|;命题2 若a2﹣5a+5=0,则;命题3 若x的不等式(m+3)x>1的解集是x<,则m<﹣3;命题4 若方程x2+mx﹣1=0中m>0,则该方程有一正根和一负根,且负根的绝对值较大.其中正确的命题的个数是()A.1 B.2 C.3 D.44.如图,四边形ABCD中,∠BAD=90°,AB=BC=2,AC=6,AD=3,则CD的长为()A.4 B.4C.3D.35.已知三角形的每条边长的数值都是2001的质因数,那么这样的不同的三角形共有()A.6 B.7 C.5 D.96.12块规格完全相同的巧克力,每块至多被分为两小块(可以不相等),如果这12块巧克力可以平均分给n名同学,则n可以为()A.26 B.23 C.17 D.15二、填空题(共8小题,每小题5分,满分40分)7.若=3,=2,且ab<0,则a﹣b=_________.8.如图,D、E、F分别是△ABC的边BC、CA、AB上的点,且DE∥BA,DF∥CA,(1)要使四边形AFDE是菱形,则要增加条件:_________;(2)要使四边形AFDE是矩形,则要增加条件:_________.9.方程的解是_________.10.要使26+210+2x为完全平方数,那么非负整数x可以是_________.(要求写出x的3个值)11.如图,直线y=﹣2x+6与x轴、y轴分别交于P、Q两点,把△POQ沿PQ翻折,点O落在R处,则点R的坐标是_________.12.如图,已知八边形ABCDEFGH中4个正方形的面积分别为25,144,48,121个平方单位,PR=13(单位),则该八边形的面积=_________平方单位.13.如图,设△ABC的两边AC与BC之和为a,M是AB的中点,MC=MA=5,则a的取值范围是_________.14.如图,一个田字形的区域A、B、C、D栽种观赏植物,要求同一个区域中种同一种植物,相邻的两块种不同的植物,现有4种不同的植物可供选择,那么有_________种栽种方案.三、解答题(共4小题,满分64分)15.某商店有A种练习本出售,每本零售价为0.30元,1打(12本)售价为3.00元,买10打以上的,每打还可以按2.70付款.(1)初三(1)班共57人,每人需要1本A种练习本,则该班集体去买时,最少需付多少元?(2)初三年级共227人,每人需要1本A种练习本,则该年级集体去买时,最少需付多少元?16.设x1、x2是方程2x2﹣4mx+2m2+3m﹣2=0的两个实根,当m为何值时,x12+x22有最小值,并求这个最小值.17.(1)已知:如图1,在四边形ABCD中,BC⊥CD,∠ACD=∠ADC.求证:AB+AC>;(2)已知:如图2,在△ABC中,AB上的高为CD,试判断(AC+BC)2与AB2+4CD2之间的大小关系,并证明你的结论.18.编号为1到25的25个弹珠被分放在两个篮子A和B中.15号弹珠在篮子A中,把这个弹珠从篮子A移至篮子B中,这时篮子A中的弹珠号码数的平均数等于原平均数加,篮子B中弹珠号码数的平均数也等于原平均数加.问原来在篮子A中有多少个弹珠?2001年第16届江苏省初中数学竞赛试卷(初三C卷)参考答案与试题解析一、选择题(共6小题,每小题6分,满分36分)1.(2005•菏泽)已知,则的值为()A.5 B.6 C.3 D.4考点:二次根式的化简求值。
-初中数学竞赛题(含答案)

初中数学竞赛一、选择题(每小题7分,共56分.以下每题的4个结论中,仅有一个是正确的,请将正确答案的英文字母填在题后的圆括号内)1.在-|-3|3,-(-3)3,(-3)3,-33中,最大的是( B ). (A)-|-3|3 (B)-(-3)3 (C)(-3)3 (D)-332. “a 的2倍与b 的一半之和的平方,减去a 、b 两数平方和的4倍”用代数式表示应为( )(A)2a+(21b 2)-4(a+b)2 (B)(2a+21b)2-a+4b 2(c)(2a+21b)2-4(a 2+b 2) (D)(2a+21b)2-4(a 2+b 2)23.若a 是负数,则a+|-a|( C ),(A)是负数 (B)是正数 (C)是零 (D)可能是正数,也可能是负数 4.如果n 是正整数,那么表示“任意负奇数”的代数式是( ). (A)2n+l (B)2n-l (C)-2n+l (D)-2n-l5.已知数轴上的三点A 、B 、C 分别表示有理数a 、1、-l ,那么|a+1|表示( ). (A)A 、B 两点的距离 (B)A 、C 两点的距离 (C)A 、B 两点到原点的距离之和 (D)A 、C 两点到原点的距离之和6.如图,数轴上标出若干个点,每相邻两点相距1个单位,点A 、B 、C 、D 对应的数分别是整数a 、b 、c 、d ,且d-2a =10,那么数轴的原点应是( ). (A)A 点 (B)B 点 (C)C 点 (D)D 点7.已知a+b =0,a≠b ,则化简a b (a+1)+ba(b+1)得( ).(A)2a (B)2b (C)+2 (D)-28.已知m<0,-l<n<0,则m ,mn ,mn 2由小到大排列的顺序是 ( ).(A)m ,mn ,mn 2 (B)mn ,mn 2,m (C)mn 2,mn ,m (D)m ,mn 2,mn 二、填空题(每小题?分,共84分)9.计算:31a -(21a -4b -6c)+3(-2c+2b)=10.计算:0.7×194+243×(-15)+0.7×95+41×(-15)=ll.某班有男生a(a>20)人,女生20人,a-20表示的实际意义是12.在数-5,-3,-1,2,4,6中任取三个相乘,所得的积中最大的是13.下表中每种水果的重量是不变的,表的左边或下面的数是所在行或所在列水果的总重量,则表中问号“?”表示的数是 梨 梨 苹果 苹果 30 梨 型 梨 梨 28 荔枝 香蕉 苹果 梨 20 香蕉 香蕉 荔枝 苹果 ? 19 20 25 3014.某学生将某数乘以-1.25时漏了一个负号,所得结果比正确结果小0.25,则正确结果应是 .15.在数轴上,点A 、B 分别表示-31和51,则线段AB 的中点所表示的数是 .16.已知2a x b n-1与-3a 2b 2m (m 是正整数)是同类项,那么(2m-n)x =17.王恒同学出生于20世纪,他把他出生的月份乘以2后加上5,把所得的结果乘以50后加上出生年份,再减去250,最后得到2 088,则王恒出生在 年 月. 18.银行整存整取一年期的定期存款年利率是2.25%,某人1999年12月3日存入1 000元,2000年12月3日支取时本息和是 元,国家利息税税率是20%,交纳利息税后还有 元.19.有一列数a 1,a 2,a 3,a 4,…,a n ,其中 a 1=6×2+l ; a 2=6×3+2; a 3=6×4+3; a 4=6×5+4;则第n 个数a n = ;当a n =2001时,n = . 20.已知三角形的三个内角的和是180°,如果一个三角形的三个内角的度数都是小于120的质数,则这个三角形三个内角的度数分别是第十五届江苏省初中数学竞赛参考答案初一年级第一试一、1.B 2.C 3.C 4.C 5.B 6.B 7.D 8.D二、9.一6a+1 06. 10.一43.6.11.男生比女生多的人数.1 2.90. 1 3.1 6. 1 4.0.1 2 5. 1 5.-1511 6.1. 1 7.1988;1. 18.1022.5;101 8. 1 9.7n+6;2 8 5.2 O .2,8 9,8 9或2,7 1,1 07(每填错一组另扣2分).一、选择题1.已知x=2是关于x 的方程3x-2m=4的根,则m 的值是( ) (A)5 (B)-5 (C)1 (D)-12.已知a+2=b-2=2c=2001,且a+b+c=2001k ,那么k 的值为( )。
全国初中数学竞赛历年竞赛试题及参考答案

初中数学竞赛试题答题时注意:1.用圆珠笔或钢笔作答; 2.解答书写时不要超过装订线; 3.草稿纸不上交.一、选择题(共5小题,每小题7分,共35分. 每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是准确的. 请将准确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.设1a =,则代数式32312612a a a +--的值为( ).(A )24 (B )25 (C )10 (D )12 2.对于任意实数a b c d ,,,,定义有序实数对a b (,)与c d (,)之间的运算“△”为:(a b ,)△(c d ,)=(ac bd ad bc ++,).如果对于任意实数u v ,, 都有(u v ,)△(x y ,)=(u v ,),那么(x y ,)为( ).(A )(0,1) (B )(1,0) (C )(﹣1,0) (D )(0,-1)3.若1x >,0y >,且满足3y y xxy x x y==,,则x y +的值为( ).(A )1 (B )2 (C )92(D )1124.点D E ,分别在△ABC 的边AB AC ,上,BE CD ,相交于点F ,设1234BDF BCF CEF EADF S S S S S S S S ∆∆∆====四边形,,,,则13S S 与24S S 的大小关系为( ).(A )1324S S S S < (B )1324S S S S = (C )1324S S S S > (D )不能确定 5.设3333111112399S =++++,则4S 的整数部分等于( ).(A )4 (B )5 (C )6 (D )7二、填空题(共5小题,每小题7分,共35分)6.若关于x 的方程2(2)(4)0x x x m --+=有三个根,且这三个根恰好可 以作为一个三角形的三条边的长,则m的取值范围是 .7.一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3,3,4;另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8. 同时掷这两枚骰子,则其朝上的面两数字之和为奇数的概率是 .8.如图,点A B ,为直线y x =上的两点,过A B ,两点分别作y 轴的平行线交双曲线1y x=(x >0)于C D ,两点. 若2BD AC =,则224OC OD - 的值为 .9.若112y x x =-+-的最大值为a ,最小值为b ,则22a b +的值为 .10.如图,在Rt △ABC 中,斜边AB 的长为35,正方形CDEF 内接于△ABC ,且其边长为12,则△ABC 的周长为 .三、解答题(共4题,每题20分,共80分)11.已知关于x 的一元二次方程20x cx a ++=的两个整数根恰好比方程20x ax b ++=的两个根都大1,求a b c ++的值.12.如图,点H 为△ABC 的垂心,以AB 为直径的⊙(第8题)(第10题)1O 和△BCH 的外接圆⊙2O 相交于点D ,延长AD 交CH 于点P ,求证:点P 为CH 的中点.13.如图,点A 为y 轴正半轴上一点,A B ,两点关于x 轴对称,过点A 任作直线交抛物线223y x=于P ,Q 两点. (1)求证:∠ABP =∠ABQ ;(2)若点A 的坐标为(0,1),且∠PBQ =60º,试求所有满足条件的直线PQ 的函数解析式.14.如图,△ABC 中,60BAC ∠=︒,2AB AC =.点P 在△ABC 内,且352PA PB PC ===,,,求△ABC 的面积.(第13题)(第12题)(第14题)初中数学竞赛试题参考答案一、选择题 1.A解:因为71a =-, 17a +=, 262a a =-, 所以322312612362126261261260662126024.a a a a a a a a a a a +--=-+---=--+=---+=()()()2.B解:依定义的运算法则,有ux vy u vx uy v +=⎧⎨+=⎩,,即(1)0(1)0u x vy v x uy -+=⎧⎨-+=⎩,对任何实数u v ,都成立. 因为实数u v ,的任意性,得(x y ,)=(1,0).3.C解:由题设可知1y y x -=,于是341y y x yx x -==,所以 411y -=, 故12y =,从而4x =.于是92x y +=.4.C解:如图,连接DE ,设1DEFS S ∆'=,则1423S S EF S BF S '==,从而有1324S S S S '=.因为11S S '>,所以1324S S S S >.5.A解:当2 3 99k =,,,时,因为()()()32111112111k k k k k k k ⎡⎤<=-⎢⎥-+-⎣⎦, 所以 3331111115111239922991004S ⎛⎫<=++++<+-< ⎪⨯⎝⎭. (第4题)于是有445S <<,故4S 的整数部分等于4.二、填空题 6.3<m ≤4解:易知2x =是方程的一个根,设方程的另外两个根为12 x x ,,则124x x +=,12x x m =.显然1242x x +=>,所以122x x -<, 164m ∆=-≥0,即()2121242x x x x +-<,164m ∆=-≥0,所以1642m -<, 164m ∆=-≥0,解之得 3<m ≤4.7.19解: 在36对可能出现的结果中,有4对:(1,4),(2,3),(2,3),(4,1)的和为5,所以朝上的面两数字之和为5的概率是41369=. 8.6解:如图,设点C 的坐标为a b (,),点D 的坐标为c d (,),则点A 的坐标为a a (,),点B 的坐标为.c c (,) 因为点C D ,在双曲线1y x=上,所以11ab cd ==,. 因为AC a b =-,BD c d =-, 又因为2BD AC =,于是22222242c d a b c cd d a ab b -=--+=-+,(),所以 22224826a b c d ab cd +-+=-=()(),即224OC OD -=6.9.32解:由1x -≥0,且12x -≥0,得12≤x ≤1.22213113122()2222416y x x x =+-+-=+--+. 因为13124<<,所以当34x =时,2y 取到最大值1,故1a =. (第8题)当12x =或1时,2y 取到最小值12,故2b =.所以,2232a b +=. 10.84解:如图,设BC =a ,AC =b ,则22235a b +==1225. ①又Rt △AFE ∽Rt △ACB ,所以FE AFCB AC=,即1212b a b-=,故 12()a b ab +=. ② 由①②得2222122524a b a b ab a b +=++=++()(), 解得a +b =49(另一个解-25舍去),所以493584a b c ++=+=.三、解答题11.解:设方程20x ax b ++=的两个根为αβ,,其中αβ,为整数,且α≤β,则方程20x cx a ++=的两根为11αβ++,,由题意得()()11a a αβαβ+=-++=,,两式相加得 2210αβαβ+++=, 即 (2)(2)3αβ++=,所以 2123αβ+=⎧⎨+=⎩,; 或232 1.αβ+=-⎧⎨+=-⎩,解得 11αβ=-⎧⎨=⎩,; 或53.αβ=-⎧⎨=-⎩,又因为[11]a b c αβαβαβ=-+==-+++(),,()(),所以 012a b c ==-=-,,;或者8156a b c ===,,,(第10题)故3a b c ++=-,或29.12.证明:如图,延长AP 交⊙2O 于点Q , 连接 AH BD QB QC QH ,,,,.因为AB 为⊙1O 的直径, 所以∠ADB =∠BDQ =90°, 故BQ 为⊙2O 的直径. 于是CQ BC BH HQ ⊥⊥,.又因为点H 为△ABC 的垂心,所以.AH BC BH AC ⊥⊥,所以AH ∥CQ ,AC ∥HQ ,四边形ACQH 为平行四边形. 所以点P 为CH 的中点.13.解:(1)如图,分别过点P Q , 作y 轴的垂线,垂足分别为C D , . 设点A 的坐标为(0,t ),则点B 的坐标为(0,-t ). 设直线PQ 的函数解析式为y kx t =+,并设P Q ,的坐标分别为 P P x y (,),Q Q x y (,).由223y kx t y x =+⎧⎪⎨=⎪⎩,, 得 2203x kx t --=, 于是 32P Q x x t =-,即 23P Q t x x =-.于是222323P P Q Qx t y t BC BD y t x t ++==++22222()333.222()333P P Q P P Q P Q Q P Q Q Q P x x x x x x x x x x x x x x --===--- 又因为P Q x PC QD x =-,所以BC PCBD QD=. 因为∠BCP =∠90BDQ =︒,所以△BCP ∽△BDQ ,(第12题)(第13题)故∠ABP =∠ABQ .(2)解法一 设PC a =,DQ b =,不妨设a ≥b >0,由(1)可知∠ABP =∠30ABQ =︒,BC ,BD ,所以 AC 2-,AD =2.因为PC ∥DQ ,所以△ACP ∽△ADQ .于是PC ACDQ AD=,即a b ,所以a b +=.由(1)中32P Q x x t =-,即32ab -=-,所以322ab a b =+=,于是可求得2a b ==将2b =代入223y x =,得到点Q ,12).再将点Q 的坐标代入1y kx =+,求得3k =-所以直线PQ 的函数解析式为1y =+.根据对称性知,所求直线PQ 的函数解析式为1y =+,或1y +. 解法二 设直线PQ 的函数解析式为y kx t =+,其中1t =. 由(1)可知,∠ABP =∠30ABQ =︒,所以2BQ DQ =.故 2Q x =.将223Q Q y x =代入上式,平方并整理得 4241590Q Q x x -+=,即22(43)(3)0Q Q x x --=.所以 2Q x =又由 (1)得3322P Q x x t =-=-,32P Q x x k +=. 若3Q x =,代入上式得 3P x =-, 从而 23()3P Q k x x =+=-.同理,若3Q x =, 可得32P x =-, 从而 23()3P Q k x x =+=.所以,直线PQ 的函数解析式为31y x =-+,或31y x =+. 14.解:如图,作△ABQ ,使得QAB PAC ABQ ACP ∠=∠∠=∠,,则△ABQ ∽△ACP . 因为2AB AC =,所以相似比为2. 于是22324AQ AP BQ CP ====,.60QAP QAB BAP PAC BAP BAC ∠=∠+∠=∠+∠=∠=︒.由:2:1AQ AP =知,90APQ ∠=︒,于是33PQ AP ==.所以 22225BP BQ PQ ==+,从而90BQP ∠=︒. 于是222()2883AB PQ AP BQ =++=+ .故 213673sin 60282ABC S AB AC AB ∆+=⋅︒==.(第14题)。
历年初中数学竞赛真题库含答案
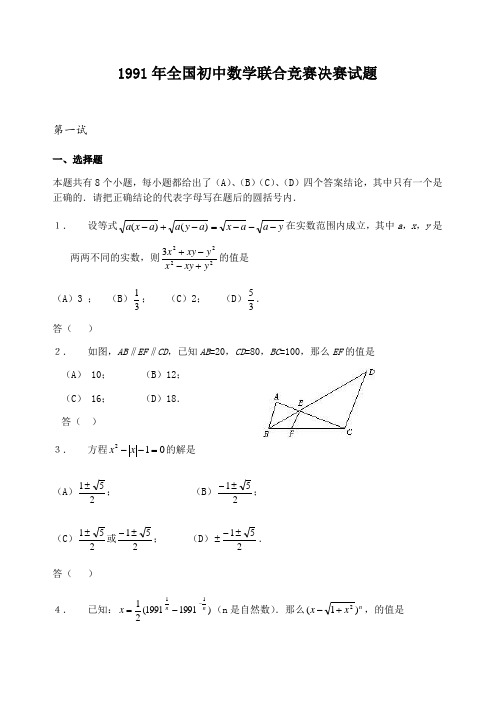
1991年全国初中数学联合竞赛决赛试题第一试一、选择题本题共有8个小题,每小题都给出了(A )、(B )(C )、(D )四个答案结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1. 设等式y a a x a y a a x a ---=-+-)()(在实数范围内成立,其中a ,x ,y 是两两不同的实数,则22223yxy x y xy x +--+的值是 (A )3 ; (B )31; (C )2; (D )35. 答( )2. 如图,AB ‖EF ‖CD ,已知AB =20,CD =80,BC =100,那么EF 的值是(A ) 10; (B )12;(C ) 16; (D )18.答( )3. 方程012=--x x 的解是(A )251±; (B )251±-; (C )251±或251±-; (D )251±-±. 答( )4.已知:)19911991(2111n n x --=(n 是自然数).那么n x x )1(2+-,的值是(A)11991-; (B)11991--;(C)1991)1(n -; (D)11991)1(--n .答( )5. 若M n 1210099321=⨯⨯⨯⨯⨯ ,其中M为自然数,n 为使得等式成立的最大的自然数,则M(A)能被2整除,但不能被3整除;(B)能被3整除,但不能被2整除;(C)能被4整除,但不能被3整除;(D)不能被3整除,也不能被2整除.答( )6. 若a ,c ,d 是整数,b 是正整数,且满足c b a =+,d c b =+,a d c =+,那么 d c b a +++的最大值是(A)1-;(B)5-;(C)0;(D)1.答( )7. 如图,正方形OPQR 内接于ΔABC .已知ΔAOR 、ΔBOP 和ΔCRQ 的面积分别是11=S ,32=S 和13=S ,那么,正方形OPQR 的边长是 (A)2;(B)3;(C)2 ;(D)3.答( )8. 在锐角ΔABC 中,1=AC ,c AB =, 60=∠A ,ΔABC 的外接圆半径R ≤1,则 (A)21< c < 2 ; (B)0< c ≤21; 答( )(C )c > 2; (D )c = 2.答( )二、填空题1.E是平行四边形ABCD 中BC 边的中点,AE 交对角线BD 于G ,如果ΔBEG 的面积是1,则平行四边形ABCD 的面积是 . 2.已知关于x 的一元二次方程02=++c bx ax 没有实数解.甲由于看错了二次项系数,误求得两根为2和4;乙由于看错了某一项系数的符号,误求得两根为-1和4,那么,=+ac b 32 .3.设m ,n ,p ,q 为非负数,且对一切x >0,qpn m x x x x )1(1)1(+=-+恒成立,则 =++q p n m 22)2( .4.四边形ABCD 中,∠ ABC 135=,∠BCD 120=,AB 6=,BC 35-=,CD = 6,则AD = .第二试x + y , x - y , x y , yx 四个数中的三个又相同的数值,求出所有具有这样性质的数对(x , y ).二、ΔABC中,AB<AC<BC,D点在BC上,E点在BA的延长线上,且BD=BE=AC,ΔBDE的外接圆与ΔABC的外接圆交于F点(如图).求证:BF=AF+CF三、将正方形ABCD分割为2n个相等的小方格(n是自然数),把相对的顶点A,C染成红色,把B,D染成蓝色,其他交点任意染成红、蓝两色中的一种颜色.证明:恰有三个顶点同色的小方格的数目必是偶数.1992年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.满足1=+-ab b a 的非负整数),(b a 的个数是(A)1; (B)2; (C)3; (D)4.2.若0x 是一元二次方程)0(02≠=++a c bx ax 的根,则判别式ac b 42-=∆与平方式20)2(b ax M +=的关系是(A)∆>M (B)∆=M (C)∆>M ; (D)不确定.3.若01132=+-x x ,则44-+x x 的个位数字是(A)1; (B)3; (C)5; (D)7.答( )4.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为(A)7; (B)6; (C)5; (D)4.答( )5.如图,正比例函数)0(>==a ax y x y 和的图像与反比例函数)0(>=k xk y 的图像分别相交于A 点和C 点.若AOB Rt ∆和COD ∆的面积分别为S 1和S 2,则S 1与S 2的关系是 (A)21S S > (B)21S S =(C)21S S < (D)不确定 答( )6.在一个由88⨯个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为1S ,把圆周经过的所有小方格的圆内部分的面积之和记为2S ,则21S S 的整数部分是 (A)0; (B)1; (C)2; (D)3.答( )7.如图,在等腰梯形ABCD 中, AB //CD , AB=2CD ,︒=∠60A ,又E 是底边AB 上一点,且FE=FB=AC , FA=AB .则AE :EB 等于(A)1:2 (B)1:3(C)2:5 (D)3:10答( )8.设9321,,,,x x x x ⋅⋅⋅均为正整数,且921x x x <⋅⋅⋅<<,220921=+⋅⋅⋅++x x x ,则当54321x x x x x ++++的值最大时,19x x -的最小值是(A)8; (B)9; (C)10; (D)11.答( )二.填空题1.若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________.2.若0≠x ,则x x x x 44211+-++的最大值是__________.3.在ABC ∆中,B A C ∠∠=∠和,90 的平分线相交于P 点,又AB PE ⊥于E 点,若3,2==AC BC ,则=⋅EB AE .4.若b a ,都是正实数,且0111=+--b a b a ,则=+33)()(ba ab . 第二试一、设等腰三角形的一腰与底边的长分别是方程062=+-a x x 的两根,当这样的三角形只有一个时,求a 的取值范围.二、如图,在ABC ∆中,D AC AB ,=是底边BC 上一点,E 是线段AD 上一点,且A CED BED ∠=∠=∠2.求证:CD BD 2=.三、某个信封上的两个邮政编码M 和N 均由0,1,2,3,5,6这六个不同数字组成,现有四个编码如下:A :320651B :105263C :612305D :316250已知编码A 、B 、C 、D 各恰有两个数字的位置与M 和N 相同.D 恰有三个数字的位置与M 和N 相同.试求:M 和N.1993年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个小题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.多项式1612+-x x 除以12-x 的余式是(A)1; (B)-1; (C)1-x ; (D)1+x ;2.对于命题Ⅰ.内角相等的圆内接五边形是正五边形.Ⅱ.内角相等的圆内接四边形是正四边形,以下四个结论中正确的是(A )Ⅰ,Ⅱ都对 (B )Ⅰ对,Ⅱ错 (C )Ⅰ错,Ⅱ对. (D )Ⅰ,Ⅱ都错.3.设x 是实数,11++-=x x y .下列四个结论:Ⅰ.y 没有最小值;Ⅱ.只有一个x 使y 取到最小值;Ⅲ.有有限多个x (不止一个)使y 取到最大值;Ⅳ.有无穷多个x 使y 取到最小值.其中正确的是(A )Ⅰ (B )Ⅱ (C )Ⅲ (D )Ⅳ4.实数54321,,,,x x x x x 满足方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=++=++=++.;;;;52154154354324321321a x x x a x x x a x x x a x x x a x x x其中54321,,,,a a a a a 是实常数,且54321a a a a a >>>>,则54321,,,,x x x x x 的大小顺序是(A)54321x x x x x >>>>; (B )53124x x x x x >>>>;(C )52413x x x x x >>>>; (D )24135x x x x x >>>>.5.不等式73)1(12+<-<-x x x 的整数解的个解(A )等于4 (B )小于4 (C )大于5 (D )等于56.在ABC ∆中,BC AO O A =∠,,是垂心是钝角,则)cos(OCB OBC ∠+∠的值是 (A)22- (B)22 (C)23 (D)21-. 答( )7.锐角三角ABC 的三边是a , b , c ,它的外心到三边的距离分别为m , n ,p ,那么m :n :p 等于 (A)c b a 1:1:1; (B)c b a :: (C)C B A cos :cos :cos (D)C B A sin :sin :sin .答( )8.13333)919294(3-+-可以化简成 (A))12(333+; (B))12(333- (C)123- (D)123+答( )二.填空题1. 当x 变化时,分式15632212++++x x x x 的最小值是___________. 2.放有小球的1993个盒子从左到右排成一行,如果最左面的盒里有7个小球,且每四个相邻的盒里共有30个小球,那么最右面的盒里有__________个小球.3.若方程k x x =--)4)(1(22有四个非零实根,且它们在数轴上对应的四个点等距排列,则k =____________.4.锐角三角形ABC 中,︒=∠30A .以BC 边为直径作圆,与AB , AC分别交于D , E ,连接DE , 把三角形ABC 分成三角形ADE 与四边形BDEC ,设它们的面积分别为S 1, S 2,则S 1:S 2=___________. 第二试一.设H 是等腰三角形ABC 垂心,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积HBC ABC S S ∆∆⋅的值变小,变大,还是不变?证明你的结论.二.ABC ∆中, BC =5, AC =12, AB =13, 在边AB ,AC 上分别取点D , E , 使线段DE 将ABC ∆分成面积相等的两部分.试求这样的线段DE 的最小长度.三.已知方程0022=++=++b cx x c bx x 及分别各有两个整数根21,x x 及21,x x '',且,021>x x 021>''x x . (1)求证:;0,0,0,02121<'<'<<x x x x (2)求证:1-b ≤c ≤1+b ; (3)求c b ,所有可能的值.1994年全国初中数学联赛试题第一试(4月3日上午8:30—9:30)考生注意:本试共两道大题,满分80分.一、选择题(本题满分48分,每小题6分)本题共有8个小题都给出了A,B、C,D,四个结论,其中只有一个是正确的,请把你认为正确结论的代表字母写在题后答案中的圆括号内,每小题选对得6分;不选、选错或选出的代表字母超过一个(不论是否写在圆括号内),一律得0分.〔答〕( )2.设a,b,c是不全相等的任意实数,若x=a2-bc,y=b2-ca,z=c2-ab,则x,y,zA.都不小于0B.都不大于0C.至少有一个小0于D.至少有一个大于0〔答〕( )3.如图1所示,半圆O的直径在梯形ABCD的底边AB上,且与其余三边BC,CD,DA相切,若BC=2,DA=3,则AB的长A.等于4B.等于5C.等于6D.不能确定〔答〕( )A.1 B.-1 C.22001D.-22001〔答〕( )5.若平行直线EF,MN与相交直线AB,CD相交成如图2所示的图形,则共得同旁内角A.4对B.8对C.12对D.16对〔答〕( )〔答〕( )7.设锐角三角形ABC的三条高AD,BE,CF相交于H。
初二数学竞赛试题及参考答案

八年级数学竞赛试题及参考答案一、选择题(每小题5分,共30分) 1.已知2220082008,2ca b a b c k k +=-==++=,且那么的值为( ). A .4 B .14 C .-4 D .14- 2.若方程组312433x y k x y k x y x y +=+⎧<<-⎨+=⎩的解为,,且,则的取值范围是( ). A .102x y <-<B .01x y <-<C .31x y -<-<-D .11x y -<-< 3.计算:2399100155555++++++=( ). A .10151- B .10051- C .101514- D .100514- 4.如图,已知四边形ABCD 的四边都相等,等边△AEF 的顶点E 、F 分别在BC 、CD 上,且AE=AB ,则∠C=( ). A .100° B .105° C .110° D .120°5.已知5544332222335566a b c d a b c d ====,,,,则、、、的大小关系是( ).A .a b c d >>>B .a b d c >>>C .b a c d >>>D .a d b c >>>6.如果把分数97的分子、分母分别加上正整数913a b 、,结果等于,那么a b +的最小(第4题图)DCB值是( ).A .26B .28C .30D .32 二、填空题:(每小题5分,共30分)7.方程组200820092007200720062008x y x y -=⎧⎨-=⎩的解是 .8.如图,已知AB 、CD 、EF 相交于点O ,EF ⊥AB ,OG 为∠COF 的平分线,OH 为∠DOG 的平分线,若∠AOC :∠COG=4:7,则∠GOH= .9.小张和小李分别从A 、B 两地同时出发,相向而行,第一次在距A 地5千米处相遇,继续往前走到各地(B 、A )后又立即返回,第二次在距B 地4千米处两人再次相遇,则A 、B 两地的距离是 千米.10.在△ABC 中,∠A 是最小角,∠B 是最大角,且2∠B=5∠A ,若∠B 的最大值为m °,最小值为n °,则m °+n °= .11.已知21()()()04b cb c a b c a a a+-=--≠=,且,则 .12.设p q ,均为正整数,且7111015p q <<,当q 最小时,pq 的值为 .以下三、四、五题要求写出解题过程. 三、(本题满分20分)13.在一次抗击雪灾而募捐的演出中,晨光中学有A 、B 、C 、D 四个班的同学参加演出,已知A 、B 两个班共16名演员,B 、C 两个班共20名演员,C 、D 两个班共34名演员,且各班演员的人数正好按A 、B 、C 、D 次序从小到大排列,求各班演员的人数.G(第8题图)HOFEDCBA(第15题图)EDCBA四、(本题满分20分)14.已知2211x x y y x y =+=+≠,,且. ⑴ 求证:1x y +=. ⑵ 求55x y +的值. 五、(本题满分20分)15.如图,在△ABC 中AC >BC ,E 、D 分别是AC 、BC 上的点,且∠BAD=∠ABE ,AE=BD . 求证:∠BAD=12∠C .参考答案一、选择题1.A 2.B 3.C 4.A 5.A 6.B二、填空题: 7、21x y =⎧⎨=⎩ 8、72.5° 9、11 10、175° 11、2 12、68213、解:依题意得:A+B=16,B+C=20,C+D=34∵A <B <C <D ,∴A <8,B >8,B <10,C >10,C <17,D >17 由8<B <10且B 只能取整数得,B=9 ∴C=11,D=23,A=7答:A 、B 、C 、D 各班演员人数分别是7人、9人、11人、23人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 001年TI 杯全国初中数学竞赛试题 一、 选择题(30分) 1. 化简)2(2)2(2234++-n n n ,得( )。
(A )8121-+n (B) 12+-n (C) 87 (D)4
7 答案:C 2. 如果c b a ,,是三个任意整数,那么
2,2,2a c c b b a +++ ( )。
(A )都不是整数 (B )至少有两个整数
(C )至少有一个整数 (D )都是整数
答案:C
3. 如果b a ,是质数,且,013,01322=+-=+-m b b m a a 那么
b a a b +的值为( )。
(A )22123 (B )222125或 (C )22125 (D )222
123或 答案:B
4. 如图,若将正方形分成k 个全等的矩形,其中上、下各横排两个,中间竖排若干个,则
k 的值为( ) ……
(A )6 (B )8 (C )10 (D )12
答案:B
5. 如图,若PA=PB ,∠APB=2∠ACB ,AC 与PB 交于点D,且PB=4,PD=3,则AD ⨯DC
等于( )。
(A )6 (B )7 (C )12 (D )16
答案:B
6. 若b a ,是正数,且满足)111)(111(12345b a -+=,则b a 和之间的大小关系是
( )。
(A )b a > (B )b a = (C )b a < (D )不能确定
答案:A
二、 填空题(30分)
7. 已知:232
3,232
3-+=+-=y x 。
那么=+2
2y x x y ____________。
答案:970 8. 若,28,1422=++=++x xy y y xy x 则y x +的值为____________。
答案:6或-7
9. 用长为1,4,4,5的线段为边作梯形,那么这个梯形的面积等于____________。
答案:36或10
10. 销售某种商品,如果单价上涨m %,则售出的数量就将减少
150m 。
为了使该商品的销售总金额最大,那么m 的值应该确定为____________。
答案:25
11. 在直角坐标系xOy 中,x 轴上的动点M (x ,0)到定点P (5,5)、Q (2,1)的距离
分别为MP 和MQ ,那么当MP+MQ 取最小值时,点M 的横坐标=x ____________。
答案:2
5 12. 已知实数b a ,满足2222,1b a ab t b ab a --==++且,那么t 的取值范围是
____________。
答案:313-≤≤-t
三、 解答题(60分)
13. 某个学生参加军训,进行打靶训练,必须射击10次。
在第6、第7、第8、第9次射击
中,分别得了9.0环、8.4环、8.1环、9.3环。
他的前9次射击所得的平均环数高于前5次射击所得的平均环数。
如果他要使10次射击的平均环数超过8.8环。
那么他在第10次射击中至少要得多少环?(每次射击所得环数都精确到0.1环)
14. 如图,已知点P 是⊙O 外一点,PS 、PT 是⊙O 的两条切线,过点P 作⊙O 的割线PAB ,
交⊙O 于A,B 两点,并交ST 于点C 。
求证:
)11(211PB
PA PC +=.
答案:P ,A ,C ,B 四点成调和点列(德站解答)
15. 如图,已知圆O 的两条半径OA 与OB 互相垂直,C 为弧AmB 上的一点,且
222BC OB AB =+,求OAC ∠的度数。
16. 对非负整数n ,满足方程n z y x =++2的非负整数),,(z y x 的组数记为n a
(1) 求3a 的值;
(2) 求2001a 的值;
o m
A
答案:。
