水力学第四章 第三节
水轮机 : r1 r2， r1 r2
2 p1 w12 p2 w2 ( r1 )2 ( r2 )2 ( z1 ) ( z2 ) h γ 2g γ 2g 2g 2g
c2
u2 w1
y
c1 2 ωy
w2
2
水轮机：液体机械能减少成为 z 有效动力及克服能量损失。 ω2r
u1 1 1 ω2x z
x
2 ω r1 )2 p1 w12 ( p2 w2 ( r2 )2 ' z1 z2 hw γ 2g 2g γ 2g 2g g ω 2 2 2 p1 w1 p2 w2 ( r1 ) ( r2 )2 ( z1 ) ( z2 ) h γ 2g γ 2g 2g 2g
4 水动力学基本原理
4.1 理想液体运动的微分方程 4.2 理想液体的伯努利方程 4.3 实际液体恒定元流的能量方程
4.4
均匀流与非均匀流
4.5 实际液体恒定总流的能量方程 4.6 恒定总流的动量方程 4.7 因次分析
4.3.1 实际液体恒定流的能量方程
从理想液体恒定流中取出一柱状微小流束，并截 取1-1和2-2断面之间的流段ds来研究，流段可以看作 横断面为dA 的柱体。 对微分段应用s方向的牛顿第二定律，则
2 ds 1 α p g 1 dA
dA
s
p+dp
2 z+dz
z 0
0
2 ds 1 α p g 1
dA
s
p+dp
du pdA ( p dpz+ )dA dAds cos dAds dz g dt
2
z
du du ds du d u 2 u （ ） dt ds dt ds ds 2 dA dAds cos dAdz 0 d p u2 （z )0 化简得 ds 2g
u1 p 2 u2 z1 ＝z 2 hw ' 2g 2g
1
p1
2
2
2
不可压缩实际液体恒定流元流的伯努利方程
在重力和离心力共同作用下，实际 c2 w2 2
u2 y 液体元流从1运动到2，则 c1 2 ωy ω2r z
w1
u1 1 1 ω2x z ω
x
2 p1 w12 ( r1 )2 p2 w2 ( r2 )2 z1 z2 h' w γ 2g 2g γ 2g 2g
积分上 式得到
u2 z C 2g
p
2
1
对微小流束上两个过水断面则有
u1 p 2 u2 z1 z2 2g 2g p1
2 2
不可压缩理想液体恒定流微小流束的能量方程 (伯努里方程) 瑞士科学家伯努里（Bernoulli，1738）
二、实际液体恒定流微小流束的能量方程式
g
2 p1 w12 p2 w 2 ( r1 )2 ( r2 )2 ( z1 ) ( z2 ) h' w γ 2g γ 2g 2g 2g
for water pump : r1 r2
2 p1 w12 p2 w 2 ( r1 )2 ( r2 )2 ( z1 ) ( z2 ) h' w γ 2g γ 2g 2g 2g
ω g
实际元流单位重量液体在转轮中的能量损失
c2
u2 w1
y
水泵：水流从转轮叶片中获得能量 z c1 2 ωy
w2
2
ω2r xຫໍສະໝຸດ u1 1 1 ω2x zω
2 p1 w12 ( r1 )2 p2 w2 ( r2 )2 z1 z2 h' w ω γ 2g 2g γ 2g 2g
对于实际液体，因为存在粘性，在流
动过程中，要消耗一部分能量用于克服摩
擦力，液体的机械能沿程减少，即存在能
量损失。
在重力作用下，实际元流从1运动到2，则
u1 p 2 u2 z1 z2 2g 2g p1
2 2
2 1
令： hw’= 单位重量的液体 从断面1-1运动至断面2-2所损失的能量，则
水力学第4章
n
1/6 1/6.6
1/7
1/8.8
α β
1.077 1.065 1.058 1.039 1.027 1.023 1.020 1.013
V/Vmax 0.791 0.807
0.817 0.850
>2 ╳ 106 1/10
1.031 1.011 0.866
2019/10/24
4.8 量纲分析和相似理论
x
x0
f (x0 ) f '(x0 )
f (x) x 2 log x 9.8021 x 0.8686 ln x 9.8021
f '(x) 1 0.8686 x
选初值x0=6。 迭代值为：6，7.961777706，7.996832646，
7.996299004，7.996299005
指数行列式不等于零。 4.用这3个基本物理量与其余的任一个物理量组成一个无
量纲数
(Q1)a (Q2 )b (Q3)c q
2019/10/24
例4-11 管道水流。管段的压强差Δp与管段长
度l, 平均流速V，水的密度ρ ，动力粘度μ，
管道直径D，绝对粗糙度Δ有关。试用π定理 决定本流动现象的无量纲数，并列出Δp与 其 他物理量关系的一般表达式。
第四章 流态和水头损失
4.1 水头损失的分类 流体从截面1运动到截面2,机械能减少:
z1
p1 g
1
V12 2g
z2
p2 g
2
V22 2g
z1
p1
g
1
V12 2g
z2
p2
g
北航水力学 第四章理想流体动力学和恒定平面势流解读
z1
p1
u12 2g
z2
p2
u22 2g
4.2.2 由动能定理推导理想流体的伯努利方程
推导过程同学们自学
z1
p1
u12 2g
z2
p2
u22 2g
本公式是由动能定理推导而得，它使伯努利方程有更加明确的 物理意义，说明伯努利方程是一能量方程。
第三节 元流伯努利方程的意义和应用
4.3.1 沿流线的伯努利方程的水力学意义
可见，在同一流线上各点的流函数为一常数，故等流函数线就是流线。
2、平面内任意两点流函数值的差等于通过这两点连线的流量。
y ABdrBnA x
d r dxi dy j
n cos i sin j dy i dx j
dr dr V ui v j
dq V
ndr
u
dy dr
v
dx dr
等 线和等Ψ线，这两族曲线互相垂直，构
成流网。
两族曲线所构成的正交网络，称为流网
流网的特征：
流网
等 线和速度矢量垂直，或者说， 等 线与等Ψ线（流线）垂直，
【例题】
已知90度角域内无粘流动，速度分布
ux kx uy ky
(k 0, x 0, y 0)
求：（1）判断该流场是否存在速度势函数， 若存在请给出并画出等势线；
流动。但粘滞性对流动 的影响很微小时，影响可以忽略。 --机械能守恒
引入势流的意义：使问题简化。
波浪运动，无分离的边界层外部的流动，多孔介质的流动（渗流） 等等可以看为势流。
4.4.1 流速势函数
以二维流动为例，根据流体运动学，它与无旋流动等价
由 ux 0 无旋流的条件→涡量 z 0
水力学第4章
γJ 2 u r0 r 2 4μ
γJ 2 r0 4μ
断面平均速度：
V
udA u 2πrdr
A
r0
A
0
πr02
umax 2
二.沿程损失系数：
umax γJ 2 γh f 2 V r0 r0 2 8μ 8 μl
第四章
流态和水头损失
§4-1
水头损失及其分类
流体从1-1断面运移到2-2断面，机械能减少：
p1 V12 p2 V22 z1 α1 z2 α2 hw γ 2g γ 2g
h w为水头损失。
hw分为两类：沿程水头损失hf和局部水头损失hj。
一.圆管流动：
hf的计算公式：
l V hf λ d 2g
u*r0 V Vd u* 2.5 ln 1.75 2.5 ln 1.75 u* ν ν 2V
又因为：
V 8 u λ
故：
1 λ 8 1.75 2.5 ln Re 2 8 λ 1 (2.5 ln 10) log Re λ 1.75 2 8
2
二.液体的非圆管流动：
A 水力半径：R χ
上式中：为过流断面上液体与固壁接触的周线长，称为湿周。
例如：
1).矩形断面管道：χ （b h) 2 A bh R χ 2(b h)
2).矩形断面排水沟：χ b 2h R A bh χ b 2h
π 2 d A 4 d 3).对于液体在圆管中的流动：R 。即：d 4 R。 χ πd 4
u um
平均速度：
水力学第四章
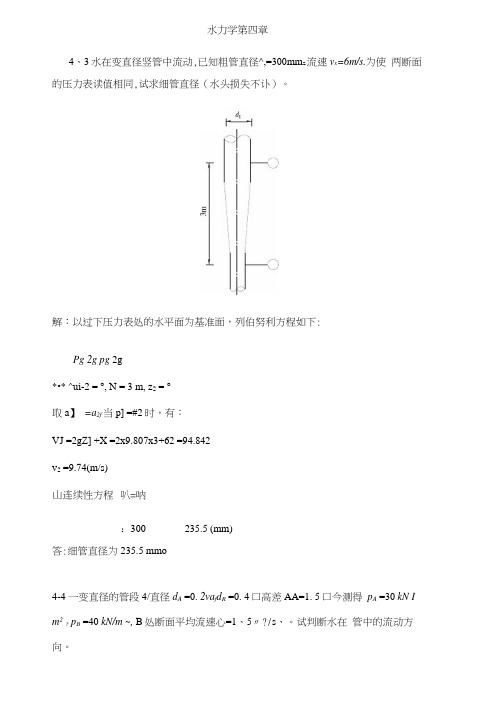
4、3水在变直径竖管中流动,已知粗管直径^,=300mm z流速v x=6m/s.为使两断面的压力表读值相同,试求细管直径（水头损失不讣）。
解：以过下压力表处的水平面为基准面，列伯努利方程如下:Pg 2g pg 2g*•* ^ui-2 = °, N = 3 m, z2 = °取a】=a2f当p] =#2时，有：VJ =2gZ] +X =2x9.807x3+62 =94.842v2 =9.74(m/s)山连续性方程叭=呐：300 235.5 (mm)答:细管直径为235.5 mmo4-4 一变直径的管段4/直径d A =0. 2va f d R =0. 4口高差AA=1. 5口今测得p A =30 kN I m2? p B =40 kN/m ~, B处断面平均流速心=1、5〃?/s、。
试判断水在管中的流动方向。
Bx—xA解：以过A的水平面为基准面，则A、B点单位重量断面平均总机械能为: …p.八30x10， l.Oxl.52 (0.4 V , ooz、H、= j +-^-+ •' ・L = 0+ ---------- + ------------x ——=4.89(m)4” pg 2g 1000x9.807 2x9.807 10.2J…P B a局七40xl03l.Oxl.52c、H R=Z R+—+—- = 1.5 + --------------------- + ------------ = 5.69 (m)〃“ pg 2g1000x9.807 2x9.807・•・水流从B点向A点流动。
答:水流从B点向A点流动。
4-5利用皮托管原理，测量水管中的点速度八 如读值A/z=60mm /求该点流速。
答:该点流速“ = 3.85m/s 。
—5用水银圧差计测虽水管中的点流速u ,如读值A li=60nim , (1)求该点流速；(2) 若管中流体是0=0.8仗/的油，Ah 不变，不计水头捉失，则该点的流速是多少？ 解:(1)况=J2g x 12.6△方=J19.6 x 12.6 x 0.06 = 3.85m/s(2)〃 = J2g x 12.8△方=\/19.6x 12.8 x 0.06 = 4.34m/s4—6利用文丘里管的喉管处负压抽吸基坑中的积水，已经知道管道直径4 = 100/7777?, 喉管亘径d 2 = 50mm , A=2w,能呈损失忽昭不计。
水力学第四章第三部分
式中μc称为流量系数；若忽略行近流速水头，则 H0≈H
00:23
Q c A 2gH
第五节 有压管道水力计算
2、淹没出流
1~1、2~2 断面列能量方程：
hH
pa
1V12
2g
pa 1
h
pa
2V22
2g
hw12
0
V1
1
hw12
LV2
d 2g
V2
2g
忽略行近流速：
H
2
32
V
h
0
3
H
L d
00:23
0
AB为流速调整段
BC为调整结束段 0
AB只考虑局部损失
00:23
BC只考虑沿程损失
第四节 局部水头损失计算 二 局部水头损失通用公式
一般情况，局部水头损失可表为下面的通用公式
h v2
j
2g
式中，ζ可由试验确定； v 为发生局部损失之前或之后的断面平均流速。
00:23
第四节 局部水头损失计算
1 过水断面突然扩大
如：水泵的吸水管、虹吸管。
长管：指管路的流速水头和局部水头损失可忽略的管路 （L/d>1000）。
00:23
第五节 有压管道水力计算
二、短管水力计算
1、自由出流 对 1~1、2~2 断面：
pa 1
V0
H
1
V2 2
H
0V02
2g
z2
p2
2V22
2g
hw12
2V22
2g
hw12
令：
H
0V02
2
p1’ 1’ θ
G
1
p2 v2
水力学第四章层流、紊流,液流阻力和水头损失
3.7d
结论2:
•紊流光滑区水流沿程水头损失系数只取决于雷诺数，粗糙度不 起作用。容易得出光滑区紊流沿程损失与流速的1.75次方成正 比。 •紊流粗糙区水流沿程水头损失系数只取决于粗糙度，由于粗糙 高度进入流速对数区，阻力大大增加，这是不难理解的。容易 得出粗糙区紊流沿程损失与流速的2.0次方成正比。 •在紊流光滑区与粗糙区之间存在紊流过渡粗糙区，此时沿 程损失系数与雷诺数和粗糙度都有关。 •尼古拉兹试验反映了圆管流动的全部情况，在其试验结果图上 能划分出层流区，过渡区、紊流光滑区、紊流过渡粗糙区，紊 流粗糙区。紊流粗糙区通常也叫做‘阻力平方区’。
ro gJ 2 2 gJ 4 1 4 gJ 4 Q (ro r )2 rdr (ro ro ) d 0 4v 4v 2 128v
上式为哈根——泊肃叶定律：圆管均匀层流的流量Q与管径d 的四次方成比例。 3、断面平均流速： V
Q gJ 2 1 ro umax A 8 2
1 1 1 1 1 , , , , 及 30 61 .2 120 252 507 1
1 1 1 1 1 1 , , , , 及 30 61 .2 120 252 507 10
层流时,
64 Re
f (Re)
1 1 1 1 1 1 , , , , 及 30 61.2 120 252 507 1014
1 u u x x dt 0 T0
2、紊流的切应力 由相邻两流层间时均流速相对运动
所产生的粘滞切应力
紊流产生附加切应力
du l t v Re
t v Re 2
纯粹由脉动流速所产生 的附加切应力
dy ( du 2 ) dy
普朗特 混合长 Re 与 du 有关，根据质点脉动引起动量交换（传递），又称为动量传递理论 dy 理论
计算水力学--第四章(3)
§5 . 内边界的处理—堰闸过流
自由出流
堰闸过流
Q ? mbh 2gh0
h0 = Zi- Zd 为上游水深 b 是闸孔净宽; h 为计算过流水深 ; 孔流 h=a ; 堰流 h=h0 ; m 为综合流量系数。计算方法同关闸情况。
Leila for 水文09 版权所有
水文09级计算水力学教学课件
第四章 河道水流计算
§5 . 内边界的处理
Qf
Qi
Q i+1
Δx i=0 集中入流
断
面
Qi
Qi+1 突
变
情
i
i+1
况
面积 A
i
i+1
河道与贮水池汇合
过闸示意
Leila for 水文09 版权所有
§5 . 内边界的处理
? 在河道水流计算中，除了外部边界条件外，还 可能遇到内部边界条件 。
? 比较可得
Leila for 水文09 版权所有
§5 . 内边界的处理—过水断面突然放大
三、河道与贮水池汇合
? 相容条件
Qi
Q i+1
令
i
i+1
断面突变情况
Leila for 水文09 版权所有
§5 . 内边界的处理—过水断面突然放大
? 上边界为水位边界条件
? 同追赶方程
? 比较可得
Leila for 水文09 版权所有
As ?t
Vi
? ?Ti ? 1 ? ?
?
? 1?
1
As ?t
Vi
? ? ? Pi?1 ?? ?
?
Vi
As ?t
水力学4
测压管水头线的定性分析
1
V0≈0
p g
O 1
H
V2 2g
则
H
hf
Q2 K2
L
简单管道水力计算的基本类型
当管道布置、断面尺寸及作用水头已知时，要求 确定管道通过的流量。 当已知管道尺寸和输水能力时，计算水头损失； 即要求确定通过一定流量时所必须的水头。
管线布置已定，当要求输送一定流量时，确定所 需的断面尺寸。
对一个已知管道尺寸、水头和流量的管道，要求确 定管道各断面压强的大小。
前进
有压管中的恒定流
有压管道 无压管道
有压流 无压流
简单管道 复杂管道
简单管道
串联管道
并联管道
长管 短管
水头损失以沿程水头损失为主，局部水头损失和流速水头在 总损失中所占比重很小，计算时可以忽略的管道
局部损失及流速水头在总损失中占有相当的比重，计算时不 能忽略的管道
自由出流 淹没出流
主要内容：
简单管道水力计算的基本公式 简单管道水力计算的基本类型 简单管道水力计算特例——虹吸管及水泵 串联管道的水力计算 并联管道的水力计算
简单管道水力计算的基本公式
1
1
自由出流
2 H 淹没出流
Z
O
2 O
O 1
O 2
按短管计算时：Q c A 2gH
其中
c
1
1
l d
1 2
Q c A 2gZ
c
1
l d
按长管计算时：
H
hf
l d
V2 2g
或
ห้องสมุดไป่ตู้
水力学 第四章
第四章 水动力学基础4. p1第四章水动力学研究的主要问题是流速和压强在空间的分布。
流速又更加重要。
水流流动时，在破坏压力和质量力平衡的同时，出现了和流速密切相关的惯性力和粘性力。
这样，水体由静到动所产生的两种力，是由流速在空间的分布和随时间的变化所决定的。
因此，水动力学的基本问题是流速的问题。
水体从静止到运动，质点获得流速，由于粘滞力的作用，改变了压强的静力特性。
但粘滞力对压强随方向变化的影响很小，在工程中可忽略不计。
以后，水体流动时的压强和静水压强，一般在概念的命名上不予区别，一律称为压强。
设在理想液体恒定流中，取一微小流束依牛顿第二定律： s s ma F ∑=其中： dtdu a s =任意两个断面： 2211221222p u p u Z Z g g g gρρ++=++00Z Z dZ +d s 12p p +dpdG=ρgdAds dA α()cos du pdA p dp dA gdAds dAds u dsραρ−+−=⋅2()02p u d Z g g ρ++=22p u Z c g gρ++=沿流线积分得：——不可压缩理想液体恒定流微小流束的能量方程式§4.2 元流的伯努利方程4.2p1第二节第四章Bernouli’s equation of real liquid方程式的物理意义2211221222p u p u Z Z g g g gρρ++=++001Z 2Z 12位置水头压强水头流速水头测压管水头总水头单位位能单位压能单位动能单位势能单位总机械能表明：在不可压缩理想液体恒定流情况下，微小流束内不同过水断面上，单位重量液体所具有的机械能保持相等（守恒）。
元流能量方程的应用——毕托管测速原理。
p a /γp b /γΔh毕托管构造：h g p p g u gu p p b a b a ∆=−=+=+22202ϕγγγ得出：b a实际液体恒定元流的伯努利方程2211221222p u p u Z Z g g g gρρ++=++w h ′+w h ′——单位重量液体从断面单位重量液体从断面1-11-11-1流至断面流至断面流至断面2-22-22-2所损失所损失的能量，称为水头损失。
第四章消防水力学基础知识
(四)膨胀性
水的体积随水温升高而增大的性质称为 水的膨胀性。根据实验，水的体积变化较小。 因此，在消防设计和火场供水中水的膨胀性 均可略去不计。
练习题：
1、水的体积随水温升高而增大的性质称为水的膨胀性。（ √ ） 2、液态水具有压缩性和膨胀性，通常状况下，二者的特性为（ A ）。 A 压缩性小，膨胀性小 B 压缩性小，膨胀性大 C 压缩性大，膨胀性小 D 压缩性大，膨胀性大 3、水的体积随水温升高而增大的性质称为水的（ C ）。 A 粘滞性 B 压缩性 C 膨胀性 D溶解性
练习题
小
1、水中含有杂质越多，电阻率越大，导电性能越差（ × ）。 2、水的导电性能与水的密度、射流形式等有关。下列说法正确的是 （ C ）。 A 杂质越少，直流射流，导电性能越大 B 杂质越少，开花射流，导电性能越大 C 杂质越多，直流射流，导电性能越大 D 杂质越多，开花射流，导电性能越大
三、水的化学性质
上海“11.15”火灾
一、水的基本特性
水有三种状态：固体、液体和气体。液体与固体的主要区 别是液体容易流动，液体与气体的主要区别是液体体积不易压 缩。 水在常温下为液体。在常压下，水温超过l00℃时，蒸发成 气体，水温下降到0℃时，即凝结成固体称为冰。
练习题 1、水有三种状态：固体，液体和气体。液体与固体的主要区别是 液体容易流动，液体与气体的主要区别是液体体积不易压缩。（√）
从表中可以看出，随着压力增加水体积变化不大。因此， 通常把水看成是不可压缩的液体，但对个别特殊情况，水的压 缩性不能忽略。如水枪开关突然关闭时，会产生一种水击现象， 在研究这一问题时，就必须考虑水的压缩性。
练习题 1、水的体积随压力减小而增加的性质称为水的压缩性。（ × ） 2、通常把水看成是不可压缩的液体。（ √ ） 3、水枪上的开关突然关闭时，会产生一种水击现象。在研究这 一问题时，就必须考虑水的（ B ）。 A 粘滞性 B 压缩性 C 膨胀性 D溶解性