2011年高中数学课件:立体几何初步《棱柱、棱锥和棱台》(苏教版必修2)
合集下载
高中数学第1章1.1.1棱柱棱锥和棱台课件苏教必修2.ppt

知新益能
1.图形平移 将一个图形上_所__有__的__点__按某一_确__定__的方向移 动相同的距离就是平移. 2.棱柱 (1)有关概念: ①一般地,由一个平面多边形沿某一方向平移 形成的空间几何体叫做棱柱.平移起止位置的 两个面叫做棱柱的底面;两底面之间的距离叫 做棱柱的高;多边形的边平移所形成的面叫做 棱柱的侧面;相邻侧面的公共边叫做棱柱的侧 棱.
变式训练2 观察下图,分别判断(1)中的三棱 镜,(2)中的螺杆头部模型有多少对互相平行 的平面,其中能作为棱柱底面的分别有几对.
解:(1)中有1对互相平行的平面,只有这1对 可以作为棱柱的底面.(2)中有4对互相平行的 平面,只有1对可以作为棱柱的底面.
考点三 棱柱、棱锥、棱台的画法
根据棱柱、棱锥、棱台的定义可以画出棱柱、 棱锥、棱台.作图时要按作图规则和作图要 求,不能随意徒手作图.
【名师点评】 (1)判断一个几何体是何种几 何体,一定要紧扣柱、锥、台的结构特征, 注意定义中的特殊字眼,切不可马虎大意. (2)本题容易错认为几何体②也是棱柱,其原 因是忽视了棱柱必须有两个面平行这个结构 特征,避免出现此类错误的方法是将教材中 的各种几何体的结构特征放在一起对比,并 且和图形对应起来记忆,要做到看到文字叙 述就想到图,看到图形就想到文字叙述.
例2 根据下列关于空间几何体的描述,说出 几何体的名称: (1)由6个平行四边形围成的几何体; (2)由7个面围成,其中一个面是六边形,其余6 个面都是有一个公共顶点的三角形; (3)由5个面围成的几何体,其中上、下两个面 是相似三角形,其余三个面都是梯形,并且这 些梯形的腰延长后能相交于一点. 【思路点拨】 审题→想象→对比定义→解答.
方法感悟
棱锥是当棱柱的一个底面收缩为一个点时形成 的空间图形,棱台则可以看成是用一个平行于 棱锥底面的平面截棱锥所得到的图形.要注意 的是,棱台的各条侧棱延长后交于一点,即棱 台可以还原成棱锥.在学习时要注意棱柱、棱 锥、棱台这三类多面体之间的联系.
高中数学 1.11.1.1 棱柱、棱锥和棱台课件 苏教版必修2

目 链
台的_顶_点__(_d_ǐn_g_d_iǎ_n,) 相邻侧面的公共边叫做棱台的侧__棱______. 接
10.棱台的侧棱的延长线_____相__交__于__一__点___.
第十一页,共35页。
栏 目 链 接
第十二页,共35页。
一、棱柱(léngzhù)的结构特征
棱柱的结构特征有:①两个底面互相平行;②侧棱都 互相平行;③棱柱的各侧棱相等,各侧面都是平行四边形.
__________.
平行四边形
6.一般地,一个面是多边形,其余各面都是
栏
________________的三角形,由这些面所围成的多面体叫做(jiàozuò)
棱有锥一.多个边公形共面顶叫点做(jiàozuò)棱锥的__________,有公共顶点的各个
目 链 接
三 角 形 叫 做 (jiàozuò) 棱 锥 的 __________底, 各面侧 面 的 公 共 顶 点 叫 做
第十四页,共35页。
截面与底面面积的比等于相似比的平方,等于所截得的小棱锥
与大棱锥对应高的比的平方.同学们要谨记:①正棱锥的底面
是正多边形,并且顶点在过正多边形中心且垂直于底面的直线 栏
目
上;②“有一个(yī ɡè)面是多边形,其余各面都是三角形”的
链 接
多面体不一定是棱锥.
第十五页,共35页。
三、棱台(léngtái)的结构特征
各个角度进行描述.主要从它的面(侧面(cèmiàn)、底面)、棱、顶点
等角度描述,棱柱、棱锥、棱台的结构特征都是用一些平面几何中的
栏 目
点、线、平面几何图形来表述的.
链 接
第二十页,共35页。
变式 训练
1.观察(guānchá)长方体模型,有多少对平行的面?能作为棱柱 底面的有多少对?观察(guānchá)六棱柱模型,有多少对平行的面?能 作为棱柱底面的有多少对?
苏教版 高中数学必修第二册 棱柱、棱锥和棱台 课件1

3.棱台的概念及特点 (1)棱台的概念
用一个平行于棱锥底面的平面去截棱锥,_截__面_和__底__面__之间的部
分称之为棱台. 侧棱:相邻侧面的公共边; (2)棱台的特点
棱台的两个底面是相__似__的多边形,侧面都是_梯_形__,侧棱延长后 都_相_交__于一点.
棱台的分类
由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……
三
四
五
棱
棱
棱
台
台
台
棱柱、棱锥与棱台的关系
多面体的基本概念 由若干个平面多边形围成的空间图形叫作多面体.
棱柱的结构特征
例1 (1)下列关于棱柱的说法: ①所有的面都是平行四边形;②每一个面都不会是三角形;③两底面平 行,并且各侧棱也平行;④被平面截成的两部分可以都是棱柱. 其中正确说法的序号是__③__④____.
√A.0个 B.1个 C.2个 D.3个
解析 ①中的平面不一定平行于底面,故①错; ②③可用反例去检验,如图所示,侧棱延长线不能相交 于一点,故②③错.
练.下列关于棱锥、棱台的说法: ①棱台的侧面一定不会是平行四边形; ②由四个平面围成的封闭图形只能是三棱锥; ③棱锥被平面截成的两部分不可能都是棱锥. 其中正确说法的序号是__①__②___.
答案:D
练 下列命题中正确的是
A.有两个面互相平行,其余各面都是四边形的几何体叫棱柱
B.棱柱中互相平行的两个面叫棱柱的底面
C.棱柱的侧面都是平行四边形,而底面不是平行四边形
√D.棱柱的侧棱都相等,侧面是平行四边形
例3.有下列三种叙述: ①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台; ②两个面平行且相似,其余各面都是梯形的多面体是棱台; ③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台. 其中正确的有
苏教版必修2数学课件-第1章立体几何初步第3节空间几何体的表面积和体积教学课件

6π [S=2π×1×2+2π×12=6π.]
栏目导航
合作探究 提素养
栏目导航
棱柱、棱锥和棱台的侧面积和表面积 【例 1】 正四棱锥的侧面积是底面积的 2 倍,高是 3,求它的 表面积. 思路探究:由 S 侧与 S 底的关系,求得斜高与底面边长之间的关系, 进而求出斜高和底面边长,最后求表面积.
所以 S 侧=3×12×(20+30)×DD′=75DD′. 又 A′B′=20 cm,AB=30 cm,则上、下底面面积之和为 S 上+S 下 = 43×(202+302)=325 3(cm2).
栏目导航
由 S 侧=S 上+S 下,得 75DD′=325 3, 所以 DD′=133 3(cm), 又因为 O′D′= 63×20=103 3(cm), OD= 63×30=5 3(cm),
错点)
运算核心素养.
3.会求简单组合体的体积及表面积.(难点)
栏目导航
自主预习 探新知
栏目导航
1.柱体、锥体、台体的体积
几何体
体积
柱体 锥体
V 柱体= Sh (S 为底面面积,h 为高), V 圆柱= πr2h (r 为底面半径) 1
V 锥体= 3Sh (S 为底面面积,h 为高), V 圆锥= π3r2h (r 为底面半径)
栏目导航
台体
V 台体= 13h(S+ SS′+S′) (S′,S 分别为上、下底面面 积,h 为高),V 圆台= 13πh(r′2+rr′+r2) (r′,r 分别为上、 下底面半径)
思考:柱体、锥体、台体的体积公式之间的关系. 提示:V=Sh―S′―=→S V=13(S′+ S′S+S)h―S′―=→0 V=13Sh.
栏目导航
[解] 如图所示,设 SE 是侧面三角形 ABS 的高,则 SE 就是正 四棱锥的斜高.
栏目导航
合作探究 提素养
栏目导航
棱柱、棱锥和棱台的侧面积和表面积 【例 1】 正四棱锥的侧面积是底面积的 2 倍,高是 3,求它的 表面积. 思路探究:由 S 侧与 S 底的关系,求得斜高与底面边长之间的关系, 进而求出斜高和底面边长,最后求表面积.
所以 S 侧=3×12×(20+30)×DD′=75DD′. 又 A′B′=20 cm,AB=30 cm,则上、下底面面积之和为 S 上+S 下 = 43×(202+302)=325 3(cm2).
栏目导航
由 S 侧=S 上+S 下,得 75DD′=325 3, 所以 DD′=133 3(cm), 又因为 O′D′= 63×20=103 3(cm), OD= 63×30=5 3(cm),
错点)
运算核心素养.
3.会求简单组合体的体积及表面积.(难点)
栏目导航
自主预习 探新知
栏目导航
1.柱体、锥体、台体的体积
几何体
体积
柱体 锥体
V 柱体= Sh (S 为底面面积,h 为高), V 圆柱= πr2h (r 为底面半径) 1
V 锥体= 3Sh (S 为底面面积,h 为高), V 圆锥= π3r2h (r 为底面半径)
栏目导航
台体
V 台体= 13h(S+ SS′+S′) (S′,S 分别为上、下底面面 积,h 为高),V 圆台= 13πh(r′2+rr′+r2) (r′,r 分别为上、 下底面半径)
思考:柱体、锥体、台体的体积公式之间的关系. 提示:V=Sh―S′―=→S V=13(S′+ S′S+S)h―S′―=→0 V=13Sh.
栏目导航
[解] 如图所示,设 SE 是侧面三角形 ABS 的高,则 SE 就是正 四棱锥的斜高.
苏教版高中数学必修二第一章 -1.1.1 棱柱、棱锥和棱台 课件 (共23张PPT)

相交于一点.
④A,B,C,D,A1,B1,C1,D1叫做四棱台的顶点.
规律总结:要认识一个几何体的结构特征,就是要从
“形”的各个角度进行描述.主要从它的面(侧面、底
栏
面)、棱、顶点等角度描述,棱柱、棱锥、棱台的结构特
目 链
接
征都是用一些平面几何中的点、线、平面几何图形来表
述的.
►变式训练
1.观察长方体模型,有多少对平行的面?能作为棱柱底
面的有多少对?观察六棱柱模型,有多少对平行的面? 栏
目
能作为棱柱底面的有多少对?
链 接
解析:观察长方体模型,有3对平行的面,能作为棱柱底
面的有3对;观察六棱柱模型,有4对平行的面,能作为
棱柱底面的有1对.
2.观察下图中的几何体,它们具有怎样的共同特征?
栏 目 链 接
解析:图中几何体的共同特征是:①均由平面图形
在直角梯形 O′OBB′中,
BB′= OO′2+(OB-O′B′)2
= 172+(8 2-2 2)2
=19 (cm) . 在直角梯形 O′OEE′中,
栏 目 链
EE′= OO′2+(OE-O′E′)2
接
= 172+(8-2)2
=5 13 (cm). 即这个棱台的侧棱长为 19 cm,斜高为 5 13 cm .
栏 目
棱把它剪开,并铺成平面图形,进而画出相应的平面
链 接
图形.将多面体的表面展开成平面图形,有利于我们
解决与多面体表面有关图,池底为一斜面,装 满水后形成的几何体由哪些简单几何体组成(答案不唯一)?
栏 目 链 接
解析:游泳池装满水后形成的几何体是一个棱柱(两底面水 平放置),但这个棱柱可看成由一个长方体补上一个三棱柱 得到[如下图(1)];也可由长方体切割下一个三棱柱得到[如 下图(2)].
苏教版高中数学必修二课件棱柱棱锥和棱台

第一步画一个三棱锥,在它的一条侧棱上取 一点 第二步从这点开始,顺次在各个侧面内画出 与底面对应边平行的线段 第三步将多余的线段擦去
例2判断下列命题是否正确。
× () (1)三棱柱是指有三条棱的几何体。 (2)由四个面围成的封闭图形只能是三 棱锥,那么由六个面围成的封闭图形 × 只能是五棱锥。 () × (3)棱柱的每个面都不会是三角形。() √ (4)棱锥的侧面只能是三角形。() √ (5)棱台的侧面一定不会是平行四边形。 ()
3.棱台的相关概念
• 棱台的概念: 用一个平行于棱锥底面的平面去截棱锥, 得到两个几何体,一个仍然是棱锥,另一 个我们称之为棱台 • 棱台的分类: 按底面多边形的边数分为三棱台、四棱台、 五棱台等
例1画一个四棱柱和一个三棱台。
第一步画上底面——画一个四边形 第二步画侧棱——从四边形的每一个顶点画 平行且相等的线段 第三步画下底面——顺次连结这些线段的另 一个端点
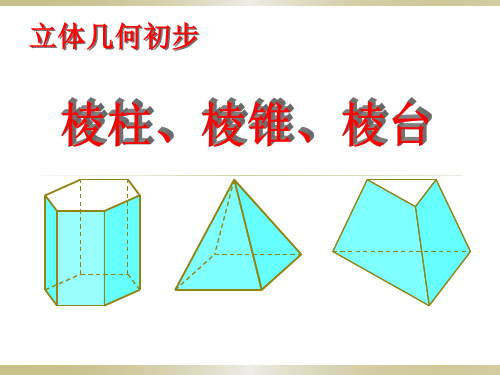
棱 柱 棱 锥 和 棱 台
教学目标: 1.棱柱、棱锥、棱台以及多面 体的几何特征 2.了解棱柱、棱锥、棱台以及 多面体的概念 3.能正确画出棱柱、棱锥、棱 台的图形
仔细观察下面的几个几何体,它们有什 么共同特点?
1.棱柱的相关概念
• 棱柱的概念: 由一个平面多边形沿某一方向平移形成的 空间几何体叫做棱柱 • 棱柱的分类: 按底面多边形的边数分为三棱柱、四棱柱、 五棱柱等 • 棱柱的特点: 两个底面是全等的多边形,且对应边互相 平行,侧面都是平行四边形
下面的几何体有什么共同特点?与图1-1-1 相比有什么变化?
2.棱锥的相关概念
• 棱锥的概念: 当棱柱的一个底面收缩为一个点时,得到 的几何体叫做棱锥 • 棱锥的分类: 按底面多边形的边数分为三棱锥、四棱锥、 五棱锥等 • 棱锥的特点: 底面是多边形,侧面是有一个公共顶点的 三角形
棱柱、棱锥和棱台-PPT课件
为平行四边形,且其交线平行。
欧式定义完善:
欧氏定义:有两个面为平行且全等多边形、 其他面均为平行四边形的几何体叫棱柱。
完善:有两个面为平行且全等多边形、 其他面均为平行四边形,且其交线平行 的几何体叫棱柱。
平移:将一个图形上所有的点按照某一确定的方
向移动相同的距离就是平移 (1)点平移, 它的移动轨迹是什么? (2)线段平移所形成的图形是什么?
D
C ①画上底面——画一个四边形;
A
B
②画侧棱——从四边形的每一个顶点
画平行且相等的线段;
D A
C ③画下底面——顺次连结这些线段的
另一个端点.
B
注意:被挡住的线要画成虚线.
数学应用
(2)画一个三棱台
S
A B
A
C C
B
①画一个三棱锥; ②在侧棱上任取一点,从这点开始,顺次在 各个侧面内画出与底面对应边平行的线段;
(12)
问题1 观察下面的几何体,有什么共同特点?
(1)
(2)
(3)
(4)
《几何原本》
欧几里得之棱柱定义
一个棱柱是一个 立体图形,它是有 一些平面构成的, 其中有两个面是相 对的、相等的、相 似且平行的,其他 各面都是平行四边 形。
Wentworth & Smith
(1913)之棱柱定义
有两个面为平行 平面上的全等多边 形、其他面均为平 行四边形的几何体 叫棱柱。
问题3 下面的几何体有什么共同特点?和上面的几何体
对比,前后发生了什么变化?
⑴
⑵
演
⑶
⑷示
棱锥的定义: 当棱柱的一个底面收缩为一个点时,
得到的几何体叫做棱锥。
顶点:由棱柱的一个
高中数学第1章立体几何初步1.1.1棱柱、棱锥和棱台课件苏教版必修2

C
顺次在各个侧面内画出与底面
对应边平行的线段
C
③将多余的线段擦去
B
棱柱、棱锥、棱台都是由一些平面多边形围成的几何体.
由若干个平面多边形围成的几何体叫做多面体.
食盐晶体
明矾晶体
石膏晶体
思考:多面体至少有几个面?这个多面体是怎样的几何体?
四
棱锥
回顾小结
• (1)通过本节课的学习,你掌握了什么? • (2)通过本节课的学习,你能否初步归纳一下学习
延长后交于一点
概念辨析:下图中的几何体是不是棱台?为什么?
回顾反思 点
线
平面多边形 棱柱
面
棱锥
空间几何图形
棱台
几何体
图形
侧棱
棱柱 侧面
底面
侧棱
棱锥
侧面
底面
棱台
上底面
侧棱 侧面 下底面
底面
侧面 侧棱
两个底面是全等 的多边形且对应 边互相平行
平行四边形
互相平行 且相等
一底面是多边形, 有一个公共顶 交于一点 另一底面缩为一点 点的三角形
类比棱柱,给棱锥各元素命名
顶点
A
C
S
B
底面
由棱柱的一个 底面收缩而成
底面
A
CA
(平面多边形)
C
侧面
B
BP
侧面
(有一个公共
顶点的三角形)
侧棱
侧棱
相邻两侧面 的公共边
D
相邻两侧面
C
的公共边
A
B 四棱锥P-ABCD
能否类比棱柱的表示法给出棱锥的表示法?
问5:如果用一个平行于棱锥底面的平面去截棱锥, 则可得到一个怎样的几何体?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)
(2)
(3)
(4)
棱锥的几个相关定义: 顶点:由棱柱的一个
S
底面收缩而成.
:
侧面
棱的
相 邻 侧
公 共 边
A
D
底面
侧面
C B
棱锥的记法: 棱锥S-ABCD 等
棱锥:有一个面是多边形,其余各面都是有
一个公共顶点的三角形,由这些面所围成的
几何体叫做棱锥。
顶点 S
侧面
侧棱
底面
D
C
A B
棱锥的结构特征
两个底面是全等的多边形底,面是多边形,侧
且对应边互相平行,侧面面是有一个公共顶
都是平行四边形
点的三角形
两个底面是相似的 多边形,且对应边 互相平行,侧面都 是梯形
课堂作业:
分别画一个三棱柱和四棱台.
把本节课所讲过的几何体集中起来审视
一下,你能发现它们有什么共同特点吗?
F`
E`
S
A`
D`
B`
C`
FE
D
C
A
DA
B
C
B
你能给它们一个共同的称呼吗? 多面体
由若干个平面多边形围成的几何体, 叫多面体
棱柱,棱锥和棱台都是由一些平面多 边形围成的几何体,由若干个平面多边形 围成的几何体称为多面体。
在现实生活中,存在着形形色色的多 面体,如食盐,明矾,石膏等晶体都呈多 面体形状。
E` D`
C`
A
C
B
FE
A
D
B
C
通过观察,你还发现棱柱具有哪些特点?
答案:两个底面是全等的多边形,且对应 的边互相平行,侧面都是平行四边形.
棱柱的结构特征
棱柱:有两个面互相平行,其余各面都是四边 形,并且每相邻两个四边形的公共边都互相平
行,由这些面所围成的几何体叫做棱柱。
顶点
侧面
底面
侧棱
用表示底面各顶点表示棱柱。
食盐晶体
明矾晶体
石膏晶体
学习了这么多的几何体了 , 你能根据要求 画出它们吗?怎样来画?
例题讲解:
例1: 请你对几何体的认识,画一个四棱柱 和一个三棱台. 画图思路:画四棱柱可分三个步骤:
第一步,画上底面-----画一个四边形 第二步,画侧棱------从四边形的每一个顶点画 平行且相等的线段. 第三步,画出地面------顺次连接线段的端点。
画三棱台的方法是: 画一个三棱锥,在它的一条侧棱上取
一点,从这点开始,顺次在各个侧面内画 出与底面的对应边平行的线段,将多余的 线段擦去。
课堂练习:
1.如图,四棱柱 的六个面都是平 行四边形, 这个 四棱柱可以由哪 几个平面图形按 怎样的方向平移 得到?
2.右图中 的 几何体是不 是棱台? 为什么?
合作探究:
观察下列的几何体,比较上下图形发生了 什么变化?变化后有什么共同的特点?
(1)
(2)
(3)
(4)
通过观察几个图形,发现它们都是 几个棱柱的一个底面缩为一个点了.
结 论:
当棱柱的一个底面收缩为一个点时, 得到的几何体叫做棱锥.
(1)
(2)
(3)
(4)
通过观察,你还发现棱锥具有哪些点?
底面是多边形,侧面是有一个 公共顶点的三角形.
3. 多面体至少有几个面? 这个多面体是怎样的几何体?
4.分别画一个三棱锥和一个 四棱台.
课堂小结:
1、平移 平移是指将一个图形上所有的点按某一 确定的方向移动相同的距离.
2、棱柱、棱锥、棱台
3、多面体的概念 4、棱柱、棱锥、棱台的画法步骤
名称 项目
棱柱
棱锥
棱台
由一个平面多边形 当棱柱的
定
沿某一方向平移形 成的空间几何体叫 做棱柱.平移起止 位置的两个面叫做
面
A
C
:
F`
E`
A`
D`
叫两
做侧
B`
C`
面
侧
侧的 棱公
共
面 FE
边A
D
B
C
B
结论:
底面为三角形,四边形,五边形‥‥‥的棱柱 分别称为三棱柱,四棱柱五棱柱‥‥‥
例如上图中的图形分别为三棱柱,六棱柱,并
分别记作:棱柱ABC-A′B′C′ 棱柱ABCDEF-A′B′C′D′E′F
A`
C`
B`
F` A`
B`
棱锥也用表 示顶点和底 面各顶点的 字母表示。
合作探究:
如果用一个平行于棱锥底面的平面去 截棱锥,想象一下,那截得的两部分几何体 会是什么样的几何体?
棱锥
棱台
说明: 棱台是棱锥被平行于底面的一个
平面所截后,截面和底面之间的部分.
上底面
侧
侧面
棱
下底面
下面我们再来看一下棱柱,棱锥,棱台 之间的关系体吗?
请同学们仔细观察下面的几何 体,它们有哪些共同的特点?
(1)
(2)
(3)
(4)
定义: 将一个图形上所有的点按某一个 确定的方向移动相同的距离就是平移.
图(1) 和 (3) 中的几何体分别由平行四边形和 五边形沿某一方向平移得来的.
平移
(1)
平移
(3)
一个底面 收缩为一 个点时,得
义
棱柱的底面,多边 到的几何 形的边平移所形成 体叫做棱
的面叫做棱柱的侧 锥.
面.两侧面的公共
边叫做棱柱的侧棱
用平行于 棱锥底面 的平面去 截棱锥,截 面和底面 之间的部 分叫做棱 台
分类
性质
根据底面多边形的边数多少,可将棱柱分为三棱柱、四棱柱、五 棱柱等;同理,棱锥、棱台也这样分类。
思考:上图中的两个几何体分别由怎么样的平
面图形,按什么样的方向平移而得的?
答:分别是由三角形和六边形进行沿同一方向 平移得来的.
结论:一般地,由一个平面 多边形沿某一个方向平
移形成的空间几何体叫做棱柱. 平移起止位置的两 个面叫做棱柱的底面. 多边形的边平移形成的面叫 做棱柱的侧面
A`
C`
B`
底
