期望与方差在生活中一些应用18页PPT
合集下载
【精品】概率论与数理统计PPT课件第四章 数学期望和方差

8
9
10
P
0.1 0.3 0.6
Y
8
9
10
P
0.2 0.5 0.3
试问哪一个人的射击水平较高? 9
例1(续)
甲、乙的平均环数可写为
EX 80.1 90.3 100.6 9.5 EY 80.2 90.5 100.3 9.1
10
例2.对产品进行抽样,只要发现废品就认为这批产 品不合格,并结束抽样。若抽样到第 n件仍未发现 废品则认为这批产品合格。假设产品数量很大,抽 查到废品的概率是 p,试求平均需抽查的件数。
6
(3)泊松分布 X的所有可能取值为0,1,2,…,且
7
(4)几何分布 X的可能取值为1,2,…, 且 P(X=k)= (1-p)k-1 p, k= 1,2,….
由于
这可以由等式
两边同时对x求导数得到。
8
例1:
甲、乙两人射击,他们的射击水平由下表给出: X:甲击中的环数; Y:乙击中的环数;
X
p)nm
29
注意到二项分布B(n , p)的数学期望,就有 于是
注: 最后一步用了泊松分布数学期望的结果.
30
例8: 设X ~ U[0,], Y =sinX,求E(Y)。
解: X 的概率密度为 所以
31
例9 设二维随机变量(X ,Y)的密度函数为 求E(X), E(Y), E( X + Y ), E(XY), E(Y / X) 解:
36
37
最终, 显然,y = 3500 时,E (Y )最大,
E(Y)max =8250万元.
38
例11.假设由自动线加工的某种零件的内径 X (mm)~
N ( ,1). 已知销售每个零件的利润T (元)与销售零件
期望在生活中的应用 人教课标版精品公开PPT课件

可以
同学们,再见!
分清问题实质,解决问题!
二项分布
应用
如图,广州到北京之间有6条不同的网络线路并联,它们能通
过的最大信息量分别为1、1、2、2、3、4.现从中任取三条网线
且使每条网线通过最大信息量,三条网线可通过的信息总量即为
三条网线各自的最大信息量之和.
1
(1)求选取的三条网线可通过信息
1
总量ξ的数学期望;
广2
北
五.比赛得分问题
( 200年 3 全国高 ,改考 编A 题 、 )B两个代表队进 对行 抗乒 赛
每队三名A队 队员 队, 员 A1, 是 A2,A3,B队队员 B1, 是 B2,B3. 按以往多次比 ,赛 对的 阵统 队计 员之 率间 如胜 下负 :概
对阵队员 A队队员胜的概率 B队队员胜的概率
A
C
1 2
C5 21
1
C
1 2
C521
1
C 321 1
C2
1 2
C2063
2C063
C2063
2C0
3 6
2C0
3 6
(1)E425365758392
20 20 20 20 20 20
13 2
(2 )P 6 1 P 4 P 5 3 4
(3) 2008年北京奥运会,为保证广州网络在ξ≥6时信息畅通 的概率超过85%,需要增加一条网线且最大信息量不低于3, 问增加的这条网线的最大信息量最少应为多少?
P ( 2 )223 221 22328 35555335575
P(3)2228 3 5 5 75
E
22 15
六.摸彩中奖问题
一个布袋内装有6个红球与6个黄球,除颜色
数学期望和方差共95页PPT

6、法律的基础有两个,而且只有两个……公平和实用。——伯克 7、有两种和平的暴力,那就是法律和礼节。——歌德
8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
EN。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
EN。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
数学期望与方差ppt课件

频率 nk n
2 13 15 10 20 30 90 90 90 90 90 90
试问:该射手每次射击平均命中靶多少环?
2
解
平均射中环数
射中靶的总环数 射击次数
0 2 113 2 15 3 10 4 20 5 30 90
0 2 1 13 2 15 3 10 4 20 90 90 90 90 90
P{ X xk } pk , k 1,2, .
若级数 xk pk 绝对收敛, 则称级数 xk pk
k 1
k 1
为随机变量 X 的数学期望, 记为 E( X ). 即
E( X ) xk pk .
k 1
5
2.连续型随机变量数学期望的定义
设连续型随机变量 X 的概率密度为 f ( x),
若积分
第一节 数学期望
一、数学期望的概念 二、数学期望的性质 三、随机变量函数的数学期望 四、小结
1
一、数学期望的概念
ห้องสมุดไป่ตู้
引例 射击问题
设某射击手在同样的条
件下,瞄准靶子相继射击90次, (命中的环数是一个随机变量). 射中次数记录如下
命中环数 k 0 1 2 3 4 5
命中次数 nk 2 13 15 10 20 30
k
k
4. 设 X, Y 是相互独立的随机变量, 则有
E( XY ) E( X )E(Y ).
说明 连续型随机变量 X 的数学期望与离散型随 机变量数学期望的性质类似.
14
数学期望在医学上的一个应用
An application of Expected Value in Medicine 考虑用验血的方法在人群中普查某种疾病。集体做法是每 10个人一组,把这10个人的血液样本混合起来进行化验。如果 结果为阴性,则10个人只需化验1次;若结果为阳性,则需对 10个人在逐个化验,总计化验11次。假定人群中这种病的患病 率是10%,且每人患病与否是相互独立的。试问:这种分组化 验的方法与通常的逐一化验方法相比,是否能减少化验次数?
期望在生活中的一些应用

1683 637 77 3 1 E 0 1 2 3 2400 2400 2400 2400 3
解(二) : (1 )略 (2)设1表示路段AC中遇到的堵车次数 ;
2 表示路段CF中遇到的堵车次数 ; 3表示路段FB中遇到的堵车次数 ; 则 1 2 3
购买股票
状态 经济形势好 经济形势中等 经济形势不好
收益 概率
40000 0.3
10000 0.5
—20000 0.2
E1 40000 0.3 10000 0.5 20000 0.2 13000 8 D1 4.4110
存入银行
状态
收益 概率
经济形势好
8000 0.3
(2)当ξ≥6时,则保证信息畅通,
求线路信息畅 通的概率;
(3) 2008年北京奥运会,为保证邯郸网络在ξ≥6时信息畅通的概 率超过85%,需要增加一条网线且最大信息量不低于3,问增加 的这条网线的最大信息量最少应为多少?
解: ξ的分布列为 ξ
4
1 C 22 3 C 20 6
5
6
7
8
9
P
1 1 1 1 1 1 1 C2 C C 1 C 3 1 C2 52 1 C2 3 2 C 1 5 2 2 2 3 3 3 3 3 C C C C 20 20 20 20 C 20 6 6 6 6 6
解:设ξ为抽到的2球钱数之和,则ξ的分布列如下:
ξP2ຫໍສະໝຸດ 2 28 C 8 2 C 45 10
6 2 1 C16 8 C2 2 C 45 10
10 1 22 C 2 C10 45
28 16 1 E 2 6 10 3.6 45 45 45
概率论与数理统计数学期望与方差专项PPT课件
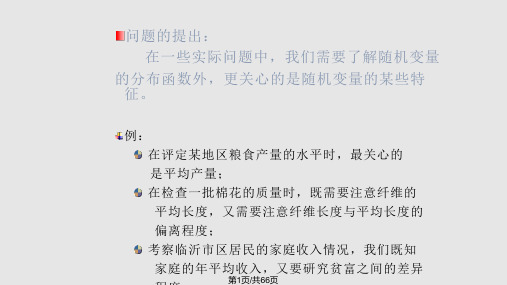
9
第9页/共66页
定理:设Y是随机变量X的函数:Y g(X )g是连续函数,
X 是离散型随机变量,它的分布律为:
P( X xk ) pk , k 1, 2,
若 g(xk )pk绝对收敛,则有E(Y ) E[g( X )] g(度为f (x)
服
从
同
一
指
数
分
布,
其
概
率密
度
为
: f (x)
1
e
x
x0
0
若将这2个电子装置串联联接
0
x0
组成整机,求整机寿命N(以小时计)的数学期望。 是
解 :X k
(k
1,
2)
的分布函数F ( x)
1
e
x
x0
0
x0
串联情况下,N min X1, X2 ,故N的分布函数为:
指 数 分 布 的
密
Fmin (x)
dx
1
x
1 x
2
3 x4
y3
dy
1
3 2x4
[
1 2y2
] |x1
x
dx
3 4
(
1
1 x6
1 x2
)dx
3 4
(
1 5
1)
3 5
考虑:先求E(Y )
yfY
(
y)dy,这里
你算对了吗?哪个更容易呢? 第14页/共66页
fY
(
y)
1 y
y
3 2x3 y2
3 2x3 y2
dx dx
0
2
2
2
sin (0 1) 0.25 sin (11) 0.2 sin (0 2) 0.15
离散型随机变量的期望与方差PPT教学课件

我的家乡在 长江边上,那里 有成片的橘园。
家乡的红橘, 真让人喜爱呀!
练习: 1、目前由于各种原因,许多人选择租车
代步,租车行业生意十分兴隆,但由于租车 者以新手居 多,车辆受损事故频频发生。据 统计,一年 中一辆车受损的概率为0.03.现保 险公司拟开设 一年期租车保险,一辆车一年的 保费为1000元,若在一年内该车受损,则保险公 司需赔偿3000元,求保险公司收益的期望。
故应选择在商场外搞促销活动。 变式1:若下雨的概率为0.6呢? 变式2:下雨的概率为多少时,在商场内、外搞
促销没有区别。
练习:
1、已知随机变量 的分布列为
0 1 2 3 4 5
P 0.1 0.2 0.3 0.2 0.1 0.1
求E
2.3
2、抛掷一枚硬币,规定正面向上得1分,反面向
上得-1分,求得分 的期望。 0
但当你走近,那阵 阵香气扑面而来, 会使你醉倒。
到了四五月,各种花竞相开放, 争奇斗艳,而橘子树却不声不响 地长出米粒大小的花骨朵。花骨 朵绽放开来,形状像茉莉,一瓣 一瓣的,有指甲那么大,小巧、 洁白、清新、朴素,一簇簇藏在 枝叶间,星星点点的,不大起眼。 但当你走近,那阵阵香气扑面而 来,会使你醉倒。
1
2
3
4
5
p
0.7
0.3× 0.32× 0.33× 0.7 0.7 0.7
0.34
E =1.43
课堂小结:
本节课我们讲了一个定义,一个公式
1)E = x1p1+x2p2+…+xnpn+…
2)若 a b ,则 E aE b
(a、b是常数)
9·家乡的 红橘
风霜考验 明媚 花骨朵竞 相开放 绽放 茉莉 一 瓣一瓣 一簇簇 朴素 又酸 又涩 成熟 沉甸甸 鲜嫩 舒畅
数学期望和方差.ppt

第四章 数学期望和方差
(2) 二项分布
X的取值为0,1,…,n. 且
P(X=k)=
n
Cnk
pk
(1-p)n-k,
k= 0, 1, …, n.
E(X) kC n kpk(1p)nk
k0
n
k
n!
pk(1p)nk
k1 k!(nk)!
nn p(n 1 )!p k 1 (1 p )(n 1 ) (k 1 )
k 1 e
k 1 ( k 1)!
k e k0 k!
(4)几何分布
第四章 数学期望和方差
X的可能取值为1,2,…, 且 P(X=k)= qk-1 p, k= 1,2,…. p+q=1.
第四章 数学期望和方差
E (X ) kkp kpk q 1p kq k 1
第四章 数学期望和方差
解:设X为停止检查时,抽样的件数,则X 的可能取值为1,2,…,n,且
P{Xk} q qn k 1 1,p,
k1,2,,n1; kn.
其中 q1p,于是
n1
E(X) kqk1pnqn1
k1
第四章 数学期望和方差
n1
E(X) kqk1(1q)nqn1
k 1 (k 1 )(n ! k )!
n1
npCn k1pk(1p)(n1)k np
k0
第四章 数学期望和方差
(3)泊松分布
X的可能取值为0,1,2,…,且
P(Xk)ke,k0,1,2,,
k!
k
E(X) kk p k
k0
