中考数学压轴题解答指导
数学中考数学压轴题知识点及练习题附解析
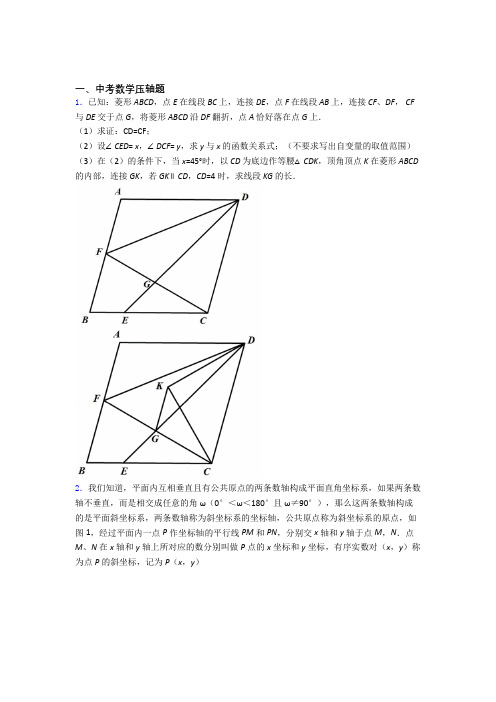
一、中考数学压轴题1.已知:菱形ABCD,点E 在线段BC 上,连接DE,点F 在线段AB 上,连接CF、DF, CF 与DE 交于点G,将菱形ABCD 沿DF 翻折,点A 恰好落在点G 上.(1)求证:CD=CF;(2)设∠CED= x,∠DCF= y,求y 与x 的函数关系式;(不要求写出自变量的取值范围)(3)在(2)的条件下,当x=45°时,以CD 为底边作等腰△CDK,顶角顶点K 在菱形ABCD 的内部,连接GK,若GK∥CD,CD=4 时,求线段KG 的长.2.我们知道,平面内互相垂直且有公共原点的两条数轴构成平面直角坐标系,如果两条数轴不垂直,而是相交成任意的角ω(0°<ω<180°且ω≠90°),那么这两条数轴构成的是平面斜坐标系,两条数轴称为斜坐标系的坐标轴,公共原点称为斜坐标系的原点,如图1,经过平面内一点P作坐标轴的平行线PM和PN,分别交x轴和y轴于点M,N.点M、N在x轴和y轴上所对应的数分别叫做P点的x坐标和y坐标,有序实数对(x,y)称为点P的斜坐标,记为P(x,y)(1)如图2,ω=45°,矩形OABC中的一边OA在x轴上,BC与y轴交于点D,OA=2,OC=1.①点A、B、C在此斜坐标系内的坐标分别为A,B,C.②设点P(x,y)在经过O、B两点的直线上,则y与x之间满足的关系为.③设点Q(x,y)在经过A、D两点的直线上,则y与x之间满足的关系为.(2)若ω=120°,O为坐标原点.①如图3,圆M与y轴相切原点O,被x轴截得的弦长OA=23,求圆M的半径及圆心M的斜坐标.②如图4,圆M的圆心斜坐标为M(23,23),若圆上恰有两个点到y轴的距离为1,则圆M的半径r的取值范围是.3.如图,AB∥CD,定点E,F分别在直线AB,CD上,平行线AB,CD之间有一动点P.(1)如图1,当P点在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为,如图2,当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为.(2)如图3,当∠EPF=90°,F P平分∠EFC时,求证:EP平分∠AEF;(3)如图4,QE,QF分别平分∠PEB和∠PFD,且点P在EF左侧.①若∠EPF=60°,则∠EQF=.②猜想∠EPF与∠EQF的数量关系,并说明理由;4.“阅读素养的培养是构建核心素养的重要基础,重庆十一中学校以‘大阅读’特色课程实施为突破口,着力提升学生的核心素养.”全校师生积极响应和配合,开展各种活动丰富其课余生活.在数学兴趣小组中,同学们从书上认识了很多有趣的数.其中有一个“和平数”引起了同学们的兴趣.描述如下:一个四位数,记千位上和百位上的数字之和为x ,十位上和个位上的数字之和为y ,如果x y =,那么称这个四位数为“和平数”. 例如:1423,14x =+,23y =+,因为x y =,所以1423是“和平数”.(1)直接写出:最小的“和平数”是________,最大的“和平数”是__________; (2)求同时满足下列条件的所有“和平数”:①个位上的数字是千位上的数字的两倍;②百位上的数字与十位上的数字之和是12的倍数;(3)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后这两个“和平数”为“相关和平数”.例如:1423于4132为“相关和平数”求证:任意的两个“相关和平数”之和是1111的倍数.5.如果关于x 的一元二次方程20ax bx c ++=有两个不相等的实数根,且其中一个根为另一个根的一半,则称这样的方程为“半等分根方程”.(1)①方程2280x x --= 半等分根方程(填“是”或“不是”);②若(1)()0x mx n -+=是半等分根方程,则代数式2252m mn n ++= ; (2)若点(,)p q 在反比例函数8x y =的图象上,则关于x 的方程260px x q -+=是半等分根方程吗?并说明理由; (3)如果方程20ax bx c ++=是半等分根方程,且相异两点(1,)M t s +,(4,)N t s -都在抛物线2y ax bx c =++上,试说明方程20ax bx c ++=的一个根为53. 6.如图,在菱形ABCD 中,AB a ,60ABC ∠=︒,过点A 作AE BC ⊥,垂足为E ,AF CD ⊥,垂足为F .(1)连接EF ,用等式表示线段EF 与EC 的数量关系,并说明理由;(2)连接BF ,过点A 作AK BF ⊥,垂足为K ,求BK 的长(用含a 的代数式表示); (3)延长线段CB 到G ,延长线段DC 到H ,且BG CH =,连接AG ,GH ,AH . ①判断AGH 的形状,并说明理由;②若12,(33)2ADH a S ==+,求sin GAB ∠的值.7.在平面直角坐标系xOy 中,对于点A 和图形M ,若图形M 上存在两点P ,Q ,使得3AP AQ =,则称点A 是图形M 的“倍增点”.(1)若图形M 为线段BC ,其中点()2,0B -,点()2,0C ,则下列三个点()1,2D -,()1,1E -,()0,2F 是线段BC 的倍增点的是_____________;(2)若O 的半径为4,直线l :2y x =-+,求直线l 上O 倍增点的横坐标的取值范围;(3)设直线1y x =-+与两坐标轴分别交于G ,H ,OT 的半径为4,圆心T 是x 轴上的动点,若线段GH 上存在T 的倍增点,直接写出圆心T 的横坐标的取值范围.8.∠MON=90°,点A ,B 分别在OM 、ON 上运动(不与点O 重合).(1)如图①,AE 、BE 分别是∠BAO 和∠ABO 的平分线,随着点A 、点B 的运动,∠AEB= °(2)如图②,若BC 是∠ABN 的平分线,BC 的反向延长线与∠OAB 的平分线交于点D ①若∠BAO=60°,则∠D= °.②随着点A ,B 的运动,∠D 的大小会变吗?如果不会,求∠D 的度数;如果会,请说明理由.(3)如图③,延长MO 至Q ,延长BA 至G ,已知∠BAO ,∠OAG 的平分线与∠BOQ 的平分线及其延长线相交于点E 、F ,在△AEF 中,如果有一个角是另一个角的3倍,求∠ABO 的度数.9.如图一,矩形ABCD 中,AB=m ,BC=n ,将此矩形绕点B 顺时针方向旋转θ(0°<θ<90°)得到矩形A 1BC 1D 1,点A 1在边CD 上.(1)若m=2,n=1,求在旋转过程中,点D 到点D 1所经过路径的长度;(2)将矩形A 1BC 1D 1继续绕点B 顺时针方向旋转得到矩形A 2BC 2D 2,点D 2在BC 的延长线上,设边A 2B 与CD 交于点E ,若161A E EC =-,求n m 的值. (3)如图二,在(2)的条件下,直线AB 上有一点P ,BP=2,点E 是直线DC 上一动点,在BE 左侧作矩形BEFG 且始终保持BE n BG m =,设AB=33,试探究点E 移动过程中,PF 是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.10.如图,直角三角形ABC ∆中,90460ACB AC A ∠︒=∠︒=,,=,O 为BC 中点,将ABC ∆绕O 点旋转180︒得到DCB ∆.一动点P 从A 出发,以每秒1的速度沿A B D →→的路线匀速运动,过点P 作直线PM ,使PM AC ⊥.(1)当点P 运动2秒时,另一动点Q 也从A 出发沿A B D →→的路线运动,且在AB 上以每秒1的速度匀速运动,在BD 上以每秒2的速度匀速运动,过Q 作直线QN 使//QN PM ,设点Q 的运动时间为t 秒,(0<t<10)直线PM 与QN 截四边形ABDC 所得图形的面积为S ,求S 关于t 的函数关系式,并求出S 的最大值.(2)当点P 开始运动的同时,另一动点R 从B 处出发沿B C D →→的路线运动,且在BC 上以每秒3的速度匀速运动,在CD 上以每秒2的速度匀度运动,是否存在这样的P R 、,使BPR ∆为等腰三角形?若存在,直接写出点P 运动的时间m 的值,若不存在请说明理由.11.问题背景:如图(1),ABC 内接于O ,过点A 作O 的切线l ,在l 上任取一个不同于点A 的点P ,连接PB PC 、,比较BPC ∠与BAC ∠的大小,并说明理由.问题解决:如图(2),A (0,2)、B (0,4),在x 轴正半轴上是否存在一点P ,使得cos APB ∠最小?若存在,求出点P 的坐标;若不存在,请说明理由.拓展应用:如图(3),四边形ABCD 中,//AB CD ,AD CD ⊥于D ,E 是AB 上一点,AE AD =,P 是DE 右侧四边形ABCD 内一点,若8AB =,11CD =,tan 2C =,9DEP S =,求sin APB ∠的最大值.12.如图所示,在平面直角坐标系中,点(),C m m 在一三象限角平分线上,点(),0B n 在x 轴上,且m=2n -+2n -+4,点A 在y 轴的正半轴上;四边形AOBC 的面积为6 (1)求点A 的坐标;(2)P 为AB 延长线上一点,//PQ OC ,交CB 延长线于Q ,探究OAP ∠、ABQ ∠、Q ∠的数量关系并说明理由;(3)作AD 平行CB 交CO 延长线于D ,BE 平分CBx ∠,BE 反向延长线交CO 延长线于,若设ADO α∠=,F β∠=,试求2αβ+的值.13.如图,矩形ABCD 中,AD >AB ,连接AC ,将线段AC 绕点A 顺时针旋转90∘得到线段AE ,平移线段AE 得到线段DF (点A 与点D 对应,点E 与点F 对应),连接BF ,分别交直线AD ,AC 于点G ,M ,连接EF .(1) 依题意补全图形;(2) 求证:EG ⊥AD ;(3) 连接EC ,交BF 于点N ,若AB =2,BC =4,设MB =a ,NF =b ,试比较()()11a b ++与9+6214.在菱形ABCD 中,点P 是对角线BD 上一点,点M 在CB 的延长线上,且PC PM =, 连接PA .()1如图①,求证:PA PM =;()2如图②,连接,AM PM 与AB 交于点,120O ADC ︒∠=求证 =PC AM ;()3连接AM ,当 90ADC ︒∠=时,PC 与AM 的数量关系是15.如图,抛物线2(40) y ax bx a =++≠与x 轴交于()() 3,0, 4,0A C -两点,与y 轴交于点B .()1求这条抛物线的顶点坐标;()2已知AD AB =(点D 在线段AC 上),有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动:同时另一个点Q 以某一速度从点B 沿线段BC 移动,经过()t s 的移动,线段PQ 被BD 垂直平分,求t 的值;()3在()2的情况下,抛物线的对称轴上是否存在一点M ,使MQ MC +的值最小?若存在,请求出点M 的坐标:若不存在,请说明理由.16.在平行四边形ABCD 中,60B ∠=︒,点E ,F 分别在边AB ,AD 上,且60ECF ∠=︒.(1)如图1,若AB BC =,求证:AE AF BC +=;(2)如图2,若4AB BC ==,且点E 为AB 的中点,连接BF 交CE 于点M ,求FM ;(3)如图3,若AB kBC =,探究线段BE 、DF 、BC 三之间的数量关系,说明理由.17.已知抛物线y=﹣x 2﹣2x+3交x 轴于点A 、C (点A 在点C 左侧),交y 轴于点B .(1)求A ,B ,C 三点坐标;(2)如图1,点D 为AC 中点,点E 在线段BD 上,且BE=2DE ,连接CE 并延长交抛物线于点M ,求点M 坐标;(3)如图2,将直线AB 绕点A 按逆时针方向旋转15°后交y 轴于点G ,连接CG ,点P 为△ACG 内一点,连接PA 、PC 、PG ,分别以AP 、AG 为边,在它们的左侧作等边△APR 和等边△AGQ ,求PA+PC+PG 的最小值,并求当PA+PC+PG 取得最小值时点P 的坐标(直接写出结果即可).18.已知:矩形ABCD 内接于⊙O ,连接 BD ,点E 在⊙O 上,连接 BE 交 AD 于点F ,∠BDC+45°=∠BFD ,连接ED .(1)如图 1,求证:∠EBD=∠EDB ;(2)如图2,点G 是 AB 上一点,过点G 作 AB 的垂线分别交BE 和 BD 于点H 和点K ,若HK=BG+AF ,求证:AB=KG ;(3)如图 3,在(2)的条件下,⊙O 上有一点N ,连接 CN 分别交BD 和 AD 于10点 M 和点 P ,连接 OP ,∠APO=∠CPO ,若 MD=8,MC= 3,求线段 GB 的长.19.已知:AB 为⊙O 的直径,点C 为弧AB 的中点,点D 为⊙O 上一点,连接CD ,交AB 于点M ,AE 为∠DAM 的平分线,交CD 于点E .(1)如图1,连接BE ,若∠ACD=22°,求∠MBE 的度数;(2) 如图2,连接DO 并延长,交⊙O 于点F ,连接AF ,交CD 于点N .①求证:DM 2+CN 2=CM 2;②如图3,当AD=1,AB=10时,请直接写出....线段ME 的长. 20.如图,抛物线25y ax bx =+-交x 轴于点A 、B (A 在B 的左侧),交y 轴于点C ,且OB OC =,()2,0A -.(1)求抛物线的解析式;(2)点P 为第四象限抛物线上一点,过点P 作y 轴的平行线交BC 于点D ,设P 点横坐标为t ,线段PD 的长度为d ,求d 与t 的函数关系式.(不要求写出t 的取值范围) (3)在(2)的条件下,F 为BP 延长线上一点,且45PFC ∠=︒,连接OF 、CP 、PB ,FOB ∆的面积为3600169,求PBC ∆的面积. 21.如图,已知ABF 为等腰直角三角形,90BAF ∠=︒,D 、C 为直线AF 上两点,且满足DF AC =,连接BD 、BC ,过点A 作AE BD ⊥于点E ,交BF 于点H ,连接CH .(1)若30BAE ∠=︒,1BE =,求DE 的长;(2)若点M 是线段BF 上的动点,连AM 并延长交BD 于N ,当M 在线段BF 的什么位置上时,AH BN =?请说明理由;(3)在(2)的结论下,判断线段CH 、AH 、BD 的数量关系.请说明理由.22.如图1,以AB 为直径作⊙O ,点C 是直径AB 上方半圆上的一点,连结AC ,BC ,过点C 作∠ACB 的平分线交⊙O 于点D ,过点D 作AB 的平行线交CB 的延长线于点E .(1)如图1,连结AD ,求证:∠ADC =∠DEC .(2)若⊙O 的半径为5,求CA •CE 的最大值.(3)如图2,连结AE ,设tan ∠ABC =x ,tan ∠AEC =y ,①求y 关于x 的函数解析式;②若CB BE =45,求y 的值. 23.发现来源于探究.小亮进行数学探究活动,作边长为a 的正方形ABCD 和边长为b 的正方形AEFG (a>b ),开始时,点E 在AB 上,如图1.将正方形AEFG 绕点A 逆时针方向旋转.(1)如图2,小亮将正方形AEFG 绕点A 逆时针方向旋转,连接BE 、DG ,当点G 恰好落在线段BE 上时,小亮发现DG ⊥BE ,请你帮他说明理由.当a=3,b=2时,请你帮他求此时DG 的长.(2)如图3,小亮旋转正方形AEFG ,点E 在DA 的延长线上,连接BF 、DF .当FG 平分∠BFD 时,请你帮他求a :b 及∠FBG 的度数.(3)如图4,BE 的延长线与直线DG 相交于点P ,a=2b .当正方形AEFG 绕点A 从图1开始,逆时针方向旋转一周时,请你帮小亮求点P 运动的路线长(用含b 的代数式表示).24.如图,二次函数23y x x m =-++的图象与x 轴的一个交点为(4,0)B ,另一个交点为A ,且与y 轴相交于C 点(1)则m =_________;C 点坐标为___________;(2)在直线BC 上方的抛物线上是否存在一点M ,使得它与B ,C 两点构成的三角形面积最大,若存在,求出此时M 点坐标;若不存在,请简要说明理由.(3)P 为抛物线上一点,它关于直线BC 的对称点为Q①当四边形PBQC 为菱形时,求点P 的坐标;②点P 的横坐标为(04)t t <<,当t =________时,四边形PBQC 的面积最大.25.附加题:在平面直角坐标系中,抛物线21y ax a =-与y 轴交于点A ,点A 关于x 轴的对称点为点B ,(1)求抛物线的对称轴;(2)求点B 坐标(用含a 的式子表示);(3)已知点11,P a ⎛⎫ ⎪⎝⎭,(3,0)Q ,若抛物线与线段PQ 恰有一个公共点,结合函数图像,求a 的取值范围.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题1.D解析:(1)见解析;(2)y=1603x +;(2)2 【解析】【分析】(1)根据翻折的性质得△DFG ≌△DFA ,从而推导得出∠FDC=∠DFG ,进而得到CF=DC ; (2)在等腰△DGC 和等腰△CFD 中,可用y 表示出∠GDC 、∠FDC 的值,从而求出∠ADF ,根据∠ADE=∠DEC ,得出y 与x 的关系式;(3)先证△KCD 是等腰直角三角形,根据CD 的长得到KC 的值,然后再△KGC 中求得KG 的值.【详解】(1)∵将菱形ABCD 沿DF 翻折,点A 恰好落在点G 上∴△DFG ≌△DFA ,∠AFD=∠FDC∴∠AFD=∠DFG∴∠FDC=∠DFG∴CF=DC ;(2)∵AD=DG=DC=FC ,∠DCF=y∴在△DGC 中,∠DGC=y ,∠GDC=180-2y在△CFD 中,∠CFD=∠CDF=902y -∴∠FDG=∠FDC -∠GDC=3902y - ∴∠ADF=∠FDG=3902y -,∴∠ADE=3y -180 ∵AD ∥BC∴∠ADE=∠DEC ,即3y -180=x化简得:y=1603x +; (3)如下图,过点K 作CD 的垂线,交CD 于点I ,延长KG 交BC 于点L ,过点C 作GL 的垂线,交GL 于点Q ,过点C 作GD 的垂线,交GD 于点N ,∵x=45°,∴y=75°,∠ADE=x=45°∴∠DGC=∠DCG=75°,∴∠NDC=30°,∴∠ADC=45°+30°=75°,∵四边形ABCD是菱形,∴∠B=75°,∵KG∥DC,∴KG∥AB,∠KGD=∠NDC=30°,∴∠GLC=∠B=75°,∠KGC=30°+75°=105°,∴∠LGC=75°,∴∠CGL=∠CGN,∴GC是∠LGN的角平分线,∴CQ=CN,∵CD=4,∠CDE=30°,∴在Rt△CND中,CN=2,∴CQ=2,∵KG∥CD,∴∠QKI=∠KIC=90°∵CQ⊥KL∴四边形CQKI是矩形,∵CK=KD,KI⊥CD,∴CI=ID=2,∴CI=CQ=2,∴矩形CQKI是正方形∴IK=CQ=2,∴在Rt△KIC中,CK=22,如下图,过点G作CK的垂线,交CK于点M,∴△KGM是等腰直角三角形,△GMC是直角三角形,且∠C=30°,设GM=x,则在Rt△GKM中,KM=GM=x,在Rt△GMC中,CG=2x,3x,∴322解得:62∴2=232x.【点睛】本题考查菱形的性质和翻折的性质,需要注意,翻折后的图形和翻折前的图形时完全相等的,这个条件不可忽略.2.B解析:(1)①(2,0),(12),(﹣12y2x;③y=﹣22x2;(2)①半径为2,M(3333);②2<r<4【解析】【分析】(1)①如图2−1中,作BE∥OD交OA于E,CF∥OD交x轴于F.求出OE、OF、CF、OD、BE即可解决问题;②如图2−2中,作BE∥OD交OA于E,作PM∥OD交OA于M.利用平行线分线段成比例定理即可解决问题;③如图3−3中,作QM∥OA交OD于M.利用平行线分线段成比例定理即可解决问题;(2)①如图3中,作MF⊥OA于F,作MN∥y轴交OA于N.解直角三角形即可解决问题;②如图4中,连接OM,作MK∥x轴交y轴于K,作MN⊥OK于N交⊙M于E、F.求出FN=NE=1时,⊙M的半径即可解决问题;【详解】解:(1)①如图2﹣1中,作BE∥OD交OA于E,CF∥OD交x轴于F.由题意OC =CD =1,OA =BC =2,∴BD =OE =1,OD =CF =BE=2, ∴A(2,0),B(1,2),C(﹣1,2),故答案为:A(2,0),B(1,2),C(﹣1,2).②如图2﹣2中,作BE ∥OD 交OA 于E ,作PM ∥OD 交OA 于M .∵OD ∥BE ,OD ∥PM ,∴BE ∥PM ,∴BE OE PM OM=, ∴21y x=, ∴y =2x .故答案为:y =2x .③如图2﹣3中,作QM ∥OA 交OD 于M .222MQ DM OA DOx y ∴=-∴= ∴222y x =-+故答案为:y=﹣22x+2.(2)①如图3中,作MF⊥OA于F,作MN∥y轴交OA于N.∵ω=120°,OM⊥y轴,∴∠MOA=30°,∵MF⊥OA,OA=23,∴OF=FA=3,∴FM=1,OM=2FM=2,∴圆M的半径为2∵MN∥y轴,∴MN⊥OM,∴MN=233,ON=2MN=433,∴M4323,33⎛⎫⎪ ⎪⎝⎭.②如图4中,连接OM,作MK∥x轴交y轴于K,作MN⊥OK于N交⊙M于E、F.∵MK∥x轴,ω=120°,∴∠MKO=60°,∵MK=OK=3∴△MKO是等边三角形,∴MN=3,当FN=1时,MF=3﹣1=2,当EN=1时,ME=3+1=4,观察图象可知当⊙M的半径r的取值范围为2<r<4.故答案为:2<r<4.【点睛】本题考查圆综合题、平行线分线段成比例定理、等边三角形的判定和性质、平面斜坐标系等知识,解题的关键是学会添加常用辅助线,构造平行线解决问题,属于中考压轴题.3.E解析:(1)∠EPF=∠AEP+∠PFC,∠AEP+∠EPF+∠PFC=360°;(2)见解析;(3)①150°,∠EQF=180°-12∠EPF【解析】【分析】(1)如下图,过点P作AB的平行线,根据平行线的性质可推导出角度关系;(2)如下图,根据(1)的结论,可得∠AEP+∠PFC=∠EPF=90°,利用△EPF内角和为180°可推导得出∠PEF+∠PFE=90°,从而得出∠PEF=∠AEP;(3)①根据(1)的结论知:∠AEP+∠PFC=∠EPF=60°,再利用角平分线的性质得出∠PEQ+∠PFQ=150°,最后在四边形EPFQ中得出结论;②根据(1)的结论知:∠AEP+∠PFC=∠EPF°,再利用角平分线的性质得出∠PEQ+∠PFQ=180°-1EPF2,最后在四边形EPFQ中得出结论.【详解】(1)如下图,过点P作PQ∥AB∵PQ∥AB,AB∥CD,∴PQ∥CD ∴∠AEP=∠EPQ,∠QPF=∠PFC 又∵∠EPF=∠EPQ+∠QPF∴∠EPF=∠AEP+∠PFC如下图,过点P作PQ∥AB同理,AB ∥QP ∥CD∴∠AEP+∠QPE=180°,∠QPF+∠PFC=180°∴∠AEP+∠EPF+∠PFC=∠AEP+∠EPQ+∠QPF+∠PFC=360°(2)根据(1)的结论知:∠AEP+∠PFC=∠EPF=90°∵PF 是∠CFE 的角平分线,∴∠PFC=∠PFE在△PEF 中,∵∠EPF=90°,∴∠PEF+∠PFE=90°∴∠PEF+∠PFE=∠AEP+∠PFC∴∠PEF=∠AEP ,∴PE 是∠AEF 的角平分线(3)①根据(1)的结论知:∠AEP+∠PFC=∠EPF=60°∴∠BEP+∠PFD=180°-∠AEP+180°-∠PFC=300°∵EQ 、QF 分别是∠PEB 和∠PFD 的角平分线∴∠PEQ=QEB ,∠PFQ=∠QFD∴∠PEQ+∠PFQ=150°在四边形PEQF 中,∠EQF=360°-∠EPF -(∠PEQ+∠PFQ)=360°-60°-150°=150° ②根据(1)的结论知:∠AEP+∠PFC=∠EPF∴∠BEP+∠PFD=180°-∠AEP+180°-∠PFC=360°-∠EPF∵EQ 、QF 分别是∠PEB 和∠PFD 的角平分线∴∠PEQ=∠QEB ,∠PFQ=∠QFD∴∠PEQ+∠PFQ=()1360EPF 2∠︒-=180°-1EPF 2∠ ∴在四边形PEQF 中: ∠EQF=360°-∠EPF -(∠PEQ+∠PFQ)=360°-EPF ∠-(180°-1EPF 2∠)=180°-1EPF 2∠ 【点睛】本题考查“M ”型模型,解题关键在过两条平行线中间的点作已知平行线的平行线,然后利用平行线的性质进行角度转化可推导结论.4.(1)1001;9999;(2)2754和4848;(3)见解析【解析】【分析】(1)根据“和平数”的定义可直接得出最小的“和平数”是1001,最大的“和平数”是9999;(2)设这个“和平数”的千位数字是a ,百位数字是m ,十位数字是n ,其中a ,m ,n 均是正整数且19a ≤≤,09m ≤≤,09n ≤≤,则个位数字是2a ,又由029a ≤≤得到a 的可能取值为1,2,3,4;根据百位上的数字与十位上的数字之和是12的倍数,可知m +n =12,得到122a m +=,由a 的可能取值可得m 的取值,即可求得符合条件的“和平数”;(3)设任意一个“和平数”千位数字为a ,百位数字为b ,十位数字为c ,个位数字为d ,则它的“相关和平数”千位数字为b ,百位数字为a ,十位数字为d ,个位数字为c ,计算它们的和,根据“和平数”的定义可知a+b=c+d ,因式分解可得原式= 1111(a+b ),即可证明.【详解】解:(1)根据“和平数”的定义可得:最小的“和平数”1001,最大的“和平数”9999,故答案为1001;9999;(2)设这个“和平数”的千位数字是a ,百位数字是m ,十位数字是n ,其中a ,m ,n 均是正整数且19a ≤≤,09m ≤≤,09n ≤≤,则个位数字是2a ,又∵029a ≤≤,∴a 的可能取值为1,2,3,4;∵百位上的数字与十位上的数字之和是12的倍数,∴m+n =0或m+n =12,∵“和平数”中a+m =n+2a ,当m+n =0时,即m=n =0,则此时a =0,不符合题意,∴m+n =12,∴a+m =12−m +2a ,解得:122a m +=, ∵a 的可能取值为1,2,3,4;且m 为正整数,∴m 的可能取值为7,8;当a =2时,m =7,这个“和平数”是2754;当a =4时,m =8,这个“和平数”是4848;综上所述,满足条件的“和平数”是2754和4848;(3)设任意一个“和平数”千位数字为a ,百位数字为b ,十位数字为c ,个位数字为d ,则它的“相关和平数”千位数字为b ,百位数字为a ,十位数字为d ,个位数字为c , ∴(100010010)(100010010)a b c d b a d c +++++++110011001111a b c d =+++1100()11()a b c d =+++由“和平数”的定义可知:a+b =c+d ,∴原式1100()11()a b a b =+++1111()a b =+,∵a ,b 为正整数,则1111()a b +能被1111整除,即(100010010)(100010010)a b c d b a d c +++++++能被1111整除,∴任意的两个“相关和平数”之和是1111的倍数.【点睛】本题考查新定义运算、因式分解的应用;能够读懂题意,根据数的特点,确定数的取值范围,进行正确的因式分解是解题关键.5.(1)①不是;②0;(2)若点(,)p q 在反比例函数8y x =的图象上,则关于x 的方程260px x q -+=是半等分根方程,理由详见解析;(3)详见解析【解析】【分析】(1)①解方程2280x x --=,根据“半等分根方程”定义作出判断即可;②解方程(1)()0x mx n -+=得11x =,2n x m =-,所以12n m -=或2n m -=,即:n =-2m 或m =-2n ,分别代入代数式2252m mn n ++=结果均为0 (2)根据点(,)p q 在反比例函数8y x =的图象上,得到8q p =,代入260px x q -+=,得到关于x 的方程2860px x p-+=,解方程,用含p 的式子表示x ,根据“半等分根方程”定义判断即可;(3)根据两点(1,)M t s +,(4,)N t s -都在抛物线上,且纵坐标相等,可以求出对称轴为52x =,根据方程20ax bx c ++=是半等分根方程,得到两根关系,根据抛物线对称轴为 12522x x +=,即可求出两个根,问题得证. 【详解】解:(1)①解方程2280x x --=得124,2x x ==-,不符合“半等分根方程”定义, 故答案为:不是;②解方程(1)()0x mx n -+=得11x =,2n x m =-,所以12n m -=或2n m -=,即:n =-2m 或m =-2n ,当n =-2m 时,()()22225522022m mn n m m n m ++=+-+-=; 当m =-2n 时,()()22225522022m mn n n n n n ++=-+-+=; 故答案为:0;(2)若点(,)p q 在反比例函数8y x =的图象上,则关于x 的方程260px x q -+=是半等分根方程理由:∵点(,)p q 在反比例函数8y x =的图象上 ∴8q p=代入方程260px x q -+=得: 2860px x p -+=解得:12x p =,24x p = ∵1212x x = ∴方程260px x q -+=是半等分根方程(3)∵相异两点(1,)M t s +,(4,)N t s -都在抛物线2y ax bx c =++上, ∴抛物线的对称轴为:(1)(4)522t t x ++-== 又∵方程20ax bx c ++=是半等分根方程∴设20ax bx c ++=的两个根分别为1x 和2x 令1212x x =则有:12522x x += 所以153x =,2103x = 所以方程20ax bx c ++=的一个根为53得证. 【点睛】本题为“新定义问题”,考查了学生自主学习的能力,解决此题关键是理解新定义概念,并结合所学数学知识进行解答.6.E解析:(1)EF =,见解析;(2)BK =;(3)①AGH 是等边三角形,见解析;②14 【解析】【分析】(1)连接EF ,AC ,由菱形的性质,可证Rt AEB Rt AFD ∆≅∆,然后得到AEF ∆为等边三角形,由解直角三角形得到AE =,即可得到答案;(2)由菱形的性质和等边三角形的性质,求出AF 的长度,然后得到BF 的长度,然后由相似三角形的性质,得到AB BK FB BA=,即可求出答案; (3)①由等边三角形的性质,先证明ABG ACH ≅,然后得到AG AH =,然后得到60BAH GAB GAH ︒∠+∠=∠=,即可得到答案;②由三角形的面积公式得到1DH =,然后得到AHF △为等腰直角三角形,再由解直角三角形的性质,即可求出答案.【详解】解:(1)EF =;理由:∵四边形ABCD 是菱形,60ABC ∠=︒,,60,//AB AD BC ABC ADC AD BC ︒∴==∠=∠=,120BAD ︒∴∠=,∵AE BC ⊥,垂足为E ,AF CD ⊥,垂足为F ,90AEB AFD ︒∴∠=∠=Rt AEB Rt AFD ∴∆≅∆,,30AE AF BAE DAF ∴=∠=∠=︒,60EAF ∴∠=︒,AEF ∴∆为等边三角形,EF AE ∴=.连接AC ,1602BAC BAD ︒∴∠=∠= 30EAC ︒∴∠= 在Rt AEC ∆中,tan EC EAC AE ∠=3AE EC ∴=,3EF EC ∴=(2)如图:∵四边形ABCD 是菱形,60,ABC AB a ︒∠==, ACD ∴是等边三角形,//,,60AB CD AD CD a ADC ︒==∠=.AF CD ⊥,垂足为F ,1,902CF DF a BAF AFD ︒∴==∠=∠= 在Rt ADF 中,sin AF ADF AD ∠=, 3AF ∴=在Rt ABF 中,22BF AB AF =+,72BF a ∴= AK BF ⊥,垂足为K ,90AKB FAB ︒∴∠=∠=ABK FBA ∠=∠~Rt AKB Rt FAB ∴∆∆,AB BK FB BA∴=, 27BK a ∴=, (3)如图:①AGH 是等边三角形.理由:连接AC .,60AB BC ABC ︒=∠=,ABC ∴为等边三角形,,60AB AC ABC ACB ︒∴=∠=∠=,120ABG ︒∴∠=. //AB CD ,60BCH ABC ︒∴∠=∠=,120ACH ︒∴∠=ABG ACH ∴∠=∠,又BG CH =,ABG ACH ∴≅,,AG AH GAB HAC ∴=∠=∠.60BAH HAC BAC ︒∠+∠=∠=,60BAH GAB GAH ︒∴∠+∠=∠=,AGH ∴为等边三角形;②ADC 为等边三角形,2,1AD DC AC CF DF ∴=====,AF ∴=.1(32ADH S =, 11(322DH ∴⨯=,1DH ∴=1CH DH CD ∴=-=,HF DH DF =-=AF HF ∴=,AHF ∴为等腰直角三角形,45AHF ︒∴∠=.过点C 作CM AH ⊥,垂足为M .在Rt CMH 中,sin CM CHM CH∠=, 12CM ∴=, 在Rt AMC 中,sin CM MAC AC ∠=, 1sin 4MAC ∴∠=. 又GAB HAC ∠=∠, 1sin sin 4GAB HAC ∴∠=∠=; 【点睛】本题考查了解直角三角形,相似三角形的判定和性质,等边三角形的判定和性质,菱形的性质,等腰三角形的判定和性质,全等三角形的判定和性质,解题的关键是熟练掌握所学的定理和性质,正确作出辅助线进行解题.7.A解析:(1)()1,1E -;(2)12m -≤≤-或01m ≤≤3)9t ≤≤.【解析】【分析】(1)首先要理解点A 是图形M 的“倍增点”的定义,将三个点逐一代入验证即可; (2)分两种情况:①点"倍增点”在O 的外部,分别求得“倍增点”横坐标的最大值和最小值,②点"倍增点"在O 的内部,依次求得“倍增点"横坐标的最大值和最小值,即可确定“倍增点”横坐标的范围;(3)分别求得线段GH 两端点为T "倍增点”时横坐标的最大值和最小值即可.【详解】(1)()1,2D -到线段BC 的距离为2,22(12)(20)1332DC =--+-=<⨯∴()1,2D -不是线段BC 的倍增点;()1,1E -到线段BC 的距离为1,22(12)(10)103EC =--+-=>,∴在线段BC 上必存在一点P 使EP=3,∴()1,1E -是线段BC 的倍增点;()0,2F 到线段BC 的距离为2,22(02)(20)2232FC =-+-=<⨯∴()0,2F 不是线段BC 的倍增点;综上,()1,1E -是线段BC 的倍增点;(2)设直线l 上“倍增点”的横坐标为m ,当点在O 外时,222(2)8,m m +-+≤解方程222(2)8m m +-+=,得1131m =+,2131m =-当点在O 内部时,22224(2)3(44(2))m m m m ++-+≥--+-+解得:m≥0或m≤-2∴直线l 上“倍增点”的橫坐标的取值范围为1312m -≤≤-或0131m ≤≤+;(3)如图所示,当点G(1,0)为T "倍增点"时,T(9,0),此时T 的横坐标为最大值,当点H(0,1)为T “倍增点”时,则T(63,此时T 的横坐标为最小值;∴圆心T(t, 0)的横坐标的取值范围为:639t -≤≤.【点睛】在正确理解点A 是图形M 的“倍增点”定义的基础上,利用(1)判断是否是倍增点的不等关系式,即可列不等式组求解范围.8.A解析:(1)135°;(2)①45°,②不发生变化,45°;(3)60°或45°【解析】【分析】(1)利用三角形内角和定理、两角互余、角平分线性质即可求解;(2)①利用对顶角相等、两角互余、两角互补、角平分线性质即可求解;②证明和推理过程同①的求解过程;(3)由(2)的证明求解思路,不难得出EAF ∠=90°,如果有一个角是另一个角的3倍,所以不确定是哪个角是哪个角的三倍,所以需要分情况讨论;值得注意的是,∠MON=90°,所以求解出的∠ABO 一定要小于90°,注意解得取舍.【详解】(1)()11801802118090180451352AEB EBA BAE OBA BAO ∠=︒-∠-∠=︒-∠+∠=︒-⨯︒=︒-︒=︒(2)①如图所示AD 与BO 交于点E ,()9060301180307521909030602180180756045OBA DBO NBC DEB OEA OAB D DBE DEB ∠=︒-︒=︒∠=∠=︒-︒=︒∠=∠=︒-∠=︒-︒=︒∠=︒-∠-∠=︒-︒-︒=︒②∠D 的度数不随A 、B 的移动而发生变化设BAD α∠=,因为AD 平分∠BAO ,所以2BAO α∠=,因为∠AOB=90°,所以180902ABN ABO AOB BAO α∠=︒-∠=∠+∠=+。
中考数学压轴题----《反比例函数综合》例题讲解
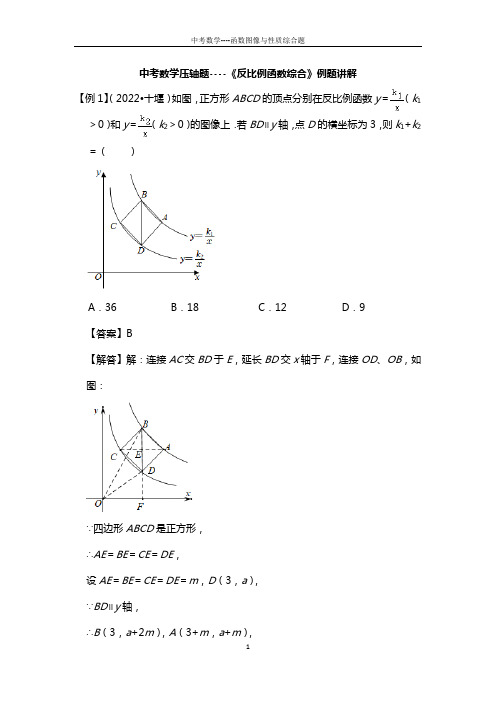
中考数学压轴题----《反比例函数综合》例题讲解【例1】(2022•十堰)如图,正方形ABCD的顶点分别在反比例函数y=(k1>0)和y=(k2>0)的图像上.若BD∥y轴,点D的横坐标为3,则k1+k2=()A.36B.18C.12D.9【答案】B【解答】解:连接AC交BD于E,延长BD交x轴于F,连接OD、OB,如图:∵四边形ABCD是正方形,∴AE=BE=CE=DE,设AE=BE=CE=DE=m,D(3,a),∵BD∥y轴,∴B(3,a+2m),A(3+m,a+m),∵A,B都在反比例函数y=(k1>0)的图像上,∴k1=3(a+2m)=(3+m)(a+m),∵m≠0,∴m=3﹣a,∴B(3,6﹣a),∵B(3,6﹣a)在反比例函数y=(k1>0)的图像上,D(3,a)在y=(k2>0)的图像上,∴k1=3(6﹣a)=18﹣3a,k2=3a,∴k1+k2=18﹣3a+3a=18;故选:B【变式1-1】(2021•鄂州)如图,点A是反比例函数y=(x>0)的图像上一点,过点A作AC⊥x轴于点C,AC交反比例函数y=(x>0)的图像于点B,点P是y轴正半轴上一点.若△PAB的面积为2,则k的值为.【答案】8【解答】解:连接OA、OB,∵AC⊥x轴,∴AC∥y轴,∴S△AOB=S△APB,∵S△APB=2,∴S△AOB=2,由反比例函数系数k的几何意义可得:S△AOC=6,S△BOC=,∴6﹣=2,解得:k=8,故答案为8.【变式2-2】(2021•荆州)如图,过反比例函数y=(k>0,x>0)图像上的四点P1,P2,P3,P4分别作x轴的垂线,垂足分别为A1,A2,A3,A4,再过P1,P2,P3,P4分别作y轴,P1A1,P2A2,P3A3的垂线,构造了四个相邻的矩形.若这四个矩形的面积从左到右依次为S1,S2,S3,S4,OA1=A1A2=A2A3=A3A4,则S1与S4的数量关系为.【答案】S1=4S4【解答】解:∵过双曲线上任意一点、向坐标轴作垂线所围成的矩形面积S是个定值,OA1=A1A2=A2A3=A3A4,∴S1=k,S2=k,S3=k,S4=k,∴S1=4S4.故答案为:S1=4S4.【变式1-3】(2022•毕节市)如图,在平面直角坐标系中,正方形ABCD的顶点A,B分别在x轴、y轴上,对角线交于点E,反比例函数y=(x>0,k >0)的图像经过点C,E.若点A(3,0),则k的值是.【答案】4【解答】解:设C(m,),∵四边形ABCD是正方形,∴点E为AC的中点,∴E(,),∵点E在反比例函数y=上,∴,∴m=1,作CH⊥y轴于H,∴CH=1,∵四边形ABCD是正方形,∴BA=BC,∠ABC=90°,∴∠OBA=∠HCB,∵∠AOB=∠BHC,∴△AOB≌△BHC(AAS),∴BH=OA=3,OB=CH=1,∴C(1,4),∴k=4,故答案为:4.【变式1-4】(2022•雁塔区校级模拟)如图,正方形ACBE的边长是,点B,C分别在x轴和y轴正半轴上,BO=2,ED⊥x轴于点D,ED的中点F在反比例函数y=(x>0)的图像上,则k=.【答案】3【解答】解:∵正方形ACBE的边长是,BO=2,∴BC=BE=,∴OC===1,∵∠ABC=90°,∴∠OBC+∠EBD=90°,∵∠OBC+∠OCB=90°,∴∠OCB=∠EBD,在△OBC和△DEB中,,∴△OBC≌△DEB(AAS),∴BD=OC=1,DE=OB=2,∴OD=3,∴E(3,2),∵点F是ED的中点,∴F(3,1),∵点F在反比例函数y=(x>0)的图像上,∴k=3×1=3,故答案为3.【变式1-5】(2021•广元)如图,点A(﹣2,2)在反比例函数y=的图像上,点M在x轴的正半轴上,点N在y轴的负半轴上,且OM=ON=5.点P (x,y)是线段MN上一动点,过点A和P分别作x轴的垂线,垂足为点D 和E,连接OA、OP.当S△OAD<S△OPE时,x的取值范围是.【答案】1<x<4【解答】解:过点B作BF⊥ON于F,连接OB,过点C作CG⊥OM于点G,连接OC,如图,∵点A(﹣2,2)在反比例函数y=的图像上,∴k=﹣4.∴y=.∵点A(﹣2,2),∴AD=OD=2.∴.设B(a,b),则ab=﹣4,OF=﹣b,BF=a.∴==2.同理:S△OCG=2.从图中可以看出当点P在线段BC上时,S△OPE>S△OBF,即当点P在线段BC上时,满足S△OAD<S△OPE.∵OM=ON=5,∴N(0,﹣5),M(5,0).设直线MN的解析式为y=mx+n,则:,解得:.∴直线MN的解析式为y=x﹣5.∴,解得:,.∴B(1,﹣4),C(4,﹣1).∴x的取值范围为1<x<4.【变式1-6】(2021•荆门)如图,在平面直角坐标系中,Rt△OAB斜边上的高为1,∠AOB=30°,将Rt△OAB绕原点顺时针旋转90°得到Rt△OCD,点A 的对应点C恰好在函数y=(k≠0)的图像上,若在y=的图像上另有一点M使得∠MOC=30°,则点M的坐标为.【答案】(,1)【解答】解:作AE⊥OB于E,MF⊥x轴于F,则AE=1,∵∠AOB=30°,∴OE=AE=,将Rt△OAB绕原点顺时针旋转90°得到Rt△OCD,点A的对应点C为(1,),∵点C在函数y=(k≠0)的图像上,∴k=1×=,∴y=,∵∠COD=∠AOB=30°,∠MOC=30°,∴∠DOM=60°,∴∠MOF=30°,∴OF=MF,设MF=n,则OF=n,∴M(n,n),∵点M在函数y=的图像上,∴n=,∴n=1(负数舍去),∴M(,1),故答案为(,1).【变式1-7】(2021•达州)如图,将一把矩形直尺ABCD和一块等腰直角三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,EF交BC于点M,反比例函数y=(x<0)的图像恰好经过点F,M,若直尺的宽CD=1,三角板的斜边FG=4,则k=.【答案】﹣12【解答】解:过点M作MN⊥AD,垂足为N,则MN=CD=1,在Rt△FMN中,∠MFN=45°,∴FN=MN=1又∵FG=4,∴NA=MB=FG﹣FN=4﹣1=3,设OA=a,则OB=a+1,∴点F(﹣a,4),M(﹣a﹣1,3),又∵反比例函数y=(x<0)的图像恰好经过点F,M,∴k=﹣4a=3(﹣a﹣1),解得,a=3,∴k=﹣4a=﹣12,故答案为:﹣12.a11。
中考数学压轴题的常见类型与解题思路

中考数学压轴题的常见类型与解题思路中考数学压轴题是中考数学试卷中的难点题目,通常是在考察学生对数学知识的深层理解和运用能力。
在中考数学压轴题中,常见的类型包括填空题、选择题、解答题等,涉及的知识点也广泛,如代数、几何、概率统计等。
下面将分别介绍中考数学压轴题的常见类型与解题思路。
一、填空题中考数学压轴题中的填空题往往考察学生对知识点的深层理解和运用能力。
填空题通常涉及代数、几何、概率统计等多个知识点,要求学生根据题目所给信息进行逻辑推理和计算,最终得出正确答案。
解题思路:1.审题:仔细阅读题目,明确要求填入的数据或公式,搞清题意。
2.列出已知条件:把题目中所给的信息一一列出,明确已知条件。
3.推理和计算:根据已知条件进行推理和计算,利用相关的数学公式或方法解题。
4.结果验证:算出结果后,需对答案进行验证,确保填入的数值或公式正确无误。
二、选择题中考数学压轴题中的选择题通常考察学生对知识点的掌握程度和运用能力。
选择题类型多样,既有单项选择题,也有不定项选择题,要求学生在有限的时间内作出正确选择。
解题思路:1.通读选项:先通读全部选项,了解每个选项的意思和含义。
2.分析题目:根据题目的要求,分析所给信息并确定相关知识点。
3.排除干扰:排除明显错误或无关的选项,缩小答案范围。
4.明确答案:通过对选项的排除及相关知识点的应用,确定最终答案。
三、解答题解题思路:1.理清思路:首先要理清解题思路,明确题目要求和解题方法。
2.列出所需步骤:根据题目要求,列出解题所需的步骤和计算方法。
3.细致计算:根据题目所给信息,进行细致计算和逻辑推理,得出正确答案。
4.解题亮点:在解答过程中,可适当突出解题亮点,以突显解题思路和方法。
总结而言,中考数学压轴题的常见类型包括填空题、选择题和解答题。
在解题过程中,学生需要通过仔细审题、列出已知条件、推理和计算、结果验证等步骤来解决填空题;而在选择题中,要通过通读选项、分析题目、排除干扰、明确答案等步骤来进行解答,而解答题则需要通过理清思路、列出所需步骤、细致计算、解题亮点等步骤来解决问题。
初中解数学压轴题技巧

初中解数学压轴题技巧初中解数学压轴题技巧一、解数学压轴题的策略解数学压轴题可分为五个步骤:1.认真默读题目,全面审视题目的所有条件和答题要求,注意挖掘隐蔽的条件和内在联系,理解好题意;2.利用重要数学思想探究解题思路;3.选择好解题的方法正确解答;4.做好检验工作,完善解题过程;5.当思维受阻、思路难觅时,要及时调整思路和方法,并重新审视题意,既要防止钻牛角尖,又要防止轻易放弃.二、解动态几何压轴题的策略近几年的数学中考试卷中都是以函数和几何图形的综合作为压轴题,用到圆、三角形和四边形等有关知识,方程与图形的综合也是常见的压轴题.动态几何问题是一种新题型,在图形的变换过程中,探究图形中某些不变的因素,把操作、观察、探求、计算和证明融合在一起.动态几何题解决的策略是:把握运动规律,寻求运动中的特殊位置;在“动”中求“静”,在“静”中探求“动”的一般规律.通过探索、归纳、猜想,获得图形在运动过程中是否保留或具有某种性质.简析:本题是一个双动点问题,是中考动态问题中出现频率最高的题型,这类题的解题策略是化动为静,注意运用分类思想.三、巧用数学思想方法解分类讨论型压轴题数学思想和方法是数学的灵魂,是知识转化为能力的桥梁 .近几年的各省市中考数学试题,越来越注重数学思想和数学方法的考查,这已成为大家的共识,为帮助读者更好地理解和掌握常用的基本数学思想和数学方法解初中数学压轴题的方法和技巧代数与几何有机结合,掌握解题策略中考压轴题主要体现在综合运用方程(组)、不等式、三角形、四边形、圆、函数知识上,对于这些内容,学生要做到一题多解、多题一解,将代数、几何知识融会贯通,会用代数的观点分析几何问题,用代数方法(方程、不等式、函数等)解决几何问题。
会从几何的角度理解代数问题,寻找几何基本图形,通过数形结合,将归纳、类比、化归、分类等方法运用到解题过程中。
平常学习中要善于归纳、总结,避免盲目的机械重复,这样我们就能找到解决问题的切入点!做好整体分析和思考,善于总结压轴题中蕴含的知识点做压轴题必须要进行全局性分析,对压轴题中蕴含的数学知识点进行剖析。
中考数学压轴题的常见类型与解题思路

中考数学压轴题的常见类型与解题思路
中考数学压轴题是考试中最难的题型,涉及的内容相对较为复杂,解题思路也较为繁琐。
以下是一些中考数学压轴题的常见类型和解题思路。
常见类型一:应用题
应用题是中考数学压轴题中最常见的类型之一。
这类题目通常涉及实际问题,需要运用数学知识进行分析和计算。
解题思路:
1. 仔细阅读题目,理解问题的背景和要求。
2. 分析问题,确定解题的核心思路和步骤。
3. 运用所学的数学知识和技巧,进行计算和推理。
4. 对结果进行合理性检验,确保解答的准确性和完整性。
解题思路:
1. 仔细观察图形,寻找图形的性质和特点。
2. 运用几何性质和定理,进行推理和证明。
3. 利用几何性质,绘制等边、等腰和直角三角形等特殊图形进行推理和计算。
4. 运用实际问题,将几何题转化为代数问题,从而更好地解决问题。
总结:
中考数学压轴题的常见类型包括应用题、几何题、代数题和概率题等。
解题时需要仔细阅读题目、分析问题、运用所学的数学知识和技巧进行计算和推理,并对结果进行合理性检验。
通过充分的准备和练习,掌握解题的方法和技巧,就能够更好地应对中考数学压轴题。
初三数学总复习之压轴题解法分析

初三数学总复习之压轴题解法分析压轴题是指考试前夕给学生的一份重要的综合试题,目的是检测学生对所学知识的掌握程度和解题能力。
在初中数学考试中,压轴题往往是整个试卷的难点,也是考察学生能力的重要环节。
在本文中,我将从解题方法的角度,分析几种常见的压轴题解法策略,帮助初三学生更好地应对数学考试。
一、代数题解法代数题是初中数学中最常见的题型之一,也是压轴题的常客。
在解代数题时,我们可以采用以下几种解法:1. 消元法:将方程组中的一个未知数表示为另一个未知数的函数,并代入到另一个方程中,从而得到一个只有一个未知数的方程。
然后通过求解这个方程,就可以得到所有未知数的值。
3. 凑整法:通过适当的变换,将方程转化为更简单的形式。
将含有平方项的方程凑成完全平方的形式,再进行求解。
以上三种解法是解代数题的常见方法,需要根据具体情况选择使用。
1. 图形分析法:通过观察图形性质和推理,找出问题中的关键信息,并推导出结论。
这种方法需要学生对几何知识的掌握程度较高。
2. 图像法:通过画图来辅助解题。
画图可以直观地表示问题中的信息,帮助学生更好地理解问题,从而找到解题的思路。
3. 字母代换法:将几何问题中的一些条件用字母代替,构建方程或者不等式,利用代数方法求解。
这种方法需要学生对代数知识的掌握程度较高。
1. 函数性质法:通过分析函数的性质和变化规律,找到函数值的范围、最值点等关键信息,从而得到解题的思路。
2. 代数方法:通过解方程或者不等式来求解函数问题。
求解函数的零点、最值等问题。
压轴题是考察学生综合能力的重要环节,解题方法的选择对于解题的效果至关重要。
在解压轴题时,学生需要根据具体题目的要求,选择合适的解题方法,并进行深入分析和思考,找到解题的关键点。
通过不断的练习和总结,学生可以逐渐提高解题的能力,更好地应对数学考试。
2024年中考数学压轴题重难点知识剖析及训练—求函数的取值范围

2024年中考数学压轴题重难点知识剖析及训练—求函数的取值范围通用的解题思路:第一步:先判定函数的增减性:一次函数、反比例函数看k ,二次函数看对称轴与区间的位置关系;第二步:当a x =时,min y y =;当b x =时,max y y =;所以max min y y y ≤≤.二次函数求取值范围之动轴定区间或者定轴动区间的分类方法:分对称轴在区间的左边、右边、中间三种情况。
(1)若自变量x 的取值范围为全体实数,如图①,函数在顶点处abx 2-=时,取到最值.(2)若abn x m 2-<≤≤,如图②,当m x =时,max y y =;当n x =时,min y y =.(3)若n x m ab≤≤<-2,如图③,当m x =,min y y =;当n x =,max y y =.(4)若n x m ≤≤,且n a b m ≤-≤2,m a b a b n -->+22,如图④,当a bx 2-=,min y y =;当n x =,max y y =.1.(中考真题)设a 、b 是任意两个不等实数,我们规定:满足不等式a ⩽x ⩽b 的实数x 的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x 与函数值y 满足:当m ⩽x ⩽n 时,有m ⩽y ⩽n,我们就称此函数是闭区间[m,n]上的“闭函数”。
(1)反比例函数xy 2013=是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由;(2)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式;(3)若二次函数5754512--=x x y 是闭区间[a,b]上的“闭函数”,求实数a ,b 的值。
【解答】解:(1)反比例函数y=是闭区间[1,2013]上的“闭函数”.理由如下:反比例函数y=在第一象限,y随x的增大而减小,当x=1时,y=2013;当x=2013时,y=1,所以,当1≤x≤2013时,有1≤y≤2013,符合闭函数的定义,故反比例函数y=是闭区间[1,2013]上的“闭函数”;(2)分两种情况:k>0或k<0.①当k>0时,一次函数y=kx+b(k≠0)的图象是y随x的增大而增大,故根据“闭函数”的定义知,,解得.∴此函数的解析式是y=x;②当k<0时,一次函数y=kx+b(k≠0)的图象是y随x的增大而减小,故根据“闭函数”的定义知,,解得.∴此函数的解析式是y=﹣x+m+n;(3)∵y=x2﹣x﹣=(x﹣2)2﹣,∴该二次函数的图象开口方向向上,最小值是﹣,且当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大;①当b≤2时,此二次函数y随x的增大而减小,则根据“闭函数”的定义知,,解得,(不合题意,舍去)或;②当a<2<b时,此时二次函数y=x2﹣x﹣的最小值是﹣=a,根据“闭函数”的定义知,b=a2﹣a﹣或b=b2﹣b﹣;a)当b=a2﹣a﹣时,由于b=(﹣)2﹣×(﹣)﹣=<2,不合题意,舍去;b)当b=b2﹣b﹣时,解得b=,由于b>2,所以b=;③当a≥2时,此二次函数y随x的增大而增大,则根据“闭函数”的定义知,,解得,,∵<0,∴舍去.综上所述,或.2.(中考真题)若关于x 的函数y ,当1122t x t -≤≤+时,函数y 的最大值为M ,最小值为N ,令函数2M N h -=,我们不妨把函数h 称之为函数y 的“共同体函数”.(1)①若函数4044y x =,当1t =时,求函数y 的“共同体函数”h 的值;②若函数y kx b =+(0k ≠,k ,b 为常数),求函数y 的“共同体函数”h 的解析式;(2)若函数21y x x=≥(),求函数y 的“共同体函数”h 的最大值;(3)若函数24y x x k =-++,是否存在实数k ,使得函数y 的最大值等于函数y 的“共同体函数”h 的最小值.若存在,求出k 的值;若不存在,请说明理由.解析:(1)解:①当1t =时,则111122x -≤≤+,即1322x ≤≤, 4044y x =,4044k =0>,y 随x 的增大而增大,314044404422202222M N h ⨯-⨯-∴===,②若函数y kx b =+,当0k >时,1122t x t -≤≤+,∴11,22M k t b N k t b ⎛⎫⎛⎫=++=-+ ⎪ ⎪⎝⎭⎝⎭,22M N k h -∴==,当0k <时,则11,22M k t b N k t b ⎛⎫⎛⎫=-+=++ ⎪ ⎪⎝⎭⎝⎭,22M N k h -∴==-,综上所述,0k >时,2k h =,0k <时,2kh =-,(2)解:对于函数()21y x x=≥, 20>,1x ≥,函数在第一象限内,y 随x 的增大而减小,112t ∴-≥,解得32t ≥,当1122t x t -≤≤+时,∴2424,11212122M N t t t t ====-+-+,()()()()()()2221221144442221212121212141t t M N h t t t t t t t +---⎛⎫∴==-=== ⎪-+-+-+-⎝⎭,∵当32t ≥时,241t -随t 的增大而增大,∴当32t =时,241t -取得最小值,此时h 取得最大值,最大值为()()4412121242h t t ===-+⨯;(3)对于函数24y x x k =-++()224x k =--++,10a =-<,抛物线开口向下,2x <时,y 随x 的增大而增大,2x >时,y 随x 的增大而减小,当2x =时,函数y 的最大值等于4k +,在1122t x t -≤≤+时,①当122t +<时,即3t 2<时,211422N t t k ⎛⎫⎛⎫=--+-+ ⎪ ⎪⎝⎭⎝⎭,211422M t t k ⎛⎫⎛⎫=-++++ ⎪ ⎪⎝⎭⎝⎭,∴h =2M N -=22111114422222t t k t t k ⎧⎫⎡⎤⎪⎪⎛⎫⎛⎫⎛⎫⎛⎫-++++---+-+⎢⎥⎨⎬ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎪⎪⎣⎦⎩⎭=2t -,∴h 的最小值为12(当32t =时),若124k =+,解得72k =-,但32t <,故72k =-不合题意,故舍去;②当122t ->时,即5t 2>时,211422M t t k ⎛⎫⎛⎫=--+-+ ⎪ ⎪⎝⎭⎝⎭,211422N t t k ⎛⎫⎛⎫=-++++ ⎪ ⎪⎝⎭⎝⎭,∴h =2M N -=2t -,∴h 的最小值为12(当52t =时),若124k =+,解得72k =-,但52t >,故72k =-不合题意,故舍去③当11222t t -≤≤+时,即3522t ≤≤时,4M k =+,i )当112222t t ⎛⎫⎛⎫--≥+- ⎪ ⎪⎝⎭⎝⎭时,即322t ≤≤时,211422N t t k⎛⎫⎛⎫=--+-+ ⎪ ⎝⎭⎝⎭22114415252222228k t t k M N h t t ⎛⎫⎛⎫++---- ⎪ ⎪-⎝⎭⎝⎭===-+ 对称轴为52t =,102>,抛物线开口向上,在322t ≤≤上,当t =2时,h 有最小值18,148k ∴=+,解得318k =-;i i )当112222t t ⎛⎫⎛⎫--≤+- ⎪ ⎪⎝⎭⎝⎭时,即522t ≤≤时,4M k =+,N =211422t t k ⎛⎫⎛⎫-++++ ⎪ ⎝⎭⎝⎭,∴2211441392222228k t t kM N h t t ⎛⎫⎛⎫+++-+- ⎪ ⎪-⎝⎭⎝⎭===-+, 对称轴为32t =,102>,抛物线开口向上,在522t <≤上,当t =2时,h 有最小值18,148k ∴=+解得318k =-,综上所述,2t =时,存在318k =-.3.(中考真题)我们不妨约定:若某函数图像上至少存在不同的两点关于原点对称,则把该函数称之为“H 函数”,其图像上关于原点对称的两点叫做一对“H 点”,根据该约定,完成下列各题(1)在下列关于x 的函数中,是“H 函数”的,请在相应题目后面的括号中打“√”,不是“H 函数”的打“×”①2y x =()②my (m 0)x=≠()③31y x =-()(2)若点()1,A m 与点(),4B n -关于x 的“H 函数”()20y ax bx c a =++≠的一对“H 点”,且该函数的对称轴始终位于直线2x =的右侧,求,,a b c 的值或取值范围;(3)若关于x 的“H 函数”223y ax bx c =++(a ,b ,c 是常数)同时满足下列两个条件:①0a b c ++=,②(2)(23)0c b a c b a +-++<,求该H 函数截x 轴得到的线段长度的取值范围.【详解】(1)①2y x =是“H 函数”②my (m 0)x=≠是“H 函数”③31y x =-不是“H 函数”;故答案为:√;√;×;(2)∵A,B 是“H 点”∴A,B 关于原点对称,∴m=4,n=1∴A(1,4),B (-1,-4)代入()20y ax bx c a =++≠,得44a b c a b c ++=⎧⎨-+=-⎩,解得40b ac =⎧⎨+=⎩,又∵该函数的对称轴始终位于直线2x =的右侧,∴-2b a >2,∴-42a >2,∴-1<a <0,∵a+c=0,∴0<c <1,综上,-1<a <0,b=4,0<c <1;(3)∵223y ax bx c =++是“H 函数”,∴设H 点为(p,q )和(-p,-q ),代入得222323ap bp c qap bp c q⎧++=⎨-+=-⎩,解得ap 2+3c=0,2bp=q ,∵p 2>0,∴a,c 异号,∴ac <0,∵a+b+c=0,∴b=-a-c ,∵(2)(23)0c b a c b a +-++<,∴(2)(23)0c a c a c a c a -----+<,∴(2)(2)0c a c a -+<,∴c 2<4a 2,∴22c a<4,∴-2<c a <2,∴-2<c a <0,设t=c a ,则-2<t <0,设函数与x 轴的交点为(x 1,0)(x 2,0),∴x 1,x 2是方程223ax bx c ++=0的两根,∴12x x -=,又∵-2<t <0,∴2<12x x -<4.(2022春•芙蓉区校级期末)在y 关于x 的函数中,对于实数a ,b ,当a ≤x ≤b 且b =a +3时,函数y 有最大值y max ,最小值y min ,设h =y max ﹣y min ,则称h 为y 的“极差函数”(此函数为h 关于a 的函数);特别的,当h =y max ﹣y min 为一个常数(与a 无关)时,称y 有“极差常函数”.(1)判断下列函数是否有“极差常函数”?如果是,请在对应()内画“√”,如果不是,请在对应()内画“×”.①y =2x ();②y =﹣2x +2();③y =x 2().(2)y 关于x 的一次函数y =px +q ,它与两坐标轴围成的面积为1,且它有“极差常函数”h =3,求一次函数解析式;(3)若,当a ≤x ≤b (b =a +3)时,写出函数y =ax 2﹣bx +4的“极差函数”h ;并求4ah 的取值范围.【解答】解:(1)①∵y =2x 是一次函数,且y 随x 值的增大而增大,∴h =2(a +3)﹣2a =6,∴y =2x 是“极差常函数”,故答案为:√;②∵y =﹣2x +2是一次函数,且y 随x 值的增大而减小,∴h =﹣2a +2﹣[﹣2(a +3)+2]=6,∴y =﹣2x +2是“极差常函数”,故答案为:√;∵y =x 2是二次函数,函数的对称轴为直线x =0,当a +3≤0时,h =a 2﹣(a +3)2=﹣9﹣6a ;当a ≥0时,h =(a +3)2﹣a 2=9+6a ;∴y =x 2不是“极差常函数”,故答案为:×;(2)当x =0时,y =q ,∴函数与y 轴的交点为(0,q ),当y =0时,x =﹣,∴函数与x 轴的交点为(﹣,0),∴S =×|q |×|﹣|=1,∴=2,当p >0时,h =p (a +3)+q ﹣(pa +q )=3,∴p =1,∴q =±,∴函数的解析式为y =x ;当p <0时,h =pa +q ﹣[p (a +3)+q ]=3,∴p =﹣1,∴q =±,∴函数的解析式为y =﹣x;综上所述:函数的解析式为y =x 或y =﹣x;(3)y =ax 2﹣bx +4=a (x ﹣)2+4﹣,∴函数的对称轴为直线x =,∵b =a +3,∴x ==+,∵,∴≤+≤,≤a +3≤,∵(a +3﹣﹣)﹣(+﹣a )=2a +2﹣,∵,∴2a +2﹣>0,∴a +3到对称轴的距离,大于a 到对称轴的距离,∴当x =a +3时,y 有最大值a (a +3)2﹣(a +3)2+4,当x =时,y 有最小值4﹣=4﹣,∴h =a (a +3)2﹣(a +3)2+4﹣4+=(a +3)2(a ﹣1+),∴4ah =(2a 2+5a ﹣3)2,∵2a 2+5a ﹣3=2(a +)2﹣,,∴≤2a 2+5a ﹣3≤9,∴≤4ah ≤81.5.(雅实)若函数1y 、2y 满足12y y y =+,则称函数y 是1y 、2y 的“融合函数”.例如,一次函数121y x =+和二次函数2234y x x =+-,则1y 、2y 的“融合函数”为21253y y y x x =+=+-.(1)若反比例函数12y x=和一次函数23y kx =-,它们的“融合函数”过点()1,5,求k 的值;(2)若21y ax bx c =++为二次函数,且5a b c ++=,在x t =时取得最值,函数2y 为一次函数,且1y 、2y 的“融合函数”为224y x x =+-,当12x -≤≤时,求函数1y 的最小值(用含t 的式子表示);(3)若二次函数21y ax bx c =++与一次函数2y ax b =--,其中0a b c ++=且a b c >>,若它们的“融合函数”与x 轴交点为()1,0A x 、()2,0B x 12x -的取值范围.【解答】解:(1)由题意可得y 1、y 2的融合函数23y kx x=+-,将点()1,5代入,可得:523k =+-,解得6k =.(2)∵12y y y =+,∴()()2222124214y y y x x ax bx c a x b x c =-=+----=-+---,∵y 2为一次函数,∴20a -=,即2a =,∴212y x bx c =++在x =t 处取得最值,∴4bt =-,即4b t =-,∴5a b c ++=,即54234c t t =+-=+,∴212434y x tx t =-++,对称轴:x t =.①若1t ≤-时,即当1x =-时,min 58y t =+,②若12t -<<时,即当x t =时,2min 234y t t =-++,③若2t ≥时,即当2x =时,min 114y t =-.(3)y 1、y 2的融合函数()2y ax b a x c b =+-+-,∵与y 轴交于点()1,0A x 、()2,0B x ,∴12b a x x a -+=,12c b x x a -⋅=,∵12||x x a -==,又∵0a b c ++=,∴b a c =--,∴12x x ==,∵a b c >>∴a a c c >--<,∴122c a -<<-,当2ca=-时,12maxx x -=,当12c a =-时,12min32x x -=12x <-<.6.(立信)已知:抛物线1C :2y ax bx c =++(0a >).(1)若顶点坐标为(1,1),求b 和c 的值(用含a 的代数式表示);(2)当0c <时,求函数220221y ax bx c =-++-的最大值;(3)若不论m 为任何实数,直线()214m y m x =--与抛物线1C 有且只有一个公共点,求a ,b ,c 的值;此时,若1k x k ≤≤+时,抛物线1C 的最小值为k ,求k 的值.【解答】解:(1)∵抛物线的顶点坐标为(1,1),∴y =a (x ﹣1)2+1=ax 2﹣2ax +a +1,∴b =﹣2a ,c =a +1;(2)∵y =ax 2+bx +c ,a >0,c <0,∴Δ=b 2﹣4ac >0,∴抛物线y =ax 2+bx +c (a >0)与x 轴有两个交点,∴|ax2+bx+c|≥0,∴﹣2022|ax2+bx+c|≤0,∴﹣2022|ax2+bx+c|﹣1≤﹣1,∴函数y=﹣2022|ax2+bx+c|﹣1的最大值为﹣1;(3)∵直线与抛物线C1有且只有一个公共点,∴方程组只有一组解,∴ax2+(b﹣m)x++m+c=0有两个相等的实数根,∴Δ=0,∴(b﹣m)2﹣4a(+m+c)=0,整理得:(1﹣a)m2﹣2(2a+b)m+b2﹣4ac=0,∵不论m为任何实数,(1﹣a)m2﹣2(2a+b)m+b2﹣4ac =0恒成立,∴,∴a=1,b=﹣2,c=1.此时,抛物线解析式为y=x2﹣2x+1=(x﹣1)2,∴抛物线的对称轴为直线x=1,开口向上,∵当k≤x≤k+1时,抛物线的最小值为k,∴分三种情况:k<0或0≤k≤1或k>1,①当k<0时,k+1<1,当k≤x≤k+1时,y随着x的增大而减小,则当x=k+1时,y的最小值为k,∴(k+1﹣1)2=k,解得:k=0或1,均不符合题意,舍去;②当0≤k≤1时,当x=1时,抛物线的最小值为0,∴k=0;③当k>1时,y随着x的增大而增大,则当x=k时,y的最小值为k,∴(k﹣1)2=k,解得:k=或,∵k>1,∴k=,综上所述,若k≤x≤k+1时,抛物线的最小值为k,k的值为0或.7.(长郡)对于一个函数给出如下定义:对于函数y,若当a≤x≤b,函数值y满足m≤y≤n,且满足n﹣m=k (b﹣a),则称此函数为“k属和合函数”,例如:正比例函数y=﹣3x,当1≤x≤3时,﹣9≤y≤﹣3,则﹣3﹣(﹣9)=k(3﹣1),求得:k=3,所以函数y=﹣3x为“3属和合函数”.(1)若一次函数y=kx﹣1(1≤x≤3)为“4属和合函数”,求k的值;(2)反比例函数kyx(k>0,a≤x≤b,且0<a<b)是“k属和合函数”,且a+b=3,请求出a﹣b的值;(3)已知二次函数y=﹣x2+2ax+3,当﹣1≤x≤1时,y是“k属和合函数”,求k的取值范围.【详解】解:(1)当k >0时,y 随x 的增大而增大,∵1≤x ≤3,∴k ﹣1≤y ≤3k ﹣1,∵函数y =kx ﹣1(1≤x ≤3)为“k 属和合函数”,∴(3k ﹣1)﹣(k ﹣1)=4(3﹣1),∴k =4;当k <0时,y 随x 的增大而减小,∴3k ﹣1≤y ≤k ﹣1,∴(k ﹣1)﹣(3k ﹣1)=4(3﹣1),∴k =﹣4,综上所述,k 的值为4或﹣4;(2)∵反比例函数y =kx,k >0,∴在第一象限,y 随x 的增大而减小,当a ≤x ≤b 且0<a <b 是“k 属和合函数”,∴k a ﹣kb=k (b ﹣a ),∴ab =1,∵a +b =3,∴(a ﹣b )2=(a +b )2﹣4ab =9﹣4=5,∴a ﹣b (3)∵二次函数y =﹣x 2+2ax +3的对称轴为直线x =a ,∵当﹣1≤x ≤1时,y 是“k 属和合函数”,∴当x =﹣1时,y =2﹣2a ,当x =1时,y =2+2a ,当x =a 时,y =a 2+3,①如图1,当a ≤﹣1时,当x =﹣1时,有y 最大值=2﹣2a ,当x =1时,有y 最小值=2+2a ∴(2﹣2a )﹣(2+2a )=k •[1﹣(﹣1)]=2k ,∴k =﹣2a ,而a ≤﹣1,∴k ≥2;②如图2,当﹣1<a ≤0时,当x =a 时,有y 最大值=a 2+3,当x =1时,有y 最小值=2+2a ,∴a 2+3﹣(2+2a )=2k ,∴k =2(1)2a -,∴12≤k <2;③如图3,当0<a ≤1时,当x =a 时,有y 最大值=a 2+3,当x =﹣1时,有y 最小值=2﹣2a ,∴a 2+3﹣(2﹣2a )=2k ,∴k =2(1)2a +,∴12<k ≤2;④如图4,当a >1时,当x =1时,有y 最大值=2+2a ,当x =﹣1时,有y 最小值=2﹣2a ,∴(2+2a )﹣(2﹣2a )=2k ,∴k =2a ,∴k >2.综上所述,当﹣1≤x ≤1时,y 是“k 属和合函数”,k 的取值范围为k ≥12.8.(师大附中博才)已知a 、b 是两个不相等的实数且a b <,我们规定:满足不等式a x b ≤≤的实数x 的所有取值的全体叫做闭区间,表示为[],.a b 对于一个函数,如果它的自变量x 与函数值y 满足:当a x b ≤≤时,有(ta y tb t ≤≤为正数),我们就称此函数是闭区间[],a b 上的“t 倍函数”.例如:正比例函数2y x =,当13x ≤≤时,26y ≤≤,则2y x =是13x ≤≤上的“2倍函数”.(1)已知反比例函数4yx=是闭区间[],m n 上的“2倍函数”,且m n +=22m n +的值;(2)①已知正比例函数y x =是闭区间[]1,2023上的“t 倍函数”,求t ;②一次函数()0y kx b k =+≠是闭区间[],m n 上的“2倍函数”,求此函数的解析式.(3)若二次函数269y x x =--是闭区间[],a b 上的“7倍函数”,求实数a 、b 的值.【详解】(1)已知反比例函数4y x=是闭区间[],m n 上的“2倍函数”,∴当m x n ≤≤时,22m y n ≤≤,当x m =时,4y m =;当x n =时,4y n=,又40k => ,∴当0x >时,y 随x 的增大而减小,当0x <时,y随x 的增大而减小,42n m ∴=,且42m n=,24mn ∴=,又m n += ,()22222023m n m mn n ∴+=++=,2220232202342019m n mn ∴+=-=-=.(2)①已知正比例函数y x =,y 随x 的增大而增大,且当1x =时,1y =;当2023x =时,2023y =,∴当12023x ≤≤时,12023y ≤≤,y x ∴=是闭区间[]1,2023上的“1倍函数”,即1t =.② 一次函数0y kx b k =+≠()是闭区间[],m n 上的“2倍函数”,∴当m x n ≤≤时,22m y n ≤≤,若0k >时,y 随x 的增大而增大,∴当x m =,则2y km b m =+=;当x n =,则2y kn b n =+=,()()2m n k m n ∴-=-,2k ∴=,将2k =代入2km b m +=,得22m b m +=,0b ∴=.∴若0k >时,函数解析式为2y x =.若0k <时,y 随x 的增大而减小,∴当x m =时,2y km b n =+=;当x n =时,2y kn b m =+=,2k ∴=-,22b m n =+.∴若0k <时,函数解析式为()22y x m n =-++,综合以上分析,函数的解析式为2y x =或()22y x m n =-++.(3)由二次函数269y x x =--解析式可知,抛物线开口向上,对称轴3x =,∴当3x <时,y 随x 的增大而减小;当3x >时,y 随x 的增大而增大, 二次函数269y x x =--是闭区间[],a b 上的“7倍函数”,∴当a x b ≤≤时,()770a y b a ≤≤≠,若3b ≤时,根据增减性,当x a =时,2697y a a b =--=;当x b =时,2697y b b a =--=,两式相减得:226677a b a b b a --+=-,()()a b a b b a ∴+-=-,1b a ∴=--,将1b a =--代入2697a a b --=得:220a a +-=,2a ∴=-或1a =,当2a =-时,1b =;当1a =时,2b =-(舍去,a b <).若3a ≥时,当x a =时,2697y a a a =--=,解得a =a =x b =时,2697y b b b =--=.解得132b =或b =均不符合a b <,舍去.若3a <,3b >时,当3x =时,236397y a =-⨯-=,187a ∴=-,则x a =时,26396949y a a =--=,若639749b =,6393343b =<,(舍去),当x b =时,2697y b b b =--=,则b =b =综上分析,2a =-,1b =或者187a =-,b =9.(长郡)定义:在平面直角坐标系中,点P (x ,y )的横、纵坐标的绝对值的和叫做点P (x ,y )的勾股值,记为[]P x y =+.(1)已知点A (1,3),B (2-,4),C 22),直接写出[]A,[]B ,[]C 的值;(2)已知点D 是直线2y x =+上一点,且[]4D =,求点D 的坐标;(3)若抛物线21y ax bx =++与直线y x =只有一个交点M ,已知点M 在第一象限,且[]24M ≤≤.令2242022t b a =-+,试求t 的取值范围.【详解】(1)解:∵A (1,3),B (−2,4),C ),∴[A ]=|1|+|3|=4,[B ]=|-2|+|4|=6,[C ;(2)设D (m ,n ),∵D 是直线y =x +2上一点,且[D ]=4,∴42m n n m ⎧+⎨+⎩==,解得13m n =⎧⎨=⎩或31m n =-⎧⎨=-⎩,∴点D 的坐标(1,3)或(-3,-1);(3)由题意方程组21y x y ax bx =⎧⎨=++⎩只有一组实数解,消去y 得2(1)10ax b x +-+=,由题意224(1)40b ac b a -=--=,∴24(1)a b =-,∴方程可以化为()()2214140b x b x -+-+=,∴1221x x b ==-,∴22,11M b b ⎛⎫ ⎪--⎝⎭,∵[]24M ≤≤,∴2121b ≤≤-或2211b -≤≤--,解得10b -≤≤或23b ≤≤,∵点M 在第一象限,∴10b -≤≤,∵22222420222(1)202222021t b a b b b b =-+=--+=++=2(1)2020b ++,∵10b -≤≤,∴20202021t ≤≤.10.(雅礼)在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:若b′=11b ab a≥⎧⎨-⎩,,<,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2,-5).(1)①点1)的限变点的坐标是;②在点A(-2,-1),B(-1,2)中有一个点是函数y=2x图象上某一个点的限变点,这个点是;(填“A”或“B”)(2)若点P在函数y=-x+3(-2≤x≤k,k>-2)的图象上,其限变点Q的纵坐标b′的取值范围是-5≤b′≤2,求k的取值范围;(3)若点P在关于x的二次函数y=x2-2tx+t2+t的图象上,其限变点Q的纵坐标b′的取值范围是b′≥m或b′<n,其中m>n.令s=m-n,求s关于t的函数解析式及s的取值范围.【详解】(1)①根据限变点的定义可知点1)1);②(-1,-2)限变点为(-1,2),即这个点是点B.(2)依题意,y=-x+3(x≥-2)图象上的点P的限变点必在函数y=31321x xx x-+≥⎧⎨--≤⎩,,<的图象上.∴b′≤2,即当x=1时,b′取最大值2.当b′=-2时,-2=-x+3.∴x=5.当b′=-5时,-5=x-3或-5=-x+3.∴x=-2或x=8.∵-5≤b′≤2,由图象可知,k的取值范围是5≤k≤8.(3)∵y=x2-2tx+t2+t=(x-t)2+t,∴顶点坐标为(t,t).若t<1,b′的取值范围是b′≥m或b′<n,与题意不符.若t≥1,当x≥1时,y的最小值为t,即m=t;当x<1时,y的值小于-[(1-t)2+t],即n=-[(1-t)2+t].∴s=m-n=t+(1-t)2+t=t2+1.∴s关于t的函数解析式为s=t2+1(t≥1),当t=1时,s取最小值2,∴s的取值范围是s≥2.。
2024年中考数学压轴题重难点知识剖析及训练—圆与射影定理结合型压轴题(含解析)

2024年中考数学压轴题重难点知识剖析及训练—圆与射影定理结合型压轴题(含解析)射影定理模型:射影定理,又称“欧几里德定理”:在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。
射影定理是数学图形计算的重要定理,在初三各名校的数学和各地中考试题中都多次考查了这一模型的应用。
图形推导过程结论因为⎩⎨⎧∠=∠∠=∠ACDABCAA∴ABC∆∽ACD∆∴ACABADAC=①ABADAC ⋅=2;②BABDBC⋅=2;③BDADCD⋅=21.(长沙中考)如图,点P在以MN为直径的半圆上运动(点P不与M,N重合),PQ⊥MN,NE平分∠MNP,交PM于点E,交PQ于点F.(1)+=.(2)若PN2=PM•MN,则=.【解答】解:(1)∵MN 为⊙O 的直径,∴∠MPN =90°,∵PQ ⊥MN ,∴∠PQN =∠MPN =90°,∵NE 平分∠PNM ,∴∠MNE =∠PNE ,∴△PEN ∽△QFN ,∴,即①,∵∠PNQ +∠NPQ =∠PNQ +∠PMQ =90°,∴∠NPQ =∠PMQ ,∵∠PQN =∠PQM =90°,∴△NPQ ∽△PMQ ,∴②,∴①×②得,∵QF =PQ ﹣PF ,∴=1﹣,∴+=1,故答案为:1;(2)∵∠PNQ =∠MNP ,∠NQP =∠NPM ,∴由射影定理得:PN 2=QN •MN ,∵PN 2=PM •MN ,∴PM =QN ,∴,∵,∴,∴,∴NQ 2=MQ 2+MQ •NQ ,即,设,则x 2+x ﹣1=0,解得,x =,或x =﹣<0(舍去).2.(北雅)如图,点P 在以MN 为直径的半圆上运动(不与M 、N 重合),PH MN ⊥于H 点,过N 点作NQ 与PH 平行交MP 的延长线于Q 点.(1)求QPN ∠的度数;(2)求证:QN 与O 相切;(3)若2PN PM MN =⋅,求MH NH 的值.【解答】(1)解:MN 是直径,90MPN ∴∠=︒,90QPN ∴∠=︒;(2)证明:PH MN ⊥ ,90PHM ∴∠=︒,//QN PH ,90QNM PHM ∴∠=∠=︒,ON QN ∴⊥,ON 是半径,QN ∴与O 相切;(3)解:90MNP PNQ ∠+∠=︒ ,90PNQ Q ∠+∠=︒,MNP Q ∴∠=∠,MPN QPN ∠=∠ ,NPM QPN ∴∆∆∽,∴PN PM QP PN=,2PN PM QP ∴=⋅,2PN PM MN =⋅ ,QP MN ∴=,//PH QN ,∴MH MP HN PQ=,∴MH MP HN MN =,同理得,MHP MPN ∆∆∽,∴MP MH MN MP =,HN MP ∴=,设PQ MN a ==,MP b =,∴MH MP HN PQ=,∴a b b b a -=,(12a b -∴=(舍)或1)2a b =∴12MH a b HN b -==.3.(长沙中考)如图,点A ,B ,C 在O 上运动,满足222AB BC AC =+,延长AC 至点D ,使得DBC CAB ∠=∠,点E 是弦AC 上一动点(不与点A ,C 重合),过点E 作弦AB 的垂线,交AB 于点F ,交BC 的延长线于点N ,交O 于点M (点M 在劣弧 AC 上).(1)BD 是O 的切线吗?请作出你的判断并给出证明;(2)记BDC ∆,ABC ∆,ADB ∆的面积分别为1S ,2S ,S ,若212()S S S ⋅=,求2(tan )D 的值;(3)若O 的半径为1,设FM x =,FE FN y ⋅=,试求y 关于x 的函数解析式,并写出自变量x 的取值范围.【解答】解:(1)BD 是O 的切线.证明:如图,在ABC ∆中,222AB BC AC =+,90ACB ∴∠=︒.又点A ,B ,C 在O 上,AB ∴是O 的直径.90ACB ∠=︒ ,90CAB ABC ∴∠+∠=︒.又DBC CAB ∠=∠,90DBC ABC ∴∠+∠=︒.90ABD ∴∠=︒.BD ∴是O 的切线.(2)由题意得,112S BC CD =⋅,212S BC AC =⋅,12S AD BC =⋅.212()S S S ⋅= ,∴2111()222BC CD AD BC BC AC ⋅⋅⋅=⋅.2CD AD AC ∴⋅=.2()CD CD AC AC ∴+=.又90D DBC ∠+∠=︒ ,90ABC A ∠+∠=︒,DBC A ∠=∠,D ABC ∴∠=∠.tan tan BC AC D ABC CD BC∴∠==∠=.2BC CD AC ∴=.又2()CD CD AC AC +=,∴4222BC BC AC AC +=.4224BC AC BC AC ∴+⋅=.241(()AC AC BC BC ∴+=.由题意,设2(tan )D m ∠=,2(AC m BC∴=.21m m ∴+=.152m ±∴=.0m > ,152m ∴=.2(tan )D ∴∠=.(3)设A α∠=,90A ABC ABC DBC ABC N ∠+∠=∠+∠=∠+∠=︒ ,A DBC N α∴∠=∠=∠=.如图,连接OM .∴在Rt OFM ∆中,OF =.1BF BO OF ∴=+=+,1AF OA OF =-=.∴在Rt AFE ∆中,tan (1tan EF AF αα=⋅=⋅,1cos cos AF AE αα==.在Rt ABC ∆中,sin 2sin BC AB αα=⋅=.(1r = ,2AB ∴=.)cos 2cos AC AB αα=⋅=.在Rt BFN ∆中,sin BF BN α==tan BF FN α==.y FE FN ∴=⋅2x =2x =2x =21x x=⋅x =.即y x =.FM AB ⊥ ,FM ∴最大值为F 与O 重合时,即为1.01x ∴< .综上,y x =,01x <.4.(长沙中考)如图,四边形ABCD 内接于⊙O ,对角线AC 为⊙O 的直径,过点C 作AC 的垂线交AD 的延长线于点E ,点F 为CE 的中点,连接DB ,DC ,DF .(1)求∠CDE 的度数;(2)求证:DF是⊙O的切线;(3)若AC=2DE,求tan∠ABD的值.解:(1)∵对角线AC为⊙O的直径,∴∠ADC=90°,∴∠EDC=90°;(2)证明:连接DO,∵∠EDC=90°,F是EC的中点,∴DF=FC,∴∠FDC=∠FCD,∵OD=OC,∴∠OCD=∠ODC,∵∠OCF=90°,∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,∴DF是⊙O的切线;(3)设DE=1,则AC=2,由射影定理得:AC2=AD×AE,∴20=AD(AD+1),∴AD=4或﹣5(舍去),∵DC2=AC2﹣AD2,∴DC=2,∴tan∠ABD=tan∠ACD==2;5.(青竹湖三模)如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A、B、D三点,CB的延长线交⊙O于点E.(1)求证:AE=CE;(2)EF与⊙O相切于点E,交AC的延长线于点F,若CD=CF=2cm,求⊙O的直径;(3)在(2)的条件下,若CF:CD=n(n>0),求sin∠CAB.解:(1)证明:连接DE,∵∠ABC=90°∴∠ABE=90°∴AE是⊙O直径,∴∠ADE =90°∴DE ⊥AC 又∵D 是AC 的中点∴DE 是AC 的垂直平分线∴AE =CE ;(2)解:在△ADE 和△EFA 中,∵∠ADE =∠AEF =90°,由射影定理得:AE 2=AD ×AF,∴AE 2=2×6,∴AE =2cm ;(3)解:∵AE 是⊙O 直径,EF 是⊙O 的切线,∵CF:CD=n,令CD=1,则CF=n ,∵∠ADE =∠AEF =90°,由射影定理得:AE 2=AD ×AF ,∴AE 2=1×(n+2),∴AE ==CE ,∵∠CAB =∠DEC,∴sin ∠CAB =sin ∠DEC ===.6.(长郡)如图,AB 为⊙O 的直径,弦CD 与AB 相交于E ,DE =EC ,过点B 的切线与AD 的延长线交于F ,过E 作EG ⊥BC 于G ,延长GE 交AD 于H .(1)求证:AH =HD ;(2)若BFBD =,DF =9,求⊙O 的半径.【解答】(1)证明:∵AB 为⊙O 的直径,DE =EC ,∴AB ⊥CD ,∴∠C +∠CBE =90°,∵EG ⊥BC ,∴∠C +∠CEG =90°,∴∠CBE =∠CEG ,∵∠CBE =∠CDA ,∠CEG =∠DEH ,∴∠CDA =∠DEH ,∴HD =EH ,∵∠A +∠ADC =90°,∠AEH +∠DEH =90°,∴AH =EH ,∴AH =HD ;(2)解:∵∠BDF =90°,BFBD =,令BD=4x ,BF=5x ,则222)5(94x x =+)(,∴2=x ,BD=12,由射影定理得:BD 2=DF •DA ,∴144=9×DA ,∴DA=16,又由射影定理得:AB 2=AF •DA ,∴AB 2=25×16,∴AB=20,即半径为10.10.如图,AB 是O 的直径,点C 是O 上一点,AD 与过点C 的切线垂直,垂足为D ,直线DC 与AB的延长线交于点P ,弦CE 平分ACB ∠,交AB 于点F ,连接BE ,BE =.(1)求证:AC 平分DAB ∠;BC=,求阴影部分的面积;(2)若5CD=,求PC的长度(射影定理).(3)若3【解答】(1)证明:连接OC.∵OA=OC,∴∠OAC=∠OCA.∵PC是⊙O的切线,AD⊥CD,∴∠OCP=∠D=90°,∴OC∥AD.∴∠CAD=∠OCA=∠OAC.即AC平分∠DAB.(2)解:连接AE.∵∠ACE=∠BCE,∴,∴AE=BE.又∵AB是直径,∴∠AEB=90°.∴AB=BE=×5=10,∵OB=5,∴BC=OB=OC=5,即△OBC是等边三角形,=×5×=,∴∠BOC=60°,∴OH==,CH=OH=,∴S△BOCS扇形BOC=×π×52=π,∴阴影部分的面积为π﹣;(3)解:过点C作CH⊥AB垂足为点H,如图:由(2)得:OC=OB=5,(2)∵AC平分∠DAB,CH⊥AB,CD⊥AD,∴CH=CD=3,∵∠ACB=∠BHC=90°,由射影定理得:CH2=BH•AH,设BH=x,AH=10-x,∴32=x(10﹣x),解得:x=1或9(舍),又由射影定理得:CH2=O H•HP,∴32=4HP,解得:HP=.7.(雅礼)如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且AD•AO=AM•AP.(1)连接OP,证明:△ADM∽△APO;(2)证明:PD是⊙O的切线;(3)若AD=24,AM=MC,求的值.解:(1)证明:连接OD、OP、CD.∵AD•AO=AM•AP,∴=,∠A=∠A,∴△ADM∽△APO.(2)∵△ADM∽△APO,∴∠ADM=∠APO,∴MD∥PO,∴∠1=∠4,∠2=∠3,∵OD=OM,∴∠3=∠4,∴∠1=∠2,∵OP=OP,OD=OC,∴△ODP≌△OCP,∴∠ODP=∠OCP,∵BC⊥AC,∴∠OCP=90°,∴OD⊥AP,∴PD是⊙O的切线.(2)连接CD.由(1)可知:PC=PD,∵AM=MC,∴AM=2MO=2R,在Rt△AOD中,OD2+AD2=OA2,∴R2+242=9R2,∴R=6,∴OD=6,MC=12,∵==,∴DP=12,∵O是MC的中点,∴==,∴点P是BC的中点,∴BP=CP=DP=12,∵MC是⊙O的直径,∴∠BDC=∠CDM=90°,在Rt△BCM中,∵BC=2DP=24,MC=12,∴BM=12,由射影定理得:MC2=MD×MB,∴122=12×MD,∴MD=4,∴=.8.(广益)如图,已知PB与⊙O相切于点B,A是⊙O上的一点,满足PA=PB,连接PO,交AB于E,交⊙O于C,D两点,E在线段OD上,连接AD,OB。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解答题在中考中占有相当大的比重,主要由综合性问题构成,就题型而言,包括计算 题、证明题和应用题等.它的题型特点和考查功能决定了审题思考的复杂性和解题设计的多 样性.一般地,解题设计要因题定法,无论是整体考虑还是局部联想,确定方法都必须遵循 的原则是:熟悉化原则、具体化原则;简单化原则、和谐化原则等. (一)解答综合、压轴题,要把握好以下各个环节:
BC,点 E 是线段 AD 上的一个动点(E 与 A、D 不重合),G、F、H 分
别是 BE、BC、CE 的中点.
(1)试探索四边形 EGFH 的形状,并说明理由.
(2)当点 E 运动到什么位置时,四边形 EGFH 是菱形?并加以证明.
图4
(3)若(2)中的菱形 EGFH 是正方形,请探索线段 EF 与线段 BC 的关系,并证明你的结论.
B
形?若不存在,请简要说明理由;若存在,请求出 EF 的长.
图1
分析:(1)中面积相等可以转化为“ △ECF 与△ACB 的 面积比为 1:2”,因为△ECF∽△
ACB,从而要求 CE 长,只要借助于相似比与面积比的关系即可得解.因为相似三角形对应边
成比例,从而第(2)题可利用比例线段来找线段间关系,再根据周长相等来建立方程.第(3)
(与点 A、C 不重合)在 AC 边上, EF ∥AB 交 BC 于点 F .
C
(1)当 △ECF 的面积与四边形 EABF 的面积相等时,求 CE 的长;
E
F
(2)当 △ECF 的周长与四边形 EABF 的周长相等时,求 CE 的长;
(3)试问在 AB 上是否存在点 P ,使得 △EFP 为等腰直角三角 A
2.寻求合理的解题思路和方法:破除模式化、力求创新是近几年中考数学试题的显著特 点,解答题体现得尤为突出,因此,切忌套用机械的模式寻求解题思路和方法,而应从各个 不同的侧面、不同的角度,识别题目的条件和结论,认识条件和结论之间的关系、图形的几 何特征与数、式的数量、结构特征的关系,谨慎地确定解题的思路和方法.当思维受阻时, 要及时调整思路和方法,并重新审视题意,注意挖掘隐蔽的条件和内在联系,既要防止钻牛 角尖,又要防止轻易放弃. (二)题型解析 类型 1 直线型几何综合题
C
E
F
5 当∠EFP=90°,EF=FP 时,同理可得 EF= 60 .
37
A
P D P' B
图1
图2
②如图 3,假设∠EPF=90°,PE=PF 时,点 P 到 EF 的距离为 1 EF . 2
设 EF=x,由△ECF∽△ACB,得
_C
_E
_F
EF
=
CD − 1 EF 2
,即 x
=
12 5
−
x 2
.解得 x = 120 ,即 EF= 120
.
_A
AB
CD
5 12
49
49
_P _D
_B
_? 2
图3
5
综上所述,在 AB 上存在点 P,使△EFP 为等腰直角三角形,此时 EF= 60 或 EF= 120 .
37
49
特别提示:因为等腰直角三角形中哪条边为斜边没有指明,所以需要就可能的情形进行讨论.
跟踪练习 1 (2007·山东烟台)如图 4,等腰梯形 ABCD 中,AD∥
①如图 2,假设∠PEF=90°,EP=EF.由 AB=5,BC=3,AC=4,得∠C=90°,
所以 Rt△ACB 斜边 AB 上高 CD= 12 .设 EP=EF=x,由△ECF∽△ACB,得 5
EF
=
CD − EP
,即
x
=
12 5
−
x
.解得 x
=
CD
5 12
37
37
BD 于点 E, AE=2, EC=1.
D
C
(1)求证: △DEC ∽ △ADC . (2)试探究四边形 ABCD 是否是梯形?若是,请你给予证明
题中假设存在符合条件的三角形,根据相似三角形中对应边成比例可建立方程.
解(:1)因为△ECF 的面积与四边形 EABF 的面积相等,所以 S△ECF:S△ACB=1:2,又因为 EF∥AB ,
1
所以△ECF∽△ACB.所以 SECF = (CE )2 = 1 . 因为 CA=4,所以 CE= 2 2 .
参考答案:1、(1)四边形 EGFH 是平行四边形.只要说明 GF//EH, GF = EH 即
可.
(2)点 E 是 AD 的中点时,四边形 EGFH 是菱形.利用全等可得 BE=CE,从而得
2
EG = EH.
根据 EGFH 是正方形,可得 EG =EH ,∠BEC = 90°.因为 G、H 分别是 BE、CE 的中点,所以 EB = EC.
这类题常见考查形式为推理与计算.对于推理,基本思路为分析与综合,即从需要证明
的结论出发逆推,寻找使其成立的条件,同时从已知条件出发来推导一些结论,再设法将它
们联系起来.对于计算,基本思路是利用几何元素(比如边、角)之间的数量关系结合方程
思想来处理.
例 1 如图 1,在 △ABC 中, AB = 5 ,BC = 3, AC = 4 ,动点 E
SACB CA
2
(2)设 CE 的长为 x,因为△ECF∽△ACB, 所以 CE = CF . 所以 CF= 3 x . 根据周长相
CA CB
4
等可得: x + EF + 3 x = (4 − x) + 5 + (3 − 3 x) + EF .解得 x = 24 .
4
4
7
(3)△EFP 为等腰直角三角形,有两种情况:
1.审题:这是解题的开始,也是解题的基础.一定要全面审视题目的所有条件和答题要求, 以求正确、全面理解题意,在整体上把握试题的特点、结构,以利于解题方法的选择和解题 步骤的设计.
审题思考中,要把握“三性”,即明确目的性,提高准确性,注意隐含性.解题实践表明: 条件暗示可知并启发解题手段,结论预告并诱导解题方向,只有细致地审题,才能从题目本 身获得尽可能多的信息.这一步,不要怕慢,其实“慢”中有“快”,解题方向明确,解题手段 合理得当,这是“快”的前提和保证.否则,欲速则不达.
因为 F 是 BC 的中点,
类型 2 .圆的综合题 常见形式为推理与计算综合,解答的基本思路仍然是分析—综合,需要注意的是,因为
综合性比较强,解答后面问题时往往需要充分利用前面的结论,这样才会简便.
例 2 如图 5,点 A、B、C、D 是直径为 AB 的⊙O 上四个点,C 是劣弧 B»D 的中点,AC 交
