【配套K12】九年级数学下册第二章二次函数2.1二次函数同步练习

合集下载

北师大版九年级下册数学第二章二次函数专题复习同步训练卷

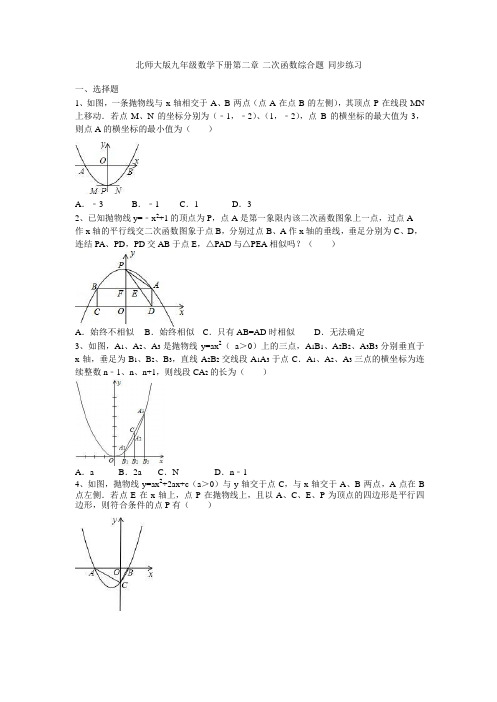
九年级下册数学第二章二次函数专题复习同步训练卷（北师大版2012）一、单选题1．二次函数y=ax 2+bx ﹣1（a ≠0）的图象经过点（1，1），则a+b+1的值是（）A ．﹣3B ．﹣1C ．2D ．3 2．二次函数y=ax 2+bx+c 的图象如图所示，对称轴是x=－1．有以下结论：①abc>0，②4ac<b 2，③2a+b=0，④a －b+c>2，其中正确的结论的个数是（）A ．1B ．2C ．3D ．43．2011年5月22日—29日在美丽的青岛市举行了苏迪曼杯羽毛球混合团体锦标赛．在比赛中，某次羽毛球的运动路线可以看作是抛物线y=－14x 2+bx+c 的一部分（如图），其中出球点B 离地面O 点的距离是1m ，球落地点A 到O 点的距离是4m ，那么这条抛物线的解析式是（）A ．213144y x x =-++B ．213144y x x =-+-C ．213144y x x =--+D ．213144y x x =--- 4．将函数的图象用下列方法平移后，所得的图象不经过点A （1，4）的方法是（）A ．向左平移1个单位B ．向右平移3个单位C ．向上平移3个单位D ．向下平移1个单位 5．如图，抛物线2(0)y ax bx c a =++≠过点(1,0)-和点(0,3)-，且顶点在第四象限，设P a b c =++，则P 的取值范围是（）．A ．31P -<<-B ．60P -<<C ．30P -<<D ．63P -<<-6．下列图像中，当0ab >时，函数2y ax =与y ax b =+的图象时（）A ．B ．C ．D ．7．二次函数y ＝ax 2+bx+c （a ≠0）的图象如图所示，有下列结论：①abc ＞0；②2a+b ＝0；③若m 为任意实数，则a+b ＞am 2+bm ；④a ﹣b+c ＞0；⑤若ax 12+bx 1＝ax 22+bx 2，且x 1≠x 2，则x 1+x 2＝2．其中，正确结论的个数为（）A ．1B ．2C ．3D ．48．函数y ＝mx 2+（m+2）x+12m+1的图象与x 轴只有一个交点，则m 的值为（） A ．0 B ．0或2C ．0或2或﹣2D ．2或﹣2 9．已知函数3()()y x m x n =---，并且a ，b 是方程3()()0x m x n ---=的两个根，则实数m ，n ，a ，b 的大小关系可能是（）A ．m n b a <<<B ．m a n b <<<C ．a m b n <<<D ．a m n b <<<10．抛物线2(0)y ax bx c a =++≠的部分图象如图所示，与x 轴的一个交点坐标为()4,0，抛物线的对称轴是1x =．下列结论中：①0abc <；②20a b +=；③0a c +>；④若点(),A m n 在该抛物线上，则2am bm c a b c ++≤++．⑤方程24ax bx c ++=有两个不相等的实数根；其中正确的有（）A ．5个B ．4个C ．3个D ．2个 A ．﹣254＜m ＜3 B ．﹣254＜m ＜2 C ．﹣2＜m ＜3 D ．﹣6＜m ＜﹣2二、填空题 11．当x = __________时，二次函数226y x x =-+ 有最小值___________.12．若函数y ＝(a －1)x 2－4x ＋2a 的图象与x 轴有且只有一个交点，则a 的值为_____．13．如图为抛物线的部分图象，抛物线y=ax 2+bx+c （a ≠0）的对称轴为直线x=1，与x 轴的一个交点坐标为（﹣1，0），下列结论：①4ac ＜b 2②方程ax 2+bx+c=0的两个根是x 1=﹣1，x 2=3③3a+c ＞0④当y ＞0时，x 的取值范围是﹣1≤x ＜3⑤当x ＜0时，y 随x 增大而增大其中正确的结论是____．14．在平面直角坐标系xOy 中，若直线y ＝kx +5k （k 为常数，k ≠0）与抛物线y ＝15x 2相交于A ，B 两点，且OA ⊥OB ，则k 的值为_____． 15．如图，在平面直角坐标系中，抛物线y ＝﹣23（x ﹣3）2+k 经过坐标原点O ，与x 轴的另一个交点为A ．过抛物线的顶点B 分别作BC ⊥x 轴于C 、BD ⊥y 轴于D ，则图中阴影部分图形的面积和为_____．三、解答题16．已知抛物线y=﹣2x 2+4x+1．（1）求这个抛物线的对称轴和顶点坐标；（2）将这个抛物线平移，使顶点移到点P(－2，0)的位置，写出所得新抛物线的表达式和平移的过程．17．小明投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y （件）与销售单价x （元）之间的关系可近似的看作一次函数：y ＝﹣10x+500，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的60%．（1）设小明每月获得利润为w （元），求每月获得利润w （元）与销售单价x （元）之间的函数关系式，并确定自变量x 的取值范围．（2）当销售单价定为多少元时，每月可获得最大利润？每月的最大利润是多少？（3）如果小明想要每月获得的利润不低于2000元，那么小明每月的成本最少需要多少元？（成本＝进价×销售量）18．如图1（注：与图2完全相同），在直角坐标系中，抛物线经过点三点0(1)A ，,(50)B ，,4(0)C ，．（1）求抛物线的解析式和对称轴；（2）P 是抛物线对称轴上的一点，求满足PA PC 的值为最小的点P 坐标（请在图1中探索）；（3）在第四象限的抛物线上是否存在点E ，使四边形OEBF 是以OB 为对角线且面积为12的平行四边形？若存在，请求出点E 坐标，若不存在请说明理由.（请在图2中探索）19．如图，已知二次函数y ＝﹣x 2+bx +3的图象与x 轴交于A 、C 两点（点A 在点C 的左侧），与y 轴交于点B ，且OA ＝OB ．（1）求线段AC 的长度；（2）若点P 在抛物线上，点P 位于第二象限，过P 作PQ ⊥AB ，垂足为Q ．已知PQ ，求点P 的坐标．20．如图1，已知二次函数y=mx 2+3mx ﹣274m 的图象与x 轴交于A ，B 两点（点A 在点B 的左侧），顶点D 和点B 关于过点A 的直线l ：y=x （1）求A 、B 两点的坐标及二次函数解析式；（2）如图2，作直线AD ，过点B 作AD 的平行线交直线1于点E ，若点P 是直线AD 上的一动点，点Q 是直线AE 上的一动点．连接DQ 、QP 、PE ，试求DQ+QP+PE 的最小值；若不存在，请说明理由：（3）将二次函数图象向右平移32个单位，再向上平移个单位，平移后的二次函数图象上存在一点M ，其横坐标为3，在y 轴上是否存在点F ，使得∠MAF=45°？若存在，请求出点F 坐标；若不存在，请说明理由．参考答案1．D2．C3．A4．D5．B6．D7．B8．C9．D10.B11．1 5 12．－1或2或1 13．①②⑤ 14．1． 15．1816．（1）对称轴是直线x=1，顶点坐标为(1，3)；（2）y=-2(x+2)2；向左平移3个单位，向下平移3个单位.17．（1）21070010000w x x =-+-（20≤x ≤32）；（2）当销售单价定为32元时，每月可获得最大利润，最大利润是2160元；（3）3600．18．（1）2545442y x x -+＝，函数的对称轴为：3x ＝；（2）点8(3)5P ，；（3）存在，点E 的坐标为12(2,)5-或12,)5(4-． 19．（1）线段AC 的长是4；（2）点P 的坐标为（﹣2，3）或（﹣1，4）．20．（1）A （﹣92，0），B （32，0）；抛物线解析式x 2x（2）12；（3）（0，（0，﹣）。

2019九年级数学下册第二章 2.1 同步练习

1 二次函数一、选择题1．2018·浦东新区一模下列函数中，是二次函数的是 ( ) A．y＝－4x＋5 B．y＝x(2x－3)C．y＝(x＋4)2－x2 D．y＝1 x22．在一定条件下，若物体所经过的路程s(m)与运动时间t(s)之间的函数关系式为s＝5t2＋2t，则当t ＝4时，该物体所经过的路程为( )A．28 m B．48 mC．68 m D．88 m3．在下列4个不同的情境中，两个变量所满足的函数关系属于二次函数关系的有( )①设正方形的边长为x，面积为y，则y与x之间的函数关系；②x个球队参加比赛，每两个队之间比赛一场，则比赛的场次数y与x之间的函数关系；③设正方体的棱长为x，表面积为y，则y与x之间的函数关系；④若一辆汽车以120 km/h的速度匀速行驶，那么汽车行驶的里程y(km)与行驶时间x(h)之间的函数关系．A．1个 B．2个C．3个 D．4个二、填空题4．二次函数y＝2(3x－1)(2－x)化为一般式为____________，其中a＝________，b＝________，c＝________.5．如果函数y＝(k－5)xk2－5k＋2＋kx＋3是二次函数，那么k的值是________．6．某厂今年一月份新产品的研发资金为a元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年三月份新产品的研发资金y(元)关于x的函数表达式为y＝______________．7．如图K－8－1所示，在宽为20 m，长为32 m的矩形地面上修筑同样宽的两条互相垂直的道路，余下的部分作为耕地，若设耕地的面积为y m2，道路的宽为x m，则y与x之间的函数表达式为________________．(写出自变量的取值范围)图K－8－1三、解答题8．已知函数y＝(m2－m)x2＋(m－1)x＋2－2m.(1)若这个函数是二次函数，求m的取值范围；(2)若这个函数是一次函数，求m的值；(3)这个函数可能是正比例函数吗？为什么？9\某工厂生产的某种产品按质量分为10个档次，第1档次(最低档次)的产品一天能生产95件，每件利润为6元．每提高一个档次，每件利润增加2元，但一天生产量减少5件．(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数，且1≤x≤10)，求出y关于x的函数表达式；(2)若生产第x档次的产品一天的总利润为1120元，求该产品的质量档次．1．[解析] B A ．y ＝－4x ＋5是一次函数；B.y ＝x (2x －3)＝2x 2－3x 是二次函数；C.y ＝(x ＋4)2－x 2＝8x＋16是一次函数；D.y ＝1x 2不是二次函数．故选B. 2．[解析] D 把t ＝4代入s ＝5t 2＋2t 中即可求出．3．[解析] C ①依题意得：y ＝x 2，属于二次函数关系，符合题意；②依题意得：y ＝12x (x －1)＝12x 2－12x ，属于二次函数关系，符合题意；③依题意得：y ＝6x 2，属于二次函数关系，符合题意；④依题意得：y ＝120x ，属于一次函数关系，不符合题意．综上所述，两个变量所满足的函数关系属于二次函数关系的有3个．故选C.4．[答案] y ＝－6x 2＋14x －4 －6 14 －4[解析] y ＝2(3x －1)(2－x )＝2(－3x 2＋7x －2)＝－6x 2＋14x －4.5．[答案] 0[解析] 由题意，得k 2－5k ＋2＝2，解得k ＝0或k ＝5.又∵k －5≠0，∴k ≠5，∴当k ＝0时，这个函数是二次函数．6．[答案] a (1＋x )27．[答案] y ＝x 2－52x ＋640(0<x ≤20)[解析] 如图所示，若把两条互相垂直的道路移到土地相邻的边上，剩余土地的宽为(20－x )m ，长为(32－x )m ，则可得y ＝(20－x )(32－x )，即y ＝x 2－52x ＋640.由于该题是实际问题，因此x 的取值要使实际问题有意义，即0<x ≤20.8．解：(1)若这个函数是二次函数，则m 2－m ≠0，解得m ≠0且m ≠1；(2)若这个函数是一次函数，则m 2－m ＝0，且m －1≠0，解得m ＝0.(3)这个函数不可能是正比例函数．理由：∵当此函数是一次函数时，m ＝0，而此时2－2m ＝2≠0，∴这个函数不可能是正比例函数．9解：(1)∵第1档次的产品一天能生产95件，每件利润为6元，每提高一个档次，每件利润增加2元，但一天生产量减少5件，第x 档次比第1档次提高了(x －1)个档次，∴y ＝[6＋2(x －1)][95－5(x －1)]，即y ＝－10x 2＋180x ＋400(x 是正整数，且1≤x ≤10)．(2)由题意可得－10x 2＋180x ＋400＝1120，整理，得x 2－18x ＋72＝0，解得x 1＝6，x 2＝12(舍去)．答：该产品的质量档次为第6档．。

[K12配套]九年级数学下册第2章二次函数2.4二次函数的应用2.4.1二次函数的应用同步练习

2.4.1二次函数的应用一、夯实基础1．如图所示的抛物线的解析式是 ( )A．y＝x2－x＋2 B．y=－x2－x＋2C．y＝x2＋x＋2 D．y=－x2＋x＋22．如图所示的是二次函数y＝ax2－x＋a2－1的图象，则a的值是．3．已知抛物线y＝4x2－11x－3，则它的对称轴是，与x轴的交点坐标是，与y轴的交点坐标是 .4．抛物线y＝x2＋bx＋c与x轴的正半轴交于A，B两点，与y轴交于C点，且线段AB 的长为1，△ABC的面积为l，则b的值是．5．用12米长的木料做成如图2－111所示的矩形窗框(包括中间的十字形)，当长、宽各为多少时，矩形窗框的面积最大?最大面积是多少?二、能力提升6.（2016·青海西宁·3分）如图，在△ABC中，∠B=90°，tan∠C=，AB=6cm．动点P从点A开始沿边AB向点B以1cm/s的速度移动，动点Q从点B开始沿边BC向点C以2cm/s 的速度移动．若P，Q两点分别从A，B两点同时出发，在运动过程中，△PBQ的最大面积是（）A．18cm2B．12cm2C．9cm2D．3cm27．如图2－112所示，△ABC的面积为2400c m2，底边BC的长为80cm，若点D在BC 上，点E在AC上，点F在AB上，且四边形BDEF为平行四边形，设BD＝x cm，S BDEF=y cm2．(1)求y与x之间的函数关系式；(2)求自变量x的取值范围；(3)当x为何值时，y最大?最大值是多少?8．如图所示，在ABCD中，AB＝4，BC＝3，∠BAD＝120°，E为BC上一动点(不与B 重合)，作EF⊥AB于F，延长FE与DC的延长线交于点G，设BE＝x，△DEF的面积为S．(1)求证△BEF∽△CEG；(2)用x表示S的函数关系式，并写出x的取值范围；(3)当E运动到何处时，S有最大值，最大值为多少?三、课外拓展9．如图所示，在边长为的正方形ABCD中，E，F是对角线AC上的两个点，它们分别从点A、点C同时出发，沿对角线以1 cm／s的相同速度运动，过E作EH垂直AC，交Rt△ADC的直角边于H；过F作FG垂直AC，交Rt△ADC的直角边于G，连接HG，EB. 设HE，EF，FG，GH围成的图形面积为S1，AE，EB，BA围成的图形面积为S2(这里规定：线段的面积为0)．若E到达C，F到达A，则停止运动．若E的运动时间为x s，解答下列问题．(1)当0＜x＜8时，直接写出以E，F，G，H为顶点的四边形是什么四边形，并求x为何值时，S1=S2；(2)①若y是S1与S2的和，求y与x之间的函数关系式；(图2－115为备用图)②求y 的最大值．四、中考链接1.（2014•菏泽第8题3分）如图，Rt△ABC中，AC=BC=2，正方形CDEF的顶点D、F分别在AC、BC边上，C、D两点不重合，设CD的长度为x，△ABC与正方形CDEF重叠部分的面积为y，则下列图象中能表示y与x之间的函数关系的是（）A BCD2.（2014•广西贺州，第26题12分）二次函数图象的顶点在原点O ，经过点A （1，14）；点F （0，1）在y 轴上．直线y=﹣1与y 轴交于点H ．（1）求二次函数的解析式；（2）点P 是（1）中图象上的点，过点P 作x 轴的垂线与直线y=﹣1交于点M ，求证：FM 平分∠OFP；（3）当△FPM 是等边三角形时，求P 点的坐标．答案1．D2．1[提示：抛物线开口向上，故a ＞0．因为图象过原点，所以a 2－1＝0，所以a ＝±1，所以a ＝1．]3．x ＝118 (3，0), (－14，0) (0，－3) 4．－35．解：设窗框的长为x 米，则窗框的宽为1233x -米，矩形窗框的面积y ＝x(1233x-)＝－x 2＋4x ．配方得y ＝－(x －2)2＋4．∵a=－l ＜0，∴函数y ＝－(x －2)2＋4有最大值．当x ＝2时，y 最大值＝4平方米，此时1233x-＝4－2＝2(米)，即当长、宽各为2米时，矩形窗框的面积最大，最大值为4平方米．6.解：∵tan∠C=，AB=6cm ，∴=，∴BC=8，由题意得：AP=t ，BP=6﹣t ，BQ=2t ，设△PBQ 的面积为S ，则S=×BP×BQ=×2t×（6﹣t ），S=﹣t 2+6t=﹣（t 2﹣6t+9﹣9）=﹣（t ﹣3）2+9， P ：0≤t≤6，Q ：0≤t≤4， ∴当t=3时，S 有最大值为9，即当t=3时，△PBQ 的最大面积为9cm 2；故选C ．7．解：(1)设A 到BC 的距离为d cm ，E 到BC 的距离为h cm ，则y=S BDEF=xh ．∵S △ABC＝12BC·d，∴2400=12×80d，∴d=60．∵ED∥AB，∴△EDC∽△ABC，∴h DC d BC =，即806080h x -=，∴h=3(80)4x -，∴y＝3(80)4x -x ＝－34x 2＋60x ．(2)自变量x 的取值范围是0＜x ＜80． (3)∵a=－34＜0，－2ba＝40，0＜40＜80，∴当x ＝40时，y 最大值＝1200．8．(1)证明：∵AB∥CD，∴∠B＝∠ECG．又∠BEF=∠CEG，∴△BEF∽△CEG． (2)解：由(1)得，∠G＝∠BFE＝90°，∴DG 为△DEF 中EF 边上的高．在Rt△BFE 中，∠B=60°，EF ＝BEsin B 在Rt△CGE 中，CE=3－x ，CG=(3－x)cos 60°=32x -，∴DG=DC＋CG=112x -，∴S=12x 2x ，其中0＜x≤3．(3)＜0，对称轴x ＝112，∴当0＜x≤3时，S 随x 的增大而增大，∴当x ＝3，即E 与C 重合时，S 有最大值，S 最大值＝．9．解：(1)以E ，F ，G ，H 为顶点的四边形是矩形．∵正方形ABCD 的边长为，∴AC=16．∵AE＝x ，过点B 作BO⊥AC 于O ，如图2－116所示，则BO ＝8，∴S 2＝4x ．∵HE=x，EF ＝16－2x ，∴S 1=x(16－2x)．当S 1＝S 2，即x(16－2x)=4x 时，解得x 1=0(舍去)，x 2＝6．∴当x ＝6时，S 1＝S 2．(2)①当0≤x＜8时，如图2－116所示．y=x(16－2x)＋4x ＝－2x 2＋20x ．当8≤x≤16时，如图所示，AE ＝x ，CE=HE ＝16－x ，EF ＝16－2(16－x)=2x －16，∴S 1＝(16－x)(2x －16)，∴y＝(16－x)(2x －16)＋4x=－2x 2＋52x －256．(2)解法1：②当0≤x＜8时，y ＝－2x 2＋20x ＝－2(x 2－10x ＋25)＋50=－2(x －5)2＋50，∴当x ＝5时，y 的最大值为50．当8≤x≤16时，y ＝－2x 2＋52x －256=－2(x －13)2＋82，∴当x ＝13时，y 的最大值为82．综上可得，y 的最大值为82．解法2：②y ＝－2x 2＋20x(0≤x＜8)，当x ＝－202(2)⨯-＝5时，y 最大值＝2204(2)-⨯-＝50．y=－2x2＋52x－256(8≤x≤16)，当x=－522(2)⨯-＝13时，y最大值=24(2)(256)524(2)⨯-⨯--⨯-＝82．综上可得，y的最大值为82．中考链接：1.A2.解答：（1）解：∵二次函数图象的顶点在原点O，∴设二次函数的解析式为y=ax2，将点A（1，14）代入y=ax2得：a=14，∴二次函数的解析式为y=14x2；（2）证明：∵点P在抛物线y=14x2上，∴可设点P的坐标为（x，14x2），过点P作PB⊥y轴于点B，则BF=14x2﹣1，PB=x，∴Rt△B PF中，PF==14x2+1，∵PM⊥直线y=﹣1，∴PM=14x2+1，∴PF=PM，∴∠PFM=∠PMF，又∵PM∥x轴，∴∠MFH=∠PMF，∴∠PFM=∠MFH，∴FM平分∠OFP；（3）解：当△FPM是等边三角形时，∠PMF=60°，∴∠FMH=30°，在Rt△MFH中，MF=2FH=2×2=4，∵PF=PM=FM，∴14x2+1=4，解得：x=±2，∴14x2=14×12=3，∴满足条件的点P的坐标为（2，3）或（﹣2，3）．。

北师大版九年级数学下册第二章2.1《二次函数》同步练习题(共6份)

《二次函数》同步练习3一、选择题1、下列是二次函数的是（） A ．281y x =+ B ．81y x =+ C ．xy 8=D ．281y x =+2、抛物线2x y -=不具有的性质是( ). A 、开口向下B 、对称轴是y 轴C 、与y 轴不相交D 、最高点是原点3、二次函数222+-=x x y 有( ). A 、最小值1 B 、最小值2 C 、最大值1D 、最大值24、已知点A ()1,1y 、B ()2,2y -、C ()3,2y -在函数()21122-+=x y 上，则1y 、2y 、3y 的大小关系是( ).A 、321y y y >>B 、131y y y >>C 、213y y y >>D 、312y y y >>5、二次函数()02≠++=a c bx ax y 图象如图所示，下面五个代数式：ab 、ac 、c b a +-、ac b 42-、b a +2中，值大于0的有( )个. A 、2B 、3C 、4D 、56、232m m y mx ++=是二次函数，则m 的值为（）A ．0，-3B ．0，3C ．0D ．-3二、填空题7、二次函数()223+-=x y 的对称轴是__________.8、当m __________时12)1(+-=mx m y 是二次函数．9、若点A ()m ,2在函数12-=x y 上，则A 点的坐标为_______. 10、当k =______时，y =（k -2）x42-+k k 是关于x 的二次函数．-1xOy11、抛物线x x y 622+=与x 轴的交点坐标是_______________.12、抛物线2x y =向左平移4个单位，再向上平移3个单位可以得到抛物线__________________的图像.13、将322+-=x x y 化为()k h x a y +-=2的形式，则=y _____________.14、抛物线x x y 32-=的顶点在第____象限.15、试写出一个二次函数，它的对称轴是直线1=x ，且与y 轴交于点()3,0._________________.16、抛物线()31212+-=x y 绕它的顶点旋转180°后得到的新抛物线的解析式为________________.17、已知抛物线c x x y -+=422的顶点在x 轴上，则c 的值为______.18、如图，将边长为1的正方形OAPB 沿x 轴正方向连续翻转2007次，点P 依次落在点20074321,,,,,P P P P P 的位置，则2007P 的坐标为___________.三、解答题19、(8分)已知抛物线的顶点坐标是()1,2-，且过点()2,1-，求该抛物线的解析式.20、(8分) 写出下列各函数关系，并判断它们是什么类型的函数．（1）写出正方体的体积V （cm 3）与正方体棱长a （cm ）之间的函数关系；（2）写出圆的面积y （cm 2）与它的半径x （cm ）之间的函数关系；21、(8分)如图，矩形的长是4cm ，宽是3cm .如果将矩形的长和宽都增加cm x ，那么面积增加2cm y .①求y 与x 之间的函数关系式；②求当边长增加多少时，面积增加82cm .22、(8分) 为了改善小区环境，某小区决定要在一块一边靠墙（墙长25m ）的空地上修建一个矩形绿化带ABCD ，绿化带一边靠墙，另三边用总长为40m 的栅栏围住（如图）．若设绿化带的BC 边长为x m ，绿化带的面积为y m 2．求y 与x 之间的函数关系式，并写出自变量x 的取值范围．23、(8分)画函数()122--=x y 的图象，并根据图象回答：(1)当x 为何值时，y 随x 的增大而减小. (2)当x 为何值时，0>y .24、(8分)利用右图，运用图象法求下列方程的解.012432=--x x (精确到0.1).34xx25、(8分)某广告公司要为客户设计一幅周长为12m 的矩形广告牌，广告牌的设计费为每平方米1000元.请你设计一个广告牌边长的方案，使得根据这个方案所确定的广告牌的长和宽能使获得的设计费最多，设计费最多为多少元？26、(8分)行驶中的汽车刹车后，由于惯性的作用，还会继续向前滑行一段距离，这段距离称为“刹车距离”，刹车距离是分析交通事故的重要依据.在一条限速120h km /的高速公路上，甲、乙两车相向而行，发现情况不对，同时刹车，但还是相撞了.事后现场测得甲车的刹车距离为21m ，乙车的刹车距离超过20m ，但小于21m . 根据两车车型查阅资料知：甲车的车速()h km x /与刹车距离()m s 甲之间有下述关系：2002.001.0x x s +=甲；乙车的车速()h km x /与刹车距离()m s 乙之间则有下述关系：x s 61=乙. 请从两车的速度方面分析相撞的原因.27、(13分)如图①，扇形ODE 的圆心O 重合于边长为3得正三角形ABC 的内心O ，扇形的圆心角∠DOE＝120°，且OD ＞OB.将扇形ODE 绕点O 顺时针方向旋转(旋转角α满足条件：0°＜α＜120°)，四边形OFBG 是旋转过程中扇形与三角形的重叠部分(如图②) (1)在上述旋转过程中，CG 、BF 有怎样的数量关系？四边形OFBG 的面积有怎样的变化？证明你发现的结论？(2)若连结FG ，设CG ＝x ，△OFG 的面积为y ，求y 与x 之间的函数关系式，并写出自变量x 的取值范围.(3)在(2)的前提下，是否存在某一位置，使△OFG 的面积最小？若存在，求出此时x 的值，若不存在，说明理由.图①28、(13分)如图，已知抛物线t ax ax y ++=42()0>a 交x 轴于A 、B 两点，交y 轴于点C ，抛物线的对称轴交x 轴于点E ，点B 的坐标为(-1，0). (1)求抛物线的对称轴及点A 的坐标；(2)过点C 作x 轴的平行线交抛物线的对称轴于点P ，你能判断四边形ABCP•是什么四边形？并证明你的结论；(3)连结CA 与抛物线的对称轴交于点D ，当∠APD=∠ACP 时，求抛物线的解析式.【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

北师大九年级数学下册《2.1二次函数》同步训练含参考答案

北师大九年级数学下册第二章二次函数 2.1 二次函数同步训练学校：__________ 班级：__________ 姓名：__________ 考号：__________一、选择题（本题共计 10 小题，每题 3 分，共计30分，）1. 下列函数中，能表示y是x的二次函数是（）A.y=1x2B.y=−x22C.y2=2x−1D.y=x(3x−1)−3x22. y=mx m2+2m+2是二次函数，则m的值为（）A.0，−2B.0，2C.0D.−23. 如果函数y=(m−3)x m2−3m+2是二次函数，那么m的值一定是（）A.0B.3C.0，3D.1，24. 下列函数关系中，可以看做二次函数y=ax2+bx+c模型的是（）A.在一定距离内，汽车行驶的速度与行驶的时间的关系B.我国人中自然增长率为1%，这样我国总人口数随年份变化的关系C.竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系（不计空气阻力）D.圆的周长与半径之间的关系5. 下列函数中，是二次函数的为（）A.y=2x+1B.y=(x−2)2−x2C.y=2x2D.y=2x(x+1)6. 若函数y=−2(x−1)2+(a−1)x2为二次函数，则a的取值范围为（）A.a≠0B.a≠1C.a≠2D.a≠37. 下列函数中，不是二次函数的是（）A.y=1−2x2B.y=2(x−1)2+4C.y=1x +x D.y=12(x−1)(x+4)8. 如果y=(m−2)x m2−m是关于x的二次函数，则m=()A.−1B.2C.−1或2D.m不存在9. 等腰三角形底角与顶角之间的函数关系是（）A.正比例函数B.一次函数C.反比例函数D.二次函数10. 圆的面积公式S=πR2中，S与R之间的关系是（）A.S是R的正比例函数B.S是R的一次函数C.S是R的二次函数D.以上答案都不对二、填空题（本题共计 8 小题，每题 3 分，共计24分，）11. 函数y=(m+1)x|m|+1+4x−5是二次函数，则m=________．12. 下列函数：①y=6x2+1；②y=6x+1；③y=6x +1；④y=6x+1．其中属于二次函数的有________（只要写出正确答案的序号）．13. 若函数y=(m+1)x m2+3m+4是二次函数，则m的值为________．14. 已知y=(k+2)x k2−2是二次函数，则k=________．15. 已知函数y=mx2m−4−2x2+2x−1(x≠0)是关于x的二次函数，则m的值为________．16. 已知两个变量x，y之间的关系式为y=(a−2)x2+(b+2)x−3．(1)当________时，x，y之间是二次函数关系；(2)当________时，x，y之间是一次函数关系．17. 若二次函数y=mx2+x+m(m−2)的图象经过原点，则m的值为________．18. 函数y=2x2中，自变量x的取值范围是________，函数值y的取值范围是________．三、解答题（本题共计 8 小题，共计46分，）19.(4分) 若y=(a−4)x a2−3a−2+a是二次函数，求：（1）a的值；(2)函数的关系式．x2．y是x的二次函数吗？20. （6分）某汽车的行驶路程y(m)与行驶时间x(s)之间的函数表达式为y=3x+12求汽车行驶60s的路程．21.(6分) 已知函数y=(n+2)x n2+n−4是关于x的二次函数．(1)求满足条件的n的值；(2)当n为何值时，抛物线有最低点？求出这个最低点的坐标，并写出y随x的增大而增大的x的取值范围．22. （6分）y=(m2−2m−3)x2+(m−1)x+m2是关于x的二次函数，则m满足的条件是什么？23.(6分) 关于x的函数是二次函数的有________．（1）y=ax2（2）y=−x(x−2)（3）y=3x2−4−x3（4）y=2xπ2x2（5）y=−2−13（6）y=12−x2=2+x（7）yx−3(8)(3+x)(x−2)=y−x2．24.(6分) 已知函数y=(m+3)x m2+6m+10是关于x的二次函数．(1)求m的值；（2）m为何值时，函数有最大值？最大值是多少？此时x在什么范围时，y随x的增大而减小？25. （6分）已知y=(m2−m)x m2−2m−1+(m−3)x+m2是x的二次函数，求m的值和二次函数的解析式．26.(6分) 已知y是x的二次函数，当x=2时，y=−4，当y=4时，x恰为方程2x2−x−8=0的根．(1)解方程 2x2−x−8=0(2)求这个二次函数的解析式．答案1. B2. D3. A4. C5. D6. D7. C8. A9. B10. C11.12. ①13.14.15. 或16. 且17.18. 全体实数19. 解：(1)∵y=(a−4)x a2−3a−2+a是二次函数，∴a2−3a−2=2，且a−4≠0，整理，得(a−4)(a+1)=0，且a−4≠0，解得a=−1；(2)由(1)知，a=−1，则该函数解析式为：y=−5x2−1．20. 解：y=3x+12x2满足二次函数的一般形式，所以y是x的二次函数，当x=60时，y=3×60+12×602=1980．21. 解：(1)根据题意得n+2≠0且n2+n−4=2，解n2+n−4=2得n1=−3，n2=2，所以n的值为−3或2；(2)当n+2>0，即n>−2时，抛物线开口向上，抛物线有最低点，所以n=2，此时解析式为y=4x2，这个最低点的坐标为(0, 0)，当x>0时，y随x的增大而增大．22. 解：∵y是x的二次函数，∴m2−2m−3≠0，∴m≠−1且m≠3，故满足的条件是m≠−1且m≠3．23. (2)，(5)，(7)．24. 解：(1)由题意得，m2+6m+10=2，m+3≠0，解得：m=−2或m=−4；(2)当m=−4时，m+3=−1<0，函数有最大值，最大值是0，根据二次函数的性质，当x>0时，y随x的增大而减小．25. 解：∵y=(m2−m)x m2−2m−1+(m−3)x+m2是x的二次函数，∴ m2−m≠0m2−2m−1=2，解得m=3或m=−1，∴此二次函数的解析式为：y=6x2+9或y=2x2−4x+1．26. 解：(1)∵2x2−x−8=0，∴a=2，b=−1c=−8，∴△=1+64=65>0，∴x1=1+654，x2=1−654；(2)设方程2x2−x−8=0的根为x1、x2，则当x=x1，x=x2时，y=4，可设y=a(2x2−x−8)+4，把x=2，y=−4代入，得−4=a(2×22−2−8)+4，解得a=4，所求函数为y=4(2x2−x−8)+4，即y=8x2−4x−28．。

北师大版九年级数学下册第二章同步测试题及答案

北师大版九年级数学下册第二章同步测试题及答案2.1二次函数一、选择题1．下列函数是二次函数的是（）A．y=-4x+5 B．y=x（2x-3）C．y=（x+4）2-x2D．y=2．若y=2xm2-2是二次函数，则m等于（）A．-2 B．2 C．±2 D．不能确定3．在一定条件下，若物体运动的路程s（米）与时间t（秒）之间的函数表达式为s=5t2+2t，则当t=4时，该物体所经过的路程为（）A．28米B．48米C．68米D．88米4．如果函数y=（k-3）+kx+1是二次函数，那么k的值一定是（）A．3 B．0 C．0或3 D．0或-35．如图，在Rt△AOB中，AB⊥OB，且AB=OB=3，设直线x=t（0<t<3）截此三角形所得阴影部分的面积为S，则S与t之间的函数关系式为（）A．S=t B．S=t2 C．S=t2D．S=t2-1二、填空题6．将二次函数y=（2x-1）（1-x）化为一般式为______，其中a=_____，b=_____，c=____．7．某企业今年第一个月新产品的研发资金为100万元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年第三个月新产品的研发资金y（万元）关于x的函数关系式为y=________．8．现用一条长为6 m的木料做成如图的窗框，窗框的面积S（m2）与窗框的宽x（m）之间的函数关系式为______________．9．汽车刹车距离s（m）与速度v（km/h）之间的函数表达式是s=v2，在一辆车速为100 km/h的汽车前方80 m处，发现停放着一辆故障车，此时刹车________有危险．（填“会”或“不会”）三、解答题10．在一块长方形镜面玻璃的四周镶上与它的周长相等的边框，制成一面镜子．镜子的长与宽的比是2：1．已知镜面玻璃的价格是每平方米120元，边框的价格是每米30元，另外制作这面镜子还需加工费45元．设制作这面镜子的总费用是y元，镜子的宽度是x m．（1）求y与x之间的函数关系式；（2）如果制作这面镜子共花了195元，求这面镜子的长和宽．参考答案一、1．B 2．C 3．D 4．B5．B二、6．y=-2x2+3x-1；-2；3；-1 7．100（1+x）2 8．S=-x2+3x9．会三、10．解：（1）由题意，得y=（2x+2x+x+x）×30+45+2x2×120=240x2+180x+45．（2）当y=195时，240x2+180x+45=195，整理得8x2+6x-5=0，即（2x-1）（4x+5）=0，解得x1=0.5，x2=-1.25（舍去）．∴2x=1．∴这面镜子的长和宽分别是1 m和0.5 m．2.2二次函数的图象与性质一、选择题1. 抛物线y =（x-2）2 +3的顶点坐标是（）A．（2，3） B．（-2，3） C．（2，-3）D．（-2，-3）2. 把抛物线y =-x2先向右平移1个单位长度长度，再向下平移3个单位长度长度，则平移后抛物线的表达式为（）A．y =-（x-1）2 +3 B．y =-（x +1）2 +3C．y =-（x-1）2-3 D．y =-（x +1）2-33. 若抛物线y =（k-7）x2-5的开口向下，则k的取值范围是（）A．k<7 B．k>7 C．k<0 D．k>04. 抛物线y =2x2-3的顶点在（）A．第一象限B．第二象限C．x轴上D．y轴上5. 已知二次函数y = -x2+bx+c 中函数y与自变量x之间的部分对应值如下表，点A（x1，y1），B（x2 ，y2）在函数的图象上，当0<x1<1，2<x2<3时，y1与y2 的大小关系正确的是（）A．y1 ≥y2 B．y1 > y2 1 2 D．y1 ≤y26. 若把函数y = x的图象用E（x，x）表示，函数y =2x+1的图象用E（x，2x+1）表示，…，则E（x，x2-2x+1）可以由E（x，x2）（）A．向上平移1个单位长度长度平移得到B．向下平移1个单位长度长度平移得到C．向左平移1个单位长度长度平移得到D．向右平移1个单位长度长度平移得到7. 下列抛物线，开口最大的是（）A．y =-x2B．y =-x2C．y =-x2D．y =-x28. 抛物线y =x2-4x+3的顶点坐标和对称轴分别是（）A．（1，2），直线x =1 B．（-1，2），直线x =-1C．（-4，-5），直线x =-4 D．（4，-5），直线x =49. 关于二次函数y=-2x2+3，下列说法正确的是（）A．它的开口方向是向上B．当x<-1时，y随x的增大而增大C．它的顶点坐标是（-2，3）D．当x=0时，y有最小值是310. 已知函数y =-3x2 +1的图象是抛物线，若该抛物线不动，把x轴向上平移2个单位长度长度，y轴向左平移1个单位长度长度，则该函数在新的直角坐标系内的函数关系式为（）A．y =-3（x +1）2+2 B．y =-3（x-1）2-1C．y =3（x +1）2 +2 D．y =3（x-1）2-211. 在平面直角坐标系中，函数y=-x+1与y=（x-1）2的图象大致是（）A B C D12. 在二次函数y=ax2+bx+c中，b2=ac，且当x=0时，y=-4，则（）A．y最大值=-4 B．y最小值=-4 C．y最大值=-3 D．y最小值=-3二、填空题13. 将y=2x2-12x-12变为y=a（x-m）2 + n 的形式，则mn =__________．14. 当x=______时，二次函数y=x2+2x-2有最小值．15. 若抛物线y=2x2-bx+3的对称轴是直线x=1，则b的值为__________．16. 已知抛物线y=ax2+bx+c（a >0）的对称轴为直线x=1，且经过点（-1，y1），（2，y2），试比较y1和y2的大小：y1 ________ y2 （填“>”“<”或“=”）．17. 抛物线y=ax2+bx+c的形状与y=2x2-4x-1相同，对称轴平行于y轴，且当x=2时，y有最大值-5，该抛物线的关系式为____________．18. 若抛物线y=x2-k的顶点为P，与x轴交于点A，B，且△ABP是等边三角形，则k的值是_______．19. 任给一些不同的实数n，得到不同的抛物线y=2x2+n，如当n=0，n=±2时，关于这些抛物线有以下结论：①开口方向都相同；②对称轴都相同；③形状都相同；④都有最低点．其中判断正确的是_______．（填序号）三、解答题20. 把二次函数y=-x2的图象向上平移2个单位长度长度．（1）求新图象的表达式、顶点坐标和对称轴；（2）画出平移后的函数图象；（3）求平移后的函数的最大值或最小值，并求对应的x的值．21. 二次函数y=ax2-2与直线y=2x-1的图象交于点P（1，m）．（1）求a，m的值；（2）写出二次函数的表达式，并指出当x取何值时，y随x的增大而增大．22. 已知抛物线y=（m-1）x2+m2-2m-2的图象开口向下，且经过点（0，1）．（1）求m的值．（2）求此抛物线的顶点坐标及对称轴．（3）当x为何值时，y随x的增大而增大？答案一、1．A 2．C 3．A 4．D5．C 6．D7．D 8．D 9．B 10．B 11．D12．C二、13．-90 14．-1 15．416．>17．y=-2（x-2）2-5 18．3 19．①②③④三、20．解：（1）把y=-x2的图象向上平移2个单位长度后得到抛物线的表达式为y=-x2+2，所以它的顶点坐标是（0，2），对称轴是直线x=0，即y轴．（2）由y=-x2+2，列表如下：其函数图象如图：；（3）如图，当x=0时，y最大=2．21．解：（1）将（1，m）代入y=2x-1，得m=2×1-1=1．所以点P的坐标为（1，1）．将点P的坐标（1，1）代入y=ax2，得1=a×12，解得a=1．即a=1，m=1．（2）由（1）知，二次函数的表达式为y=x2，所以当x>0时，y随x的增大而增大．（3）顶点坐标为（0，0），对称轴为y轴．22．解：（1）由题意，得解得m=-1．（2）当m=-1时，抛物线的表达式为y=-2x2+1，其顶点坐标为（0，1），对称轴为y轴．（3）因为抛物线y=-2x2+1的开口向下，所以在对称轴的左侧，即当x<0时，y随x的增大而增大．2.3确定二次函数的表达式一、选择题1．若二次函数y=x2+bx-2的图象与x轴的一个交点为（1，0），则该二次函数的表达式为（）A．y=x2-2x B．y=x2+x-1 C．y=x2+x-2 D．y=x2-x-22．若二次函数的图象经过点（1，10），顶点坐标为（-1，-2），则此二次函数的表达式为（）A．y=3x2+6x+1 B．y=3x2+6x-1 C．y=3x2-6x+1 D．y=-3x2-6x+13．如图，抛物线的函数表达式是（）A．y=x2-x+2 B．y=x2+x+2 C．y=-x2-x+2 D．y=-x2+x+24．若y=ax2+bx+c，则由表格中信息可知y与x之间的函数表达式是（）A．y=x2-4x+3 B．y=x2-3x D．y=x2-4x+85．已知二次函数y=x2+bx+c，若b+c=0，则它的图象一定过点（）A．（-1，-1）B．（1，-1）C．（-1，1）D．（1，1）二、填空题6．在二次函数y=x2+bx+c中，函数y与自变量x的部分对应值如下表，则m的值为________．7．若抛物线y=ax2+bx+c的顶点是A（2，1），且经过点B（1，0），则此抛物线的表达式为___________．8．如果一条抛物线的形状与抛物线y=-x2+2的形状相同，且顶点坐标是（4，-2），那么它的函数表达式是__________．9．二次函数的图象如图，则其表达式为__________．10．如果抛物线经过A（-1，-6），B（1，-2），C（2，3）三点，那么抛物线的函数表达式为__________．三、解答题11．如图，已知抛物线y=x2+bx+c的顶点坐标为M（0，-1），与x轴交于A，B两点．（1）求抛物线的函数表达式；（2）判断△MAB的形状，并说明理由．12．如图，一拱桥的截面呈抛物线形状，拱桥两端点与水面的距离都是1 m，拱桥的跨度为10 m，拱桥与水面的最大距离是5 m，桥洞两侧壁上各有一盏距离水面4 m的景观灯．（1）建立适当的直角坐标系并求出抛物线对应的函数表达式；（2）求两盏景观灯之间的水平距离．13．如图，已知二次函数y=x2+mx+n的图象经过点P（-3，1），对称轴是经过点（-1，0）且平行于y轴的直线．（1）求m，n的值；（2）若一次函数y=kx+b的图象经过点P，与x轴相交于点A，与二次函数的图象相交于另一点B，点B在点P的右侧，PA：PB=1：5，求一次函数的表达式．14．已知二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）的图象经过A，B，C，D四个点，其中横坐标x 与纵坐标y的对应值如下表：求：（1）二次函数的表达式；（2）△ABD的面积．15．如图，已知抛物线y=ax2+bx+c（a≠0）经过A（-1，0），B（3，0），C（0，-3）三点，直线l是抛物线的对称轴．（1）求抛物线的函数关系式；（2）设P是直线l上的一个动点，当点P到点A，B的距离之和最小时，求点P的坐标．16．如图，已知抛物线y=x2+bx+c经过A（-1，0），B（3，0）两点．（1）求抛物线的表达式和顶点坐标；（2）当0<x<3时，求y的取值范围；（3）P为抛物线上一点，若S△PAB =10，求出此时点P的坐标．参考答案一、1．C2．A 3．D 4．A 5．D二、6．-1 7．y=-x2+4x-3 8．y=（x-4）2-2或y=-（x-4）2-29．y=-x2+2x+310．y=x2+2x-5三、11．解：（1）∵在抛物线的函数表达式中二次项系数为1，且顶点为M（0，-1），∴其函数表达式为y=x2-1．（2）△MAB是等腰直角三角形．理由如下：当y=0时，x2-1=0，∴x=±1．∵点M的坐标为（0，-1），∴OA=OB=OM，∴∠OAM=∠OMA=∠OBM=∠OMB=45°，∴∠AMB=90°，∴△MAB是直角三角形，且MA=MB，∴△MAB是等腰直角三角形．12．解：（1）答案不唯一，如建立如图的平面直角坐标系．由题意知，抛物线的顶点坐标为（5，5），与y轴的交点坐标是（0，1）．设抛物线对应的函数表达式是y=a（x-5）2+5．把（0，1）代入y=a（x-5）2+5，得a=-，∴y=-（x-5）2+5（0≤x≤10）．（2）由题意知，两盏景观灯的纵坐标都是4，令4=-（x-5）2+5，∴425（x-5）2=1，∴x1=，x2=．∴两盏景观灯之间的水平距离为-=5（m）．13．解：（1）∵抛物线的对称轴是经过点（-1，0）且平行于y轴的直线，∴-=-1，解得m=2．∵二次函数y=x2+mx+n的图象经过点P（-3，1），∴9-3m+n=1，∴n=3m-8=-2．（2）∵m=2，n=-2，∴二次函数的表达式为y=x2+2x-2．如图，分别过点P，B作PC⊥x轴于点C，BD⊥x轴于点D，则PC∥BD，∴．∵点P的坐标为（-3，1），∴PC=1．∵PA：PB=1：5，∴，∴BD=6，∴点B的纵坐标为6．令6=x2+2x-2，解得x1=2，x2=-4（舍去），∴点B的坐标为（2，6）．∴解得∴一次函数的表达式为y=x+4．14．解：（1）把A，B，C三点的坐标分别代入y=ax2+bx+c，得解得所以二次函数的表达式为y=-x2+3x+3．（2）S△ABD =×3×4=6．15．解：（1）分别将A（-1，0），B（3，0），C（0，-3）代入y=ax2+bx+c，得解得∴抛物线的函数关系式为y=x2-2x-3．（2）当点P在x轴上时，P，A，B三点在一条直线上，则点P到点A，B的距离之和最小，此时点P的横坐标x=-=1．∴点P的坐标为（1，0）．16．解：（1）把A（-1，0），B（3，0）分别代入y=x2+bx+c，得解得∴抛物线的表达式为y=x2-2x-3．∵y=x2-2x-3=（x-1）2-4，∴抛物线的顶点坐标为（1，-4）．（2）由图象可知，当0<x<3时，-4≤y<0．（3）∵A（-1，0），B（3，0），∴AB=4．设P（x，y），则S△PAB =AB·|y|=2|y|=10，∴|y|=5，∴y=±5．①当y=5时，x2-2x-3=5，解得x1=-2，x2=4，此时点P的坐标为（-2，5）或（4，5）．②当y=-5时，x2-2x-3=-5，方程无实数解．综上所述，点P的坐标为（-2，5）或（4，5）．2.4二次函数的应用一、选择题1．如图，假设篱笆（虚线部分）的长度是16 m，则所围成矩形ABCD的最大面积是（）A．60 m2B．63 m2C．64 m2D．66 m22．河北省赵县的赵州桥的桥拱是近似的抛物线形，建立如图示的平面直角坐标系，其函数关系式为y=-x2，当水面离桥拱顶的高度DO是4 m时，这时水面宽度AB为（）A．-20 m B．10 m C．20 m D．-10 m3．竖直向上发射的小球的高度h（m）关于运动时间t（s）的函数表达式为h=at2 +bt，其图象如图．若小球在发射后第2 s与第6 s时的高度相等，则小球的高度最高的是第（）A．3 s B．3.5 s C．4 s D．6.5 s4．如图，在一场篮球赛中，篮球运动员跳起投篮，已知球出手时离地面2.2 m，与篮圈中心的水平距离为8 m，当球出手后水平距离为4 m时达到最大高度4 m，篮圈运行的轨迹为抛物线的一部分，篮圈中心距离地面3 m，运动员发现未投中，若假设出手的角度和力度都不变，要使此球恰好通过篮圈中心，运动员应该跳得（）A．比开始高0.8 m B．比开始高0.4 m C．比开始低0.8 m D．比开始低0.4 m5．毕节某旅行社在十一黄金周期间接团去外地旅游，经计算所获的营业额y（元）与旅行团人员x（人）之间满足关系式y=-x2 +100x+28 400，要使所获的营业额最大，则旅行团应有（）A．30人B．40人C．50人D．55人6．一件工艺品的进价为100元，标价135元售出，每天可售出100件．根据销售统计，一件工艺品每降价1元出售，则每天可多售出4件，要使每天获得的利润最大，每件需降价的钱数为（）A．5元B．10元C．0元D．36元二、填空题7．某农场拟建三间长方形种牛饲养室，饲养室的一面靠墙（墙长50 m），中间用两道墙隔开（如图）．已知计划中的建筑材料可建墙的总长度为48 m，则这三间长方形种牛饲养室的总占地面积的最大值为________m2．8．如图，在△ABC中，∠B=90°，AB=12 mm，BC=24 mm，动点P从点A开始沿边AB向点B以2 mm/s 的速度移动（不与点B重合），动点Q从点B开始沿边BC向点C以4 mm/s的速度移动（不与点C重合）．如果P，Q分别从A，B同时出发，那么经过________s，四边形APQC的面积最小．9．如图，小明的父亲在相距2 m的两棵树间拴了一根绳子，给他做了一个简易的秋千，拴绳子的地方距地面的高都是2.5 m，绳子自然下垂呈抛物线状，身高1 m的小明距较近的那棵树0.5 m时，头部刚好接触到绳子，则绳子的最低点距地面的距离为________m.10．若两个数的和为6，则这两个数的积最大可以达到________．11．某果园有90棵橘子树，平均每棵树结520个橘子．根据经验估计，每多种一棵橘子树，平均每棵树就会少结4个橘子．设果园里增种x棵橘子树，橘子总个数为y个，则果园里增种________棵橘子树时，橘子总个数最多．12．如图，正方形ABCD的边长为4，E，F分别是边BC，CD上的两个动点，且AE⊥EF，则AF的最小值是________．三、解答题13．为了改善小区环境，某小区决定要在一块一边靠墙（墙长25 m）的空地上修建一个矩形绿化带ABCD，绿化带一边靠墙，另三边用总长为40 m的栅栏围住（如图）．设绿化带的BC边长为x m，绿化带的面积为y m2．（1）求y与x之间的函数关系式，并写出自变量x的取值范围．（2）当x为何值时，绿化带的面积最大？14．某中学课外兴趣活动小组准备围建一个矩形苗圃，其中一边靠墙，另外三边由长为30 m的篱笆围成．已知墙长为18 m（如图），设这个苗圃垂直于墙的一边长为x m．（1）若苗圃的面积为72 m2，求x．（2）若平行于墙的一边长不小于8 m，这个苗圃的面积有最大值和最小值吗？如果有，求出最大值和最小值；如果没有，请说明理由．（3）当这个苗圃的面积不小于100 m2时，直接写出x的取值范围．15．如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE，ED，DB 组成，已知河底ED是水平的，ED=16 m，AE=8 m，抛物线的顶点C到ED的距离是11 m．以ED所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系．（1）求抛物线的函数表达式；（2）已知从某时刻开始的40 h内，水面与河底ED的距离h（m）随时间t（h）的变化满足函数表达式h=-（t-19）2+8（0≤t≤40），且当水面到顶点C的距离不大于5 m时，需禁止船只通行，请通过计算说明：在这一时段内，禁止船只通行的时间是多少．16．有这样一个例题：有一个窗户形状如图①，上部是一个半圆，下部是一个矩形．如果制作窗框的材料总长为6 m，如何设计这个窗户，才能使其透光面积最大？这个例题的答案是：当窗户半圆的半径约为0.35 m时，透光面积的最大值约为1.05 m2．我们如果改变这个窗户的形状，上部改为由两个正方形组成的矩形，如图②，材料总长仍为6 m．利用图③，解答下列问题：（1）若AB为1 m，求此时窗户的透光面积．（2）与例题比较，改变窗户的形状后，窗户透光面积的最大值有没有变大？请通过计算说明．17．某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量y（件）与销售单价x（元/件）符合一次函数y=kx+b，且当x=65时，y=55；x=75时，y=45．（1）求一次函数y=kx+b的表达式．（2）若该商场获得利润为W元，试写出利润W与销售单价x之间的关系式．当销售单价定为多少时，商场可获得最大利润，最大利润是多少？18．生物学家为了推测最适合某种珍奇植物生长的温度，将这种植物分别放在不同温度的环境中，经过一定时间测量出这种植物高度的增长情况（如下表）．（1）求y与x之间的函数表达式；（2）推测最适合这种植物生长的温度，并说明理由．19．在端午节前夕，三位同学到某超市调研一种进价为2元的粽子的销售情况．请根据小丽提供的信息，解答小明和小华提出的问题．20．经市场调查，某种商品在第x天的售价与销量的相关信息如下表：已知该商品的进价为每件30（1）求y与x之间的函数关系式．（2）销售该商品第几天时，当天销售的利润最大？最大利润是多少？21．某商贸公司购进某种水果的成本为20元/千克，经过市场调研发现，这种水果在未来48天的销售单价p（元/千克）与时间t（天）之间的函数关系式为且其日销售量y（千克）与时间t（天）的关系如下表：（1）已知y（2）问：哪一天的销售利润最大？最大日销售利润为多少？（3）在实际销售的前24天中，公司决定每销售1千克水果就捐款n元利润（n<9）给“精准扶贫”对象．现发现：在前24天中，每天扣除捐款后的日销售利润随时间t的增大而增大，求n的取值范围．答案一、1．C 2．C 3．C 4．A 5．C 6．A二、7．1448．39．0.5 10．9 11．20 12．5三、13．解：（1）∵四边形ABCD为矩形，BC=x m，∴AB=m．根据题意，得y=AB·BC=·x=-x2+20x（0<x≤25）．（2）∵y=-x2+20x=-（x-20）2+200，∴当x=20时，绿化带的面积最大．14．解：（1）苗圃与墙平行的一边长为（30-2x）m．由题意，得x（30-2x）=72，即x2-15x+36=0．解得x1=3（不符合题意，舍去），x2=12．即x的值为12．（2）依题意，得8≤30-2x≤18，解得6≤x≤11．面积S=x（30-2x）=-2（x-）2+（6≤x≤11）．①当x=时，S有最大值，S最大=m2；②当x=11时，S有最小值，S最小=11×（30-22）=88（m2）．（3）令x（30-2x）=100，得x2-15x+50=0．解得x1=5，x2=10．∴x的取值范围是5≤x≤10．15．解：（1）由题意可知，顶点C的坐标为（0，11）．设抛物线的函数表达式为y=ax2+11．由抛物线的对称性可知，点B的坐标为（8，8），∴8=64a+11，解得a=-，∴抛物线的函数表达式为y=-x2+11．（2）当水面到顶点C的距离不大于5 m时，h≥6．把h=6代入h=-（t-19）2+8（0≤t≤40），得t1=35，t2=3．∴禁止船只通行的时间为|t1-t2|=32（h）．答：禁止船只通行的时间为32 h．16．解：（1）由题意，得AD =m，∴此时窗户的透光面积为m2．（2）设AB=x m，则AD=（3-x）m．∵3-x>0，∴0<x<．设窗户的透光面积为S．由题意，得S=AB·AD=x（3-x）=-x2+3x=-（x-）2+．∵x=在0<x<内，∴当x=时，S最大值=m2>1.05 m2，∴与例题比较，现在窗户透光面积的最大值变大了．17．解：（1）根据题意，得解得∴一次函数的表达式为y=-x+120．（2）根据题意，得W=（x-60）（-x+120）=-x2+180x-7 200=-（x-90）2+900．∵抛物线的开口向下，∴当x<90时，W随x的增大而增大．又∵60≤x≤87，∴当x=87时，W最大= -（87-90）2+900=891．∴当销售单价定为87元/件时，商场可获得最大利润，最大利润是891元．18．解：（1）设y=ax2+bx+c（a≠0）．选（0，49），（2，41），（-2，49）分别代入，得解得∴y与x之间的函数表达式为y=-x2-2x+49．（2）最适合这种植物生长的温度是-1 ℃．理由：由（1）可知，当x=-=-1时，y取最大值50，即说明最适合这种植物生长的温度是-1 ℃．19．解：（1）小华的问题解答：设利润为W元，每个定价为x元，则W=（x-2）·[500-100（x-3）]=-100x2+1 000x-1 600=-100（x-5）2+900．当W=800时，解得x=4或x=6．因为2×240%=4.8（元），所以x=6不符合题意，舍去．故当每个定价为4元时，每天的利润为800元．（2）小明的问题解答：因为当x<5时，W随x的增大而增大，所以当x=4.8时，W最大，最大值为-100（4.8-5）2+900=896（元）．故800元的销售利润不是最多，当每个定价为4.8元时，才会使每天的利润最大．20．解：（1）当1≤x<50时，y=（200-2x）（x+40-30）=-2x2+180x+2 000．当50≤x≤90时，y=（200-2x）（90-30）=-120x+12 000．（2）当1≤x<50时，二次函数图象的开口向下，对称轴为直线x=-=45，∴当x=45时，y最大= -2×452+180×45+2 000=6 050．当50≤x≤90时，y随x的增大而减小，∴当x=50时，y最大=-120×50+12 000=6 000．综上所述，销售该商品第45天时，当天销售的利润最大，最大利润是6 050元．21．解：（1）由题意，得y=120-2t．当t=30时，y=120-60=60．答：在第30天的日销售量为60千克．（2）设日销售利润为W元，则W=（p-20）y．当1≤t≤24时，W=（t+30-20）（120-2t）=-t2+10t+1 200=-（t-10）2+1 250．当t=10时，W最大=1 250．当25≤t≤48时，W=（-t+48-20）（120-2t）=t2-116t+3 360=（t-58）2-4．由二次函数的图象及性质知，当t=25时，W最大=1 085．∵1 250>1 085，∴在第10天的销售利润最大，最大日销售利润为1 250元．（3）依题意，得每天扣除捐款后的日销售利润W=（t+30-20-n）（120-2t）=-t2+2（n+ 5）t+1 200-120n，其图象的对称轴为直线t=2n+10，要使W随t的增大而增大．由二次函数的图象及性质知，2n+10≥24，解得n≥7．又∵n<9，∴7≤n<9．2.5二次函数与一元二次方程一、选择题1．抛物线y=-3x2-x+4 与坐标轴的交点个数是（）A．3 B．2 C．1 D．02．若二次函数y=2x2+mx+8的图象如图，则m的值是（）A．-8 B．8 C．±8 D．63．若二次函数y=x2-4x+m（m为常数）的图象与x轴的一个交点为（1，0），则关于x的一元二次方程x2-4x+m=0的两个实数根是（）A．x1=1，x2=-1 B．x1=-1，x2=2 C．x1=-1，x2=0 D．x1=1，x2=34．若函数y=mx2+（m+2）x+m+1的图象与x轴只有一个交点，则m的值为（）A．0 B．0或2 C．2或-2 D．0，2或-25．若m，n（m<n）是关于x的方程1-（x-a）（x-b）=0的两根，且a<b，则a，b，m，n的大小关系是（）A．m<a<b<n B．a<m<n<b C．a<m<b<n D．m<a<n<b6．若二次函数y=x2-mx的图象的对称轴是直线x=2，则关于x的方程x2-mx=5的解为（）A．x1=1，x2=5 B．x1=1，x2=3C．x1=1，x2=-5 D．x1=-1，x2=57．如图，已知抛物线与x轴的一个交点为A（1，0），对称轴是直线x=-1，则抛物线与x轴的另一个交点坐标是（）A．（-3，0）B．（-2，0）C．（0，0）D．（2，0）8．下表是满足二次函数y=ax2+bx+c的五组数据，x1是方程ax2+bx+c=0的一个解，则下列选项正确的是（）A.1.6<x1<1.8 B．1119．根据关于x的二次函数y=x2+px+q，可列表如下：则方程x2+px+q=0A．解的整数部分是0，十分位是5 B．解的整数部分是0，十分位是8C．解的整数部分是1，十分位是1 D．解的整数部分是1，十分位是210．已知二次函数y=ax2+bx+c的y与x的部分对应值如下表，则下列判断正确的是（）A．抛物线开口向上C．当x=3时，y>0 D．方程ax2+bx+c=0的正根在2与3之间二、填空题11．若二次函数y=kx2-6x+3的图象与x轴有交点，则k的取值范围是______．12．如图，二次函数y=x2-4x+3的图象与x轴交于A，B两点，与y轴交于点C，则△ABC的面积为________．13．已知关于x的二次函数y=ax2+（a2-1）x-a的图象与x轴的一个交点的坐标为（m，0）．若2<m<3，则a的取值范围是________．14．抛物线y=x2-2x+0.5如图，利用图象可得方程x2-2x+0.5=0的近似解为________（结果精确到0.1）．15．如图，已知抛物线y=x2+bx+c经过点（0，-3），请你确定一个b的值，使该抛物线与x轴的一个交点在（1，0）和（3，0）之间．你所确定的b的值是________．三、解答题16．已知二次函数y=x2+4x+k-1.（1）若抛物线与x轴有两个不同的交点，求k的取值范围；（2）若抛物线的顶点在x轴上，求k的值．17．已知抛物线y=（x-m）2 -（x-m），其中m是常数．（1）求证：不论m为何值，该抛物线与x轴一定有两个公共点．（2）若该抛物线的对称轴为直线x =．①求该抛物线的函数表达式．②把该抛物线沿y轴向上平移多少个单位长度后，得到的抛物线与x轴只有一个公共点？18．利用二次函数的图象估计一元二次方程x2-2x-1=0的近似根（结果精确到0.1）．19．已知二次函数y=ax2+bx+c（a>0）的图象与x轴交于A（x1，0），B（x2，0）（x1<x2）两点，与y轴交于点C，x1，x2是方程x2+4x-5=0的两根．（1）若抛物线的顶点为D，求S△ABC：S△ACD的值；（2）若∠ADC=90°，求二次函数的表达式．参考答案一、1．A 2．B 3．D4．D 5．A 6．D 7．A8．C 9．C 10．D二、11．k≤3且k≠012．3 13．<a<或-3<a<-214．x1≈0.3，x2≈1.7 15．-三、16．解：（1）∵二次函数y=x2+4x+k-1的图象与x轴有两个交点，∴b2-4ac=42-4×1×（k-1）=20-4k>0，解得k<5．则k的取值范围为k<5．（2）根据题意，得==0，解得k=5．17．（1）证明：y=（x-m）2-（x-m）=x2-（2m+1）x+m2+m．∵Δ=（2m+1）2-4（m2+m）=1>0，∴不论m为何值，该抛物线与x轴一定有两个公共点．（2）解：①∵x=-=，∴m=2，∴抛物线的函数表达式为y=x2-5x+6．②设抛物线沿y轴向上平移k个单位长度后，得到的抛物线与x轴只有一个公共点，则平移后抛物线的函数表达式为y=x2-5x+6+k．∵抛物线y=x2－5x+6+k与x轴只有一个公共点，∴Δ=52-4（6+k）=0，解得k=．即把该抛物线沿y轴向上平移个单位长度后，得到的抛物线与x轴只有一个公共点．18．解：方程x2-2x-1=0的根是函数y=x2-2x-1的图象与x轴交点的横坐标．作出二次函数y=x2-2x-1的图象，如图．由图象可知，方程有两个根，一个在-1和0之间，另一个在2和3之间．先求-1和0之间的根，当x=-0.4时，y=-0.04；当x=-0.5时，y=0.25．因此，x≈-0.4是方程的一个近似根，同理可知，x≈2.4是方程的另一个近似根．即方程x2-2x-1=0的近似根为x1≈-0.4，x2≈2.4．19．解：（1）因为x2+4x-5=0的两根分别是x1=-5，x2=1，所以A，B两点的坐标分别为（-5，0），（1，0），所以抛物线的对称轴为直线x=-2．由二次函数的图象与一元二次方程的解的关系，可设二次函数的表达式为y=a（x2+4x-5）（a>0），则点C，D的坐标分别为C（0，-5a），D（-2，-9a），从而可画出大致图象，如图．所以S△ABC =AB·OC=15a．设AC与抛物线的对称轴交于点E，则由三角形相似，得点E的坐标为（-2，-3a），所以S△ACD = S△AED + S△DEC =（9a-3a）×3+（9a-3a）×2=15a．所以S△ABC ：S△ACD的值为1．（2）当∠ADC=90°时，△ADC是直角三角形，所以由勾股定理，得AC2=AD2+DC2．因为AC2=52+（5a）2，AD2=32+（9a）2，DC2=22+（9a-5a）2，所以52+（5a）2=32+（9a）2+22+（9a-5a）2，解得a=±（负值不符合题意，舍去）．所以二次函数的表达式为y=（x2+4x-5）=x2+x-．。

初中北师大版数学九年级下册2.1【同步练习】《二次函数》

《二次函数》同步练习1．下列函数解析式中，一定为二次函数的是（）A ．y =3x -1B ．y=a 2x +bx +cC ．s =22t -2t +1D ．y =2x +1x A ．y =2x B ．y ＝21xC ．y =k 2xD ．y =k 2x 4. 当m 不为何值时，函数y =（m -2）2x +4x -5（m 是常数）是二次函数（）A ．-2B ．2C ．3D ．-35. 在下列函数关系式中，y 是x 的二次函数的是（）A ．x y=6 B ．xy =-6 C ．2x +y =6 D ．y =-6x 6. 下列函数中，一定是二次函数的是（）A ．y ＝2xB ．y=a 2x +bx+cC ．y ＝21xD ．y=（k 2+1）x 7. 下列函数是二次函数的是（）A ．y =2x +1B ．y=a 2x -2x +1C ．y =2x +2D ．y =2x -18. 已知函数y =（m 2+m ）2x +mx +4为二次函数，则m 的取值范围是（）A ．m ≠0B ．m ≠-1C ．m ≠0，且m ≠-1D ．m =-19. 下列函数关系中，可以看做二次函数y=a 2x +bx+c 模型的是（）A ．在一定距离内，汽车行驶的速度与行驶的时间的关系B ．我国人中自然增长率为1%，这样我国总人口数随年份变化的关系C ．竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系（不计空气阻力）D ．圆的周长与半径之间的关系10. 下列各式中，y 是x 的二次函数的是（）A ． y=a 2x +bx+cB ．x 2+y -2=0C ．y 2-ax =-2D ．2x -y 2+1=011. 下列函数关系中，y 是x 的二次函数的是（）A ．y =2x +3B ．yC ．y=2x -1D ．y=21x +1 12. 下列函数中，是二次函数的为（）A ．y =82x +1B ．y =8x +1C ．y =8x D ．y =28x16.如果函数y =（a -1）x 是二次函数，那么a 的取值范围是________ 17.若y =（a -1）x 3a 2−1是关于x 的二次函数，则a =________18.若函数2213(3)m m y m x +-=-是二次函数，则m =________ 21. 当k 为何值时，函数2(1)1k k y k x +=-+为二次函数？2. 函数y =（kx -1）（x-3），当k 为何值时，y 是x 的一次函数？当k 为何值时，y 是x 的二次函数？23.若232(3)m m y m x -+=-是二次函数，求m 的值 24.已知2(1)mm y m x -=+是二次函数，求m 的值。

北师大版九年级数学下册第二章二次函数综合题同步练习

北师大版九年级数学下册第二章二次函数综合题同步练习一、选择题1、如图，一条抛物线与x 轴相交于A、B 两点（点A 在点B 的左侧），其顶点P 在线段MN 上移动．若点M、N 的坐标分别为（﹣1，﹣2）、（1，﹣2），点B 的横坐标的最大值为3，则点A 的横坐标的最小值为（）A．﹣3 B．﹣1 C．1 D．32、已知抛物线y=﹣x2+1 的顶点为P，点A 是第一象限内该二次函数图象上一点，过点A作x 轴的平行线交二次函数图象于点B，分别过点B、A 作x 轴的垂线，垂足分别为C、D，连结PA、PD，PD 交AB 于点E，△PAD 与△PEA 相似吗？（）A．始终不相似B．始终相似C．只有AB=AD 时相似D．无法确定3、如图，A1、A2、A3 是抛物线y=ax2（a＞0）上的三点，A1B1、A2B2、A3B3 分别垂直于x 轴，垂足为B1、B2、B3，直线A2B2 交线段A1A3 于点C．A1、A2、A3 三点的横坐标为连续整数n﹣1、n、n+1，则线段CA2 的长为（）A．a B．2a C．N D．n﹣14、如图，抛物线y=ax2+2ax+c（a＞0）与y 轴交于点C，与x 轴交于A、B 两点，A 点在B 点左侧．若点E 在x 轴上，点P 在抛物线上，且以A、C、E、P 为顶点的四边形是平行四边形，则符合条件的点P 有（）A ．1 个B ．2 个C ．3 个D ．4 个5、如图，抛物线 y=﹣x 2+2x+m+1 交 x 轴于点 A （a ，0）和 B （b ，0），交 y 轴于点 C ，抛物线的顶点为 D ，下列四个命题：①当 x ＞0 时，y ＞0；②若 a=﹣1，则 b=4；③抛物线上有两点 P （x 1，y 1）和 Q （x 2，y 2），若 x 1＜1＜x 2，且 x 1+x 2＞2，则 y 1＞y 2； ④点 C E ，点 G ，F 分别在 x 轴和 y 轴上，当 m=2 时，四边形 EDFG 周长的最小值为．其中真命题的序号是（）A ．①B ．②C ．③D ．④6、抛物线 y=ax 2+3ax+b 的一部分图象如图，设该抛物线与 x 轴的交点为 A （﹣5，0）和 B ，与 y 轴的交点为 C ，若△ACO ∽△CBO ，则∠CAB 的正切值为（）A B D ．77、如图，抛物线 y=x 2﹣12x ﹣32与直线 y=x ﹣2 交于 A 、B 两点（点 A 在点 B 的左侧），动点 P 从 A 点出发，先到达抛物线的对称轴上的某点 E ，再到达 x 轴上的某点 F ，最后运动到点 B ．若使点 P 运动的总路径最短，则点 P 运动的总路径的长为（）A ．2B ．3C ．52D ．538、如图，OABC 是边长为 1 的正方形，OC 与 x 轴正半轴的夹角为 15°，点 B 在抛物线 y=ax 2 （a ＜0）的图象上，则 a 的值为（）A．B．C．﹣2 D．9、如图，抛物线m：y=ax2+b（a＜0，b＞0）与x 轴于点A、B（点A 在点B 的左侧），与y 轴交于点C．将抛物线m 绕点B 旋转180°，得到新的抛物线n，它的顶点为C1，与x 轴的另一个交点为A1．若四边形AC1A1C 为矩形，则a，b 应满足的关系式为（）A．ab=﹣2 B．ab=﹣3 C．ab=﹣4 D．ab=﹣510、定义：若抛物线的顶点与x 轴的两个交点构成的三角形是直角三角形，则这种抛物线就称为：“美丽抛物线”．如图，直线l：y=x+b 经过点M（0，），一组抛物线的顶点B1（1，y1），B2（2，y2），B3（3，y3），…B n（n，y n）（n 为正整数），依次是直线l 上的点，这组抛物线与x 轴正半轴的交点依次是：A1（x1，0），A2（x2，0），A3（x3，0），…A n+1（x n+1，0）（n 为正整数）．若x1=d（0＜d＜1），当d 为（）时，这组抛物线中存在美丽抛物线．A．或B．或 C．或D．二、填空题11、如图，二次函数y=x2﹣4x+3 的图象交x 轴于A，B 两点，交y 轴于C，则△ABC 的面积为（）12、如图，在平面直角坐标系中，二次函数y=ax2+mc（a≠0）的图象经过正方形ABOC 的三个顶点，且ac=﹣2，则m 的值为.13、如图，一条抛物线与x 轴相交于A、B 两点，其顶点P 在折线C﹣D﹣E 上移动，若点C、D、E 的坐标分别为（﹣1，4）、（3，4）、（3，1），点B 的横坐标的最小值为1，则点A 的横坐标的最大值为.14、如图，点A，B 的坐标分别为（1，4）和（4，4），抛物线y=a（x﹣m）2+n 的顶点在线段AB 上运动，与x 轴交于C、D 两点（C 在D 的左侧），点C 的横坐标最小值为﹣3，则点D 的横坐标最大值为．15、如图，矩形ABCD 的长AB=6cm，宽AD=3cm．O 是AB 的中点，OP⊥AB，两半圆的直径分别为AO 与OB．抛物线y=ax2 经过C、D 两点，则图中阴影部分的面积是cm2．16、如图．抛物线y=﹣x2﹣2x+3 与x 轴相交于点A 和点B，与y 轴交于点C．设点M 是第=6，点M 的坐标为，若点P 在线段BA 上以每秒二象限内抛物线上的一点，且S△MA B1 个单位长度的速度从点B 向点A 运动（不与B，A 重合），同时，点Q 在射线AC 上以每秒2 个单位长度的速度从A 向C 运动．设运动的时间为t 秒，当t 为时，△APQ 的面积最大，最大面积是．三、解答题17、如图，已知抛物线y=﹣12x2+bx+c 与坐标轴分别交于点A（0，8）、B（8，0）和点E，动点C 从原点O 开始沿OA 方向以每秒1 个单位长度移动，动点D 从点B 开始沿BO 方向以每秒1 个单位长度移动，动点C、D 同时出发，当动点D 到达原点O 时，点C、D 停止运动．（1）直接写出抛物线的解析式：；（2）求△CED 的面积S 与D 点运动时间t 的函数解析式；当t 为何值时，△CED 的面积最大？最大面积是多少？（3）当△CED 的面积最大时，在抛物线上是否存在点P（点E 除外），使△PCD 的面积等于△CED 的最大面积？若存在，求出P 点的坐标；若不存在，请说明理由．18、如图，在直角坐标系中，抛物线经过点A（0，4），B（1，0），C（5，0），其对称轴与x 轴相交于点M．（1）求抛物线的解析式和对称轴；（2）在抛物线的对称轴上是否存在一点P，使△PAB 的周长最小？若存在，请求出点P 的坐标；若不存在，请说明理由；（3）连接AC，在直线AC 的下方的抛物线上，是否存在一点N，使△NAC 的面积最大？若存在，请求出点N 的坐标；若不存在，请说明理由．19、如图，已知抛物线y=x2﹣ax+a2﹣4a﹣4 与x 轴相交于点A 和点B，与y 轴相交于点D （0，8），直线DC 平行于x 轴，交抛物线于另一点C，动点P 以每秒2 个单位长度的速度从C 点出发，沿C→D 运动，同时，点Q 以每秒1 个单位长度的速度从点A 出发，沿A→B 运动，连接PQ、CB，设点P 运动的时间为t 秒、（1）求a 的值；（2）当四边形ODPQ 为矩形时，求这个矩形的面积；（3）当四边形PQBC 的面积等于14 时，求t 的值；（4）当t 为何值时，△PBQ 是等腰三角形？（直接写出答案）20、如图，已知抛物线y= 34x2+bx+c 与坐标轴交于A、B、C 三点，A 点的坐标为（﹣1，0），过点C 的直线334y xt=-与x 轴交于点Q，点P 是线段BC 上的一个动点，过P 作PH 垂直OB 于点H，若PB=5t，且0＜t＜1，是否存在使P，H，Q 为顶点的三角形与三角形COQ 相似的t 的值．21、如图，直线y=x+2 与抛物线y=ax2+bx+6（a≠0）相交于A（12，52）和B（4，m），点P是线段AB 上异于A、B 的动点，过点P 作PC⊥x 轴于点D，交抛物线于点C．（1）求抛物线的解析式；（2）是否存在这样的P 点，使线段PC 的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；（3）求△PAC 为直角三角形时点P 的坐标．22、已知在平面直角坐标系xOy 中，O 为坐标原点，线段AB 的两个端点A（0，2），B（1，0）分别在y 轴和x 轴的正半轴上，点C 为线段AB 的中点，现将线段BA 绕点B 按顺时针方向旋转90°得到线段BD，抛物线y=ax2+bx+c（a≠0）经过点D．（1）如图1，若该抛物线经过原点O，且a=﹣13．①求点D 的坐标及该抛物线的解析式；②连结CD，问：在抛物线上是否存在点P，使得∠POB 与∠BCD 互余？若存在，请求出所有满足条件的点P 的坐标，若不存在，请说明理由；（2）如图2，若该抛物线y=ax2+bx+c（a≠0）经过点E（1，1），点Q 在抛物线上，且满足∠QOB 与∠BCD 互余．若符合条件的Q 点的个数是4 个，请直接写出a 的取值范围．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 二次函数
一、选择题
1．2018·浦东新区一模下列函数中，是二次函数的是 ( )
A．y＝－4x＋5 B．y＝x(2x－3)
C．y＝(x＋4)2－x2 D．y＝1 x2
2．在一定条件下，若物体所经过的路程s(m)与运动时间t(s)之间的函数关系式为s＝5t2＋2t，则当t＝4时，该物体所经过的路程为( )
A．28 m B．48 m
C．68 m D．88 m
3．在下列4个不同的情境中，两个变量所满足的函数关系属于二次函数关系的有( )
①设正方形的边长为x，面积为y，则y与x之间的函数关系；
②x个球队参加比赛，每两个队之间比赛一场，则比赛的场次数y与x之间的函数关系；
③设正方体的棱长为x，表面积为y，则y与x之间的函数关系；
④若一辆汽车以120 km/h的速度匀速行驶，那么汽车行驶的里程y(km)与行驶时间x(h)之间的函数关系．
A．1个 B．2个
C．3个 D．4个
二、填空题
4．二次函数y＝2(3x－1)(2－x)化为一般式为____________，其中a＝________，b＝________，c＝________.
5．如果函数y＝(k－5)xk2－5k＋2＋kx＋3是二次函数，那么k的值是________．
6．某厂今年一月份新产品的研发资金为a元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年三月份新产品的研发资金y(元)关于x的函数表达式为y＝______________．7．如图K－8－1所示，在宽为20 m，长为32 m的矩形地面上修筑同样宽的两条互相垂直的道路，余下的部分作为耕地，若设耕地的面积为y m2，道路的宽为x m，则y与x之间的函数表达式为________________．(写出自变量的取值范围)
图K－8－1
三、解答题
8．已知函数y＝(m2－m)x2＋(m－1)x＋2－2m.
(1)若这个函数是二次函数，求m的取值范围；
(2)若这个函数是一次函数，求m的值；
(3)这个函数可能是正比例函数吗？为什么？
9\某工厂生产的某种产品按质量分为10个档次，第1档次(最低档次)的产品一天能生产95件，每件利润为6元．每提高一个档次，每件利润增加2元，但一天生产量减少5件．
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数，且1≤x≤10)，求出y关于x 的函数表达式；
(2)若生产第x档次的产品一天的总利润为1120元，求该产品的质量档次．
1．[解析] B A ．y ＝－4x ＋5是一次函数；B.y ＝x (2x －3)＝2x 2－3x 是二次函数；C.y ＝(x ＋
4)2－x 2＝8x ＋16是一次函数；D.y ＝1x 2不是二次函数．故选B. 2．[解析] D 把t ＝4代入s ＝5t 2
＋2t 中即可求出．
3．[解析] C ①依题意得：y ＝x 2，属于二次函数关系，符合题意；②依题意得：y ＝12
x (x －1)＝12x 2－12
x ，属于二次函数关系，符合题意；③依题意得：y ＝6x 2，属于二次函数关系，符合题意；④依题意得：y ＝120x ，属于一次函数关系，不符合题意．综上所述，两个变量所满足的函数关系属于二次函数关系的有3个．故选C.
4．[答案] y ＝－6x 2＋14x －4 －6 14 －4
[解析] y ＝2(3x －1)(2－x )＝2(－3x 2＋7x －2)＝－6x 2＋14x －4.
5．[答案] 0
[解析] 由题意，得k 2－5k ＋2＝2，解得k ＝0或k ＝5.又∵k －5≠0，∴k ≠5，∴当k ＝0时，
这个函数是二次函数．
6．[答案] a (1＋x )2
7．[答案] y ＝x 2－52x ＋640(0<x ≤20)
[解析] 如图所示，若把两条互相垂直的道路移到土地相邻的边上，剩余土地的宽为(20－x )m ，
长为(32－x )m ，则可得y ＝(20－x )(32－x )，即y ＝x 2－52x ＋640.由于该题是实际问题，因此x 的
取值要使实际问题有意义，即0<x ≤20.
8．解：(1)若这个函数是二次函数，则m 2－m ≠0，解得m ≠0且m ≠1；
(2)若这个函数是一次函数，则m 2－m ＝0，且m －1≠0，解得m ＝0.
(3)这个函数不可能是正比例函数．
理由：∵当此函数是一次函数时，m ＝0，而此时
2－2m ＝2≠0，
∴这个函数不可能是正比例函数．
9解：(1)∵第1档次的产品一天能生产95件，每件利润为6元，每提高一个档次，每件利润增加2元，但一天生产量减少5件，第x 档次比第1档次提高了(x －1)个档次，
∴y ＝[6＋2(x －1)][95－5(x －1)]，
即y ＝－10x 2＋180x ＋400(x 是正整数，且1≤x ≤10)．
(2)由题意可得－10x 2＋180x ＋400＝1120，
整理，得x 2－18x ＋72＝0，
解得x 1＝6，x 2＝12(舍去)．
答：该产品的质量档次为第6档．。