巩固练习- 函数的单调性-基础
高一函数的单调性-基础练习题含答案

人教A 版高中数学必修一第一章 《1.3函数的基本性质》练习题11.3.1函数的单调性[基础练习]1.判断1)(2-=xx f 在(0,+∞)上是增函数还是减函数 2.判断x x x f 2)(2+-=在( —∞,0)上是增函数还是减函数3.下列函数中,在(0,2)上为增函数的是( )(A )y=x1 (B ) y=2x-1 (C ) y=1-x (D )y=2)12(-x 4. 函数y=x1-1的单调 递 区间为 5.证明函数 f (x )=-2x +x 在(21,+∞)上为减函数[巩固练习]1.已知f (x )=(2k+1)x+1在(-∞,+∞)上是减函数,则( )(A )k >21 (B )k <21 (C )k >-21 (D k <-21 2.在区间(0,+∞)上不是增函数的是 ( ) (A )y=2x+1 (B )y=32x +1 (C )y=x 2 (D ) y=32x +x +1 3.若函数f (x )=2x +2(a-1)x+2在区间(-∞,4)上为增函数,则实数a 的取值范围是 ( )(A ) a ≤ -3 (B )a ≥-3 (C )a ≤ 3 (D )a ≥34.如果函数f (x )是实数集R 上的增函数,a 是实数,则 ( )(A )f (2a )>f (a+1) (B )f (a )< f (3a )(C )f (2a +a )>f (2a ) (D )f (2a -1)<f (2a )5.函数y=11+x 的单调减区间为 6.函数y=1+x +x -2的增区间为 减区间为7.证明:21)(x x f =在(0,+∞)上是减函数[能力提高]1.证明函数xx x f 1)(+=在(0,1)上是减函数2.定义域为R 的函数f (x )在区间( —∞,5)上单调递减,对注意实数t 都有)5()5(t f t f -=+,那么f (—1),f (9),f (13)的大小关系是 3.若f (x )是定义在[]1,1-上的减函数,f (x-1)<f (2x -1),求x 的取值范围答案[基础练习]1、增2、增3、B4、减,()0,∞-和()+∞,05、略[巩固练习]1、D2、C3、A4、D5、()1,-∞-和()+∞-,16、[)+∞,2,(]1,-∞-7、略[能力提高]1、略2、f(9)<f(—1)<f(13)3、(0,1)。
函数的单调性和奇偶性知识归纳和典型题型

奇函数在其对称区间[a,b]和[-b,-a]上具有相同的单调性,即已知 是奇函数,它在区间[a,b]上是增函数(减函数),则 在区间[-b,-a]上也是增函数(减函数);偶函数在其对称区间[a,b]和[-b,-a]上具有相反的单调性,即已知 是偶函数且在区间[a,b]上是增函数(减函数),则 在区间[-b,-a]上也是减函数(增函数).
若a>0,在区间 ,函数是减函数;在区间 ,函数是增函数;
若a<0,在区间 ,函数是增函数;在区间 ,函数是减函数.
要点三、一些常见结论
(1)若 是增函数,则 为减函数;若 是减函数,则 为增函数;
(2)若 和 均为增(或减)函数,则在 和 的公共定义域上 为增(或减)函数;
(3)若 且 为增函数,则函数 为增函数, 为减函数; 若 且 为减函数,则函数 为减函数, 为增函数.
(1) ; 1)x∈[5,10]; 2)x∈(-3,-2)∪(-2,1);
(2) ;
(3) ;
(4) .
举一反三:
【变式1】已知 当 的定义域为下列区间时,求函数的最大值和最小值.
(1)[0,3];(2)[-1,1];(3)[3,+∞).
例5.(2015 西安周至县一模)已知函数 ,x∈[―5,5],
(2) 存在 ,使得 ,那么,我们称 是函数的最大值(或最小值).
要点诠释:
①最值首先是一个函数值,即存在一个自变量 ,使 等于最值;
②对于定义域内的任意元素 ,都有 (或 ),“任意”两字不可省;
③使函数 取得最值的自变量的值有时可能不止一个;
④函数 在其定义域(某个区间)内的最大值的几何意义是图象上最高点的纵坐标;最小值的几何意义是图象上最低点的纵坐标.
《3.1.2函数的单调性》作业设计方案-高中数学人教B版19必修第一册

《3.1.2 函数的单调性》作业设计方案(第一课时)一、作业目标本作业设计旨在帮助学生巩固和深化对“函数的单调性”的理解,通过实际操作和练习,掌握判断函数单调性的方法和技巧,为后续学习打下坚实的基础。
二、作业内容1. 基础知识巩固- 要求学生复习函数单调性的定义,理解增函数和减函数的概念,并能够正确使用数学语言描述函数的单调性。
- 布置相关练习题,如填空题和选择题,考察学生对基本概念的掌握情况。
2. 函数单调性判断- 指导学生通过图像、导数、差分等方法判断函数的单调性。
- 设计一定数量的应用题,让学生在具体情境中应用单调性的概念。
3. 函数单调性与实际生活的联系- 通过实例分析,如气温变化、商品销售量与价格的关系等,让学生理解函数单调性在实际生活中的意义。
- 要求学生分析生活中的一些现象,用数学语言表达其单调性,并给出简要的解释。
4. 综合练习- 设计一组综合题目,涵盖函数单调性的判断、计算和实际应用等内容。
- 要求学生独立完成综合练习,并在课堂上进行讨论和交流。
三、作业要求1. 学生需在规定时间内独立完成作业,并保证答案的准确性和规范性。
2. 对于每个题目,学生需写出详细的解题步骤和思路,以便于教师了解学生的掌握情况。
3. 学生在完成作业过程中,应注重理解题目的意图和解题方法,而不仅仅是追求答案的正确性。
4. 对于涉及图像的题目,学生需使用数学软件绘制准确的函数图像,并标注关键点。
5. 学生在完成作业后,需进行自我检查和修正,确保答案的准确性。
四、作业评价1. 教师将根据学生的答案,对学生的理解和应用能力进行评估。
2. 教师将对解题步骤和思路的规范性、准确性和完整性进行评价。
3. 对于有创意的解题思路和方法,教师将给予额外的加分和表扬。
4. 对于存在的问题和不足,教师将给出具体的指导和建议。
五、作业反馈1. 教师将在课堂上对作业进行讲解和点评,帮助学生纠正错误并加深理解。
2. 学生需根据教师的反馈和建议,对作业进行修正和完善。
高一数学必修1第一章函数单调性-学生

教学目标1.了解函数单调性的概念,掌握判断简单函数单调性的方法2.能用文字语言和数学符号语言描述增函数、减函数、单调性等概念,能准确理解这些定义的本质特点重难点 3.会求一些简单函数的定义域、函数值。
【知识回顾与能力提升】1.函数的概念(1)函数的定义:设A,B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x),x∈A.(2)函数的定义域与值域:函数y=f(x)中,x叫做自变量,x的取值范围A叫做函数的定义域,与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.显然,值域是集合B 的子集.2.区间概念(a,b为实数,且a<b)定义名称符号数轴表示{x|a≤x≤b}闭区间[a,b]{x|a<x<b}开区间(a,b){x|a≤x<b}半开半闭区间[a,b){x|a<x≤b}半开半闭区间(a,b]3.其他区间的表示定义R{x|x≥a}{x|x>a}{x|x≤a}{x|x<a}符号(-∞,+∞)[a,+∞)(a,+∞)(-∞,a](-∞,a)4.函数相等如果两个函数定义域相同,并且对应关系完全一致,我们称这两个函数相等.【新知识梳理与重难点点睛】1.定义域为I的函数f(x)的增减性2.函数的单调性与单调区间如果函数y=f(x)在区间D上是增函数或减函数,就说函数y=f(x)在区间D上具有(严格)的单调性,区间D叫做y=f(x)的单调区间.要点一函数单调性的判定与证明例1求证:函数f(x)=1x2在(0,+∞)上是减函数,在(-∞,0)上是增函数.跟踪演练1已知函数f(x)=2-xx+1,证明:函数f(x)在(-1,+∞)上为减函数.A .(-∞,2]B .[2,+∞)C .[3,+∞)D .(-∞,3]3.已知函数f (x )是(-∞,+∞)上的增函数,若a ∈R ,则( ) A .f (a )>f (2a ) B .f (a 2)<f (a ) C .f (a +3)>f (a -2) D .f (6)>f (a )4.函数y =f (x )在R 上为增函数,且f (2m )>f (-m +9),则实数m 的取值范围是( ) A .(-∞,-3) B .(0,+∞) C .(3,+∞)D .(-∞,-3)∪(3,+∞)5.如图所示为函数y =f (x ),x ∈[-4,7]的图象,则函数f (x )的单调递增区间是________.【新方法、新技巧练习与巩固】一、基础达标1.下列说法中,正确的有( )①若任意x 1,x 2∈I ,当x 1<x 2时,f (x 1)-f (x 2)x 1-x 2>0,则y =f (x )在I 上是增函数;②函数y =x 2在R 上是增函数; ③函数y =-1x在定义域上是增函数;④函数y =1x 的单调区间是(-∞,0)∪(0,+∞).A .0个B .1个C .2个D .3个2.下列函数中,在区间(0,1)上是增函数的是( ) A .y =|x | B .y =3-x。
专题1第一章集合与函数的概念知识点与基础巩固题(原卷版)高一数学复习巩固练习(人教A版)
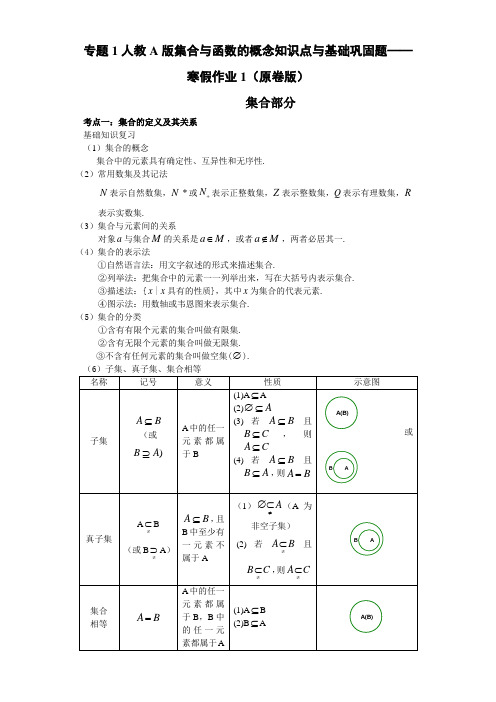
专题1人教A 版集合与函数的概念知识点与基础巩固题——寒假作业1(原卷版)集合部分考点一:集合的定义及其关系 基础知识复习 (1)集合的概念集合中的元素具有确定性、互异性和无序性. (2)常用数集及其记法N 表示自然数集,N *或N +表示正整数集,Z 表示整数集,Q 表示有理数集,R表示实数集.(3)集合与元素间的关系对象a 与集合M 的关系是a M ∈,或者a M ∉,两者必居其一. (4)集合的表示法①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合. ③描述法:{x |x 具有的性质},其中x 为集合的代表元素. ④图示法:用数轴或韦恩图来表示集合. (5)集合的分类①含有有限个元素的集合叫做有限集. ②含有无限个元素的集合叫做无限集. ③不含有任何元素的集合叫做空集(∅).(7)已知集合A 有(1)n n ≥个元素,则它有2n 个子集,它有21n -个真子集,它有21n -个非空子集,它有22n -非空真子集.考点二:集合的基本运算 基础知识复习1.交集的定义:一般地,由所有属于A 且属于B 的元素所组成的集合,叫做A,B 的交集.记作A ∩B(读作”A 交B ”),即A ∩B={x|x ∈A ,且x ∈B}.2、并集的定义:一般地,由所有属于集合A 或属于集合B 的元素所组成的集合,叫做A,B 的并集。
记作:A ∪B(读作”A 并B ”),即A ∪B={x|x ∈A ,或x ∈B}.3、交集与并集的性质:A ∩A = A ,A ∩φ= φ, A ∩B = B ∩A ,A ∪A = A ,A ∪φ= A , A ∪B = B ∪A.4、全集与补集(1)全集:如果集合S 含有我们所要研究的各个集合的全部元素,这个集合就可以看作一个全集。
通常用U 来表示。
(2)补集:设S 是一个集合,A 是S 的一个子集(即A ⊆S ),由S 中 所有不属于A 的元素组成的集合,叫做S 中子集A 的补集(或余集)。
高中数学高考总复习---函数的最值和及值巩固练习题(基础、提高)含答案解析

(Ⅰ)求 a、b 的值;
(Ⅱ)若对于任意的 x∈[0,3],都有 f(x)<c2 成立,求 c 的取值范围。
14.(2015 金凤区校级一模)已知函数
.
(1)求
的单调区间和极值;
(2)若对任意
,
恒成立,求实数 的最大值.
15. (2016 海淀区模拟)已知函数
.
(Ⅰ)当 时,求函数 的单调区间;
(Ⅱ)若关于 的不等式
14
②当
时,由(1)知
,
所以
随 的变化情况如下表:
0
0
↗
极大值
↘
极小值
↗
所以 的极大值点为 ,极小值点为 。
综上所述,当
时,
有一个极大值点
,没有极小值点;
当
时, 有一个极大值点 ,一个极小值点 。
16.【解析】
(1)由已知,函数 f(x)的定义域为(0,+∞),
,
所以
.
当
时,g(x)在区间
在区 间
上单调递减;
当
时,g(x)在区间(0,+∞)上单调递增.
(2)由
,解得
上单调递增, .
12
令
.
则 故存在 x0∈(1,e),使得 令
, .
,
由
知,函数 u(x)在区间(1,+∞)上单调递增.
所以
.
即 a0∈(0,1).
当 a=a0 时,有
,
由(1)知,函数 f'(x)在区间(1,+∞)上单调递增.
故当 x∈(1,x0)时,有 f'(x0)<0,从而 f(x)>f(x0)=0; 当 x∈(x0,+∞)时,有 f'(x0)>0,从而 f(x)>f(x0)=0; 所以,当 x∈(1,+∞)时,f(x)≥0.
2022年初升高暑期数学精品讲义专题11 函数的单调性与最值分层训练【含答案】

x
1 2
,
2
,使
2
x2
x
1
0
成立,则实数
的取值范围是
______________.
【答案】 (2 2, ) 【解析】 【分析】
利用不等式的基本性质分离参数,利用函数的单调性求相应最值即可得到结论. 【详解】 由 2x2 x 1 0 可得, x 2x2 1,
因为
x
1 2
,
2
,所以
2x
1 x
当 a 0 时,函数 f (x) 2x 1在 R 上单调递增,即 f (x) 在 , 6上递增,则 a 0 , 当 a 0 时,函数 f (x) 是二次函数,又 f (x) 在 , 6上单调递增,由二次函数性质知, a 0 ,
1 6
a 则有 a 0
1 a0
,解得 6
,
所以实数
a
的取值范围是
即 x x 2 ,平方后解得 x 1 .
所以 x 的取值范围为 (, 1) .
故选:B.
8.(2022·北京市房山区房山中学高二期中)若函数 f (x) x2 mx 10 在 (- 2,1) 上是增函数,则实数 m 的取
值范围是(
)
A.[2, +)
B.[4, +)
C. (, 2]
D. (, 4]
A
不正确;
对于 B,函数 y = x2 在区间 , 0上是减函数,故 B 正确;
对于 C,函数 y x3 在 , 0上是增函数,故 C 不正确;
对于 D,函数 y x 在 , 0上是增函数,故 D 不正确.
故选:B.
2.(2022·江苏·高一)已知函数 f x x2 2ax 4 在[0, ) 上是增函数,则实数 a 的取值范围为
三角函数总内容练习巩固

阶段滚动训练一(范围:§1.1~§1.3)一、选择题1.(2018·湖南衡阳二十六中高二期中)已知角α的终边经过点P ⎝⎛⎭⎫32,12,则cos α等于( )A.12B.32C.33 D .±122.角29π12的终边所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限3.(2018·河南林州第一中学高二期末)若角α是第二象限角,则α2是( )A .第一象限角B .第二象限角C .第一或第三象限角D .第二或第四象限角4.(2018·天津河东区高二期中)若θ是第二象限角,则下列选项中能确定为正值的是( ) A .sin θ2B .cos θ2C .tan θ2D .cos 2θ 5.n 为整数,化简sin (n π+α)cos (n π+α)的结果是( )A .±tan αB .-tan αC .tan αD .tan nα6.已知P (-3,y )为角β的终边上的一点,且sin β=1313,则2sin 2βsin 2β-cos 2β等于( )A .±12B .-211 C.36D .±27.若cos θ<0,且cos θ-sin θ=1-2sin θcos θ,那么θ是( ) A .第一象限角 B .第二象限角 C .第三象限角 D .第四象限角8.下列三角函数: ①sin ⎝⎛⎭⎫n π+43π; ②cos ⎝⎛⎭⎫2n π+π6; ③sin ⎝⎛⎭⎫2n π+π3; ④cos ⎣⎡⎦⎤(2n +1)π-π6; ⑤sin ⎣⎡⎦⎤(2n +1)π-π3(n ∈Z ). 其中与sin π3数值相同的是( )A .①②B .①③④C .②③⑤D .②③二、填空题9.下列说法中正确的有________.(写出所有正确说法的序号) ①正角的正弦值是正的,负角的正弦值是负的,零角的正弦值是零;②若有一三角形的两内角α,β满足sin α·cos β<0,则此三角形必为钝角三角形; ③对任意的角α,都有|sin α+cos α|=|sin α|+|cos α|;④对任意角α⎝⎛⎭⎫α≠k π2,k ∈Z ,都有⎪⎪⎪⎪tan α+1tan α=|tan α|+⎪⎪⎪⎪1tan α. 10.已知sin α=14,且α∈⎝⎛⎭⎫π2,π,则sin α-2cos 2α=________. 考点 运用基本关系式求三角函数值 题点 运用基本关系式求三角函数值11.sin 20°+cos 200°sin 340°-cos 160°+tan 19°+cos 341°tan 161°+cos 199°的值为________.12.已知角α的终边经过点P (m ,22),sin α=223且α为第二象限角.(1)求m 的值;(2)若tan β=2,求sin αcos β+3sin ⎝⎛⎭⎫π2-αsin βcos (π+α)cos (-β)-3sin αsin β的值.13.证明:(1)1-cos 2αsin α-cos α-sin α+cos αtan 2α-1=sin α+cos α; (2)(2-cos 2α)(2+tan 2α)=(1+2tan 2α)(2-sin 2α).14.已知集合M =⎩⎨⎧⎭⎬⎫x ⎪⎪ x =-2cos n π3,n ∈Z ,集合N =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪x =2sin 2n -36π,n ∈Z ,那么M 与N 之间的关系是( ) A .M N B .NMC .M ∩N =∅D .M =N15.化简:sin ⎝⎛⎭⎫4n -14π-α+cos ⎝⎛⎭⎫4n +14π-α(n ∈Z ).阶段滚动训练二(范围:§1.4~§1.5)1.(2018·江西景德镇一中高二期末)函数y =tan x ⎝⎛⎭⎫x ≠k π+π2,k ∈Z 的单调性为( ) A .在整个定义域上为增函数 B .在整个定义域上为减函数C .在每一个开区间⎝⎛⎭⎫-π2+k π,π2+k π(k ∈Z )上为增函数 D .在每一个开区间⎝⎛⎭⎫-π2+2k π,π2+2k π(k ∈Z )上为增函数2.已知函数y =sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2的部分图象如图所示,则( )A .ω=1,φ=π6B .ω=1,φ=-π6C .ω=2,φ=π6D .ω=2,φ=-π63.函数y =tan x +sin x -|tan x -sin x |在区间⎝⎛⎭⎫π2,3π2内的图象是( )4.函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2的部分函数图象如图所示,为了得到函数f (x )的图象,只需将g (x )=sin ωx 的图象( )A .向右平移π6个单位长度B .向右平移5π6个单位长度C .向左平移π6个单位长度D .向左平移5π6个单位长度5.设点P 是函数f (x )=sin ωx 的图象C 的一个对称中心,若点P 到图象C 的对称轴的距离的最小值为π4,则f (x )的最小正周期为( )A .2πB .π C.π2 D.π46.已知函数f (x )=A cos(ωx +φ)(A >0,ω>0)的部分图象如图所示,f ⎝⎛⎭⎫π2=-23,则f (0)等于( )A .-23 B.23 C .-12 D.127.函数f (x )=⎝⎛⎭⎫1-21+2x tan x 的图象( )A .关于x 轴对称B .关于y 轴对称C .关于直线y =x 对称D .关于原点对称8.函数f (x )=M sin(ωx +φ)(ω>0)在区间(a ,b )上是增函数,且f (a )=-M ,f (b )=M ,则函数g (x )=M cos(ωx +φ)在[a ,b ]上( ) A .是增函数B .是减函数C .可以取到最大值MD .可以取到最小值-M9.方程2x =cos x 解的个数为( ) A .1 B .2 C .0 D .无数个二、填空题10.(2018·福建闽侯第八中学高二期末)函数y =lg(sin x -cos x )的定义域为________. 11.若f (x )=2sin(ωx +φ)+m ,对任意实数t 都有f ⎝⎛⎭⎫π8+t =f ⎝⎛⎭⎫π8-t ,且f ⎝⎛⎭⎫π8=-3,则实数m 的值等于________.12.函数y =cos(2x +φ)(-π≤φ<π)的图象向右平移π2个单位长度后,与函数y =sin ⎝⎛⎭⎫2x +π3的图象重合,则φ=________.三、解答题13.求函数y =sin ⎝⎛⎭⎫π3+4x +cos ⎝⎛⎭⎫4x -π6的周期、单调区间及最大值、最小值.14.已知函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫A >0,ω>0,|φ|<π2的部分图象如图所示.(1)求函数f (x )的解析式;(2)设112π<x <1112π,且方程f (x )=m 有两个不同的实数根,求实数m 的取值范围和这两个根的和.15.已知函数f (x )=2cos ωx ,且函数y =f (x )图象的两相邻对称轴间的距离为π2.(1)求f ⎝⎛⎭⎫π8的值;(2)将函数y =f (x )的图象向右平移π6个单位长度后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y =g (x )的图象,求g (x )的单调递减区间.阶段滚动训练三(范围:§1.1~§1.5)一、选择题1.若sin(π-θ)<0,tan(π+θ)>0,则θ的终边在( ) A .第一象限 B .第二象限C .第三象限D .第四象限2.已知角α的终边上一点的坐标为⎝⎛⎭⎫sin 2π3,cos 2π3,则角α的最小正值为( ) A.5π6 B.2π3 C.4π3 D.11π63.函数y =2cos x -1的最大值、最小值分别是( ) A .2,-2 B .1,-3 C .1,-1 D .2,-14.若函数f (x )=2sin(ωx +φ)对任意x 都有f ⎝⎛⎭⎫π3+x =f (-x ),则f ⎝⎛⎭⎫π6等于( ) A .2或0 B .0 C .-2或0D .-2或2 5.若cos ⎝⎛⎭⎫3π2-α=-53,则sin(-5π+α)等于( ) A.23 B .-23 C.53 D .-536.已知tan α=3,则sin αcos α等于( ) A.310 B.35 C.710 D.457.已知a 是实数,则函数f (x )=1+a sin ax 的图象不可能是( )二、填空题8.函数y =2sin ⎝⎛⎭⎫m 3x +π3的最小正周期在⎝⎛⎭⎫23,34内,则正整数m 的值是________. 9.函数y =f (x )=A sin(ωx +φ)⎝⎛⎭⎫A >0,ω>0,|φ|<π2的部分图象如图所示,则f (1)+f (2)+f (3)+…+f (2 018)+f (2 019)的值等于________.10.已知一扇形的弧所对的圆心角为54°,半径r =20 cm ,则扇形的周长为________ cm. 11.已知函数f (x ),任意x 1,x 2∈⎝⎛⎭⎫-π2,π2(x 1≠x 2),给出下列结论: ①f (x +π)=f (x );②f (-x )=f (x );③f (0)=1; ④f (x 1)-f (x 2)x 1-x 2>0;⑤f ⎝⎛⎭⎫x 1+x 22>f (x 1)+f (x 2)2.当f (x )=tan x 时,正确结论的序号为________.12.关于函数f (x )=4sin ⎝⎛⎭⎫2x -π3(x ∈R ),有下列说法:①y =f ⎝⎛⎭⎫x +43π为偶函数; ②要得到函数g (x )=-4sin 2x 的图象,只需将f (x )的图象向右平移π3个单位长度; ③y =f (x )的图象关于直线x =-π12对称; ④y =f (x )在[0,2π]内的增区间为⎣⎡⎦⎤0,512π和⎣⎡⎦⎤1112π,2π. 其中正确说法的序号为________.三、解答题13.已知扇形AOB 的周长为10 cm.(1)若这个扇形的面积为4 cm 2,求扇形圆心角的弧度数;(2)求该扇形的面积取得最大值时圆心角的大小及弧长.14.设f (x )=4sin ⎝⎛⎭⎫2x -π3+ 3. (1)求f (x )在⎣⎡⎦⎤0,π2上的最大值和最小值; (2)把y =f (x )的图象上的所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移2π3个单位长度,得到函数y =g (x )的图象,求g (x )的单调递减区间.15.已知函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π),在同一周期内,当x =π12时,f (x )取得最大值3;当x =7π12时,f (x )取得最小值-3. (1)求函数f (x )的解析式;(2)求函数f (x )的单调递减区间;(3)若x ∈⎣⎡⎦⎤-π3,π6时,函数h (x )=2f (x )+1-m 有两个零点,求实数m 的取值范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【巩固练习】
1.定义域R 上的函数()f x 对任意两个不相等的实数,a b ,总有
()()0f a f b a b ->-,则必有( ) A .函数()f x 先增后减
B .函数()f x 先减后增
C .函数()f x 是R 上的增函数
D .函数()f x 是R 上的减函数
2.在区间)0,(-∞上为增函数的是( )
A .1=y
B .21+-=x x y
C .122---=x x y
D .21x y +=
3.函数()(2)f x x x =--的一个单调递减区间可以是( )
A.[-2,0]
B.[0,2]
C.[1,3]
D. [0,+∞)
4.若函数2
()2(1)2f x x a x =+-+在区间(],4-∞上是减函数,则实数a 的取值范围是( ) A.3a ≥ B. 3a ≤ C. 3a ≥- D. 3a ≤-
5.函数y =( )
A .(
]2,∞- B .(]
2,0 C .[)
+∞,2 D .[)+∞,0
6.设0a >,函数2()f x ax bx c =++的图象关于直线1x =对称,则(1),f f f 之间的大小
关系是( )
A. (1)f f f <<
B. (1)f f f <<
C. (1)f f f <<
D. (1)f f f <<
7.函数11
y x =-的单调区间是____________________.
8.函数2y x =+____________.
9.若函数2()23f x x px =++在(],1-∞上是减函数,[)1,+∞是增函数,则p = .
10.已知一次函数(1)y k x k =++在R 上是增函数,且其图象与x 轴的正半轴相交,则k 的取值范围
是 .
11.已知函数2
()(0)f x ax bx c a =++≠是(,0)-∞上的减函数,且()f x 的最小值为正数,则()f x 的解析式可以为 .(只要写出一个符合题意的解析式即可,不必考虑所有可能情形)
12.设a R ∈,判断函数()(2)3()f x a x x R =++∈的单调性,并写出单调区间.
13.已知函数()f x 的定义域为()1,1-,且同时满足下列条件:(1)()f x 是奇函数;(2)()f x 在定义域上单调递减;(3)2(1)(1)0,f a f a -+-<求a 的取值范围.
14.已知函数[]2()22,5,5f x x ax x =++∈-.
① 当1a =-时,求函数的最大值和最小值;
② 求实数a 的取值范围,使()y f x =在区间[]5,5-上是单调函数. 【答案与解析】
1. 【答案】C. 【解析】由()()0f a f b a b
->-知,当a b >时,()()f a f b >,当a b <时,()()f a f b <,所以()f x 在R 上单调递增,故选C.
2. 【答案】B. 【解析】2121111
x x y x x x -=+==-+---,故选B . 3. 【答案】C. 【解析】函数2()(1)1f x x =--+,图象开口向下,对称轴是1x =,故选C.
4. 【答案】D.
【解析】 函数的对称轴是1x a =-,依题意,14a -≥,解得3a ≤-.
5. 【答案】B.
【解析】 1
y x =
≥,y 是x 的减函数,当1,x y y ==<≤ 6. 【答案】A.
【解析】 由于0a >,且函数2()f x ax bx c =++图象的对称轴为1,x =所以函数()f x 在[)1,+∞上
单调递减.因为1<<(1)f f f <<.
7.【答案】()(),1,1,-∞+∞
【解析】 函数11y x =-的图象是由函数1y x =的图象向右平移1个单位得到的,故把1y x
=的单调区间向右平移1个单位即可.
8. 【答案】[2,)-+∞
【解析】 1,x y ≥-是x 的增函数,当1x =-时,min 2y =-.
9. 【答案】-4
【解析】依题意函数的对称轴是1x =,所以14
p -
=. 10. 【答案】10k -<< 【解析】 依题意10,01
k k k +>⎧⎪-⎨>⎪+⎩ ,解得10k -<<. 11. 【答案】答案不唯一,如2
()1f x x =+等.
12.【答案】
【解析】当2a >-时,此函数为R 上的增函数;
当2a =-时,函数(即为3y =)为常数函数,不具有单调性; 当2a <-时,此函数为R 上的减函数. 13.【解析】22(1)(1)(1)f a f a f a -<--=-,则2211111111a a a a -<-<⎧⎪-<-<⎨⎪->-⎩
,
∴01a <<
14.【解析】2
(1)1,()22,a f x x x =-=-+对称轴min max 1,()(1)1,()(5)37x f x f f x f ===== ∴max m ()37,()1in f x f x ==
(2)对称轴,x a =-当5a -≤-或5a -≥时,()f x 在[]5,5-上单调 ∴5a ≥或5a ≤-.。
