求圆中阴影部分的面积讲解
圆求阴影部分面积方法

学生姓名:年级:课时数:辅导科目:数学学科教师:课题求阴影部分面积方法专题授课日期及其时段教学内容一、阴影部分面积的求法(一)、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,右图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了。
(二)、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,右图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可。
(三)、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分析发现它是一个底2,高4的三角形,就可以直接求面积了。
(四)、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求右图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了。
(五)、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可。
如右图,右图中大小正方形的边长分别是9厘米和5厘米,求阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便.(六)、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如右图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半.(七)、平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.例如,如上页最后一图,欲求阴影部分面积,可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
求圆的阴影面积和周长

求圆的阴影面积和周长圆是几何学中最基本的图形之一,它具有许多有趣的性质和应用。
在本文中,我们将讨论圆的阴影面积和周长,并且提供一些计算方法和实际应用的指导。
首先,让我们来了解一下圆的定义。
圆是由一个连续的点组成的,这些点与一个固定点的距离是相等的。
这个固定点称为圆心,距离被称为半径。
圆可以在平面上任何位置,不过在计算阴影面积和周长时,我们通常使用标准的圆形。
阴影面积是圆在光照下产生的暗部的面积。
想象一下,当太阳光投射到一个圆形物体上时,它在圆的背面产生了一个阴影。
阴影面积可以通过将整个圆的面积减去光线照射到的部分来计算出来。
圆的面积公式是πr²(其中,π约等于3.14,r为圆的半径)。
因此,阴影面积可以表示为A = πr² - 光线照射到的部分的面积。
接下来,让我们谈谈圆的周长。
周长是圆形物体边界的长度。
描述一下,就是画一条线沿着圆的外部边界走一圈,这条线的长度就是圆的周长。
圆的周长公式是2πr。
其中,π约等于3.14,r为圆的半径。
计算圆的阴影面积和周长可以通过以下步骤来完成:1. 确定圆的半径:测量或已知圆的半径大小。
2. 使用公式计算阴影面积:使用公式A = πr²计算圆的面积。
3. 确定光线照射的部分:根据实际情况确定光线照射到的部分的面积。
4. 计算阴影面积:将整个圆的面积减去光线照射到的部分的面积,得到阴影面积。
5. 使用公式计算周长:使用公式C = 2πr计算圆的周长。
圆的阴影面积和周长在生活中有许多应用。
例如,在建筑设计中,当考虑建筑物遮阳和采光的影响时,需要计算圆的阴影面积。
此外,圆的周长用于计算各种环形物体的长度,如车轮、圆形跑道、自行车轮胎等。
总结起来,圆的阴影面积和周长是计算圆形物体的重要指标。
通过了解圆的定义和相应的公式,我们可以准确计算阴影面积和周长,并将其应用于日常生活和实际问题中。
五年级《圆》求阴影部分面积的十大方法
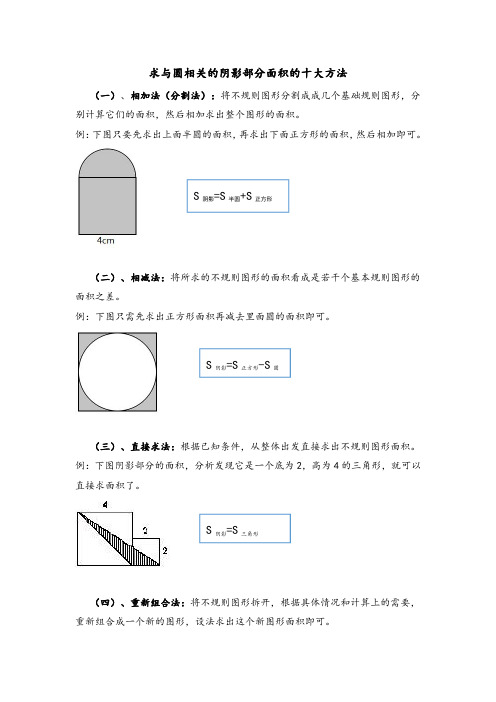
求与圆相关的阴影部分面积的十大方法(一)、相加法(分割法):将不规则图形分割成成几个基础规则图形,分别计算它们的面积,然后相加求出整个图形的面积。
例:下图只要先求出上面半圆的面积,再求出下面正方形的面积,然后相加即可。
(二)、相减法:将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。
例:下图只需先求出正方形面积再减去里面圆的面积即可。
(三)、直接求法:根据已知条件,从整体出发直接求出不规则图形面积。
例:下图阴影部分的面积,分析发现它是一个底为2,高为4的三角形,就可以直接求面积了。
(四)、重新组合法:将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可。
S 阴影=S 半圆+S 正方形S 阴影=S 正方形-S 圆S 阴影=S 三角形例:下图可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了。
(五)、辅助线法:根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可。
例:下图虽然可以用相减法解决,但不如添加一条辅助线后用直接法计算2个三角形面积之和更简便。
(六)、割补法:把原图形的一部分切割下来,补在图形中的另一部分,使之成为规则图形,从而使问题得到解决。
例:下图只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半。
(七)、平移法:将图形中某一部分切割下来,平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积。
S 阴影=S 正方形-S 圆S 阴影=S 正方形÷2S 阴影=S 三角形①+S 三角形②例:下图可先沿中间切开,把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
(八)、旋转法:将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度,贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积。
专题8 巧求圆中阴影部分的面积(含答案)

专题8 巧求圆中阴影部分的面积【知识解读】求与圆有关的阴影部分的面积,能考查同学们的观察能力、随机应变能力和综合运用数学知识的能力,解答此类问题要注意观察和分析图形的形成,学会分解和组合图形,消除思路中的“阴影”,明确要计算图形的面积,可以通过哪些图形的和或差得到,就能给解决问题带来一片光明,切勿盲目计算;下面介绍几种常用的解法.培优学案【典例示范】等积变换法:是在不改变图形面积的前提下,利用“等底、等高的两个三角形的面积相等”,将不规则图形转化为规则图形的面积来求解的方法.例1 如图1-8-1,点P 是半径为1的⊙O 外一点,OP =2,P A 切⊙O 于点A ,弦AB ∥OP ,连接PB ,则图中阴影部分的面积是.图181AB OP图182ABCDEMNO【跟踪训练】如图1-8-2,AB 是⊙O 的直径,MN 是⊙O 的切线,C 为切点,过点A 作AD ⊥MN 于点D ,交⊙O 于点E .已知AB =6,BC =3,求图中阴影部分的面积.【解答】和差法:是指将阴影部分看作两个规则图形的和或差.例2 如图1-8-3,扇形OAB 中,∠AOB =60°,扇形半径为4,点C 在BC 上,CD ⊥OA ,垂足为点D ,当CD =OD 时,图中阴影部分的面积为.图183BCD图184CEF【跟踪训练】如图1-8-4,在等腰直角三角形ABC 中,∠C =90°,点D 为AB 的中点,已知扇形EAD 和扇形FBD 的圆心分别为点A 、点B ,且AC =2,则图中阴影部分的面积为(结果不取近似值).割补法:是在不改变图形面积的前提下,通过割补,将发散的图形面积集中在一起,把不规则的图形凑合成规则图形的方法.例3 如图1-8-5,半径为2cm ,圆心角为90°的扇形OAB 中,分别以OA ,OB 为直径作半圆,则图中阴影部分的面积为cm 2.图185ABO图186A 'O 'O ABC【跟踪训练】如图1-8-6,将半圆O 绕直径AB 的端点B 逆时针旋转30°,得到半圆O ′,A ′B 交直径AB 于点C ,若BC =23,则图中阴影部分的面积为 .【提示】连接O ′C ,A ′C ,将阴影部分的面积通过割补,转化为△BO ′C 的面积加上扇形O ′AC 的面积.特殊位置法:是在不改变题意的前提下,通过取特殊位置,将图形特殊化,以方便求解.例4 如图1-8-7,一个半径为r 的圆形纸片在边长为a (a >3r )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“接触不到的部分”的面积是()A .23r πB 233π- C .()233r πD .2r π【提示】解答本题的关键是搞清楚圆形纸片“不能接触到的部分”的面积,即圆形纸片与正三角形的相邻两边都相切时,两切点与正三角形的一个顶点形成的曲边三角形的面积.图187图188【跟踪训练】如图1-8-8,一张半径为1的圆形纸片在边长为a (a ≥3)的正方形内任意移动,则该正方形内,这张圆形纸片“不能接触到的部分”的面积是() A .2a π-B .()24a π-C .πD .4π-整体代换法:是指在解答过程中,可将某些不易求的且不发生变化的量看作整体处理. 例5 如图1-8-9,在Rt △ABC 中,∠C =90°,CA =CB =4,分别以A ,B ,C 为圆心,以12AC 为半径画弧,三条弧与边AB 所围成的阴影部分的面积是.图189CBA【提示】直接求阴影部分的面积是不可能的,根据题意结合图形,知阴影部分的面积等于直角三角形的面积减去三个扇形的面积,其中A ,B 两个扇形的面积无法直接求出,但若把它们看作一个“整体”,则问题易求.【跟踪训练】1.如图1-8-10,正方形的边长a ,以各边为直径在正方形内画半圆,则图中阴影部分的面积为 . 【提示】图中阴影部分的面积可以看作四个半圆的面积之和与正方形的面积之差.CBAOFEDCBA2.如图1-8-11,⊙A ,⊙B ,⊙C 两两不相交,且半径都是2cm ,则图中三个扇形(即阴影部分)面积之和是 cm 2.【提示】图中3个扇形正好拼成一个圆心角为180°的大扇形。
初三数学圆阴影部分面积10种解题方法

初三数学圆阴影部分面积10种解题方法01和差法对于不规则图形实施分割、叠合后,把所求的图形面积用规则图形面积的和、差表示,再求面积.贵港中考如图1,在扇形OAB中,C是OA的中点,CD⊥OA,CD与弧AB交于点D,以O为圆心,OC的长为半径作弧CE交OB于点E,若OA= 4,∠AOB=120°,则图中阴影部分的面积为( 结果保留π) .图1解析: 图形中的阴影部分是不规则图形,较难直接计算.注意到阴影部分是环形BECA的一部分,因此阴影部分面积等于环形BECA的面积减去图形DCA的面积,又图形DCA的面积等于扇形DOA 的面积减去△ODC的面积.图2如图2,连接OD交弧CE于M.因为OA=4,C是OA的中点,CD⊥OA,所以OD=4,OC=2,DC=2√3,所以∠ODC=30°,∠DOC=60°02割补法对图形合理分割,把不规则图形补、拼成规则图形会,再求面积.吉林中考如图3,将半径为3的圆形纸片,按下列顺序折叠,若弧AB和弧BC都经过圆心O,则阴影部分的面积是( 结果保留π) .图3解析: 观察图形可以发现: 下方树叶形阴影部分的面积分成左右两块后,可以补到上方两个空白的新月形的位置.是否能够完全重合,通过计算验证即可.图4如图4,过点O作OD⊥AB于D,连接OA、OC、OB.由折叠性质知OD=1/2r=1/2AO,03等积变形法运用平行线性质或其他几何图形性质把不规则图形面积转化为与它等面积的规则图形来进行计算.天水中考如图5,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B、E 是半圆弧的三等分点,弧BE的长为2π/3,则阴影部分的面积为图5解析: 阴影部分是Rt△ABC的一部分,运用平行线的性质可将图形ABE面积转化成扇形BOE面积.连接BD、BE、BO、OE,如图6.图6因为点E、B是半圆弧的三等分点,所以∠DOB=∠BOE=∠EOA=60°,所以∠BAD=∠EBA=∠BAE=30°,所以BE∥AD.04平移法一些图形看似不规则,将某一个图形进行平移变换后,利用平移的性质,把不规则的图形的面积转化为规则图形的面积来计算.2019年黄石中考模拟如图7,从大半圆中剪去一个小半圆( 小半圆的直径在大半圆的直径MN上),点O为大半圆的圆心,AB是大半圆的弦,且与小半圆相切,AB∥MN,已知AB=12cm,则阴影部分的面积是.图7解析: 因为AB∥MN,由平行线间的距离处处相等,可以平移小半圆,使小半圆的圆心与大半圆的圆心重合,这样不规则的阴影图形就变成一个环形.图8如图8.过点O作OC⊥AB,垂足为C,连接OB,设大半圆的半径为R,小半圆的半径为r.05旋转法一些图形看似不规则,把某个图形进行旋转变换后,利用旋转的性质,把不规则图形的面积转化为规则图形的面积,再进行计算.安顺中考如图9,矩形ABCD中,BC=2,DC=4,以AB 为直径的⊙O与DC相切于点E,则阴影部分的面积为图9解析: 若直接利用弓形面积公式求解相当繁琐,根据已知条件及圆的旋转不变性,利用图形的旋转可实现解题.图10如图10,连接OE 交BD于M.因为CD 是⊙O 的切线,所以OE⊥CD,又AB∥CD,则OE⊥AB,而OE=OB,易知△OBM ≌△EDM,把△OBM绕点M旋转180°就会转到△EDM,阴影部分就转化为扇形BOE,恰好是半径为2的圆的四分之一,06对称法一些图形看似不规则,利用轴对称和中心对称的性质,把不规则图形进行轴对称和中心对称变换,转化为规则图形的面积,再进行计算.赤峰中考如图11,反比例函数y=k/x( k>0) 的图象与以原点(0,0)为圆心的圆交A、B两点,且A( 1,√3) ,图中阴影部分的面积等于 (结果保留π) .图11解析: 根据反比例函数图象及圆的对称性———既是轴对称图形,又是中心对称图形,可知图中两个阴影面积的和等于扇形AOB的面积.过点A作AD⊥x轴于D,如图12.图12因为A( 1,√3) ,所以∠AOD=60°,OA=2,又因为点A、B关于直线y=x对称,所以∠AOB=2×( 60°-45°)=30°.07整体法当已知条件不能或不足以直接求解时,可整体思考,化单一、分散为整体,把所求的未知量整体转换为已知量,再将问题整体化求解.安徽中考如图13,半径均为1的⊙A、⊙B、⊙C、⊙D、⊙E两两外离,A、B、C、D、E分别为五边形的五个顶点,则图中阴影部分的面积是图13解析: 由已知条件,分别求阴影部分的圆心角不易求得,但将五个扇形的圆心角合为一整体,它们的圆心角的和也是五边形的外角之和360°,所以阴影部分面积是一个整圆的面积,所以S阴影=π.08方程法有些图形的局部可以看成某个规则图形,或某些图形具有等面积的性质,这时可以把它们的关系用方程( 组) 来表示,再解方程( 组) ,求出图形的面积.2019年武汉模拟如图14,在边长为2的正方形ABCD 中,分别以2为半径,A、B、C、D 为圆心作弧,则阴影部分的面积是 ( 结果保留π) .图14解析: 仔细观察图形,有两种相同特征的图形在正方形内部,一起围成所求的阴影部分.设弧AC与弧BD交于点G,连接BE、EC,如图15.图15设形如AED 图形的面积为x,形如DEG 图形的面积为y,那么S阴影= S正-4 ( x+y) ,只需求出(x+y)的结果即可.09推算法某些题目运用已知条件,和图形的性质或定理进行推理,可把阴影部分面积用某个式子表示,从而求得不规则图形的面积.南宁中考如图16,Rt△ABC 中,AC=8,BC=6,∠C=90°,分别以AB、BC、AC 为直径作三个半圆,那么阴影部分的面积为平方单位.图16解析: 设左边阴影部分面积为S1,右边阴影部分面积为S2,整个图形的面积可以表示成: 以AC 为直径的半圆+ 以BC为直径的半圆+△ABC.也可以表示成: S1+S2+以AB为直径的半圆。
圆求阴影部分面积方法

圆求阴影部分面积方法圆的阴影部分面积可以通过多种方法求解。
下面将介绍两种常用的方法:几何解法和积分解法。
1.几何解法:首先,我们需要明确阴影的形成原理。
当一个圆形物体在光源的照射下,会在其周围产生一个暗影区域。
暗影区域形状类似于圆形,阴影的大小与光源与圆心之间的位置有关。
在这个问题中,我们假设光源位于圆的正上方,圆位于坐标原点(0,0),光源到圆心的距离为r,圆的半径为R。
首先,我们可以将圆分为四个象限,每个象限的阴影部分面积相同。
以第一象限为例,阴影部分面积可以通过扇形面积和三角形面积之和求解。
扇形面积的计算公式为:A1 = πR^2 θ / 360°,其中θ为扇形的圆心角,可以通过余弦定理计算得到:cosθ = r / (r+R)。
将θ代入公式可得:A1 = πR^2 cosθ。
三角形面积的计算公式为:A2 = (1/2)R^2 sinθ。
四个象限的阴影部分面积之和即为圆的阴影部分面积:A = 4(A1 +A2) = 4(πR^2 cosθ + (1/2)R^2 sinθ)。
2.积分解法:在这种方法中,我们将阴影部分分为无限多个面积微元,然后对每个面积微元求和来计算阴影部分的总面积。
设一些面积微元的宽度为dx,圆上该位置的半径为r(x),根据图形关系可知,r(x) = (R/x) * sqrt(x^2 - r^2)。
那么微元dA的面积可以表示为:dA = 2πr(x)dx,由此可得阴影部分面积的积分公式为:A =∫dA = ∫2πr(x)dx。
所以,我们需要确定积分的上下限。
当x从-r到r变化时,即为圆的直径上的每个点,阴影部分面积的范围。
将r(x)代入积分公式,可得:A = ∫(-r,r)2π(R/x) * sqrt(x^2 - r^2)dx。
这个积分在计算上可能比较复杂,可以改写为:A = 2πR * ∫(-r,r)(1 / sqrt(1 - (r/x)^2))dx。
使用换元法,令 u = r/x,可得到:dx= -r/u^2 du。
圆中阴影部分面积的计算

圆中阴影部分面积的计算要计算圆中阴影部分的面积,我们首先需要了解圆和阴影的几何属性。
阴影是由光线被物体遮挡而产生的暗部分。
在计算阴影部分的面积时,我们需要知道光源的位置和其对圆产生的阴影形状。
假设光源位于圆的正上方,这样阴影将呈现半圆形状。
为了计算阴影部分的面积,我们可以将圆分为两个部分:圆的整体部分和阴影部分。
我们可以先计算出整个圆的面积,然后减去阴影部分的面积即可得到阴影部分的面积。
首先,我们需要确定光源的位置。
假设光源的位置位于圆的正上方。
此时,光线与圆周的切点即为阴影部分的起始点。
请参考以下步骤来计算圆中阴影部分的面积:1.确定圆的半径。
2.使用圆的半径计算整个圆的面积。
公式为:A=πr²。
3.根据光源的位置,确定阴影部分的起始点和终止点。
4.计算阴影部分的面积。
由于阴影呈半圆形状,因此可以使用半圆的面积计算公式:A=0.5πr²。
其中,r为阴影部分的半径。
5.将整个圆的面积减去阴影部分的面积,即可得到阴影部分的面积。
下面我们通过一个实例来进一步解释计算阴影部分的面积:假设圆的半径为10单位长度,我们要计算半径为5单位长度的阴影部分的面积。
1.圆的半径(r)=10。
2.整个圆的面积(A)=π(10)²=100π。
3.阴影部分的半径(r)=54.阴影部分的面积(A)=0.5π(5)²=12.5π。
5.阴影部分的面积=整个圆的面积-阴影部分的面积=100π-12.5π=87.5π。
因此,半径为5单位长度的阴影部分的面积约为87.5π单位²。
总之,要计算圆中阴影部分的面积,需要确定圆的半径和阴影的形状,然后使用相应的几何公式进行计算。
圆阴影部分面积
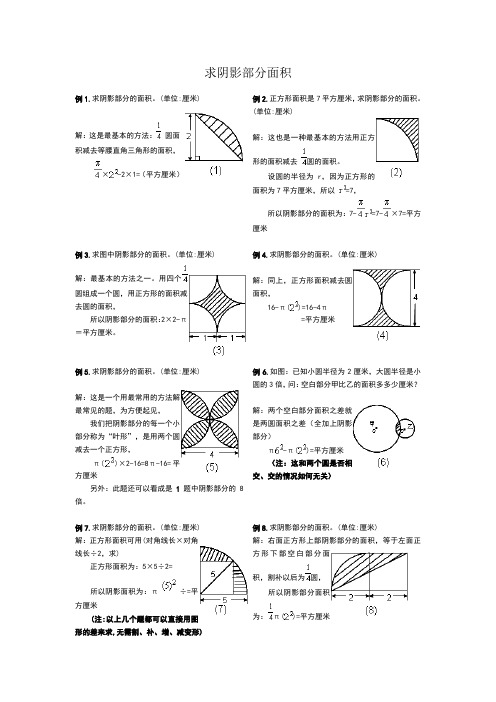
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为 r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=所以阴影面积为:π÷=平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=平方厘米例9.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AB为直径סּC,求此圆与y轴围成的
阴影部分的面积
4π-
3
3
。
0y
B
C
O
A
0x
回顾与思考
反思自我
驶向胜利 的彼挑战
自我岸
•想一想,你有哪些收获?
•说出来,与同学们分享.
回顾与思考
反思自我
驶向胜利 的彼挑战
自我岸
(1)学会了求不规则图形的面积的一般 方法。
(2)深入理解了转化的数学思想。
(3)体会到了数学的灵活性,多变性。
成正六边形、平行四边形、正三角形,将
圆心连线外侧的六个扇形(阴影部分)的
面积之和依次记为S、P、Q则( D )
A.S>P>Q
B.S>Q>P
C.S>P=Q
D.S=P=Q
2. סּA、סּB、סּC、סּD、סּE相互外离,
它们的半径都是1,顺次连结五个圆
心,得到五边形ABCDE,则图中五
个扇形的面积之和为
。23 π
A
B
E
C
D
3. 在∆ABC中,∠BAC=90°, AB=AC=2,以AB为直径的圆交 BC于D,则图中阴影部分的面 为1 。
B
D
C
A
4.图中正比例函数与反 比例函数的图象相交于 A、B两点,分别以A、B 两点为圆心,画与y轴
2. 边长为1的正方形ABCD绕点A逆
时针旋转30 °到正方形AEFH,
图中阴影部分的面积为 3 。 3
C
B
E
P
F
D
A
H
3 2
目标导学(二)
3.在△ABC中,分别以点
A、B、C为圆心的扇形,
半径相同为4。那么图中
三个扇形(即阴影部分)
的面积之和为
。
8π 。
目标导学(三)
4. 在两个同心圆中,三条直径把大 圆分成相等的六部分,若大圆半径
结束寄语
下课了!
数学使人聪明,数学 使人陶醉,数学的美陶冶 着你、我、他。
2. 在直角△ABC中,∠A=90度, AB=8, AC=6, 两个相等的圆 ⊙A 、⊙ B外切,那么图中两个扇
形(即阴影部分)的面积之和
为 25π 。。
2. 有六个等圆按如图甲、乙、丙三种形状
摆放,使邻圆互相外切,且圆心线分别构
D
A
C
B
7.矩形ABCD中,BC=2,DC=4,以AB 为直径的半圆O与DC相切于点E,
则阴影部分的面积是π 。
9.AB是סּO的直径,点D、E是半圆
的三等分点,AE、BD的延长线交
于点C,若CE=2,则图中阴影部分
的面积为
4π-
3
3
。
8.直线y=kx+b过M(1,3)N(-1,
3 3)与坐标轴的交点为A、B,以
π 相切的两个圆。若点A
的坐标为(1,2),则 图中两个阴影面积的和
为π 。
5.∆ABC中BC=4,以点A为圆心,以2 为半径的⊙ A与BC相切于D,P为⊙ A上一点,∠EPF=40°,则阴影 部分的面积4 - 8π 。
9
A
P
E
F
B
D
C
6.某种商品的商标图案如图(阴影部分) 已知菱形ABCD的边长为4,∠A=60°, B⌒D是以A为圆心AB长为半径的弧,C⌒D 是以B 为圆心BC为半径的弧,则该商标图案的 面积为 4 3 。
归纳总结:
1.和差法: 2. 整体求解法。(化零为整) 3.移动法:包括割补法、平移法、等
积代换法。
把不规则图形面积转化成 几个规则图形面积之和(或 差)。
达标练习
1 .某长方形广场的四角 都有一块半径相同的四 分之一圆形的草地,若圆 形的半径为r米,长方形 的长为a米,宽为b米,用 代数式表示空地的面积 是 ab- πr2 。
求圆中阴影部分的面积
九年级数学备课组
学习目标
1.学会求圆中不规则图形面积 的一般方法。
2.深入理解数学的转化思想。 3.体会数学的灵活性,多变性, 激发我们学习数学的兴趣。
课前测评
说说你知道的平面图形 及它们的面积计算公式?
目标导学(一)
1. 正方形ABCD边 长为2cm,以B点 为圆心,AB长为半 径作弧,则图中阴 影部分的面积 为 (4-π)cm2 。
为2,则阴影部分面积为 2π 。
5. סּO2的弦AB切סּO1于C点且
AB∥O1O2,AB=8,则阴影部 A C
B
O1 O2
分的面积为 16π 。
6. A是半径为2的סּO外一点,OA=4
AB切סּO于B,弦BC∥OA,连接AC
则阴影部分面为
。2 π 3
O
A
C
B
通过做以上三组题,你 能总结出求图中阴影面积的 方法吗?(相互交流)
