六年级数学下册正反比例应用题
(完整)六年级正反比例实例练习题

(完整)六年级正反比例实例练习题六年级正反比例实例练题
问题一
在某个比例中,正比例常数是4。
如果当x等于6时,y等于8,那么y是多少时,x等于10?
根据正比例的定义,我们可以得到以下比例关系式:
x y
- = -
6 8
再根据比例的性质,我们可以发现两个关键点:(6, 8) 和 (10, y)。
现在我们可以利用已知的关键点来求解未知的值:
6/8 = 10/y
通过交叉相乘的运算,我们可以得到:
6y = 80
最后,我们将上式解为y:
y = 80/6
因此,当x等于10时,y的值为13.33。
问题二
某公司的收入和投资之间存在着正反比例关系。
该公司的收入是100万美元,而投资是200万美元。
如果该公司的收入增加至150万美元,那么投资会减少到多少?
根据正反比例的定义,我们可以得到以下比例关系式:
收入投资
---- = ------
100万 200万
现在我们可以利用已知的比例关系来解决问题。
已知收入增加到150万美元,我们要求投资的值。
150/100 = 200/投资
通过交叉相乘的运算,我们可以得到:
150 * 投资 = 100 * 200
最后,我们将上式解为投资:
投资 = (100 * 200) / 150
因此,当收入增加到150万美元时,投资会减少到133.33万美元。
以上是关于六年级正反比例实例练习题的解答,希望对您有帮助。
如果还有其他问题,请随时提问。
六年级正反比例易错题应用题

六年级正反比例易错题应用题一、正比例应用题1. 题目一辆汽车2小时行驶140千米,照这样的速度,从甲地到乙地共行驶5小时。
甲乙两地之间的公路长多少千米?解析:根据题意可知汽车行驶的速度是一定的。
因为速度 = 路程÷时间,当速度一定时,路程和时间成正比例关系。
设甲乙两地之间的公路长x千米。
先求出汽车的速度,已知汽车2小时行驶140千米,速度为140÷2 = 70(千米/小时)。
根据正比例关系可列出比例式:(140)/(2)=(x)/(5)。
然后交叉相乘得到2x = 140×5,2x=700,解得x = 350千米。
2. 题目小明买9本练习本花了4.5元,如果买同样的练习本20本需要付多少钱?解析:因为练习本的单价是一定的,单价 = 总价÷数量,当单价一定时,总价和数量成正比例关系。
设买20本练习本需要付x元。
先求出单价,4.5÷9 = 0.5(元/本)。
列出比例式:(4.5)/(9)=(x)/(20)。
交叉相乘得9x = 4.5×20,9x = 90,解得x = 10元。
二、反比例应用题1. 题目一间房子要用方砖铺地,用面积是9平方分米的方砖,需要96块,如果改用面积是4平方分米的方砖,需要多少块?解析:房间地面的总面积是一定的。
因为每块砖的面积×砖的块数 = 房间地面总面积,当房间地面总面积一定时,每块砖的面积和砖的块数成反比例关系。
设改用面积是4平方分米的方砖需要x块。
房间地面总面积为9×96 = 864平方分米。
根据反比例关系可列出方程4x = 9×96。
解得x=(9×96)/(4)=216块。
2. 题目一辆汽车从甲地开往乙地,每小时行60千米,5小时到达。
如果要4小时到达,每小时应行多少千米?解析:甲乙两地的路程是一定的。
因为速度×时间 = 路程,当路程一定时,速度和时间成反比例关系。
精选练习六年级下册 正比例、反比例应用题专项训练 含答案解析

正比例、反比例应用题一、应用题1.小兰的身高1.5m,她的影长是2.4m。
如果同一时间同一地点测得一棵树的影子长4米,这棵树有多高?2.一间房子要用方砖铺地,用边长5分米的方砖需用2000块,如果改用边长是4分米的方砖,需用多少块?(用比例解)3.用同样的砖铺地,铺18平方米要用618块砖.如果铺地24平方米,要用多少块砖?(用比例知识来解)4.测量小组要测量一棵树的高度,先量得树的影子长12米,接着在树的附近直立了一根长2米的竹竿,量得竹竿的影子长1.2米.这棵树的高度是多少米?5.王师傅完成一批零件,计划每天加工240个,20天完成。
实际每天多加工60个,多少天完成任务?(用比例知识解答)6.青艺农场收割小麦.前6天收割了114公顷,剩下152公顷.(1)照前几天的工作效率,剩下的还要多少天才能完成?(用比例解)(2)前几天收割的比后几天收割的少百分之几?(3)每公顷平均收小麦7.5吨,这个农场用载重5吨的卡车运回全部小麦,需要运多少次?7.小华的身高是1.6米,他的影长是2.4米.如果在同一时间、同一地点测得一棵树的影长为6米,这棵树有多高?8.市政工程队铺一条路,原计划每天铺0.6千米,24天完成.实际每天铺0.8千米,实际用多少天完成?9.给学校教务处办公室铺地砖,原计划选用3分米的方砖,需要960块;后来实际选用了4分米的方砖铺地,实际用了多少块4分米的方砖?10.甲乙两地相距360千米,一辆汽车从甲地到乙地计划7小时行完全程,汽车时间234….(小时)路程100150200….(千米)4.5千米,20天完成,实际每天修6千米,实际几天可修完?(用比例解)12.一辆汽车3小时行了135千米,照这样计算,行驶315千米需要几小时?(用比例解)13.一辆汽车从甲地出发,每小时行45千米,4小时到达乙地.如果每小时行60千米,几小时可到达乙地?(用比例解)14.(2015•邹城市)一艘轮船从甲港开往乙港,去时顺水,每小时行24千米,15小时到达.返回时逆水,速度降低了25%,多少小时返回甲港?(用比例解)15.用边长是40厘米的方砖给教室铺地需500块,如果改用边长是50厘米的方砖铺地,可节省多少块?16.六年级甲、乙、丙三个班植树,任务分配是:甲班要植三个班总棵数的40%,乙、丙两班植树棵数的比是4:3.当甲班植了200棵树时,正好完成三个班植.求丙班植树多少棵?树总棵数的2717.一间房子要用方砖铺地,用边长是5分米的方砖需要400块,如果改用边长是4分米的方砖,需要多少块?(用比例解)18.育美小学的六年级同学参加军校的行军训练,3小时行了15千米.照这样计算,再行17.5千米就可到达目的地,到达目的地还要行几小时?(用比例解) 19.A、B两地相距360km,一辆汽车从甲地到乙地,原计划每小时行90km,实际这辆汽车是按照下表的速度行驶的.问这辆汽车能否在原计划时间内到达目的时间(h)234…10…路程(km)100150200…500…平方米的客厅要用87.5块,那么18平方米的卧室要用多少块?21.印刷厂用一批纸装订英语练习本.如果每本36页,能订4000本,如果每本32页,能订多少本?车厢种类车厢节数每节车厢可乘人数硬座7108硬卧1678软卧43423.一间房子要用方砖铺地,用面积是9平方分米的方砖,需用96块,如果改用边长是4分米的方砖,需用多少块?(用比例解)24.在春游活动中,我班共创建了8个活动小组,每组5人。
六年级数学下册第四单元正反比例、比例尺应用题

精心整理六年级数学下册第四单元正反比例、比例尺应用题正反比例的应用题1、用同样的方砖铺地,铺20平方米要320块,如果铺42平方米,23辆同样4周约56、7、修一条公路,4天修了200米,照这样计算,又修了6天,又修了多少米?8、小明读一本书,每天读12页,8天可以读完。
如果每天多读4页,几天可以读完?9、今春分配给学校一些植树任务,每天栽200棵6天可以完成任务,现在需要4天完成任务,实际每天比原计划多栽多少棵?10、农场用3辆拖拉机耕地,每天共耕225公顷,照这样速度,用511小时到12、吨,1390141516、一个机器零件长5毫米,画在图纸上是4厘米,求这幅图纸的比例尺。
(5分)17、地图上的26厘米,在比例尺为1∶1300000的地图上约是多少千米?(5分)18、李师傅计划生产450个零件,工作8小时后还差330个零件没有完成,照这样速度,共要几小时完成任务?19、用一批纸装订同样的练习本,如果每本30页,可以装订80本。
如果每本页数减少20%,这批纸可以装订多少本?20、某印刷厂计划四月份印刷课本20000本,结果8天就印刷了56002122、40 2316 24比是25例尺?25、一列火车从甲地开往乙地,5小时行了350千米,照这样计算,共要行9小时。
甲乙两地相距多少千米?26、英华小学有一块长120米、宽80米的长方形操场,画在比例尺为1:4000的平面图上,长和宽各应画多少厘米?(6分)27、修一条路,如果每天修120米,8天可以修完;如果每天修150米,几天可以修完?(用比例方法解)28、同学们做操,每行站20人,正好站18行。
如果每行站24人,294小30、千米,31用324033超产80个,可以提前几天完成?(用比例方法解)34、小明买4本同样的练习本用了4.8元,3.6元可以买多少本这样的练习本?35.甲乙两地在比例尺是1:20000000的地图上长4厘米,乙丙两地相距500千米,画在这幅地图上,应画多长?一辆汽车以每小时200千米的速度从甲地经过乙地,去丙地需要多少小时?参考答案1.正比例2.3.60:4.3:3.6=20:XX=245.正比例3:7.5=X:19.5X=7.86.正比例240:3=X:5 X=4007.8.X=69.X=300 10.正比例225:3=X:5 X=37511.反比例20+4=24(千米)20×12=24XX=1012.13.14.40X=20×60X=3015.正比例3:1.2=X:4.8X=1216.4cm:5mm =40mm:5mm=8:118.19.20.正比例四月份有30天5600:8=x:30 X=210021.反比例90x=105×30X=3535-30=5(天)22.23.300÷3=100km/h甲:100÷5×2=40km/h乙:100÷5×3=60km/h25.20cm:10km=20:1000000=1:5000026.120m=12000cm80m=8000cm 长:12000÷4000=3cm宽:8000÷4000=2cm27.反比例28.29.30.0.6x=0.5x36X=3031.正比例100t=100000kg500:15=100000:xX=300032.反比例40x=50x6033.34.X=335.500km=50000000cm50000000÷20000000=2.5cm 4x20000000=80000000=800km(800+500)÷200=6.5h。
完整版六年级正反比例练习题
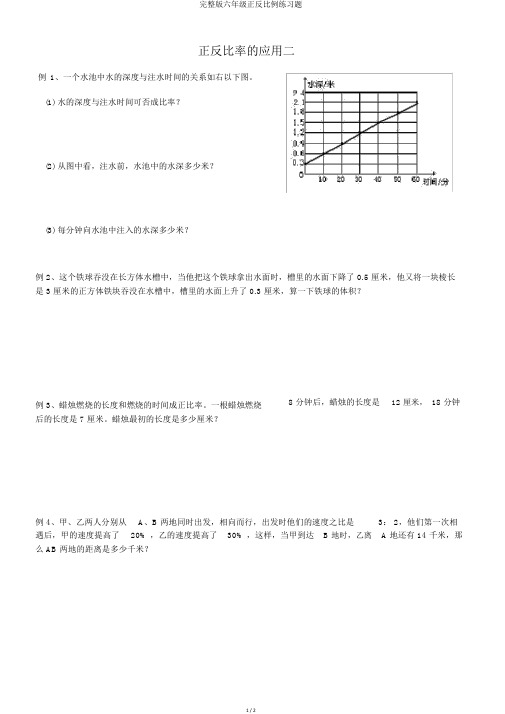
正反比率的应用二例1、一个水池中水的深度与注水时间的关系如右以下图。
(1)水的深度与注水时间可否成比率?(2)从图中看,注水前,水池中的水深多少米?(3)每分钟向水池中注入的水深多少米?例 2、这个铁球吞没在长方体水槽中,当他把这个铁球拿出水面时,槽里的水面下降了 0.5 厘米,他又将一块棱长是 3 厘米的正方体铁块吞没在水槽中,槽里的水面上升了 0.3 厘米,算一下铁球的体积?例 3、蜡烛燃烧的长度和燃烧的时间成正比率。
一根蜡烛燃烧后的长度是 7 厘米。
蜡烛最初的长度是多少厘米?8 分钟后,蜡烛的长度是12 厘米,18 分钟例 4、甲、乙两人分别从A、B 两地同时出发,相向而行,出发时他们的速度之比是遇后,甲的速度提高了20% ,乙的速度提高了30% ,这样,当甲到达 B 地时,乙离3: 2,他们第一次相A 地还有 14 千米,那么 AB 两地的距离是多少千米?看看你会做吗?1、用不相同的杯子装水,水的高度与杯子的底面积的关系如右图。
( 1)从图中看,水的高度与杯子的底面积可否成比率?成什么比率?为什么?( 2)从图中估计,当杯子的底面积是50 平方厘米时,水深多少厘米?当水深25 厘米时,杯子的底面积是多少平方厘米?2、将一个圆柱体完好吞没在一个装满水的水槽中,拿出后水面下降了9 厘米。
尔后放入一个底面积和圆柱体相同,高是圆柱体1的圆锥,这时水面会上升多少厘米?23、蜡烛燃烧的长度和燃烧的时间成正比率。
一根蜡烛燃烧12 分钟后,蜡烛的长度是17 厘米, 18 分钟后的长度是 9 厘米。
蜡烛最初的长度是多少厘米?4、甲、乙两人分别从A、 B 两地同时出发,相向而行,出发时他们的速度之比是后,甲的速度提高了20% ,乙的速度提高了40% ,当甲到达目的地后,乙还有AB 两地的距离是多少千米?4: 3,他们第一次相遇44 千米到达目的地,那么。
六年级正反比例题100道

六年级正反比例题100道正比例题:1. 如果一个苹果的价格是2元,那么5个苹果的价格是多少元。
2. 5本书的价格是20元,那么每本书的价格是多少元。
3. 一个足球的价格是50元,购买3个足球需要多少钱。
4. 如果一辆车每小时行驶60公里,行驶2小时后能行驶多少公里。
5. 4个橙子的总价是16元,1个橙子多少钱。
6. 一条绳子长6米,3条绳子总长多少米。
7. 如果每辆车能载5人,10辆车能载多少人。
8. 一盒巧克力有10块,3盒巧克力有多少块。
9. 每个学生要交100元的学费,10个学生总共交多少钱。
10. 一台电脑的价格是4000元,4台电脑的总价是多少元。
11. 如果1升油的价格是8元,5升油的价格是多少元。
12. 一辆自行车的价格是300元,7辆自行车总共需要多少钱。
13. 1本书的页数是200页,5本书的总页数是多少页。
14. 如果每个学生需要2支铅笔,20个学生需要多少支铅笔。
15. 一棵树的高度是3米,5棵树的总高度是多少米。
16. 1块蛋糕的价格是15元,3块蛋糕总共多少钱。
17. 如果每本杂志售价10元,9本杂志总共多少钱。
18. 一辆车每小时行驶80公里,4小时能行驶多少公里。
19. 如果1公斤米的价格是5元,2公斤米总共多少钱。
20. 每个孩子要喝250毫升的牛奶,8个孩子需要多少牛奶。
21. 一支笔的价格是3元,12支笔总共多少钱。
22. 如果一个篮球的价格是120元,3个篮球的价格是多少元。
23. 一根铅笔的长度是20厘米,4根铅笔的总长度是多少厘米。
24. 如果一个人的工资是3000元,5个人的总工资是多少元。
25. 每条鱼的重量是200克,10条鱼的总重量是多少克。
26. 如果1个西瓜的价格是30元,4个西瓜的价格是多少元。
27. 一辆车的油耗是每公里8升,行驶100公里需要多少升油。
28. 每个学生要用5张纸,25个学生需要多少张纸。
29. 如果一个房间的面积是50平方米,5个这样的房间总面积是多少平方米。
人教版数学六年级下册:《正反比例》作业题

人教版数学六年级下册:《正反比例》作
业题
题目一
1. 小明用3个小时跑了18公里的路程,那么他用6个小时能跑多少公里?
题目二
2. 小王花了180元买了6个苹果,那么他花多少钱可以买到10个苹果?
题目三
3. 如果6个工人在10天内修好一台机器,那么4个工人需要多少天才能完成同样的任务?
题目四
4. 铅球比赛中,小明用3次机会扔出了150米的距离,那么他要扔多少次才能达到300米的距离?
题目五
5. 一瓶洗衣液可以洗20件衣服,那么洗60件衣服需要多少瓶洗衣液?
题目六
6. 一只牛在10天内吃掉了60千克的草,那么3只牛需要多少天才能吃掉180千克的草?
题目七
7. 小红用5秒钟跑完了50米的距离,那么她要跑多少秒才能跑完100米的距离?
题目八
8. 小明用8个小时做完了40道数学题,那么他需要多少小时才能做完80道数学题?
题目九
9. 一家工厂用30个机器生产了3000个产品,那么他需要多少个机器才能生产5000个产品?
题目十
10. 小王用200元买了5个篮球,那么他需要多少钱才能买到12个篮球?
以上就是本次《正反比例》作业题。
请同学们根据题目进行计算,并将答案填写到答题卡上。
完成后请交给老师检查。
祝大家顺利完成!。
人教版六年级下册数学用正反比例解决问题练习题(含答案)

用正反比例解决问题练习题一、填空1.一种盐水,是由盐和水按1:50 配制而成的。
其中,盐的重量占盐水的(),水的重量占盐水的()。
2.一幅地图,图上A、B距离3厘米,地面上A、B距离150千米。
这幅图的比例尺是()。
3.如果x÷y = 11×5,那么x和y成()比例;如果x:4=5:y,那么x和y成()比例。
4.如果甲÷乙=丙,那么,甲一定时,乙和丙成()比例;乙一定时,甲和丙成()比例;丙一定时,甲和乙成()比例。
5.在比例尺为1:8的图纸上,甲、乙两圆的直径比是2:3,那么甲、乙两圆的实际的直径比是()。
二、选择1.如果3x=8y(x、y都不等于0),那么x和y()A、成正比例B、成反比例不成比例 D、以上说法都不对2.如果x3= y8(x、y都不等于0),那么x和y()A、成正比例B、成反比例C、不成比例D、以上说法都不对3.下列表示x和y成反比例的式子是()A、x+3y=12B、y=4xC、y=23x D、y=-32x4.已知kx=y,且x和y都不为0,当k一定时,x和y()A、成正比例B、成反比例C、不成比例D、以上说法都不对5.甲数的34是乙数,那么甲数与乙数()A、成正比例 B、成反比例C 、不成比例D 、以上说法都不对三、判断题1.正方形的边长和周长成正比例。
( )2.正方形的边长和面积成正比例。
( )3.a 是b 的57,数a 和数b 成正比例。
( )4.如果4a=3b,那么a ∶b=3∶4 。
( )5.A8= B ,那么A 和B 成反比例。
( )6.长方体的体积一定,底面积和高成反比例。
( )7.如果x 与y 成反比例,那么3 x 与y 也成反比例。
( )8.圆的面积与半径的平方成正比例。
( )9.圆锥的体积一定,底面积和高成反比例。
( ) 10.全班总人数一定,出勤人数和出勤率成正比例。
( )四、根据比例关系填表1.根据yx=10,填写下表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
做一做
食堂买3桶油用780元,照这样计算,买8桶油要 用多少元?(用比例知识解答) 每桶油的单价一定,总价和数量成正比例. 解:设买8桶油要用 780 3 3
数 学
x 元. x =
8
x = 780×8 x = 2080
答:买8桶油要用2080元.
做一做
同学们做广播操,每行站20人,正好站18行. 如果每行站24人,可以站多少行? 学生总数一定,每行的人数与行数成反比例. 解:设可以站 24
数 学
比例的应用
复习 判断下面每题中的两种量成什么比例? (1)速度一定,路程和时间. 正比例 (2)路程一定,速度和时间.
数 学
反比例
正比例
(3)单价一定,总价和数量.
(4)每小时耕地的公顷数一定,耕地的总公顷数和时间. 正比例 (5)全校学生做操,每行站的人数和站的行数. 反比例
例题 一辆汽车从甲地开往乙地,每小时行70千米,5 小时到达.如果要4小时到达,每小时要行多少千米? 70× 5÷ 4 = 350 ÷ 4 = 87.5(千米)
(1)设要求的问题为x;
(2)判断题目中哪个量是一定的?另外两种
量成正比例关系(除的关系)还是成反比例关系 (乘的关系)? (3)列比例式; (4)解比例,验算,作答。
4ⅹ=70×5
变式 一辆汽车从甲地开往乙地,每小时行70千米,5 小时到达.如果每小时行87.5千米,需要几小时到达? 解:设需要 小时到达.
数 学
x 87.5 x = 70×5 ×5 x = 70 87.5 x
= 4
答:需要4小时到达.
小结
数 学
用比例知识解答应用题的关键:是正确找出
题中的两种相关联的量,判断它们成哪种比例, 然后根据正反比例的意义列出方程.
数 学
x = 20×18 ×18 x = 2024 x
= 15
x 行.
答:可以站15行.
加工一批零件,每小时加工90 个,需要5小时,如果要3小时 完成,每小时加工多少个? (用比列解答)
解:设每小时加工ⅹ个。
3Ⅹ=90×5 3Ⅹ÷3=450÷3 Ⅹ=150
答:每小时加工150个。
用比例解这类问题的过程可以归纳为以 下几个步成 ( 反)比例.
所以两次行驶的(速度)和( 时间)的( 积 ) 是相等的.
例题 一辆汽车从甲地开往乙地,每小时行70千米,5 小时到达.如果要4小时到达,每小时要行多少千米?
数 学
解:设每小时要行 x 千米.
4Ⅹ÷4=350÷4 Ⅹ=87.5
答:每小时要行87.5千米。
