(完整版)六年级数学正比例练习题
新人教版六年级下册数学正反比例精选练习题

数 学
两种相关联的量,一种量变化,另一种量 也随着变化。
比值(也就是商)一定 y =K(一定)
x
积一定
x×y=k(一定)
例7
数
观察下面的两个表,再回答问题。
学
1、表中各有哪两种相关联的量?
2、在各表的两种相关联的量中,一种量是怎样随着另一 种量的变化而变化的?它们的变化规律各有什么特征?
3、哪个表中的两种量成正比例关系?哪个表中的两种量 成反比例关系?
1
●
09
8
7
6
●
5
4
●
3
2
●
1
⑵图1是表示汽车所行路程与相应耗油量关系 的图像,说一说有什么特点。
答:汽车所行路程与相应的耗油量是两种相 关联的量,耗油量随着所行路程和变化而变 化。所行路程增加,耗油量随着增加,所行 路程减少,耗油量也随着减少。 ⑶利用图像估计一下,汽车行驶55㎞的耗油 量是多少?
速度、时间、路程
数
速度×时间=路程
学
路程
= 速度
时间
路程
= 时间
速度
当速度一定时,也就是路程和时间的比的比值一 定,路程和时间成正比例。
当路程一定时,也就是速度和时间的乘积一定, 速度和时间成反比例。
当时间一定时,也就是路程和速度的什么一定, 这时,路程和速度成什么比例?
路程(千米)
180
150
●
B
120
●
90
●
60
●
A
30 ●
速度(千米/时)
180 150
120 ● A 90
60 ●
●
30
● ●B
0 2 4 6 8 10 12 时间(时) 0 2 4 6 8 10 12
苏教版六年级下册数学正比例和反比例 试卷 (含答案)

苏教版六年级下册数学正比例和反比例试卷 (含答案)第6章正比例和反比例单元测试卷一.选择题(共16小题)1.已知,当y一定时,x与z()。
A。
成正比例关系 B。
成反比例关系 C。
不成比例关系2.下面x和y成正比例关系的是()。
A。
y/x = 常数 B。
3x = 4y C。
y = x - 33.如图表示的数量之间的关系是()。
A。
正比例 B。
反比例 C。
不成比例4.正方形的周长和它的边长()。
A。
成正比例 B。
成反比例 C。
不成比例5.汽车从甲地开往乙地,汽车行驶的速度与行驶的时间()。
A。
成正比例 B。
成反比例 C。
不成比例6.下列各种关系中,反比例关系的是()。
A。
平行四边形的面积一定,它的底与高B。
三角形的高不变,它的底和面积C。
圆的面积固定,它的半径与圆周率7.XXX从家到学校,她每小时所走的路程与所用时间()。
A。
成正比例 B。
成反比例 C。
不成比例 D。
无法确定8.圆的周长和它的直径()。
A。
成正比例 B。
成反比例 C。
不成比例 D。
无法判断9.下面各选项中的两种量,成正比例关系的是()。
A。
当xy = 8时,x和y B。
购买物品的总价和数量C。
正方形的周长和它的边长 D。
圆锥的高一定,体积和底面半径10.XXX从家里去学校,所需时间与所行速度()。
11.下面几句话中,正确的有()。
①路程一定,速度和时间成反比例;②正方形的面积和边长成正比例;③三角形面积一定,底和高成反比例;④x+y=25,x与y成反比例。
A。
①和② B。
①和③ C。
①和④ D。
③和④12.下面各题中,()成反比例关系。
A。
一本书看过的页数和剩余的页数B。
圆的周长和直径C。
长方形的面积一定,它的长和宽D。
行驶时间一定,速度和路程13.一本书,已经看的页数与剩余的页数如下表,它们()。
已看的页数剩余的页数10 9020 8030 7014.比例尺一定,图上距离与实际距离()。
A。
成正比例 B。
成反比例 C。
可成正比例也可成反比例D。
新版六年级数学下册试题第四单元正比例和反比例专项练习题人教版(附答案)

人教版六年级下册正比例和反比例专项练习题学校:___________姓名:___________班级:___________考号:___________一、选择题1.xy -9=k (一定),x 和y 的关系是( )。
A .成正比例B .成反比例C .不成比例D .无法确定2.一架民航机从A 地匀速飞往B 地,飞行速度和所用时间( )。
A .成正比例B .成反比例C .不成比例D .无法确定3.下面各题中的各种量不成比例的是( )。
A .梯形的上、下底的和不变,梯形的面积和高 B .在一块菜地上种南瓜和茄子的面积C .如果ba 14⨯=,a 和b 4.将8L 水倒入正方体形状的容器里,水的高度与容器的底面积( ) A .成正比例关系B .成反比例关系C .不成比例关系5.10个小星星可以换4面小红旗,淘气用x 个小星星换了18面小红旗.那么下列比例中,不符..合题意...的是( ). A .10:4:18x = B .10:4:18x = C .4:1018:x =D .4:10:18x =6.下面两种量成反比例关系的是( )。
A .订阅《数学报》的份数和总钱数 B .三角形的面积一定,它的底和高C .长方形的周长一定,它的长和宽7.如果xy= 8,x 和y ( )比例. A .成正B .成反C .不成8.下面图( )表示的是成反比例关系的图像。
A .B .C .9.表示a 、b 成正比例关系的是( ) A .a+b=18B .ab=18C .a=18b 10.下列x 和y 成反比例关系的是( )。
A .y =7+xB .x +y =48C .x =3y D .y =4二、图形计算11.如图:正方形的边长为1米,==,求四边形ABGD的面积.三、其他计算12.求未知数X.(1)1.5:0.3=x:2.7;(2)5x﹣1.2=2.8;(3)x+x=.四、填空题13.一间房子用方砖铺地。
用面积9平方分米的方砖,需要96块。
六年级正比例应用题

六年级正比例应用题一、行程问题中的正比例关系。
1. 一辆汽车2小时行驶120千米,照这样的速度,5小时行驶多少千米?- 解析:因为速度一定,路程和时间成正比例关系。
先求出速度,速度 = 路程÷时间,即120÷2 = 60(千米/小时)。
设5小时行驶x千米,根据正比例关系可得(120)/(2)=(x)/(5),解得x = 300千米。
2. 小明步行的速度是一定的,他走1500米用了30分钟,那么他走2500米需要多少分钟?- 解析:速度一定,路程与时间成正比例。
先求速度,速度=1500÷30 = 50(米/分钟)。
设走2500米需要x分钟,可得(1500)/(30)=(2500)/(x),交叉相乘得1500x = 2500×30,x=(2500×30)/(1500)=50分钟。
3. 飞机飞行的速度不变,飞行1800千米需要3小时,若要飞行3000千米需要多少小时?- 解析:速度不变,路程和时间成正比例。
速度为1800÷3 = 600(千米/小时)。
设飞行3000千米需要x小时,(1800)/(3)=(3000)/(x),解得x = 5小时。
二、工作效率问题中的正比例关系。
4. 工人师傅3小时生产零件180个,照这样计算,7小时生产多少个零件?- 解析:工作效率一定,工作总量和工作时间成正比例。
工作效率=180÷3 = 60(个/小时)。
设7小时生产x个零件,(180)/(3)=(x)/(7),解得x = 420个。
5. 某工厂的一台机器,4天可以生产240个产品,照这样计算,8天能生产多少个产品?- 解析:工作效率一定,工作总量和工作时间成正比例。
这台机器的工作效率为240÷4 = 60(个/天)。
设8天生产x个产品,(240)/(4)=(x)/(8),解得x = 480个。
6. 一个打字员2小时打了12000字,按照这样的速度,5小时能打多少字?- 解析:打字速度一定,打字总量和打字时间成正比例。
正比例六年级练习题

正比例六年级练习题1. 小明骑自行车从家到学校的距离是5千米,花费的时间是20分钟。
如果小明骑自行车的速度保持不变,那么他骑自行车10千米要花费多长时间?解析:根据题意可知,小明骑自行车的速度是不变的,那么他骑自行车的速度可以用速度和时间的关系式 v = s / t 来表示。
假设他骑自行车10千米要花费的时间是 t1,那么根据题意可得: 5千米 / 20分钟 = 10千米 / t1。
求解上述比例式可以得到:t1 = (10千米 × 20分钟) / 5千米 = 40分钟。
答案:小明骑自行车10千米要花费40分钟。
2. 一箱苹果有24个,重4千克,那么重6千克的苹果需要多少个?解析:根据题意可知,苹果的重量和苹果的个数之间是成正比例的,苹果的重量可以用重量和个数的关系式 g = w / n 来表示。
假设重6千克的苹果需要的个数是 n1,那么根据题意可得: 4千克 / 24个 = 6千克 / n1。
求解上述比例式可以得到:n1 = (6千克 × 24个) / 4千克 = 36个。
答案:重6千克的苹果需要36个。
3. 甲用4根绳子拉一辆车,用了12分钟拉了100米;乙用6根绳子拉相同的车,需要多少时间才能拉行走200米?解析:根据题意可知,拉车的速度和所用的绳子的根数之间是成正比例的,速度可以用速度和时间的关系式 v = s / t 来表示。
假设乙用6根绳子拉相同的车需要的时间是 t2,那么根据题意可得: 4根绳子 / 12分钟 = 6根绳子 / t2。
求解上述比例式可以得到:t2 = (6根绳子 × 12分钟) / 4根绳子 = 18分钟。
答案:乙用6根绳子拉行走200米需要18分钟。
4. 甲种植一批小麦可以收获10千克,需要耕种10天;乙种植相同的一批小麦,需要多少天才能收获25千克?解析:根据题意可知,小麦的收获量和种植的天数之间是成正比例的,小麦的收获量可以用收获量和天数的关系式 y = x / t 来表示。
北师大版六年级数学下册第四单元《正比例和反比例》专项练习卷(含答案)

北师大版六年级数学下册第四单元《正比例和反比例》专项练习卷(全卷共5页,共22题,70分钟完成)1.一个工程队3天修了57米路。
照这样计算再修133米,一共需要几天?(用比例知识解)2.买4个本子用了6元。
如果买3个同样的本子,要用多少钱?(用比例解)3.工程队要修一条路,计划每天修150米,60天可以修好,实际每天比计划多修30米,多少天可以修好?(用比例解)4.给一间小型会议室铺地砖,用面积0.09m2的方砖铺地,正好需要100块,如果改用边长0.2m的方砖铺地,需要多少块?(用比例解)5.一架飞机顺风每小时飞行1500km,逆风每小时飞行1200km,燃油够飞9小时,飞机起飞时为顺风,飞机飞出多远就得往回飞?(用比例知识解答)6.学校会议室,用边长0.6m的方砖铺地,正好需要200块,如果改用边长0.5m的方砖铺地,需要多少块?(用比例解)7.六年级教师办公室购进一包白纸,计划每天用20张,可以用28天。
由于有了节约用纸的意识,实际每天只用了16张,实际可以用多少天?8.李师傅原来加工一个零件需要3.5分钟,后来改进了工艺,加工同样的一个零件只需2.8分钟。
原来准备做600个零件的时间,现在可以多做多少个?(用比例知识解决)9.从芜湖到上海的路程全程约360千米。
一辆轿车1.5小时行驶了135千米,照这样的速度行驶,行完全程需要多长时间?10.学校食堂运来30袋大米,每袋40kg,第1周(5天)用了400kg照这样计算,这批大米能用多少天?(列比例解答)11.食堂运来一批煤,原计划每天烧0.4t,可以烧63天,改进技术后,每天只烧0.28t,这批煤实际能烧多少天?(用比例知识解答)12.李老师读《新教育》一书,如果每天读10页,26天能读完。
李老师想提前6天读完,平均每天要读多少页?(请用比例的知识解答)13.有一间大客厅,用面积9平方分米的方砖铺地,需要1200块,如果改用边长40厘米的方砖铺地,需要多少块?(用比例解)14.工厂加工一批零件,原计划每天做80个,30天可以完成任务。
完整版)六年级数学正比例练习题

完整版)六年级数学正比例练习题1.判断XXX的单价和购买XXX的数量与总价是否成正比例,并给出理由。
XXX的单价一定,购买XXX的数量和总价成正比例。
因为购买的数量和总价是随着单价的不变而相应变化的。
2.判断轮船行驶的速度与行驶的路程和时间是否成正比例,并给出理由。
轮船行驶的速度一定,行驶的路程和时间成正比例。
因为行驶的路程和时间是随着速度的不变而相应变化的。
3.判断每小时织布米数与织布的米数和时间是否成正比例,并给出理由。
每小时织布米数一定,织布的米数和时间成正比例。
因为织布的米数和时间是随着每小时织布米数的不变而相应变化的。
4.判断幼儿园老师分给每个小朋友的饼干的块数与小朋友的人数和所需的饼干数是否成正比例,并给出理由。
幼儿园老师分给每个小朋友的饼干的块数一定,小朋友的人数和所需的饼干数成正比例。
因为所需的饼干数是随着小朋友的人数的增加而相应增加的,而每个小朋友分得的饼干块数是不变的。
5.判断订阅《中国小年报》的份数与钱数是否成正比例,并给出理由。
订阅《中国小年报》的份数和钱数成正比例。
因为订阅的份数越多,需要支付的钱数也就越多。
6.判断XXX跳高的高度与他的身高是否成正比例,并给出理由。
XXX跳高的高度与他的身高成正比例。
因为身高越高,跳高的高度也就越高。
7.判断长方形的宽一定,它的面积与长是否成正比例,并给出理由。
长方形的宽一定,它的面积与长成正比例。
因为长方形的面积是由长和宽相乘得到的,而宽是不变的,所以面积随着长的增加而相应增加。
8.判断长方形的宽一定,它的周长与长是否成正比例,并给出理由。
长方形的宽一定,它的周长与长成正比例。
因为长方形的周长是由长和宽相加再乘以2得到的,而宽是不变的,所以周长随着长的增加而相应增加。
9.判断小麦的每公顷产量一定,小麦的公顷数与总产量是否成正比例,并给出理由。
小麦的每公顷产量一定,小麦的公顷数与总产量成正比例。
因为每公顷产量不变,所以总产量随着公顷数的增加而相应增加。
(完整版)小学六年级正比例、反比例练习题
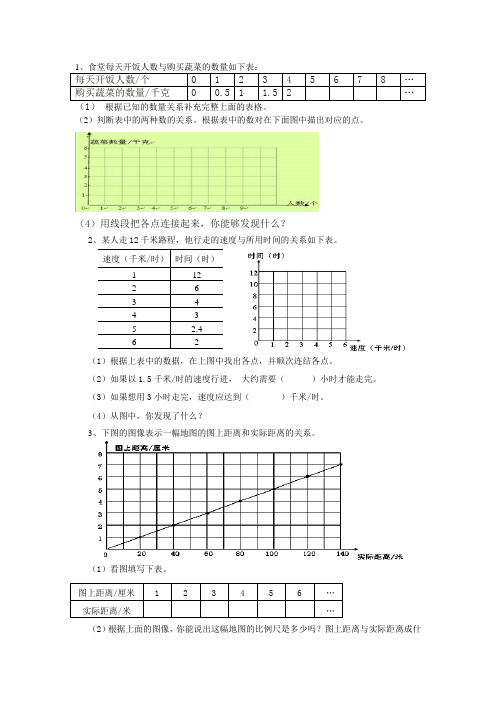
1、食堂每天开饭人数与购买蔬菜的数量如下表:
每天开饭人数/个
012345678…
购买蔬菜的数量/千克 0 0.5 1 1.5 2
…
(1) 根据已知的数量关系补充完整上面的表格。
(2)判断表中的两种数的关系。根据表中的数对在下面图中描出对应的点。
(4)用线段把各点连接起来,你能够发现什么?
2、某人走 12 千米路程,他行走的速度与所用时间的关系如下表。
强强到 A 地用了多长时间? (2)强强骑车 2.5 小时可以行多少千米? (3)按这样的速度行使 36 千米,强强需要多少时间?
6、同一时间,同一地点测得树高和影长如下图:
影பைடு நூலகம்/m
˙˙˙˙˙˙˙˙ 5.6
4.8 4.0 3.2 2.4 1.6 0.8 0
1 2 3 4 5 6 7 8 树高/m
(1)看图填写下表:
所行路程(km)
16
32
48
64
耗油量(L)
2
4
6
8
(1) 表中的耗油量与所行路程成正比 例吗?为什么?
14
12
(2) 右图是表示汽车所行路程与相应
10
耗油量关系的图像,说一说有什么
8
特点。
6
4
2
(3) 利用图像估计一下,汽车行驶 60km 0 的耗油量是多少?
耗油量(L)
路程(km)
8 16 24 32 40 48 56 64
9、给一间屋子铺地砖,每一块地砖的面积与所需地砖的块数如下:
每一块地砖面积/m2
0.16
0.4
0.5
……
需要地砖的块数/块
300
120
(1) 根据表中的数量关系,补充完整表格。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
+正比例练习题一
判断下面的两种量是否成正比例,并说明理由。
1.苹果的单价一定,购买苹果的数量和总价。
()( )○( )=单价( )
所以和()正比例。
2. 轮船行驶的速度一定,行驶的路程和时间。
()
( )○( )=速度( )
所以和()正比例。
3.每小时织布米数一定,织布的米数和时间。
()
( )○( )=每小时织布米数( )
所以和()正比例。
4.幼儿园老师分给每个小朋友的饼干的块数一定,小朋友的人数和所需的饼干数。
()
( )○( )=( )
所以和()正比例。
5.订阅《中国小年报》的份数和钱数。
()
( )○( )=( )
所以和()正比例。
6.小新跳高的高度和他的身高。
()
所以和()正比例。
7.长方形的宽一定,它的面积和长。
()
( )○( )=( )
所以和()正比例。
8. 长方形的宽一定,它的周长和长。
()
( )○( )=( )
所以和()正比例。
9.小麦的每公顷产量一定,小麦的公顷数和总产量()。
( )○( )=( )
所以和()正比例。
10.平行四边形的高一定,它的面积和底。
( ) ( )○( )=( )
所以和()正比例。
11. 三角形的高一定,它的面积和底。
( )
( )○( )=( )
所以和()正比例。
12.圆的周长和半径。
()
( )○( )=( )
所以和()正比例。
13.圆的面积和半径。
()
( )○( )=( )
所以和()正比例。
14.甲地到乙地,已行的路程和剩下的路程。
()
( )○( )=( )
所以和()正比例。
15.小明要做了12到数学题,做完的题和没做的题。
()
( )○( )=( )
所以和()正比例。
16.三(1)班的出勤率一定,全班人数和出勤人数。
()
( )○( )=( )
所以和()正比例。
正比例练习题二
一、判断下面各题的两个量是否成正比例,并说明理由。
(1)小明买《扬子晚报》,数量与总价。
关系式:
(2)王老师的体重和身高。
关系式:
(3)同样一台织布机,工作时间和工作总量。
关系式:
(4)圆的直径和周长。
关系式:
(5)神州6号在轨道上飞行的速度是一定的,飞行的路程与飞行的时间。
关系式:
(6)被减数一定,减数与差。
关系式:
(7)圆的周长与它的半径。
关系式:
(8)圆的半径与它的面积。
关系式:
(9)假定某一景点每天的游客数一定,游客总数和天数。
关系式:
(10)平行四边形的高一定,它的底和面积。
关系式:
(11)被除数一定,商和除数。
关系式:
(12)小明的年龄和他的体重。
关系式:
(13)做一件衬衫的用布量一定,生产这种衬衫的总用布量和件数。
关系式:
(14)一个因数不变,积与另一个因数成正比例。
关系式:
(15)长方形的长一定,宽和面积成正比例。
关系式:(16)大米的总量一定,吃掉的和剩下的成正比例。
关系式:
(17)圆的半径和周长成正比例。
关系式:
(18)分数的分子一定,分数值和分母成正比例。
关系式:
(19)铺地面积一定,方砖的边长和所需块数成正比例。
关系式:
(20)圆的周长和直径成正比例。
关系式:
(21)除数一定,被除数和商成正比例。
关系式:
(22)和一定,加数和另一个加数成正比例。
关系式:
二、填空。
(1)如果x和y是两种相关联的量,并且y=3x,
那么y和x成()比例。
(2)x÷12=y(x≠0),那么x与y成()比例。
(3)3、当a+b=5,那么a与b()比例。
三、选择。
(1)甲数的与乙数的相等,甲数与乙数()。
A、成正比例
B、不成比例
C、无法判断
(2)表示X和Y成正比例关系的式子是()。
(3)全班人数一定,出勤人数和缺勤人数()。
A、成正比例
B、不成比例
C、无法判断
(4)每袋大米的质量一定,大米总质量和袋数()。
A、成正比例
B、不成比例
C、无法判断
(5)正方体的体积和棱长()。
A、成正比例
B、不成比例
C、无法判断
(6)X=7Y,X和Y()。
A、成正比例
B、不成比例
C、无法判断。
