中考数学总复习检测卷-圆
苏教版初三数学中考-圆-复习

(第2题) 苏教版初三数学“圆”中考复习一、选择题1. 当两圆无公共点时,这两圆的位置关系一定是 ··········· ( )A .外离B .内含C .同心圆D .外离或内含 答案:D .解析:本题为容易题,考查了圆与圆的位置关系.根据两圆的位置关系,当两圆外离或内含时,两圆没有公共点,因此本题选D .2. 如图,已知AB 为⊙O 的直径,点C 在⊙O 上,若∠B =50°,则∠A 等于······················· ()A .80°B .60°C .50°D .40° 答案:D .解析:本题为容易题,考查了直径所对圆周角的特征.直径所对的圆周角是直角,故∠A 与∠B 互余,因此本题选D .3. 如图,圆周角∠ACB 的度数为48°,则圆心角∠AOB 的度数为······················· ( ) A .48° B .24° C .96°D .90°答案:C .解析:本题为容易题,考查了圆周角与圆心角的关系.同弧所对的圆周角是圆心角的一半,因此本题选C .4. 如图,⊙O 的半径为5,弦AB 的长为8,M 是弦AB 上的动点,则线段OM 长的最小值 ················ ( )A .2B .3C .4D .5答案:B .解析:本题为容易题,考查了垂径定理及其推论.当OM ⊥AB 时OM 最短,由垂径定理得AM =BM =4,根据勾股定理解得OM =3,因此本题选B .5. 两圆半径分别为2 cm 和6 cm ,若两圆相切,则圆心距为 ······· ( )A .4 cmB .8 cmC .10 cm 或2 cmD .8 cm 或4 cmA(第3题)O CBA BMO(第4题)解析:本题为容易题,考查了圆与圆的位置关系.两圆相切分为外切与内切,当两圆外切时,圆心距d =R +r ,当两圆内切时,圆心距d =R -r ,因此本题选D .6. 如图,P 为正△ABC 外接圆上一点,则∠APB 为 ··· ( )A .150°B .135°C .115°D .120°答案:D .解析:本题为容易题,考查了圆周角与圆心角的关系.由圆内接四边形的性质得∠P +∠C =180°,因此本题选D .7. 一个扇形的圆心角是120°,它的面积为3π cm 2,那么这个扇形的半径是 ( )AB .3 cmC .6 cmD .9 cm答案:B .解析:本题为容易题,考查了计算扇形的面积.扇形面积公式为S =2360n r ,因此本题选B .8. 已知两圆的圆心距是3,两圆半径分别是一元二次方程x 2-3x +2=0的两个根,则这两个圆的位置关系是 ······················ ( )A .外离B .外切C .相交D .内切答案:B .解析:本题为容易题,考查了圆与圆的位置关系.方程的两个根为1和2,由d =R +r 得两圆外切,因此本题选B .9. 如图,四边形ABCD 为⊙O 的内接四边形,∠BOD =120°,则∠BCD的度数为 ··················· ( )A .120°B .90°C .60°D .30°答案:A .解析:本题为容易题,考查了圆周角与圆心角的关系.由题意得∠A =60°,又根据圆内接四边形的性质得∠A +∠C =180°,因此本题选A .10.在半径为R 的圆中有一条长度为R 的弦,则该弦所对的圆周角的度数是( )A .30°B .30°或150°C .60°D .60°或120°BDC OA(第9题)AB C P(第6题)解析:本题为容易题,考查了圆周角与圆心角的关系.该弦与两半径围成一个正三角形,因此圆心角为60°,根据同弧所对的圆周角是圆心角的一半得30°,再根据圆内接四边形性质得优弧所对的圆周角为150°,因此本题选B.11.在Rt△ABC中,∠C=90°,AB=10 cm,AC=5 cm,若以C为圆心,4 cm为直径的⊙C 与AB的关系是··························· ( ) A.相离B.相交C.相切D.不能确定答案:A.解析:本题为中档题,考查了直线与圆的位置关系.通过计算可得BC=C到AB>2,因此本题选A.12.如图,梯形ABCD内接于⊙O,AB∥CD,AB为直径,DO平分∠ADC,则∠DAO的度数是···············( )A.90°B.80°C.70°D.60°答案:D.解析:本题为中档题,考查了圆的有关概念和平行的性质.由条件可得△AOD为正三角形,因此本题选D.13.过⊙O内一点M的最长弦长为10 cm,最短弦长为8 cm,那么OM的长为( )A.3 cm B.6 cm CD.9 cm答案:A.解析:本题为中档题,考查了垂径定理及其推论.最长弦为直径,故半径为5 cm,最短弦为垂直于直径的弦,由垂径定理构造直角三角形后由勾股定理得OM=3,因此本题选A.14.若圆锥的母线长为4 cm,底面半径为3 cm,则圆锥的侧面展开图的面积是( )A.6π cm2B.12π cm2C.18π cm2D.24π cm2答案:B.解析:本题为中档题,考查了计算圆锥的侧面积.圆锥的底面周长为6π,即为扇形的弧长,由扇形面积公式S=12lR,因此本题选B.15.如图,在△ABC中,AB=2,AC=1,以AB为直径的圆与AC相切,与边BC交于点D,则AD的长为··········· ( )ABA BOD C(第12题)A BDC(第15题)C.235D.435答案:A.解析:本题为中档题,考查了切线与过切线的半径之间的关系和直径所对圆周角的性质.由切线的概念得△ABC为Rt△,可得BC=5,又由直径所对圆周角是90°,用面积法可解出AD,因此本题选A.16.两圆相交,圆心距为5 cm,两圆半径分别为3 cm和4 cm,则公共弦长为( )A.2.4 cm B.4.8 cm C.1.8 cm D.3.6 cm答案:B.解析:本题为稍难题,考查了圆与圆的位置关系和解直角三角形.由条件可得,圆心和一个交点围成一个直角三角形,且斜边上的高为2.4 cm,因此本题选B.17. 已知Rt△ABC的两条直角边长为6和8,则它的内切圆与外接圆的圆心距为( )A.32B.332C.3 D.5答案:D.解析:本题为稍难题,考查了切线长定理和三角形的内心、外心.外心是三条边垂直平分线的交点,在斜边中点。
中考数学复习《圆的有关性质》测试题(含答案)

中考数学复习《圆的有关性质》测试题(含答案)一、选择题(每题5分,共30分)1.[2014·梧州]已知⊙O的半径是5,点A到圆心O的距离是7,则点A与⊙O 的位置关系是(C) A.点A在⊙O上B.点A在⊙O内C.点A在⊙O外D.点A与圆心O重合【解析】∵⊙O的半径是5,点A到圆心O的距离是7,即点A到圆心O 的距离大于圆的半径,∴点A在⊙O外.2.[2015·珠海]如图29-1,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠BOD的度数是(D)A.25°B.30°C.40°D.50°图29-1【解析】∵在⊙O中,直径CD垂直于弦AB,∴AD︵=BD︵,∴∠DOB=2∠C=50°.3.[2015·遂宁]如图29-2,在半径为5 cm的⊙O中,弦AB=6 cm,OC⊥AB于点C,则OC=(B) A.3 cm B.4 cm C.5 cm D.6 cm图29-2【解析】 显然利用垂径定理.如答图,连结OA , ∵AB =6 cm ,AC =12AB = 3 cm , 又⊙O 的半径为5 cm ,所以OA =5 cm , 在Rt △AOC 中, OC =AO 2-AC 2=52-32=4(cm).4.[2015·宁波]如图29-3,⊙O 为△ABC 的外接圆,∠A =72°,则∠BCO 的度数为(B)A .15°B .18°C .20°D .28°图29-3【解析】 连结OB ,如答图,∠BOC =2∠A =2×72°=144°,∵OB =OC ,∴∠CBO =∠BCO ,∴∠BCO =12(180°-∠BOC )=12×(180°-144°)=18°.5.[2015·巴中]如图29-4,在⊙O 中,弦AC ∥半径OB ,∠BOC =50°,则∠OAB 的度数为(A)A .25°B .50°C .60°D .30° 【解析】 ∵∠BOC =2∠BAC ,∠BOC =50°,第3题答图第4题答图∴∠BAC=25°,∵AC∥OB,∴∠BAC=∠B=25°,∵OA=OB,∴∠OAB=∠B=25°.图29-4 图29-56.[2014·荆门]如图29-5,AB是半圆O的直径,D,E是半圆上任意两点,连结AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件其中错误的是(D) A.∠ACD=∠DAB B.AD=DEC.AD2=BD·CD D.AD·AB=AC·BD【解析】由题意可知,∠ADC=∠ADB=90°,A.∵∠ACD=∠DAB,∴△ADC∽△BDA,故A正确;B.∵AD=DE,∴AD︵=DE︵,∴∠DAE=∠B,∴△ADC∽△BDA,故B正确;C.∵AD2=BD·CD,∴AD∶BD=CD∶AD,∴△ADC∽△BDA,故C正确;D.∵AD·AB=AC·BD,∴AD∶BD=AC∶AB,但∠ADC=∠ADB不是夹角,故D错误.二、填空题(每题5分,共30分)7.[2015·贵州]如图29-6,A ,B ,C 三点均在⊙O 上,若∠AOB =80°,则∠ACB =__40°__.【解析】 ∠ACB =12∠AOB =12×80°=40°.图29-6 图29-78.[2015安徽]如图29-7,点A ,B ,C 在⊙O 上,⊙O 的半径为9,AB ︵的长为2π,则∠ACB 的大小是__20°__.9.[2015·娄底]如图29-8,在⊙O 中,AB 为直径,CD 为弦,已知∠ACD =40°,则∠BAD =__50__度. 【解析】 ∵在⊙O 中,AB 为直径,∴∠ADB =90°,∵∠B =∠ACD =40°,∴∠BAD =90°-∠B =50°.10.[2015·泰州]如图29-9,⊙O 的内接四边形ABCD 中,∠A =115°,则∠BOD 等于__130°__.【解析】 ∵∠A =115°,∴∠C =180°-∠A =65°,∴∠BOD =2∠C =130°.图29-9 图29-10图29-811.[2015·绍兴]如图29-10,已知点A (0,1),B (0,-1),以点A 为圆心,AB 为半径作圆,交x 轴的正半轴于点C ,则∠BAC 等于__60__度. 【解析】 ∵A (0,1),B (0,-1), ∴AB =2,OA =1,∴AC =2, 在Rt △AOC 中,cos ∠BAC =OA AC =12, ∴∠BAC =60°.12.某居民区一处圆形下水管道破裂,修理人员准备更换一段与原管道同样粗细的新管道.如图29-11,水面宽度原有60 cm ,发现时水面宽度只有50 3 cm ,同时水位也下降65 cm ,则修理人员应准备的半径为__50__cm 的管道.图29-11【解析】 如答图所示:过点O 作EF ⊥AB 于点F ,交CD 于点E ,连结OC ,OA , ∵CD ∥AB ,∴EF ⊥CD ,∵CD =60 cm ,AB =50 3 cm , ∴CE =12CD =12×60=30 cm , AF =12AB =12×503=25 3 cm ,设⊙O 的半径为r ,OE =h cm ,则OF =65-h (cm), 在Rt △OCE 中,OC 2=CE 2+OE 2,即r 2=302+h 2,①第12题答图在Rt△OAF中,OA2=AF2+OF2,即r2=(253)2+(65-h )2,②①②联立,解得r=50 cm.三、解答题(共10分)13.(10分)[2014·湖州]如图29-12,已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D.(1)求证:AC=BD;(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.图29-12解:(1)证明:如答图,过点O作OE⊥AB于点E.则CE=DE,AE=BE.∴AE-CE=BE-DE,即AC=BD;(2)由(1)可知,OE⊥AB且OE⊥CD,第13题答图如答图,连结OA,OC,∴CE=OC2-OE2=82-62=27.AE=OA2-OE2=102-62=8.∴AC=AE-CE=8-27.14.(8分)[2015·安顺]如图29-13,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为(C)图29-13A.2 2 B.4C.4 2 D.8【解析】∵∠A=22.5°,∴∠BOC=2∠A=45°,∵⊙O的直径AB垂直于弦CD,∴CE=DE,△OCE为等腰直角三角形,∴CE=22OC=22,∴CD=2CE=4 2.15.(10分)某地有一座圆弧形拱桥,圆心为O,桥下水面宽度为7.2 m,如图29-14,过O作OC⊥AB于D,交圆弧于C,CD=2.4 m.现有一艘宽3 m,船舱顶部为方形并高出水面(AB)2 m的货船要经过拱桥,此货船能否顺利通过这座拱桥?图29-14解:如答图,连结ON,OB.∵OC⊥AB,∴D为AB的中点.∵AB=7.2 m,∴BD=12AB=3.6 m.第15题答图设OB=OC=ON=r,则OD=OC-CD=r-2.4.在Rt△BOD中,根据勾股定理得r2=(r-2.4)2+3.62,解得r=3.9(m).∵CD=2.4 m,船舱顶部为方形并高出水面AB为2 m,∴CE=2.4-2=0.4(m),∴OE=r-CE=3.9-0.4=3.5(m).在Rt△OEN中,EN2=ON2-OE2=3.92-3.52=2.96,∴EN= 2.96 m,∴MN=2EN=2× 2.96≈3.44(m)>3(m),∴此货船能顺利通过这座拱桥.16.(12分)[2015·台州]如图29-15,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.(1)若∠CBD=39°,求∠BAD的度数;(2)求证:∠1=∠2.图29-15解:(1)∵BC=DC,∴BC︵=DC︵.∴∠BAC=∠CAD=∠CBD.∵∠CBD=39°,∴∠BAC=∠CAD=39°.∴∠BAD=∠BAC+∠DAC=78°;(2)证明:∵EC=BC,∴∠CBE=∠CEB.∵∠CBE=∠1+∠CBD,∠CEB=∠2+∠BAC,∴∠1+∠CBD=∠2+∠BAC.又∵∠BAC=∠CBD,∴∠1=∠2.。
中考数学一轮复习圆检测题

圆检测试题(总分:120分,时间:120分钟)一、选择题(每题3分,共30分)1,⊙O 的半径为5,圆心O 的坐标为(0,0),点P 的坐标为(4,2),则点P 与⊙O 的位置关系是( )A.点P 在⊙O 内B.点P 的⊙O 上C.点P 在⊙O 外D.点P 在⊙O 上或⊙O 外2,⊙O 的半径为2,点P 是⊙O 外一点,OP 的长为3,那么以P 为圆心,且与⊙O 相切的圆的半径一定是( )A.1或5B.1C.5D.1或43,A 是半径为5的⊙O 内一点,且OA =3,过点A 的弦长是整数的弦有( ) A.1条 B.2条 C.3条 D.4条4,如图1,△PQR 是⊙O 的内接正三角形,四边形ABCD 是⊙O 的内接正方形,BC ∥QR ,则∠AOQ 中( )A.60°B. 65°C. 72°D. 75°5,如图2,⊙O 1和⊙O 2内切,它们的半径分别为3和1,过O 1作⊙O 2的切线,切点为A ,则O 1A 的长为( )A.2B.4C.D.6,设⊙O 的直径为m ,直线L 与⊙O 相离,点O 到直线L 的距离为d ,则d 与m 的关系是( )A.d =mB.d >mC.d >D.d < 7,如图3,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中∠AOB 为120°,OC 长为8cm ,CA 长为12cm ,则阴影部分的面积为( )A.64πcm 2B.112πcm 2C.144πcm 2D.152πcm 28,如图4,AB 、AC 为⊙O 的切线,B 、C 是切点,延长OB 到D ,使BD =OB ,连接AD ,352m 2mO 2O 1A 图2ACOB图3D 第10题图QP ODCBA Q图1如果∠DAC =78°,那么∠ADO 等于( )A.70°B.64°C.62°D.51°9,将一个半径为8cm ,面积为32πcm 2的扇形铁皮围成一个圆锥形容器(不计接缝),那么这个圆锥形容器的高为( )A.4cmB.4cmC.4cmD.2cm10,如图5,已知EF 是⊙O 的直径,把∠A 为60°的直角三角板ABC 的一条直角边BC 放在直线EF 上,斜边AB 与⊙O 交于点P ,点B 与点O 重合;将三角形ABC 沿OE 方向平移,使得点B 与点E 重合为止.设∠POF =x °,则x 的取值范围是( )A.60≤x ≤120B.30≤x ≤60C.30≤x ≤90D.30≤x ≤120 二、填空题(每题3分,共24分)11,点A 的坐标为(3,0),点B 的坐标为(0,4),则点B 在以A 为圆心,6 为半径的圆的___.12,如图6,⊙O 的直径为10,弦AB =8,P 是弦AB 上的一个动点,那么OP 长的取值范围是___.13,如图7,在⊙O 中,AB 、AC 是互相垂直且相等的两条弦,OD ⊥AB ,OE ⊥AC ,垂足分别为D 、E ,若AC =2cm ,则⊙O 的半径为_____cm.14,如图8,⊙O 为△ABC 的内切圆,D 、E 、F 为切点,∠DOB =73°,∠DOE =120°.则∠DOF =_______度,∠C =______度,∠A =_______度.15,若小唐同学掷出的铅球在场地上砸出一个直径约为10cm 、深约为2cm 的小坑,则该铅球的直径约为___.3514B PAO 图6FO ECDBA 图8图7EDC BAO图4OCDBA图5OF CAPE(B ) DCAB图916,如图9所示的圆柱体中底面圆的半径是,高为2,若一只小虫从A 点出发沿着圆柱体的侧面爬行到C 点,则小虫爬行的最短路程是.(结果保留根号)17,已知⊙O 1、⊙O 2的圆心距O1O 2=5,当⊙O 1与⊙O 2相交时,则⊙O 1的半径R = ,⊙O 2的半径r =______.(写出一组满足题意的R 与r 的值即可)18,如图10,P 1是一块半径为1的半圆形纸板,在P 1的左下端剪去一个半径为的半圆后得到图形P 2,然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆的半径)得图形P 3,P 4,…,P n …,记纸板P n 的面积为S n ,试计算求出S 2= ;S 3=___;并猜想得到S n -S n -1= (n ≥2).三、解答题(第19-21题,每题10分,第22-24题,每题12分,共66分) 19,如图11-①,在定宽度的纸条上打个简单的结,然后系紧、压平,使它成为平面的结(如图11-②),证明该结具有正五边形的形状.20,如图12,AB 是⊙O 的直径,∠BAC =60 ,P 是OB 上一点,过P 作AB 的垂线与AC 的延长线交于点Q ,过点C 的切线CD 交PQ 于D ,连结OC .(1)求证:△CDQ 是等腰三角形; (2)如果△CDQ ≌△COB ,求BP ∶PO 的值.21,如图13是一纸杯,它的母线AC 和EF 延长后形成的立体图形是圆锥,该圆锥的侧面展开图形是扇形OAB ,经测量,纸杯上开口圆的直径为6cm ,下底面直径为4cm ,母线长EF =8cm ,求扇形OAB 的圆心角及这个纸杯的表面积.(面积计算结果用π表示)2π12图12图10图11①②22,如图14,BC是⊙O的直径,点A在圆上,且AB=AC=4.P为AB上一点,过P作PE⊥AB分别BC、OA于E、F.(1)设AP=1,求△OEF的面积.(2)设AP=a (0<a<2),△APF、△OEF的面积分别记为S1、S2.①若S1=S2,求a的值;②若S=S1+S2,是否存在一个实数a,使S<?若存在,求出一个a的值;若不存在,说明理由.23,如图15,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B 点的切线相交于点D,E为CH中点,连接AE并延长交BD于点F,直线CF交直线AB于点G.(1)求证:点F是BD中点;(2)求证:CG是⊙O的切线;(3)若FB=FE=2,求⊙O的半径.24,如图①,AD是圆O的直径,BC切圆O于点D,AB、AC与圆O相交于点E、F.(1)求证:AE·AB=AF·AC;(2)如果将图①中的直线BC向上平移与圆O相交得图②,或向下平移得图③,此时,AE·AB=AF·AC是否仍成立?若成立,请证明,若不成立,说明理由.15图15图16备用题:1,如图,在Rt△ABC,将△ABC 绕点B 旋转至△A′BC′的位置,且使点A,B,C′三点在同一直线上,则点A 经过的最短路线长是 2,如图,扇形AOB 的圆心角为60°,半径为6cm,C 、D 分别是的三等分点, 则阴影部分的面积是________.cm 23,已知⊙O 的半径为6cm,P 为线段OA 的中点,若点P 在⊙O 上,则OA 的长( ) B A.等于6cm B.等于12cm ; C.小于6cm D.大于12cm4,⊙O 1、⊙O 2、⊙O 3两两外切,且半径分别为2cm,3cm,10cm,则△O 1O 2O 3 的形状是( )D A.锐角三角形 B.等腰直角三角形; C.钝角三角形 D.直角三角形5,圆锥的母线长为5cm,底面半径为3cm,那么它的侧面展开图的圆心角是( )D A.180° B.200° C.225° D.216°6,小明要制作一个圆锥模型,其侧面是由一个半径为9cm,圆心角为240 °的扇形纸板制成的,还需要用一块圆形纸板做底面,那么这块圆形纸板的直径为( )B A.15cm B.12cm C.10cm D.9cm7,圆锥的底面直径为30cm,母线长为50cm, 那么这个圆锥的侧面展开图的圆心角为( A )A .108° B.120° C.135° D.216°8,一个扇形的弧长是20cm,面积是240cm 2,那么扇形的圆心角是( )BA.120°B.150°C.210°D.240°9,某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上, 向内放入两个半径为5cm 的钢球,测得上面一个钢球顶部高DC=16cm(钢管的轴截面如图所示), 求钢管的内直径AD 的长.过O 1作O 1E⊥AD 于E,过O 2作O 2F⊥AD 于F,过O 2作O 2G⊥O 1E 于G,则AE=DF=5cm, O 1G=16-AB 2πππOCDBAA 'C 'CBA5-5=6cm,O 2O 1=5+5=10cm,故O 2G==8cm,所以EF=8cm,从而AD=5+5+8=18cm.10,如图,AB 是半圆O 的直径,C 为半圆上一点,过C 作半圆的切线,连接AC, 作直线AD,使∠DAC=∠CAB,AD 交半圆于E,交过C 点的切线于点D. (1)试判断AD 与CD 有何位置关系,并说明理由;(2)若AB=10,AD=8,求AC 的长.(1)AD⊥CD.理由:连接OC,则OC⊥CD.∵OA=OC,∴∠OAC=∠OCA,又∠OAC= ∠DAC,∴ ∠DAC=∠OCA,∴AD∥OC,∴AD⊥CD.(2)连接BC,则∠ACB=90°由(1)得∠ADC=∠ACB,又 ∠DAC=∠CAB.∴△ACD∽△ABC,∴,即AC 2=AD ·AB=80,故AC=.11,如图13,A 是半径为12cm 的⊙O 上的定点,动点P 从A 出发,以2πcm/s 的速度沿圆周逆时针运动,当点P 回到A 地立即停止运动.(1)如果∠POA =90°,求点P 运动的时间;(2)如果点B 是OA 延长线上的一点,AB =OA ,那么当点P 运动的时间为2s 时,判断直线BP 与⊙O 的位置关系,并说明理由.(1)当∠POA =90°时,点P 运动的路程为⊙O 周长的或.设点P 运动的时间为t s.22106-AC AD AB AC=8045=1434O ECD BAO 2O 1CDBAAPBO图13当点P 运动的路程为⊙O 周长的时,2πt =×2π×12,解得t =3,当点P 运动的路程为⊙O 周长的时,2πt =×2π×12,解得t =9,所以当∠POA =90°时,点P 运动的时间为3s 或9s.(2)如图,当点P 运动的时间为2s 时,直线BP 与⊙O 相切.理由如下:当点P 运动的时间为2s 时,点P 运动的路程为4πcm.连接OP ,PA .因为⊙O 的周长为24πcm ,所以的长为⊙O 周长的,所以∠POA =60°.因为OP =OA ,所以△OAP 是等边三角形.即OP =OA =AP ,∠OAP =60°,因为AB =OA ,所以AP =AB .因为∠OAP =∠APB +∠B ,所以∠APB =∠B =30°.所以∠OPB =∠OPA +∠APB =90°,所以OP ⊥BP .即直线BP 与⊙O 相切.参考答案:一、1,A ;2,A ;3,D ;4,D .点拨:因为BC ∥QR ,所以PO 所在的直线既是正三角形的一条对称轴,又是正方形的一条对称轴.所以∠AOQ =∠POQ -∠AOP .又因为正三角形的中心角为120°,正方形的中心角90°,所以∠AOQ =∠POQ -∠AOP =120°-45°=75°.故应选D ;5,C ;6,C ;7,B .点拨:因为扇形AOB 的面积=π(8+12)2=π,扇形COD 的面积=π×82=π,所以阴影部分的面积=π-π=112π.故应选B ;8,B ;9,B ;10,B .点拨:因为开始时点B 与点O 重合,所以∠POF =30°,又因为当三角形ABC 沿OE 方向平移时,∠POF 逐渐增大,只到使得点B 与点E 重合为止时,∠PEF =30°,所以∠POF =60°.所以x 的取值范围是30至60之间.故应选B .二、11,内部;12,3≤OP ≤5;13,;14,146°、60°、86°; 15,14.5cm.点拨:如图,AB =10cm ,CD =2cm ,由垂径定理可知,OC ⊥AB ,所以AD =BD =5cm ,设半径OA =R ,则OD =R -2,在Rt △ADO 中,由勾股定理,得OA 2=AD 2+OD 2,所以R 2=52+( R -2)2,14143434AP 16120360400312036064340036432CD BA O BAPO解得2R =14.5.16,点拨:如图,此时的AC 即为小虫爬行的最短路程.在 Rt △ABC 中,BC =2,AB =×2π×=2,所以由勾股定 理,得AC ===2.17,显然答案不惟一.由两圆相交必须满足<5<R +r 的正数R 、r 即可.如,⊙O 1的半径R =7,⊙O 2的半径r =3.等等;18,根据条件,得S 1=π,S 2=π-π×=π,S 3=π-π×-π×=π,S 4=π-π×-π×-π×=π,…,所以S 2-S 1=π-π=π(-1)=-π×,S 3-S 2=π-π=π(-)=-π×,S 4-S 3=π-π=π(-)=-π×,…,由此可以猜想S n -S n -1=-π×.所以应分别填上π、π、-π×. 三、19,根据折叠,可知四边形DEAB 和BCDE 是等腰梯形,于是ED =AB =BC =CD =AE ,∠BAE =∠AED =∠BCD =∠CDE =∠ABC .20,(1)证明 由已知得∠ACB =90︒,∠ABC =30︒,所以∠Q =30︒,∠BCO =∠ABC =30︒.因为CD 是⊙O 的切线,CO 是半径,所以CD ⊥CO ,所以∠DCQ =∠BCO =30︒,所以∠DCQ =∠Q ,故△CDQ 是等腰三角形.(2)设⊙O 的半径为1,则AB =2,OC =1,AC =AB =1,BC =.因为等腰三角形CDQ 与等腰三角形COB 全等,所以CQ =BC =.于是AQ =AC +CQ =1+,122π22AB BC +2222+2R r -121212212⎛⎫ ⎪⎝⎭381212212⎛⎫⎪⎝⎭12214⎛⎫ ⎪⎝⎭11321212212⎛⎫ ⎪⎝⎭12214⎛⎫ ⎪⎝⎭12218⎛⎫⎪⎝⎭431283812123412114113238121116341221443128113212436411161231412114n -38113212114n -12333D CBA进而AP =AQ =(1 +),所以BP =AB -AP =2-(1 +)=(3-),所以PO =AP -AO =(1 +)-1=(-1),所以BP ∶PO =. 21,由题意可知:=6π,=4π,设∠AOB =n °,AO =R ,则CO =R -8,由弧长公式得=6π,=4π,解方程组n =45,可求表面积为44π.22,(1)因为BC 是⊙O 的直径,所以∠BAC =90°.因为AB =AC ,所以∠B =∠C =45°,因为OA ⊥BC ,所以∠B=∠BAO =45°.又PE ⊥ AB ,∠AFP =∠BAO =45°.即∠OEF =∠OFE =45°.则△APF、△OEF 与△OAB 均为等腰直角三角形.而AP =l ,AB =4,所以AF ,OA =,即OE =OF .所以△OEF 的面积为OE ×OF =1.(2)①因为PF =AP =a,所以S 1=a 2,且AF a ,所以OE =OF =a (2-a ),所以S 2=×OE ×OF =(2-a )2.当S 1=S 2时,有a 2=(2-a )2,所以a =4±,因为0<a <2,所以a =4-.②S =S 1+S 2=a 2+(2-a )2=a 2-4a +4=( a -)2+,当a =时,S 取得最小值为.<,所以不存在这样实数a ,使S .23,(1)证明:因为CH ⊥AB ,DB ⊥AB ,所以△AEH ∽△AFB ,△ACE ∽△ADF ,所以==,因为HE =EC ,所以BF =FD .(2)连接CB 、OC ,因为AB 是直径,所以∠ACB =90°,因为F 是BD 中点,所以∠BCF =∠CBF =90°-∠CBA =∠CAB =∠ACO ,所以∠OCF =90°,所以CG 是⊙O 的切线.(3)由FC =FB =FE ,得∠FCE =∠FEC ,可证得FA =FG ,且AB =BG ,因为△GBC ∽△GCA ,所以=,即CG 2=AG ·BG .所以(2+FG )2=BG ×AG =121231231231231233AB CD 180n R π(8)180n R π-618041808nR nR n⨯=⎧⎨⨯=-⎩121212121232324343434343EHBFAE AF CEFDGC AG BG GC2BG2,在Rt△BGF中,由勾股定理,得BG2=FG2-BF2,所以FG2-4FG-12=0.解之得FG1=6,FG2=-2(舍去).所以AB=BG=4,所以⊙O半径为2.24,(1)如图①,连接DE.因为AD是圆O的直径,所以∠AED=90°,又因为BC切圆O于点D,所以AD⊥BC,∠ADB=90°,在Rt△AED和Rt△ADB中,∠EAD=∠DAB,所以Rt△AED∽Rt△ADB,所以=,即AE·AB=AD2,同理连接DF,可证Rt△AFD∽Rt△ADC,即AF·AC=AD2,所以AE·AB=AF·AC.(2)AE·AB=AF·AC;仍然成立.如图②,连接DE,因为BC在上下平移时始终与AD垂直,设垂足为D′.则∠AD′B=90°.因为AD 是圆O的直径,所以∠AED=90°,又因为∠D′AB=∠EAD,所以Rt△AD′B∽Rt△AED,所以=,即AE·AB=AD′·AD;同理AF·AC=AD′·AD,所以AE·AB=AF·AC.同理可证,当直线BC向下平移与圆O相离如图③时,AE·AB=AF·AC仍然成立.22AEADADABABADADAB。
中考数学《圆》专项复习综合练习题-附带答案
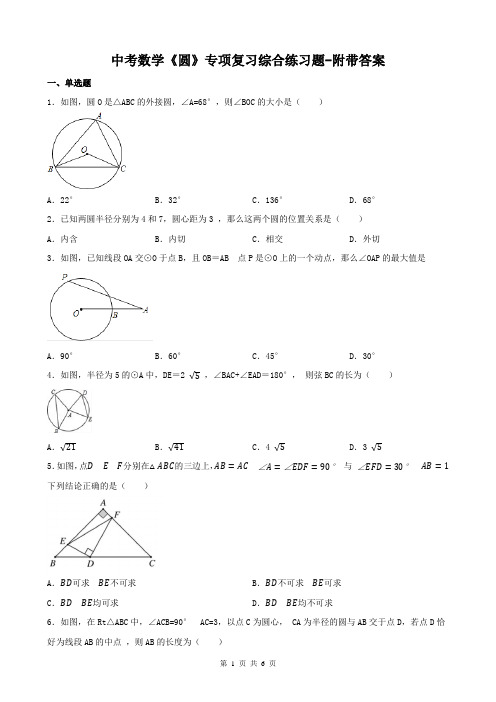
中考数学《圆》专项复习综合练习题-附带答案一、单选题1.如图,圆O是△ABC的外接圆,∠A=68°,则∠BOC的大小是()A.22°B.32°C.136°D.68°2.已知两圆半径分别为4和7,圆心距为3 ,那么这两个圆的位置关系是()A.内含B.内切C.相交D.外切3.如图,已知线段OA交⊙O于点B,且OB=AB 点P是⊙O上的一个动点,那么∠OAP的最大值是A.90°B.60°C.45°D.30°4.如图,半径为5的⊙A中,DE=2 √5,∠BAC+∠EAD=180°,则弦BC的长为()A.√21B.√41C.4 √5D.3 √55.如图,点D E F分别在△ABC的三边上,AB=AC∠A=∠EDF=90°与∠EFD=30°AB=1下列结论正确的是()A.BD可求BE不可求B.BD不可求BE可求C.BD BE均可求D.BD BE均不可求6.如图,在Rt△ABC中,∠ACB=90° AC=3,以点C为圆心, CA为半径的圆与AB交于点D,若点D恰好为线段AB的中点,则AB的长度为()B.3 C.9 D.6A.327.如图,⊙O是△ABC的外接圆,弦BD交AC于点E,AE=DE, BC=CE,过点O作OF⊥AC于点F,延长FO 交BE于点G ,若DE=6,EG=4,则AB的长为()A.4√5B.8√3C.13 D.148.如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形…,重复上述过程,经过2018次后所得到的正六边形边长是原正六边形边长的()A.(√2)2016倍B.(√3)2017倍C.(√3)2018倍D.(√2)2019倍二、填空题9.如图,PA、PB切⊙O于点A、B ,已知⊙O半径为2 且∠APB=60°,则AB= .10.如图,矩形ABCD中,BC=4 CD=2 以AD为直径的半圆O与BC相切于点E,连接BD,则阴影部分的面积为.(结果保留π)11.如图,两边平行的刻度尺在圆上移动当刻度尺的一边与直径为6.5cm的圆相切时另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm)则刻度尺的宽为 cm.12.如图,两圆相交于A、B两点小圆经过大圆的圆心O 点C D分别在两圆上若∠ADB=100°则∠ACB的度数为。
2023年九年级数学中考复习 圆综合压轴题 解答题专题训练(含解析)

2022-2023学年九年级数学中考复习《圆综合压轴题》解答题专题训练(附答案)1.如图.在Rt△ABC中,∠ACB=90°,D为AB边的中点,连接CD.以CD为直径作⊙O,分别与AC,BC相交于点M,N.过点N作⊙O的切线交AB于点E.(1)求证:∠BEN=90°.(2)若AB=10,请填空:①迮接OE,ON,当NE=时,四边形OEBN是平行四边形;②连接DM,DN,当AC=时,四边形CMDN为正方形.2.如图,以AB为直径的半圆中,点O为圆心,点C在圆上,过点C作CD∥AB,且CD =OB.连接AD,分别交OC,BC于点E,F,与⊙O交于点G,若∠ABC=45°.(1)求证:①△ABF∽△DCF;②CD是⊙O的切线.(2)求的值.3.如图,△ABC内接于⊙O,AB为直径,点D为半径OA上一点,过点D作AB的垂线交AC于点E,交BC的延长线于点P,点F在线段PE上,且PF=CF.(1)求证:CF是⊙O的切线;(2)连接AP与⊙O相交于点G,若∠ABC=2∠P AC,求证:AB=BP;(3)在(2)的条件下,若AC=4,BC=3,求CF的长.4.如图,△ABC内接于⊙O,AB是⊙O的直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.(1)判断直线AF与⊙O的位置关系并说明理由;(2)若⊙O的半径为6,AF=2,求AC的长;(3)在(2)的条件下,求阴影部分的面积.5.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F,连接AD.(1)求证:EF是⊙O的切线.(2)求证:△FBD∽△FDA.(3)若DF=4,BF=2,求⊙O的半径长.6.如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG.(1)判断CG与⊙O的位置关系,并说明理由;(2)求证:2OB2=BC•BF;(3)如图2,当∠DCE=2∠F,DG=2.5时,求DE的长.7.已知:△ABC内接于⊙O,连接AO并延长交BC于点D,且AD⊥BC于点D.(1)如图1,求证:∠B=∠C;(2)如图2,点E在上,连接AE,CE,∠ACE=∠ACB,求证:∠CAE=2∠ACE;(3)如图3,在(2)的条件下,过点A作AF⊥CE交CE的延长线于点F,若AE=5,AB=13,求AF的长.8.在Rt△ABC中,∠ACB=90°,AC=6,∠B=30°,点M是AB上的动点,以M为圆心,MB为半径作圆交BC于点D,(1)若圆M与AC相切,如图1,求圆的半径;(2)若AM=2MB,连接AD,如图2.①求证:AD与圆M相切;②求阴影部分的面积.9.如图,已知AB是⊙O的直径,C是⊙O上的一点,D是AB上的一点,DE⊥AB于D,DE交BC于F,且EF=EC.(1)求证:EC是⊙O的切线;(2)求证:△OAC∽△ECF;(3)若BD=4,BC=8,圆的半径OB=5,求EC的长.10.如图,已知以BC为斜边的Rt△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,过点D作DE∥BC交AB的延长线于点E,连接DB,DC.(1)求证:ED为⊙O的切线;(2)求证:BC2=2ED•FC;(3)若tan∠ABC=2,AD=,求BC的长.11.已知△ABC内接于⊙O,D是弧AC上一点,连接BD、AD,BD交AC于点M,∠BMC =∠BAD.(1)如图1,求证:BD平分∠ABC;(2)如图2,过点D作⊙O的切线,交BA的延长线于点F,求证:DF∥AC;(3)如图3,在(2)的条件下,BC是⊙O的直径,连接DC,AM=1,DC=,求四边形BFDC的面积.12.如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,P为弧AD上一点.(1)如图1,连接AC、PC、P A,求证:∠APC=∠ACD;(2)如图2,连接PB,PB交CD于E,过点P作⊙O的切线交CD的延长线于点F,求证:FE=PF;(3)如图3,在(2)的条件下,连接AE,且∠P AE=∠F,过点A作AG⊥PF,垂足为G,若PG=6,,求BH的长.13.如图,⊙O的半径为1,点A是⊙O的直径BD延长线上的一点,C为⊙O上的一点,AD=CD,∠A=30°.(1)求证:直线AC是⊙O的切线;(2)求△ABC的面积;(3)点E在上运动(不与B、D重合),过点C作CE的垂线,与EB的延长线交于点F.①当点E运动到与点C关于直径BD对称时,求CF的长;②当点E运动到什么位置时,CF取到最大值,并求出此时CF的长.14.如图所示,AB是⊙O的直径,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,作AF ⊥PC于点F,连接CB.(1)求证:AC平分∠F AB.(2)求证:BC2=CE•CP.(3)当AB=4时,求劣弧BC长度(结果保留π).15.已知:如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,连接CE,BD是⊙O的切线与OE的延长线相交于点D.(1)求证:∠D=∠AEC;(2)求证:CE2=EH•EA;(3)若⊙O的半径为5,,求FH的长.16.如图,在平面直角坐标系xOy中,已知点A(0,8),点B是x轴正半轴上一点,连接AB,过点A作AC⊥AB,交x轴于点C,点D是点C关于点A的对称点,连接BD,以AD为直径作⊙Q交BD于点E,连接并延长AE交x轴于点F,连接DF.(1)求线段AE的长;(2)若∠ABE=∠FDE,求EF的值.(3)若AB﹣BO=4,求tan∠AFC的值.17.如图,在Rt△ABC中,∠B=90°,AE平分∠BAC,交BC于点E,点D在AC上,以AD为直径的⊙O经过点E,点F在⊙O上,且EF平分∠AED,交AC于点G,连接DF.(1)求证:△DEF∽GDF;(2)求证:BC是⊙O的切线;(3)若cos∠CAE=,DF=10,求线段GF的长.18.如图,⊙O是△ABC的外接圆,AC是⊙O的直径,过圆心O的直线PF⊥AB于D,交⊙O于E,F,PB是⊙O的切线,B为切点,连接AP,AF.(1)求证:直线P A为⊙O的切线;(2)求证:AC2=4OD•OP;(3)若BC=6,,求AC的长.19.如图,AB是半圆O的直径,AB=10.C是弧AB上一点,连接AC,BC,∠ACB的平分线交AB于点P,过点P分别作PE⊥AC,PF⊥BC,垂足分别为E、F.(1)求证:四边形CEPF是正方形;(2)当sin A=时,求CP的长;(3)设AP的长为x,图中阴影部分的面积为y,求y与x之间的函数关系式,并写出y 的最大值.20.问题提出(1)如图①,△ABC为等边三角形,若AB=2,则△ABC的面积为.问题探究(2)如图②,在Rt△ABC中,∠ABC=90°,AC=3,BD是△ABC的角平分线,过点D作DE⊥BD交BC边于点E.若AD=1,求图中阴影部分的面积.问题解决(3)如图③,是某公园的一个圆形施工区示意图,其中⊙O的半径是4米,公园开发部门计划在该施工区内设计一个四边形绿化区域ABCD,连接AC、BD,现准备在△ADC 区域种植花卉供游人欣赏.按设计要求,A、B、C、D四个点都在圆上,∠ADB=∠BDC =60°.设BD的长为x米,△ADC的面积为y平方米.①求y与x之间的函数关系式;②按照设计要求,为让游人有更好的观赏体验,△ADC花卉区域的面积越大越好,那么请求出花卉区域△ADC面积的最大值.参考答案1.(1)证明:如图,连接ON,DN,∵CD是⊙O的直径,∴∠CND=∠DNB=90°,∵NE是⊙O的切线,∴∠ONE=90°,∴∠BNE=∠OND,∵ON=OD,∴∠ODN=∠OND,∴∠ODN=∠BNE,∵D是斜边AB的中点,∴CD=AD=BD,∴∠B=∠BCD,∵∠BCD+∠ODN=90°,∴∠B+∠BNE=90°,∴∠NEB=90°;(2)解:①∵四边形OEBN是平行四边形,∴BE=ON=,∵E为BD的中点,∴N为BC的中点,∴NE为△BCD的中位线,∴NE∥CD,且NE=CD=.故答案为:;②∵四边形CMDN为正方形,∴∠MCD=∠MDC=45°,∠CMD=90°,∴MC=MD=CD,∵AD=DC,∴M是AC的中点,AC=2MC=CD,∴CD=AB=5,∴AC=5.故答案为:5.2.(1)证明:①∵CD∥AB,∴∠F AB=∠D,∵∠AFB=∠DFC,∴△ABF∽△DCF;②∵∠ABC=45°,∴∠AOC=2∠ABC=90°,∵CD∥AB,∴∠DCO=∠AOC=90°,∵OC是半圆的半径,∴CD是⊙O的切线;(2)解:过点F作FH∥AB交OC于H,设圆的半径为2a,∵CD=OB=OA,CD∥AB,∴CE=OE=a,AE=DE,由勾股定理得:AE==a,∴AD=2a,∵△ABF∽△DCF,∴==,∵FH∥AB,∴==,∵FH∥AB,∴==,∴EF=,∵CD是⊙O的切线,∴DC2=DG•DA,即(2a)2=DG•2a,解得:DG=,∴FG=a﹣﹣=,∴==.3.(1)证明:连接OC,∵PF=FC,OC=OB,∴∠PCF=∠CPF,∠OCB=∠OBC,∵PD⊥AB,∴∠PDB=90°,∴∠CPF+∠OBC=90°,∴∠PCF+∠OCB=90°,∴∠FCO=90°,∴OC⊥CF,∴CF是⊙O的切线.(2)证明:连接BG,∵,∴∠P AC=∠PBG,∵∠PBA=2∠P AC,∴∠PBA=2∠PBG,∵AB为⊙O的直径,∴∠AGB=∠PGB=90°,∴∠APB=∠P AB,∴AB=BP;(3)解:∵AB为⊙O的直径,∴∠ACB=90°,∵AC=4,BC=3,∴AB===5,∴AB=BP=5,∴PC=2,∵∠PDA=∠PCA=90°,P A=P A,∠APB=∠P AB,∴△APC≌△APD(AAS),∴AD=PC=2,PD=AC=4,∠P AC=∠APD,∴AE=PE,设DE=x,AE=PE=4﹣x,在Rt△AED中,AD2+DE2=AE2,即22+x2=(4﹣x)2,解得x=,∴EP=4﹣x=,∵∠PEC=90°﹣∠EPC,∠FCE=90°﹣∠PCF,即∠PEC=∠FCE,∴EF=CF=PF,∴CF=.4.解:(1)直线AF与⊙O相切.理由如下:连接OC,∵PC为圆O切线,∴CP⊥OC,∴∠OCP=90°,∵OF∥BC,∴∠AOF=∠B,∠COF=∠OCB,∵OC=OB,∴∠OCB=∠B,∴∠AOF=∠COF,∵在△AOF和△COF中,,∴△AOF≌△COF(SAS),∴∠OAF=∠OCF=90°,∴AF⊥OA,又∵OA为圆O的半径,∴AF为圆O的切线;(2)∵∠AOF=∠COF,OA=OC,∴E为AC中点,即AE=CE=AC,OE⊥AC,∵∠OAF=90°,OA=6,AF=2,∴tan∠AOF=,∴∠AOF=30°,∴AE=OA=3,∴AC=2AE=6;(3)∵AC=OA=6,OC=OA,∴△AOC是等边三角形,∴∠AOC=60°,OC=6,∵∠OCP=90°,∴CP=OC=6,∴S△OCP=OC•CP==18,S扇形AOC==6π,∴阴影部分的面积为S△OCP﹣S扇形AOC=18﹣6π.5.(1)证明:连接OD,如图所示:∵AB为⊙O的直径,∴∠ADB=90°.∴AD⊥BC.∵AB=AC,∴CD=BD=BC.∵OA=OB,∴OD是△ABC的中位线,∴OD∥AC.∵EF⊥AC,∴EF⊥OD.∵OD是半径,∴EF与⊙O相切.(2)证明:∵AB为直径,∴∠ADB=90°,∴∠BAD+∠ABD=90°,∵OD⊥DE,∴∠FDB+∠ODB=90°,∵OB=OD,∴∠OBD=∠ODB,∴∠BAD=∠FDB,∵∠F=∠F,∴△FBD∽△FDA;(3)解:设⊙O的半径为r,则AB=2r,∵△FBD∽△FDA,∴,∵DF=4,BF=2,∴,∴r=3.6.解:(1)CG与⊙O相切,理由如下:如图1,连接CO,∵AB是⊙O的直径,∴∠ACB=∠ACF=90°,∵点G是EF的中点,∴GF=GE=GC,∴∠AEO=∠GEC=∠GCE,∵OA=OC,∴∠OCA=∠OAC,∵OF⊥AB,∴∠OAC+∠AEO=90°,∴∠OCA+∠GCE=90°,即OC⊥GC,∵OC是圆的半径,∴CG与⊙O相切;(2)证明:∵∠AOE=∠FCE=90°,∠AEO=∠FEC,∴∠OAE=∠F,又∵∠B=∠B,∴△ABC∽△FBO,∴,即BO•AB=BC•BF,∵AB=2BO,∴2OB2=BC•BF;(3)由(1)知GC=GE=GF,∴∠F=∠GCF,∴∠EGC=2∠F,又∵∠DCE=2∠F,∴∠EGC=∠DCE,∵∠DCE=∠AOD=45°,∴∠EGC=45°,又∵∠OCG=90°,∴△OCG为等腰直角三角形,∴GC=OC,OG=OC,∴OD+DG=OC,即OC+2.5=OC,解得OC=,∵GF=GE=GC=OC,∴DE=GE﹣DG=OC﹣DG=.7.(1)证明:∵AD⊥BC,AD过圆心O,∴BD=CD,且AD⊥BC,∴AB=AC,∴∠B=∠C;(2)证明:连接BE,设∠ACE=α,则∠ACB=3α,∴∠ABC=∠ACB=3α,∵∠ABE=∠ACE=α,∴∠CBE=∠ABC﹣∠ABE=3α﹣α=2α,∴∠CAE=∠CBE=2α=2∠ACE;(3)解:过点E作EG⊥AC于点G,在CG上截取GH=AG,连接EH,∴EH=AE=5,∴∠AHE=∠EAH=2α,∴∠CEH=∠AHE﹣∠ECH=2α﹣α=α=∠ECH,∴CH=EH=5,∵AC=AB=13,∴AH=AC﹣CH=13﹣5=8,∴AG=GH=4,∴CG=4+5=9,在Rt△AEG中,EG===3,在Rt△CEG中,CE===3,∵,∴,∴.8.解:(1)过点M作MN⊥AC于点N,∵圆M与AC相切,∴MN=MB,∵∠ACB=90°,AC=6,∠B=30°,∴AB=12,设MN=MB=R.∴AM=12﹣R,∵∠ACB=90°,MN⊥AC,∴MN∥BC,∴∠B=∠AMB=30°,∴,∴,解得R=24﹣36.(2)①连接DM,由题意可知MB=MD,∴∠B=∠MDB=30°,∴∠AMD=60°,∵AM=2MB,∴AM=2MD,∵∠ACB=90°,∠B=30°,∴AB=2AC,∠BAC=60°,∴△AMD∽△ABC,∴∠ADM=∠ACB=90°,∴AD与圆M相切;②∵AB=12,AM=2MB,∴BM=4,AM=8,∵∠ADM=90°,∴AD==4,∴S阴影部分=4.9.(1)证明:∵OC=OB,∴∠OBC=∠OCB,∵DE⊥AB,∴∠OBC+∠DFB=90°,∵EF=EC,∴∠ECF=∠EFC=∠DFB,∴∠OCB+∠ECF=90°,∴OC⊥CE,∴EC是⊙O的切线;(2)证明:∵AB是⊙O的直径,∴∠ACB=90°,∴∠ABC+∠A=90°,∠ABC+∠BFD=90°,∴∠BFD=∠A,∴∠A=∠BFD=∠ECF=∠EFC,∵OA=OC,∴∠OCA=∠A=∠BFD=∠ECF=∠EFC,∴△OAC∽△ECF;(3)解:∵AB是⊙O的直径,∴∠ACB=90°,∵OB=5,∴AB=10,∴AC===6,∵cos∠ABC=,∴,∴BF=5,∴CF=BC﹣BF=3,∵△OAC∽△ECF,∴,∴EC==.10.(1)证明:如图1,连接OD.∵BC为⊙O的直径,∴∠BAC=90°.∵AD平分∠BAC,∴.∴OD⊥BC,∵DE∥BC,∴OD⊥ED,又∵OD为半径,∴ED为⊙O的切线;(2)证明:由(1)可得△BCD为等腰直角三角形.∵DE∥BC,∴∠E=∠ABC=∠ADC,∠BDE=∠DBC=∠DCB=45°.∴△BED∽△FDC,∴,即BD2=DE•FC,又,∴BC2=2ED•FC;(3)解:如图2,过点D作DG⊥AD,交AC的延长线于点G.∴∠CDG+∠ADC=90°,∠DGC=∠DAG=45°.又∵∠ADB+∠ADC=90°,∴∠ADB=∠GDC,∵DB=DC,∠BAD=∠DGC=45°,∴△ABD≌△GCD(AAS),∴AB=CG.∵∠DAG=45°,∠ADG=90°,∴△ADG为等腰直角三角形,∴AB+AC=AG=AD==3,∵tan∠ABC=2,∴设AB=x,则AC=2x.∴3x=3,∴x=1.即AB=1,AC=2.∴BC===.11.(1)证明:∵∠BMC=∠BAD,又∵∠BMC=∠BAC+∠ABD,∠BAD=∠BAC+∠DAM,∴∠ABD=∠DAC,又∵弧DC=弧DC,∴∠DAC=∠DBC,∴∠ABD=∠CBD,∴BD平分∠ABC;(2)证明:连接OA、OB、OD,OD交AC于点N,∵FD是⊙O的切线,D为切点,OD是⊙O的半径,∴OD⊥FD,∴∠FDO=90°,又∵∠AOD=2∠ABD,∠DOC=2∠DBC,∠ABD=∠CBD,∴∠AOD=∠COD,又∵AO=CO,∴ON⊥AC,∴∠ANO=90°,∴∠ANO=∠FDO,∴AC∥FD;(3)解:连接OD,交AC于N,∵BC是⊙O的直径,∴∠BAC=∠BDC=90°,∴∠F AC=180°﹣∠BAC=90°,又∵∠ANO=∠FDN=90°,∴四边形ANDF是矩形,∴AF=DN,∠F=90°,又∵ON⊥AC,∴AN=CN,∴设MN=a,则AN=CN=MN+AM=a+1,∴CM=MN+CN=2a+1,在Rt△MDC中,cos∠ACD=,在Rt△NDC中,cos∠ACD=,∴,解得a1=﹣(舍去),a2=1,∴MN=1,CN=a+1=2,∴DN=AF==,又∵MN=AM=1,∠AMB=∠NMD,∠BAM=∠MND=90°,∴△BAM≌△DNM(AAS),∴BA=ND=,∴BF=AB+AF=2,∴AN=FD=a+1=2,∴BD==2,∴S△BFD=,S△DBC=BD•CD==3,∴S四边形BFDC=S△BFD+S△BDC=2.12.(1)证明:连接AD,∵AB是⊙O的直径,弦CD⊥AB,∴,∴∠ACD=∠DC,∵,∴∠APC=∠ADC,∴∠APC=∠ACD;(2)证明:连接OP,∵PF是⊙O的切线,∴OP⊥PF,即∠EPF+∠OPE=90°,∵OP=OB,∴∠OPB=∠OBP,∵CD⊥AB,∴∠HEB+∠HBE=90°,∵∠PEF=∠HEB,∴∠PEF=∠FPE,∴FE=PF;(3)解:过E作EM⊥PF,垂足为M,∵AG⊥PF,∴∠GAP+∠GP A=90°,∵∠APE=90°,∴∠GP A+∠EPM=90°,∵∠AGP=∠EMP=90°,∴△GP A∽△MEP,∴,∵∠P AE=∠F,∴tan∠P AE=tan∠F,则,∵,∴,∴MF=PG=6,设PM=x,∵PE2﹣PM2=EF2﹣FM2,∴,解得:x1=﹣10,x2=4,即PM=4,∴EM==8,∵,即,∴P A=3,∵CD⊥AB,AB是直径,∴∠BHE=∠APB=90°,∴∠HEB=∠BAP,∵∠MPE=∠HEB,∴tan∠P AB=,即,∴PB=6,∴BE=PB﹣PE=2,∵sin∠HEB=,即,∴BH=4.13.(1)证明:连接OC,如图1,∵AD=CD,∠A=30°,∴∠ACD=30°,∴∠CDB=60°,∵OD=OC,∴∠OCD=60°,∴∠ACO=∠ACD+∠OCD=90°,∵OC是半径,∴直线AC是⊙O的切线;(2)解:∵∠OCD=60°,OC=OD,∴△DCO是等边三角形,∴CD=AD=OD=1,作CH⊥BD于点H,则DH=,如图2,∴CH===,∵AB=AD+BD=3,∴S△ABC==.(3)①当点E运动到与点C关于直径AB对称时,CE⊥AB于点K,如图3,∵BD为⊙O的直径,CK=,∴CE=2CK=,∵CF⊥CE,∴∠ECF=90°,∵∠CDB=∠CEB=60°,∴CF=CE•tan60°==3,②∵点E在上运动过程中,∠CDB=∠CEB=60°,在Rt△ECF中,tan60°=,∴CF=CE,∴当CE最大时,CF取得最大值,∴当CE为直径,即CE=2时,CF最大,最大值为2.14.(1)证明:连接AC,BC,∵OC=OA,∴∠OCA=∠OAC,∵PF是⊙O的切线,CE⊥AB,∴∠OCP=∠F=90°,∴AF∥OC,∴∠F AC=∠OCA,∴∠F AC=∠OAC,∴CA平分∠F AB.(2)证明:∵CD是直径,∴∠CBD=90°,∴∠CBP=90°,∵CE⊥OB,∴∠CEB=∠CBP=90°,∵PC切⊙O于点C,∴∠PCB=∠CAB,∵AB是直径,∴∠ACB=90°,∴∠ABC+∠CAB=90°,∠BCE+∠ABC=90°,∵∠CAB=∠BCE,∴∠PCB=∠BCE,∴△BCE∽△PCB,∴,∴BC2=CE•CP;(3)解:,设CF=3a,CP=4a,∵BC2=CE•CP=3a•4a=12a2,∴BC=2a,在Rt△BCE中,sin∠CBE=,∴∠CBE=60°,∴∠BCE=30°,∴△COB是等边三角形,∵AB=4,∴OB=BC=2,∴劣弧BC的长==π.15.(1)证明:∵BD是⊙O的切线,∴∠OBD=90°,∠ABC+∠DBC=90°,∵BC⊥OD,∴∠D+∠DBC=90°,∴∠ABC=∠D,∵∠AEC=∠ABC,∴∠D=∠AEC;(2)证明:连接AC,如图所示:∵OF⊥BC,∴,∴∠CAE=∠ECB,∵∠CEA=∠HEC,∴△CEH∽△AEC,∴,∴CE2=EH•EA;(3)解:连接BE,过O作OG⊥BE于G,如图所示:∵AB是⊙O的直径,∴∠AEB=90°,∵⊙O的半径为5,∴AB=10,∵cos∠BCE=,∴cos∠BAE==,∴AE=8,∴BE===6,∵,∴BE=CE=6,∵CE2=EH•EA,∴EH=,在Rt△BEH中,BH=.∵OG⊥BE,OB=OE,∴BG=3,∴OG===4,∴BF•OE,∴BF=,∴HF=BH﹣BF=.16.解:(1)∵点A(0,8),∴AO=8,∵AD是⊙Q的直径,∴∠AEB=∠AED=90°,∴∠AEB=∠AOB=90°,∵BA垂直平分CD,∴BC=BD,∴∠ABO=∠ABE在△ABE和△ABO中,,∴△ABE≌△ABO(AAS),∴AE=AO=8;(2)∵∠ABE=∠FDE,∴AB∥DF,∴△CAB∽△CDF,∴,又∵∠ABE=∠FDE,∠AEB=∠FED∴△DEF∽△BEA,∴,∴EF=2AE=16;(3)设BO=x,则AB=x+4,在Rt△ABO中,由AO2+OB2=AB2得:82+x2=(x+4)2,解得:x=6,∴OB=BE=6,AB=10,∵∠EAB+∠ABE=90°,∠ACB+∠ABC=90°,∴∠EAB=∠ACB,∵∠BF A=∠AFC,∴△BF A∽△AFC,∴;设EF=m,则AF=8+m,BF=(8+m),∵在Rt△BEF中,BE2+EF2=BF2,∴62+m2=[(8+m)]2,解得:m=,即EF=,∴tan∠AFC=.17.(1)证明:如图1,∵EF平分∠AED,∴∠AEF=∠FED,∵∠AEF=∠ADF,∴∠FED=∠ADF,∵∠GFD=∠DFE,∴△GFD∽△DFE;(2)证明:如图2,∵AE平分∠BAC,∴∠BAE=∠EAO,∵OA=OE,∴∠EAO=∠OEA,∴∠BAE=∠OEA,∴AB∥OE,∴∠OEC=∠B,∵∠B=90°,∴∠OEC=90°,∵OE为半径,∴BC是⊙O的切线;(3)解:如图3,连接OF、AF,∵AD为直径,∴∠AFD=∠AED=90°,∵EF平分∠AED,∴∠AEF=∠FED=45°,∴∠AFD=∠AEF=45°,∴△AFD为等腰直角三角形,∵DF=10,OA=OD∴AD=DF=×10=20,OF⊥AD,OA=OD=OF=10,∵cos∠CAE=,∴AE=AD•cos∠CAE=20×=10,∵∠AEF=∠ADF,∠AGE=∠FGD,∴△AGE∽△FGD,∴,∴AG=GF,∵AG=AO+OG=10+OG,∴10+OG=GF,∴OG=GF﹣10,在Rt△FOG中,GF2=OF2+OG2,∴GF2=102+(GF﹣10)2,解得:GF=或(不符合题意,舍去),∴线段GF的长为.18.(1)证明:连接OB,∵PB是⊙O的切线,∴∠PBO=90°,∵OA=OB,BA⊥PO于D,∴AD=BD,∠POA=∠POB,又∵PO=PO,∴△P AO≌△PBO(SAS),∴∠P AO=∠PBO=90°,∵OA为圆的半径,∴直线P A为⊙O的切线;(2)证明:∵∠P AO=∠PDA=90°,∴∠OAD+∠AOD=90°,∠OP A+∠AOP=90°,∴∠OAD=∠OP A,∴△OAD∽△OP A,∴,∴OA2=OD•OP,又∵AC=2OA,∴AC2=4OD•OP;(3)解:∵OA=OC,AD=BD,BC=6,∴OD=BC=3,设AD=x,∵tan∠F=,∴FD=2x,OA=OF=2x﹣3,在Rt△AOD中,由勾股定理,得,(2x﹣3)2=x2+32,解之得,x1=4,x2=0(不合题意,舍去),∴AD=4,OA=2x﹣3=5,∵AC是⊙O的直径,∴AC=2OA=10.∴AC的长为10.19.(1)证明:∵∠ACB=90°,PE⊥AC,PF⊥BC,∴四边形PECF是矩形,∵CP平分∠ACB,PE⊥AC,PF⊥BC,∴PE=PF,∴四边形CEPF是正方形;(2)解:∵sin A=,AB=10,∴,∴BC=8,∴AC===6,∴tan A=,设PE=CE=m,则AE=6﹣m,∴tan A=,∴m=,∴PC=PE=;(3)解:∵四边形CEPF是正方形,∴PE=PF,∠APE+∠BPF=90°,∠PEA=∠PFB=90°,∴将△APE绕点P顺时针旋转90°,得到△A′PF,P A′=P A,如图所示:则A′、F、B三点共线,∠APE=∠A′PF,∴∠A′PF+∠BPF=90°,即∠A′PB=90°,∴S△P AE+S△PBF=S△P A′B=P A′•PB=x(10﹣x),∴y与x之间的函数关系式为y=﹣+5x,∵y=﹣+5x=﹣,∴x=5时,y有最大值为.20.解:(1)如图①,AD⊥BC,∵△ABC为等边三角形,AB=2,∴∠B=60°,BC=AB=2,∵AD⊥BC,∴∠ADB=90°,在Rt△ABD中,=sin B=sin60°,∴=,∴AD=,∴△ABC的面积=AB•AD=×2×=,故答案为:;(2)如图②,过点D作DH⊥BC于点H,∵∠ABC=90°,BD是△ABC的角平分线,∴∠DBC=∠ABD=45°,∵DE⊥BD,∴∠BDE=90°,∴∠DEB+∠DBE=90°,∴∠DEB=90°﹣∠DBE=90°﹣45°=45°,∴BD=ED,∵DH⊥BC,∴BH=EH,∴DH=BE=BH=EH,设DH=BH=EH=a,∵∠ABC=90°,∴AB⊥BC,∵DH⊥BC,∴AB∥DH,∴△CDH∽△CAB,∴==,∵AD=1,AC=3,∴CD=3﹣1=2,∴==,∴AB=a,CE=a,∴BC=CE+BE=a+2a=3a,∵AB2+BC2=AC2,∴a2+9a2=9,∴a2=1,∴S阴影=S△ABC﹣S△BDE=AB•BC﹣BE•DH=×a•3a﹣×2a•a=a2﹣a2=a2=1;(3)①设AC与BD相交于点E,连接OB,OA,OC,过点O作OH⊥AB于点H,∵∠ADB=∠BDC=60°,∴AB=BC,∠BAC=∠BDC=60°,∴△ABC是等边三角形,∴∠ACB=60°,AB=AC=BC,在△ABO和△ACO中,,∴△ABO≌△ACO(SSS),同理△ABO≌△CBO(SSS),∴S△ABO=S△ACO=S△CBO,∴S△ABC=3S△ABO,∵∠AOB=2∠ACB,∴∠AOB=120°,在Rt△OAH和Rt△OBH中,,∴Rt△OAH≌Rt△OBH(HL),∴∠AOH=∠BOH,AH=BH,在Rt△OAH中,OA=4,∠AOH=∠AOB=60°,∴cos∠AOH=cos60°==,sin∠AOH=sin60°==,∴OH=OA=2,AH=OA=2,∴AB=2AH=4,∴S△ABC=3S△ABO=3××4×2=12,∵∠ABE=∠DBA,∠BAE=∠BDA=60°,∴△ABE∽△DBA,∴===,即S△DBA=S△ABE,∵∠CBE=∠DBC,∠BCE=∠BDC=60°,∴△CBE∽△DBC,∴===,即S△DBC=S△CBE,∴S四边形ABCD=S△DBA+S△DBC=S△ABE+S△CBE,=(S△ABE+S△CBE)=S△ABC=×12=x2,∴S△ADC=S四边形ABCD﹣S△ABC=x2﹣12,即y=x2﹣12;∵BD的长度大于AB,小于等于直径,∴4<x≤8,∴y与x之间的函数关系式为y=x2﹣12(4<x≤8);②由①知,y与x之间的函数关系式为y=x2﹣12,则对称轴为y轴,∵>0,∴x>0时,y随x的增大而增大,∵4<x<8,∴当x=8时,y有最大值,即当BD为⊙O的直径时,y取最大值,即y=×82﹣12=4,∴花卉区域△ADC面积的最大值是4.。
中考数学总复习《圆综合解答题》专题训练-附答案

中考数学总复习《圆综合解答题》专题训练-附答案学校:___________班级:___________姓名:___________考号:___________ 1.如图△ABC内接于⊙O AB、CD是⊙O的直径E是DA长线上一点且∠CED=∠CAB.(1)求证:CE是⊙O的切线;求线段CE的长.(2)若DE=3√5tanB=122.如图在△ABC中AB=AC以AB为直径作⊙O交BC于点D.过点D作DE⊥AC 垂足为E延长CA交⊙O于点F.(1)求证:DE是⊙O的切线;⊙O的半径为5 求线段CF的长.(2)若tanB=123.如图△ABC内接于⊙O直径DE⊙AB于点F交BC于点M DE的延长线与AC的延长线交于点N连接AM.(1)求证:AM=BM;(2)若AM⊙BM DE=8 ⊙N=15° 求BC的长.4.如图△ABC内接于⊙O AB是⊙O的直径D是⊙O上的一点CO平分∠BCD CE⊥AD垂足为E AB与CD相交于点F.(1)求证:CE是⊙O的切线;时求CE的长.(2)当⊙O的半径为5sinB=355.如图1 锐角△ABC内接于⊙O⊙BAC=60°若⊙O的半径为2√3.(1)求BC的长度;(2)如图2 过点A作AH⊙BC于点H若AB+AC=12 求AH的长度.6.如图AB是⊙O的直径M是OA的中点弦CD⊥AB于点M过点D作DE⊥CA交CA的延长线于点E.(1)连接AD则∠AOD=_______;(2)求证:DE 与⊙O 相切;(3)点F 在BC ⏜上 ∠CDF =45° DF 交AB 于点N .若DE =6 求FN 的长.7.如图 AB 是⊙O 的直径 点C 为⊙O 上一点 OF ⊥BC 垂足为F 交⊙O 于点E AE 与BC 交于点H 点D 为OE 的延长线上一点 且∠ODB =∠AEC .(1)求证:BD 是⊙O 的切线(2)求证:CE 2=EH ⋅EA(3)若⊙O 的半径为52 sinA =35 求BH 和DF 的长. 8.如图 在⊙ABC 中 ⊙C=90° 点O 在AC 上 以OA 为半径的⊙O 交AB 于点D BD 的垂直平分线交BC 于点E 交BD 于点F 连接DE .(1)求证:直线DE 是⊙O 的切线(2)若AB=5 BC=4 OA=1 求线段DE 的长.9.如图 AB 是⊙O 的直径 弦CD 与AB 交于点E 过点B 的切线BP 与CD 的延长线交于点P 连接OC CB .(1)求证:AE ·EB =CE ·ED(2)若⊙O 的半径为 3 OE =2BE CE DE =95 求tan∠OBC 的值及DP 的长.10.如图菱形ABCD中AB=4以AB为直径作⊙O交AC于点E过点E作EF⊥AD于点F.(1)求证:EF是⊙O的切线(2)连接OF若∠BAD=60°求OF的长.(3)在(2)的条件下若点G是⊙O上的一个动点则线段CG的取值范围是什么?11.如图点C在以AB为直径的半圆O上(点C不与A B两点重合)点D是弧AC的中点DE⊥AB于点E连接AC交DE于点F连接OF过点D作半圆O的切线DP 交BA的延长线于点P.(1)求证:AC∥DP(2)求证:AC=2DE的值.(3)连接CE CP若AE⊙EO=1⊙2求CECP12.如图1 AB为⊙O直径CB与⊙O相切于点B D为⊙O上一点连接AD OC若AD//OC.(1)求证:CD为⊙O的切线(2)如图2 过点A作AE⊥AB交CD延长线于点E连接BD交OC于点F若AB=3AE=12求BF的长.13.已知:如图在⊙O中∠PAD=∠AEP AF=CF AB是⊙O的直径CD⊥AB于点G.(1)求证:AP是⊙O的切线.(2)若AG=4tan∠DAG=2求△ADE的面积.(3)在(2)的条件下求DQ的长.14.如图已知AB是⊙O的直径点E是⊙O上异于A B的点点F是弧EB的中点连接AE AF BF过点F作FC⊙AE交AE的延长线于点C交AB的延长线于点D⊙ADC的平分线DG交AF于点G交FB于点H.(1)求证:CD是⊙O的切线(2)求sin⊙FHG的值(3)若GH=4√2HB=2 求⊙O的直径.15.如图⊙O的两条弦AB、CD互相垂直垂足为E且AB=CD.(1)求证:AC=BD.(2)若OF⊥CD于F OG⊥AB于G问四边形OFEG是何特殊四边形?并说明理由.(3)若CE=1,DE=3求⊙O的半径.16.【问题提出】如图1 △ABC为⊙O内接三角形已知BC=a圆的半径为R 探究a R sin∠A之间的关系.【解决问题】如图2 若∠A为锐角连接BO并延长交⊙O于点D连接DC则∠A=∠D在△DBC中BD为⊙O的直径BC=a所以BD=2R,∠BCD=90°.所以在Rt△DBC中建立a R sin∠D的关系为________________.所以在⊙O内接三角形△ABC中a R sin∠A之间的关系为________________.类比锐角求法当∠A为直角和钝角时都有此结论.【结论应用】已知三角形△ABC中∠B=60°,AC=4则△ABC外接圆的面积为________.17.已知AB为⊙O的直径PA PC是⊙O的的切线切点分别为A C过点C作CD//AB交⊙O于D.(1)如图当P D O共线时若半径为r求证CD=r(2)如图当P D O不共线时若DE=2CE=8求tan∠POA.18.如图1 已知矩形ABCD中AB=2√3AD=3 点E为射线BC上一点连接DE以DE为直径作⊙O(1)如图2 当BE=1时求证:AB是⊙O的切线(2)如图3 当点E为BC的中点时连接AE交⊙O于点F连接CF求证:CF=CD (3)当点E在射线BC上运动时整个运动过程中CF长度是否存在最小值?若存在请直接写出CF长度的最小值若不存在请说明理由.19.已知四边形ABCD为⊙O的内接四边形直径AC与对角线BD相交于点E作CH⊥BD于H CH与过A点的直线相交于点F∠FAD=∠ABD.(1)求证:AF为⊙O的切线(2)若BD平分∠ABC求证:DA=DC(3)在(2)的条件下N为AF的中点连接EN若∠AED+∠AEN=135°⊙O 的半径为2√2求EN的长.20.如图1 直线l1⊥l2于点M以l1上的点O为圆心画圆交l1于点A B交l2于点C D OM=4 CD=6 点E为弧AD上的动点CE交AB于点F AG⊙CE 于点G连接DG AC AD.(1)求⊙O的半径长(2)若⊙CAD=40° 求劣弧弧AD的长(3)如图2 连接DE是否存在常数k使CE−DE=k·EG成立?若存在请求出k的值若不存在请说明理由(4)若DG⊙AB则DG的长为(5)当点G在AD的右侧时请直接写出⊙ADG面积的最大值.参考答案1.(1)证明:⊙AB是⊙O的直径⊙∠ACB=90°⊙∠CAB+∠B=90°⊙∠CED=∠CAB∠B=∠D⊙∠CED+∠D=90°⊙∠DCE=∠ACB=90°⊙CD⊥CE⊙CD是⊙O的直径即OC是⊙O半径⊙CE是⊙O的切线(2)由(1)知CD⊥CE在Rt△ABC和Rt△DEC中⊙∠B=∠D tanB=12⊙tan∠B=tan∠D=CECD =12⊙CD=2CE在Rt△CDE中CD2+CE2=DE2DE=3√5⊙(2CE)2+CE2=(3√5)2解得CE=3(负值舍去)即线段CE的长为3.2.解:(1)⊙OB=OD⊙∠ABC=∠ODB⊙AB=AC⊙∠ABC=∠ACB⊙∠ODB=∠ACB⊙OD∥AC⊙DE⊥AC OD是半径⊙DE⊥OD⊙DE是⊙O的切线.(2)连接BF AD⊙⊙O的半径为5 AB为直径⊙AB=10∠ADB=90°∠BFC=90°⊙tanB=1设AD=x则BD=2x2在Rt△ABD中由勾股定理得:AD2+BD2=AB2即x2+(2x)2=102解得:x=2√5或x=−2√5(舍去)⊙BD=2x=4√5⊙AB=AC∠ADB=90°⊙BD=CD⊙BC=2BD=8√5由(1)知OD∥AC⊙∠ODB=∠C⊙OB=OD⊙∠B=∠ODB=∠C⊙tanC=tanB=1即CF=2BF2在Rt△BCF中BF2+CF2=BC2即BF2+(2BF)2=(8√5)2解得BF=8或BF=−8(舍去)⊙CF=2BF=16.3.(1)证明:⊙直径DE⊙AB于点F⊙AF=BF⊙AM=BM(2)连接AO BO如图由(1)可得AM=BM⊙AM⊙BM⊙⊙MAF=⊙MBF=45°⊙⊙CMN=⊙BMF=45°⊙AO=BO DE⊙AB∠AOB⊙⊙AOF=⊙BOF=12⊙⊙N=15°⊙⊙ACM=⊙CMN+⊙N=60° 即⊙ACB=60°∠AOB.⊙⊙ACB=12⊙⊙AOF=⊙ACB=60°.⊙DE=8⊙AO=4.得AF=2√3在Rt⊙AOF中由sin∠AOF=AFAO在Rt⊙AMF中AM=√2AF=2√6.得BM= AM=2√6得CM=2√2在Rt⊙ACM中由tan∠ACM=AMCM⊙BC=CM+BM=2√2+2√6.4.(1)证明:⊙弧AC=弧AC⊙∠ADC=∠B.⊙OB=OC⊙∠B=∠OCB.⊙CO平分∠BCD⊙∠OCB=∠OCD⊙∠ADC=∠OCD.⊙CE⊥AD⊙∠ADC+∠ECD=90°⊙∠OCD+∠ECD=90°即CE⊥OC.⊙OC为⊙O的半径⊙CE是⊙O的切线.(2)连接OD得OD=OC⊙∠ODC=∠OCD.⊙∠OCD=∠OCB=∠B⊙∠ODC=∠B⊙CO=CO⊙△OCD≌△OCB⊙CD=CB.⊙AB是⊙O的直径⊙∠ACB=90°⊙AC=AB⋅sinB=10×35=6⊙CB=√AB2−AC2=√102−62=8⊙CD=8⊙CE=CD⋅sin∠ADC=CD⋅sinB=8×35=245.5.解:(1)连接OB OC过点O作OD⊙BC于点D⊙BD =CD =12BC⊙⊙A =60°⊙⊙BOC =2⊙A =120°⊙OB =OC⊙⊙OBC =⊙OCB =180°−∠BOC2=30°⊙OB =2√3⊙BD =OB •cos30°=2√3×√32=3⊙BC =2BD =6.(2)设点G 为此三角形ABC 内切圆的圆心(角平分线的交点) 过G 分别向ABAC BC 作垂线GM GN GQ⊙GM =GN =GQ CQ =CN BQ =BM AM =AN⊙AM +AN =AB +AC -BC =6⊙AM =AN =3.在Rt △AGM 中⊙⊙GAM =30°⊙GM =√3⊙S △ABC =12BC •AH =S △ABG +S △BCG +S △ACG=12AB •GM +12BC •GQ +12AC •GN=12GM(AB+AC+CB)=9√3∵BC=6, S△ABC=12BC•AH⊙AH=3√3.6.(1)解:如图1 连接OD AD⊙AB是⊙O的直径CD⊥AB⊙AB垂直平分CD⊙M是OA的中点⊙OM=12OA=12OD⊙cos∠DOM=OMOD =12⊙∠DOM=60°即∠AOD=60°故答案为:60°(2)解:⊙CD⊥AB AB是⊙O的直径⊙CM=MD⊙M是OA的中点⊙AM=MO又⊙∠AMC=∠DMO⊙△AMC≌△OMD⊙∠ACM=∠ODM⊙CA∥OD⊙DE⊥CA⊙∠E=90°⊙∠ODE=180°−∠E=90°⊙DE⊥OD⊙DE与⊙O相切(3)如图2 连接CF CN⊙OA⊥CD于M⊙M是CD中点⊙NC=ND⊙∠CDF=45°⊙∠NCD=∠NDC=45°⊙∠CND=90°⊙∠CNF=90°由(1)可知∠AOD=60°∠AOD=30°⊙∠ACD=12在Rt△CDE中∠E=90°∠ECD=30°DE=6=12⊙CD=DEsin30°在Rt△CND中∠CND=90°∠CDN=45°CD=12⊙CN=CD•sin45°=6√2⊙∠AOD=60°,OA=OD⊙△OAD是等边三角形⊙∠OAD=60°∠CAD=2∠OAD=120°⊙∠CFD=180°−∠CAD=60°在Rt△CNF中∠CNF=90°∠CFN=60°CN=6√2 =2√6.⊙FN=CNtan60°7.(1)证明:如图1所示⊙∠ODB=∠AEC∠AEC=∠ABC⊙∠ODB=∠ABC⊙OF⊥BC⊙∠BFD=90°⊙∠ODB+∠DBF=90°⊙∠ABC+∠DBF=90°即∠OBD=90°⊙BD⊥OB⊙AB是⊙O的直径⊙BD是⊙O的切线(2)证明:连接AC如图2所示⊙OF⊥BC⊙弧BE=弧CE⊙∠CAE=∠ECB⊙∠CEA=∠HEC⊙△AEC ∽△CEH⊙CE EH =EACE⊙CE 2=EH ⋅EA(3)解:连接BE 如图3所示⊙AB 是⊙O 的直径⊙∠AEB =90°⊙⊙O 的半径为52 sin∠BAE =35 ⊙AB =5 BE =AB ⋅sin∠BAE =5×35=3 ⊙EA =√AB 2−BE 2=4⊙弧BE =弧CE⊙BE =CE =3⊙CE 2=EH ⋅EA⊙EH =94⊙在Rt △BEH 中 BH =√BE 2+EH 2=√32+(94)2=154 ⊙∠A =∠C⊙sinC =sinA⊙OF ⊥BC 垂足为F⊙在Rt △CFE 中 FE =CE ⋅sinC =3×35=95 ⊙CF =√CE 2−EF 2=√32−(95)2=125 ⊙BF =CF =125⊙OF =√BO 2−BF 2=√(52)2−(125)2=710 ⊙∠ODB =∠ABC⊙tan∠ODB =tan∠ABC⊙BFDF =OFBF⊙BF 2=OF ⋅DF⊙(125)2=710DF ⊙DF =28835.8.解:(1)连接OD 如图⊙EF 垂直平分BD⊙ED=EB⊙⊙EDB=⊙B⊙OA=OD⊙⊙A=⊙ODA⊙⊙A+⊙B=90°⊙⊙ODA+⊙EDB=90°⊙⊙ODE=90°⊙OD⊙DE⊙直线DE 是⊙O 的切线(2)作OH⊙AD 于H 如图 则AH=DH 在Rt △OAB 中 sinA=BC AB =45在Rt △OAH 中 sinA=OH OA =45⊙OH=45⊙AH=√12−(45)2=35⊙AD=2AH=65 ⊙BD=5﹣65=195⊙BF=12BD=1910在Rt⊙ABC 中 cosB=45 在Rt⊙BEF 中 cosB=BF BE =45⊙BE=54×1910=198 ⊙线段DE 的长为198.9.((1)证明:连接AD∵∠A =∠BCD ∠AED =∠CEB ∴ΔAED ∽ΔCEB∴ AECE =EDEB∴AE ·EB =CE ·ED(2)解:∵⊙O 的半径为 3 ∴OA =OB =OC =3∵OE =2BE∴OE =2 BE =1 AE =5 ∵ CEDE =95 ∴设CE =9x DE =5x∵AE ·EB =CE ·ED∴5×1=9x ·5x解得:x 1=13 x 2=−13(不 合题意舍去) ∴CE =9x =3 DE =5x =53 过点C 作CF ⊥AB 于F∵OC =CE =3∴OF =EF =12OE =1∴BF =2在RtΔOCF中∵∠CFO=90°∴CF2+OF2=OC2∴CF=2√2在RtΔCFB中∵∠CFB=90°∴tan∠OBC=CFBF =2√22=√2∵CF⊥AB于F∴∠CFB=90°∵BP是⊙O的切线AB是⊙O的直径∴∠EBP=90°∴∠CFB=∠EBP在ΔCFE和ΔPBE中{∠CFB=∠PBE EF=BE ∠FEC=∠BEP∴ΔCFE≅ΔPBE(ASA)∴EP=CE=3∴DP=EP−ED=3−53=43.10.:解:(1)证明:如图连接OE.⊙四边形ABCD是菱形∴∠CAD=∠CAB∵OA=OE∴∠CAB=∠OEA∴∠CAD=∠OEA∴OE∥AD∵EF⊥AD∴OE⊥EF又⊙OE是⊙O的半径⊙EF是⊙O的切线.(2)解:如图连接BE.⊙AB是⊙O的直径∴∠AEB=90°∵∠BAD=60°∴∠CAD=∠CAB=30°在Rt△ABE中AE=AB·cos30°=2√3在Rt△AEF中EF=AE·sin30°=√3AB=2在Rt△OEF中OE=12⊙OF=√OE2+EF2=√4+3=√7.(3)解:如图过点C作CM垂直AB交AB延长线于点M由(2)知∠BAD=60°∴∠ACB=∠CAB=30°,∠CBM=60°∴AB=BC=4,BM=2,CM=2√3∴AM=6,OM=6−2=4.⊙OC=√OM2+CM2=√42+(2√3)2=2√7⊙CG近=2√7−2CE远=2√7+2⊙线段CG的取值范围是:2√7−2≤CG≤2√7+211.(1)证明:连接OD∵D为弧AC的中点∴OD⊥AC又∵DP为⊙O的切线∴OD⊥DP∴AC∥DP(2)证明:∵DE⊥AB∴∠DEO=90°由(1)可知OD⊥AC设垂足为点M∴∠OMA=90°∴∠DEO=∠OMA AC=2AM又∵∠DOE=∠AOM OD=OA∴△ODE≌△OAM(AAS)∴DE=AM∴AC=2AM=2DE(3)解:连接OD OC CE CP∵∠ODP=∠OED=90°∠DOE=∠DOP ∴△DOE∽△POD∴ODOP =OEOD∴OD2=OE⋅OP ∵OC=OD∴OC2=OE⋅OP∴OCOE =OPOC又∵∠COE=∠POC ∴△COE∽△POC∴CECP =OEOC∵AE:EO=1:2∴OEOA =23∴OEOC =23∴CECP =23.12.解:(1)连接OD⊙CB与⊙O相切于点B⊙OB⊥BC⊙AD//OC⊙∠A=∠COB,∠ADO=∠DOC⊙OA=OD⊙∠A=∠ADO=∠COB=∠DOC⊙△DOC≌△BOC(SAS)⊙∠ODC=∠OBC=90°⊙OD⊥DC又OD为⊙O半径⊙CD为⊙O的切线(2)解:设CB=x⊙AE⊥EB⊙AE为⊙O的切线⊙CD CB为⊙O的切线⊙ED=AE=4,CD=CB=x,∠DOC=∠BCO⊙BD⊥OC过点E作EM⊥BC于M则EM=12,CM=x−4⊙(4+x)2=122+(x−4)2解得x=9⊙CB=9⊙OC=√62+92=3√13⊙AB是直径且AD⊙OC⊙⊙OFB=⊙ADB=⊙OBC=90°又⊙⊙COB=⊙BOF⊙⊙OBF⊙⊙OCB⊙OB BF =OCBC⊙BF=OB⋅BCOC =6×93√13=1813√1313.(1)证明:如图所示连接AC ⊙AB是⊙O的直径CD⊥AB⊙弧AD=弧AC⊙∠AEP=∠ADC⊙∠PAD=∠AEP⊙∠PAD=∠ADC⊙AP∥CD⊙AP⊥AB⊙AB是⊙O的直径⊙AP是⊙O的切线(2)解:如图所示连接BD⊙AF=CF⊙∠FAC=∠FCA⊙弧CE=弧AD⊙弧AD=弧AC⊙弧AD=弧AC=弧CE⊙∠ADG=∠QDG⊙AB⊥CD⊙∠AGD=∠QGD=90°又⊙OG=OG⊙△AGD≌△OGD(ASA)⊙QG=AG=4∠DQG=∠DAG=2在Rt△ADG中tan∠DAG=DGAG⊙DG=2AG=8⊙QD=√DG2+QG2=4√5连接OD过点E作EH⊥AB于H设圆O的半径为r则OG=r−4在Rt△ODG中由勾股定理得OD2=OG2+DG2⊙r2=(r−4)2+82解得r=10⊙AB=20⊙BQ=12⊙∠AEQ=∠DBQ,∠EAQ=∠BDQ⊙△AQE∽△DQB⊙QE BQ =AQDQ即QE12=84√5⊙QE=12√55⊙∠EQH=∠DQG=∠DAG⊙在Rt△EQH中tan∠EQH=EHQH=2⊙EH=2QH⊙EH2+QH2=QE2⊙4QH2+QH2=1445⊙QH=125⊙EH=245⊙S△ADE=S△ADQ+S△AEQ=12AQ⋅DG+12AQ⋅EH=12×8×8+12×8×245=70.4.(3)解:由(2)得DQ=4√5.14.(1)证明:连接OF.⊙OA=OF⊙⊙OAF=⊙OF A⊙EF̂=FB̂,⊙⊙CAF=⊙F AB⊙⊙CAF=⊙AFO⊙OF∥AC⊙AC⊙CD⊙OF⊙CD⊙OF是半径⊙CD是⊙O的切线.(2)⊙AB是直径⊙⊙AFB=90°⊙OF⊙CD⊙⊙OFD=⊙AFB=90°⊙⊙AFO=⊙DFB⊙⊙OAF=⊙OF A⊙⊙DFB=⊙OAF⊙GD平分⊙ADF⊙⊙ADG=⊙FDG⊙⊙FGH=⊙OAF+⊙ADG⊙FHG=⊙DFB+⊙FDG⊙⊙FGH=⊙FHG=45°⊙sin⊙FHG=sin45°=√22(3)解:过点H作HM⊙DF于点M HN⊙AD于点N.⊙HD平分⊙ADF⊙HM=HNS△DHF⊙S△DHB= FH⊙HB=DF ⊙DB⊙⊙FGH是等腰直角三角形GH=4√2⊙FH=FG=4⊙DF DB =42=2设DB=k DF=2k⊙⊙FDB=⊙ADF⊙DFB=⊙DAF ⊙⊙DFB⊙⊙DAF⊙DF2=DB•DA⊙AD=4k⊙GD平分⊙ADF⊙FG AG =DFAD=12⊙AG=8⊙⊙AFB=90° AF=12 FB=6∴AB=√AF2+BF2=√122+622=6√5⊙⊙O的直径为6√515.(1)证明:⊙AB=CD⊙弧AB=弧CD⊙弧AB−弧BC=弧CD−弧BC即弧AC=弧BD⊙AC=BD(2)解:四边形OFEG是正方形.理由如下:⊙AB⊥CD OF⊥CD OG⊥AB⊙∠AED=∠OGE=∠OFE=90°⊙四边形OFEG是矩形.如图连接OA OD.⊙OF⊥CD OG⊥AB⊙CF=DF AG=BG.⊙CD=AB⊙AG=DF.⊙OG=√OA2−AG2OF=√OD2−DF2OA=OD⊙OG=OF⊙四边形OFEG是正方形(3)解:⊙CE=1 DE=3⊙CD=4⊙CF=DF=2⊙EF=CF-CE=2-1=1.⊙四边形OFEG是正方形⊙OF=EF=1.在Rt△OED中OD=√OF2+DF2=√5⊙⊙O的半径为√5.16.:解:【解决问题】如图连接BO并延长交⊙O于点D连接DC则∠A=∠D 在△DBC中⊙BD为⊙O的直径BC=a⊙BD=2R,∠BCD=90°⊙sinD=BCBD =a2R⊙sinA=a2R故答案为:sinD=a2R sinA=a2R【结论应用】解:设△ABC外接圆的半径为R ⊙∠B=60°,AC=4⊙sinB=AC2R⊙√3 2=42R解得:R=43√3⊙△ABC外接圆的面积为π×(43√3)2=163π.故答案为:163π17.(1)证明:连接OC⊙PA PC是⊙O的切线切点分别为A C ⊙PA=PC∠PAO=∠PCO=90°在RtΔPAO和RtΔPCO中{PA=PCPO=PO⊙RtΔPAO≌RtΔPCO(HL)⊙∠POA=∠POC⊙CD//AB⊙∠CDO=∠DOA⊙∠CDO=∠COD⊙CD=OC=r(2)解:设OP交CD于E连接OC过O作OH⊥CD于点H由(1)可知RtΔPAO≌RtΔPCO⊙∠POA=∠POC⊙CD//AB⊙∠CEO=∠EOA⊙∠CEO=∠COE⊙CE=CO=8⊙CD=CE+ED=10⊙OH⊥CD⊙CH=DH=5⊙EH=DH−DE=3在RtΔCHO中⊙OH=√OC2−CH2=√82−52=√39在RtΔOHE中⊙tan∠POA=tan∠HEO=OHEH =√393⊙tan∠POA=√393.18.解:(1)如图过点O作OM⊥AB且OM的反向延长线交CD于点N.由题意可知四边形BCNM为矩形⊙MN=AD=3⊙O为圆心即O为DE中点⊙N为DC中点即线段ON为△DEC中位线又⊙CE=BC−BE=3−1=2⊙ON=12CE=1⊙OM=MN -ON=3-1=2.在Rt △DEC 中 DE =√CD 2+CE 2=√(2√3)2+22=4. ⊙OD=DE=OM=2.即AB 为⊙O 的切线.(2)设⊙O 与AD 交于点G 连接CG EG DF FG ⊙DE 为直径⊙∠EGD =∠EFD =90°.⊙∠GEC =90°⊙CG 为直径.⊙∠CFG =∠CDG =90°⊙E 为BC 中点⊙G 为AD 中点在Rt △AFD 中 FG 为中线⊙AG=DG=FG在Rt △CFG 和Rt △CDG 中 {FG =DG CG =CG⊙△CFG ≅△CDG(HL).⊙CF=CD .(3)如图 取AD 中点H 连接CH FH FD .由(2)可知FH =12AD =32 在Rt △CDH 中 CH =√CD 2+HD 2=√(2√3)2+(32)2=√572 ⊙CF ≥CH −FH =√572−32. ⊙当F 点在CH 上时CF 长有最小值 最小值为√572−32.19.解:(1)⊙AC 为⊙O 的直径⊙⊙ADC =90°⊙⊙DAC +⊙DCA =90°.⊙弧AD =弧AD⊙⊙ABD =⊙DCA .⊙⊙F AD =⊙ABD⊙⊙F AD =⊙DCA⊙⊙F AD +⊙DAC =90°⊙CA ⊙AF⊙AF 为⊙O 的切线.(2)连接OD .⊙弧AD =弧AD⊙⊙ABD=1⊙AOD.2⊙弧DC=弧DC⊙DOC.⊙⊙DBC=12⊙BD平分⊙ABC⊙⊙ABD=⊙DBC⊙⊙DOA=⊙DOC⊙DA=DC.(3)连接OD交CF于M作EP⊙AD于P.⊙AC为⊙O的直径⊙⊙ADC=90°.⊙DA=DC⊙DO⊙AC⊙⊙F AC=⊙DOC=90° AD=DC=√(2√2)2+(2√2)2=4 ⊙⊙DAC=⊙DCA=45° AF⊙OM.⊙AO=OCAF.⊙OM=12⊙⊙ODE+⊙DEO=90° ⊙OCM+⊙DEO=90°⊙⊙ODE=⊙OCM.⊙⊙DOE=⊙COM OD=OC⊙⊙ODE⊙⊙OCM⊙OE=OM.设OM=m⊙OE =m AE =2√2−m AP =PE =2−√22m⊙DP =2+√22m . ⊙⊙AED +⊙AEN =135° ⊙AED +⊙ADE =135°⊙⊙AEN =⊙ADE .⊙⊙EAN =⊙DPE⊙⊙EAN ⊙⊙DPE⊙AE DP =AN PE ⊙2√2−m 2+√22m =m2−√22m⊙m =2√23⊙AN =2√23 AE =4√23由勾股定理得:NE =2√103.20.解:(1)连接OD⊙AB 是⊙O 的直径 l 1⊥l 2 CD =6⊙CM =DM =12CD =3在Rt △DOM 中 OM =4⊙OD=√OM2+CM2=5即⊙O的半径长为5(2)⊙AB是⊙O的直径l1⊥l2⊙弧BC=弧BD⊙∠BAD=∠BAC=12∠CAD=20°⊙∠BOD=2∠BAD=40°⊙∠AOD=180°−∠BOD=140°⊙劣弧弧AD的长为140×π×5180=35π9(3)存在常数k=2理由如下:如图在CG上截取CH=DE连接AH AE⊙AB垂直平分CD⊙AC=AD又⊙⊙ACH=⊙ADE⊙⊙ACH⊙⊙ADE(SAS)⊙AH=AE⊙ AG⊙HE⊙HG=EG⊙CE-DE=2EG⊙k=2(4)⊙DG⊙AB⊙⊙CFM⊙⊙CGD⊙FM DG =CFCG=CMCD=12⊙CF=FG DG=2FM⊙⊙CMF=⊙AGF⊙CFM=⊙AFG ⊙⊙CFM⊙⊙AFG⊙CF AF =FMFG⊙FM×AF=CF×FG=CF2设FM=x则AF=9-x⊙x(9−x)=32+x2解得:x=32或3⊙DG=3或6(5)如图取AC的中点P当PG⊙AD时⊙ADG的面积最大在Rt△AMC中⊙CMA=90° CM=3 AM=OA+OM=5+4=9⊙AD=AC=√CM2+AM2=√32+92=3√10在Rt△AGC中⊙CGA=90° 点P为AC的中点⊙PG=12AC=3√102过点C作CN⊙AD于点N在Rt⊙CDN和Rt⊙ADM中⊙⊙CND=⊙AMD=90° ⊙CDN=⊙ADM ⊙Rt⊙CDN~Rt⊙ADM⊙CN AM =CDAD⊙CN=AM⋅CDAD =9×63√10=9√105设PG交AD于点K ⊙PK⊙AD CN⊙AD ⊙PK⊙CN⊙⊙APK⊙⊙CAN⊙PK CN =APAC=12⊙PK=12CN=9√1010⊙GK=PG−PK=3√102−9√1010=3√105⊙⊙ADG面积的最大值为12AD⋅GK=12×3√10×3√105=9.。
2020年九年级数学中考《圆》综合专题复习试题(含答案)

1 ∵AH=2AC= 3,
AH ∴OA=sin60°=2. ∴⊙O 半径的长为 2. (2)证明:在 BM 上截取 BE=BC,连接 CE, ∵∠ABC=120°,BM 平分∠ABC, ∴∠MBA=∠MBC=60°. ∵BE=BC, ∴△EBC 是等边三角形.
∴CE=CB=BE,∠BCE=60°. ∴∠BCD+∠DCE=60°. ∵∠ACM=∠ABM=60°,∴∠ECM+∠DCE=60°. ∴∠ECM=∠BCD. ∵∠CAM=∠CBM=60°,∠ACM=∠ABM=60°. ∴△ACM 是等边三角形.∴AC=CM. ∴△ACB≌△MCE(SAS).∴AB=ME. ∵ME+EB=BM, ∴AB+BC=BM.
基础题组
1.(2019·保定一模)已知⊙O 的半径 OA 长为 2,若 OB= 3,则可以得到的正确图形可
能是(A)
2.(2019·广州)平面内,⊙O 的半径为 1,点 P 到 O 的距离为 2,过点 P 可作⊙O 的切线条
数为(C)
A.0 条
B.1 条
C.2 条
D.无数条
3.如图,在 Rt△ABC 中,∠C=90°,AC=3,BC=4,以点 A 为圆心作圆.如果⊙A 与线
则∠D=27°.
基础题组
1.(2019·柳州)如图,A,B,C,D 是⊙O 上的点,则图中与∠A 相等的角是(D)
A.∠B
B.∠C
C.∠DEB
D.∠D
A︵B
A︵B
2.(2019·吉林)如图,在⊙O 中, 所对的圆周角∠ACB=50°.若 P 为 上一点,
∠AOP=55°,则∠POB 的度数为(B)
A.30°
3 切,连接 OC,则 tan∠OCB= 5 .
2020年中考数学总复习单元综合检测六:圆

单元综合检测六圆(120分钟150分)1.如图,☉O中,弦AB,CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是A.35°B.42°C.43°D.44°2.如图,已知在☉O中,OA⊥BC,∠AOB=70°,则∠ADC的度数为A.30°B.35°C.45°D.70°3.如图,☉O的半径为2,A为☉O上一点,半径OD⊥弦BC于点D.如果∠BAC=60°,那么OD 的长是A.2B.C.1D.【解析】∵OD⊥弦BC,∴∠BDO=90°.∵∠BOD=∠A=60°,∴OD=OB=1.4.如图,△ABC的内切圆☉O与AB,BC,CA分别相切于点D,E,F,且AD=2,△ABC的周长为14,则BC的长为A.3B.4C.5D.6【解析】∵☉O与AB,BC,CA分别相切于点D,E,F,∴AF=AD=2,BD=BE,CE=CF.∵△ABC 的周长为14,∴AD+AF+BE+BD+CE+CF=14,∴2(BE+CE)=10,即BC=5.5.如图,☉O的直径BA的延长线与弦DC的延长线交于点E,且CE=OB.已知∠DOB=72°,则∠E等于A.36°B.30°C.26°D.24°【解析】如图,连接OC,则CE=OB=CO,∴∠E=∠1,∴∠2=∠E+∠1=2∠E.∵OC=OD,∴∠D=∠2=2∠E.∴∠3=∠E+∠D=∠E+2∠E=3∠E.又∠3=72°,∴3∠E=72°,解得∠E=24°.6.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示.已知EF=CD=4 cm,则球的半径长是A.2 cmB.2.5 cmC.3 cmD.4 cm【解析】取EF的中点M,连接OM,OF.设球的半径为r cm,易得Rt△OFM中,OF=r,OM=4-r,FM=EF=2,(4-r)2+22=r2,解得r=2.5,则球的半径长为2.5 cm.7.一个圆锥的高为3 cm,侧面展开图是一个半圆,则圆锥的侧面积是A.6π cm2B.9π cm2C.6π cm2D.9π cm2【解析】设圆锥的底面圆的半径为r,母线长为l,由题意得2πr=πl,即l=2r,又∵r2+32=l2,解得r=,l=2,∴圆锥的侧面积是πrl=×2π=6π(cm2).8.如图,在半径为5的☉O中,弦AB=6,C是优弧上一点(不与点A,B重合),则cos C的值为A. B.C. D.【解析】连接OA,OB,过点O作OD⊥AB于点D,∴BD=AB=3,∠BOD=∠AOB=∠C.在Rt△BOD中,OB=5,BD=3,∴OD=4,∴cos ∠BOD=,即cos C=.9.小颖同学在制作手工时,把一个边长为12 cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为A.2cmB.6cmC.4cmD.8cm【解析】如图,☉O是等边△ABC的外接圆,连接OB,作OD⊥BC于点D,∵△ABC是等边三角形,∴∠ABC=60°.∵☉O是等边△ABC的外接圆,∴∠OBD=∠ABC=30°.∵OD⊥BC,∴BD=BC=6,∴OB==4(cm).10.如图,在平面直角坐标系xOy中,直线AB经过点A(6,0),B(0,6),☉O的半径为2(O为坐标原点),P是直线AB上的动点,过点P作☉O的一条切线PQ,Q为切点,则切线长PQ的最小值为A. B.3C.3D.【解析】连接OQ,OP,在Rt△OPQ中,PQ=.∵OQ=2,当OP取最小值时,PQ最小,且OP≥3,∴PQ≥.二、填空题(本大题共4小题,每小题5分,满分20分)11.如图,已知扇形的圆心角∠AOB=120°,半径OA=2,则扇形的弧长为.【解析】由弧长公式得扇形的弧长=.12.(2019·四川雅安)如图,△ABC内接于☉O,BD是☉O的直径,∠CBD=21°,则∠A的度数为69°.【解析】∵△ABC内接于☉O,BD是☉O的直径,∴∠BCD=90°.∵∠CBD=21°,∴∠A=∠D=90°-21°=69°.13.如图,AB是☉O的直径,弦CD⊥AB,∠BCD=30°,CD=4,则S阴影=.【解析】连接OC,设AB与CD交于点E,∵AB是☉O的直径,弦CD⊥AB,∴CE=DE=CD=2.∵∠BCD=30°,∴∠DOE=60°.又∵∠DEO=90°,∠ODE=30°,∴△CEB ≌△DEO(ASA),∴S△CEB=S△DEO,∴S阴影=S扇形BOD.∵sin ∠EOD=,∴OD=4,∴S阴影=S=π.扇形BOD14.如图,在△ABC中,∠ACB=90°,CD为AB边上的高,P为AC的中点,连接PD,BC=6,DP=4.O为边BA上一点,以点O为圆心,OB为半径作☉O,当☉O与∠PCD的边所在直线相切时,☉O的半径等于.【解析】∵∠ADC=90°,P是AC的中点,∴AC=2DP=8,又∵BC=6,∴AB=10,∴CD=,∴BD=.如图1,若☉O与CD相切,则☉O的半径r=BD=.如图2,若☉O与CP相切,则BO=OE=r,AO=10-r,由OE⊥AC知OE∥BC,∴△AOE∽△ABC,∴,即,解得r=.综上,☉O的半径等于.三、(本大题共2小题,每小题8分,满分16分)15.如图,四边形ABCD的顶点都在☉O上,∠ABC=135°,AC=4,求☉O的半径长.解:∵四边形ABCD的顶点都在☉O上,∠ABC=135°,∴∠D=180°-∠ABC=45°,∴∠AOC=2∠D=90°.∵OA=OC,且AC=4,∴OA=OC=AC=2,即☉O的半径长为2.16.如图,已知一条圆弧经过点A(0,4),B(4,4),C(6,2),在图中作出点A,B,C所确定的圆的圆心M,并直接写出圆心M的坐标.解:图略,圆心M(2,0).四、(本大题共2小题,每小题8分,满分16分)17.如图,在△ACE中,AC=CE,☉O经过点A,C,且与边AE,CE分别交于点D,F,B是劣弧上的一点,且,连接AB,BC,CD.求证:△CDE≌△ABC.证明:∵,∴∠DCE=∠BAC.∵四边形ABCD内接于☉O,∴∠CDE=∠ABC.又∵CE=AC,∴△CDE≌△ABC.18.如图,☉O是△ABC的外接圆,CA=CB,连接BO并延长交AC于点D.(1)求证:∠C=2∠CBD;(2)若AB=6,sin C=,则☉O的半径为5.解:(1)连接CO,AO.∵CA=CB,OA=OB,OC=OC,∴△COA≌△COB,∴∠ACO=∠BCO.∵OC=OB,∴∠BCO=∠CBD,∴∠C=2∠CBD.(2)提示:如图,作☉O的直径AK,连接BK,∴∠ABK=90°,∠C=∠K.∵AB=6,sin C=,∴sinK=,∴AK=10,∴☉O的半径为5.五、(本大题共2小题,每小题10分,满分20分)19.如图,△ABC内接于☉O.(1)作∠B的平分线与☉O交于点D;(用尺规作图,不写作法,保留作图痕迹)(2)在(1)中,连接AD,若∠BAC=60°,∠C=66°,求∠DAC的大小.解:(1)如图所示,BD即为所求.(2)∵∠BAC=60°,∠C=66°,∴∠ABC=180°-∠BAC-∠C=54°.由作图可知BD平分∠ABC,∴∠DAC=∠DBC=∠ABC=27°.20.如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.(1)求圆弧所在圆的半径r的长.(2)当洪水泛滥到跨度只有30米时,要采取紧急措施.若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?解:(1)连接OA.由题意得AD=AB=30,OD=r-18.在Rt△ADO中,由勾股定理得r2=302+(r-18)2,解得r=34.(2)连接OA',OE=OP-PE=30.在Rt△A'EO中,由勾股定理得A'E2=A'O2-OE2,即A'E2=342-302,解得A'E=16,∴A'B'=32.∵A'B'=32>30,∴不需要采取紧急措施.六、(本题满分12分)21.如图,四边形ABDC内接于☉O,∠BAC=60°,AD平分∠BAC交☉O于点D,连接OB,OC,BD,CD.(1)求证:四边形OBDC是菱形;(2)若∠ABO=15°,OB=1,求弦AC的长.解:(1)连接OD,由圆周角定理得∠BOC=2∠BAC=120°.∵AD平分∠BAC,∴,∴∠BOD=∠COD=60°.∵OB=OD,OC=OD,∴△BOD和△COD都是等边三角形,∴OB=BD=DC=OC,∴四边形OBDC是菱形.(2)连接OA,∵OB=OA,∠ABO=15°,∴∠AOB=150°,∴∠AOC=360°-150°-120°=90°,∴AC=.七、(本题满分12分)22.如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆☉O于点D,连接BD,CD,过点D作直线DM,使∠BDM=∠DAC.(1)求证:直线DM是☉O的切线;(2)若DF=2,AF=5,求BD的长.解:(1)连接OD.∵点E是△ABC的内心,∴∠BAD=∠CAD,∴,∴OD⊥BC.∵∠BDM=∠DAC,∠DAC=∠DBC,∴∠BDM=∠DBC,∴BC∥DM,∴OD⊥DM.又∵OD为☉O的半径,∴直线DM是☉O的切线.(2)∵,∴∠DBF=∠DAB.又∵∠BDF=∠ADB(公共角),∴△DBF∽△DAB,∴,即BD2=DF·DA.∵DF=2,AF=5,∴DA=DF+AF=7,∴BD2=14,∴BD=.八、(本题满分14分)23.如图,AB是☉O的直径,过☉O上一点C作☉O的切线,交AB的延长线于点E.过点A作CE的垂线,垂足为D,AD交☉O于点F,设∠ABC=α(0°<α<90°).(1)用含α的代数式表示∠DAC;(2)若AB=10,sin α=,求AD的长;(3)若α=60°,AB=10,求图中阴影部分的面积.解:(1)连接OC.∵AB为☉O的直径,∴∠ACB=90°.∵OB=OC,∴∠OCB=∠ABC=α,∴∠ACO=90°-α.∵DE切☉O于点C,∴OC⊥DE.∵AD⊥CE,∴AD∥OC,∴∠DAC=∠ACO=90°-α.(2)在Rt△ABC中,∵sin α=,AB=10,∴AC=8.易得∠ACD=α,∴sin ∠ACD=sin α=,即,∴AD=.(3)连接OF,交AC于点G.∵∠DAC=90°-α=90°-60°=30°,∴∠FOC=2∠DAC=60°.∵OB=OC,∠ABC=60°,∴△OBC是等边三角形,∴∠BOC=60°,∴∠AOF=60°.∵OA=OF,∴△OAF是等边三角形,∴AF=OF=OC,∠AFO=60°.在△AFG和△COG中,∴△AFG≌△COG,∴S△AFG=S△COG.∵AB=10,∴☉O的半径r=5,∴S阴影=S扇形OFC=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学总复习第三次周考试卷--圆
班级:___________姓名:___________座号:___________ 2016.3.26
一、选择题(每小题3分,共30分)
1.如图,线段AB 是⊙O 的直径,弦CD ⊥AB ,∠CAB =20°,则∠AOD 等于( ) A .160° B .150° C .140° D .120°
第1题 第2题 第3题 第4题
2.如图,在直角坐标系中,以原点为圆心,半径为5的圆内有一点P(0,-3),那么经过点P 的所有弦中,最短的弦的长为( )
A .4
B .5
C .8
D .10 3.如图,AB 是⊙O 的直径,CD 切⊙O 于点C ,若∠BCD =25°,则∠B 等于( ) A .25° B .65° C .75° D .90°
4.如图,AB 是⊙O 的直径,AC 是⊙O 的切线,A 为切点,连接BC 交⊙O 于点D ,连接AD ,若∠ABC =45°,则下列结论正确的是( )
A .AD =12BC
B .AD =1
2
AC C .AC >AB D .AD >DC
5.如图,△ABC 的内切圆⊙O 与AB ,BC ,CA 分别相切于点D ,E ,F ,若∠DEF =52°,则∠A 的度数是( )
A .52°
B .76°
C .26°
D .128°
第5题 第6题 第7题 第8题 6.如图,⊙O 与正方形ABCD 的两边AB ,AD 相切,且DE 与⊙O 相切于点E.若⊙O 的半径为5,且AB =11,则DE 的长度为( )
A .5
B .6
C .30
D .11
2
7.如图是一个废弃的扇形统计图,小华利用它的阴影部分来制作一个圆锥,则这个圆锥的底面半径是( )
A .3.6
B .1.6
C .3
D .6
8.如图,在⊙O 内有折线OABC ,其中OA =8,AB =12,∠A =∠B =60°,则BC 的长为( )
A .19
B .16
C .18
D .20
9.如图,一个半径为r 的圆形纸片在边长为a(a >23r)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“接触不到的部分”的面积是( )
A .π3r 2
B .33-π3
r 2 C .(33-π)r 2 D .πr 2 10.如图,在平面直角坐标系中,⊙P 的圆心坐标是(3,a)(a >3),半径为3,函数y =x 的图象被⊙P 截得的弦AB 的长为42,则a 的值是( )
A .4
B .3+ 2
C .3 2
D .3+ 3
第9题 第10题 第11题 第12题
二、填空题(每小题3分,共24分)
11.如图,在⊙O 中,AB ︵=CD ︵
,∠DCB =28°,则∠ABC =_____________度. 12.如图,四边形ABCD 是⊙O 的内接四边形,若∠C =130°,则∠BOD =_____________度.
13.如图,AB 是⊙O 的直径,点C 在AB 的延长线上,CD 与⊙O 相切于点D ,若∠C =20°,则∠CDA =_____________°.
第13题 第14题 第16题 第18题
14.如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足为E ,连接AC ,若∠CAB =22.5°,CD =8 cm ,则⊙O 的半径为_____________cm .
15.用半径为12 cm ,圆心角为90°的扇形纸片围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为_____________cm .
16.如图,MN 是⊙O 的弦,正方形OABC 的顶点B ,C 在MN 上,且点B 是CM 的中点,若正方形OABC 的边长为7,则MN 的长为_____________.
17.直径为10 cm 的⊙O 中,弦AB =5 cm ,则弦AB 所对的圆周角是_______________. 18.如图,在△ABC 中,AB =6,将△ABC 绕点B 顺时针旋转60°后得到△DBE ,点A 经过的路径为弧AD ,则图中阴影部分的面积是_____________.
三、解答题(共46分)
19.(9分)如图,在⊙O 中,AB 是直径,点D 是⊙O 上的一点,点C 是AD ︵
的中点,弦CM 垂直AB 于点F ,连接AD ,交CF 于点P ,连接BC ,∠DAB =30°.
(1)求∠ABC 的度数;
(2)若CM =83,求AC ︵
的长度.(结果保留π)
20.(9分)已知△ABC内接于⊙O,过点A作直线EF.
(1)如图①,若AB为⊙O的直径,要使EF成为⊙O的切线,还需要添加的一个条件是(要求写出两种情况):_____________或_____________;
(2)如图②,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是⊙O的切线吗?试证明你的判断.
21.(9分)如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′·OP=r2,则称点P′是点P关于⊙O的“反演点”.如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是A,B关于⊙O的反演点,求A′B′的长.
22.(9分)如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E.
(1)求∠OCA的度数;
(2)若∠COB=3∠AOB,OC=23,求图中阴影部分面积.(结果保留π和根号)
23.(10分)如图,等腰三角形ABC 中,AC =BC =10,AB =12,以BC 为直径作⊙O 交AB 于点D ,交AC 于点G ,DF ⊥AC ,垂足为F ,交CB 的延长线于点E.
(1)求证:直线EF 是⊙O 的切线; (2)求cos E 的值.
附加题.(10分)如图,在△ABC 的外接圆⊙O 中,△ABC 的外角平分线CD 交⊙O 于
点D ,F 为AD ︵上一点,且AF ︵=BC ︵
,连接DF ,并延长DF 交BA 的延长线于点E.
(1)判断DB 与DA 的数量关系,并说明理由; (2)求证:△BCD ≌△AFD ;
(3)若∠ACM =120°,⊙O 的半径为5,DC =6,求DE 的长.。
