欧拉法解常微分方程
欧拉法matlab程序

欧拉法matlab程序1. 介绍在数学和工程领域中,欧拉法(Euler’s Method)是一种用于数值求解常微分方程的方法。
它是一种简单而有效的方法,通过离散化时间和空间,将微分方程转化为差分方程,在计算机程序中实现求解。
由于其易于理解和实现,欧拉法被广泛用于教学和工程实践中。
在本文中,我们将详细讨论如何使用MATLAB编写欧拉法程序。
我们将探讨欧拉法的原理、步骤、程序实现以及示例应用。
2. 欧拉法的原理欧拉法基于微分方程的初值问题,通过近似求解微分方程得到数值解。
它将连续的问题离散化为离散的差分问题。
对于一阶常微分方程,具有以下形式:dy=f(t,y)dt其中,t是自变量,y是因变量,f(t,y)是给定的函数。
假设我们已经知道初值条件t0和y(t0),以及步长ℎ,则欧拉法通过以下递推公式求解数值解:y n+1=y n+ℎ⋅f(t n,y n)其中,y n是第n步的数值解,t n=t0+n⋅ℎ。
欧拉法的基本原理是通过在每个时间步长上使用切线来逼近函数曲线,从而得到数值解。
该方法的准确性取决于步长的选择,较小的步长可以提高准确性,但增加了计算复杂度。
3. MATLAB实现欧拉法程序的步骤3.1 定义微分方程首先,我们需要定义要求解的微分方程。
在MATLAB中,可以使用一个匿名函数来=−αy,可以定义如下:表示微分方程。
例如,对于一个简单的线性微分方程dydtf = @(t, y) -alpha * y;3.2 设置初始条件和步长接下来,我们需要设置初始条件和步长。
初始条件包括t0和y(t0),步长ℎ表示每个时间步长的间隔。
t0 = 0;y0 = 1;h = 0.1;3.3 迭代计算使用欧拉法进行迭代计算,直到达到所需的终止条件。
在每个时间步长上,根据欧拉法的递推公式,更新数值解。
t = t0;y = y0;while t <= tf % 终止条件为t <= tfy = y + h * f(t, y);t = t + h;end3.4 可视化结果最后,我们可以使用MATLAB的绘图功能将结果可视化。
第五章:常微分方程数值解法第一节欧拉法

常微分方程数值解法-欧拉法、改进欧拉法与四阶龙格库塔法常微分方程数值解法

y( xn1)
y( xn
Байду номын сангаас
h)
y(xn )
hy'( xn )
h2 2!
y''( )
进一步: 令
h2 y( xn ) hy'( xn ) 2! y''( xn )
常微分方 yn1 y( xn1 ) , yn y( xn )
程数值解
法-欧拉法 yn1 yn hf ( xn , yn ) h2
、改进欧 y( xn1 ) yn1
2
max y''( x)
a xb
拉法和四
三、Euler方法
已 知 初 值 问 题 的 一 般 形式 为:
dy
dx
f (x, y)
a xb
(1)
y( x0 ) y0
常微分方 用差商近似导数 程数值解 问题转化为
yn1 yn dy
h
dx
法-欧拉法 yn1 yn hf ( xn , yn )
法-欧 y(拉0) 法1
、改进欧
拉法和四
四、几何意义
由 x0 , y0 出发取解曲线 y yx 的切线(存在!),则斜率
dy
f x0, y0
dx x y
,
0
0
常微分方 由于 f x0, y0 及 x0, y0 已知,必有切线方程。
由点斜式写出切程线方数程:值解
法、-改欧进拉欧法 ddxy y y0 x x0
常微分方 程数值解 能用解析方法求出精确解的微分方程为数不多,
而且有的方程即使有解析解,也可能由于解的表达
法-欧拉法 式非常复杂而不易计算,因此有必要研究微分方程
欧拉近似方法求常微分方程

欧拉近似方法求常微分方程朱翼1、编程实现以下科学计算算法,并举一例使用之。
“欧拉近似方法求常微分方程”算法说明:欧拉法是简单有效的常微分方程数值解法,欧拉法有多种形式的算法,其中简单欧拉法是一种单步递推算法。
其基本原理为对简单的一阶方程的初值问题:y’=f(x,y)其中y(x0 )=y0欧拉法等同于将函数微分转换为数值微分,由欧拉公式可得y n+1 =y n+hf(x n ,y n)程序代码:function [tout,yout]=myeuler(ypfun,t0,tfinal,y0,tol,trace) %初始化pow=1/3;if nargin<5,tol=1.e-3;endif nargin<6,trace=0;endt=t0;hmax=(tfinal-t)/16;h=hmax/8;y=y0(:);chunk=128;tout=zeros(chunk,1);yout=zeros(chunk,length(y));k=1;tout(k)=t;yout(k,:)=y.';if trace %绘图 clc,t,h,yendwhile (t<tfinal)&(t+h>t) %主循环if t+h>tfinal,h=tfinal-t;end% Compute the slopesf=feval(ypfun,t,y);f=f(:);%估计误差并设定可接受误差delta=norm(h*f,'inf');tau=tol*max(norm(y,'inf'),1.0);%当误差可接受时重写解if delta<=taut=t+h;y=y+h*f;k=k+1;if k>length(tout)tout=[tout;zeros(chunk,1)];yout=[yout;zeros(chunk,length(y))];endtout(k)=t;yout(k,:)=y.';endif tracehome,t,h,yend% Update the step sizeif delta~=0.0h=min(hmax,0.9*h*(tau/delta)^pow);endendif (t<tfinal)dish('Singularity likely.')tendtout=tout(1:k);yout=yout(1:k,:);流程图:用欧拉法求y’=-y+x+1,y(0)=1。
常微分方程数值解法欧拉法

)
f ( xn1, yn1)
hL
y(k ) n 1
yn1
L
hL
k 1
y(0) n 1
yn1
Q
hL 1,
y (k 1) n 1
yn1 (k
)
在迭代公式中取极限,有
yn1 yn h f ( xn1, yn1 ) 因此yn(k1)的极限就是隐式方程的解
几何意义
y
设已知曲线上一点 Pn (xn , yn ),过该 点作弦线,斜率为(xn+1 , yn +1 ) 点的 方向场f(x,y)方向,若步长h充分小, 可用弦线和垂线x=xn+1的交点近似 曲线与垂线的交点。
式。隐式公式不能直接求解,一般需要用Euler显式公式
得到初值,然后用Euler隐式公式迭代求解。因此隐式公
式较显式公式计算复杂,但稳定性好
y0 n1
yn
h
y(k 1) n1
yn
h
f (xn , yn )
f
( xn1 ,
y(k) n1
)
收敛性
y (k 1) n 1
yn1
h
f
( xn1,
y(k ) n 1
如何求解
解析解法:(常微分方程理论)
只能求解极少一类常微分方程;实际中给定的问题不一 定是解析表达式,而是函数表,无法用解析解法。
数值解法: 求解所有的常微分方程
计算解函数 y(x) 在一系列节点 a = x0< x1<…< xn= b
处的近似值 yi y( xi ) (i 1, ... , n)
y(xn1) y(xn ) hy(xn ) y(xn ) yn
y(xn1) yn1 yn h f (xn , yn )
常微分方程的数值解法(欧拉法、改进欧拉法、泰勒方法和龙格库塔法)
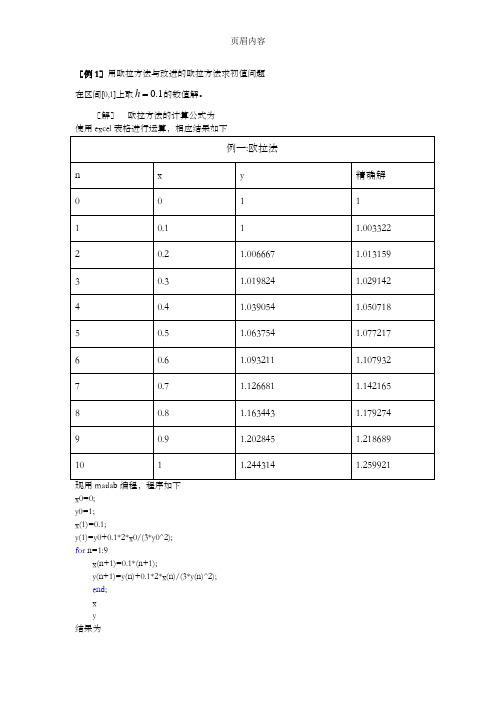
[例1]用欧拉方法与改进的欧拉方法求初值问题h 的数值解。
在区间[0,1]上取0.1[解]欧拉方法的计算公式为x0=0;y0=1;x(1)=0.1;y(1)=y0+0.1*2*x0/(3*y0^2);for n=1:9x(n+1)=0.1*(n+1);y(n+1)=y(n)+0.1*2*x(n)/(3*y(n)^2);end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0067 1.0198 1.0391 1.0638 1.0932 1.1267 1.1634 Columns 9 through 101.2028 1.2443改进的欧拉方法其计算公式为本题的精确解为()y x=x0=0;y0=1;ya(1)=y0+0.1*2*x0/(3*y0^2);y(1)=y0+0.05*(2*x0/(3*y0^2)+2*x0/(3*ya^2));for n=1:9x(n+1)=0.1*(n+1);ya(n+1)=ya(n)+0.1*2*x(n)/(3*ya(n)^2);y(n+1)=y(n)+0.05*(2*x(n)/(3*y(n)^2)+2*x(n+1)/(3*ya(n+1)^2));end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0099 1.0261 1.0479 1.0748 1.1059 1.1407 1.1783 Columns 9 through 101.2183 1.2600[例2]用泰勒方法解x=0.1, 0.2, …, 1.0处的数值解,并与精确解进行比较。
欧拉法求解微分方程matlab

欧拉法求解微分方程matlab引言微分方程是数学中一类重要的方程,广泛应用于物理、工程、经济等领域。
而求解微分方程是数学建模与计算科学中的一个关键问题,其中欧拉法是一种常用的数值求解微分方程的方法。
本文将介绍欧拉法的原理和具体实现方法,并用MATLAB进行实例演示。
欧拉法原理欧拉法是一种基于近似和离散化的数值求解微分方程的方法。
它的基本思想是将微分方程转化为差分方程,通过近似求解差分方程来得到微分方程的近似解。
以一阶常微分方程为例,我们设方程为dy/dx = f(x, y),其中f(x, y)为已知函数。
欧拉法的基本思想是通过将自变量x的区间[a, b]离散化为多个小区间,然后在每个小区间上用线性插值来计算近似解。
具体步骤如下:1.将区间[a, b]平均分割成n个小区间,每个小区间的宽度为h = (b - a) /n。
2.初始化近似解的初始值,通常是在初始点(a, y0)处,其中y0为已知的初始条件。
3.根据差分方程的递推关系式,依次计算每个小区间上的近似解,直到达到终点(b, yn)。
递推关系式为:yn+1 = yn + h * f(xn, yn),其中xn为当前区间的起点。
欧拉法的优缺点欧拉法作为一种简单直观的数值求解方法,具有以下优点:•简单易懂,易于理解和实现。
•计算代价较小,在有限的计算资源下能够快速求解微分方程。
•在某些情况下能够得到较为精确的近似解。
然而,欧拉法也存在一些缺点:•求解精度有限,特别是在计算步长较大或方程非线性的情况下,误差会积累导致结果偏差较大。
•对于某些特殊的微分方程,欧拉法可能不收敛或产生不稳定的结果。
•仅适用于离散化步长较小的情况,对于某些复杂的微分方程,求解效果可能较差。
在实际应用中,我们需要根据具体的问题和求解要求来选择合适的数值求解方法,欧拉法只是其中的一种选择。
欧拉法的MATLAB实现以下是欧拉法在MATLAB中的实现代码:function [x, y] = eulerMethod(f, a, b, y0, n)h = (b - a) / n;x = a:h:b;y = zeros(1, n+1);y(1) = y0;for i = 1:ny(i+1) = y(i) + h * f(x(i), y(i));endend在该代码中,我们定义了一个名为eulerMethod的函数,该函数接受以下参数:•f:已知函数f(x, y),表示微分方程dy/dx = f(x, y)的右侧项。
数学物理方程的数值解法

数学物理方程的数值解法数学物理方程是自然界和科学中描述物体运动、能量转化和相互作用的基本规律。
我们通常使用数值解法来求解这些方程,以得到近似的解析解。
数值解法既可以用于数学问题,也可以用于物理问题。
本文将介绍几种常见的数学物理方程的数值解法。
一、微分方程的数值解法微分方程是描述物体运动和变化的重要工具。
常见的微分方程有常微分方程和偏微分方程。
常见的数值解法包括:1. 欧拉法(Euler's method)欧拉法是最简单的数值解法之一,通过将微分方程离散化为差分方程,在每个小时间步长上近似计算微分方程的导数。
欧拉法易于实现,但精度相对较低。
2. 龙格-库塔法(Runge-Kutta method)龙格-库塔法是一类常用的数值解法,包括二阶、四阶等不同的步长控制方法。
龙格-库塔法通过计算多个离散点上的导数来近似微分方程,精度较高。
3. 有限差分法(Finite difference method)有限差分法是一种常用的数值解法,将微分方程转化为差分方程并在网格上逼近微分方程的导数。
有限差分法适用于边值问题和初值问题,且精度较高。
二、积分方程的数值解法积分方程描述了给定函数的积分和积分变换之间的关系。
常见的数值解法有:1. 数值积分法数值积分法是通过数值逼近求解积分方程,常用的数值积分法包括梯形法则、辛普森法则等。
数值积分法适用于求解一维和多维积分方程。
2. 蒙特卡洛法(Monte Carlo method)蒙特卡洛法通过随机采样和统计分析的方法,将积分方程转化为概率问题,并通过大量的随机样本来估计积分值。
蒙特卡洛法适用于高维空间和复杂积分方程。
三、优化问题的数值解法优化问题是寻找在给定约束条件下使目标函数取得极值的数学问题。
常见的数值解法有:1. 梯度下降法(Gradient descent method)梯度下降法是一种常用的优化算法,通过迭代和梯度方向来寻找目标函数的局部最优解。
梯度下降法适用于连续可导的优化问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
错误!未定义书签。
数学与计算科学学院
实验报告
实验项目名称Eular方法求解一阶常微分方程数值解
所属课程名称偏微分方程数值解
实验类型验证性
实验日期2015-3-26
班级
学号
姓名
成绩
一、实验概述:
【实验目的】
熟练掌握应用显性Eular法和隐式Eular法求解一般一阶常微分方程的近似数值解。
【实验原理】
虽然求解常微分方程有各种各样的解析方法,但解析方法只能用来求解一些特殊类型的方程。
求解从实际问题当中归结出来的微分方程主要靠数值解法。
欧拉方法是一类重要的数值解法。
这类方法回避解y(x)的函数表达式,而是寻求它在一系列离散节点上的近似值,相邻的两个节点的间距称作步长。
假定步长为定数。
欧拉方法是一类离散化方法,这类方法将寻求解y(x)的分析问题转化为计算离散值值的代数问题,从而使问题获得了实质性的简化。
然而随之带来的困难是,由于数据量往往很大,差分方法所归结出的可能是个大规模的代数方程组。
【实验环境】
1.硬件环境
2.2.软件环境
MATLAB7.0
二、实验内容:
【实验结论】
A步长h=0.001时进行数据测试。
结果如下:迭代第一次时,
结果与方程描述内容相符。
迭代第二次时,
结果与方程描述内容基本相符。
迭代三次时,
结果与方程描述内容基本相符。
迭代1000次时,
模拟结果已经严重脱离事实,故当选择delta为0.001时,该迭代方法不收敛。
时间与个变量直接的变化关系如图所示:
从上述图形可以明显看出,在迭代的不断进行时,各变量与时间的变化越来越大,且严重脱离了方程所描述的现实意义。
B.当选择h=0.00000001时,模拟结果如下:
迭代第一次,
与A中结果相同。
迭代第二次,
跌二次迭代结果明显优于一中。
跌三次迭代结果,
并未产生误差。
地1000次迭代结果,
结果明显是收敛的。
时间与个变量直接的变化关系如图所示:
从图中能够清晰看出,当h=0.00000001时,模拟结果与方程所表示的显示意义相吻合。
说明了显性Eualr方法的收敛性是与步长的选择是相关。
这就对我们们选择步长造成了困难,由于选择的步长不合适有可能得出错误的结论。
附录:源程序。
