2021年北师大版七年级数学下册第一章《整式的除法(二)》导学案.doc
(完整)北师大版七年级数学下册第一章整式的乘除导学案
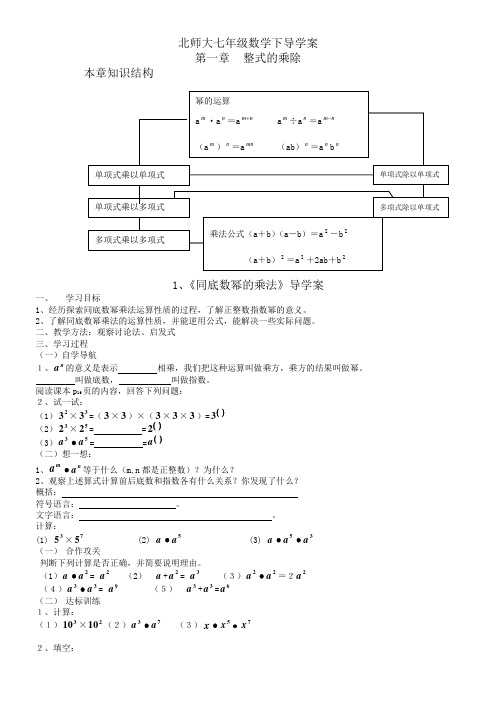
北师大七年级数学下导学案 第一章 整式的乘除本章知识结构1、《同底数幂的乘法》导学案一、 学习目标1、经历探索同底数幂乘法运算性质的过程,了解正整数指数幂的意义。
2、了解同底数幂乘法的运算性质,并能逆用公式,能解决一些实际问题。
二、教学方法:观察讨论法、启发式 三、学习过程 (一)自学导航1、na 的意义是表示 相乘,我们把这种运算叫做乘方,乘方的结果叫做幂。
叫做底数, 叫做指数。
阅读课本p 16页的内容,回答下列问题: 2、试一试:(1)23×33=(3×3)×(3×3×3)=()3(2)32×52= =()2 (3)3a •5a = =()a(二)想一想:1、ma •n a 等于什么(m,n 都是正整数)?为什么?2、观察上述算式计算前后底数和指数各有什么关系?你发现了什么? 概括: 符号语言: 。
文字语言: 。
计算:(1) 35×75 (2) a •5a (3) a •5a •3a (一) 合作攻关判断下列计算是否正确,并简要说明理由。
(1)a •2a = 2a (2) a +2a = 3a (3)2a •2a =22a(4)3a •3a = 9a (5) 3a +3a =6a (二) 达标训练 1、计算:(1)310×210(2)3a •7a (3)x •5x •7x2、填空:5x •( )=9x m •( )=4m 3a •7a •( )=11a3、计算:(1)m a •1+m a (2)3y •2y +5y (3)(x+y)2•(x+y)64、灵活运用:(1)x 3=27,则x= 。
(2)9×27=x3,则x= 。
(3)3×9×27=x3,则x= 。
(三) 总结提升1、怎样进行同底数幂的乘法运算?2、练习:(1)53×27= (2)若ma =3,na =5,则nm a += 。
北师大版七年级数学下册第一章 整式的乘除 导学案

第一章 整式的运算1.整式导学案学习目标1.了解整式产生的背景和整式的概念;2.会识别单项式、多项式和整式,确定次数和项数. 重点:目标2 难点:识别单项式与多项式的次数学习过程一、知识回顾1.什么叫同类项?答:所含字母相同,相同字母的指数也相同的项 .例如: (略). 2.化简:)45(2)2(32222y x xy y x xy ---=-7y x x y222+二、自主探究1.阅读P 2 (1)图1-1中装饰物所占的面积是b216∆,窗户中能射进阳光 的部分的面积是bab 216∆-; (2)写出做一做中各小题答案:①mn ab 2121-;②x 53;③h a 2;2.阅读P 3,回答:(1)单项式的特 数与字母的乘积 ;(2)多项式的主要特征是 几个单项式的和 ,举两个例子. 单项式 和 多项式 称为整式.(3)单项式的次数是指 所有字母的指数和 ,单独一个非零数的次数是 O ; (4) 一个多项式钟,次数最高的项的次数 叫多项式的次数。
3.“读一读”P 4~P 5皮克公式 三、课堂练习1.判断下列各代数式是否单项式,如果不是,说明理由;① x +1 ② x 1 ③ πr 2④ -23a 2b ⑤ -abc ⑥πb a 23(1)(2)不是,;(3)(4)(5)(6)是2.下面说法:①单项式m 即没有系数,也没有次数;②单项式5×105t 的系数是5;③-2009是单项式;④11+x 是多项式;⑤π1是单项式;正确的个数有(B ) A.1 B.2 C.3 D.43.单项式232xy π-的系数是∆23-,次数是 3 ;32-的系数是32-,次数是 0 .4.多顶式52132--x x 的各项分别是5;21;32--x x . 5.多项式10232011323-+-x yx 是 四 次 三 项式;最高次项的系数是 -3/2 , 常数项是201110-.6.一个n 次多项式(n 为正整数),它的每一项的次数( D ) A.都是n B.都小于n C.都不小于n D.都不大于n 四、小结与反思本节的知识点有;单项式,多顶式的概念以及它们的次数 ;我的困惑是 . 五、拓展延伸1. 已知多项式12513212--+-+z y x y x m 是六次四项式,单项式n m y x 25--与该多项式次数相同,求m 、n 的值.解;由题意可得;2+m +1=6; 5-m +2n =6 所以 m =3; n =22. 已知多项式12112101112b ab b a b a a-++-+-Λ.(1)请你按照上述规律写出该多项式的第5项,并指出它的系数和次数. (2)这个多项式是几次几项式?解;(1)第5项是 ba 48-,系数是-1,次数是12;(2)这个多项式是12次13项式.第一章 整式的运算 2.整式的加减导学案(1)学习目标1.经历用字母表示数量关系的过程;2.会进行整式的加减运算,并能说明其中的算理; 重点和难点:目标2学习过程一、知识回顾1.单项式y x 222-的系数是 ,次数是 ;多项式431323b a b a a x -++的次数与单项式c b a 4322的次数相同,则x = .2.3ab -(3ab -4a 2b )是否为整式?答: .上式的计算结果是 , 在计算过程中,我应用了学过的知识 . 二、自主探究1.阅读课本P 7并按课文要求“做一做”(1),(2),(3)写在练习本上,再举几个两位数重复上面的过程.我发现这些和有一个规律 ,这个规律对任意一个两位数都成立吗?答: .2.用字母表示两位数后,把相加的结果填在书上的空格中,从运算结果再看前面的规律你的感悟是 ;3.“做一做”P 7下半部分,得到的结论是 .4.在上面的两个问题中,前一个式子用到了整式的 运算,后一个式子用到了整式的 运算,口述你是如何运算的. 5.相信你能够顺利完成P 8例1问:你在做整式加减的过程中会遇到的两个主要步骤是 , 注意事项为 .三、随堂练习1.P 9 随堂练习写在下面.2.化简求值:)4()(242222y x y x y ,其中3-=x ,6=y .四、小结与反思本节课的知识点有 ; 我的困惑是 . 五、拓展1.对于有理数a 、b 定义b a b a 23+=⊕,试化简x y x y x 3)]()[(⊕-⊕+.2.已知2223y xy x M +-=,2232y xy x N -+=,求 ①N M + ; ②N M 32-.达州外国语学校校本课程◆初2014级数学◆导学:第一章 整式的运算2.整式的加减导学案(2)学习目标1.进一步体会符号表示数的意义,提高符号感; 2.熟练地进行整式运算,解决实际问题;重点:熟练进行整式加减运算 难点:准确计算,对实际问题会归纳学习过程一、知识回顾1.整式的加减的实质是 ;如果遇到括号时,则要 。
2021年北师大版七年级数学下册第一章《整式的除法(2)》公开课课件 (2)

1 2
vt 2
小明下山所用时间为:(v1t1 2v2t)4v1 4t18 1t2
∴小明下山所用时间为: 1 4
t1
1 8
t2
小结(2分钟)
本节课你的收获是什么?
1、单项式相除
1、系数相除; 2、同底数幂相除; 3、只在被除式里的幂不变。
2、多项式除以单项式
先把这个多项式的每一项分别除以单项式, 再把所得的商相加。
a
2a
(1)瓶子
8
1a 2
(2)杯子
(x 1 )(2 x 1 )(2 x 2 1 )(4 x 4 1 )(1 6 x 8 1 ) (2 5 6 x 1 6 1)
2
2 4 1 6 2 5 6
当堂训练答案
1.计算题答案
(1)2y 1
( 2) 8x45x22
( 3) 71m2n215m3125n3( 4) 9a6b
3、单项式除以单项式结果仍是单项式, 多项式除以单项式结果仍是多项式。
当堂训练 18分钟)
1.计算下列各式
( 1) (2xyx)x (2)(8x55x32x)x
(3( )7 5m 2n31 5m 3n22 3n5) 5n( 2 4 ) ( 3 a b ) 2 b 2 a
No 2.一个多项式除以 2 x 2 y 其商为 (4x3y26x3y2x4y2) 求这个多项式。
1.7 整式的除法(2)
学习目标(1分钟)
1.探索多项式除以单项式的法则 2.运用法则进行简单计算
自学指导(1分钟)
请同学们认真阅读P30--31页,完成下列问题。
1、完成“议一议”之前的填空,能说出你的理 由吗? 2、如何进行多项式除以单项式的运算? 3、认真看例2的解题过程,看商式的项数与被除
【最新】北师大版七年级数学下册第一章《整式的乘法(2)》导学案 (2)

精品资料新北师大版七年级数学下册第一章《整式的乘法(2)》导学案课题 1.4整式的乘法(2)课时 1 课型预习+展示学生活动(自主参与、合作探究、展示交流)学习目标经历探索整式的乘法运算法则的过程,会进行简单的整式的乘法运算三、巩固提升例题讲解(1))6-)(21-10-12(-3322yxyyxxy(2)222(-2)()5()a ab b a a b ab*+++练一练1. -3x(-y-xyz)[来源:Z§xx§]2.(x3)2―2x3[x3―x(2x2―1)]3.已知有理数a、b、c满足|a―b―3|+(b+1)2+|c-1|=0,求(-3ab)·(a2c-6b2c)的值。
4.已知:2x·(x n+2)=2x n+1-4,求x的值。
5.若a3(3a n-2a m+4a k)=3a9-2a6+4a4,求-3k2(n3mk+2km2)的值。
重难点整式的乘法运算推测整式乘法的运算法则学生活动(自主参与、合作探究、展示交流)一、预习交流1、思考:单项式与多项式相乘最容易出错的是哪点?2、预习作业:(1)2(ab-3) =(2)(2xy2)·3yx=(3)(―2a3b) (―6ab6c) =(4)-3(ab2c+2bc-c) =3、写一个多项式,并说出它的次数和项数。
4、你在预习中还有哪些疑惑?二、探究释疑如图所示,公园中有一块长mx米、宽y米的空地,根据需要在两边各留下宽为a米、b米的两条小路,其余部分种植花草,求种植花草部分的面积.你是怎样列式表示种植花草部分的面积的?是否有不同的表示方法?其中包含了什么运算?方法一:可以先表示出种植花草部分的长与宽,由此得到种植花草部分面积为方法二:可以用总面积减去两条小路的面积,得到种植花草部分面积为由上面的探索,我们得到了上面等式从左到右运用了乘法分配律,将单项式乘以多项式转化为单项式乘以单项式单项式与多项式相乘:。
北师大版七年级数学下册第1章1.7整式的除法第2课时多项式除以单项式(教案)

一、教学内容
本节课我们将深入探讨北师大版七年级数学下册第1章“整式的除法”中的1.7节,第2课时“多项式除以单项式”的内容。具体包括以下要点:
1.理解并掌握多项式除以单项式的运算法则;
2.能够正确运用多项式除以单项式的运算解决实际问题;
五、教学反思
在今天的课程中,我们探讨了多项式除以单项式的知识点。回顾整个教学过程,我觉得有几个方面值得反思和总结。
首先,从学生的反馈来看,他们对这个Байду номын сангаас识点的掌握程度参差不齐。在讲解过程中,我尽量用简单的语言和生动的案例进行解释,但仍有部分学生在实际操作时遇到困难。针对这一点,我考虑在接下来的课程中增加一些针对性的练习,以巩固学生对多项式除以单项式的理解和运用。
-指导学生如何处理除法运算中出现的余数,以及如何将余数转化为分数或小数;
-强调检查计算结果的重要性,包括验证商与余数是否正确。
举例:学生在解决类似“计算(3x^3 - 5x^2 + 2x) ÷ (2x - 1)”这样的问题时,可能会在合并同类项或处理余数时遇到困难。
四、教学流程
(一)导入新课(用时5分钟)
2.培养学生运用数学语言进行表达和交流,增强数学建模和抽象思维能力;
3.在解决多项式除以单项式问题时,学会分析问题、归纳总结,提高数学推理和数据分析能力;
4.培养学生合作探究、自主学习的意识,提高数学学习的兴趣和自信心;
5.引导学生关注数学在现实生活中的应用,增强数学应用的意识和实践能力。
三、教学难点与重点
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
数学:1.9.1《整式的除法(2)》学案(北师大七年级下)

1.9整式的除法(2)【目标导航】理解多项式除以单项式的运算法则,并能用法则进行计算;理解有理数的运算律在整式的加、减、乘、除运算中仍然适用,能比较熟练地进行整式计算。
【知识梳理】一般地,多项式除以单项式,先把这个多项式的分别除以,再把所得的商 .【学法导航】同底数幂的除法是学习整式除法的基础,在复习过程中一定要落实好同底数幂的除法法则。
此外,可以适当选择几个单项式除法的计算题让学生完成,一方面巩固旧知识,另一方面为学习新知识打基础。
【预习检查】填空题(1)(625+125+50)÷25=()÷()+()÷()+()÷()=(2)(4a+6)÷2=()÷()+()÷()=(3)(2a-a)÷(-2a)=()÷(-2a)+()÷(-2a)=【课堂探究】一、课本探究1.课本p41页教科书做一做计算下列各题,说说你的理由(课题:多项式除以单项式)a b+3ab) ÷a1、(ad+bd)÷d2、(23、(x3y-2xy) ÷(xy)二、典例展示知识点1:多项式除以单项式【例】1计算:(1)(6ab +8b )÷(2b );(2)(27a 3-15a 2+6a )÷(3a );(3)(9x 2y -6xy 2)÷(3xy );(4)(3x 2y -xy 2+21xy )÷(-21xy )【变式】计算:(1)(28a 3-14a 2+7a )÷(7a );(2)(36x 4y 3-24x 3y 2+3x 2y 2)÷(-6x 2y );(3)[(2x +y )2-y (y +4x )-8x ]÷2x .分析:1.多项式除以单项式,被除式有几项,商仍有几项,不可丢项,其中(1)容易丢掉最后一项;2.可以利用乘除是互逆运算,检验计算是否正确;3.每一步运算都要求学生说出变形的依据;4.(4)题要分清运算顺序,把计算结果写完整.【自主操练】1.一个多项式除以2x 2y ,其商为(4x 3y 2-6x 3y +2x 4y 2),则这个多项式为( )A.2xy -3x +x 2y B.8x 6y 2-12x 6y +4x 8y 2C.2x -3xy +x 2y D.8x 5y 3-12x 5y 2+4x 6y 32.一个x 的四次三项式被一个x 的二次单项式整除,其商式为( )A.二次三项式 B.三次三项式 C.二次二项式 D.三次二项式3. (-8x 4y +12x 3y 2-4x 2y 3)÷(4x 2y )等于( )A.-2x 2y +3xy -y 2B.-2x 2+3xy -y 2C.-2x 2+3xy -yD.-2x 2+3xy 2-y 24.计算正确的是( )A.(9x 4y 3-12x 3y 4)÷3x 3y 2=3xy -4xy 2B.(28a 3-14a 2+7a )÷7a =4a 2-2a +7aC.(-4a 3+12a 2b -7a 3b 2)÷(-4a 2)=a -3b +47ab 2D.(25x 2+15x 2y -20x 4)÷(-5x 2)=-5-3xy +4x 25. ÷(-4a 2)=12a 4-16a 3+4a 2.6.(6a 2+4a -10ab )÷(2a )= .(1)(5x 2y 3-4x 3y 2+6x )÷6x ;(2)[x (3-4x )+2x 2(x -1)]÷(-2x );(3)(28a 3-14a 2+7a)÷7a ;(4)(36x 4y 3-24x 3y 2+3x 2y 2)÷(-6x 2y)8.化简,求值÷(xy),其中x=10,y=251。
北师大版七年级数学下册第一章整式的运算导学案

课题:1.1 同底数幂的乘法【课型】新授【学习目标】1.能够在实际情境中,抽象概括出所要研究的数学问题,增强学生的数感符号感。
2.在已有的对幂的知识的了解基础之上,通过与同伴合作,经历探索同底数幂乘法运算性质过程,进一步体会幂的意义,发展合作交流能力、推理能力和有条理的表达能力。
3. 了解同底数幂乘法的运算性质,并能解决一些实际问题,感受数学与现实生活的密切联系,增强学生的数学应用意识,训练他们养成学会分析问题、解决问题的良好习惯。
【重点】掌握同底数幂乘法的运算性质。
【难点】应用同底数幂乘法的运算性质解决一些实际问题。
【教学准备】多媒体课件【教学过程】一、复习检测复习七年级上册数学课本中介绍的有关乘方运算知识:二、导入新课以课本上有趣的天文知识为引例,让学生从中抽象出简单的数学模型,实际在列式计算时遇到了同底数幂相乘的形式,给出问题,启发学生进行独立思考,也可采用小组合作交流的形式,结合学生现有的有关幂的意义的知识,进行推导尝试,力争独立得出结论。
三、自主探究,讨论交流1.利用乘方的意义,提问学生,引出法则:计算103×102.解:103×102=(10×10×10)×(10×10)(幂的意义)=10×10×10×10×10 (乘法的结合律)=105.2.引导学生建立幂的运算法则:将上题中的底数改为a,则有 a3•a2=(aaa)•(aa)=aaaaa=a5,即a3•a2=a5=a3+2.用字母m,n表示正整数,则有即am•an=am+n.3.引导学生剖析法则(1)等号左边是什么运算? (2)等号两边的底数有什么关系?(3)等号两边的指数有什么关系?(4)公式中的底数a可以表示什么(5)当三个以上同底数幂相乘时,上述法则是否成立?要求学生叙述这个法则,并强调幂的底数必须相同,相乘时指数才能相加.四、课堂小结:师生互相交流总结本节课上应该掌握的同底数幂的乘法的特征,教师对课堂上学生掌握不够牢固的知识进行强调与补充,学生也可谈一谈个人的学习感受。
北师大版数学七年级下册1.7《整式的除法》说课稿2

北师大版数学七年级下册1.7《整式的除法》说课稿2一. 教材分析《整式的除法》是北师大版数学七年级下册第1.7节的内容。
本节课主要介绍整式除法的基本概念、方法和步骤。
整式除法是代数运算的重要组成部分,它在解决实际问题和进一步学习高级数学中具有重要意义。
本节课的内容为后续学习多项式乘法、因式分解等知识打下基础。
二. 学情分析学生在七年级上学期已经学习了整式的加减运算,对整式的概念有了一定的了解。
但是,对于整式除法这种新的运算方法,学生可能存在一定的困难。
因此,在教学过程中,需要注重引导学生理解整式除法的本质,并通过大量的练习让学生熟练掌握整式除法的运算方法。
三. 说教学目标1.知识与技能:让学生掌握整式除法的基本概念、方法和步骤,能够正确地进行整式除法的运算。
2.过程与方法:通过自主学习、合作交流的方式,培养学生解决实际问题的能力。
3.情感态度与价值观:激发学生对数学学习的兴趣,培养学生的耐心和细心。
四. 说教学重难点1.教学重点:整式除法的基本概念、方法和步骤。
2.教学难点:整式除法运算中,如何正确地确定商的首项和尾项。
五. 说教学方法与手段1.教学方法:采用自主学习、合作交流、教师讲解相结合的方法。
2.教学手段:利用多媒体课件进行教学,让学生更直观地理解整式除法的运算过程。
六. 说教学过程1.引入新课:通过复习整式的加减运算,引出整式除法这种新的运算方法。
2.讲解示范:利用多媒体课件,讲解整式除法的基本概念、方法和步骤,让学生直观地理解整式除法的运算过程。
3.学生练习:让学生独立完成一些整式除法的练习题,巩固所学知识。
4.合作交流:让学生分组进行讨论,分享彼此在练习过程中遇到的问题和解决方法。
5.教师点评:对学生的练习情况进行点评,指出存在的问题,并进行讲解。
6.总结提升:对本节课的内容进行总结,强调整式除法的注意事项。
七. 说板书设计板书设计要简洁明了,能够突出整式除法的基本概念、方法和步骤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、探究释疑
计算下列各题,说说你的理由
。
。
。
以上法则的语言生活动
(自主参与、合作探究、展示交流)
一、预习交流
1.计算并回答问题:
(1)4a3b4c÷2a2b2c;(2)(- a2b2c)÷3ab2.
以上的计算是什么运算?能否叙述这种运算的法则?
2.计算并回答问题:
(1)3x(x2- x+1);(2)-4a·( a2-a+2).
以上的计算是什么运算?能否叙述这种运算的法则?
新北师大版七年级数学下册第一章《整式的除法(二)》导学案
课
题
1.7整式的除法(二)
课
时
1
课
型
自学+展示
学生活动
(自主参与、合作探究、展示交流)
学习目标
1.经历探索整式除法运算法则的过程,会进行简单的整式除法运算;
2.理解整式除法运算的算理,发展有条理的思考及表达能力。
三、巩固提高
1.计算:
(l)(28a3-14a2+7a)÷7a;(2)(36x4y3-24x3y2+3x2y2)÷(-6x2y).
2.计算:
(1)(6xy+5x)÷x;(2)(15x2y-10xy2)÷5xy;
(3)(8a2b-4ab2)÷4ab;(4)(4c2d+c3d3)÷(-2c2d).
拓展延伸迁移升华
化简[(2x+y)2-y(y+4x)-8x]÷2x.
四小结
本节课你都有哪些收获?
重难点
多项式除以单项式的法则是本节的重点
