Global Bifurcations in Rayleigh-Benard Convection Experiments, Empirical Maps and Numerical
替罗非班在急性进展性脑梗死中应用

现代医学Modern Medical Journal2020,Aug ;48(8):966-970[收稿日期]2020-03-23[修回日期]2020-08-11[作者简介]尹其舵(1982-),男,安徽巢湖人,主治医师。
E -mail :Yqd19820815@163.com[通信作者]吴清阳E -mail :qingyangwumd@163.com[引文格式]尹其舵,李正侠,耿万杰,等.替罗非班在急性进展性脑梗死中应用[J ].现代医学,2020,48(8):966-970.·论著·替罗非班在急性进展性脑梗死中应用尹其舵1,李正侠1,耿万杰1,吴清阳2(1.安徽省阜阳市太和县人民医院神经内科,安徽阜阳236600;2.南京医科大学附属无锡市人民医院影像科,江苏无锡214023)[摘要]目的:探讨替罗非班联合阿司匹林、氯吡格雷对急性进展性脑梗死患者的临床疗效、生活质量ADL 评分、神经功能缺损NIHSS 评分的影响。
方法:前瞻性分析90例急性进展性脑梗死患者,随机分为观察组和对照组,各45例。
对照组给予服用阿司匹林、氯吡格雷治疗,观察组在经替罗非班联合治疗(24 72)h 后贯续服用阿司匹林及氯吡格雷。
比较2组患者治疗后临床疗效、NIHSS 评分(24h 、72h 、7d 及14d )、ADL 评分及不良反应发生率。
结果:观察组总有效率为88.99%,高于对照组的71.11%(P <0.05);观察组治疗后NIHSS 评分低于对照组,且观察组治疗后与治疗前ADL 评分差值高于对照组(P <0.05);不良反应发生率:观察组为13.85%,对照组为7.69%(P >0.05)。
结论:替罗非班联合阿司匹林、氯吡格雷能有效地改善急性进展性脑梗死患者脑组织血流,提高患者生活质量,改善神经功能,安全性较好。
[关键词]急性进展性脑梗死;替罗非班;NIHSS 评分;生活质量[中图分类号]R743.3[文献标识码]A[文章编号]1671-7562(2020)08-0966-05doi :10.3969/j.issn.1671-7562.2020.08.006Effect of tirofiban in patients with acute cerebral infarctionYIN Qiduo 1,LI Zhengxia 1,GENG Wanjie 1,WU Qingyang 2(1.Department of Neurology ,Taihe County People 's Hospital ,Fuyang 236600,China ;2.Department of Radiology ,the Affiliated Wuxi People 's Hospital of Nanjing Medical University ,Wuxi 214023,China )[Abstract ]Objective :To study the clinical efficacy of tirofiban combined with aspirin and clopidogrel on scores ofDaily Living Ability Scale (ADL )and National Institute of Health Stroke Scale (NIHSS )in patients with acute pro-gressive cerebral infarction.Methods :90patients with acute progressive cerebral infarction admitted to our hospi-tal from July 2018to July 2019were randomly divided into observation group and control group (45cases ).The control group was treated with aspirin and clopidogrel ,on top of which the observation group was given tirofiban.The clinical efficacy ,ADL ,NIHSS and adverse reactions between the two groups were statistically analyzed.Results :The total effective rate was 88.89%in the observation group ,71.11%in the control group (P <0.05).In the observation group ,the NIHSS were lower than those during the time of 24h ,72h ,7d and 14d ,respectively (P <0.05)and meanwhile ,the differentials of ADL between post treatment and prior treatment were high than those in the control group (P <0.05).The incidence of adverse reactions was 13.85%in the observation group ,7.69%in the control group (P >0.05).Conclusion :Tirofiban combined with aspirin and clopidogrel has a cura-tive effect in acute progressive cerebral infarction ,improving the brain microcirculation blood flow and nerve func-tion ,enhancing life quality of patients ,and ensuring the safety of the therapy.[Key words ]acute progressive stroke ;tirofiban ;score of NIHSS ;quality of life·669·急性脑梗死是临床常见的一种脑血管疾病,病理生理学基础为脑血供突然中断,可导致脑组织坏死,神经元细胞、星形胶质细胞、胶质细胞不同程度损伤,是出现致残、致死的严重脑血管疾病之一。
布里斯托大学著名校友

布里斯托大学(University of Bristol),简称布大,始建于1876年,是位于英格兰西南部第一大城市布里斯托市的一所世界30强顶尖名校,历年最高世界排名为全球第27名,布里斯托大学是全英大学十强之一。
1909年,布里斯托大学被英国国王爱德华七世授予皇家宪章,正式成为真正意义上的大学。
学校建校至今共计培养了11位诺贝尔奖得主。
布里斯托大学是素有英国常春藤盟校之称的“罗素大学集团(The Russell Group)”创始成员,也是英国历史上著名的六所“红砖大学”之一、科英布拉集团(The Coimbra Group)创始成员、世界大学联盟(Worldwide Universities Network)成员、欧洲大学协会(European University Association)成员。
著名校友360教育集团介绍说,毕业生的荣耀能反映一间学校的成就,培养好的人才,是每一所好大学的终极目标,布里斯托大学是一所很全面的学校,从科学家到艺术家,从国家政要到奥运级健将,都有非常出众的校友。
Sir Winston Churchill-英国著名政治家,两次就任英国首相,曾任该校校监。
The Right Honourable the Baroness Hale of Richmond-英国最高法院副院长。
Charles Bolden-现任美国国家航空航天局局长,美国航天局首位非洲裔局长。
Sir Liam Joseph Donaldson-英国首席医疗官。
Dr Dale Wigley FRS-英国伦敦癌症研究中心首席科学家。
Geoffrey Tovey-英国血清学家,英国移植服务创始人。
Debby Reynolds-英国首席兽医官。
J. M. G. Le Clézio-法国作家,诺贝尔文学奖获得者。
Harold Pinter-英国剧作家,诺贝尔文学奖获得者。
Max Delbrück-美国生物学家,诺贝尔生理学或医学奖获得者。
第二类皮奥拉-基尔霍夫应力

第二类皮奥拉-基尔霍夫应力
《高级宏观经济学》是一本关于新凯恩斯主义理论的经济学著作,作者是美国哥伦比亚大学的经济学家保罗·罗默。
该书在宏观经济学领域有很高的声誉,是一份详细阐述新凯恩斯主义宏观经济学的全面指南。
新凯恩斯主义是一种对凯恩斯主义的进一步发展,认为在短期内宏观经济政策才有可能影响经济增长和就业。
新凯恩斯主义主张采取积极的货币和财政政策,以控制失业率和通货膨胀。
它的理论关注市场失灵和信息不对称的影响,认为政府可以通过干预市场来促进贸易,而这也体现了罗默等学者对政府干预市场的积极支持。
总之,通过学习《高级宏观经济学》可以更好地了解新凯恩斯主义宏观经济学的理论和实践,以及政府在促进经济增长和就业方面的作用。
可持续性资本理论

B OSTON U NIVERSITY Center for Energy and Environmental Studies Working Papers SeriesNumber 9501 September 1995 THE CAPITAL THEORY APPROACH TO SUSTAINABILITY:A CRITICAL APPRAISALbyDavid Stern675 Commonwealth Avenue, Boston MA 02215Tel: (617) 353-3083Fax: (617) 353-5986E-Mail: dstern@WWW: /sterncv.htmlThe Capital Theory Approach to Sustainability:A Critical AppraisalDavid I. SternBoston UniversityNovember 1995______________________________________________________________________________ Center for Energy and Environmental Studies, Boston University, 675 Commonwealth Avenue, Boston MA 02215, USA. Tel: (617) 353 3083 Fax: (617) 353 5986, E-Mail: dstern@The Capital Theory Approach to Sustainability:A Critical Appraisal______________________________________________________________________________ SummaryThis paper examines critically some recent developments in the sustainability debate. The large number of definitions of sustainability proposed in the 1980's have been refined into a smaller number of positions on the relevant questions in the 1990's. The most prominent of these are based on the idea of maintaining a capital stock. I call this the capital theory approach (CTA). Though these concepts are beginning to inform policies there are a number of difficulties in applying this approach in a theoretically valid manner and a number of critics of the use of the CTA as a guide to policy. First, I examine the internal difficulties with the CTA and continue to review criticisms from outside the neoclassical normative framework. The accounting approach obscures the underlying assumptions used and gives undue authoritativeness to the results. No account is taken of the uncertainty involved in sustainability analysis of any sort. In addition, by focusing on a representative consumer and using market (or contingent market) valuations of environmental resources, the approach (in common with most normative neoclassical economics) does not take into account distributional issues or accommodate alternative views on environmental values. Finally, I examine alternative approaches to sustainability analysis and policy making. These approaches accept the open-ended and multi-dimensional nature of sustainability and explicitly open up to political debate the questions that are at risk of being hidden inside the black-box of seemingly objective accounting.I.INTRODUCTIONThe Brundtland Report (WCED, 1987) proposed that sustainable development is "development that meets the needs of the present generation while letting future generations meet their own needs". Economists initially had some difficulty with this concept, some dismissing it1 and others proliferating a vast number of alternative definitions and policy prescriptions (see surveys by: Pezzey, 1989; Pearce et al., 1989; Rees, 1990; Lélé, 1991).In recent years, economists have made some progress in articulating their conception of sustainability. The large number of definitions of sustainability proposed in the 1980's have been refined into a smaller number of positions on the relevant questions in the 1990's. There is agreement that sustainability implies that certain indicators of welfare or development are non-declining over the very long term, that is development is sustained (Pezzey, 1989). Sustainable development is a process of change in an economy that does not violate such a sustainability criterion. Beyond this, the dominant views are based on the idea of maintaining a capital stock as a prerequisite for sustainable development. Within this school of thought there are opposing camps which disagree on the empirical question of the degree to which various capital stocks can be substituted for each other, though there has been little actual empirical research on this question.There is a consensus among a large number of economists that the CTA is a useful means of addressing sustainability issues.2 Capital theory concepts are beginning to inform policy, as in the case of the UN recommendations on environmental accounting and the US response to them (Beardsley, 1994; Carson et al., 1994; Steer and Lutz, 1993). There are, however, a growing number of critics who question whether this is a useful way to address sustainability (eg. Norgaard, 1991; Amir, 1992; Common and Perrings, 1992; Karshenas, 1994; Pezzey, 1994; Common and Norton, 1994; Faucheux et al., 1994; Common, 1995). The literature on sustainable development and sustainability is vast and continually expanding. There are also a large number ofsurveys of that literature (eg. Tisdell, 1988; Pearce et al., 1989; Rees, 1990; Simonis, 1990; Lélé, 1991; Costanza and Daly, 1992; Pezzey, 1992; Toman et al., 1994). I do not intend to survey this literature.The aim of this paper is to present a critique of the capital theory approach to sustainability (CTA henceforth) as a basis for policy. This critique both outlines the difficulties in using and applying the CTA from a viewpoint internal to neoclassical economics and problems with this approach from a viewpoint external to neoclassical economics. I also suggest some alternative approaches to sustainability relevant analysis and policy. The neoclasscial sustainability literature generally ignores the international dimensions of the sustainability problem. I also ignore this dimension in this paper.The paper is structured as follows. In the second section, I discuss the background to the emergence of the capital theory approach, while the third section briefly outlines the basic features of the approach. The fourth section examines the limitations of the CTA from within the viewpoint of neoclassical economics and the debate between proponents of "weak sustainability" and "strong sustainability". The following sections examine the drawbacks of this paradigm from a viewpoint external to neoclassical economics and discuss alternative methods of analysis and decision-making for sustainability. The concluding section summarizes the principal points.SHIFTING DEBATE: EMERGENCE OF THE CAPITAL THEORY II. THEAPPROACHMuch of the literature on sustainable development published in the 1980's was vague (see Lélé, 1991; Rees, 1990; Simonis, 1990). There was a general lack of precision and agreement in defining sustainability, and outlining appropriate sustainability policies. This confusion stemmed in part from an imprecise demarcation between ends and means. By "ends" I mean the definition ofsustainability ie. what is to be sustained, while "means" are the methods to achieve sustainability or necessary and/or sufficient conditions that must be met in order to do the same. As the goal of policy must be a subjective choice, considerable debate surrounded and continues to surround the definition of sustainability (eg. Tisdell, 1988). As there is considerable scientific uncertainty regarding sustainability possibilities, considerable debate continues to surround policies to achieve any given goal.Sharachchandra Lélé (1991) stated that "sustainable development is in real danger of becoming a cliché like appropriate technology - a fashionable phrase that everyone pays homage to but nobody cares to define" (607). Lélé pointed out that different authors and speakers meant very different things by sustainability, and that even UNEP's and WCED's definitions of sustainable development were vague, and confused ends with means. Neither provided any scientific examination of whether their proposed policies would lead to increased sustainability. "Where the sustainable development movement has faltered is in its inability to develop a set of concepts, criteria and policies that are coherent or consistent - both externally (with physical and social reality) and internally (with each other)." (613). Judith Rees (1990) expressed extreme skepticism concerning both sustainable development and its proponents. “It is easy to see why the notion of sustainable development has become so popular ... No longer does environmental protection mean sacrifice and confrontation with dominant materialist values” (435). She also argued that sustainable development was just so much political rhetoric. A UNEP report stated: "The ratio of words to action is weighted too heavily towards the former" (quoted in Simonis, 1990, 35). In the early days of the sustainability debate, vagueness about the meaning of sustainability was advantageous in attracting the largest constituency possible, but in the longer run, greater clarity is essential for sustaining concern.In the 1990's many people have put forward much more precisely articulated definitions of sustainable development, conditions and policies required to achieve sustainability, and criteria toassess whether development is sustainable. This has coincided with a shift from a largely politically-driven dialogue to a more theory-driven dialogue. With this has come a clearer understanding of what kinds of policies would be required to move towards alternative sustainability goals, and what the limits of our knowledge are. There is a stronger awareness of the distinction between ends and means. Most, but not all (eg. Amir, 1992), analysts agree that sustainable development is a meaningful concept but that the claims of the Brundtland Report (WCED, 1987) that growth just had to change direction were far too simplistic.There is a general consensus, especially among economists, on the principal definition of sustainable development used by David Pearce et al. (1989, 1991): Non-declining average human welfare over time (Mäler, 1991; Pezzey, 1992; Toman et al., 1994).3 This definition of sustainability implies a departure from the strict principle of maximizing net present value in traditional cost benefit analysis (Pezzey, 1989), but otherwise it does not imply a large departure from conventional economics. John Pezzey (1989, 1994) suggests a rule of maximizing net present value subject to the sustainability constraint of non-declining mean welfare. It encompasses many but not all definitions of sustainability. For example, it excludes a definition of sustainability based on maintaining a set of ecosystem functions, which seems to be implied by the Holling-sustainability criterion (Common and Perrings, 1992; Holling, 1973, 1986) or on maintaining given stocks of natural assets irrespective of any contribution to human welfare. A sustainable ecosystem might not be an undesirable goal but it could be too strict a criterion for the goal of maintaining human welfare (Karshenas, 1994) and could in some circumstances lead to declining human welfare. Not all ecosystem functions and certainly not all natural assets may be necessary for human welfare. Some aspects of the natural world such as smallpox bacteria may be absolutely detrimental to people. In the context of the primary Pearce et al. definition, the Holling-sustainability criterion is a means not an end.The advantage of formalizing the concept of sustainability is that this renders it amenable to analysis by economic theory (eg. Barbier and Markandya, 1991; Victor, 1991; Common and Perrings, 1992; Pezzey, 1989, 1994; Asheim, 1994) and to quantitative investigations (eg. Repetto et al., 1989; Pearce and Atkinson, 1993; Proops and Atkinson, 1993; Stern, 1995). Given the above formal definition of sustainability, many economists have examined what the necessary or sufficient conditions for the achievement of sustainability might be. Out of this activity has come the CTA described in the next section. The great attractiveness of this new approach is that it suggests relatively simple rules to ensure sustainability and relatively simple indicators of sustainability. This situation has seemingly cleared away the vagueness that previously attended discussions of sustainability and prompted relatively fast action by governments and international organizations to embrace specific goals and programs aimed at achieving this notion of the necessary conditions for sustainability.III. THE ESSENCE OF THE CAPITAL THEORY APPROACHThe origins of the CTA are in the literature on economic growth and exhaustible resources that flourished in the 1970s, exemplified by the special issue of the Review of Economic Studies published in 1974 (Heal, 1974). Robert Solow (1986) built on this earlier literature and the work of John Hartwick (1977, 1978a, 1978b) to formalize the constant capital rule. In these early models there was a single non-renewable resource and a stock of manufactured capital goods. A production function produced a single output, which could be used for either consumption or investment using the two inputs. The elasticity of substitution between the two inputs was one which implied that natural resources were essential but that the average product of resources could rise without bound given sufficient manufactured capital.The models relate to the notion of sustainability as non-declining welfare through the assumption that welfare is a monotonically increasing function of consumption (eg. Mäler, 1991). The path ofconsumption over time (and therefore of the capital stock) in these model economies depends on the intertemporal optimization rule. Under the Rawlsian maxi-min condition consumption must be constant. No net saving is permissible as this is regarded as an unjust burden on the present generation. Under the Ramsey utilitarian approach with zero discounting consumption can increase without bound (Solow, 1974). Here the present generation may be forced to accept a subsistence standard of living if this can benefit the future generations however richer they might be. Paths that maximize net present value with positive discount rates typically peak and then decline so that they are not sustainable (Pezzey, 1994). Pezzey (1989) suggested a hybrid version which maximizes net present value subject to an intertemporal constraint that utility be non-declining. In this case utility will first increase until it reaches a maximum sustainable level. This has attracted consensus as the general optimizing criterion for sustainable development. Geir Asheim (1991) derives this condition more formally.Under the assumption that the elasticity of substitution is one, non-declining consumption depends on the maintenance of the aggregate capital stock ie. conventional capital plus natural resources, used to produce consumption (and investment) goods (Solow, 1986). Aggregate capital, W t,and the change in aggregate capital are defined by:W t=p Kt K t + p Rt S t (1)∆W t=p Kt∆K t + p Rt R t (2)where S is the stock of non-renewable resources and R the use per period. K is the manufactured capital stock and the p i are the relevant prices. In the absence of depreciation of manufactured capital, maintenance of the capital stock implies investment of the rents from the depletion of the natural resource in manufactured capital - the Hartwick rule (Hartwick 1977, 1978a, 1978b). Income is defined using the Hicksian notion (Hicks, 1946) that income is the maximum consumption in a period consistent with the maintenance of wealth. Sustainable income is,therefore, the maximum consumption in a period consistent with the maintenance of aggregate capital intact (Weitzman, 1976; Mäler, 1991) and for a flow of income to be sustainable, the stock of capital needs to be constant or increasing over time (Solow, 1986).The initial work can be extended in various ways. The definition of capital that satisfies these conditions can be extended to include a number of categories of "capital": natural, manufactured, human, and institutional.4 Natural capital is a term used by many authors (it seems Smith (1977) was the first) for the aggregate of natural resource stocks that produce inputs of services or commodities for the economy. Some of the components of natural capital may be renewable resources. Manufactured capital refers to the standard neoclassical definition of "a factor of production produced by the economic system" (Pearce, 1992). Human capital also follows the standard definition. Institutional capital includes the institutions and knowledge necessary for the organization and reproduction of the economic system. It includes the ethical or moral capital referred to by Fred Hirsch (1976) and the cultural capital referred to by Fikret Berkes and Carl Folke (1992). For convenience I give the name 'artificial capital' to the latter three categories jointly. None of these concepts is unproblematic and natural capital is perhaps the most problematic. Technical change and population growth can also be accommodated (see Solow, 1986).Empirical implementation of the CTA tends to focus on measurement of sustainable income (eg. El Serafy, 1989; Repetto, 1989) or net capital accumulation (eg. Pearce and Atkinson, 1993; Proops and Atkinson, 1993) rather than on direct estimation of the capital stock.5 The theoretical models that underpin the CTA typically assume a Cobb-Douglas production function with constant returns to scale, no population growth, and no technological change. Any indices of net capital accumulation which attempt to make even a first approximation to reality must take these variables into account. None of the recent empirical studies does so. For example, David Pearce and Giles Atkinson (1993) present data from eighteen countries on savings and depreciation of natural andmanufactured capital as a proportion of GNP. They demonstrate that only eight countries had non-declining stocks of total capital, measured at market prices, and thus passed a weak sustainability criterion of a constant aggregate capital stock, but their methodology ignores population growth, returns to scale or technological change.IV.INTERNAL APPRAISAL OF THE CAPITAL THEORY APPROACHIn this section, I take as given the basic assumptions and rationale of neoclassical economics and highlight some of the technical problems that are encountered in using the CTA as an operational guide to policy. From a neoclassical standpoint these might be seen as difficulties in the positive theory that may lead to difficulties in the normative theory of sustainability policy. In the following section, I take as given solutions to these technical difficulties and examine some of the problems inherent in the normative neoclassical approach to sustainability.a.Limits to Substitution in Production and "Strong Sustainability"Capital theorists are divided among proponents of weak sustainability and strong sustainability. This terminology is confusing as it suggests that the various writers have differing ideas of what sustainability is.6 In fact they agree on that issue, but differ on what is the minimum set of necessary conditions for achieving sustainability. The criterion that distinguishes the categories is the degree of substitutability believed to be possible between natural and artificial capital.7The weak sustainability viewpoint follows from the early literature and holds that the relevant capital stock is an aggregate stock of artificial and natural capital. Weak sustainability assumes that the elasticity of substitution between natural capital and artificial capital is one and therefore that there are no natural resources that contribute to human welfare that cannot be asymptotically replaced by other forms of capital. Reductions in natural capital may be offset by increases inartificial capital. It is sometimes implied that this might be not only a necessary condition but also a sufficient condition for achieving sustainability (eg. Solow, 1986, 1993).Proponents of the strong sustainability viewpoint such as Robert Costanza and Herman Daly (1992) argue that though this is a necessary condition for sustainability it cannot possibly be a sufficient condition. Instead, a minimum necessary condition is that separate stocks of aggregate natural capital and aggregate artificial capital must be maintained. Costanza and Daly (1992) state: "It is important for operational purposes to define sustainable development in terms of constant or nondeclining total natural capital, rather than in terms of nondeclining utility" (39).8 Other analysts such as members of the "London School" hold views between these two extremes (see Victor, 1991). They argue that though it is possible to substitute between natural and artificial capital there are certain stocks of "critical natural capital" for which no substitutes exist. A necessary condition for sustainability is that these individual stocks must be maintained in addition to the general aggregate capital stock.The weak sustainability condition violates the Second Law of Thermodynamics, as a minimum quantity of energy is required to transform matter into economically useful products (Hall et al., 1986) and energy cannot be produced inside the economic system.9 It also violates the First Law on the grounds of mass balance (Pezzey, 1994). Also ecological principles concerning the importance of diversity in system resilience (Common and Perrings, 1992) imply that minimum quantities of a large number of different capital stocks (eg. species) are required to maintain life support services. The London School view and strong sustainability accommodate these facts by assuming that there are lower bounds on the stocks of natural capital required to support the economy, in terms of the supply of materials and energy, and in terms of the assimilative capacity of the environment, and that certain categories of critical natural capital cannot be replaced by other forms of capital.Beyond this recognition it is an empirical question as to how far artificial capital can substitute for natural capital. There has been little work on this at scales relevant to sustainability. However, the econometric evidence from studies of manufacturing industry suggest on the whole that energy and capital are complements (Berndt and Wood, 1979).In some ways the concept of maintaining a constant stock of aggregate natural capital is even more bizarre than maintaining a non-declining stock of total capital. It seems more reasonable to suggest that artificial capital might replace some of the functions of natural capital than to suggest that in general various natural resources may be substitutes for each other. How can oil reserves substitute for clean air, or iron deposits for topsoil? Recognizing this, some of the strong sustainability proponents have dropped the idea of maintaining an aggregate natural capital stock as proposed by Costanza and Daly (1992) and instead argue that minimum stocks of all natural resources should be maintained (Faucheux and O'Connor, 1995). However, this can no longer really be considered an example of the CTA. Instead it is an approach that depends on the concept of safe minimum standards or the precautionary principle. The essence of the CTA is that some aggregation of resources using monetary valuations is proposed as an indicator for sustainability.The types of models which admit an index of aggregate capital, whether aggregate natural capital or aggregate total capital, is very limited. Construction of aggregate indices or subindices of inputs depend on the production function being weakly separable in those subgroups (Berndt and Christensen, 1973). For example it is only possible to construct an index of aggregate natural capital if the marginal rate of substitution between two forms of natural capital is independent of the quantities of labor or capital employed. This seems an unlikely proposition as the exploitation of many natural resources is impractical without large capital stocks. For example, in the production of caught fish, the marginal rate of substitution, and under perfect competition the price ratio, between stocks of fresh water fish and marine fish should be independent of the number of fishingboats available. This is clearly not the case. People are not likely to put a high value on the stock of deep sea fish when they do not have boats to catch them with.If substitution is limited, technological progress might reduce the quantity of natural resource inputs required per unit of output. However, there are arguments that indicate that technical progress itself is bounded (see Pezzey, 1994; Stern, 1994). One of these (Pezzey, 1994) is that, just as in the case of substitution, ultimately the laws of thermodynamics limit the minimization of resource inputs per unit output. Stern (1994) argues that unknown useful knowledge is itself a nonrenewable resource. Technological progress is the extraction of this knowledge from the environment and the investment of resources in this activity will eventually be subject to diminishing returns.Limits to substitution in production might be thought of in a much broader way to include nonlinearities and threshold effects. This view is sometimes described as the "ecological" viewpoint on sustainability (Common and Perrings, 1992; Common, 1995) or as the importance of maintaining the "resilience" of ecological systems rather than any specific stocks or species. This approach derives largely from the work of Holling (1973, 1986). In this view ecosystems are locally stable in the presence of small shocks or perturbations but may be irreversibly altered by large shocks. Structural changes in ecosystems such as those that come about through human interference and particularly simplification, may make these systems more susceptible to losing resilience and being permanently degraded. There is clearly some substitutability between species or inorganic elements in the role of maintaining ecosystem productivity, however, beyond a certain point this substitutability may suddenly fail to hold true. This approach also asks us to look at development paths as much less linear and predictable than is implied in the CTA literature.All things considered, what emerges is a quite different approach to sustainability policy. It is probable that substitution between natural and artificial capital is limited, as is ultimately technicalchange. Additionally the joint economy-ecosystem system may be subject to nonlinear dynamics. This implies that eventually the economy must approach a steady state where the volume of physical economic activity is dependent on the maximum economic and sustainable yield of renewable resources or face decline ie. profit (or utility) maximizing use of renewable resources subject to the sustainability constraint. As in Herman Daly's vision (Daly, 1977) qualitative change in the nature of economic output is still possible. Sustainability policy would require not just maintaining some stocks of renewable resources but also working to reduce "threats to sustainability" (Common, 1995) that might cause the system to pass over a threshold and reduce long-run productivity.The notion of Hicksian income originally applied to an individual price-taking firm (Faucheux and O'Connor, 1995). However, even here it is not apparent that the myopic policy of maintaining capital intact from year to year is the best or only way to ensure the sustainability of profits into the future. If a competing firm makes an innovation that renders the firm's capital stock obsolete, the latter's income may drop to zero. This is despite it previously following a policy of maintaining its capital intact. The firm's income measured up to this point is clearly seen to be unsustainable. In fact its policy has been shown to be irrelevant to long-run sustainability. In the real world firms will carry out activities that may not contribute to the year to year maintenance of capital and will reduce short-run profits such as research and development and attempts to gain market share.10 These activities make the firm more resilient against future shocks and hence enhance sustainability.b.Prices for AggregationSupposing that the necessary separability conditions are met so that aggregation of a capital stock is possible, analysts still have to obtain an appropriate set of prices so that the value of the capital stock is a sustainability relevant value. The CTA is more or less tautological if we use the "right" prices. However, these correct "sustainability prices" are unknown and unknowable. A number of。
极限实验室
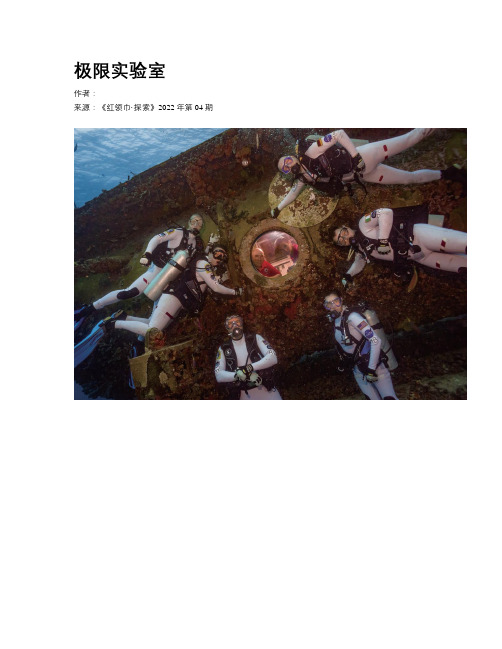
极限实验室作者:来源:《红领巾·探索》2022年第04期如果你的夢想是成为一名科学家,那么除了“白大褂”“实验室”,你可能还会与这些装备亲密接触:连体羽绒服、冰镐、冰爪、头盔、水壶……是不是很像要去极限攀登?因为我们今天要去的第一个实验室,坐落在喜马拉雅山上。
这里的科学家在极端环境中冒险工作,只为获得有关气候、环境与地质的宝贵资料。
海拔5050米金字塔实验室在喜马拉雅山的尼泊尔萨加玛塔国家公园内,珠穆朗玛峰脚下海拔5000多米处。
它涉及包括地质、气候、环境和人体生理学等多个研究领域;主要目标是改善尼泊尔及周边国家原住民的生活水平,保护脆弱的高海拔生态系统。
每年的4月23日,是世界实验室日。
世界各地的实验室会在这一天表彰那些努力取得新发现、发明新事物或取得科学突破的研究人员。
地下2000米萨德伯里微中子观测站(英文简称SNOLAB)是一个深层地下实验室,位于加拿大安大略省一处地下2000米的矿井内。
实验室拥有5000平方米的洁净空间,为研究包括超新星、宇宙暗物质与太阳中微子等物理现象提供了理想环境。
水下20米宝瓶座水下研究实验室,位于佛罗里达群岛海洋保护区的水面以下20米处。
它的主要任务是帮助科学家研究这里的珊瑚、鱼类和海草等生物。
除此之外,它还是训练潜水员和航天员的理想场所。
风速372千米/时华盛顿山气象站位于美国新罕布什尔州。
气象站所在的山顶,是一个“严寒、浓雾、大雪和风速创纪录”的地方,这里曾记录到世界最快风速之一(风速达372千米/时)。
科学家们坚守在这里,研究影响地球天气和气候的自然系统。
你知道吗?风洞是一种产生人造气流的管道,用来模拟飞行器、汽车、导弹等物体周围气体的流动情况。
目前已建成的超高速风洞LENS-X,位于美国纽约卡斯潘大学布法罗研究中心,风速高达30马赫(声速的30倍)。
我国的JF-22超高速风洞位于北京的怀柔科学城,将在今年建成。
耗资1500亿美元国际空间站是目前所有人造极限实验室中条件最极端的:距离地表370千米~460千米,绕地球运行的速度近28000千米/时。
二叠纪-三叠纪灭绝事件

二叠纪-三叠纪灭绝事件二叠纪-三叠纪灭绝事件(Permian–Triassic extinction event)是一个大规模物种灭绝事件,发生于古生代二叠纪与中生代三叠纪之间,距今大约2亿5140万年[1][2]。
若以消失的物种来计算,当时地球上70%的陆生脊椎动物,以及高达96%的海中生物消失[3];这次灭绝事件也造成昆虫的唯一一次大量灭绝。
计有57%的科与83%的属消失[4][5]。
在灭绝事件之后,陆地与海洋的生态圈花了数百万年才完全恢复,比其他大型灭绝事件的恢复时间更长久[3]。
此次灭绝事件是地质年代的五次大型灭绝事件中,规模最庞大的一次,因此又非正式称为大灭绝(Great Dying)[6],或是大规模灭绝之母(Mother of all mass extinctions)[7]。
二叠纪-三叠纪灭绝事件的过程与成因仍在争议中[8]。
根据不同的研究,这次灭绝事件可分为一[1]到三[9]个阶段。
第一个小型高峰可能因为环境的逐渐改变,原因可能是海平面改变、海洋缺氧、盘古大陆形成引起的干旱气候;而后来的高峰则是迅速、剧烈的,原因可能是撞击事件、火山爆发[10]、或是海平面骤变,引起甲烷水合物的大量释放[11]。
目录? 1 年代测定? 2 灭绝模式o 2.1 海中生物o 2.2 陆地无脊椎动物o 2.3 陆地植物? 2.3.1 植物生态系统? 2.3.2 煤层缺口o 2.4 陆地脊椎动物o 2.5 灭绝模式的可能解释? 3 生态系统的复原o 3.1 海洋生态系统的改变o 3.2 陆地脊椎动物? 4 灭绝原因o 4.1 撞击事件o 4.2 火山爆发o 4.3 甲烷水合物的气化o 4.4 海平面改变o 4.5 海洋缺氧o 4.6 硫化氢o 4.7 盘古大陆的形成o 4.8 多重原因? 5 注释? 6 延伸阅读? 7 外部链接年代测定在西元二十世纪之前,二叠纪与三叠纪交界的地层很少被发现,因此科学家们很难准确地估算灭绝事件的年代与经历时间,以及影响的地理范围[12]。
人口变动在大城市碳排放中的作用与影响——以北京市为例

人口变动在大城市碳排放中的作用与影响——以北京市为例童玉芬;韩茜【摘要】碳排放是表征一个国家或地区环境状况的重要指标,与经济发展、技术和人口等都有着密切的联系.本文采用了基于环境压力等式IPAT的STIRPAT模型来定量分析北京市人口因素及其他相关因素对北京市碳排放的影响.研究结果显示,北京市的经济水平、城镇人口规模、就业结构、城镇化率和年龄因素对北京市的碳排放具有正效应,即随着上述因素的增大,碳排放也呈现增加趋势,而碳排放强度(技术因素)与碳排放呈现反相关关系.从1980-2010年的上述各类因素的变化以及对碳排放的影响程度上看,经济水平的提高对碳排放的贡献最大,人口规模的增加对碳排放的贡献紧随其后,产业结构升级和城镇化提高都对碳排放产生了明显的促进作用.【期刊名称】《北京社会科学》【年(卷),期】2013(000)002【总页数】7页(P113-119)【关键词】北京市;人口因素;碳排放【作者】童玉芬;韩茜【作者单位】首都经济贸易大学劳动经济学院,北京100070【正文语种】中文【中图分类】C922一、前言近一个世纪以来,矿物燃料 (如煤、石油等)被大量使用,森林被大肆砍伐和焚烧,其排放出大量的二氧化碳等多种温室气体,成为全球气候变暖的主要原因。
政府间气候变化问题小组根据气候模型预测,到2100年为止,全球气温估计将上升大约1.4-5.8℃ (2.5-10.4华氏度)(IPCC,2007)。
根据这一预测,全球气温将出现过去10,000年中从未有过的巨大变化,其后果会使全球降水量重新分配、冰川和冻土消融、海平面上升等,既危害自然生态系统的平衡,更威胁人类的食物供应和居住环境。
改革开放以来,我国国民经济持续增长。
在经济高速增长和社会转型的大背景下,我国的人口发展和居民生活消费方式正发生着深刻变化。
北京作为中国的首都和特大城市,更是经历了社会发展的深刻变革和经济增长的巨大改变,同时伴随着人口的快速增长和结构变化。
思力华-原研品质-值得信赖资料讲解

位于德国比布拉赫的生物技术中心投入使用,是德国第一个生物制药 生产厂
1988-presence: Value through Innovation 创新展现价值
1999 2002
Launch of micardis® for hypertension 抗高血压药物美卡素上市 Launch of spiriva® for COPD 治疗COPD药物 思力华上市
mirapex®/mirapexin®森福罗
Nevirapine
奈韦拉平
virmaune®
维乐命
Indication 适应症
First launch 首次上市
Prevention of venous thromboembolic events
深静脉血栓栓塞预防
2008
Chronic Obstructive Pulmonary Disease (COPD)
1885
Albert Boehringer becomes a pioneer of large-scale biotech production by using bacteria to produce lactic acid
阿尔伯特勃林格使用细菌生产乳酸,成为大规模生物技术生产的先锋
1917 1941
Hale Waihona Puke COPD Anticholinergic Broncho-dilator 慢阻肺/抗胆碱能药物
AIS & AMI & PE / r-TPA 急性心梗,脑梗&肺栓塞
Inflammation & pain / NSAID 炎症&疼痛/非甾体抗炎药
Cough / Mucolytic anti-tussive 止咳化痰
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a rXiv:c omp-ga s/9354v127May1993Global Bifurcations in Rayleigh-B´e nard Convection:Experiments,Empirical Maps and Numerical Bifurcation Analysis I.G.Kevrekidis and R.Rico-Mart´ınez Department of Chemical Engineering,Princeton University,Princeton,NJ 08544-5263R.E.Ecke 1,R.M.Farber 2and pedes 21Physics Division and Center for Nonlinear Studies 2Theoretical Division Los Alamos National Laboratory,Los Alamos,NM 87545February 6,2008Abstract We use nonlinear signal processing techniques,based on artificial neural networks,to construct an empirical mapping from experimen-tal Rayleigh-B´e nard convection data in the quasiperiodic regime.The data,in the form of a one-parameter sequence of Poincar´e sections in the interior of a mode-locked region (resonance horn),are indicative of a complicated interplay of local and globalbifurcations with respect to the experimentally varied Rayleigh number.The dynamic phenomena apparent in the data include period doublings,complex intermittent behavior,secondary Hopf bifurcations,and chaotic dynamics.We use the fitted map to reconstruct the experimental dynamics and to ex-plore the associated local and global bifurcation structures in phase ing numerical bifurcation techniques we locate the stable and1unstable periodic solutions,calculate eigenvalues,approximate invari-ant manifolds of saddle type solutions and identify bifurcation points. This approach constitutes a promising data post-processing procedure for investigating phase space and parameter space of real experimental systems;it allows us to infer phase space structures which the exper-iments can only probe with limited measurement precision and only at a discrete number of operating parameter settings.21IntroductionWhen presented with experimental observations of the dynamics of a nonlin-ear system at a discrete number of operating parameter settings,it is often difficult to interpret the global phase space structure underlying the exper-imental time series,or to get a good picture of the state of the system at intermediate parameter values.It would therefore be desirable to develop a model of the experimental dynamics that could be implemented,simu-lated and analyzed on the computer.Several approaches are possible:one could start from the fundamental equations for the system,impose realis-tic boundary conditions,and simulate the resulting set of equations.For experiments described by partial differential equations,such an approach is often untenable,requiring extensive computational resources.Even though necessary for the fundamental understanding of the instabilities underlying the dynamics,this approach may not quantitatively reproduce thefiner de-tails of the observed behavior.This may be because of small deviations from the idealizations of the model,imperfections of the apparatus,oversimplified boundary conditions,imperfect estimation of physical properties,inaccurate readings of the experimental settings,etc.The second approach,which more practically aims at interpreting the particular experimental observations,is tofit the observed dynamics with a dynamical system(a map,or a set of ODEs)of the appropriate phase space dimension.As we shall see,this ap-proach is capable,at least for the experimental data we have considered,of reproducing significant features of the dynamics and yielding insight into the properties of the phase-space structure underlying the observed behavior. Techniques for the reconstruction of phase-space mappings have been devel-oped for dynamical systems analysis[11,21]and recently for the purpose of prediction and forecasting of time series(see for example[4]and references therein).These methods include functional approximation using radial basis functions,local-linear maps,and neural network algorithms.In this paper we use the latter approach(i.e.,fitting the observed dy-namics)incorporating in the model a functional dependence on a bifurcation parameter;this can easily be generalized to multiple parameters.This type of empirical modeling provides crucial assistance in conjunction with nu-merical bifurcation analysis[3,24]for interpreting the bifurcation structures “contained in”(or consistent with)the experimental data.More generally, such techniques can play a significant role in real-time prediction and control3applications for a large class of physical systems(see for example the re-cent experimental literature on stabilizing unstable periodic orbits[25,26]). They can be thought of as a useful data compression and post-processing tool,which assists the concise presentation and interpretation of experimen-tal time series.In this work we consider the dynamics of data from a Rayleigh-B´e nard convection experiment in a region of parameter space where the behavior is complicated and difficult to interpret by visual inspection of the Poincar´e section data alone.The paper is organized as follows:the next section is a description of the experiment and of the experimental data.We then outline briefly the data processing technique used(Artificial Neural Net-works,ANNs)and discuss its performance infitting the ing the fitted map(s)we construct a plausible picture of the bifurcation structures in phase and parameter space using numerical bifurcation methods.Finally, we discuss the applicability of this approach to a wider class of problems. 2Experimental DataThe experimental data presented here are obtained from a rectangular small-aspect-ratio convection cell used for studies of low-dimensional nonlinear dy-namics.The convectingfluid is a1.46%solution of3He in superfluid4He and thermal convection is induced by applying afixed heating current to the top plate while maintaining the bottom plate atfixed temperature.Details of the experimental apparatus and properties of the superfluid mixture are described elsewhere[8,19].Here we discuss the measurement probe and present a brief characterization of the parameter space of thermal convection in this system.For afixed geometry,two dimensionless parameters characterize the con-vective state.The Rayleigh number R,proportional to the temperature difference across thefluid layer∆T,is a measure of the driving force ap-plied to the system.The other dimensionless parameter in the problem is the Prandtl numberσ,which measures the ratio of the rates of molecular diffusion of momentum and heat and controls details of the secondary insta-bilities in thermal convection.In3He-4He mixturesσis a strong function of the mean temperature T m of the cell,and is varied over the quasiperiodic regime in the range0.06<σ<0.08by varying the mean temperature in the4Figure1:Convective dynamic states in two-parameter(Rayleigh number and Prandtl number)space.Dynamic behavior in the various regions is described in the text.range0.83<T m<0.90K.For small R,thefluid conducts heat diffusively.At R≈2000there is a forward(supercritical)bifurcation to steady convection[19]where thefluid motion is believed to be two convection rolls oriented parallel to the short side of the rectangular convection cell.At higher values of R theflow becomes time dependent,going through a sequence of bifurcations from periodic to quasiperiodic to chaotic dynamics.The state of the time-dependent convec-tiveflow is partially determined from measurements of the spatially-averaged convective heat transport.In small-aspect-ratio convection,however,the side walls severely constrain the spatial structure of thefluidflow,and measure-ment of the dynamics of the system at a single point is often adequate to characterize the dynamical nature of the state.Therefore,in addition to a global measure of the temperaturefield from the time dependence of the top-bottom temperature difference,we use a thermal probe which measures a local temperature difference near the center of the cell top plate with a temperature sensitivity of0.3×10−7K/Hz1/2[19].We denote the measured temperature difference at the local probe byδT(t).The output of this probe is digitized to produce a time series record of the system dynamics.In order to understand the context of the data,we now describe briefly5the relevant regions of parameter space,see Fig.1.Thefirst time dependent solution“begins”at the transition to periodic oscillations of frequency f1 (typically f1≈0.6Hz).This transition is a forward Hopf bifurcation in R [8],and its critical R value depends strongly onσ.Another Hopf bifurcation at higher R gives rise to a second frequency f2,incommensurate with thefirst. This second mode is only weakly interacting with the initial limit cycle mode and not until there is a discontinuous transition to a different second mode does measurable mode-locking occur.Within a region of parameter space above the discontinuous transition,quasiperiodic(incommensurate frequen-cies),mode-locked and chaotic states exist[9,10,13].Fig.2shows the various data processing stages of a“typical”experimen-tal run,in this case for R/R c=12.01,1/σ=14.97.(a)shows a segment of the experimental time series;(b)shows the corresponding power spectrum (calculated from the time series using an FFT algorithm with standard win-dowing techniques),marking the frequencies f1and f2fromfitting.Standard techniques of phase space reconstruction[11,21]are used to produce phase space trajectories of the dynamical system;(c)shows a projection of the con-tinuous attractor reconstructed with two time delays,τ1=2s andτ2=1s (the phase space for all the attractors in this paper has been normalized so that the limits of the attractors are±1);andfinally(d)shows the Poincar´e section obtained from this attractor by transversely intersecting it with a plane defined by x(t)=-0.15and only plotting intersections in a single direc-tion.How this particular section arises will be discussed later.The location and orientation of the Poincar´e plane is variable,so that we can choose sec-tions with the minimum of overlappings and projection singularities usually arising in delay coordinate reconstructions of dynamical ing these techniques we can characterize the evolution of dynamical states of the system as R is varied.The dynamics in the quasiperiodic regime are often“summarized”in terms of a single number,the winding or rotation number W≡f2/f1,where f1and f2are the fundamental frequencies(practically determined from spec-tral analysis of the time series data).The mode-locking structure known as the“devil’s staircase”is constructed from a sequence of such spectra as a function of R/R c atfixedσ.Such a representative structure is illustrated in Fig.3,obtained from experimental data(the Rayleigh number is normalized with the critical R c=2000).By making a series of such measurements at different values ofσ,the locking regions in the{R/R c,σ}parameter space6Figure2:The various data processing stages of the experimental run:(a)a segment of the experimental time series,(b)the power spectrum,(c)a pro-jection of the reconstructed attractor using time delays(notice the location of the plane(x(t)=-0.15)used to generate the Poincar´e section shown in (d)).7are determined,Fig.4.These regions,called“Arnol’d horns”or“resonance”horns,are seen to broaden asσdecreases(this is why we plot1/σin the ordi-nate in Fig.4)indicating that the coupling or nonlinearity of the oscillatory modes varies roughly with1/σ.Similarly the value of the winding number is controlled primarily by changing R/R c.For1/σ<14,the dynamics of the system are well described by the circle map model[7,10,13].For special irrational winding numbers,the universal-ity predicted for the attractor has been verified in this system[10,20].Some-what higher up in the horns more complicated behavior appears,arising via global bifurcations[9,15].It is this region of parameter space that concerns us here.In Fig.5we illustrate the detailed structure in the neighborhood of the W=2/13locking.Significant features in addition to quasiperiodic and mode-locked regions include secondary Hopf bifurcations of the mode-locked periodic orbit,period doubling bifurcations,regions of complicated transient behavior,and apparently chaotic states whose appearance is probably associ-ated with the occurrence of global bifurcations.Hysteresis in the transitions between these states can be thought of as indicative of such global bifurca-tions,as computational and theoretical work on many model systems shows. Fig.6is a representative experimental plot of the hysteretic behavior of the winding number for ascending and descending sequences of R/R c[15].The effective winding number of the Poincar´e sections,ρ,is related to W mea-sured from the power spectra byρ=1/W,mod1.So for W=2/13we get ρ=1/2which gives a period-2cycle with two points in the Poincar´e sec-tion[7,13].Our purpose in the next sections is to describe the complicated dynamics represented by these data with a simple empirical mapping as a function of a single control parameter,R/R c.We will usefitting techniques to generate such an input-output map that can be analyzed with numerical bifurcation methods.3Empirical Map ConstructionWe used a standard ANN configuration[17]to process the time series from the experimental results sampled in Fig.7.The experimental information is in the form of a(nonlinear)map F:−→X n+1X n F(X,R)8Figure3:Frequency ratio f2/f1vs.R/R c showing experimental devil’s stair-case of mode-locked intervals for1/σ=14.9.Prominent lockings are indicated. Figure4:Experimental regions of mode locking in the1/σand R/R c pa-rameter space.The dashed lines represent the hysteretic discontinuity at low R/R c,increasing R/R c(-----)and decreasing(––––),and a transition to high dimensional chaos at large R/R c.For1/σ>15there is structure in the horns not shown on this global plot.9Figure5:Fine structure of the2/13resonance horn.Secondary Hopf bifur-cations(S.H.B.),period doublings,hysteresis,intermittency and resonance horn overlaps are shown.where X=[x y]T are the coordinates of the intersections of the trajectory with the Poincar´e plane,X n and X n+1are two such successive intersections, and R is the value of the operating parameter,the Rayleigh number.While afirst visual inspection of the phase portraits in Fig.7might indi-cate that a map of the plane would constitute a satisfactory representation of the data,a more careful study reveals that there exist folds in the pro-jection used(see for example Fig.7H or Fig.7L).We were not able tofind a two-dimensional plane that would“get rid of”these projection singulari-ties for all the phase portraits involved in this one-parameter cut.For that reason,and in order to obtain a deterministic map,we used one more delay in the reconstruction of the attractor.This means that we chose tofit a (four-dimensional)map F of the form X n+1=F(X n,X n−1,R).Artificial neural networks(see Fig.8)are structures composed of many interconnected processing units(neurons).A fully connected network dis-tributes the outputs of every neuron in a given layer to all the neurons of the layer above.The input layer is composed of“fan-out”units whose function is only to distribute their inputs to the neurons in the next layer.10Figure6:W vs R/R c for ascending(+)and descending(◦)sequences(1/σ= 14.97).Prominent lockings are labeled.The neurons of the intermediate or“hidden”layers compute as their output a scalar nonlinear function(usually of sigmoidal shape)of a weighted sum of their inputs.The input to one of the neurons of thefirst hiddenlayer is the sumi a i X i+b;X i are the outputs of the layer below(the inputlayer),and the constants a i and b(which are different for each neuron and are called“weights”and“offsets”,respectively)will be determined,as we discuss below,by“training”the network.The outputs of the neurons of thisfirst hidden layer will then serve as inputs of the neurons of the second hidden layer,with new weights and offsets,and so on.The neurons of the output(final)layer simply produce linear functions(linear combinations plus a scalar offset)of their inputs.These structures have been found to have universal approximator proper-ties:they can be used to construct approximations(outputs)of continuous functions of n real variables(inputs)with support in the unit hypercube [5,14].The standard ANN architecture used in this work consists of a four layered network:input layer,output layer and two hidden layers.This11Figure7:A sampling of the experimental Poincar´e sections used for training the ANN.The experimental observations depicted in the“upper”sequence (O through L)are indicative of a large amplitude invariant circle while the ones in the“lower”sequence(A through J)are related to the period-2res-onant solution.The contiguous sequence A through J was broken in the figure only because of space limitations.The overlap zone demonstrates the observed bistability(hysteresis).The parameter values(R/R c)are as follows A:12.057,B:12.040,C:12.032,D:12.019,E:12.0150,F:12.011,G:12.007, H:12.002,I:11.986,J:11.982,K:11.987,L:11.983,M:11.979,N:11.950 and O:11.946.12Figure8:Schematic representation of the ANN configuration used.All layers are fully interconnected;a few of the connections are depicted. particular structure has been found to be,in practice,successful in the iden-tification of nonlinear mappings based on time series data(e.g.[17]).The feedforward artificial neural networks we used had an input layer con-sisting of four neurons for the system state and one neuron for the operating parameter.The output layer consisted of two neurons that predict the point at which the continuous time trajectory will next intersect the plane which defines the Poincar´e section.In order to successively iterate the ANN,both outputs have to be fed back into the corresponding inputs(schematically depicted in Fig.8with dash–dot lines).The weights and offsets of the ANN that provide the“best”approxi-mation(outputs)of the observed measurements as a function of previous measurements(inputs)are determined by“training”the network:a least squares minimization problem.The objective function is the norm of the difference between ANN predictions and actual experimental measurements of the states after one iteration of the Poincar´e map.Training was performed13using a conjugate gradient algorithm,with the map and derivative evalua-tions performed in parallel using a SIMD computer(the64,000processor CM-200)at the Advanced Computing Laboratory at LANL.The implemen-tation we used is therefore ideally suited to very large sets(many thousands) of data points.In the process of this research we trained several ANNs,all of them con-taining two hidden layers;the“best”results presented here were obtained with10nonlinear neurons per hidden layer,each neuron with activation function g(X)=14Interpretation of the dataIn what follows,we will present our a priori“best guess”of a consistent se-quence of bifurcations underlying the phase portraits in Fig.7as illustrated in the schematic bifurcation diagram of Fig.9.While some of our interpre-tations may appear somewhat arbitrary atfirst,a reader experienced in the study of resonance phenomena for maps or periodically-forced oscillators will find such bifurcation sequences in the quasiperiodic regime quite familiar.Our data start at R/R c=12.052,roughly in the middle of the2/13 resonance horn;we clearly see a period-2attractor,phase portrait A in Fig.7. We will call this the“resonant”period-2;it is associated with the2/13 resonance horn,and the boundaries of the horn correspond to saddle-node bifurcations involving this period-2solution.At higher values of the Prandtl number(lower down the horn in Figs.4and5)the data clearly indicate that this saddle-node bifurcation occurs on a smooth invariant circle,Fig.10[15]. One therefore expects a saddle period-2to coexist with the stable period-2,and a“minimal”requirement of thefitted map would be to predict the existence of such a solution.Thefitted map should also exhibit a saddle-node bifurcation involving this saddle and the resonant period-2at low values of R,i.e.at the boundary of the resonance horn.A supercritical(soft)Hopf bifurcation occurs with decreasing R,giving rise to a small amplitude period-2invariant circle(phase portrait B).The model should be capable of predicting this Hopf bifurcation,i.e.,the stable period-2solution should lose stability with two eigenvalues of its linearization exiting the unit circle in the complex plane.Furthermore,the model should predict an unstable(source)period-2solution surrounded by the period-2 stable invariant circle.The period-2invariant circles grow in amplitude and deform(phase por-traits C and D),and thefirst“nontrivial”transition occurs between phase portraits D(showing a period-2“cuspy”invariant circle)and phase portrait E,showing a period-16stable solution.The period-16points are obviously located close to the eight“cusps”or corners developed by the period-2cir-cles.It is in principle possible that these apparent cusps may be the result of a singularity due to the projection to a two-dimensional picture.Because of the intensely deformed nature of the circles,however,we do not believe that this period16is the result of frequency-locking on the circles.We sug-gest that a saddle-node of period-8solutions occurs away from the period-215Figure9:Tentative schematic bifurcation diagram of the transitions ob-served in the experimental data.Solid lines indicate stable periodic solutions, broken lines indicate unstable solutions andfilled circles indicate period-2 small amplitude invariant circles(small)or large amplitude invariant circles (large).16Figure10:A sequence of Poincar´e sections obtained at1/σ=14.749,lower down the2/13resonance horn.They clearly indicate the birth of a stable (resonant)period-2in a saddle-node bifurcation on the invariant circle.17circles.The period-2circles,growing in amplitude,are then lost via a global bifurcation involving their interaction with the saddle period-8solution(this is consistent with the pronounced cusps developing on the invariant circles). The stable period-8solution then undergoes a cascade of period doublings, resultingfirst in the observed period-16(phase portrait E)and eventually in an8-horseshoe-piece apparently chaotic attractor(phase portrait F).This attractor then undergoes a reverse sequence of period doublings,coming back to a period16(phase portrait G),a period8,andfinally resulting in phase portrait H.Fig.9summarizes our interpretation of these transitions:the stable period-2undergoes a“soft”Hopf bifurcation,and the resulting stable period-2invariant circle grows and is eventually destroyed in a global bifurcation involving the stable and unstable manifolds of the saddle-type period-8so-lutions.These period-8solutions exist on an isola:a saddle-node pair of period-8solutions is born and eventually disappears in saddle-node period-8bifurcations.The stable node period-8becomes a focus,then an inverse node,andfinally undergoes a period-doubling cascade,followed by a re-verse cascade,and disappearing in the“other”saddle-node end of the isola. Notice that our interpretation predicts a small hysteresis interval where sta-ble period-8solutions coexist with a stable period-2invariant circle.It is in principle possible to avoid this by assuming that the period-8solution results from frequency locking on the period-2invariant circles;it is the“pointed”nature of the shape of the circles that argues against such an interpretation.It is tempting to consider that the reverse sequence of these bifurcations occurs as the bifurcation parameter R is further reduced:A global bifurca-tion involving the saddle period-8stable and unstable manifolds“gives rise”again to large amplitude period-2invariant circles(slightly wrinkled)in phase portrait H.The amplitude of the circles diminishes(phase portraits I and J), but here the analogy with the high R behavior stops:there is no evidence of a low-R Hopf bifurcation,nor is there a stable period-2observed in the data.Instead,the behavior“jumps”directly from large amplitude period-2 invariant circles to a large amplitude attractor.Indeed,this large amplitude attractor coexists with the large amplitude period-2invariant circle(that is the hysteresis observed at the edge of the resonance horn in Fig.6).The large amplitude attractor gradually develops into a smooth large amplitude invariant circle in phase portrait N,and shows clearly a saddle-node period-5 frequency locking between phase portraits N and O.That this latter bifurca-18tion is indeed a saddle-node bifurcation on the invariant circle is supported by the accumulation of experimental points on the large invariant circle in phase portrait N,occurring atfive distinct locations.The stable period-5should be accompanied by a saddle period-5,and has rotation number f2/f1=5/33. This would then imply that frequency lockings predicted by the Farey se-quence should exist(and the largest ones could be detected)between the 5/33and the2/13resonances:there is experimental evidence of the12/79 and7/46lockings in the data.The large amplitude invariant circle(denoted by largefilled circles in Fig.9)develops a number of frequency lockings(indicated by the“flat”parts of its evolution in the bifurcation diagram),reminiscent of the truly flat intervals of frequency locking in a rotation number vs.R plot.Based on this information,here is a plausible explanation of what occurs as R grows from lower to higher values:At some point an“invisible”saddle-node(saddle-source)bifurcation of period-2solutions occurs,away in phase space from the large amplitude invariant circle.A global bifurcation,involv-ing the saddle-type period-2solutions gives rise tofinite-amplitude period-2 invariant circles,thus leading to an interval of hysteresis between the stable period-2invariant circles and the large amplitude attractor;this is the hys-teresis observed experimentally close to the boundary of the horn.In this case of multistability,the basin boundary between the two attractors(the large-amplitude invariant circle and the period-2invariant circles)is provided by the stable manifolds of the saddle-type period-2solutions.Finally,these same saddle period-2s are responsible for the end of the hysteresis interval: the large amplitude invariant circle approaches these two saddle points,and is lost in a global bifurcation involving their stable and unstable manifolds.This interpretation is“realistic”in that it involves only generic codimension-1bifurcations,which are furthermore known to occur in similar regimes for maps of the plane(see for example[1,12,23].)The only“unusual”ele-ment is that the saddle-node bifurcation at the boundary of the resonance horn is now a saddle-source;both period-2solutions born there are unstable. This interpretation is due to the fact that no stable period-2points were ob-served for low R in the one-parameter diagram.We saw that“lower down”the resonance horn(lower1/σ)this saddle-node bifurcation yields a stable node(Fig.10);this would then imply the existence(in a two-parameter continuation)of a Takens-Bogdanov point[2,27](two eigenvalues of the res-onant period-2solution at1)on the boundary of the resonance horn some-19where in the vicinity of our experimental one-parameter cut.Since secondary Hopf bifurcation curves emanate from such codimension-2bifurcation points [23,12,22],this interpretation is also corroborated by the existence of period-2invariant circles nearby,and the observation of secondary Hopf bifurcations along the experimental one-parameter cut.A plausible embedding of this one-parameter cut in a two-parameter diagram is presented and discussed in Section6.This inferred sequence of bifurcations is consistent with the observed phase portraits.The important question is whether a model based on–and consistent with–the experimental data will indeed exhibit these bifurcations at intermediate values of the control parameter(R).5The ANN based models and their predic-tionsAs we discussed in section3,we chose to train an ANN withfive neurons in the input layer,two in the output layer and two-hidden layers with10neurons each.The training set consisted of data obtained at ascending(Fig.22)and descending(Fig.23)values of R;the entire set of available data was used.The training was successful,in that the resulting map was capable of accurately predicting the one-step-ahead data it wasfitted to.More importantly,when this map was iterated indefinitely,the qualitative nature and quantitative location of its attractors was comparable to the experimental ones.We will start investigating and comparing the numerically predicted and experimen-tally observed(actually inferred)bifurcations from the interior of the horn R/R c≈12.049towards its left boundary with decreasing values of R/R c. Figure11shows a sequence of qualitative transitions between experimental phase portraits(top row)and predicted long-term attractors(bottom row).A bifurcation diagram constructed using the model is also shown in Fig.11: the stable period-2indeed undergoes a Hopf bifurcation at R/R c=12.0257 (the experimental value is somewhat higher,at R/R c≈12.046).Stable and unstable solutions have been calculated through Newton iteration and standard continuation techniques.Local bifurcations were found using stan-dard numerical bifurcation algorithms(e.g.the package AUTO by Prof.E. Doedel[6]).The model does predict the supercritical“soft”nature of the20。
