著名机构讲义春季16-八年级培优版-图形运动中函数关系的确立-教师版

合集下载

八年级数学培优教材讲义

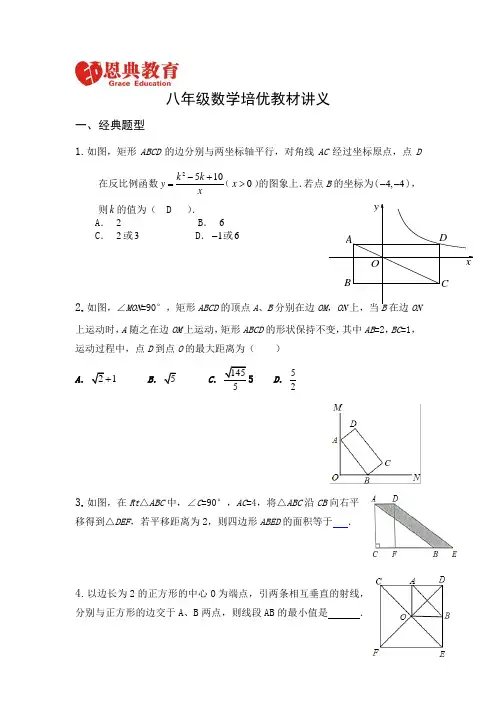
八年级数学培优教材讲义一、经典题型1.如图，矩形ABCD的边分别与两坐标轴平行，对角线AC经过坐标原点，点D在反比例函数2510k kyx-+=（0x>）则k的值为（ D ）．A．2 B．6C．2或3 D．1-或62.如图，∠MON=90°，矩形ABCD的顶点A、B上运动时，A随之在边OM上运动，矩形ABCD运动过程中，点D到点O的最大距离为（）A1B C．55 D．523.如图，在Rt△ABC中，∠C=90°，AC=4，将△ABC沿CB向右平移得到△DEF，若平移距离为2，则四边形ABED的面积等于．4.以边长为2的正方形的中心O为端点，引两条相互垂直的射线，分别与正方形的边交于A、B两点，则线段AB的最小值是．5.如图，Rt△ABC 中，∠C=90°，以斜边AB 为边向外作正方形ABDE ，且正方形对角线交于点O ，连接OC ，已知AC=5，OC=6，则另一直角边BC 的长？．6.已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．7.已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F8.如图，分别以△ABC 的AC 和BC 为一边，在△ABC的外侧作正方形ACDE和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB9. 如图，将矩形ABCD 沿直线EF 折叠，使点C 与点A 重合，折痕交AD 于点E ，交BC 于点F ，连接AF 、CE ，（1）求证：四边形AFCE 为菱形；（2）设AE=a ，ED=b ，DC=c ．请写出一个a 、b 、c 三者之间的数量关系式．10. 已知：如图，在菱形ABCD 中，F 为边BC 的中点，DF 与对角线AC 交于点M ，过M 作ME ⊥CD 于点E ，∠1=∠2．（1）若CE=1，求BC 的长；（2）求证：AM=DF+ME11.如图所示，现有一张边长为4的正方形纸片ABCD ，点P 为正方形AD 边上的一点（不与点A 、点D 重合）将正方形纸片折叠，使点B 落在P 处，点C 落在G 处，PG 交DC 于H ，折痕为EF ，连接BP 、BH ．（1）求证：∠APB =∠BPH ；（2）当点P 在边AD 上移动时，△PDH 的周长是否发生变化？并证明你的结论；A B CDEFG H PA CDEF GH P（备用图）二、动点问题1.如图，△ABC中，点O为AC边上的一个动点，过点O作直线MN∥BC，设MN 交∠BCA的外角平分线CF于点F，交∠ACB内角平分线CE于E．（1）试说明EO=FO；（2）当点O运动到何处时，四边形AECF是矩形并证明你的结论；（3）若AC边上存在点O，使四边形AECF是正方形，猜想△ABC的形状并证明你的结论．2.如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，已知AD=AB=3，BC=4，动点P从B点出发，沿线段BC向点C作匀速运动；动点Q从点D出发，沿线段DA向点A作匀速运动．过Q点垂直于AD的射线交AC于点M，交BC于点N．P、Q两点同时出发，速度都为每秒1个单位长度．当Q点运动到A点，P、Q两点同时停止运动．设点Q运动的时间为t秒．（1）求NC，MC的长（用t的代数式表示）；（2）当t为何值时，四边形PCDQ构成平行四边形；（3）是否存在某一时刻，使射线QN恰好将△ABC的面积和周长同时平分？若存在，求出此时t的值；若不存在，请说明理由；（4）探究：t为何值时，△PMC为等腰三角形．3.直线y=- 34x+6与坐标轴分别交于A、B两点，动点P、Q同时从O点出发，同时到达A点，运动停止．点Q沿线段OA运动，速度为每秒1个单位长度，点P 沿路线O⇒B⇒A运动．（1）直接写出A、B两点的坐标；（2）设点Q的运动时间为t（秒），△OPQ的面积为S，求出S与t之间的函数关系式；（3）当S= 485时，求出点P的坐标，并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标．4.已知,矩形ABCD 中,4AB cm =,8BC cm =,AC 的垂直平分线EF 分别交AD 、BC于点E 、F ,垂足为O .(1)如图1,连接AF 、CE .求证四边形AFCE 为菱形,并求AF 的长；(2)如图2,动点P 、Q 分别从A 、C 两点同时出发,沿AFB ∆和CDE ∆各边匀速运动一周.即点P 自A →F →B →A 停止,点Q 自C →D →E →C 停止.在运动过程中,已知点P 的速度为每秒5cm ,点Q 的速度为每秒4cm ,运动时间为t 秒,当A 、C 、P 、Q 四点为顶点的四边形是平行四边形时,求t 的值.AB C DEF 图1O 图2备用图三、探究题型1.如图，第①个图形中一共有1个平行四边形，第②个图形中一共有5个平行四边形，第③个图形中一共有11个平行四边形，…则第⑩个图形中平行四边形的个数是（） A ．54 B ．110 C ．19 D ．1092.如图所示，直线y=x+1与y 轴相交于点A 1，以OA 1为边作正方形OA 1B 1C 1，记作第一个正方形；然后延长C 1B 1与直线y=x+1相交于点A 2，再以C 1A 2为边作正方形C 1A 2B 2C 2，记作第二个正方形；同样延长C 2B 2与直线y=x+1相交于点A 3，再以C 2A 3为边作正方形C 2A 3B 3C 3，记作第三个正方形；…，依此类推，则第5个正方形的边长为_______________；第n 个正方形的边长为_______________________。

著名机构讲义春季01-八年级培优版-一次函数的图像与性质-学生版

教师姓名学生姓名年级初二上课时间学科数学课题名称一次函数的图像与性质一次函数的图像与性质知识模块Ⅰ：一次函数【答案】A【例3】已知一次函数y kx b =+，当1x =-时，3y =；当2x =时，5y =；求这个一次函数的解析式. 【答案】21133y x =+【例4】已知正比例函数（a ＜0）与反比例函数的图象有两个公共点，其中一个公共点的纵坐标为4．（1）求这两个函数的解析式；（2）在坐标系中画出它们的图象（可不列表）；（3）利用图像直接写出当x 取何值时，．【例5】某一次函数y ＝kx +b 的自变量取值范围为2≤x ≤4时，函数值的取值范围为5≤y ≤9，求这个函数解析式.xy xy xy xyDCB A OOOOx a y )3(1+=xa y 32-=21y y >OABxy知识模块Ⅱ：一次函数图像的变换变换平移对称旋转关于x 轴关于y 轴关于垂直于坐标轴的直线旋转图象上的两个点，由旋转后的两点坐标确定解析式方法 ⑴k 值不变，平移图象上的一个点；⑵k 值不变，“上加下减，左加右减”⑴对称图象上的两个点； ⑵k b 、均变为相反数⑴对称图象上的两个点；⑵k 变为相反数，b 不变对称图象上的两个点，由对称后的两点坐标确定解析式【例6】直线2(13)(22)y k x k =-+-与已知直线21y x =-+平行，且不经过第三象限，求k 的值．【例7】把一次函数的图像向上平移73个单位，得到的函数解析式为23y x =-，求平移前的函数图像与函数23y x =--的图像和坐标轴所围成的图形面积．【例8】直线313y x =-+和x 轴、y 轴分别相交于点A 、点B ，以线段AB 为边在第一象限内作等边三角形ABC ，如果在第一象限内有一点P （12m ，）且△ABP 的面积与△ABC 的面积相等，求m 的值．ABCPOxy【例9】函数12y y y =+且12y x m =+，2131y x m =+-．（1）若12y y 与图像的交点的纵坐标为4，求y 关于x 的函数解析式；（2）若（1）中函数y 的图像与x 轴、y 轴交于A 、B 两点，若将此函数绕A 点顺时针旋转90°后交y 轴于C 点，求直线AC 的解析式．知识模块Ⅲ：一些特殊直线大致图象等等等举例1y x =-+，2y x =-等2233y x y x =-+=-，等11122y x y x =+=--，等重要性质⑴与y x =或y x =-平行⑵与x y ，轴的夹角为45︒，并与坐标轴围成等腰直角三角形k b ，互为相反数即0k b +=k b =【例10】根据下列条件求解相应函数解析式：（1）直线经过点(45)，且与y =2x +3无交点；（2）直线的截距为-3且经过点(123)，．【例11】如图，已知函数1y x =+的图象与y 轴交于点A ，一次函数y kx b =+的图象经过点 B （0，1-），并且与x 轴以及1y x =+的图象分别交于点C 、D ；（1）若点D 的横坐标为1，求四边形AOCD 的面积（即图中阴影部分的面积）；（2）在第（1）小题的条件下，在y 轴上是否存在这样的点P ，使得以点P 、B 、D 为顶点的三角形是等腰三角形；如果存在，求出点P 坐标；如果不存在，说明理由；（3）若一次函数y kx b =+的图象与函数1y x =+的图象的交点D 始终在第一象限，则系数k 的取值范围是________（请直接写出结果）．【习题1】当m ___________时，一次函数的函数值y 随x 的减小而减小．【习题2】若一次函数的图像不经过第一象限，则的取值范围是___________．【习题3】老师给出一个一次函数，甲乙丙丁四位同学各指出这个函数的一个性质：甲说函数图像不经过第三象限；乙说函数图像经过第一象限；丙说当2x <时，y 随x 的增大而减小；丁说当2x <时，0y >.(21)3y m x =-+12(1)12y k x k =-+-k A BC DO xy。

著名机构讲义春季16-八年级培优版-图形运动中函数关系的确立-学生版

八年级(上)培优讲义：第11讲图形与坐标(1)

第11讲图形与坐标1一、知识建构1.确定位置常用的方法：一般由两种：1、2、.2.平面直角坐标系：（1）定义：具有的两条的数轴组成平面直角坐标系，两条数轴分别称轴轴或轴轴，这两系数轴把一个坐标平面分成的四个部分，我们称作是四个（2）有序数对：在一个坐标平面内的任意一个点可以用一对来表示，如A （a.b），（a.b）即为点A的其中a是该点的坐标，b是该点的坐标平面内的点和有序数对具有的关系.（3）平面内点的坐标特征:①P（a .b）：第一象限第二象限第三象限第四象限X轴上Y轴上②对称点：P（a ,b）关于y轴的对称点，关于y轴的对称点，关于原点的对称点。

③特殊位置点的特点：P（a .b）若在一、三象限角的平分线上，则若在二、四象限角的平分线上，则④到坐标轴的距离：P（a .b）到x轴的距离到y轴的距离到原点的距离⑤坐标平面内点的平移：将点P（a .b）向左（或右）平移h个单位，对应点坐标为（或），向上（或下）平移k个单位，对应点坐标为（或）.二、经典例题例1.某船从A港出发,先向正东行驶3千米到达B港，再向北航行3千米到达C港,求船只相对于A港的方位和距离.例2．小兰上学路上看见小雪,她一口气追上小雪,对小雪说:“刚才你在我的北偏西300方向”。

小雪说：“那你在我的西偏北300方向”。

小雪说得对吗？例3．如果规定行写在前面，列号写在后面，试用数对的方法表示出图中各点的位置.例4. 在平面直角坐标系中画出点A(0，－2)，B(1 ，2) ，C(－1，2)，D(－3，0)然后用线段把各点顺次连结起来.例5. 点P（3a－9,a+1）在第二象限，则a的取值范围为是多少？若a是整数请写出所有满足条件的点的坐标.例6.已知P(m,n)在第二象限，有序数对(m,n)中的整数m,n满足m－n=－6,写出所有符合条件的点坐标，并在平面直角坐标系中表示出来.三、基础演练1．(1)在教室里从讲台开始从前往后、从左往右数你的位置是4排3座，用有序实数对记作。

著名机构初中数学培优讲义.函数及图像.第05讲(B级).教师版

内容基本要求略高要求较高要求一次函数理解正比例函数，能结合具体情境了解一次函数的意义;会画一次函数的图像，理解一次函数的性质会根据已知条件确定一次函数解析式;会根据一次函数解析式求其图像与坐标轴的交点坐标；能根据一次函数图像求二元一次方程组的近似解能用一次函数解决实际问题一、函数的相关概念1．常量与变量在某一变化过程中，可以取不同数值的量叫做变量，取值始终保持不变的量叫做常量．如在圆的面积公式2πS R =中，π是常数，是一个常量，而S 随R 的变化而变化，所以S 、R 是变量．2．自变量、因变量与函数在某一变化过程中，有两个量，例如x 和y ，对于x 的每一个值，y 都有唯一的值与之对应，其中x 是自变量，y 是因变量，此时也称y 是x 的函数．函数不是数，它是指在一个变化过程中两个变量之间的关系，函数本质就是变量间的对应关系．注意：⑴对于每一个给定的x 值，y 有一个唯一确定的值与之对应，否则y 就不是x 的函数．例如2y x =就不是函数，因为当4x =时，2y =±，即y 有两个值与x 对应．⑵对于每一个给定的y 值，x 可以有一个值与之对应，也可以有多个值与之对应．例如在函数2(3)y x =-中，2x =时，1y =；4x =时，1y =．二、函数自变量的取值范围函数自变量的取值范围是指是函数有意义的自变量的取值的全体．求自变量的取值范围通常从两方面考虑，一是要使函数的解析式有意义；二是符合客观实际．在初中阶段，自变量的取值范围考虑下面几个方面： ⑴整式：自变量的取值范围是任意实数．例题精讲中考要求⑵分式：自变量的取值范围是使分母不为零的任意实数． ⑶根式：当根指数为偶数时，被开方数为非负数． ⑷零次幂或负整数次幂：使底数不为零的实数．注意：在一个函数关系式中，同时有各种代数式，函数自变量的取值范围是各种代数式中自变量取值范围的公共部分．在实际问题中，自变量的取值范围应该符合实际意义，通常往往取非负数，整数之类．三、函数的表示方法1．函数的三种表示方法：⑴列表法：通过列表表示函数的方法．⑵解析法：用数学式子表示函数的方法叫做解析法．譬如：30S t =，2S R π=． ⑶图象法：用图象直观、形象地表示一个函数的方法．2．对函数的关系式（即解析式）的理解：⑴函数关系式是等式．例如4y x =就是一个函数关系式．⑵函数关系式中指明了那个是自变量，哪个是函数．通常等式右边代数式中的变量是自变量，等式左边的一个字母表示函数．例如：y =x 是自变量，y 是x 的函数．⑶函数关系式在书写时有顺序性．例如：31y x =-+是表示y 是x 的函数，若写成13yx -=就表示x 是y 的函数．求y 与x 的函数关系时，必须是只用变量x 的代数式表示y ，得到的等式右边只含x 的代数式．三、函数的图象1．函数图象的概念：对于一个函数，如果把自变量x 和函数y 的每对值分别作为点的横坐标与纵坐标，在平面直角坐标系内描出相应的点，这些点所组成的图形，就是函数的图象．2．函数图象的画法⑴列表； ⑵描点； ⑶连线．3．函数解析式与函数图象的关系：由函数图象的定义可知，图象上任意一点(),P x y 中的x ，y 都是解析式方程的一个解．反之，以解析式方程的任意一个解为坐标的点一定在函数的图象上．判断一个点是否在函数图象上的方法是：将这个点的坐标值代入函数的j 解析式，如果满足函数解析式，这个店就在函数的图象上，否则就不在这个函数的图象上．模块一、函数及其自变量取值范围1.分别指出下列关系式中的变量与常量：球的表面积2cm S （）与球半径(cm)R 的关系式是24S R π=；设圆柱的底面半径()R m 不变，圆柱的体积3()V m 与圆柱的高()h m 的关系式是2V R h π=。

著名机构数学讲义寒假01-八年级培优版-一次函数的概念图像与性质-教师版

教师姓名冯娜娜学生姓名年级初二上课时间单击此处输入日期。

学科数学课题名称一次函数的概念图像与性质知识模块Ⅰ：一次函数的概念（1）一般地，解析式形如y kx b =+（k ，b 是常数，且0k ≠）的函数叫做一次函数；（2）一次函数y kx b =+的定义域是一切实数；（3）当0b =时，解析式y kx b =+就成为y kx =（k 是常数，且0k ≠），这时y 是x 的正比例函数，所以正比例函数是一次函数的特例；一次函数的概念图像与性质（4）一般地，我们把函数y c =（为常数）叫做常值函数．它的自变量由所讨论的问题确定．【例1】下列函数中，哪些是一次函数?（1）12y x =；（2）2y x =-+；（3）2(21)y x x =-+；（4）5y x=；（5）2y x x =-；（6）()()y ax bx a a b =-+≠．【答案】（1）、（2）、（6）．【例2】已知y 与x 的关系式是(3)y a x a =-+（其中a 是常数），那么y 是x 的一次函数吗?请说明．【答案】当3a ≠时，y 是x 的一次函数；当3a =时，y =3，y 不是x 的一次函数，是常值函数；【例3】已知一次函数解析式为()21345m y m x x +=-+-，求实数m 的值．【答案】0m =或3m =或12m =-．知识模块Ⅱ：一次函数的图像与性质（一）一次函数的图像：1、一次函数的图像：一次函数的y kx b =+（其中k 、b 是常数，且k ≠0）的图像是一条直线。

2、一次函数的图像的画法：y kx b =+示意图（草图）经过的象限变化趋势性质（增减性）0k >0b >一、二、三从左向右上升y 随x 的增大而增大， y 随x 的减小而减小0b <一、三、四 0k <0b >一、二、四从左向右下降y 随x 的增大而减小，y 随x 的减小而增大0b <二、三、四 OyxOyxxyO Oyx画一次函数的图像可通过“列表、描点、连线”获得，也可由“两点确定一条直线”的知识，通过“只需描出图像上的两个点，然后过这两点做一条直线” 获得 3、直线与截距：一条直线与y 轴的交点的纵坐标叫做这条直线在y 轴上的截距，简称直线的截距。

著名机构初中数学培优讲义图形初步.第06讲(C级).教师版

内容基本要求略高要求较高要求立体图形的展开图会画基本几何体（直棱柱、圆柱、圆锥、球）；了解直棱柱、圆锥的侧面展开图；了解基本几何体的展开图（球除外）；观察与现实生活有关的图片，并能对形状、大小和相互位置作做简单的描述．能根据直棱柱、圆锥的展开图判断立体模型．直线、射线、线段会表示点、线段、射线、直线，知道它们之间的联系和区别；结合图形理解两点之间的距离的概念；会比较两条线段的大小，并能进行与线段有关的简单计算会用尺规作图：做一条线段等于已知线段，做已知线段的垂直平分线；会用线段中点的知识解决简单问题；结合图形认识线段间的数量关系会运用两点间的距离解决有关问题角、角平分线会识别角并会表示；认识角、分、秒，并会进行简单换算；会度量角的大小并进行简单计算；会比较两个角的大小；了解角平分线的概念并会表示会尺规作图：作一个角等于已知角，做已知角的角平分线；会用角平分线的性质解决简单问题；会结合图形认识角与角之间的数量关系一、立体图形的展开图正方形展开图的知识要点：第一类：有6种。

特点：是4个连成一排的正方形，其两侧各有一个正方形.简称“141型”第二类：有3种。

特点：是有3个连成一排的正方形，其两侧分别有1个和两个相连的正方形;简称“132型”例题精讲中考要求图形初步第三类：仅有一种。

特点：是两个连成一排的正方形的两侧又各有两个连成一排的正方形；简称“222型”第四类：仅有1种，三个连成一排的正方形的一侧，还有3个连成一排的正方形，可简称“33型”正方形展开图的识别方法：1.排除法：（1）由少于或多于6个的正方形组成的图形不是正方形的平面展开图（2）有“凹”字型或“田”字型部分的平面图形不是正方体的展开图2.对比法：对照上面的四种规则进行对照；从展开图可以看出，在正方形的展开图中不会出现如下图所示的“凹”字型和“田”字型结构。

二、直线、射线、线段的概念：①在直线的基础上定义射线、线段：直线上的一点和这点一旁的部分叫射线，这个点叫做射线的端点．直线上两点和中间的部分叫线段，这两个点叫线段的端点．②在线段的基础上定义直线、射线：把线段向一方无限延伸所形成的图形叫射线，把线段向两方无限延伸所形成的图形是直线．点与直线的关系：点在直线上；点在直线外．两个重要公理：①经过两点有且只有一条直线，也称为“两点确定一条直线”．②两点之间的连线中，线段最短，简称“两点之间，线段最短”．两点之间的距离：两点确定的线段的长度．⑴点的表示方法：我们经常用一个大写的英文字母表示点：A，B，C，D，……⑵直线的表示方法：①用两个大写字母来表示，这两个大写字母表示直线上的点，不分先后顺序，如直线AB，如下图⑴也可以写作直线BA．(1) (2)lA B② 用一个小写字母来表示，如直线l，如上图⑵．注意：在直线的表示前面必须加上“直线”二字；用两个大写字母表示时字母不分先后顺序．⑶射线的表示方法：① 用两个大写字母来表示．第一个大写字母表示射线的端点，第二个大写字母表示射线上的点．如射线OA ，如图⑶，但不能写作射线AO ． ② 用一个小写字母来表示，如射线l ，如图⑷．(3) (4)lAO注意：在射线的表示前面必须加上“射线”二字．用两个大写字母表示射线时字母有先后顺序，射线的端点在前．⑷ 线段的表示方法：① 用两个大写字母来表示，这两个大写字母表示线段的两个端点，无先后顺序之分，如线段AB ，如图⑸，也可以写作线段BA ．② 也可以用一个小写字母来表示：如线段l ，如图⑹．(5) (6)lAB注意：在线段的表示前面必须加上“线段”二字．用两个大写字母表示线段时字母不分先后顺序．中点：把线段分成两条相等的线段的点叫做这条线段的中点．三、角与角平分线 1、定义定义1：有公共端点的两条射线组成的图形叫角，这个公共端点是角的顶点，这两条射线是角的两条边.角的大小只与开口的大小有关，而与角的边画出部分的长短无关．这是因为角的边是射线而不是线段．定义2：角由一条射线绕着它的端点旋转到另一个位置所成的图形，处于初始位置的那条射线叫做角的始边，终止位置的那条射线叫做角的终边.(1) 如果角的终边是由角的始边旋转半周而得到，这样的角叫平角. (2) 如果角的终边是由角的始边旋转一周而得到，这样的角叫周角. 注意：由角的定义可知：（1）角的组成部分为：两条边和一个顶点；（2）顶点是这两条边的交点；（3）角的两条边是射线，是无限延伸的.（4）射线旋转时经过的平面部分称为角的内部，平面的其余部分称为角的外部.角平分线：从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线。

著名机构讲义春季09-八年级培优版-期中复习-学生版

教师姓名学生姓名年级初二上课时间学科数学课题名称期中复习知识模块Ⅰ：一次函数的图像与性质1、一般地，一次函数（是常数，且）的图像是一条直线2、一般地，直线（）与轴的交点坐标是（0，）。

直线（）的截距是。

3、一般地，一次函数（）的图像可由正比例函数的图像平移得到。

当时，向上平移个单位；当时，向下平移个单位。

如果，那么直线与直线b kx y +=b k ，0k ≠b kx y +=0≠k y b b kx y +=0≠k b b kx y +=0b ≠kx y =0>b b 0<b b 21b b ≠1b kx y +=期中复习平行。

反过来，如果，直线与直线平行，那么，。

4、由一次函数的函数值（或），就得到关于的一元一次不等式（或），在一次函数的图像上且位于轴上方（或下方）的所有点，他们的横坐标的取值范围就是不等式（或）的解集。

5、一般来说，一次函数（为常数，且）具有以下性质：当时，函数值随自变量的值增大而增大；当时，函数值随自变量的值增大而减小。

6、正比例函数是特殊的一次函数，它的性质与一次函数的性质是一致的。

7、直线（）过点（0，）且与直线平行。

由直线在直角坐标平面内的位置情况可知：当，且时，直线经过第一、二、三象限；当时，直线经过第一、三、四象限；当时，直线经过第一、二、四象限；当时，直线经过第二、三、四象限。

把上述判断反过来叙述也是正确的知识模块Ⅱ：代数方程（一）整式方程1．一元整式方程：如果方程中只有一个未知数且两边都是关于未知数的整式,这个方程叫做一元整式方程．2．一元n 次方程：一元整式方程中含未知数的项的最高次数是n （n 是正整数），这个方程叫做一元次方程．3．一元高次方程：一元整式方程中含有未知数的项的最高次数是n ，若次数n 是大于2的正整数，这样的方程统称为一元高次方程．4．（1）二项方程：如果一元n 次方程的一边只有含未知数的一项和非零的常数项，另一边是零，那么2b kx y +=11b x k y +=22b x k y +=21k =k 21b ≠b b kx y +=0>y 0<y x 0>+b kx 0<+b kx b kx y +=x 0>+b kx 0<+b kx b kx y +=b k ,0≠k 、a 0>k y x 、b 0<k y x b kx y +=0,0≠≠b k b kx y =kx y =、a 0>k 0>b b kx y +=、b 00<>b k ，且b kx y +=、c 00><b k ，且b kx y +=、d 00<<b k ，且b kx y +=n这样的方程就叫做二项方程．（2）二项方程的一般形式为0(0,0,)nax b a b n +=≠≠是正整数（3）二项方程根的情况：当n 为奇数时，方程有且只有一个实数根当n 为偶数时，如果ab <0，那么方程有两个实数根，且这两个根互为相反数；如果ab >0，那么方程没有实数根.（二）分式方程1.分式方程：分母中含有未知数的方程叫做分式方程2.基本思想：通过去分母把分式方程转化为整式方程，在求解。

著名机构数学讲义暑假16-八年级基础版-函数的应用-教师版

教师姓名学生姓名年级初二上课时间学科数学课题名称函数的应用函数的应用知识模块Ⅰ：反比例函数构造面积 1. 反比例函数图像上任意一点到x 轴y 轴的垂线，所得矩形的面积为k 的绝对值。

2. 过反比例函数图像上任一点作坐标轴的垂线，则垂足，已知点及原点这三点构成的三角形的面积k s 21= 【例1】如图，过双曲线k y x =（k 是常数，k ＞0，x ＞0）的图象上两点A ，B 分别作AC ⊥x 轴于C ，BD ⊥x 轴于D ，则△AOC 的面积S 1和△BOD 的面积S 2的大小关系为（）A ．S 1＞S 2B ．S 1=S 2C ．S 1＜S 2D ．S 1与S 2无法确定【答案】B【例2】如图，已知点P 是双曲线k y x=（k ≠0）上一点，过点P 作P A ⊥x 轴于点A ，且S △P AO =2，则该双曲线的解析式为（）A ．y =﹣B ．y =﹣C ．y =D ．y =【答案】B【例3】如图，已知点P （x ，y ）是反比例函数图象上一点，O 是坐标原点，P A ⊥x 轴，S △P AO =4，且图象经过（1，3m ﹣1）；求：（1）反比例函数解析式．（2）m 的值．【答案】（1）8y x=（2）3m =【例4】已知：在平面直角坐标系xOy 中，过点A （﹣5，2）向x 轴作垂线，垂足为B ，连接AO ，点C在线段AO上，且AC：CO=2：3，反比例函数kyx=的图象经过点C，与边AB交于点D．（1）求反比例函数的解析式；（2）求△BOD的面积．【答案】（1）185yx=-（2）95知识模块Ⅱ：正反比例函数交点问题和面积1.K值几何意义2.图形的对称性3.面积公式、面积等积转换【例5】正比例函数y=x与反比例函数1yx=的图象相交于A、C两点．AB⊥x轴于B，CD⊥x轴于D（如图），则四边形ABCD的面积为（）A．1B．C．2D．【答案】C【例6】若函数y=kx（k＞0）与函数kyx=的图象相交于A，C两点，AB垂直x轴于B，则△ABC的面积为（）A．1B．2C．K D．k2【答案】A【例7】如图，反比例函数4yx=-的图象与直线13y x=-x的交点为A，B，过点A作y轴的平行线与过点B作x轴的平行线相交于点C，则△ABC的面积为（）A．8B．6C．4D．2【答案】A【例8】已知正比例函数y=mx与反比例函数6myx+=的图象有两个交点，其中一个交点的横坐标为2．（1）求这两个函数的解析式；（2）在同一直角坐标内画出它们的图象．【答案】（1）93y x yx==（2）省略知识模块Ⅲ：正反例函数的应用1、行程问题2、面积周长3、正反比例结合【例9】一辆汽车在行驶过程中，路程y（千米）与时间x（小时）之间的函数关系如图所示，当0≤x≤1时，y关于x的函数解析式为y = 60x，那么汽车在第二小时内的平均速度为 _____________千米/小时。

著名机构初中数学培优讲义一次函数与几何综合.第09讲(C级).教师版

内容基本要求略高要求较高要求一次函数理解正比例函数，能结合具体情境了解一次函数的意义;会画一次函数的图像，理解一次函数的性质会根据已知条件确定一次函数解析式;会根据一次函数解析式求其图像与坐标轴的交点坐标；能根据一次函数图像求二元一次方程组的近似解能用一次函数解决实际问题一、一次函数的应用【例1】如果等腰三角形的周长为16，那么它的底边长y 与腰长x 之间的函数图像为（）A1684816y xOB1684816y xOC1684816y xOD1684816y xO【解析】由题意得函数关系式为y 216x =-+，根据三角形三边关系2x y >，即2216x x >-+，得4x >，例题精讲中考要求一次函数与几何综合又因为216x <，所以8x <，确定自变量的取值范围48x <<【答案】A【例2】 2007年5月，第五届中国宜昌长江三峡国际龙舟拉力赛在黄陵庙揭开比赛帷幕．20日上午9时，参赛龙舟从黄陵庙同时出发．其中甲、乙两队在比赛时，路程y （千米）与时间x （小时）的函数关系如图所示．甲队在上午11时30分到达终点黄柏河港． ⑴哪个队先到达终点？乙队何时追上甲队？ ⑵在比赛过程中，甲、乙两队何时相距最远？时间/时【解析】⑴乙队先达到终点，对于乙队，1x =时，16y =，所以16y x =，对于甲队，出发1小时后，设y 与x 关系为y kx b =＋，将1x =，20y =和 2.5x =，35y =分别代入上式得： 2035 2.5k bk b =+⎧⎨=+⎩解得：1010y x =＋解方程组161010y x y x =⎧⎨=+⎩ 得：53x =，即：出发1小时40分钟后（或者上午10点40分）乙队追上甲队．⑵1小时之内，两队相距最远距离是4千米，乙队追上甲队后，两队的距离是16(1010)610x x x -+=-，当x 为最大，即3516x =时，610x -最大，此时最大距离为35610 3.125416⨯-=<，（也可以求出AD CE 、的长度，比较其大小）所以比赛过程中，甲、乙两队在出发后1小时（或者上午10时）相距最远【答案】⑴乙队先达到终点，甲队出发1小时40分钟后（或者上午10点40分）乙队追上甲队；⑵甲、乙两队在出发后1小时（或者上午10时）相距最远【例3】如图表示甲、乙两名选手在一次自行车越野赛中，路程y （km ）随时间x （min ）的变化的图像（全程），根据图像回答以下问题：⑴求比赛开始多少分钟时，两人第一次相遇？⑵求这次比赛的全程是多少？⑶求比赛开始多少分钟时，两人第二次相遇？【解析】⑴由图可知，线段OD 过点481200（，）（，，）可知其解析式为14y x =，他们相遇时6y =，此时24x =，故比赛开始24分钟时，两人第一次相遇． ⑵由图可知，这次比赛的全程为12km ．⑶点B （33，7）、点C （43，12），故线段BC 的解析式为：()1192y x =-，而线段OD 的解析式为()10484y x =<<，故它们的交点坐标为（38，192），即比赛开始38分钟时，两人第二次相遇．【答案】⑴24；⑵12；⑶38【例4】为了保护环境，某企业决定购买10台污水处理设备，现有A B ，两种型号的设备，其中每台的价⑴求购买设备的资金y 万元与购买A 型x 台的函数关系，并设计该企业有几种购买方案； ⑵若企业每月产生的污水量为2040吨，利用函数的知识说明，应选择哪种购买方案；⑶在第⑵问的条件下，若每台设备的使用年限为10年，污水厂处理污水费为每吨10元，请你计算，该企业自己处理污水与将污水排到污水厂处理相比较，10年节约资金多少万元？（注：企业处理污水的费用包括购买设备的资金和消耗费）【解析】⑴购买污水处理设备A 型x 台，则B 型()10x -台，由题意知：()121010y x x =+- 即2100y x =+ 2100105y x =+≤ ∴ 2.5x ≤又∵x 是非负整数 ∴x 可取0,1,2∴有三种购买方案：①购A 型D 台，B 型10台；②购A 型1台，B 型9台；③购A 型2台，B 型8台；⑵由题意得()240200102040x x +-≥，解得1x ≥∴x 为1或2∵由2100y x =+得20k =>，y 随x 的增大而增大．为了节约资金，应选购A 型1台，B 型9台．⑶10年企业自己处理污水的总资金为：1021010202+⨯=（万元）若将污水排到污水厂处理，10年所需费用为： 20401210102448000⨯⨯⨯＝（元）244.8=（万元）∵244.820242.8-=（万元） ∴能节约资金42.8万元．【答案】⑴2100105y x =+≤，有三种购买方案：①购A 型D 台，B 型10台；②购A 型1台，B 型9台；③购A 型2台，B 型8台； ⑶42.8【例5】一次时装表演会预算中票价定位每张100元，容纳观众人数不超过2000人，毛利润y （百元）关于观众人数x （百人）之间的函数图象如图所示，当观众人数超过1000人时，表演会组织者需向保险公司交纳定额平安保险费5000元（不列入成本费用）请解答下列问题：⑴求当观众人数不超过1000人时，毛利润y （百元）关于观众人数x （百人）的函数解析式和成本费用s （百元）关于观众人数x （百人）的函数解析式；⑵若要使这次表演会获得36000元的毛利润，那么要售出多少张门票？需支付成本费用多少元？（注：当观众人数不超过1000人时，表演会的毛利润=门票收入—成本费用；当观众人数超过1000人时，表演会的毛利润=门票收入—成本费用—平安保险费）【解析】⑴由图象可知：当010x ≤≤时，设y 关于x 的函数解析100y kx =-，∵(10,400)在100y kx =-上，∴40010100k =-，解得50k = ∴50100y x =-，100(50100)s x x =--），∴50100s x =+ ⑵当1020x <≤时，设y 关于x 的函数解析式为y mx b =+， ∵(10,350)，(20,850)在y mx b =+上， 1035020580m b m b +=⎧⎨+=⎩，解得50150m b =⎧⎨=-⎩∴50150y x =-，∴()100501505050100s x x s x ∴=---∴=+ ∴()()50100010501501020x x y x x ⎧-⎪=⎨-<⎪⎩≤≤≤令360y =当010x ≤≤时，50100360x -= 解得9.2x =50100509.2100560s x =+=⨯+=当1020x <≤时，50150360x -=解得10.2x = 501005010.2100610s x =+=⨯+=．要使这次表演会获得36000元的毛利润．要售出920张或1020张门票，相应支付的成本费用分别为56000元或61000元．【答案】⑴50100s x =+；⑵要售出920张或1020张门票，相应支付的成本费用分别为56000元或61000元【例6】某汽车运输公司根据实际需要计划购买大、中型两种客车共20辆，已知大型客车每辆62万元，中型客车每辆40万元，设购买大型客车x （辆），购车总费用为y （万元）．（1）求y 与x 的函数关系式（不要求写出自变量x 的取值范围）；（2）若购买中型客车的数量少于大型客车的数量，请你给出一种费用最省的方案，并求出该方案所需费用．【解析】略【答案】（1）因为购买大型客车x 辆，所以购买中型客车()20x -辆．()62402022800y x x x =+-=+．（2）依题意得()20x x -<.解得x >10．∵ 22800y x =+，y 随着x 的增大而增大，x 为整数，∴ 当x=11时，购车费用最省，为22×11+800=1 042（万元）．此时需购买大型客车11辆，中型客车9辆．答：购买大型客车11辆，中型客车9辆时，购车费用最省，为1 042万元．二、一次函数与几何综合【例7】已知直线3y x =+的图象与x y 、轴交于A B 、两点，直线l 经过原点，与线段AB 交于点C ，把AOB ∆的面积分为2:1的两部分，求直线l 的解析式。

上海1对3春季讲义-数学-八年级-第1讲-一次函数的图像与性质

精锐教育1对3辅导讲义问题一汽车以60千米/时的速度匀速行驶，行驶里程为s千米，行驶时间为t小时，填下面的表:60120180240300说说你是如何得到的：路程 =试用含t的式子表示s在一根弹簧的下端挂重物，改变并记录重物的质量，观察并记录弹簧长度的变化，探索它们的变化规律。

如果弹簧原长为10cm，每1千克重物使弹簧伸长0.5cm，怎样用含重物质量x（单位：kg）的式子表示受力后的弹簧长度L(单位：cm)?【知识梳理1】1、一次函数的概念2、一次函数与正比例函数的关系3、一次函数图像经过的象限4、一次函数的增减性xyxyOO4．关于x 的一次函数21y kx k =++的图像可能是（）．5．若一次函数的图像经过点（1，3）与（2，﹣1），则它的解析式为．6．已知一次函数3(3)y x =-+在y 轴上的截距是；如果一次函数235y x m =--在y 轴上的截距是7，则_________m =．7．过点P （8，2）且与直线1y x =+平行的一次函数解析式为_________．1．将直线向上平移3个单位得到的函数解析式是． 2．函数，随的增大而．3．直线如图所示，化简：．4．已知函数轴交点的纵坐标为，且当，则此函数的解析式为．5．如图，表示一次函数与正比例函数（为常数，且）图象的是（）xyxyxyxyDCBAOOOO13y x =-34y x =-y x y mx n =+2m n m --=y kx b y =+的图象与5-12x y ==时，y mx n =+y mnx =m n ，mn 0≠xy xy xy xyDCB A OOOO1．甲、乙两人到距离A 地35千米的B 地办事，甲步行先走，乙骑车后走，两人行进的时间和路程的关系如图所示，根据图示提供的信息解答：（1）乙比甲晚小时出发；（2）乙出发小时后追上甲；（3）求乙比甲早几小时到达B 地？2．如图，线段AB ，CD 分别是一辆轿车和一辆客车在行驶过程中油箱内的剩余油量1y （升）、2y （升）关于行驶时间x （小时）的函数图像。

著名机构数学讲义暑假12-八年级培优版-正比例函数的图象与性质-学生版

教师姓名学生姓名年级初二上课时间学科数学课题名称正比例函数的图像与性质正比例函数的图像与性质知识模块Ⅰ：正比例函数的定义1.思考：下列问题中的变量对应规律可用怎样的函数表示？（1）圆的周长L随半径r的大小变化而变化。

（2）每个练习本的厚度为0.5cm,一些练习本摞在一起总的厚度h(单位：cm)随这些练习本的本数m的变化而变化。

（3）冷冻一个0℃的物体，使它每分下降2℃，物体温度T（单位：℃）随冷冻时间m（单位：分）的变化而变化。

2.观察发现，得出正比例函数的定义一般地，形如y＝kx (K是常数、k≠0) 的函数，叫正比例函数，其中k叫做比例系数。

强调两点：①k≠0(即自变量系数不为0) ②x的指数为1【例1】下列关系中的两个量成正比例的是（）A．从甲地到乙地，所用的时间和速度B．正方形的面积与边长C．买同样的作业本所要的钱数和作业本的数量D．人的体重与身高【例2】下列关系式中，表示y是x的正比例函数的是（）A．y=B．y=1C．y=x+1D．y=2x【例3】若函数y=（4m﹣1）x+m﹣4是正比例函数，则m的取值范围是（）A．m=4B．C．m≤4D．【例4】已知函数y=2x2a+2b是正比例函数，则a+b=__________知识模块Ⅱ：正比例函数的图像1.（1）列表（2）描点（3）连线2.正比例函数的图像根据两点确定一条直线，可以确定两个点（两点法）画正比例函数的图象．正比例函数图像是经过原点（0，0）和点(1,k)的一条直线。

【例5】画出y＝-3x的图像【例6】在平面直角坐标系中，正比例函数y=-x的图象的大体位置是（）A ．B ．C ．D ．知识模块Ⅲ：正比例函数的性质当k >0时，直线y =kx 依次经过第三、一象限，从左向右上升，y 随x •的增大而增大；当k <0时，直线y =kx 依次经过第二、四象限，从左向右下降，y 随x •的增大而减小【例7】已知正比例函数y =（5m ﹣3）x ，如果y 随着x 的增大而减小，那么m 的取值范围为__________【例8】如果点A （﹣1，2）在一个正比例函数y =f （x ）的图象上，那么y 随着x 的增大而__________ （填“增大”或“减小”）．【例9】正比例函数y =（2a ﹣1）x 的图象经过第二、四象限，那么a 的取值范围是__________ 【例10】如果正比例函数y =（k ﹣3）x 的图象经过第一、三象限，那么k 的取值范围是__________ 【例11】正比例函数y =kx 的图象如图所示，则k 的取值范围是（） A ．k ＞0 B ．k ＜0C ．k ＞1D ．k ＜1【例12】关于函数y =2x ，下列结论中正确的是（）A ．函数图象都经过点（2，1）B ．函数图象都经过第二、四象限C ．y 随x 的增大而增大D ．不论x 取何值，总有y ＞0（第1题）k ＞0 （第1题）k <0【例13】下列关于正比例函数y=3x的说法中，正确的是（）A．当x=3时，y=1B．它的图象是一条过原点的直线C．y随x的增大而减小D．它的图象经过第二、四象限知识模块Ⅳ：用待定系数法求正比例函数待定系数法：先设代求函数关系式，在根据条件列方程或方程组，求出未知系数，从而得到所求结果的方法。

著名机构讲义春季03-八年级培优版-一次函数章节复习-教师版

教师姓名学生姓名年级初二上课时间学科数学课题名称一次函数章节复习一次函数章节复习【答案】 D【例4】若，且的图像不经过第四象限，则点所在象限为______．【答案】四．【例5】若函数与轴交于点A ，直线上有一点M ，若△AOM 的面积为8，则点M 的坐标______．【答案】(04)-，或(84)-，．【例6】如图所示，直线经过A （1，2）和B （3，0）两点，则不等式组的解集是多少? 【答案】10x -<<．【例7】如图所示，直线与轴、轴分别交于点A 和点B ，D 是轴上的一点，若将△DAB 沿直线DA 折叠，点B 恰好落在轴正半轴上的点C 处，求直线CD 的解析式．0abc <b cy x a a=-()a b c +，4y x =--x y kx b =+--13x kx b -+<+<323y x =-+x y y x ABCDxyO ．A BOxy【答案】3233y x =-．【例8】如图所示，直线L 与轴、轴分别交于A （6，0）、B （0，3）两点，点C （4，0）为轴上一点，点P 在线段AB （包括端点A 、B ）上运动．（1）求直线L 的解析式；（2）当点P 的纵坐标为1时，按角的大小进行分类，请你确定△P AC 是哪一类三角形，并说明理由；（3）是否存在这样的点P ，使得△POC 为直角三角形?若存在，求出点P 的坐标；若不存在，请说明理由．【答案】（1）132y x =-+；（2）直角三角形；（3）（0，3），（4，1），（2，2），P 186()55，．【例9】已知一次函数中随的增大而增大，它的图像与两坐标轴构成的直角三角形的面积不超过，反比例函数的图像在第二、四象限．求满足以上条件的的整数值．【答案】1或2．x y x 1121y x k =+-y x 3223k y x-=k ABC DO xy 346ABCP x yL【例10】如图，在平面直角坐标系中，多边形OABCDE 的顶点坐标分别是，，，，，．若直线经过点，且将多边形OABCDE 分割成面积相等的两部分，求直线的函数表达式．【答案】11133y x =-+．【习题1】如图，直线与x 轴交于点（-4，0）则当y ＞0时，x 的取值范围是（） A ．x ＞-4 B ．x ＞0 C ．x ＜-4 D ．x ＜0【答案】 AxOy (00)O ，(06)A ，(46)B ，(44)C ，(64)D ，(60)E ，l (23)M ，l y kx b =+AB CDE PMOxy 0-4xy【习题2】小明、小强两人进行百米赛跑，小明比小强跑得快，如果两人同时跑，小明肯定赢，现在小明让小强先跑若干米，图中的射线a 、b 分别表示两人跑的路程与小明追赶时间的关系，根据图象判断：小明的速度比小强的速度每秒快（） A ．1米 B ．1.5米C ．2米D ．2.5米【答案】 D【习题3】如图，在直角梯形ABCD 中，动点P 从点B 出发，沿BC 、CD 运动至点D 停止．设点P 运动的路程为，△ABP 的面积为y ，如果y 关于x 的函数图像如图所示，则△BCD的面积是（）A ．3B ．4C ．5D ．6【答案】 A【习题4】直线y =(m +1)x +m 2+1与y 轴的交点坐标是（0，3），且直线经过第一、二、四象限，则m =______．【答案】2m =-．【习题5】如图一次函数的图像如图所示，如果，那么x 的取值范围是____________．【答案】x ＜2x y kx b =+0kx b +>864200s （米）t （秒）ba ABC DP xy52Oxy324302s （千米） BCDt （小时）A【习题6】如图，已知A 地在B 地正南方3千米处，甲乙两人同时分别从A 、B 两地向正北方向匀速直行，他们与A 地的距离S （千米）与所行的时间t （小时）之间的函数关系图象如图所示的AC 和BD 给出，当他们行走3小时后，他们之间的距离为______千米．【答案】1.5．【习题7】如图，直线与轴、轴分别相交于点A 、B ，△AOB 与△ACB 关于直线对称，则点C 的坐标为________．【答案】33()22，．【习题8】在平面直角坐标系中，O 为坐标原点，已知A （1，）在直线上，在坐标轴上确定点P ，使△AOP 为等腰三角形，则符合条件的点P 的个数有__________个．【答案】 8【习题9】A 市、B 市和C 市分别有某种机器10台、10台、8台，现在决定把这些机器支援给D 市18台，E 市10台．已知：从A 市调运1台机器到D 市、E 市的运费分别为200元和800元；从B 市调运1台机器到D 市、E 市的运费分别为300元和700元；从C 市调运1台机器到D 市、E 市的运费分别为400元和500元．设从A 市、B 市各调台机器到D 市，当28台机器调运完毕后，求总运费W （元）关于（台）的函数关系式，并求W 的最大值和最小值．【答案】W =-800x +17200，最大值13200元，最小值10000元．:33l y x =-+x y l a 2y x =-+x x ABCOxyl【习题10】如图所示，在矩形OABC中，O为直角坐标系的原点，A 、C两点的坐标为（3，0），（0，5）（1）请直接写出点B的坐标；（2）若过点C的直线CD交AB边于点D，且把矩形OABC的周长分为1:3的两部分，求直线CD 的解析式．【答案】（1）B（3，5）；（2）153y x=-+．ABCO xy。

浙教版数学八年级上册专题培优讲义《专题12 函数与方程思想》

浙教版数学八年级上册专题培优讲义专题12函数与方程思想【知识梳理】函数思想，是指用函数的概念和性质去分析问题、转化问题和解决问题，函数思想的实质是用联系和变化的观点研究问题，将问题中的量转化为函数关系去解决．方程思想是从问题的数量关系入手，运用数学语言将问题中的条件转化为方程或方程组，然后通过解方程(组)来使问题获解．方程与函数联系密切，我们可以用方程思想解决函数问题，也可以用函数思想讨论方程问题．在确定函数解析式中的待定系数、函数图象与坐标轴的交点、函数图象的交点等问题时，将问题转化为解方程或方程组，而在讨论方程、方程组的解的个数、解的分布情况等问题时，借助函数图象能获得直观简洁的解答．【例题探究】【例1】若A (－1，2)，B (2，－1)，C (m ，m )三点在同一条直线上，则m 的值等于________．【思路点拨】先用待定系数法求出经过点A (－1，2)，B (2，－1)的直线的表达式，再把点C 的坐标代入表达式，解方程即可得出m 的值．【例2】如图，将边长为6cm 的正方形纸片ABCD 折叠，使点D 落在AB 边的中点E 处，点C 落在点Q 处，折痕为FH ，则线段AF 的长为()A ．32B ．3C ．94D ．154【思路点拨】由正方形的性质和折叠的性质，可得EF ＝DF ，∠A ＝90°，在Rt △AEF 中，根据勾股定理列出方程即可得出AF 的长．【例3】设直线y＝kx＋6和直线y＝(k＋1)x＋6(k是正整数)及x轴围成的三角形的面积为S k(k＝1，2，3，…，8)，则S1＋S2＋S3＋…＋S8的值是()A．49B．634C．16D．14【思路点拨】先求出直线y＝kx＋6和直线y＝(k＋1)x＋6的交点，再求出这两条直线与x轴围成的三角形的面积S k的表达式，将其代入S1＋S2＋S3＋…＋S8即可得出结果．【例4】甲、乙两家体育器材商店出售同样的乒乓球拍和乒乓球，球拍一副定价60元，乒乓球每盒定价10元．世界乒乓球锦标赛期间，两家商店都进行促销活动：甲商店规定每买一副乒乓球拍赠两盒乒乓球；乙商店规定所有商品打九折．某校乒乓球队需要买2副乒乓球拍，乒乓球若干盒(不少于4盒)．设该校要买乒乓球x盒，所需商品在甲商店购买需用y1元，在乙商店购买需用y2元．(1)请分别写出y1，y2与x之间的函数关系式(不必注明自变量x的取值范围)；(2)对x的取值情况进行分析，试说明在哪一家商店买所需商品比较便宜；(3)若该校要买2副乒乓球拍和20盒乒乓球，在不考虑其他因素的情况下，请设计一个最省钱的购买方案．【思路点拨】先根据题意建立费用y与购买数量x的函数关系式，再结合方程与不等式求解．【例5】如图1，在平面直角坐标系xOy中，直线l1：y＝x＋1与x轴交于点A，直线l2：y＝3x－3与x轴交于点B，与l1相交于点C.图1(1)求点A，B，C的坐标；(2)如图2，动直线x＝t分别与直线l1，l2交于P，Q两点．①若PQ＝2，求t的值；＝2S△ABC？若存在，求出此时点Q的坐标；若不存在，请②是否存在一点Q，使得S△AQC说明理由．图2【思路点拨】(1)在两个函数表达式中令y＝0即可求得点A，B的坐标，联立两个函数表达式即可求得点C的坐标；(2)①由题意可得点P(t，t＋1)，点Q(t，3t－3)，根据PQ＝2列出方程即可求得t的值；②先求出△ABC的面积，即可得出△AQC的面积，再根据△AQC的面积等于水平宽与铅垂高乘积的一半列方程求解．【例6】工厂某车间需加工一批零件，甲组工人加工中因故停产检修机器一次，然后以原来的工作效率继续加工，由于时间紧任务重，乙组工人也加入共同加工零件．设甲组加个)，乙组加工零件的数量为y乙(个)，其函数图象如工时间t(时)，甲组加工零件的数量为y甲(图所示．(1)求y乙与t之间的函数关系式，并写出t的取值范围；(2)求a的值，并说明a的实际意义；(3)甲组加工多长时间时，甲、乙两组加工零件的总数为480个？与t之间的函数关系式，结合图象可写出t 【思路点拨】(1)用待定系数法即可求得y乙的取值范围；(2)由图象知，甲3小时加工零件120，可求得甲加工零件的速度，从而可求得甲加工8小时的零件个数；(3)设甲组加工m小时，根据甲、乙两组加工零件的总数为480个，列出方程即可解答．【例7】某市是著名的苹果生产基地，果品公司从A村收购苹果400吨，从B村收购苹果600吨．现在要将这些苹果运到C，D两个冷藏仓库储存，已知C库可储存300吨，D 库可储存700吨苹果；从A村运往C，D两处的费用分别为每吨20元和25元，从B村运往C，D两处的费用分别为每吨15元和18元．请你设计一个方案使苹果的运输费用最小，最小费用是多少．【思路点拔】设从A村运x吨苹果到C库，则可以用x的代数式表示苹果的运输费用y元的函数关系式，再结合函数增减性就能求出最小费用．【答案解析】【知识梳理】函数思想，是指用函数的概念和性质去分析问题、转化问题和解决问题，函数思想的实质是用联系和变化的观点研究问题，将问题中的量转化为函数关系去解决．方程思想是从问题的数量关系入手，运用数学语言将问题中的条件转化为方程或方程组，然后通过解方程(组)来使问题获解．方程与函数联系密切，我们可以用方程思想解决函数问题，也可以用函数思想讨论方程问题．在确定函数解析式中的待定系数、函数图象与坐标轴的交点、函数图象的交点等问题时，将问题转化为解方程或方程组，而在讨论方程、方程组的解的个数、解的分布情况等问题时，借助函数图象能获得直观简洁的解答．【例题探究】【例1】若A(－1，2)，B(2，－1)，C(m，m)三点在同一条直线上，则m的值等于________．【解题过程】设经过A(－1，2)，B(2，－1)两点的直线的表达式为y＝kx＋b(k≠0)，k ＋b ＝2，k ＋b ＝－1.＝－1，＝1.∴y ＝－x ＋1.把C (m ，m )代入表达式，得m ＝－m ＋1.解得m ＝12.故填12.【方法归纳】①经过两点用待定系数法即可得出直线的表达式；②点在直线上，其坐标满足直线的表达式．【例2】如图，将边长为6cm 的正方形纸片ABCD 折叠，使点D 落在AB 边的中点E 处，点C 落在点Q 处，折痕为FH ，则线段AF 的长为()A ．32B ．3C ．94D ．154【解题过程】∵将边长为6cm 的正方形纸片ABCD 折叠，使点D 落在AB 边的中点E 处，∴EF ＝DF ，AB ＝AD ＝6cm ，∠A ＝90°.∵点E 是AB 的中点，∴AE ＝BE ＝3cm.在Rt △AEF 中，EF 2＝AF 2＋AE 2，∴(6－AF )2＝AF 2＋9．解得AF ＝94.故选C.【方法归纳】本题是典型的利用方程思想解决几何计算的问题．几何的计算一般分为两类，一类是利用题中已知线段或角度直接进行计算，另一类就是直接计算有困难的情况下，引入方程，通过设未知数，然后根据未知线段之间的关系列出方程，把几何问题代数化．【例3】设直线y ＝kx ＋6和直线y ＝(k ＋1)x ＋6(k 是正整数)及x 轴围成的三角形的面积为S k (k ＝1，2，3，…，8)，则S 1＋S 2＋S 3＋…＋S 8的值是()A ．49B ．634C ．16D ．14【解题过程】联立两直线的表达式成方程组，＝kx ＋6，＝（k ＋1）x ＋6.＝0，＝6.∴两直线的交点是(0，6)．∵直线y ＝kx ＋6与x 轴的交点为(－6k ，0)，直线y ＝(k ＋1)x ＋6与x 轴的交点为(－6k ＋1，0)，∴S k ＝12×6×|－6k －(－6k ＋1)|＝18(1k －1k ＋1)．∴S 1＋S 2＋S 3＋…＋S 8＝18×(1－12＋12－13＋13－14＋…＋18－19)＝18×(1－19)＝16.故选C.【方法归纳】两个函数图象的交点坐标即为两个函数表达式联立得到的二元一次方程组的解．【例4】甲、乙两家体育器材商店出售同样的乒乓球拍和乒乓球，球拍一副定价60元，乒乓球每盒定价10元．世界乒乓球锦标赛期间，两家商店都进行促销活动：甲商店规定每买一副乒乓球拍赠两盒乒乓球；乙商店规定所有商品打九折．某校乒乓球队需要买2副乒乓球拍，乒乓球若干盒(不少于4盒)．设该校要买乒乓球x 盒，所需商品在甲商店购买需用y 1元，在乙商店购买需用y 2元．(1)请分别写出y 1，y 2与x 之间的函数关系式(不必注明自变量x 的取值范围)；(2)对x 的取值情况进行分析，试说明在哪一家商店买所需商品比较便宜；(3)若该校要买2副乒乓球拍和20盒乒乓球，在不考虑其他因素的情况下，请设计一个最省钱的购买方案．【解题过程】(1)由题意知，在甲商店购买所需商品可获赠4盒乒乓球，∴还需再购买(x －4)盒乒乓球．∴y 1＝10(x －4)＋60×2＝10x ＋80，即y 1＝10x ＋80．∵乙商店规定所有商品打九折，∴y 2＝0.9(10x ＋60×2)＝9x ＋108，即y 2＝9x ＋108.(2)假设y 1>y 2，即10x ＋80>9x ＋108，解得x >28.∴当x >28时，在乙商店购买所需商品比较便宜．当x＝28时，y1＝10x＋80＝10×28＋80＝360(元)，y2＝9x＋108＝9×28＋108＝360(元)，∴y1＝y2，∴当x＝28时，在甲商店购买所需商品和在乙商店购买所需商品一样便宜．当4≤x<28时，在甲商店购买所需商品比较便宜．(3)若所需商品全部在一个商店购买，由(2)知，购买2副球拍和20盒乒乓球时，在甲商店购买比在乙商店购买便宜，需10×20＋80＝280(元)．若所需商品在两个商店购买，可以到甲商店购买2副乒乓球拍，需要2×60＝120(元)，同时获赠4盒乒乓球，到乙商店购买16盒乒乓球，需要16×10×90%＝144(元)，共需120＋144＝264(元)．∵264<280，∴最佳的购买方案是到甲商店购买2副乒乓球拍，获赠4盒乒乓球，再到乙商店购买16盒乒乓球．【方法归纳】这是一道决策问题的选择，解题的关键是建立两种函数的表达式，用方程或不等式进行比较，综合分析后选择最佳方案．【例5】如图1，在平面直角坐标系xOy中，直线l1：y＝x＋1与x轴交于点A，直线l2：y＝3x－3与x轴交于点B，与l1相交于点C.图1(1)求点A，B，C的坐标；(2)如图2，动直线x＝t分别与直线l1，l2交于P，Q两点．①若PQ＝2，求t的值；＝2S△ABC？若存在，求出此时点Q的坐标；若不存在，请②是否存在一点Q，使得S△AQC说明理由．图2【解题过程】(1)对于直线l 1：y ＝x ＋1，令y ＝0，0＝x ＋1，x ＝－1，∴点A (－1，0)，对于直线l 2：y ＝3x －3，令y ＝0，0＝3x －3，x ＝1，∴点B (1，0)，y ＝3x －3，y ＝x ＋1，x ＝2，y ＝3.∴点C (2，3)．(2)①由题意可得，点P (t ，t ＋1)，点Q (t ，3t －3)，则PQ ＝|(t ＋1)－(3t －3)|＝|4－2t |＝2，解得t ＝1或3.②∵S △ABC ＝12AB ·y C ＝12×2×3＝3，∴S △AQC ＝2S △ABC ＝6，∵S △AQC ＝12PQ ·(x C －x A )，∴12×|4－2t |×3＝6，∴t ＝0或t ＝4，∴存在，点Q 的坐标为(0，－3)或(4，9)．【方法归纳】直角坐标系中三角形的面积可以用水平宽与铅垂高乘积的一半来表示．解题时还要注意分类讨论，避免遗漏．【例6】工厂某车间需加工一批零件，甲组工人加工中因故停产检修机器一次，然后以原来的工作效率继续加工，由于时间紧任务重，乙组工人也加入共同加工零件．设甲组加工时间t (时)，甲组加工零件的数量为y 甲(个)，乙组加工零件的数量为y 乙(个)，其函数图象如图所示．(1)求y 乙与t 之间的函数关系式，并写出t 的取值范围；(2)求a 的值，并说明a 的实际意义；(3)甲组加工多长时间时，甲、乙两组加工零件的总数为480个？【解题过程】(1)设y 乙与t 之间的函数关系式是y 乙＝kt ＋b ，由题意，k ＋b ＝0，k ＋b ＝360.＝120，＝－600.∴y 乙与t 之间的函数关系式是y 乙＝120t －600(5≤t ≤8)．(2)由图象可得，甲加工零件的速度为120÷3＝40(个/时)，∴a ＝120＋40×(8－4)＝280，实际意义是：当甲加工8小时时，一共加工了280个零件．(3)设甲组加工m 小时，甲、乙两组加工零件的总数为480个，由题意，得120＋40(m －4)＋(120m －600)＝480，解得m ＝7，∴甲组加工7小时时，甲、乙两组加工零件的总数为480个．【方法归纳】本题考查一次函数的应用．解答本题时，要明确题意，充分利用函数图象提供的信息，灵活运用函数和方程的知识解决．【例7】某市是著名的苹果生产基地，果品公司从A 村收购苹果400吨，从B 村收购苹果600吨．现在要将这些苹果运到C ，D 两个冷藏仓库储存，已知C 库可储存300吨，D 库可储存700吨苹果；从A 村运往C ，D 两处的费用分别为每吨20元和25元，从B 村运往C ，D 两处的费用分别为每吨15元和18元．请你设计一个方案使苹果的运输费用最小，最小费用是多少．【解题过程】设苹果的运输费用为y 元，从A 村运x 吨苹果到C 库，则从A 村运(400－x)吨苹果到D库；从B村运(300－x)吨苹果到C库，运(x＋300)吨苹果到D库．由题意，得y＝20x＋25(400－x)＋15(300－x)＋18(x＋300)＝－2x＋19900(0≤x≤300)．∵k＝－2<0，∴y随x的增大而减小．＝－2×300＋19900＝19300.∴当x＝300时，y最小答：从A村运300吨苹果到C库，运100吨苹果到D库，从B村运600吨苹果到D库，这样苹果的运输费用最小，最小费用是19300元．【方法归纳】在本题的求解过程中，所建立的是一次函数模型．因此，这里的函数何时有最值及最值是多少，完全由自变量的取值范围所确定．一般地，根据一次函数的图象可知，对一次函数y＝ax＋b(a≠0，m≤x≤n)，若a>0，则当x＝m时，函数有最小值am＋b；当x＝n时，函数有最大值an＋b；若a<0，则当x＝m时，函数有最大值am＋b；当x＝n时，函数有最小值an＋b.。

著名机构初中数学培优讲义.二次函数.第10讲(C).教师版

内容基本要求略高要求较高要求二次函数1.能根据实际情境了解二次函数的意义； 2.会利用描点法画出二次函数的图像；1.能通过对实际问题中的情境分析确定二次函数的表达式；2.能从函数图像上认识函数的性质；3.会确定图像的顶点、对称轴和开口方向；4.会利用二次函数的图像求出二次方程的近似解；1.能用二次函数解决简单的实际问题；2.能解决二次函数与其他知识结合的有关问题；1．能从函数图像上认识函数的性质； 2．会确定图像的顶点、对称轴和开口方向； 3． .能用二次函数解决简单的实际问题．愤怒的小鸟和人类对抛物线的迷恋人类似乎沉迷于对抛物线轨迹的预测，否则，你如何解释高尔夫运动？或者我们为何如此尊敬橄榄球运动中的四分卫和板球运动中的出色投球手？我们的身体在对准目标投掷物品上很在行。

在投射物离开手指之前，首先在头脑中预测轨道，转动肩膀，活动肩胛骨，扭动屁股，弯曲胳膊，伸展手指。

中考要求重难点课前预习二次函数这是一系列运动的精确配合。

发射！当投射物全速冲向目标的时候，会有短暂的焦虑和期待。

人类的祖先在早期的狩猎活动中，就已经开始投射标枪，远程制服猎物。

这种活动展示了速度和力量，以及对运动轨迹的预测，并且有丰盛的食物作为报酬。

对抛物线的利用体现了人类作为高级生物的智慧，因为相比直线投射来说，抛物线投射通过对角度的调节，能够为攻击提供更多的灵活性和准确性。

其它动物的捕猎行为更多的是利用直线发射：除了射水鱼 ——它的捕猎行为是针对特定方位喷射水柱，将昆虫打下树叶——没有其它动物使用抛物线。

变色龙喷吐舌头（捕食）时是直线，狗能够捕捉球但无法投射。

没有其它动物有我们这样善于投射的臂膀……鸟类，无论疯狂与否，唯一接近投射的行为是埃及秃鹰向大致方位投射石头，试图打碎鸵鸟蛋的时候。

现代人早已无需通过狩猎获取食物，但是那种原始的快感却一直保留着。

也许这就是愤怒的小鸟成功的原因，当弹弓射出小鸟的那一刻，我们原始的欲望得到了满足，而焦虑得到了释放。

著名机构数学讲义暑假15-八年级培优版-函数的应用-学生版

教师姓名学生姓名年级初二上课时间学科数学课题名称函数的应用函数的应用知识模块Ⅰ：反比例函数构造面积1. 反比例函数图像上任意一点到x 轴y 轴的垂线，所得矩形的面积为k 的绝对值。

2. 过反比例函数图像上任一点作坐标轴的垂线，则垂足，已知点及原点这三点构成的三角形的面积k s 21=【例1】如图，A ，C 是函数1y x=的图象上任意两点，过点A 作y 轴的垂线，垂足为B ，过点C 作y 轴的垂线，垂足为D ，记Rt △AOB 的面积为S 1，Rt △COD 的面积为S 2，则S 1和S 2的大小关系是（） A ．S 1＞S 2 B ．S 1＜S 2 C ．S 1=S 2 D ．由A ，C 两点的位置确定【例2】一个反比例函数在第二象限的图象如图所示，点A 是图象上任意一点，AM ⊥x 轴，垂足为 M ，O 是原点，如果△AOM 的面积是3，求这个反比例函数的解析式是（） A ．3y x =- B ．3y x = C ．6y x = D ．6y x=-【例3】如图，点P 是x 轴正半轴上的一动点，过点P 作x 轴的垂线，交双曲线1y x=于点Q ，连接OQ ．当点P 沿x 轴的正方向运动时，Rt △QOP 的面积（）A ．逐渐增大B ．逐渐减小C ．保持不变D ．无法确定【例4】如图，在直角坐标系中，O 为坐标原点．已知反比例函数ky x=（k ＞0）的图象经过点A （2，m），过点A作AB⊥x轴于点B，且△AOB的面积为．（1）求k和m的值；（2）求当x≥1时函数值y的取值范围．【例5】如图，点A（a，b）是双曲线8yx=（x＞0）上的一点，点P是x轴负半轴上的一动点，AC⊥y轴于点C，过点A作AD⊥x轴于点D，连接AP交y轴于点B．（1）△P AC的面积是___________（2）当a=2，点P的坐标为（﹣2，0）时，求△ACB的面积．【例6】如图，A，B分别在反比例函数1yx=，kyx=（k＞1）图象上且在第一象限内，且AB∥x轴，AD⊥x轴，BC⊥x轴，垂足分别为点D，点C．（1）若AD=2AB=2，求k的值；（2）当k=4时，求矩形ABCD的面积．知识模块Ⅱ：正反比例函数交点问题和面积1.K值几何意义2.图形的对称性3.面积公式、面积等积转换【例7】如图，直线y=mx与双曲线kyx=交于A，B两点，过点A作AM⊥x轴，垂足为点M，连接BM，若S△ABM=4，则k的值为（）A．﹣2B．﹣4C．4D．﹣8【例8】如图，直线y=mx与函数2yx=的图象交于A、B两点，BC∥x轴，AC∥y轴，△ABC的面积记为S，则（）A．S=2B．2＜S＜4C．S=4D．S随m的变化而变化【例9】如图，已知直线y=x与双曲线kyx=（k＞0）交于A、B两点，且点A的横坐标为4（1）求k的值（2）若双曲线kyx=（k＞0）上一点C的纵坐标为8，求△AOC的面积AB单家 O 路程（千米）时间（分钟）128 312 4第24题图·（3）过原点O 的另一条直线l 交双曲线ky x（k ＞0）于P 、Q 两点（P 点在第一象限），若△AOP 的面积为6，求直线l 的解析式．【例10】某人从甲地行走到乙地的路程S （千米）与时间t （时）的函数关系如图，那么此人行走5.千米，所用的时间______________（时）【例11】王师傅从家门口骑车去单位上班，先走平路到达点A ，再走上坡路到达点B ，最后走下坡路到达工作单位，所用的时间与路程的关系如图所示．下班后，如果他沿原路返回，且走平路、上坡路、下坡路的速度分别保持和去上班时一致．请根据图像所提供的信息，解答下列问题：（1）王师傅从家门口到单位需要_____________分钟；（2）王师傅从单位到家门口需要_____________分钟．【例12】等腰三角形周长20，腰长为x ，底边为y ，写出y 关于x 的函数解析式_______________，定义域是______________【例13】下列变化过程中的两个变量成反比例的是（） A 、圆的周长C 与该圆半径r ；B 、扇形的面积一定时，所对圆心角的度数n 与扇形所在半径r ；C 、平行四边形的面积一定时，平行四边形的一条边长a 和这条边上的高h ；D 、平行四边形的一条边长一定时，平行四边形的面积S 和这条边上的高h .【例14】为预防某种流感，某校对教室进行“药熏消毒”．已知药物燃烧阶段，室内每立方米空气中的含药量y （毫克）与燃烧时间x （分钟）成正比例；燃烧阶段后，y 与x 成反比例（这两个变量之间的关系如图所示）．现测得药物10分钟燃完，此时教室内每立方米空气含药量为8毫克．据以上信息解答下列问题：（1）求药物燃烧时y 与x 的函数解析式．（2）求药物燃烧阶段后y 与x 的函数解析式．（3）当教室内每立方米空气含药量不低于4毫克时消毒有效，问消毒有效的时间是几分钟？知识模块Ⅲ：正反例函数的应用1、行程问题2、面积周长3、正反比例结合【例15】如图，在矩形ABCD 中，AB =1，BC =2，动点E 从点C 出发，以每秒1个单位的速度沿路线C →D →A 作匀速运动，点E 到达A 点运动停止，那么△BEC 的面积y 与点E 运动的时间x 秒之间的函数图象大y (毫克)x (分)810致是（）A ．B ．C ．D ．【例16】一根蜡烛长20厘米，共燃烧4小时，下列图像中表示其燃烧时剩下的高度h （厘米）与燃烧时间t （小时）之间的函数关系的是（）【例17】下列说法正确的是（）A ．周长为10的长方形的长与宽成正比例B ．面积为10的等腰三角形的腰长与底边长成正比例C ．面积为10的长方形的长与宽成反比例D ．等边三角形的面积与它的边长成正比例【例18】为了预防“流感”，某学校对教室采用“药熏”消毒法进行消毒．已知药物燃烧时，室内每立方米空气中的含药量y （毫克）与时间x （分钟）成正比例，药物燃烧完后，y 与 x 成反比例（如图所示）．现测得药物4分钟燃毕，此时室内空气中每立方米含药量为 8毫克．请根据题中所提供的信息，解答下列问题：（1）求药物燃烧时，y 关于x 的函数解析式及定义域；（2）求药物燃烧完后，y 关于x 的函数解析式及定义域；（3）研究表明，当空气中每立方米的含药量不低于2毫克时，才能有效地杀灭空气中的病菌，那么此次消毒有效时间有多长？-4 O th(A )204 O th (B )204 O th (D )204O th(C )204知识模块Ⅳ：函数表示法【例19】根据生物学研究结果，青春期男女生身高增长速度呈现如图的规律，由图可以判断，下列说法错误的是（）A 、男生在13岁时身高增长速度最快；B 、女生在10岁以后身高增长速度放慢；C 、11岁时男女生身高增长速度基本相同；D 、女生身高增长的速度总比男生慢．【习题1】如图，反比例函数ky x=（k ＜0），点M 是它在第二象限内的图象上一点，MP 垂直x 轴于点P ，如果△OMP 的面积为1，该函数的解析式为_____________【习题2】如图：在反比例函数()0ky k x=≠图象上取一点A 分别作AC ⊥x 轴，AB ⊥y 轴，且S ABOC =6，（第4题那么这个函数解析式为_____________【习题3】如图，原点O 是矩形ABCD 的对称中心，顶点A 、C 在反比例函数图象上，AB 平行x 轴．若矩形ABCD 的面积为8，那么反比例函数的解析式是_____________【习题4】矩形的长为x ，宽为y ，面积为9，则y 与x 之间的函数关系及定义域是_____________ 【习题5】已知一圆的直径为x ，周长为y ，则y 关于x 的函数关系式为_____________ 【习题6】如图，已知直线y =kx （k ＞0）与双曲线8y x=交于A 、B 两点，且点A 的纵坐标为4，第一象限的双曲线上有一点P （1，a ），过点P 作PQ ∥y 轴交直线AB 于点Q ．（1）直接写出k 的值及点B 的坐标；（2）求线段PQ 的长；（3）如果在直线y =kx 上有一点M ，且满足△BPM 的面积等于12，求点M 的坐标．【答案】（1）()22,4y x B =--（2）6 （3） ()()2,46,12--【习题7】小华和小晶上山游玩，小华步行，小晶乘坐缆车，相约在山顶缆车的终点会合．已知小华步行的路程是缆车所经线路长的2倍，小晶在小华出发后50分钟才坐上缆车，缆车的平均速度为每分钟180米．图中的折线反映了小华行走的路程y （米）与时间x （分钟）之间的函数关系．（1）小华行走的总路程是_____________米，他途中休息了_____________分钟；（2）当0≤x ≤30时，y 与x 的函数关系式是_____________ （3）小华休息之后行走的速度是每分钟_____________米；（4）当小晶到达缆车终点时，小华离缆车终点的路程是_____________米．。

著名机构初中数学培优讲义.函数及图像.第06讲(B级).学生版

内容基本要求略高要求较高要求一次函数理解正比例函数，能结合具体情境了解一次函数的意义;会画一次函数的图像，理解一次函数的性质会根据已知条件确定一次函数解析式;会根据一次函数解析式求其图像与坐标轴的交点坐标；能根据一次函数图像求二元一次方程组的近似解能用一次函数解决实际问题平移规律：一次函数的图象与几何变换，熟知“上加下减，左加右减”的原则模块一一次函数的平移【例1】在平面直角坐标系中，把直线21y x =-向右平移一个单位长度后，其直线解析式为（）A ．2y x =B ．21y x =-C ．22y x =+D ．23y x =-【巩固】直线22y x =+向右平移3个单位，再向下平移2个单位，所得到的直线的解析式是．【巩固】一次函数经过沿y 轴向下平移3个单位，在向右平移2个单位，所得的直线的解析式为()23y x =-，则原来的一次函数解析式为．【例2】（2005•聊城）直线l 1是正比例函数的图象，将1l 沿y 轴向上平移2个单位得到的直线2l 经过点()11P ，，那么（）A ．1l 过第一．三象限B ．2l 过第二．三．四象限C ．对于1l ，y 随x 的增大而减小D ．对于2l ，y 随x 的增大而增大例题精讲中考要求一次函数与平移、解析式、及不等式模块二用待定系数法求一次函数解析式先设出函数解析式，再根据条件确定解析式中未知的系数，从而具体写出这个式子的方法，叫做待字系数法．用待定系数法求函数解析式的一般步骤： ①根据已知条件写出含有待定系数的解析式；②将x y ，的几对值，或图象上的几个点的坐标代入上述的解析式中，得到以待定系数为未知数的方程或方程组；③解方程（组），得到待定系数的值；④将求出的待定系数代回所求的函数解析式中，得到所求的函数解析式．☞待定系数法【例3】已知y n +与x m +成正比例，其中m 、n 是常数，当1x =时，1y =-，当1x =-时，7y =-.求y与x 的函数关系．【巩固】已知一次函数y kx b =+，当31x -≤≤时，对应的y 值为19y ≤≤，求kb 的值.【例4】（1）（★★★）(09山东泰安)已知y 是x 一次函数，表给出了部分对应值，m 的值是．（2）（★★★）（08永州）如图，一次函数的图象经过M 点，与x 轴交于A 点，与y 轴交于B 点，根据图中信息求：求这个函数的解析式．【例5】（1）如果直线y ax b =+经过第一、二、三象限，那么ab 0（填“>”、“<”、“=”）．（2）已知一次函数()22312y a x a =-+-．求：①a 为何值时，一次函数的图象经过原点．②a 为何值时，一次函数的图象与y 轴交于点()0,9．☞对称【例6】若直线y kx b =+与直线22y x =+关于x 轴对称，则k b ，的值分别是（）A 、﹣2，﹣2B 、﹣2，2C 、2，﹣2D 、2，2【巩固】若正比例函数y =kx 与y =2x 的图象关于x 轴对称，则k 的值= ．。