陕西省2019年中考数学试题研究 类型3 线段最值问题练习
精品解析:陕西省2019年中考数学试题(解析版)
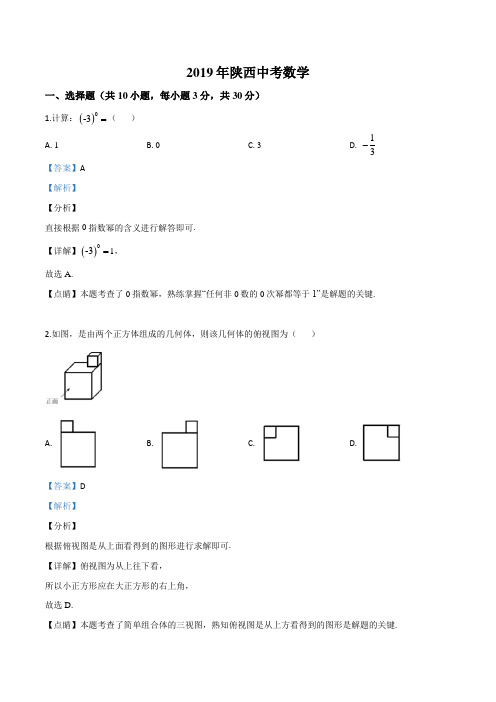
2019年陕西中考数学一、选择题(共10小题,每小题3分,共30分)1.计算:()0-3=()A. 1B. 0C. 3D.1 3 -【答案】A【解析】【分析】直接根据0指数幂的含义进行解答即可.【详解】()0-3=1,故选A.【点睛】本题考查了0指数幂,熟练掌握“任何非0数的0次幂都等于1”是解题的关键.2.如图,是由两个正方体组成的几何体,则该几何体的俯视图为()A. B. C. D.【答案】D【解析】【分析】根据俯视图是从上面看得到的图形进行求解即可.【详解】俯视图为从上往下看,所以小正方形应在大正方形的右上角,故选D.【点睛】本题考查了简单组合体的三视图,熟知俯视图是从上方看得到的图形是解题的关键.3.如图,OC 是∠AOB 的角平分线,l //OB,若∠1=52°,则∠2的度数为( )A. 52°B. 54°C. 64°D. 69°【答案】C 【解析】 【分析】先根据两直线平行,同旁内角互补求出∠AOB=128°,再根据角平分线的定义得到∠BOC=64°,继而根据平行线的性质即可求得答案. 【详解】∵l//OB , ∴∠1+∠AOB=180°, ∴∠AOB=128°, ∵OC 平分∠AOB , ∴∠BOC=64°, 又∵l//OB , ∴∠2=∠BOC=64°, 故选C.【点睛】本题考查了平行线的性质,角平分线的定义,熟练掌握平行线的性质是解本题的关键.4.若正比例函数2y x =-的图象经过点O (a -1,4),则a 的值为( ) A. -1 B. 0C. 1D. 2【答案】A 【解析】 【分析】把点(a-1,4)直接代入正比例函数y=-2x 中求解即可.【详解】∵函数2y x =-过O(a-1,4), ∴2(1)4a --=, ∴1a =-, 故选A.【点睛】本题考查了正比例函数图象上点的坐标特征,熟知正比例函数图象上的点的坐标一定满足正比例函数的解析式是解题的关键.5.下列计算正确的是( ) A. 222236a a a ⋅= B. ()224236a b a b -=C. ()222a b a b -=- D. 2222a a a -+=【答案】D 【解析】 【分析】根据单项式乘法法则、积的乘方法则、完全平方公式,合并同类项法则逐一进行计算即可. 【详解】A. 422236a a a ⋅=,故A 选项错误; B. ()224239a b a b -=,故B 选项错误;C. ()2222a b a ab b -=-+,故C 选项错误; D. 2222a a a -+=,正确, 故选D.【点睛】本题考查了单项式乘法、积的乘方、完全平方公式、合并同类项等运算,熟练掌握各运算的运算法则是解题的关键.6.如图,在△ABC 中,∠B=30°,∠C=45°,AD 平分∠BAC 交BC 于点D ,DE ⊥AB ,垂足为E 。
人教版九年级数学下册2019年陕西省中考数学试卷及答案解析

2019年陕西省中考数学试卷一、选择题(共10小题,每小题3分,共30分)1.(3分)(2019•陕西)计算:0(3)(-= )A .1B .0C .3D .13- 2.(3分)(2019•陕西)如图,是由两个正方体组成的几何体,则该几何体的俯视图为 ( )A .B .C .D .3.(3分)(2019•陕西)如图,OC 是AOB ∠的角平分线,//l OB ,若152∠=︒,则2∠的度数为( )A .52︒B .54︒C .64︒D .69︒4.(3分)(2019•陕西)若正比例函数2y x =-的图象经过点(1,4)O a -,则a 的值为( )A .1-B .0C .1D .25.(3分)(2019•陕西)下列计算正确的是( )A .222236a a a =gB .2242(3)6a b a b -=C .222()a b a b -=-D .2222a a a -+=6.(3分)(2019•陕西)如图,在ABC ∆中,30B ∠=︒,45C ∠=︒,AD 平分BAC ∠交BC 于点D ,DE AB ⊥,垂足为E .若1DE =,则BC 的长为( )A .22+B .23+C .23+D .37.(3分)(2019•陕西)在平面直角坐标系中,将函数3y x =的图象向上平移6个单位长度,则平移后的图象与x 轴的交点坐标为( )A .(2,0)B .(2,0)-C .(6,0)D .(6,0)-8.(3分)(2019•陕西)如图,在矩形ABCD 中,3AB =,6BC =,若点E ,F 分别在AB ,CD 上,且2BE AE =,2DF FC =,G ,H 分别是AC 的三等分点,则四边形EHFG 的面积为( )A .1B .32C .2D .49.(3分)(2019•陕西)如图,AB 是O e 的直径,EF ,EB 是O e 的弦,且EF EB =,EF 与AB 交于点C ,连接OF ,若40AOF ∠=︒,则F ∠的度数是( )A .20︒B .35︒C .40︒D .55︒10.(3分)(2019•陕西)在同一平面直角坐标系中,若抛物线2(21)24y x m x m =+-+-与2(3)y x m n x n =-++关于y 轴对称,则符合条件的m ,n 的值为( )A .57m =,187n =-B .5m =,6n =-C .1m =-,6n =D .1m =,2n =-二、填空题(共4小题,每小题3分,共12分)11.(3分)(2019•陕西)已知实数12-,0.16,3π,25,34,其中为无理数的是 .12.(3分)(2019•陕西)若正六边形的边长为3,则其较长的一条对角线长为 . 13.(3分)(2019•陕西)如图,D 是矩形AOBC 的对称中心,(0,4)A ,(6,0)B ,若一个反比例函数的图象经过点D ,交AC 于点M ,则点M 的坐标为 .14.(3分)(2019•陕西)如图,在正方形ABCD 中,8AB =,AC 与BD 交于点O ,N 是AO 的中点,点M 在BC 边上,且6BM =.P 为对角线BD 上一点,则PM PN -的最大值为 .三、解答题(共78分)15.(5分)(2019•陕西)计算:231227|13|()2--⨯-+-- 16.(5分)(2019•陕西)化简:22282()242a a a a a a a-++÷+-- 17.(5分)(2019•陕西)如图,在ABC ∆中,AB AC =,AD 是BC 边上的高.请用尺规作图法,求作ABC ∆的外接圆.(保留作图痕迹,不写作法)18.(5分)(2019•陕西)如图,点A ,E ,F 在直线l 上,AE BF =,//AC BD ,且AC BD =,求证:CF DE =.19.(7分)(2019•陕西)本学期初,某校为迎接中华人民共和国建国七十周年,开展了以“不忘初心,缅怀革命先烈,奋斗新时代”为主题的读书活动.校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”(下面简称:“读书量”)进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,如图所示:根据以上信息,解答下列问题:(1)补全上面两幅统计图,填出本次所抽取学生四月份“读书量”的众数为.(2)求本次所抽取学生四月份“读书量”的平均数;(3)已知该校七年级有1200名学生,请你估计该校七年级学生中,四月份“读书量”为5本的学生人数.20.(7分)(2019•陕西)小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45︒;再在BD的延长线上确定一点G,使5DG=米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得2FG=米,小明眼睛与地面的距离 1.6CD=米.已知点F、G、D、B在同一水平直线上,EF=米,测倾器的高度0.5且EF、CD、AB均垂直于FB,求这棵古树的高度AB.(小平面镜的大小忽略不计)21.(7分)(2019•陕西)根据记录,从地面向上11km 以内,每升高1km ,气温降低6C ︒;又知在距离地面11km 以上高空,气温几乎不变.若地面气温为(C)m ︒,设距地面的高度为()x km 处的气温为(C)y ︒(1)写出距地面的高度在11km 以内的y 与x 之间的函数表达式;(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为26C ︒-时,飞机距离地面的高度为7km ,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面12km 的高空,飞机外的气温是多少度呢?请求出假如当时飞机距离地面12km 时,飞机外的气温.22.(7分)(2019•陕西)现有A 、B 两个不透明袋子,分别装有3个除颜色外完全相同的小球.其中,A 袋装有2个白球,1个红球;B 袋装有2个红球,1个白球.(1)将A 袋摇匀,然后从A 袋中随机取出一个小球,求摸出小球是白色的概率;(2)小华和小林商定了一个游戏规则:从摇匀后的A ,B 两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平.23.(8分)(2019•陕西)如图,AC 是O e 的一条弦,AP 是O e 的切线.作BM AB =并与AP 交于点M ,延长MB 交AC 于点E ,交O e 于点D ,连接AD .(1)求证:AB BE =;(2)若O e 的半径5R =,6AB =,求AD 的长.24.(10分)(2019•陕西)在平面直角坐标系中,已知抛物线2:()L y ax c a x c =+-+经过点(3,0)A -和点(0,6)B -,L 关于原点O 堆成的抛物线为L '.(1)求抛物线L 的表达式;(2)点P 在抛物线L '上,且位于第一象限,过点P 作PD y ⊥轴,垂足为D .若POD ∆与AOB ∆相似,求复合条件的点P 的坐标.25.(12分)(2019•陕西)问题提出:(1)如图1,已知ABC ∆,试确定一点D ,使得以A ,B ,C ,D 为顶点的四边形为平行四边形,请画出这个平行四边形;问题探究:(2)如图2,在矩形ABCD 中,4AB =,10BC =,若要在该矩形中作出一个面积最大的BPC ∆,且使90BPC ∠=︒,求满足条件的点P 到点A 的距离;问题解决:(3)如图3,有一座草根塔A ,按规定,要以塔A 为对称中心,建一个面积尽可能大的形状为平行四边形的草根景区BCDE .根据实际情况,要求顶点B 是定点,点B 到塔A 的距离为50米,120CBE ∠=︒,那么,是否可以建一个满足要求的面积最大的平行四边形景区BCDE ?若可以,求出满足要求的平行四边形BCDE 的最大面积;若不可以,请说明理由.(塔A 的占地面积忽略不计)2019年陕西省中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,共30分)1.(3分)计算:0(3)(-= )A .1B .0C .3D .13-【考点】零指数幂【分析】直接利用零指数幂的性质计算得出答案.【解答】解:0(3)1-=. 故选:A .2.(3分)如图,是由两个正方体组成的几何体,则该几何体的俯视图为( )A .B .C .D .【考点】简单组合体的三视图【分析】找到从上面看所得到的图形即可.【解答】解:从上往下看,所以小正方形应在大正方形的右上角. 故选:D .3.(3分)如图,OC 是AOB ∠的角平分线,//l OB ,若152∠=︒,则2∠的度数为()A .52︒B .54︒C .64︒D .69︒【考点】平行线的性质【分析】依据平行线的性质以及角平分线的定义,即可得到64BOC ∠=︒,再根据平行线的性质,即可得出2∠的度数.【解答】解://l OB Q ,1180AOB ∴∠+∠=︒,128AOB ∴∠=︒,OC Q 平分AOB ∠,64BOC ∴∠=︒,又//l OB ,且2∠与BOC ∠为同位角,264∴∠=︒,故选:C .4.(3分)若正比例函数2y x =-的图象经过点(1,4)O a -,则a 的值为( )A .1-B .0C .1D .2【考点】一次函数图象上点的坐标特征【分析】由正比例函数图象过点O ,可知点O 的坐标满足正比例函数的关系式,由此可得出关于a 的一元一次方程,解方程即可得出结论.【解答】解:Q 正比例函数2y x =-的图象经过点(1,4)O a -,42(1)a ∴=--,解得:1a =-.故选:A .5.(3分)下列计算正确的是( )A .222236a a a =gB .2242(3)6a b a b -=C .222()a b a b -=-D .2222a a a -+=【考点】整式的混合运算【分析】根据各个选项中的式子可以计算出正确的结果,本题得以解决.【解答】解:224236a a a =Q g ,故选项A 错误, 2242(3)9a b a b -=Q ,故选项B 错误,222()2a b a ab b -=-+Q ,故选项C 错误,2222a a a -+=Q ,故选项D 正确,故选:D .6.(3分)如图,在ABC ∆中,30B ∠=︒,45C ∠=︒,AD 平分BAC ∠交BC 于点D ,DE AB ⊥,垂足为E .若1DE =,则BC 的长为( )A .22+B .23+C .23+D .3【考点】角平分线的性质【分析】过点D 作DF AC ⊥于F 如图所示,根据角平分线的性质得到1DE DF ==,解直角三角形即可得到结论.【解答】解:过点D 作DF AC ⊥于F 如图所示,AD Q 为BAC ∠的平分线,且DE AB ⊥于E ,DF AC ⊥于F , 1DE DF ∴==,在Rt BED ∆中,30B ∠=︒,22BD DE ∴==,在Rt CDF ∆中,45C ∠=︒,CDF ∴∆为等腰直角三角形,22CD DF ∴==,22BC BD CD ∴=+=+,故选:A .7.(3分)在平面直角坐标系中,将函数3y x =的图象向上平移6个单位长度,则平移后的图象与x 轴的交点坐标为( )A .(2,0)B .(2,0)-C .(6,0)D .(6,0)-【考点】一次函数图象与几何变换【分析】根据“上加下减”的原则求得平移后的解析式,令0y =,解得即可.【解答】解:由“上加下减”的原则可知,将函数3y x =的图象向上平移6个单位长度所得函数的解析式为36y x =+,Q 此时与x 轴相交,则0y =,360x ∴+=,即2x =-,∴点坐标为(2,0)-,故选:B .8.(3分)如图,在矩形ABCD 中,3AB =,6BC =,若点E ,F 分别在AB ,CD 上,且2BE AE =,2DF FC =,G ,H 分别是AC 的三等分点,则四边形EHFG 的面积为( )A .1B .32C .2D .4【考点】:矩形的性质;平行四边形的判定与性质【分析】由题意可证//EG BC ,2EG =,//HF AD ,2HF =,可得四边形EHFG 为平行四边形,即可求解.【解答】解:2BE AE =Q ,2DF FC =,∴12AE BE =,12CF DF = G Q 、H 分别是AC 的三等分点 ∴12AG GC =,12CH AH = ∴AE AG BE GC= //EG BC ∴ ∴13EG AE BC AB ==,且6BC = 2EG ∴=,同理可得//HF AD ,2HF =∴四边形EHFG 为平行四边形,且EG 和HF 间距离为1 212EHFG S ∴=⨯=四边形,故选:C .9.(3分)如图,AB 是O e 的直径,EF ,EB 是O e 的弦,且EF EB =,EF 与AB 交于点C ,连接OF ,若40AOF ∠=︒,则F ∠的度数是( )A .20︒B .35︒C .40︒D .55︒【考点】圆周角定理;圆心角、弧、弦的关系【分析】连接FB ,得到140FOB ∠=︒,求出EFB ∠,OFB ∠即可. 【解答】解:连接FB .40AOF ∠=︒Q ,18040140FOB ∴∠=︒-︒=︒, 1702FEB FOB ∴∠=∠=︒EF EB =Q55EFB EBF ∴∠=∠=︒, FO BO =Q ,20OFB OBF ∴∠=∠=︒, EFO EBO ∴∠=∠,35EFO EFB OFB ∠=∠-∠=︒,故选:B .10.(3分)在同一平面直角坐标系中,若抛物线2(21)24y x m x m =+-+-与2(3)y x m n x n =-++关于y 轴对称,则符合条件的m ,n 的值为( ) A .57m =,187n =- B .5m =,6n =-C .1m =-,6n =D .1m =,2n =-【考点】二次函数图象与几何变换【分析】根据关于y 轴对称,a ,c 不变,b 变为相反数列出方程组,解方程组即可求得. 【解答】解:Q 抛物线2(21)24y x m x m =+-+-与2(3)y x m n x n =-++关于y 轴对称, ∴21324m m n m n -=+⎧⎨-=⎩,解之得12m n =⎧⎨=-⎩,故选:D .二、填空题(共4小题,每小题3分,共12分)11.(3分)已知实数12-,0.16,3,π,25,34,其中为无理数的是3,π,34 .【考点】立方根;算术平方根;无理数【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.【解答】解:255=,12-、0.16是有理数;无理数有3、π、34. 故答案为:3、π、34.12.(3分)若正六边形的边长为3,则其较长的一条对角线长为 6 . 【考点】正多边形和圆【分析】根据正六边形的性质即可得到结论. 【解答】解:如图所示为正六边形最长的三条对角线,由正六边形性质可知,AOB ∆,COD ∆为两个边长相等的等边三角形, 26AD AB ∴==,故答案为6.13.(3分)如图,D 是矩形AOBC 的对称中心,(0,4)A ,(6,0)B ,若一个反比例函数的图象经过点D ,交AC 于点M ,则点M 的坐标为 3(2,4) .【考点】反比例函数图象上点的坐标特征;矩形的性质;中心对称【分析】根据矩形的性质求得(6,4)C,由D是矩形AOBC的对称中心,求得(3,2)D,设反比例函数的解析式为kyx=,代入D点的坐标,即可求得k的值,然后根据反比例函数图象上点的坐标特征即可求得M点的坐标.【解答】解:(0,4)AQ,(6,0)B,(6,4)C∴,DQ是矩形AOBC的对称中心,(3,2)D∴,设反比例函数的解析式为kyx =,326k∴=⨯=,∴反比例函数的解析式为6yx =,把4y=代入得64x=,解得32x=,故M的坐标为3(2,4).故答案为3(2,4).14.(3分)如图,在正方形ABCD中,8AB=,AC与BD交于点O,N是AO的中点,点M在BC边上,且6BM=.P为对角线BD上一点,则PM PN-的最大值为2.【考点】轴对称-最短路线问题;正方形的性质【分析】作以BD为对称轴作N的对称点N',连接PN',MN',依据PM PN PM PN MN ''-=-„,可得当P ,M ,N '三点共线时,取“=”,再求得13CM CN BM AN '==',即可得出////PM AB CD ,90CMN '∠=︒,再根据△N CM '为等腰直角三角形,即可得到2CM MN '==.【解答】解:如图所示,作以BD 为对称轴作N 的对称点N ',连接PN ',MN ', 根据轴对称性质可知,PN PN '=,PM PN PM PN MN ''∴-=-„,当P ,M ,N '三点共线时,取“=”, Q 正方形边长为8,AC ∴==O Q 为AC 中点,AO OC ∴==N Q 为OA 中点,ON ∴=,ON CN ''∴==AN '∴=6BM =Q ,862CM AB BM ∴=-=-=,∴13CM CN BM AN '==' ////PM AB CD ∴,90CMN '∠=︒, 45N CM '∠=︒Q ,∴△N CM '为等腰直角三角形,2CM MN '∴==,即PM PN -的最大值为2, 故答案为:2.三、解答题(共78分)15.(5分)计算:231227|13|()2--⨯-+--【考点】实数的运算;负整数指数幂【分析】直接利用立方根的性质以及负指数幂的性质和绝对值的性质分别化简得出答案. 【解答】解:原式2(3)314=-⨯-+-- 13=+.16.(5分)化简:22282()242a a a a a a a-++÷+-- 【考点】分式的混合运算【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.【解答】解:原式2(2)8(2)[(2)(2)2a a a a a a a -+-=+-+g2(2)(2)(2)(2)2a a a a a a +-=+-+ga =.17.(5分)如图,在ABC ∆中,AB AC =,AD 是BC 边上的高.请用尺规作图法,求作ABC ∆的外接圆.(保留作图痕迹,不写作法)【考点】等腰三角形的性质;三角形的外接圆与外心;作图-复杂作图【分析】作线段AB 的垂直平分线,交AD 于点O ,以O 为圆心,OB 为半径作O e ,O e 即为所求.【解答】解:如图所示:O e 即为所求.18.(5分)如图,点A ,E ,F 在直线l 上,AE BF =,//AC BD ,且AC BD =,求证:CF DE =.【考点】全等三角形的判定与性质【分析】根据平行线的性质得到CAF DBE ∠=∠,证明ACF BDE ∆≅∆,根据全等三角形的性质证明结论.【解答】证明:AE BF =Q ,AE EF BF EF ∴+=+,即AF BE =,//AC BD Q , CAF DBE ∴∠=∠,在ACF ∆和BDE ∆中, AC BD CAF DBE AF BE =⎧⎪∠=∠⎨⎪=⎩, ()ACF BDE SAS ∴∆≅∆ CF DE ∴=.19.(7分)本学期初,某校为迎接中华人民共和国建国七十周年,开展了以“不忘初心,缅怀革命先烈,奋斗新时代”为主题的读书活动.校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”(下面简称:“读书量”)进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,如图所示:根据以上信息,解答下列问题:(1)补全上面两幅统计图,填出本次所抽取学生四月份“读书量”的众数为3.(2)求本次所抽取学生四月份“读书量”的平均数;(3)已知该校七年级有1200名学生,请你估计该校七年级学生中,四月份“读书量”为5本的学生人数.【考点】众数;用样本估计总体;加权平均数;条形统计图;扇形统计图【分析】(1)根据统计图可知众数为3;(2)平均数3118221312455331821126⨯+⨯+⨯+⨯+⨯==++++;(3)四月份“读书量”为5本的学生人数6120012060=⨯=(人).【解答】解:(1)根据统计图可知众数为3,故答案为3;(2)平均数3118221312455331821126⨯+⨯+⨯+⨯+⨯==++++;(3)四月份“读书量”为5本的学生人数6120012060=⨯=(人),答:四月份“读书量”为5本的学生人数为120人.20.(7分)小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B ,如图所示.于是他们先在古树周围的空地上选择一点D ,并在点D 处安装了测量器DC ,测得古树的顶端A 的仰角为45︒;再在BD 的延长线上确定一点G ,使5DG =米,并在G 处的地面上水平放置了一个小平面镜,小明沿着BG 方向移动,当移动带点F 时,他刚好在小平面镜内看到这棵古树的顶端A 的像,此时,测得2FG =米,小明眼睛与地面的距离1.6EF =米,测倾器的高度0.5CD =米.已知点F 、G 、D 、B 在同一水平直线上,且EF 、CD 、AB 均垂直于FB ,求这棵古树的高度AB .(小平面镜的大小忽略不计)【考点】解直角三角形的应用-仰角俯角问题;相似三角形的应用【分析】过点C 作CH AB ⊥于点H ,则CH BD =,0.5BH CD ==.解Rt ACH ∆,得出AH CH BD ==,那么0.5AB AH BH BD =+=+.再证明EFG ABG ∆∆∽,根据相似三角形对应边成比例求出17.5BD =,进而求出AB 即可. 【解答】解:如图,过点C 作CH AB ⊥于点H , 则CH BD =,0.5BH CD ==. 在Rt ACH ∆中,45ACH ∠=︒, AH CH BD ∴==,0.5AB AH BH BD ∴=+=+.EF FB ⊥Q ,AB FB ⊥,90EFG ABG ∴∠=∠=︒.由题意,易知EGF AGB ∠=∠, EFG ABG ∴∆∆∽,∴EF FG AB BG =即 1.620.55BD BD=++, 解之,得17.5BD =,17.50.518()AB m ∴=+=.∴这棵古树的高AB 为18m .21.(7分)根据记录,从地面向上11km 以内,每升高1km ,气温降低6C ︒;又知在距离地面11km 以上高空,气温几乎不变.若地面气温为(C)m ︒,设距地面的高度为()x km 处的气温为(C)y ︒(1)写出距地面的高度在11km 以内的y 与x 之间的函数表达式;(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为26C ︒-时,飞机距离地面的高度为7km ,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面12km 的高空,飞机外的气温是多少度呢?请求出假如当时飞机距离地面12km 时,飞机外的气温. 【考点】一次函数的应用【分析】(1)根据气温等于该处的温度减去下降的温度列式即可; (2)根据(1)的结论解答即可.【解答】解:(1)根据题意得:6y m x =-;(2)将7x =,26y =-代入6y m x =-,得2642m -=-,16m ∴=∴当时地面气温为16C ︒1211x =>Q ,1661150(C)y ︒∴=-⨯=-假如当时飞机距地面12km 时,飞机外的气温为50C ︒-.22.(7分)现有A 、B 两个不透明袋子,分别装有3个除颜色外完全相同的小球.其中,A 袋装有2个白球,1个红球;B 袋装有2个红球,1个白球.(1)将A 袋摇匀,然后从A 袋中随机取出一个小球,求摸出小球是白色的概率; (2)小华和小林商定了一个游戏规则:从摇匀后的A ,B 两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平.【考点】列表法与树状图法;游戏公平性【分析】(1)P(摸出白球)23 =;(2)由上表可知,共有9种等可能结果,其中颜色不相同的结果有4种,颜色相同的结果有5种P(颜色不相同)49=,P(颜色相同)59=,4599<这个游戏规则对双方不公平【解答】解:(1)共有3种等可能结果,而摸出白球的结果有2种P∴(摸出白球)23 =;(2)根据题意,列表如下:A B红1红2白白1(白1,红1)(白1,红2)(白1,白)白2(白2,红1)(白2,红2)(白2,白)红(红,红1)(红,红2)(白1,白)由上表可知,共有9种等可能结果,其中颜色不相同的结果有4种,颜色相同的结果有5种P∴(颜色不相同)49=,P(颜色相同)59=Q 45 99 <∴这个游戏规则对双方不公平23.(8分)如图,AC是Oe的一条弦,AP是Oe的切线.作BM AB=并与AP交于点M,延长MB交AC于点E,交Oe于点D,连接AD.(1)求证:AB BE=;(2)若Oe的半径5R=,6AB=,求AD的长.【考点】切线的性质;相似三角形的判定与性质【分析】(1)根据切线的性质得出90EAM ∠=︒,等腰三角形的性质MAB AMB ∠=∠,根据等角的余角相等得出BAE AEB ∠=∠,即可证得AB BE =;(2)证得ABC EAM ∆∆∽,求得C AME ∠=∠,485AM =,由D C ∠=∠,求得D AMD ∠=∠,即可证得485AD AM ==.【解答】(1)证明:AP Q 是O e 的切线,90EAM ∴∠=︒,90BAE MAB ∴∠+∠=︒,90AEB AMB ∠+∠=︒.又AB BM =Q ,MAB AMB ∴∠=∠,BAE AEB ∴∠=∠,AB BE ∴=(2)解:连接BCAC Q 是O e 的直径,90ABC ∴∠=︒在Rt ABC ∆中,10AC =,6AB =,8BC ∴=,BE AB BM ==Q ,12EM ∴=,由(1)知,BAE AEB ∠=∠,ABC EAM ∴∆∆∽C AME ∴∠=∠,EM AMAC BC =, 即12108AM=,485AM ∴=又D C ∠=∠Q ,D AMD ∴∠=∠485AD AM ∴==.24.(10分)在平面直角坐标系中,已知抛物线2:()L y ax c a x c =+-+经过点(3,0)A -和点(0,6)B -,L 关于原点O 堆成的抛物线为L '.(1)求抛物线L 的表达式;(2)点P 在抛物线L '上,且位于第一象限,过点P 作PD y ⊥轴,垂足为D .若POD ∆与AOB ∆相似,求复合条件的点P 的坐标.【考点】二次函数综合题【分析】(1)将点A 、B 的坐标代入抛物线表达式,即可求解;(2)分POD BOA ∆∆∽、OPD AOB ∆∆∽两种情况,分别求解.【解答】解:(1)将点A 、B 的坐标代入抛物线表达式得:93()06a c a c c -++=⎧⎨=-⎩,解得:16a c =⎧⎨=-⎩, 2:56L y x x ∴=--(2)Q 点A 、B 在L '上的对应点分别为(3,0)A '-、(0,6)B '-,∴设抛物线L '的表达式26y x bx =++,将(3,0)A '-代入26y x bx =++,得5b =-,∴抛物线L '的表达式为256y x x =-+,(3,0)A -,(0,6)B -,3AO ∴=,6OB =,设:(P m ,256)(0)m m m -+>,PD y ⊥Q 轴,∴点D 的坐标为2(0,56)m m -+,PD m =Q ,256OD m m =-+,Rt POD ∆与Rt AOB ∆相似,①POD BOA ∆∆∽时,PD OD OB OA=,即22(56)m m m =-+, 解得:32m =或4; ②当OPD AOB ∆∆∽时,同理可得:1m =或6;1P Q 、2P 、3P 、4P 均在第一象限,∴符合条件的点P 的坐标为(1,2)或(6,12)或(23,43)或(4,2).25.(12分)问题提出:(1)如图1,已知ABC ∆,试确定一点D ,使得以A ,B ,C ,D 为顶点的四边形为平行四边形,请画出这个平行四边形;问题探究:(2)如图2,在矩形ABCD 中,4AB =,10BC =,若要在该矩形中作出一个面积最大的BPC ∆,且使90BPC ∠=︒,求满足条件的点P 到点A 的距离; 问题解决:(3)如图3,有一座草根塔A ,按规定,要以塔A 为对称中心,建一个面积尽可能大的形状为平行四边形的草根景区BCDE .根据实际情况,要求顶点B 是定点,点B 到塔A 的距离为50米,120CBE ∠=︒,那么,是否可以建一个满足要求的面积最大的平行四边形景区BCDE ?若可以,求出满足要求的平行四边形BCDE 的最大面积;若不可以,请说明理由.(塔A 的占地面积忽略不计)【考点】四边形综合题【分析】(1)利用平行四边形的判定方法画出图形即可.(2)以点O 为圆心,OB 长为半径作O e ,O e 一定于AD 相交于1P ,2P 两点,点1P ,2P 即为所求.(3)可以,如图所示,连接BD ,作BDE ∆的外接圆O e ,则点E 在优弧¶BD 上,取·BED 的中点E ',连接E B ',E D ',四边形BC DE ''即为所求.【解答】解:(1)如图记为点D 所在的位置.(2)如图,4AB =Q ,10BC =,∴取BC 的中点O ,则OB AB >. ∴以点O 为圆心,OB 长为半径作O e ,O e 一定于AD 相交于1P ,2P 两点, 连接1BP ,1PC ,1PO ,90BPC ∠=︒Q ,点P 不能再矩形外; BPC ∴∆的顶点1P 或2P 位置时,BPC ∆的面积最大,作1PE BC ⊥,垂足为E ,则3OE =, 1532AP BE OB OE ∴==-=-=,由对称性得28AP =.(3)可以,如图所示,连接BD ,A Q 为BCDE Y 的对称中心,50BA =,120CBE ∠=︒, 100BD ∴=,60BED ∠=︒作BDE ∆的外接圆O e ,则点E 在优弧¶BD 上,取·BED 的中点E ',连接E B ',E D ', 则E B E D '=',且60BE D ∠'=︒,∴△BE D '为正三角形. 连接E O '并延长,经过点A 至C ',使E A AC '=',连接BC ',DC ', E A BD '⊥Q ,∴四边形E D '为菱形,且120C BE ∠''=︒,作EF BD ⊥,垂足为F ,连接EO ,则EF EO OA E O OA E A +-'+='„, 1122BDE E BD S BD EF BD E A S ∆'∴='=V g g g g „,)2221006050003E BD BCDE BC DE S S S sin m '''∴==⋅︒=V 平行四边形平行四边形„ 所以符合要求的BCDE Y 的最大面积为250003m .。
2019年陕西中考数学试题(含解析)(2021年整理精品文档)

(完整版)2019年陕西中考数学试题(含解析)
编辑整理:
尊敬的读者朋友们:
这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整版)2019年陕西中考数学试题(含解析))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整版)2019年陕西中考数学试题(含解析)的全部内容。
2019陕西中考数学试卷及解析
H
答这棵古树的高度为18米
解得:x =18(米)EF AB =FG GB 1.6x =2x -0.5+5∴EFG∽ABG
EF ⊥AB AB ⊥FB 由题意得:∠EGF =∠AGB 在EFG 和ABG 中CH =BD =x -0.5∴CH =AH =AB -HB =x -0.5∵∠ACH=45°过C 作AB 的垂线CH ,垂足为H ,则BH =CD =0.5米解:设古树AB 高度为x
∴SΔBE'D 3
2
3×10000
25003。
2019年陕西中考数学题型专练-线段最值问题

线段最值问题1.(1)如图①,已知⊙O及⊙O外一点C,请在⊙O上找一点P,使其到点C的距离最近;(2)如图②,已知正方形ABCD的边长为4.点M和N分别从点B、C同时出发,以相同的速度沿BC、CD方向向终点C和D运动.连接AM和BN,交于点P.请在图中画出点P的运动路径,并求出点P到点C的最短距离;(3)如图③,AC为边长为4的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA方向向终点C和A运动,连接AM和BN,交于点P,求点P到直线CD的最短距离.第1题图解:(1)如解图①,连接OC交⊙O于点P,点P即为所求;第1题解图①(2)由题知BM=CN,在△ABM和△BCN中,⎪⎩⎪⎨⎧=∠=∠=CN BM BCN ABM BC AB ,∴△ABM ≌△BCN (SAS),∴∠AMB =∠BNC ,又∵∠PBM =∠CBN ,∴△PBM ∽△CBN ,∴∠BPM =∠BCN =90°,∴∠APB =90°,如解图②,连接AC 、BD 交于点O ,取AB 中点E ,则以点E 为圆心,BE 为半径的BO ︵即为点P 的运动路径,连接EC 交BO ︵于点F ,则点P 与点F 重合时,点P 到点C 距离最近.第1题解图②在Rt △BCE 中,CE =BC 2+BE 2,∵BE =12AB =2,BC =4,∴CE =25,∵EF =B ′E =12AB =2,∴CF =CE -EF =25-2,∴点P 到点C 的最短距离为25-2;(3)由题知BM =CN .∵四边形ABCD 为菱形,且∠ABC =60°,∴∠ACB =12∠BCD =60°,∴∠ABC =∠ACB .在△ABM 和△BCN 中,⎪⎩⎪⎨⎧=∠=∠=CN BM ACB ABC BC AB ,∴△ABM ≌△BCN ,∴∠AMB =∠BNC ,∴△BPM ∽△BCN ,∴∠BPM =∠BCN =60°,∴∠APB =180°-∠BPM =120°.如解图③,分别作线段AB 、BP 的垂直平分线,两线交于一点E ,则以点E 为圆心,EB 为半径的BA ︵为点P 的运动路径.连接EC ,交BA ︵于点F ,当点P 与点F 点重合时,点P 到CD 的距离最近.∵∠ABC =∠ACB =60°,且AB =BC ,∴△ABC 是等边三角形,∴CE 为AB 的垂直平分线,∴∠BCE =30°,BF ︵=F A ︵,∵∠BEC =2∠BAP =60°, 第1题解图③∴∠EBC =90°,∴在Rt △EBC 中,CE =BC sin60°=432=833,BE =BC tan60°=43=433, 又∵EF =BE ,∴CF =CE -EF =433.∴点P 到直线CD 的最短距离为433.2. 问题探究(1)请在图①的△ABC 的边BC 上作一点P ,使AP 最短;(2)如图②,点P 为△ABC 内部一点,且满足∠APB =∠BPC =∠APC . 求证:点P 到点A 、B 、C 的距离之和最短,即P A +PB +PC 最短; 问题解决(3)如图③,某高校有一块边长为400米的正方形草坪ABCD ,现准备在草坪内放置一对石凳及垃圾箱在P 点处,使点P 到B 、C 、D 三点的距离之和最小,那么是否存在符合条件的点P ?若存在,请作出点P 的位置,并求出这个最短距离;若不存在,请说明理由.第2题图(1)解:如解图①所示,过点A 作BC 的垂线,垂足为P ,点P 即为所求;第2题解图(2)证明:如解图②,将AB绕点B逆时针旋转60°,得到A1B,将PB绕点B逆时针旋转60°,得到P1B,连接P1A1,P1P,A1A,A1B,根据作图可知△AA1B和△PP1B均为等边三角形,则PP1=PB,∵△AA1B、△PP1B为等边三角形,∴A1B=AB,BP1=BP,∠A1BA=∠P1BP=60°,∴∠A1BP1+∠P1BA=∠PBA+∠P1BA,∴∠A1BP1=∠PBA,∴△A1BP1≌△ABP,∴P1A1=P A,∴P1A1+PP1+PC=P A+PB+PC,连接A1C,根据两点之间线段最短可知,当P1A1+PP1+PC=A1C时,P A+PB +PC最短,∵∠APB=∠BPC=∠APC=13×360°=120°,∴∠A1P1B=∠APB=∠BPC=120°,又∵△BP1P为等边三角形,∠A1P1B+∠BP1P=∠BPP1+∠BPC=180°,∴A1、P1、P、C四点共线,∴P1A1+PP1+PC=A1C,∴当∠APB=∠BPC=∠APC时,P A+PB+PC最短;(3)解:存在符合条件的点P.如解图③,以CD为边作等边△CDE,再作△CDE的外接圆⊙O,连接BE,交⊙O于点P,此时PB+PC+PD最小.在PE 上截取PQ =PC .∵在等边△CDE 中,∠DCE =∠CDE =60°,∴∠CPE =∠CDE =60°(同弧所对的圆周角相等),第2题解图③∴△CPQ 为等边三角形,∴CQ =CP ,∠PCQ =60°,∴∠PCD +∠DCQ =∠DCQ +∠ECQ =60°,∴∠PCD =∠ECQ ,又∵CD =CE ,PC =QC ,∴△PCD ≌△QCE (SAS),∴PD =QE ,∴PB +PC +PD =PB +PQ +QE =BE 最小,理由如下:设点M 为正方形ABCD 内任意一点,连接BM ,CM 、DM ,将△CMD 绕点C 顺时针旋转60°得到△CGE ,∵BE <GE +GM +MB =MD +MC +MB ,∴BE 为PB +PC +PD 的最短距离.在Rt △CEF 中,∠ECF =30°,CE =400米,∴EF =12CE =200(米),CF =CE ·cos30°=2003(米),∴BF=BC+CF=400+2003(米),在Rt△BEF中,BE=BF2+EF2=(400+2003)2+2002=200(6+2)≈773米.∴点P到B、C、D三点的距离之和最小值为200(6+2)米(或约为773米).。
2019年陕西省中考数学试题及答案【Word版】

2019年陕西省中考数学试题及答案【Word版】

2019年陕西中考数学试卷第Ⅰ卷(选择题 共30分)一.选择题(共10小题,每小题3分,计30分。
每小题只有一个选项是符合题意的)1。
4的算术平方根是( )A .-2 B.2 C.21- D. 21 2.下面是一个正方体被截去一个直三棱柱得到的几何体,则该几何体的左视图是( )3.若点A (—2,m)在正比例函数y=21-x 的图像上,则m 的值是( ) A .41 B 。
41- C 。
1 D. -1 4.小军旅行箱的密码是一个六位数,由于他忘记了密码的末位数字,则小军能一次打开该旅行箱的概率是( ) A .101 B. 91 C. 61 D 。
51 5.把不等式组的解集表示在数轴上,正确的是( )6.某区10名学生参加市级汉字听写大赛,他们得分情况如下表:人数3 4 2 1 得分 80 85 90 95那么这10名学生所得分数的平均数和众数分别是( )A 。
80和82.5 B.85.5和85 C.85和85 D.85。
5和807.如图,AB ∥CD ,∠A=45°,∠C=28°,则∠AEC 的大小为( )A 。
17°B 。
62°C 。
63°D 。
73°8.若x=—2是关于x 的一元二次方程02522=+-a ax x 的一个根,则a 的值为 ( ) A.1或4 B. -1或—4 C 。
-1或4 D 。
1或—49。
如图,在菱形ABCD 中,AB=5,对角线AC=6,若过点A 作AE ⊥BC ,垂足为E ,则AE 的长为( )A .4 B. 512 C. 524 D 。
5 10。
二次函数)0(2≠++=a c bx ax y 的图像如图所示,则下列结论中正确的是( )A .c >—1 B.b >0 C 。
2a+b ≠0 D 。
92a +c >3b第Ⅱ卷(非选择题 共90分)二.填空题(共6小题,每小题3分,计18分)11。
计算:2)31(--=______。
2019年陕西省中考数学试卷(详解版)

1计算:2如图,是由两个正方体组成的几何体,则该几何体的俯视图为(3如图,4若正比例函数5下列计算正确的是(6如图,在7在平面直角坐标系中,将函数8如图,在矩形9如图,10在同一平面直角坐标系中,若抛物线11已知实数12若正六边形的边长为13如图,14如图,在正方形15计算:16化简:17如图,在18如图,点19本学期初,某校为迎接中华人民共和国建国七十周年,开展了以20小明利用刚学过的测量知识来测量学校内一棵古树的高度,一天下午,他和学习小组的同学们带答案解析米.设树高为米,为米,由物理学知识知:,∴,∴,代入数值即①,过点作,垂足为.∵,,∴为等腰直角三角形∴,代入数值即②联立①②,解得,答:这棵古树的高度高为米.答案解析根据记录,从地面向上以内,每升高,气温降低;又知在距地面以上的高空,气温几乎不变.若地面气温为,设距地面的高度为处的气温为.21写出距地面的高度在以内的于之间的函数表达式.(1)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为时,飞机距地面的高度为,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距地面的高空,飞机外的气温是多少度呢?请求出假如当时飞机距地面时,飞机外的气温.(2).(1)若在距地面的高空飞机外的温度为.(2).(1)把代入上式,得,∴,∴当时底面的气温为,当时,,∴若在距地面的高空飞机外的温度为.(2)现有22如图,2324在平面直角坐标系中,已知抛物线25回答下列问题.∴,∴平行四边形的最大面积为,故最大面积为.。
2019年陕西省中考数学试题及答案【Word版】

2019年陕西中考数学试卷第Ⅰ卷(选择题 共30分)一.选择题(共10小题,每小题3分,计30分、每小题只有一个选项就是符合题意得)1、4得算术平方根就是( )A.-2 B 、2 C 、21- D 、 21 2、下面就是一个正方体被截去一个直三棱柱得到得几何体,则该几何体得左视图就是( )3、若点A(-2,m)在正比例函数y=21-x 得图像上,则m 得值就是( ) A.41 B 、 41- C 、1 D 、 -1 4、小军旅行箱得密码就是一个六位数,由于她忘记了密码得末位数字,则小军能一次打开该旅行箱得概率就是( ) A.101 B 、 91 C 、 61 D 、 51 5、把不等式组得解集表示在数轴上,正确得就是( ):人数3 4 2 1 得分 80 85 90 95那么这10名学生所得分数得平均数与众数分别就是( )A 、80与82、5B 、85、5与85C 、85与85D 、85、5与807、如图,AB ∥CD,∠A=45°,∠C=28°,则∠AEC 得大小为( )A 、17°B 、62°C 、63°D 、73°8、若x=-2就是关于x 得一元二次方程02522=+-a ax x 得一个根,则a 得值为 ( ) A 、1或4 B 、 -1或-4 C 、 -1或4 D 、 1或-49、如图,在菱形ABCD 中,AB=5,对角线AC=6,若过点A 作AE ⊥BC,垂足为E,则AE 得长为( )A.4 B 、 512 C 、 524 D 、5 10、二次函数)0(2≠++=a c bx ax y 得图像如图所示,则下列结论中正确得就是( )A.c >-1 B 、b >0 C 、2a+b ≠0 D 、 92a +c >3b第Ⅱ卷(非选择题 共90分)二.填空题(共6小题,每小题3分,计18分)11、计算:2)31(--=______、12、因式分解:m(x-y)+n(x-y)=_____________、13、请从以下两个小题中任选一个....作答,若多选,则按所选做得第一题计分、 A 、一个正五边形得对称轴共有_____条、B 、用科学计算器计算:︒+56tan 331≈________、(结果精确到0、01)14、如图,在正方形ABCD 中,AD=1,将△ABD 绕点B 顺时针旋转45°得到△A ′BD ′,此时A ′D ′与CD 交于点E,则DE 得长度为_______、15、已知),(111y x P ,),(222y x P 就是同一个反比例函数图像上得两点、若212+=x x ,且211112+=y y ,则这个反比例函数得表达式为_________、 16、如图,⊙O 得半径就是2,直线l 与⊙O 相交于A 、B 两点,M 、N 就是⊙O 上两个动点,且在直线l 得异侧,若∠AMB=45°,则四边形MANB 面积得最大值就是________、三.解答题(共9小题,计72分、解答应写出过程)17、(本题满分5分)先化简,再求值: 11222+--x x x x ,其中x=21-、 18、(本题满分6分)如图,在Rt △ABC 中,∠ABC=90°,点D 在边AB 上,使DB=BC,过点D 作EF ⊥AC,分别交AC 于点E 、CB 得延长线于点F 、求证:AB=BF 、19、(本题满分7分)根据《2019年陕西省国民经济与社会发展统计公报》提供得大气污染物(A —二氧化硫,B —氮氧化物,C —化学需氧量,D —氨氮)排放量得相关数据,我们将这些数据用条形统计图与扇形统计图统计如下:根据以上统计图提供得信息,解答下列问题:(1)补全上面得条形统计图与扇形统计图;(2)国务院总理李克强在十二届全国人大二次会议得政府工作报告中强调,建设美好家园、加大节能减排力度,今年二氧化硫、化学需氧量得排放量在去年基础上都要减少2%、按此指示精神,求出陕西省2019年二氧化硫、化学需氧量得排放量共需减少约多少万吨?(结果精确到0、1)20、(本题满分8分)某一天,小明与小亮来到一河边,想用遮阳帽与皮尺测量这条河得大致宽度,两人在确保无安全隐患得情况下,先在河岸边选择了一点B(点B 与河对岸岸边上得一棵树得底部点D 所确定得直线垂直于河岸)、①小明在B 点面向树得方向站好,调整帽檐,使视线通过帽檐正好落在树得底部点D 处,如图所示,这时小亮测得小明眼睛距地面得距离AB=1、7米;②小明站在原地转动180°后蹲下,并保持原来得观察姿态(除身体重心下移外,其她姿态均不变),这时视线通过帽檐落在了DB 延长线上得点E 处,此时小亮测得BE=9、6米,小明得眼睛距地面得距离CB=1、2米、根据以上测量过程及测量数据,请您求出河宽BD 就是多少米?21、(本题满分8分)小李从西安通过某快递公司给在南昌得外婆寄一盒樱桃,快递时,她了解到这个公司除收取每次6元得包装费外,樱桃不超过1kg 收费22元,超过1kg,则超出部分按每千克10元加收费用、设该公司从西安到南昌快寄樱桃得费用为y(元),所寄樱桃为x(kg)、(1)求y 与x 之间得函数关系式;(2)已知小李给外婆快寄了2、5kg 樱桃,请您求出这次快寄得费用就是多少元?22、(本题满分8分)小英与她得父亲、母亲计划外出旅游,初步选择了延安、西安、汉中、安康四个城市、由于时间仓促,她们只能去其中一个城市,到底去哪一个城市三人意见不统一、在这种情况下,小英父亲建议,用小英学过得摸球游戏来决定、规则如下:①在一个不透明得袋子中装一个红球(延安)、一个白球(西安)、一个黄球(汉中)与一个黑球(安康),这四个球除颜色不同外,其余完全相同;②小英父亲先将袋中球摇匀,让小英从袋中随机摸出一球,父亲记录下其颜色,并将这个球放回袋中摇匀,然后让小英母亲从袋中随机摸出一球,父亲记录下它得颜色;③若两人所摸出球得颜色相同,则去该球所表示得城市旅游,否则,前面得记录作废,按规则②重新摸球,直到两人所摸出球得颜色相同为止、按照上面得规则,请您解答下列问题:(1)已知小英得理想旅游城市就是西安,小英与母亲随机各摸球一次,均摸出白球得概率就是多少?(2)已知小英母亲得理想旅游城市就是汉中,小英与母亲随机各摸球一次,至少有一人摸出黄球得概率就是多少?23、(本题满分8分)如图,⊙O 得半径为4,B 就是⊙O 外一点,连接OB,且OB=6、过点B 作⊙O 得切线BD,切点为D,延长BO 交⊙O 于点A,过点A 作切线BD 得垂线,垂足为C 、(1)求证:AD 平分∠BAC;(2)求AC 得长、24、(本题满分10分)已知抛物线C:c bx x y ++-=2经过A(-3,0)与B(0,3)两点、将这条抛物线得顶点记为M,它得对称轴于x 轴得交点记为N 、(1)求抛物线C 得表达式;(2)求点M 得坐标;(3将抛物线C 平移到C ′,抛物线C ′得顶点记为M ′,它得对称轴于x 轴得交点记为N ′、如果以点M 、N 、M ′、N ′为顶点得四边形就是面积为16得平行四边形,那么应将抛物线C 怎样平移?为什么?25、(本题满分12分)问题探究(1)如图①,在矩形ABCD 中,AB=3,BC=4、如果BC 边上存在点P,使△APD 为等腰三角形,那么请画出满足条件得一.个.等腰△APD,并求出此时BP 得长; (2)如图②,在△ABC 中,∠ABC=60°,BC=12,AD 就是BC 边上得高,E 、F 分别为边AB 、AC 得中点、当AD=6时,BC 边上存在一点Q,使∠EQF=90°,求此时BQ 得长;问题解决(3)有一山庄,它得平面图为如图③得五边形ABCDE,山庄保卫人员想在线段CD 上选一点M 安监控装置,用来监视边AB 、现只要使∠AMB 大约为60°,就可以让监控装置得效果达到最佳、已知∠A=∠E=∠D=90°,AB=270m,AE=400m,ED=285m,CD=340m 、问在线段CD 上就是否存在点M,使∠AMB=60°?若存在,请求出符合条件得DM得长;若不存在,请说明理由、图①图②图③参考答案1、B2、A3、C4、A5、D6、B7、D8、B9、C 10、D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
类型3 线段最值问题
6. 问题探究
(1)如图①,点M、N在直线l异侧,在直线l上找一点P,使P到M、N两点的距离之和最短;
(2)如图②,点M、N在直线l同侧,若MN=2,点M、N到直线l的距离分别为2和1,在直线l上找一点P,使P到M、N两点的距离之和最短,求最短距离为多少?
问题解决
(3)聪聪的爸爸是供电公司的线路设计师,公司准备在输电农田区l上连接一个分支线路,为M、N两个村落同时输电.如图③所示,农田区两侧AB与CD平行,且农田区宽为0.5千米,村落M到农田AB一侧的距离为2千米,村落N到农田CD一侧的距离为1千米,两村落M、N的连线与农田区l所夹锐角恰好为45°,根据架线要求,当线路通过农田区时,要求线路与农田区垂直.请你帮助聪聪的爸爸设计出最短的分支线路,并根据所画示意图计算出最短线路.(要求:写出计算过程,结果保留根号)
第6题图
解:(1)如解图①,连接MN,与直线l相交于点P,点P即为所求;
第6题解图①第6题解图②
(2)如解图②,连接MN,作点N关于l的对称点N′,连接MN′交l于点P,此时P到M、N 两点的距离最短.
过点M作MO⊥l于点O,并延长到点C,使OC=1,过点N作NF⊥MO于点F,连接N′C,根据作图可知四边形NDOF为矩形,即ND=N′D=FO=OC=1.
又∵MO=2, MN=2,则MF=MO-FO=2-1=1,MC=MO+OC=3,
∴N′C=FN=MN2-MF2=22-12=3,
∴N′M=MC2+N′C2=32+(3)2=23;
(3)如解图③,过点M作l的垂线,过点N作l的平行线,两条线交于点O,再在MO上找一点P,使得点P与点O关于l对称,连接PN,与农田区CD一侧的交点为点F,过点F作农田区AB一侧的垂线,垂足为E,然后连接MN及ME.
第6题解图③
根据题意可知在Rt△MON中,∵∠MNO=45°,
∴△MON为等腰直角三角形,故OM=ON=3.5千米,
结合作图中的对称性,可知PO=3千米,
∴MP=MO-PO=3.5-3=0.5(千米),
又∵EF⊥l,MO⊥l,且MP=EF, ∴四边形MPFE为平行四边形,∴ME=PF,即ME+FN+EF=PN+EF,
∴线路ME→EF→FN的线路为最短线路.
∵在Rt△PON中,PN=OP2+ON2=32+3.52=85
2
(千米),
∴ME+EF+FN=PN+EF=85+1
2
(千米).
∴最短线路长为85+1
2
千米.
7. 问题探究
(1)如图①,点M、N分别是△ABC边AB、AC上任意一点,在BC边上确定一点P,使得PM+PN的值最小;
(2)如图②,点M是边长为2的正方形ABCD对角线AC上一动点,点N为CD边的中点,求△DMN 周长的最小值;
问题解决
(3)如图③,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB边的中点,在OA上取一点D,将△BDA 沿BD翻折,使点A落在BC边上的点F处.若M为x轴上任意一点,N为y轴上任意一点,当四边形MNFE的周长最小时,求出点M、N的坐标,并求出周长的最小值.
第7题图
解:(1)如解图①,作点M关于BC的对称点M′,连接M′N交BC于点P,则点P就是所求的点;
第7题解图
(2)如解图②,连接BD 交AC 于点O , ∵正方形的对角线互相垂直平分, ∴点D 关于AC 的对称点为点B , 连接BN ,交AC 于点M ,连接DM , ∴DM +MN =MB +MN =BN .
在AC 上任取一点M ′,连接BM ′、DM ′、M ′N , 则DM ′+M ′N =BM ′+M ′N >BN , ∴点M 就是所求的点, ∵线段DN 的长为定值,
∴当DM +MN 的值最小时△DMN 的周长最小, 即周长的最小值为BN +DN 的值.
∵正方形ABCD 的边长为
2,N 为DC 的中点,
∴DN =1,BN =22
+12
=5,
∴△DMN 的周长的最小值为5+1;
(3)∵在矩形OABC 中,OA =3,OC =2,点E 是AB 的中点, ∴点E 坐标为(3,1).
又∵△BDA 沿BD 翻折,使点A 落在BC 边上的点F 处, 可知四边形ADFB 是正方形, ∴BF =AB =OC =2, CF =BC -BF =3-2=1, ∴点F 的坐标为(1,2).
如解图③,作点E 关于x 轴的对称点E ′,作点F 关于y 轴的对称点F ′,连接E ′F ′,分别与x 轴、y 轴交于点M 、N ,连接FN 、ME 、EF ,在OC 上任取一点N ′,在OA 上任取一点M ′,连接F ′N ′、N ′M ′、M ′E ′、FN ′、EM ′,则EF +FN ′+N ′M ′+M ′E =EF +F ′N ′+N ′M ′+M ′E ′>E ′F ′,则取M 、N 点时四边形MNFE 的周长最小.
第7题解图③
∴E ′(3,-1),F ′(-1,2),
设直线E ′F ′的解析式为y =kx +b ,将点E ′、F ′的坐标分别代入,
得⎩
⎪⎨⎪⎧3k +b =-1
-k +b =2,解得⎩
⎪⎨⎪⎧k =-
34b =54
,
∴直线E ′F ′的解析式为y =-34x +5
4.
当y =0时,x =53,故点M 的坐标为(5
3,0),
当x =0时,y =54,故点N 的坐标为(0,5
4
).
∵点E 与E ′关于x 轴对称,点F 与F ′关于y 轴对称,
∴NF =NF ′,ME =ME ′,F ′B =4,E ′B =3.
在Rt △BE ′F ′中,E ′F ′=BE ′2
+BF ′2
=32
+42
=5, ∴FN +NM +ME =F ′N +NM +ME ′=F ′E ′=5, 在Rt △BEF 中,EF =BE 2
+BF 2
=12
+22
=5, ∴FN +NM +ME +EF =5+5,
∴四边形MNFE 周长的最小值是5+ 5.。
