《步步高 学案导学设计》2013-2014学年高中数学苏教版选修1-2【备课资源】2.1.3
《步步高 学案导学设计》2013-2014学年高中数学苏教版选修1-2【备课资源】第二章推理与证明 章末复习课

1 π (1-cos α>0,当且仅当 cos α= ,即 α= 时取等号) 2 3 1 ∴4cos α≤ . 1-cos α
研一研·题型解法、解题更高效
章末复习课
∵α∈(0,π),∴sin α>0.
本 课 时 栏 目 开 关
sin α ∴4sin αcos α≤ . 1-cos α
sin α ∴2sin 2α≤ . 1-cos α
研一研·题型解法、解题更高效
章末复习课
本 课 时 栏 目 开 关
③设 3 个两两垂直的侧面形成的侧棱长分别为 a,b,c,则这 a2+b2+c2 个四面体的外接球的半径为 R= . 2
研一研·题型解法、解题更高效
章末复习课
② 跟踪训练 1 (1)下列推理是归纳推理的是________, 是类比推 ③④ 理的是________.
当 n=3 时,有 sin3x+cos3x=(sin2x+cos2x)(sin x+cos x)- sin xcos x· x+cos x). (sin
因为(sin x+cos x)2=(-1)2,
研一研·题型解法、解题更高效
章末复习课
所以 sin2x+2sinxcos x+cos2x=1.
所以 sin xcos x=0.
例 3 设二次函数 f(x)=ax2+bx+c(a≠0)中的 a、b、c 都为整 数,已知 f(0)、f(1)均为奇数,求证:方程 f(x)=0 无整数根. 证明 假设方程 f(x)=0 有一个整数根 k,
本 课 时 栏 目 开 关
则 ak2+bk+c=0
∵f(0)=c,f(1)=a+b+c 都为奇数,∴a+b 必为偶数.
章末复习课
综上可知方程 f(x)=0 无整数根.
《步步高学案导学设计》2013-2014学年高中数学苏教版选修1-2【备课资源】2.2.1直接证明习题课

开 a2+b2≥a+2 b2.
(3)若 a,b∈(0,+∞),则a+2 b≥ ab,特别地ba+ab≥2.
(4)a2+b2+c2≥ab+bc+ca(a,b,c∈R).
研一研·题型解法、解题更高效
习题课
跟踪训练 1 (1)已知:a,b,c 都是正实数,且 ab+bc+ca= 1.求证:a+b+c≥ 3.
时 栏
(2)证明:PD⊥平面 ABE.
目
开 证明 (1)在四棱锥 P-ABCD 中,
∵PA⊥底面 ABCD,CD⊂底面 ABCD,
∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,
习题课
研一研·题型解法、解题更高效
∴CD⊥平面 PAC, 而 AE⊂平面 PAC, 本 ∴CD⊥AE.
课
时 (2)由 PA=AB=BC,∠ABC=60°,
栏
目 可得 AC=PA,
开
∵E 是 PC 的中点, ∴AE⊥PC. 由(1)知,AE⊥CD,
习题课
研一研·题型解法、解题更高效
且 PC∩CD=C,
所以 AE⊥平面 PCD.
而 PD⊂平面 PCD,
本
课 时
∴AE⊥PD.
栏
目 ∵PA⊥底面 ABCD,
开
∴PA⊥AB,
又 AB⊥AD,∴AB⊥平面 PAD,
研一研·题型解法、解题更高效
习题课
题型一 选择恰当的方法证明不等式
例 1 设 a,b,c 为任意三角形三边长,I=a+b+c,S=
本 课
ab+bc+ca,试证:3S≤I2<4S.
时
栏 目
证明 I2=(a+b+c)2=a2+b2+c2+2ab+2bc+2ca
开
=a2+b2+c2+2S.
《步步高 学案导学设计》2013-2014学年高中数学(苏教版)选修2-1【配套备课资源】第二章 2.3.1

标准 方程
研一研·问题探究、课堂更高效
2.3.1
问题 2 两种形式的标准方程怎样进行区别?能否统一?
答案
本 课 栏 目 开 关
两个标准方程的区别:双曲线标准方程中 x2 与 y2
研一研·问题探究、课堂更高效
解 矩形灾民区ABCD中的点可分为三类,第
2.3.1
一类沿道路PA送药较近,第二类沿道路PB送 药较近,第三类沿道路PA和PB送药一样远
本 课 栏 目 开 关
近.依题意,界线是第三类点的轨迹.
设 M 为界线上的任一点, 则 PA+MA=PB+MB,MA-MB=PB-PA=50(定值).
研一研·问题探究、课堂更高效
2.3.1
小结
本 课 栏 目 开 关
(1)解答与双曲线有关的应用问题时,不但要准确把
握题意,了解一些实际问题的相关概念,同时还要注意双 曲线的定义及性质的灵活应用. (2)实际应用问题要注意其实际意义以及在该意义下隐藏着 的变量范围.
研一研·问题探究、课堂更高效
跟踪训练3 2008年5月12日,四川汶川发生
c= 7,所以焦点为(± 7,0),顶点为(± 4,0).于是双曲线 经过点(± 7,0),焦点为(± 4,0),则 a′= 7,c′=4,所 x2 y2 以 b′2=9,所以双曲线的标准方程为 - =1. 7 9
研一研·问题探究、课堂更高效
探究点二 例2
2.3.1
双曲线定义及标准方程的应用 x2 y2 已知双曲线的方程是 - =1,点 P 在双曲线上,且 16 8
《步步高 学案导学设计》2013-2014学年高中数学苏教版选修 排列(一)

m 个元素的所有排列?
本 课 时 栏 目 开 关
干排列按一定的顺序一一写出来, 为了省略前面与上一行相 同的元素而画出的像树枝一样的图形, 能很好的表达排列中 各元素的先后顺序,利用树形图具体地列出各种情况,可避 免排列的重复或遗漏.
研一研·问题探究、课堂更高效
(1)首先要保证元素的无重复性,否则不是排列问题;
(2)其次是保证选出的元素在被安排时的有序性,否则不是排列 问题,而检验它是否有顺序的标准是变换某一结果中两元素的 位置,看结果是否变化,有变化就是有顺序,无变化就是无 顺序.
研一研·问题探究、课堂更高效
例1 判断下列问题是否是排列问题:
§1.2(一)
解析 问题. 根据排列的定义,选出的元素有顺序的才是排列
练一练·当堂检测、目标达成落实处
§1.2(一)
2.从甲、乙、丙三人中选两人站成一排的所有排列为
甲乙,甲丙,乙甲,乙丙,丙甲,丙乙 ______________________________________.
本 课 时 栏 目 开 关
解析
选出两人,两人的不同站法都要考虑.
解
(1)列出每一个起点和终点情况,如图所示,共有 12 种
机票.
研一研·问题探究、课堂更高效
故符合题意的机票种类有:
§1.2(一)
北京广州,北京南京,北京天津,广州南京,广州天津,广州 北京,南京天津,南京北京,南京广州,天津北京,天津广州,
本 课 时 栏 目 开 关
天津南京,共 12 种.
(2)因为 A 不排第一,排第一位的情况有 3 类(可从 B、C、D 中 任选一人排),而此时兼顾分析 B 的排法,列树图如图.
《步步高学案导学设计》2013-2014学年高中数学苏教版选修1-2【备课资源】2.1.3
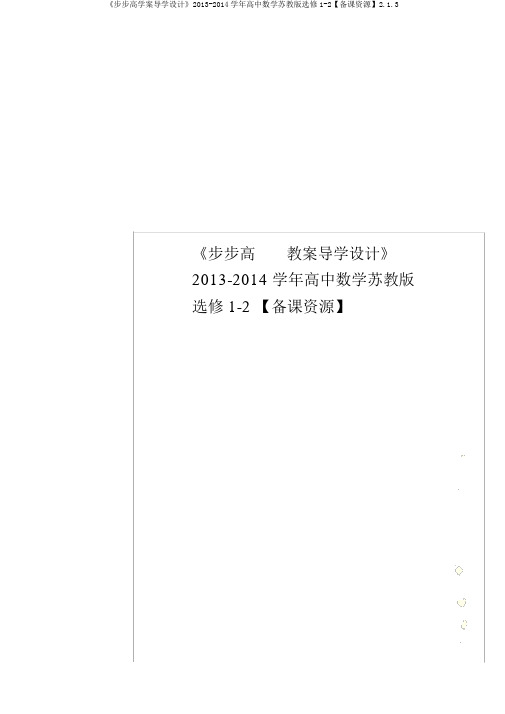
《步步高教案导学设计》2013-2014 学年高中数学苏教版选修 1-2 【备课资源】2. 1.3推理事例赏析一、基 关1.有两栽花色的正六 形地板 ,按下边的 律拼成若干个 案, 第 6 个 案中有底 的正六 形的个数是 ________.111112. 察以下不等式:1>2,1+2+3>1,1+2+3+⋯1311111+7>2,1+2+3+⋯+15>2,1+2+3+⋯+1 531>2,⋯由此猜第n个 等 式______________(n ∈N *).3.已知数列 {a n }的前 n 和 S n ,且 S n =n 2+1. 此数列的前 4 分 a 1=______,a 2=________,a 3=________,a 4=________.据此猜 ,数列 {a n }的通 公式 a n =________________________________________________________________________.4.正方形ABCD 中,对角线AC⊥BD.运用类比的方法,猜想正方体 ABCD —A1B1C1D1中,有关结论: ________________________.5.假如函数f(x)是奇函数,那么f(0)=0.由于函1数 f(x)=x是奇函数,因此 f(0)=0.这段演绎推理错误的原由是 ______________.二、能力提高6.已知△ABC 中,AD ⊥BC 于D,三边是a,b,c,则有 a= ccos B+ bcos C;类比上述推理结论,写出以下条件下的结论:四周体 P—ABC 中,△ABC,△ PAB,△ PBC,△ PCA 的面积分别是 S,S1,S2,S3,二面角 P—AB—C,P—BC—A,P—AC—B 的度数分别是α,β,γ,则S=__________________________________________________________.7.已知等式: (tan 5 +°1)(tan 40 +°1)=2;(tan 15 +°1)(tan 30 +°1)=2;(tan 25 +°1)(tan 20 +°1)=2;据此可猜想出一个一般性命题:____________________________________________.8.设M 是拥有以下性质的函数f(x)的全体:关于随意s>0,t>0,都有f(s)+f(t)<f(s+t).给出函数 f1(x)=log2x,f2(x)=2x-1.以下判断正确的是 ________.① f 1(x)∈M ;② f 1(x)?M ;③f 2(x)∈M ;④ f 2(x)?M.9.已知命 :平面直角坐 系xOy 中,△ ABCx2的 点 A(-p,0)和 C(p,0), 点 B 在 m 2+2ny2=1 (m>n>0,p = m2-n 2)上, 的离心率是 e ,sin A +sin C 1sin B=e .将 命 比到双曲 中, 出一个命 :__________________________________________________________________________________________________________.10.已知等式: 3tan 30 ·°tan 30 +°tan 30 +°tan30°= 3,3tan 20 ·°tan 40 +°tan 20 +°tan 40 =° 3,3tan 15 ·°tan 45 +°tan 15 +°tan 45 =° 3.据此猜想出一个一般性命 ,并 明你的猜想.11.在平面中有命 :等腰三角形底 上任一点到两腰距离之和等于一腰上的高.把此 比到空的正三棱 ,猜想并 明有关 .三、研究与拓展12. S n 数列 {a n }的前 n 和, 出两个数列:(Ⅰ)5,3,1,- 1,- 3,- 5,- 7,⋯(Ⅱ)-14,- 10,- 6,- 2,2,6,10,14,18,⋯(1)于数列 (Ⅰ),算 S1,S2,S4,S5;于数列(Ⅱ),算 S1,S3,S5,S7;(2)依据上述果,于存在正整数k,足 a k +a k+1=0 的一等差数列 {a n}的和的律,猜想一个正确的,并加以明.答案1.311+1+⋯+1>n2.1+n232-1 23.23572,n=1 2n-1, n≥24.角面 AA1C1C⊥BB1D1D5.大前提6.S1cos α+S2cos β+S3cos γ7.(tan α+1)[tan(45 -°α)+1]=28.②③9.平面直角坐系xOy 中,△ ABC 的点 A(-x2y2p,0)和 C(p,0),点 B 在双曲m2-n2=1 (m,n>0,p= m2+n2)上,双曲的离心率e,|sin A-sin C| 1sin B=e10.解猜想: 3tan α·tan β+tan α+tan β=3,此中α+β=60 °.tan α+tan β明:∵tan( α+β)=,1-tan α·tan βtan α+tan β即=.31-tan α·tan β整理,得3tan α·tan β+tan α+tan β= 3.11.解猜想结论:正三棱锥底面上任一点到三个侧面的距离之和等于以侧面为底时三棱锥的高.证明以下:设 P 为正三棱锥 A—BCD 底面上任一点,点 P 到平面 ABC、ACD 、ABD 的距离分别为 h1、h2、h3,以侧面 ABC 为底时对应的高为 h,则:V P—ABC+V P—ACD+V P—ABD=V D—ABC .111即: 3S△ABC·h1+3S△ACD·h2+3S△ABD·h31=3S△ABC·h.∵S△ABC=S△ACD=S△ABD∴h1+h2+h3=h,此即要证的结论.12.解(1)关于数列 (Ⅰ),S1=S5=5,S2=S4=8;关于数列 (Ⅱ),S1=S7=- 14,S3= S5=- 30. (2)关于等差数列 {a n},当 a k+a k+1=0 时,猜想 S n=S2k-n(n≤2k,n,k∈N* ).下边给出证明:设等差数列 {a n}的前项为 a1,公差为 d.∵a k+a k+1=0,∴a1+(k-1)d+a1+kd=0,∴2a1=(1-2k)d.又 S-S =(2k-n)a +2k-n 2k-n-1d-2k- n n12n n-1na1-2d2k-n2k-n-1= [(k - n)(1 - 2k) +2-n n-1]d=0.2∴S2k-n=S n,猜想正确.。
《步步高 学案导学设计》2013-2014学年高中数学苏教版选修1-2【备课资源】3.1数系的扩充

本 课 时 栏 目 开 关
mm+2 (1)要使 z 是实数, 需满足 m +2m-3=0, m 且 m-1
2
有意义即 m-1≠0,解得 m=-3. mm+2 (2)要使 z 是虚数,m 需满足 m +2m-3≠0,且 有 m-1
2
意义即 m-1≠0,解得 m≠1 且 m≠-3.
mm+2 (3)要使 z 是纯虚数,m 需满足 =0, m-1 且 m2+2m-3≠0, 解得 m=0 或 m=-2.
答 对于复数 z=a+bi(a,b∈R),当 b≠0 时叫做虚数;当 a=0 且 b≠0 时,叫做纯虚数.
研一研·问题探究、课堂更高效§3.1例 1 请说出下列复数的实部和虚部,并判断它们是实数,虚 数还是纯虚数. 1 ①2+3i;②-3+ i;③ 2+i;④π;⑤- 3i;⑥0. 2
本 课 时 栏 目 开 关
练一练·当堂检测、目标达成落实处
§3.1
3.如果 z=m(m+1)+(m2-1)i 为纯虚数,则实数 m 的值为
本 课 时 栏 目 开 关
0 ________.
解析
mm+1=0 由题意知 2 m -1≠0
,∴m=0.
练一练·当堂检测、目标达成落实处
4.下列几个命题: ①两个复数相等的一个必要条件是它们的实部相等;
本 课 时 栏 目 开 关
§3.1
【学习要求】 1.了解引进虚数单位 i 的必要性,了解数集的扩充过程. 2.理解在数系的扩充中由实数集扩展到复数集出现的一些基
本 课 时 栏 目 开 关
本概念. 3.掌握复数代数形式的表示方法,理解复数相等的充要条件. 【学法指导】 可以从实际需求和数系的扩充认识引入复数的必要性, 认识 复数代数形式的结构, 从本质上理解复数和有序数对的对应 关系.
《步步高 学案导学设计》2013-2014学年高中数学苏教版选修 排列(二)

研一研·题型解法、解题更高效
方法二
§1.2(二)
5 (插空法)将其余 5 人全排列,有 A5种排法,5 人之间
及两端共有 6 个位置, 任选 2 个排甲、 乙两人, A2种排法. 有 6 故 共有 A5· 2=3 600(种)排法. 5 A6 (3)(捆绑法)将甲、乙、丙三人捆绑在一起与其余 4 人全排列,
练一练·当堂检测、目标达成落实处
§1.2(二)
2.6 人站成一排,甲、乙、丙 3 个人不能都站在一起的排法种 数为________. 576
本 课 时 栏 目 开 关
解析
3 (间接法)甲、乙、丙三人在一起的排法种数为 A4×A3; 4
6 不考虑任何限制,6 人的全排列有 A6. 6 3 ∴符合题意的排法种数为:A6-A4×A3=576. 4
本 课 时 栏 目 开 关
小结
本题两小题的区别在于: 第(1)小题是从 5 本不同的书中
选出 3 本分别送给 3 名同学,各人得到的书不同,属于求排列 数问题;而第(2)小题中,给每人的书均可以从 5 种不同的书中 任选 1 本,各人得到哪本书相互之间没有联系,要用分步计数 原理进行计算.
研一研·题型解法、解题更高效
§1.2(二)
小结
处理元素“相邻”“不相邻”问题应遵循“先整体, 后
局部”的原则.元素相邻问题,一般用“捆绑法”,先把相邻
本 课 时 栏 目 开 关
的若干个元素“捆绑”为一个大元素与其余元素全排列, 然后 再松绑,将这若干个元素内部全排列.元素不相邻问题,一般 用“插空法”,先将不相邻元素以外的“普通”元素全排列, 然后在“普通”元素之间及两端插入不相邻元素.
研一研·题型解法、解题更高效
跟踪训练 3 对于本例中的 7 人, (1)甲、乙两人之间只有 1 人的排法有多少种? (2)甲、乙、丙排序一定时,有多少种排法?
《步步高 学案导学设计》2013-2014学年高中数学苏教版选修1-2【备课资源】1.2(一)

§1.2 回归分析(一) 一、基础过关 1.下列各关系中是相关关系的是________.①路程与时间(速度一定)的关系;②加速度与力的关系;③产品成本与产量的关系;④圆周长与圆面积的关系;⑤广告费支出与销售额的关系.2.在以下四个散点图中,其中适用于作线性回归的散点图为__________.(填序号) 3.对于回归分析,下列说法正确的是________.①在回归分析中,变量间的关系若是非确定关系,那么因变量不能由自变量惟一确定②线性相关系数可以是正的,也可以是负的2③回归分析中,如果r=1,说明x与y之间完全相关④样本相关系数r∈(-1,1) 4.下表是x和y之间的一组数据,则y关于x的线性回归方程必过点________. x 1 2 3 4 y 1 3 5 7 ^5.工人月工资y(元)按劳动生产率x(千元)变化的回归方程为y =50+80x,下列判断正确的是________.①劳动生产率为1 000元时,则月工资为130元;②劳动生产率提高1 000元时,则月工资提高80元;③劳动生产率提高1 000元时,则月工资提高130元;④当月工资为210元时,劳动生产率为2 000元.二、能力提升6.某医院用光电比色计检验尿汞时,得尿汞含量(mg/L)与消光系数计数的结果如下:尿汞含量x 2 4 6 8 10 消光系数y 64 138 205 285 360 若y与x具有线性相关关系,则线性回归方程是________________.7.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,算得数据如下:101022x=55,y=91.7,x=38 500,y =87 777,iii1i1==1xy=55 950.则y与x的相关系数约为______.(保留四位有效数字) iii1=^8.若线性回归方程中的回归系数b =0,则相关系数r等于________.9.某产品的广告费用x与销售额y的统计数据如下表:广告费用x(万元) 4 2 3 5 销售额y(万元) 49 26 39 54 ^^^^根据上表可得线性回归方程y =b x+a 中的b 为9.4,据此模型预报广告费用为6万元时销售额为________万元.10.在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为: 1 2 3 4 5 价格x 1.4 1.6 1.8 2 2.2 需求量y 12 10 7 5 3 552已知∑xy=62,∑x=16.6. iiii1i1==(1)画出散点图; (2)求出y对x的线性回归方程;(3)如果价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t).11.一机器可以按各种不同的速度运转,其生产物有一些会有缺点,每小时生产有缺点物件的个数随机器运转速度而变化,用x表示转速(单位:转/秒),用y表示每小时生产的有缺点物件的个数,现观测得到(x,y)的4组观测值为(8,5),(12,8),(14,9),(16,11).(1)假定y与x之间有线性相关关系,求y对x的线性回归方程;(2)若实际生产中所容许的每小时最大有缺点物件数为10,则机器的速度不得超过多少转/秒.(精确到1转/秒) 三、探究与拓展12.某运动员训练次数与运动成绩之间的数据关系如下:次数(x) 30 33 35 37 39 44 46 50 成绩(y) 30 34 37 39 42 46 48 51 (1)作出散点图; (2)求出线性回归方程;(3)进行相关性检验;(4)试预测该运动员训练47次及55次的成绩.答案1.③⑤ 2.①③ 3.①②③ 4.(2.5,4) ^5.② 6.y =-11.3+36.95x 7.0.999 8 8.0 9.65.5 10.解 (1)散点图如下图所示: 1(2)因为x=×9=1.8,51y=×37=7.4,5552∑xy=62,∑x=16.6, iiii1i1==5∑xy-5xy^iii1=所以b = 522∑x-5xii1=62-5×1.8×7.4==-11.5,216.6-5×1.8^^ a =y-b x=7.4+11.5×1.8=28.1, ^故y对x的线性回归方程为y =28.1-11.5x. ^(3)y =28.1-11.5×1.9=6.25(t).故价格定为1.9万元,预测需求量大约为6.25 t. ^^^11.解(1)设线性回归方程为y =b x+a ,x=12.5,y=8.25,442∑x=660,∑xy=438. iiii1i1==^438-4×12.5×8.2525.5于是b ==235660-4×12.551=,70^^513351256 a =y-b x=8.25-×12.5=-×=-. 7047027^516∴所求的线性回归方程为y =x-. 707^516(2)由y =x-≤10,707760得x≤≈15,51即机器速度不得超过15转/秒.12.解(1)作出该运动员训练次数(x)与成绩(y)之间的散点图,如下图所示,由散点图可知,它们之间具有线性相关关系.(2)列表计算:22次数x 成绩y x y xy iiiiii30 30 900 900 900 33 34 1 089 1 156 1 122 35 37 1 225 1 369 1 295 37 39 1 369 1 521 1 443 39 42 1 521 1 764 1 638 44 46 1 936 2 116 2 024 46 48 2 116 2 304 2 208 50 51 2 500 2 601 2 550 由上表可求得x=39.25,y=40.875,82∑x=12 656,ii1=882∑y=13 731,∑xy=13 180,iiii1i1==8∑xy-8x y^iii1=∴b =≈1.041 5,822∑x-ii1=^^a =y-b x=-0.003 88,^∴线性回归方程为y =1.041 5x-0.003 88. (3)计算相关系数r=0.992 7>r=0.707,因此有95%的把握认为运动员的成绩和训练次数有0.05关. (4)由上述分析可知,我们可用回归方程^y =1.041 5x-0.003 88 作为该运动员成绩的预报值.将x =47和x=55分别代入该方程可得y=49和y=57.故预测该运动员训练47次和55次的成绩分别为49和57.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.1.3 推理案例赏析
一、基础过关
1.有两种花色的正六边形地板砖,按下面的规律拼成若干个图案,则第6个图案中有底纹的正六边形的个数是________.
2.观察下列不等式:1>12,1+12+13>1,1+12+13+…+17>32,1+12+13+…+115>2,1+12+13
+…+131>52
,… 由此猜测第n 个等式为______________(n ∈N *).
3.已知数列{a n }的前n 项和为S n ,且S n =n 2+1.则此数列的前4项分别为a 1=______,a 2=________,a 3=________,a 4=________.据此猜测,数列{a n }的通项公式为a n = ________________________________________________________________________.
4.正方形ABCD 中,对角线AC ⊥BD .运用类比的方法,猜想正方体ABCD —A 1B 1C 1D 1中,相关结论:________________________.
5.如果函数f (x )是奇函数,那么f (0)=0.因为函数f (x )=1x
是奇函数,所以f (0)=0.这段演绎推理错误的原因是______________.
二、能力提升
6.已知△ABC 中,AD ⊥BC 于D ,三边是a ,b ,c ,则有a =c cos B +b cos C ;类比上述推理结论,写出下列条件下的结论:四面体P —ABC 中,△ABC ,△P AB ,△PBC ,△PCA 的面积分别是S ,S 1,S 2,S 3,二面角P —AB —C ,P —BC —A ,P —AC —B 的度数分别是α,β,γ,则S =__________________________________________________________.
7.已知等式:(tan 5°+1)(tan 40°+1)=2;
(tan 15°+1)(tan 30°+1)=2;
(tan 25°+1)(tan 20°+1)=2;
据此可猜想出一个一般性命题:____________________________________________.
8.设M 是具有以下性质的函数f (x )的全体:对于任意s >0,t >0,都有f (s )+f (t )<f (s +t ).给出函数f 1(x )=log 2x ,f 2(x )=2x -1.下列判断正确的是________.
①f 1(x )∈M ;②f 1(x )∉M ;
③f 2(x )∈M ;④f 2(x )∉M .
9.已知命题:平面直角坐标系xOy 中,△ABC 的顶点A (-p,0)和C (p,0),顶点B 在椭圆x 2
m 2+y 2n 2=1 (m >n >0,p =m 2-n 2)上,椭圆的离心率是e ,则sin A +sin C sin B =1e .
将该命题类比到双曲线中,给出一个命题:__________________________________ ________________________________________________________________________. 10.已知等式:3tan 30°·tan 30°+tan 30°+tan 30°=3,
3tan 20°·tan 40°+tan 20°+tan 40°=3,
3tan 15°·tan 45°+tan 15°+tan 45°= 3.
据此猜想出一个一般性命题,并证明你的猜想.
11.在平面中有命题:等腰三角形底边上任一点到两腰距离之和等于一腰上的高.把此结论类比到空间的正三棱锥,猜想并证明相关结论.
三、探究与拓展
12.记S n为数列{a n}的前n项和,给出两个数列:
(Ⅰ)5,3,1,-1,-3,-5,-7,…
(Ⅱ)-14,-10,-6,-2,2,6,10,14,18,…
(1)对于数列(Ⅰ),计算S1,S2,S4,S5;
对于数列(Ⅱ),计算S1,S3,S5,S7;
(2)根据上述结果,对于存在正整数k,满足a k+a k+1=0的这一类等差数列{a n}的和的规
律,猜想一个正确的结论,并加以说明.
答案
1.31
2.1+12+13+…+12n -1>n 2
3.2 3 5 7 ⎩⎪⎨⎪⎧
2, n =12n -1, n ≥2 4.对角面AA 1C 1C ⊥BB 1D 1D
5.大前提错误
6.S 1cos α+S 2cos β+S 3cos γ
7.(tan α+1)[tan(45°-α)+1]=2
8.②③
9.平面直角坐标系xOy 中,△ABC 的顶点A (-p,0)和C (p,0),顶点B 在双曲线x 2m 2-y 2
n 2=1 (m ,n >0,p =m 2+n 2)上,双曲线的离心率为e ,则|sin A -sin C |sin B =1e
10.解 猜想:3tan α·tan β+tan α+tan β=3,其中α+β=60°.
证明:∵tan(α+β)=tan α+tan β1-tan α·tan β
, 即3=tan α+tan β1-tan α·tan β
. 整理,得3tan α·tan β+tan α+tan β= 3.
11.解 猜想结论:正三棱锥底面上任一点到三个侧面的距离之和等于以侧面为底时三棱锥的高.
证明如下:设P 为正三棱锥A —BCD 底面上任一点,点P 到平面ABC 、ACD 、ABD 的距离分别为h 1、h 2、h 3,以侧面ABC 为底时对应的高为h ,则:
V P —ABC +V P —ACD +V P —ABD =V D —ABC .
即:13S △ABC ·h 1+13S △ACD ·h 2+13
S △ABD ·h 3 =13
S △ABC ·h . ∵S △ABC =S △ACD =S △ABD
∴h 1+h 2+h 3=h ,此即要证的结论.
12.解 (1)对于数列(Ⅰ),S 1=S 5=5,S 2=S 4=8;
对于数列(Ⅱ),S 1=S 7=-14,S 3=S 5=-30.
(2)对于等差数列{a n },当a k +a k +1=0时,
猜想S n =S 2k -n (n ≤2k ,n ,k ∈N *).
下面给出证明:
设等差数列{a n }的前项为a 1,公差为d . ∵a k +a k +1=0,∴a 1+(k -1)d +a 1+kd =0, ∴2a 1=(1-2k )d .
又S 2k -n -S n =(2k -n )a 1+(2k -n )(2k -n -1)2d -na 1-n (n -1)2
d =[(k -n )(1-2k )+2k -n 2k -n -1 2-n n -1 2
]d =0. ∴S 2k -n =S n ,猜想正确.。
