MSA(线性)分析
新版MSA线性

RL/QR-C0611 年 月 日
计算并绘图
表格制作:杨清松 2005年2月14日
0偏倚线 ta是否小于 tb是否小于 0.5 拟合优度 或等于 大于0.8 是否在置 或等于 线性判定 tgm-2,1-a/3 0.4 信区间内 tgm-2,1-a/2 0.3
0.2
FALSE
#DIV/0!
#NUM!
#NUM!
0.1 0 0 2 4 6 参考值 8 10 12
结论
#DIV/0!
评价人/日期
测量系统分析 MSA 线性分析
量具名称/编号: 基准值 零件数(g) 1 2 3 4 5 测 量 次 数 (m) 6 7 8 9 10 11 12 13 14 15 零件平均值 基准值 偏倚 极差 m 0 g 0 a #DIV/0! #DIV/0! 0 #DIV/0! 0 b #DIV/0! 0 #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! 0 #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! 0 #DIV/0! 0 Y=aX+b
2
tgm-2,1-α #NUM! b∑Yi
/2
ta
tb
1.194363 0.501485 a∑XiYi Xbar
偏倚平均值24.0692 #DIV/0! 95%置信区间上限 95%置信区间下限
参考值Xi 0 1 i #DIV/0! 偏倚均值Y 0.9 上限
0.8 下限
0 线性图 #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
MSA线性分析报告

MSA线性分析报告一、背景介绍MSA(Measurement System Analysis)是衡量一个测量系统可靠性和准确性的一种分析方法。
线性分析是MSA的一种常用方法,用于评估测量系统在不同测量条件下的偏差和重复性。
本报告对测量系统进行了线性分析,旨在评估该测量系统的稳定性和可靠性。
二、实验设计本次实验选择了20个随机样本点,并在不同的测量条件下对这些样本进行了测量。
实验中,测量条件包括不同的测量设备、不同的操作人员和不同的测试时间。
三、数据收集在实验中,我们记录了每个测量点的测量结果,并根据不同的测量条件进行了分类。
在统计过程中,我们忽略了任何测量超过正常范围的数据。
四、数据处理我们首先对每个测量条件下的测量结果进行了平均计算,然后计算了每个测量条件下的平均值、偏差和方差。
接下来,我们使用Shewhart控制图对测量系统的稳定性进行了分析,用于检测任何特殊原因变异。
五、结果分析1.平均值分析:通过对不同测量条件下的平均值进行分析,发现测量设备A的平均值为10.25,测量设备B的平均值为10.45,测量设备C的平均值为10.35、由此可见,不同的测量设备在测量结果上存在一定的差异。
2.偏差分析:我们计算了每个测量条件下的偏差,并对其进行了平均。
结果显示,测量设备A的偏差为0.25,测量设备B的偏差为0.15,测量设备C的偏差为0.20。
根据偏差分析结果,测量设备B的偏差最小,表明其测量结果相对更加准确。
3.方差分析:方差分析是评估测量系统重复性的一种方法。
我们计算了每个测量条件下的方差,并对其进行了平均。
结果显示,测量设备A的方差为0.10,测量设备B的方差为0.08,测量设备C的方差为0.12、根据方差分析结果,测量设备B的重复性最好,表明其测量结果具有较高的可靠性。
4.控制图分析:我们使用Shewhart控制图对测量系统的稳定性进行了评估。
控制图显示,测量设备A和测量设备B在样本均值上呈稳定的趋势,但测量设备C的样本均值存在一定的波动。
MSA测量系统线性分析报告

MSA测量系统线性分析报告测量系统分析(MSA)是一种评估和验证测量系统能力的方法,用于确保使用的测量设备和方法是准确和可靠的。
线性分析是MSA的一种方法,用于评估测量系统的线性性能。
本报告将对我们使用的测量系统进行线性分析,并评估其可靠性和准确性。
在进行线性分析之前,我们首先选择了一组参考物件,这些参考物件涵盖了我们使用测量系统的范围。
接下来,我们使用该测量系统对这些参考物件进行测量,并记录了测量结果。
我们重复了一定次数的测量,在不同条件下进行了多次测量,以考察测量系统的稳定性。
下面是我们的线性分析结果:1.线性度评估:我们对测量结果进行了回归分析,以确定测量系统的线性度。
通过绘制回归线并计算其斜率和截距,我们可以得出结论测量系统相对于参考物体的线性度良好。
我们还计算了线性度指标R-square,用于衡量回归方程的拟合程度。
大于等于0.95的R-square值表示测量系统的线性度较好,我们的测量系统达到了这个标准。
2.斜率稳定性:为了评估测量系统的斜率稳定性,我们分析了在不同时间点、不同测量人员和不同测量条件下的测量结果,并计算了它们的标准差。
通过比较标准差,我们可以判断测量系统的斜率稳定性。
较小的标准差表示测量系统的斜率较为稳定。
根据我们的分析,测量系统的斜率稳定性得到了验证。
3.截距稳定性:我们还评估了测量系统的截距稳定性。
通过分析在不同条件下的截距差异,我们可以评估测量系统的稳定性。
较小的截距差异表示系统的截距较为稳定。
根据我们的分析,测量系统的截距稳定性也得到了验证。
4.线性系统鉴别能力:为了评估测量系统的线性系统鉴别能力,我们进行了线性系统鉴别实验。
我们选择了一组具有已知线性关系的物体,并对其进行测量。
然后,我们通过计算测量值与实际值之间的误差,来评估测量系统的鉴别能力。
较小的误差表示测量系统能够准确地鉴别线性关系。
我们的测量系统在线性系统鉴别能力方面表现良好。
综上所述,我们的测量系统通过线性分析表明其具有良好的线性度、斜率稳定性、截距稳定性和线性系统鉴别能力。
MSA线性分析报告

0 平均值 #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
0
(xi-
(xi-
x)
x)
xi yi 上限
0
0
0
0
0
0
0
0
0
0
0
#VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE!
零偏倚
0
0
0
0
0
0
0
0
0
0
0
1 yi 0.9 0.8 0.7 0.6
线性研究图示法
名称 表达式 计算值
斜率 中心 偏差
拟合优度
a = #VALUE! b = #DIV/0! s = #DIV/0! R2 = #VALUE!
0.5
H:a=0 t a = #VALUE!
0.4
H:b=0 t b = #DIV/0!
0.3
t = gm-2 , 1 - a / 2
#NUM!
0.2
判定标准
0.1
1) 如果“偏倚=0”的整个
0
xi 直线都位于置信度区间内,
0
0
0
0
0
0
0
0
0
0
0
则该测量系统的线性是可以
零偏倚
Yi
上限
下限
接受的。 2) 如果图示法表示该测量
评价:
系统可接受,则假设H: a=0 (斜率=0)应该为真 , 当 ta ≤ t gm-2 , 1 - a / 2 时则不能被否定; 3) 如果以上假设为真 , 则测 量相系同统的对偏所倚有,这的个参偏考移值必具须有 为
【MSA】确定线性的指南

【MSA】线性(Linearity)线性是在测量设备预期的工作(测量)量程内,偏倚值的差异。
线性可被视为偏倚对于量程大小不同所发生的变化。
注意:不可接受的线性会增添不同结果。
不要假设偏倚是不变的。
造成线性误差的可能原因如下:●仪器需要校准,缩短校准周期●仪器、设备或夹具的磨损●维护保养不好—空气、动力、液体、过滤器、腐蚀、尘土、清洁●基准的磨损或损坏,基准的误差—最小/ 最大●不适当的校准(没有涵盖操作范围)或使用基准设定●仪器质量不好—设计或符合性●缺乏稳健的仪器设计或方法●应用了错误的量具●不同的测量方法—作业准备、载入、夹紧、技巧●随着测量尺寸不同,(量具或零件)变形量不同●环境—温度、湿度、振动、清洁●错误的假设,应用的常数不对●应用—零件数量、位置、操作者技能、疲劳、观测误差(易读性、视差)如果测量设备存偏差,把每一个范围内刻度做一张对照表,配合使用。
当然前提是稳定性比较好。
【MSA】确定线性的指南进行研究可使用以下指南进行线性评价:1)由于存在过程变差,选择g≥5个零件,使这测量涵盖这量具的整个工作量程。
2)对每个零件进行全尺寸测量,从而确定其参考值,并确定涵盖了这量具的工作量程。
3)让经常使用该量具的操作者测量每个零件m≥10次。
V要随机的选择零件,从而减少评价者对测量中偏倚的“记忆”。
结果分析-图示法4)计算零件每次测量的偏倚,以及每个零件的偏倚平均值。
5)在线性图上画出相对于参考值的每个偏倚及偏倚平均值。
(参见图II-B 3)6)应用以下公式,计算并画出最适合的线及该线的置信度区间。
对最适合的线,用公式:式中以及σ重复性=S按下式计算,确定重复性是否可接受%EV= 100 [EV/TV] =100[σ重复性/TV]这里的总变差(TV)是基于预期的过程变差(首选)或规格范围除以6。
( 见下面的GRR研究)如果%EV是大的(详情见第二章,第D节),那么这个测量系统的变差不可接受,因为偏倚分析中假设重复性是可接受的,所以继续对一个%EV值大的测量系统进行分析会导致误导与混淆的结果。
测量系统分析MSA(偏倚、线性、稳定性、GAA)学习资料
-0.010 0.870 0.010 1.050
0.010 0.850 -0.010 1.040
-0.003 0.865 0.005 1.045
偏移 0.010
0.000 -0.050 -0.030 -0.010 -0.010 0.000 0.000 0.010 -0.010 0.030 0.000 -0.010 0.000 -0.010 -0.005
偏移
量測系統線性
0.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 -0.1 -0.1
0.000
0.200
0.400
y = -0.0063x + 0.0056 0.600 0.800 1.000 1.200
基準值
迴歸統計
回歸式
R 平方 調整的 R 平方 標準誤 觀察值個數
1.130 量測值
1.120
1.140 1.090 1.130 1.130 1.140 1.150 1.110 1.120 1.140 1.130 1.110 1.140 1.150 1.170 1.131
偏移 -0.010
0.010 -0.040 0.000 0.000 0.010 0.020 -0.020 -0.010 0.010 0.000 -0.020 0.010 0.020 0.040 0.001
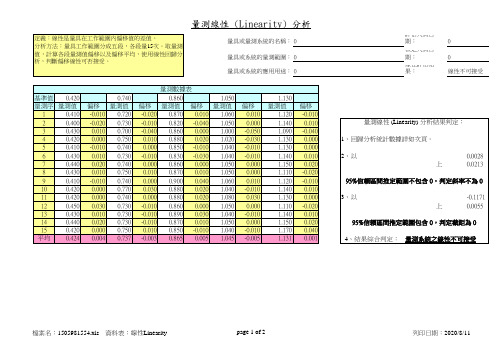
量測線性 (Linearity) 分析
定義:線性是量具在工作範圍內偏移值的差值。 分析方法:量具工作範圍分成五段,各段量15次。取量測 值,計算各段量測值偏移以及偏移平均,使用線性回歸分 析,判斷偏移線性可否接受。
量具或量測系統的名稱: 0 量具或系統的量測範圍: 0 量具或系統的應用用途: 0
MSA线性研究测量报告

MSA线性研究测量报告一、引言测量系统分析(MSA)是确保测量过程稳定、可重复和准确的一种方法。
线性研究是一种MSA方法,用于评估测量系统的线性度。
本报告旨在通过对一些测量系统进行线性研究,评估其线性度。
二、方法1.样品选择:选择一组20个样品,每个样品有不同的已知值(称作参考值)。
确保样品的值分布均匀,覆盖整个测量范围。
2.测量过程:使用待测试的测量系统对每个样品进行测量,记录测量结果。
3.数据处理:计算每个样品的测量误差,即测量结果与参考值之间的差异。
4.统计分析:将测量误差按样品进行分组,计算每组的平均值和标准差。
5.绘制散点图:将每个样品的测量误差绘制成散点图,其中x轴表示参考值,y轴表示测量误差。
6.直线回归分析:对散点图进行直线回归分析,计算回归方程的斜率和截距。
7.判断线性度:根据回归方程的斜率和截距,判断测量系统的线性度。
如果斜率接近于1且截距接近于0,则说明测量系统具有较好的线性度。
三、结果1.数据处理:计算20个样品的测量误差,并将其按样品进行分组。
计算每组的平均值和标准差。
结果如下表所示:样品编号,参考值(单位),测量误差(单位)-------,-----------,-------1,10.0,-0.12,15.5,0.23,20.0,0.04,25.5,0.35,30.0,-0.26,35.5,-0.17,40.0,0.18,45.5,-0.29,50.0,0.110,55.5,0.011,60.0,-0.112,65.5,0.213,70.0,0.114,75.5,0.315,80.0,-0.216,85.5,-0.117,90.0,-0.118,95.5,0.219,100.0,0.020,105.5,-0.2平均值:0.03标准差:0.14[散点图]3.直线回归分析:对散点图进行直线回归分析,得到回归方程为y=0.99x+0.0154.判断线性度:根据回归方程的斜率和截距,该测量系统具有较好的线性度,斜率接近于1,截距接近于0。
Msa线性分析报告

Msa线性分析报告一、引言Msa线性分析(Measurement Systems Analysis)是一种用于评估测量系统准确性和可重复性的方法。
在许多行业中,准确的测量是确保产品质量和过程控制的关键因素。
通过进行Msa线性分析,可以了解测量系统的偏差、稳定性和重复性等指标,进而帮助生产过程的改进和优化。
二、测量系统分析目的Msa线性分析的目的在于评估测量系统的能力,确定其是否能够提供准确和可靠的测量结果。
通过分析测量系统的变异性,可以判断测量误差的来源,避免产生误导性的测量结果。
具体而言,Msa线性分析可达到以下目标:1.评估测量系统的稳定性:确定测量系统的变异程度,判断其是否存在明显的漂移或不稳定的情况。
2.评估测量系统的重复性:确定测量值的重复性,即在相同条件下进行多次测量的结果是否相近。
3.评估测量系统的偏差:确定测量系统的系统性偏差,即测量结果与实际值之间的差异。
4.评估测量系统的线性:确定测量系统的线性关系,即测量结果是否与被测量对象的实际值成比例。
三、Msa线性分析方法Msa线性分析通常采用以下步骤进行:1. 收集数据首先,需要收集足够数量的测量数据,以便对测量系统进行分析。
这些数据可以来自于实际的生产环境或者实验室测试,确保数据的多样性和代表性。
2. 数据处理在收集好数据后,需要对数据进行处理,以便进行后续的分析。
常用的数据处理方法包括:•数据清洗:去除异常值和不符合实际情况的数据。
•数据平滑:采用滑动平均或其他平滑方法,消除数据中的噪声和波动。
•数据转换:对数据进行转换,以符合分析模型的要求。
3. Msa线性分析在数据处理完成后,可以进行Msa线性分析的具体步骤。
以下是常用的分析方法:a. 方差分析(ANOVA)方差分析是一种常用的统计方法,用于比较不同因素对测量系统变异性的影响。
通过方差分析,可以确定测量系统的不确定性来源,例如操作员、设备、环境等因素,进而优化测量系统。
b. 回归分析回归分析可以用来评估测量系统的线性关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
100.18 0.14 148.16 0.08
次 8 5.02
-0.1
26.84
0.03
58.84
0.02
100.1
0.06 148.18
0.1
数9
5.02
-0.1
26.84
0.03
58.82
0
100.08 0.04 148.16 0.08
(m)
10 5.04 -0.08 26.82 0.01 58.84 0.02 100.08 0.04 148.14 0.06
0.02 100.08 0.04 148.18
0.1
5 5.04 -0.08 26.85 0.04 58.82
0
100.14 0.1 148.16 0.08
6
5
-0.12 26.86 0.05 58.84 0.02 100.14 0.1 148.18 0.1
测
量7
5
-0.12 26.86 0.05 58.82
100.1
0.06 148.18
0.1
2 5.04 -0.08 26.84 0.03 58.86 0.04 100.08 0.04 148.16 0.08
3 5.02
-0.1
26.84
0.03
58.84
0.02
100.1
0.06 148.14 0.06
4 5.02
-0.1
26.82
0.01
58.84
58.82
0
58.836
58.82
0.016
0.04
100.14 0.1 100.1066667 100.04 0.066666667 0.1
148.16 0.08 148.1626667 148.08 0.082666667 0.04
mg
a
b
Y=aX+b
R2
α
S
tgm-2,1-α/2
ta
tb
15 5 0.00106 -0.05409 Y=0.00106X-0.05409 80.84% 0.05 0.05926 1.993 1.19436 0.50148
14 5.02
-0.1
26.86
0.05
58.84
0.02 100.08 0.04 148.18
0.1
15 零件平均值
基准值 偏倚 极差
5.04 -0.08 5.017333333
5.12 -0.102666667
0.06
Байду номын сангаас
26.82 0.01 26.83666667 26.81 0.026666667 0.04
11 4.98 -0.14 26.82 0.01 58.82
0
100.1 0.06 148.18 0.1
12 4.98 -0.14 26.84 0.03 58.86 0.04 100.1 0.06 148.14 0.06
13 5.02
-0.1
26.82
0.01
58.84
0.02
100.1
0.06 148.14 0.06
测量系统分析 MSA 线性分析
DEF/QER-2113/A0
量具 名称/
基准值
卡尺 N-01-35
量具规 格:
5.12
26.81
0-150mm 58.82
操作人: 100.04
148.08
零件数(g)
1
读数
偏倚
2
读数
偏倚
3
读数
偏倚
4
读数
偏倚
5
读数
偏倚
1 5.02
-0.1
26.82
0.01
58.84
0.02
小于 0
线性0 判定
TRUE
拟合优度 大于0.8
TRUE 0偏倚线 2是0 否在置 信区间内
TRUE ta是否小于 4或0 等于
tgm-2,1-a/2
TRUE tb是否小于
或60等于 tgm-2,1-a/3
-0.5 TRUE TRUE TRUE TRUE
TRUE TRUE
80
y = 0.001t1ax=mm- /s0e.05401.00106 -0.05409 tb=b/seb 0.0004 0.03405
sem
seb
100
120
140
160
-1
-1.5
结论
参考值
线性可以接受
评价人/日期
1.13394
计算参数 ∑(XiXbar)2
-0.57946 -0.92769
201.926
b∑Yi -0.00483
m
a∑XiYi Xbar
0.偏02倚1平2均8 值 24.0692
95%置信区间上限
95%置信区间下限
线性b (偏倚平均值)
偏倚
上限 0大下.5于 限
TRUE
TRUE
TRUE
TRUE
参考
1偏值.5倚Xi 均值
5.12 -0.10267
上限 0.10943
下限1 -0.20674
26.81 0.02667 0.00093 -0.05217
58.82 0.016 0.29752 -0.2808
100.04 线1性48图.08
∑Yi2
0.06667 0.08267
0.02279
0.68371
