高中数学培优试题精选集5
高中数学培优试题及答案

高中数学培优试题及答案一、选择题(每题5分,共20分)1. 若函数f(x)=2x^2-4x+3,求f(2)的值为:A. 1B. 3C. 5D. 7答案:B2. 已知等差数列{an}的首项a1=3,公差d=2,求第10项a10的值:A. 23B. 27C. 29D. 31答案:A3. 计算下列定积分的值:∫(0,2) (x^2 - 3x + 2) dx:A. 0B. 4C. 6D. 8答案:C4. 若复数z满足|z-1|=2,则z的模长|z|的最小值为:A. 1B. √3C. 2D. √5答案:B二、填空题(每题5分,共20分)5. 函数y=x^3-3x^2+4x-5的极值点个数为_______。
答案:26. 一个圆的半径为5,圆心在原点,求该圆的面积为_______。
答案:25π7. 已知函数f(x)=x^2-2x+1,求f(x)的对称轴方程为_______。
答案:x=18. 若直线y=3x+2与抛物线y^2=4x相交于点A和B,求线段AB的中点坐标为_______。
答案:(1, 5/3)三、解答题(每题15分,共30分)9. 已知等比数列{bn}的前三项依次为b1=2,b2=4,b3=8,求该数列的通项公式。
答案:bn=2^n10. 已知函数f(x)=x^3-3x^2+2x+1,求函数f(x)的单调递增区间。
答案:(-∞, 1)和(2, +∞)四、证明题(每题15分,共15分)11. 证明:若a, b, c为实数,且满足a^2+b^2+c^2=1,则(a+b+c)^2≤3。
答案:证明如下:由柯西-施瓦茨不等式可知,对于任意实数a, b, c有(a^2+b^2+c^2)(1^2+1^2+1^2)≥(a+b+c)^2,即(a^2+b^2+c^2)(3)≥(a+b+c)^2。
又因为a^2+b^2+c^2=1,所以(a+b+c)^2≤3。
五、应用题(每题15分,共15分)12. 某商场进行促销活动,规定顾客每消费满100元即可获得一张优惠券,每张优惠券可以抵用10元。
高三数学理科培优班综合测试卷五试题

汤阴一中2021届高三数学理科培优班综合测试卷五制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日一. 选择题〔本大题一一共12小题,每一小题5分,一共60分〕1. 假设集合{}{}P x x Q y y =≤≤=≤≤0402,,那么以下对应中,不是从P 到Q 的映射的是〔 〕 A y x B y x C y x D y x ....====121318232.a b a b a b b ==⊥+-→→→2332,||,,且与λα也互相垂直,那么λ的值是〔 〕 A B C D ....-±32323213. 数列{}a n 的前n 项和S n n n N n =-∈532()*那么n ≥2时有〔 〕A S na naB S na naC na S naD na S na n n n n n n n n ....>><<>><<11114. 双曲线C x a y b C y b x aa b 12222222221100::()-=-=>>,,,连结C 1,C 2的四个顶点的四边形的面积为S 1,连结C 1,C 2的四个焦点的四边形面积为S 2,那么S S 12的最大值为〔 〕 A. 2 B. 4 C.14 D. 125. 如下图是一批产品中抽样得到数据的频率直方图,由图可看出概率最大时数据所在的范围是〔 〕A. 〔,〕B. 〔,〕C. 〔,〕D. 〔,〕频率 组距8.1 8.2 8.3 8.4 8.5 8.6 8.7 数据6. 平面直角坐标系中,O 为坐标原点,A 〔3,1〕,B 〔-1,3〕假设点C 满足→→→+=OB OA OC βα,其中α、R ∈β,且1=+βα,那么点C 的轨迹方程为〔 〕A. 01123=-+y xB. 5)2()1(22=-+-y x C. 02=-y x D. 052=-+y x7. 9)222(-x的展开式的第7项为421,那么)(lim 2n n x x x +++∞→ 的值是〔 〕A.41 B. 43 C. 41- D. 21 8. 如下图正方体1111D C B A ABCD -中,O 是底面ABCD 的中心,M 、N 分别是棱1DD ,11C D 的中点,那么直线OM 〔 〕A. 是AC 和MN 的公垂线B. 垂直于AC ,但不垂直于MNC. 垂直于MN ,但不垂直于ACD. 与MN 、AC 都不垂直9. 设函数)(x f 在定义域内可导,)(x f y =图象如下图,那么导函数y f x ='()的图象可能为〔 〕10. 定义在R 上的函数)(x f 对于任意x 都有)(1)(1)2(x f x f x f -+=+成立,设)(n f a n =,问数列{}n a 中值不同的项最多为〔 〕 A. 4项 B. 6项 C. 8项 D. 无法确定 11. 函数)2cos()2sin()(ππ++=x x x f ,假设对于任意R x ∈,都有)()(0x f x f ≥成立,那么0x 的一个可能值是〔 〕 A.2πB. 2π-C. 4π D. 4π-12. 使不等式)0,1(11-∈+>+x x ax 在时恒成立,那么a 的取值范围是〔 〕 A. {1} B. (0, 1) C. [0, 1] D. (∞-,1 ]二. 填空题〔本大题一一共4小题,每一小题4分,一共16分〕13. 设⎩⎨⎧>+≤-==→)1(4)1(2)(,5)(lim 21x bx x ax x f x f x 而那么直线0=++c by ax 的倾斜角为_____________。
高三数学 数学数列多选题的专项培优练习题(含答案

高三数学 数学数列多选题的专项培优练习题(含答案一、数列多选题1.已知数列{}n a 的前n 项和为n S ,前n 项积为n T ,0n a ≠,且202021111212a a ++≤+( )A .若数列{}n a 为等差数列,则20210S ≥B .若数列{}n a 为等差数列,则10110a ≤C .若数列{}n a 为等比数列,则20200T >D .若数列{}n a 为等比数列,则20200a <【答案】AC 【分析】由不等关系式,构造11()212xf x =-+,易得()f x 在R 上单调递减且为奇函数,即有220200a a +≥,讨论{}n a 为等差数列、等比数列,结合等差、等比的性质判断项、前n 项和或积的符号即可. 【详解】 由202021111212a a ++≤+,得2020211110212212a a +-+-≤+, 令11()212x f x =-+,则()f x 在R 上单调递减,而1121()212212xx x f x --=-=-++, ∴12()()102121xx x f x f x -+=+-=++,即()f x 为奇函数,∴220200a a +≥,当{}n a 为等差数列,22020101120a a a +=≥,即10110a ≥,且2202020212021()02a a S +=≥,故A 正确,B 错误;当{}n a 为等比数列,201820202a a q=,显然22020,a a 同号,若20200a <,则220200a a +<与上述结论矛盾且0n a ≠,所以前2020项都为正项,则202012020...0T a a =⋅⋅>,故C 正确,D 错误. 故选:AC. 【点睛】关键点点睛:利用已知构造函数,并确定其单调性和奇偶性,进而得到220200a a +≥,基于该不等关系,讨论{}n a 为等差、等比数列时项、前n 项和、前n 项积的符号.2.设n S 是公差为()d d ≠0的无穷等差数列{}n a 的前n 项和,则下列命题正确的是( ) A .若0d <,则数列{}n S 有最大项 B .若数列{}n S 有最大项,则0d <C .若对任意*n N ∈,均有0n S >,则数列{}n S 是递增数列D .若数列{}n S 是递增数列,则对任意*n N ∈,均有0n S > 【答案】ABC 【分析】由等差数列的求和公式可得()2111222n n n d d S na d n a n -⎛⎫=+=+- ⎪⎝⎭,可看作关于n 的二次函数,由二次函数的性质逐个选项验证可得. 【详解】由等差数列的求和公式可得()2111222n n n d d S na d n a n -⎛⎫=+=+- ⎪⎝⎭, 选项A ,若0d <,由二次函数的性质可得数列{}n S 有最大项,故正确; 选项B ,若数列{}n S 有最大项,则对应抛物线开口向下,则有0d <,故正确; 选项C ,若对任意*n ∈N ,均有0n S >,对应抛物线开口向上,0d >, 可得数列{}n S 是递增数列,故正确;选项D ,若数列{}n S 是递增数列,则对应抛物线开口向上, 但不一定有任意*n ∈N ,均有0n S >,故错误. 故选:ABC . 【点睛】本题考查等差数列的求和公式的应用,()2111222n n n d d S na d n a n -⎛⎫=+=+- ⎪⎝⎭可看成是二次函数,然后利用二次函数的性质解决问题,考查分析和转化能力,属于常考题.3.设数列{}{},n n a b 的前n 项和分别为,n n S T ,1121,n n n S S S n++==,且212n n n n a b a a ++=,则下列结论正确的是( ) A .20202020a = B .()12n n n S += C .()112n b n n =-+D .1334n T n ≤-< 【答案】ABD 【分析】可由累乘法求得n S 的通项公式,再由()12n n n S +=得出n a n =,代入212n n n n a b a a ++=中可得()112n b n n =++.由裂项相消法求出n T ,利用数列的单调性证明1334n T n ≤-<.由题意得,12n n S n S n++=, ∴当2n ≥时,121121112n n n n n S S S n n S S S S S n n ---+=⋅⋅⋅⋅⋅=⋅⋅⋅⋅--()13112n n +⋅=,且当1n =时也成立, ∴ ()12n n n S +=,易得n a n =,∴ 20202020a =,故,A B 正确; ∴ ()()()211111112222n n b n n n n n n +⎛⎫==+=+- ⎪+++⎝⎭,∴11111111111111112324351122212n T n n n n n n n n ⎛⎫⎛⎫=+-+-+-++-+-=++-- ⎪ ⎪-++++⎝⎭⎝⎭3111342124n n n n ⎛⎫=+-+<+ ⎪++⎝⎭, 又n T n -随着n 的增加而增加, ∴1113n T n T -≥-=,∴1334n T n ≤-<,C 错误,D 正确, 故选:ABD. 【点睛】使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源与目的.4.已知等差数列{}n a 中,59a a =,公差0d >,则使得前n 项和n S 取得最小值的正整数n 的值是( ) A .5 B .6C .7D .8【答案】BC 【分析】分析出数列{}n a 为单调递增数列,且70a =,由此可得出结论. 【详解】在等差数列{}n a 中,59a a =,公差0d >,则数列{}n a 为递增数列,可得59a a <,59a a ∴=-,可得5975202a a a a +==>,570a a ∴<=,所以,数列{}n a 的前6项均为负数,且70a =, 因此,当6n =或7时,n S 最小. 故选:BC.方法点睛:本题考查等差数列前n 项和最大值的方法如下:(1)利用n S 是关于n 的二次函数,利用二次函数的基本性质可求得结果; (2)解不等式0n a ≥,解出满足此不等式的最大的n 即可找到使得n S 最小.5.已知数列{}n a 的前n 项和为n S ,11a =,且1n n S a λ-=(λ为常数).若数列{}n b 满足2920n n a b n n -+-=,且1n n b b +<,则满足条件的n 的取值可以为( )A .5B .6C .7D .8【答案】AB 【分析】利用11a S =可求得2λ=;利用1n n n a S S -=-可证得数列{}n a 为等比数列,从而得到12n na ,进而得到nb ;利用10nnb b 可得到关于n 的不等式,解不等式求得n 的取值范围,根据n *∈N 求得结果. 【详解】当1n =时,1111a S a λ==-,11λ∴-=,解得:2λ=21n n S a ∴=-当2n ≥且n *∈N 时,1121n n S a --=-1122n n nn n a S S a a ,即:12n n a a -=∴数列{}n a 是以1为首项,2为公比的等比数列,12n na2920n n a b n n =-+-,219202n n n n b --+-∴= ()()222111912092011280222n n n n nn n n n n n b b +--+++--+--+∴-=-=< 20n >,()()21128470n n n n ∴-+=--<,解得:47n <<又n *∈N ,5n ∴=或6 故选:AB 【点睛】关键点点睛:本题考查数列知识的综合应用,涉及到利用n a 与n S 的关系求解通项公式、等比数列通项公式的求解、根据数列的单调性求解参数范围等知识,解决本题的关键点是能够得到n b 的通项公式,进而根据单调性可构造出关于n 的不等式,从而求得结果,考查学生计算能力,属于中档题.6.设首项为1的数列{}n a 的前n 项和为n S ,已知121n n S S n +=+-,则下列结论正确的是( )A .数列{}n a 为等比数列B .数列{}n S n +为等比数列C .数列{}n a 中10511a =D .数列{}2n S 的前n 项和为2224n n n +---【答案】BCD 【分析】 由已知可得11222n n n n S n S nS n S n++++==++,结合等比数列的定义可判断B ;可得2n n S n =-,结合n a 和n S 的关系可求出{}n a 的通项公式,即可判断A ;由{}n a 的通项公式,可判断C ;由分组求和法结合等比数列和等差数列的前n 项和公式即可判断D. 【详解】因为121n n S S n +=+-,所以11222n n n n S n S nS n S n++++==++.又112S +=,所以数列{}n S n +是首项为2,公比为2的等比数列,故B 正确;所以2n n S n +=,则2nn S n =-.当2n ≥时,1121n n n n a S S --=-=-,但11121a -≠-,故A 错误;由当2n ≥时,121n n a -=-可得91021511a =-=,故C 正确;因为1222n n S n +=-,所以2311222...2221222...22n n S S S n ++++=-⨯+-⨯++-()()()23122412122...2212 (22412)2n n n n n n n n n ++--⎡⎤=+++-+++=-+=---⎢⎥-⎣⎦ 所以数列{}2n S 的前n 项和为2224n n n +---,故D 正确. 故选:BCD . 【点睛】关键点点睛:在数列中,根据所给递推关系,得到等差等比数列是重难点,本题由121n n S S n +=+-可有目的性的构造为1122n n S S n n +++=+,进而得到11222n n n n S n S nS n S n++++==++,说明数列{}n S n +是等比数列,这是解决本题的关键所在,考查了推理运算能力,属于中档题,7.在n n n A B C (1,2,3,n =)中,内角,,n n n A B C 的对边分别为,,n n n a b c ,n n n A B C 的面积为n S ,若5n a =,14b =,13c =,且222124n n n a c b ++=,222124n n n a b c ++=,则( ) A .n n n A B C 一定是直角三角形 B .{}n S 为递增数列 C .{}n S 有最大值D .{}n S 有最小值【答案】ABD 【分析】先结合已知条件得到()222211125=252n n n n b c b c +++-+-,进而得到22225=n n n b c a +=,得A 正确,再利用面积公式得到递推关系1221875=644n n S S ++,通过作差法判定数列单调性和最值即可. 【详解】 由222124n n n a c b ++=,222124n n n a b c ++=得,222222112244n n n n n n a c a b bc+++++=+()2221122n n n a b c =++()2225122n n b c =++,故()222211125=252n n n n b c b c +++-+-, 又221125=0b c +-,22250n n b c ∴+-=,22225=n n n b c a ∴+=,故n n n A B C 一定是直角三角形,A 正确;n n n A B C 的面积为12n n n S b c =,而()4222222222221124224416n n n n n n n n n n n n a b c a b c a c a b b c +++++++=⨯=, 故()42222222222111241875161875==1616641n n n n n n n n n n n a b c a b bS S c c S +++++++==+,故22212218751875==6446434n n n n n S S SS S +-+--,又22125=244n n n n n b c b c S +=≤(当且仅当=n n b c 22121875=06344n n n S SS +∴--≥,又由14b =,13c =知n n b c ≠不是恒成立,即212n n S S +>,故1n n S S +>,故{}n S 为递增数列,{}n S 有最小值16=S ,无最大值,故BD 正确,C 错误. 故选:ABD. 【点睛】本题解题关键是利用递推关系得到()222211125=252n n n n b c b c +++-+-,进而得到22225=n n n b c a +=,再逐步突破.数列单调性常用作差法判定,也可以借助于函数单调性判断.8.斐波那契数列,又称黄金分割数列、兔子数列,是数学家列昂多·斐波那契于1202年提出的数列.斐波那契数列为1,1,2,3,5,8,13,21,……,此数列从第3项开始,每一项都等于前两项之和,记该数列为(){}F n ,则(){}F n 的通项公式为( )A .(1)1()2n nF n -+=B .()()()11,2F n F n F n n +=+-≥且()()11,21F F ==C .()n nF n ⎡⎤⎥=-⎥⎝⎭⎝⎭⎦ D .()n n F n ⎡⎤⎥=+⎥⎝⎭⎝⎭⎦【答案】BC 【分析】根据数列的前几项归纳出数列的通项公式,再验证即可; 【详解】解:斐波那契数列为1,1,2,3,5,8,13,21,……,显然()()11,21F F ==,()()()3122F F F =+=,()()()4233F F F =+=,,()()()11,2F n F n F n n +=+-≥,所以()()()11,2F n F n F n n +=+-≥且()()11,21F F ==,即B 满足条件;由()()()11,2F n F n F n n +=+-≥, 所以()()()()11F n n F n n ⎤+-=--⎥⎣⎦所以数列()()1F n n ⎧⎫⎪⎪+⎨⎬⎪⎪⎩⎭为公比的等比数列, 所以()()1nF n n +-=⎝⎭1115()n F F n n -+=+, 令1nn n Fb -=⎝⎭,则11n n b ++, 所以1n n b b +=-,所以n b ⎧⎪⎨⎪⎪⎩⎭以510-所以1n n b -+,所以()1115n n n nF n --⎤⎤⎛⎫+⎥⎥=+=- ⎪ ⎪⎥⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦; 即C 满足条件; 故选:BC 【点睛】考查等比数列的性质和通项公式,数列递推公式的应用,本题运算量较大,难度较大,要求由较高的逻辑思维能力,属于中档题.二、平面向量多选题9.定义空间两个向量的一种运算sin ,a b a b a b ⊗=⋅,则关于空间向量上述运算的以下结论中恒成立的有( ) A .()()a b a b λλ⊗=⊗ B .a b b a ⊗=⊗C .()()()a b c a c b c +⊗=⊗+⊗D .若()11,a x y =,()22,b x y =,则122a b x y x y ⊗=- 【答案】BD 【分析】对于A,B,只需根据定义列出左边和右边的式子即可,对于C,当λab 时,()()1sin ,a b c b c b c λ+⊗=+⋅,()()()sin ,sin,1sin ,a c b c b c b c b c b c b c b c λλ⊗+⊗=⋅+⋅=+⋅,显然不会恒成立. 对于D,根据数量积求出cos ,a b ,再由平方关系求出sin ,a b 的值,代入定义进行化简验证即可. 【详解】解:对于A :()()sin ,a b a b a b λλ⊗=⋅,()sin ,a b a b a bλλλ⊗=⋅,故()()a b a b λλ⊗=⊗不会恒成立;对于B ,sin ,a b a b a b ⊗=⋅,=sin ,b a b a b a ⊗⋅,故a b b a ⊗=⊗恒成立; 对于C ,若λab ,且0λ>,()()1sin ,a b c b c b c λ+⊗=+⋅,()()()sin,sin ,1sin ,a c b c b c b c b c b c b c b c λλ⊗+⊗=⋅+⋅=+⋅,显然()()()a b c a c b c +⊗=⊗+⊗不会恒成立; 对于D ,1212cos ,x x y y a b a b+=⋅,212sin ,1a b a b ⎛ ⎪=- ⎪⋅⎭,即有222121212121x x y y x x y y a b a b a b a a b ⎛⎫⎛⎫++ ⎪⊗=⋅⋅-=⋅- ⎪⎪ ⎪⋅⎭⎭21y =⎪+⎭==1221x y x y =-.则1221a b x y x y ⊗=-恒成立. 故选:BD. 【点睛】本题考查向量的新定义,理解运算法则正确计算是解题的关键,属于较难题.10.数学家欧拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一条直线上,且重心到外心的距离是重心到垂心距离的一半,此直线被称为三角形的欧拉线,该定理则被称为欧拉线定理.设点O 、G 、H 分别是ABC 的外心、重心、垂心,且M 为BC 的中点,则( )A .0GA GB GC ++= B .24AB AC HM MO +=- C .3AH OM =D .OA OB OC ==【答案】ABD 【分析】向量的线性运算结果仍为向量可判断选项A ;由12GO HG =可得23HG HO =,利用向量的线性运算()266AB AC AM GM HM HG +===-,再结合HO HM MO =+集合判断选项B ;利用222AH AG HG GM GO OM =-=-=故选项C 不正确,利用外心的性质可判断选项D ,即可得正确选项. 【详解】因为G 是ABC 的重心,O 是ABC 的外心,H 是ABC 的垂心, 且重心到外心的距离是重心到垂心距离的一半,所以12GO HG =, 对于选项A :因为G 是ABC 的重心,M 为BC 的中点,所以2AG GM =, 又因为2GB GC GM +=,所以GB GC AG +=,即0GA GB GC ++=,故选项A 正确;对于选项B :因为G 是ABC 的重心,M 为BC 的中点,所以2AG GM =,3AM GM =,因为12GO HG =,所以23HG HO =, ()226663AB AC AM GM HM HG HM HO ⎛⎫+===-=- ⎪⎝⎭()646424HM HO HM HM MO HM MO =-=-+=-,即24AB AC HM MO +=-,故选项B 正确;对于选项C :222AH AG HG GM GO OM =-=-=,故选项C 不正确; 对于选项D :设点O 是ABC 的外心,所以点O 到三个顶点距离相等,即OA OB OC ==,故选项D 正确;故选:ABD. 【点睛】关键点点睛:本题解题的关键是利用已知条件12GO HG =得23HG HO =,利用向量的线性运算结合2AG GM =可得出向量间的关系.。
期中试卷】2018年 高中数学 必修5 综合培优卷(含答案)

期中试卷】2018年高中数学必修5 综合培优卷(含答案)2018年高中数学必修5综合培优卷一、选择题:1、已知等差数列{an}的前n项和为Sn,且an=S(n-1),则a1的值是()A。
0.B。
1.C。
2.D。
32、不等式ax2+bx+2>0的解集是(-2.1),则a+b的值是()A。
10.B。
-10.C。
-14.D。
143、在△ABC中,若2cosB∙sinA=sinC,则△ABC的形状一定是()A。
等腰直角三角形。
B。
直角三角形。
C。
等腰三角形。
D。
等边三角形4、在△ABC中,角A,B,C所对的边分别为a,b,c,若b(1-cosC)=c∙cosA,b=2,则△ABC的面积为()A。
1.B。
2.C。
3.D。
45、若实数x,y满足约束条件x+y=1且x2+y2≥1,则z=2x+y的最小值为()A。
2.B。
1.C。
-4.D。
06、已知偶函数f(x)在[0,+∞)单调递减,若f(-2)=0,则满足xf(x-1)>0的x的取值范围是()A。
(-∞,-1)∪(0,3)。
B。
(-1,0)∪(3,+∞)。
C。
(-∞,-1)∪(1,3)。
D。
(-1,0)∪(1,3)7、设x,y满足约束条件x2+y2=1,若目标函数z=ax+3y仅在点(1,0)处取得最小值,则a的取值范围为()A。
(-6,3)。
B。
(-6,-3)。
C。
(0,3)。
D。
(-6,0]8、已知正实数a,b满足a+b=3,则ab的最小值为()A。
1.B。
2.C。
3/2.D。
9/49、在数列{an}中,an+2=1/an+1+2/an,如果a1=1与a2的等比中项,那么a3的值是()A。
1/2.B。
1/3.C。
1/4.D。
1/5,通项公式是an=1/n(n+1)10、设数列{an}满足an+1=3an-2,a1=1,则a3的值是()A。
-1.B。
1.C。
3.D。
5,通项公式是an=2n-111、△ABC的内角A,B,C的所对的边a,b,c成等比数列,且公比为q,则q的取值范围是()A。
高三数学 导数培优专题(含解析)

培优导数专题1、(本大题满分12分) 设函数f (x )=.cos 2sin xx+(Ⅰ)求f (x )的单调区间;(Ⅱ)如果对任何,0≥x 都有f (x )ax ≤,求a 的取值范围. 2.(本小题满分12分)已知.)2()(,02xe ax x xf a -=≥函数(Ⅰ)当x 为何值时,f (x )取得最小值?证明你的结论; (Ⅱ)设)(x f 在[-1,1]上是单调函数,求a 的取值范围.3、已知函数21()ln (1)(0).2f x x ax a x a R a =-+-∈≠且(1)求函数()f x 的单调递增区间;(2)记函数()y F x =的图象为曲线C .设点A (x 1,y 1),B (x 2,y 2)是曲线C 上的不同两点.如果在曲线C 上存在点M (x 0,y 0),使得:①1202x x x +=;②曲线C 在点M 处的切线平行于直线AB ,则称函数F (x )夺在“中值相依切线”, 试问:函数f (x )是否存在“中值相依切线”,请说明理由.4、对于函数()f x ,若存在0x R ∈,使00()f x x =成立,则称0x 为()f x 的不动点。
如果函数2()(,*)x a f x b c N bx c +=∈-有且仅有两个不动点0、2,且1(2)2f -<-。
(1)试求函数()f x 的单调区间;(2)已知各项均为负的数列{}n a 满足1)1(4=nn a f s ,求证:1111ln n n n a n a ++-<<-;(3)设1n nb a =-,n T 为数列{}n b 的前n 项和,求证:201120101ln 2011T T -<<。
5、(12分)设函数f (x ) = x 2+bln (x +1),(1)若对定义域的任意x ,都有f (x )≥f (1)成立,求实数b 的值; (2)若函数f (x )在定义域上是单调函数,求实数b 的取值范围; (3)若b =-1,证明对任意的正整数n ,不等式33311......31211)1(nk f nk ++++∑=π都成立;6、(12分)已知函数)()(R x kx e x f x∈-= (1)若e k =,试确定函数)(x f 的单调区间;(2)若0>k 且对任意R x ∈,0|)(|>x f 恒成立,试确定实数k 的取值范围;(3)设函数)()()(x f x f x F -+=,求证:)()2()()2()1(21*+∈+>⋅N n en F F F nn Λ1解: (I ).)cos 2(1cos 2)cos 2()sin (sin cos )cos 2()(22x x x x x x x x f ++=+--+=' ……2分分是减函数在每一个区间是增函数在每一区间因此即时当即时当6.))(342,322()(,))(322,322()(.0)(,21cos ,)(342322;0)(,21cos ,)(322322ΛΛZ Z Z Z ∈++∈+-<'-<∈+<<+>'->∈+<<-k k k x f k k k x f x f x k k x k x f x k k x k ππππππππππππππππ(II )令则),()(x f ax x g -=.31)31cos 21(3)cos 2(3cos 22)cos 2(1cos 2)(222-+-+=+++-=++-='a x x x a x x a x g故当.)(,0)0()(,0,0)0(.0)(,31ax x f g x g x g x g a ≤=≥≥=≥'≥即时所以当又时[)[).2021)2(,0.3sin cos 2sin )(,)3arccos ,0(,.3sin ,0)0()(,)3arccos ,0(.3arccos ,0)(.0)(,3arccos ,0.3cos )(,3sin )(,310ππ⋅≥>=≤>>+=∈>=>∈>'∈-='-=<<a f a ax xx x x f a x ax x h x h a x a x h x h a x a x x h ax x x h a 有时当时当于是即时故当上单调增加在因此时故当则令时当因此,a 的取值范围是.,31⎪⎭⎫⎢⎣⎡+∞……12分2.解:(I )对函数f (x )求导数,得 .]2)1(2[)22()2()(22xx x e a x a x e a x e ax x x f --+=-+-='令0)(='x f ,得 [x 2+2(1-a )x -2a ]e x =0,从而x 2+2(1-a )x -2a =0.解得 212221,11,11x x a a x a a x <++-=+--=其中,当x 变化时,)(x f ',f (x )的变化如下表:当f (x )在x =x 1处取到极大值,在x =x 2处取到极小值,……………………4分 当a ≥0时,x 1<-1, x 2≥0,f (x )在(x 1 , x 2)为减函数,在(x 2,+ ∞)为增函数.而当x <0时,f (x )=x (x -2a )e x>0;当x =0时,f (x )=0.所以当x =a -1+21a +时, f (x )取得最小值. …………………8分(II )当a ≥0时,f (x )在[-1,1]上单调函数的充要条件是x 2≥1,即a -1+21a +≥1.解得a ≥43;综上:f (x )在[-1,1]上为单调函数的充分必要条件为a ≥43;即a 的取值范围是),43[+∞… 3、解:(Ⅰ) 函数()f x 的定义域是(0,)+∞. ………1分由已知得,1(1)()1'()1a x x a f x ax a x x-+=-+-=-. ………2分 ⅰ 当0a >时, 令'()0f x >,解得01x <<;∴函数()f x 在(0,1)上单调递增 ⅱ 当0a <时,①当11a -<时,即1a <-时, 令'()0f x >,解得10x a<<-或1x >; ∴函数()f x 在1(0,)a-和(1,)+∞上单调递增②当11a -=时,即1a =-时, 显然,函数()f x 在(0,)+∞上单调递增;③当11a ->时,即10a -<<时, 令'()0f x >,解得01x <<或1x a>-∴函数()f x 在(0,1)和1(,)a-+∞上单调递增 。
高中数学培优班专题资料(包含答案)
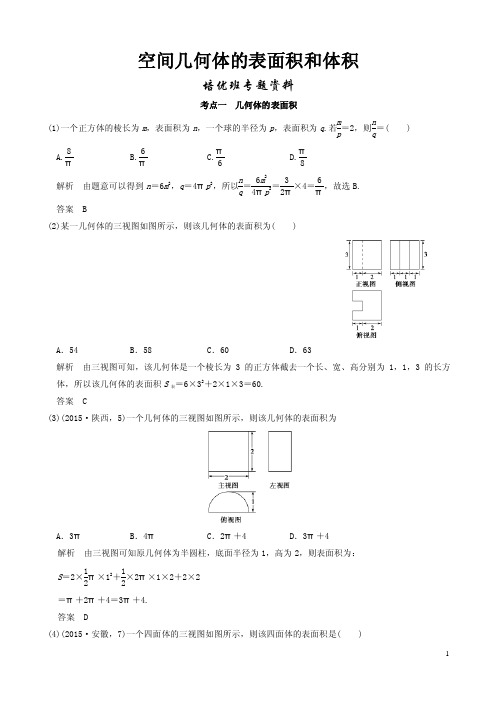
空间几何体的表面积和体积培优班专题资料考点一 几何体的表面积(1)一个正方体的棱长为m ,表面积为n ,一个球的半径为p ,表面积为q .若m p =2,则n q=( ) A.8πB.6πC.π6D.π8解析 由题意可以得到n =6m 2,q =4πp 2,所以n q =6m 24πp 2=32π×4=6πB. 答案 B(2)某一几何体的三视图如图所示,则该几何体的表面积为( )A .54B .58C .60D .63解析 由三视图可知,该几何体是一个棱长为3的正方体截去一个长、宽、高分别为1,1,3的长方体,所以该几何体的表面积S 表=6×32+2×1×3=60. 答案 C(3)(2015·陕西,5)一个几何体的三视图如图所示,则该几何体的表面积为A .3πB .4πC .2π+4D .3π+4解析 由三视图可知原几何体为半圆柱,底面半径为1,高为2,则表面积为:S =2×12π×12+12×2π×1×2+2×2=π+2π+4=3π+4. 答案 D(4)(2015·安徽,7)一个四面体的三视图如图所示,则该四面体的表面积是( )A .1+ 3B .2+ 3C .1+2 2D .2 2解析 由空间几何体的三视图可得该空间几何体的直观图,如图,∴该四面体的表面积为S 表=2×12×2×1+2×34×(2)2=2+3,故选B. 答案 B(5)(2015·新课标全国Ⅱ,9)已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点,若三棱锥O -ABC 体积的最大值为36,则球O 的表面积为( ) A .36πB .64πC .144πD .256π解析 如图,要使三棱锥O -ABC 即C -OAB 的体积最大,当且仅当点C 到平面OAB 的距离,即三棱锥C -OAB 底面OAB 上的高最大,其最大值为球O 的半径R ,则V O -ABC 最大=V C -OAB 最大=13×12S △OAB ×R =13×12×R 2×R =16R 3=36,所以R =6,得S 球O =4πR 2=4π×62=144π,选C. 答案 C(6)(2014·重庆,7)某几何体的三视图如图所示,则该几何体的表面积为( )A .54B .60C .66D .72解析 该几何体的直观图如图所示,易知该几何体的表面是由两个直角三角形,两个直角梯形和一个矩形组成的,则其表面积S =12×3×4+12×3×5+2+52×5+2+52×4+3×5=60.选B.答案 B(7)(2014·浙江,3)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )A .90 cm 2B .129 cm 2C .132 cm 2D .138 cm 2解析 由三视图可知该几何体由一个直三棱柱与一个长方体组合而成(如图),其表面积为S =3×5+2×12×4×3+4×3+3×3+2×4×3+2×4×6+3×6=138(cm 2).答案 D(8)(2014·大纲全国,8)正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( ) A.81π4B .16πC .9πD.27π4解析 设球的半径为R ,由题意可得(4-R )2+(2)2=R 2,解得R =94,所以该球的表面积为4πR 2=81π4.故选A.(9)(2014·安徽,7)一个多面体的三视图如图所示,则该多面体的表面积为( )A .21+ 3B .18+3C .21D .18解析 根据题意作出直观图如图,该多面体是由正方体切去两个角而得到的,根据三视图可知其表面积为6(22-12×1×1)+2×34×(2)2=6×72+3=21+ 3.故选A.答案 A(10)(2012·安徽,12)某几何体的三视图如图所示,该几何体的表面积是________.解析 由三视图可知,该几何体为底面是直角梯形且侧棱垂直于底面的棱柱,故该几何体的表面积为S=2×12×(2+5)×4+[2+5+4+42+(5-2)2]×4=92.答案 92考点二 几何体的体积(1)某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x 的值是( )A .2 B.92 C.32D .3解析 根据三视图判断几何体为四棱锥,其直观图是:V =13×1+22×2x =3⇒x =3. 故选D. 答案 D(2)(2015·山东,7)在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) A.2π3B.4π3C.5π3D .2π解析 如图,由题意,得BC =2,AD =AB =1.绕AD 所在直线旋转一周后所得几何体为一个圆柱挖去一个圆锥的组合体.所求体积V =π×12×2-13π×12×1=53π.答案 C(3)(2015·重庆,5)某几何体的三视图如图所示,则该几何体的体积为( )A.13+π B.23+π C.13+2π D.23+2π解析 这是一个三棱锥与半个圆柱的组合体,V =12π×12×2+13⎝⎛⎭⎫12×1×2×1=π+13,选A.答案 A (4)(2015·新课标全国Ⅱ,6)一个正方体被一个平面截去一部分后,剩余部分的三视图如图所示,则截去部分体积与剩余部分体积的比值为()A.18B.17C.16D.15解析 如图,由题意知,该几何体是正方体ABCD -A 1B 1C 1D 1被过三点A 、B 1、D 1的平面所截剩余部分,截去的部分为三棱锥A -A 1B 1D 1,设正方体的棱长为1,则截去部分体积与剩余部分体积的比值为111111A A B D B C D ABCDV V --=1111111111A AB D A BCD ABCD A A B D V V V ----=13×12×12×113-13×12×12×1=15,选D.答案 D(5)某几何体的三视图如图所示,它的体积为()A .72πB .48πC .30πD .24π解析 由三视图可知,该几何体是半个球体和一个倒立圆锥体的组合体,球的半径为3,圆锥的底面半径为3,高为4,则根据体积公式可得几何体的体积为30π,故选C.答案 C(6)(2014·陕西,5)已知底面边长为1,侧棱长为2的正四棱柱的各顶点均在同一个球面上,则该球的体积为( ) A.32π3B .4πC .2πD.4π3解析 如图为正四棱柱AC 1.根据题意得AC =2,∴对角面ACC 1A 1为正方形,∴外接球直径2R =A 1C =2,∴R =1,∴V 球=4π3,故选D.答案 D(7)(2014·湖北,8)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相乘也.又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L 与高h ,计算其体积V 的近似公式V ≈136L 2h .它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V ≈275L 2h 相当于将圆锥体积公式中的π近似取为( ) A.227B.258C.15750D.355113解析 圆锥的体积V =13πr 2h =13π⎝⎛⎭⎫L 2π2h =L 2h 12π,由题意得12π≈752,π近似取为258,故选B.答案 B(8)(2014·新课标全国Ⅱ,6)如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm ,高为6 cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.13解析 由三视图知该零件是两个圆柱的组合体.一个圆柱的底面半径为2 cm ,高为4 cm ;另一个圆柱的底面半径为3 cm ,高为2 cm.则零件的体积V 1=π×22×4+π×32×2=34π(cm 3).而毛坯的体积V =π×32×6=54π(cm 3),因此切削掉部分的体积V 2=V -V 1=54π-34π=20π(cm 3),所以V 2V =20π54π=1027.故选C.答案 C (9)(2012·新课标全国,11)已知三棱锥S ABC 的所有顶点都在球O 的球面上, △ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为( ) A.26B.36C.23D.22解析 如图,H 为△ABC 的外接圆圆心,则∠BHC =120°,设△ABC 的外接圆半径为r ,则1=BC 2=HC 2+HB 2-2HC ·HB ·cos 120°=3r 2, ∴r =33. 连接OH ,根据球的截面性质知,OH ⊥平面ABC ,∴OH =OC 2-CH 2=1-13=63∵O 为SC 的中点,∴S 到平面ABC 的距离为2OH =263,∴V S ABC =13S △ABC ×263=13×34×263=26.答案 A(10)(2015·江苏,9)现有橡皮泥制作的底面半径为5,高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥与圆柱各一个,则新的底面半径为________.解析 设新的底面半径为r ,由题意得13πr 2·4+πr 2·8=13π×52×4+π×22×8,解得r =7.答案7(11)(2014·江苏,8)设甲、乙两个圆柱的底面积分别为S 1,S 2,体积分别为V 1,V 2,若它们的侧面积相等,且S 1S 2=94,则V 1V 2的值是________.解析 设圆柱甲的底面半径为r 1,高为h 1,圆柱乙的底面半径为r 2,高为h 2.由题意得S 1S 2=πr 21πr 22=94,∴r 1r 2=32. 又∵S 甲侧=S 乙侧,即2πr 1h 1=2πr 2h 2,∴h 1h 2=r 2r 1=23, 故V 1V 2=S 1h 1S 2h 2=S 1S 2·h 1h 2=94×23=32答案 32(12)(2013·江苏,8)如图,在三棱柱A 1B 1C 1ABC 中,D ,E ,F 分别是AB ,AC ,AA 1的中点,设三棱锥F ADE 的体积为V 1,三棱柱A 1B 1C 1ABC 的体积为V 2,则V 1∶V 2=________.解析 由题意可知点F 到面ABC 的距离与点A 1到面ABC 的距离之比为1∶2,S △ADE ∶S △ABC =1∶4. 因此V 1∶V 2=13AF ·S △AED 2AF ·S △ABC=1∶24.答案 1∶24。
2023届高三数学培优试卷含详细答案解析(五)

2023届高三培优试卷(五)一、单选题1.设集合{1,2,6},{2,4},{|15}A B C x x ===∈-≤≤R ,则()A B C ⋃⋂=( ) A .{2} B .{1,2,4}C .{1,2,4,6}D .{|15}x R x ∈-≤≤2.设复数z 满足(1+i)z =2i ,则∣z ∣=( ) A .12B.2CD .23.已知函数1()3()3x x f x =-,则()f x ( )A .是奇函数,且在R 上是增函数B .是偶函数,且在R 上是增函数C .是奇函数,且在R 上是减函数D .是偶函数,且在R 上是减函数 4.设函数f (x )=cos (x +3π),则下列结论错误的是( ) A .f(x)的一个周期为−2πB .y=f(x)的图像关于直线x=83π对称 C .f(x+π)的一个零点为x=6πD .f(x)在(2π,π)单调递减 5.已知4sin cos 3αα-=,则sin 2α=( )A .79-B .29-C .29D .796.在正方体1111ABCD A B C D -中,E 为棱CD 的中点,则( ) A .11A E DC ⊥ B .1A E BD ⊥ C .11A E BC ⊥ D .1A E AC ⊥二、填空题7.若双曲线221y x m-=m =__________.8.若等差数列{}n a 和等比数列{}n b 满足111a b ==-,448a b ==,则22a b =_______.三、解答题9.设数列{}n a 满足123(21)2n a a n a n ++⋯+-=. (1)求{}n a 的通项公式;(2)求数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和.10.某种商品价格与该商品日需求量之间的几组对照数据如下表:(1)求y 关于x 的线性回归方程;(2)利用(1)中的回归方程,当价格40x =元/kg 时,日需求量y 的预测值为多少? 参考公式:线性回归方程ˆy bx a=+,其中1122211()(),()ˆˆn ni iiii i nniii i x y n x y x x y y b ay bx xn x xx ====-⋅⋅--===--⋅-∑∑∑∑2023届高三培优试卷(五)答案1.【答案】B【详解】(){1246}[15]{124}A B C =-=,,,,,, ,选B. 2.【答案】C【详解】由题意可得2i1i z =+,由复数求模的法则可得1121z z z z =,则2i 221i 2z ===+.故选C. 3.【答案】A【详解】:函数()133x xf x ⎛⎫=- ⎪⎝⎭的定义域为R ,且()()111333,333x x x x x x f x f x --⎡⎤⎛⎫⎛⎫⎛⎫-=-=-+=--=-⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦即函数()f x 是奇函数,又1y 3,3xxy ⎛⎫==- ⎪⎝⎭在R 都是单调递增函数,故函数()f x 在R 上是增函数.故选A.4.【答案】D【详解】f (x )的最小正周期为2π,易知A 正确;f 8π3⎛⎫⎪⎝⎭=cos 8ππ33⎛⎫+ ⎪⎝⎭=cos3π=-1,为f (x )的最小值,故B 正确; ∵f (x +π)=cos ππ3x ⎛⎫++ ⎪⎝⎭=-cos π3x ⎛⎫+ ⎪⎝⎭,∵f ππ6⎛⎫+ ⎪⎝⎭=-cos ππ63⎛⎫+ ⎪⎝⎭=-cos 2π=0,故C 正确;由于f 2π3⎛⎫ ⎪⎝⎭=cos 2ππ33⎛⎫+⎪⎝⎭=cosπ=-1,为f (x )的最小值,故f (x )在,2ππ⎛⎫⎪⎝⎭上不单调,故D 错误.故选D. 5.【答案】A【详解】()2sin cos 17sin 22sin cos 19ααααα--===--.所以选A.6.【答案】C【详解】画出正方体1111ABCD A B C D -,如图所示.对于选项A ,连1D E ,若11A E DC ⊥,又111DC A D ⊥,所以1DC ⊥平面11A ED ,所以可得11DC D E ⊥,显然不成立,所以A 不正确.对于选项B ,连AE ,若1A E BD ⊥,又1BD AA ⊥,所以DB ⊥平面1A AE ,故得BD AE ⊥,显然不成立,所以B 不正确.对于选项C ,连1AD ,则11AD BC .连1A D ,则得111,AD A D AD ED ⊥⊥,所以1AD ⊥平面1A DE ,从而得11AD A E ⊥,所以11A E BC ⊥.所以C 正确.对于选项D ,连AE ,若1A E AC ⊥,又1AC AA ⊥,所以AC ⊥平面1A AE ,故得AC AE ⊥,显然不成立,所以D 不正确. 故选C .7.【答案】2【详解】222222221,,13c a b a b m e m a a +=====+=,2m =.渐近线方程是2y mx x =±=±. 8.【答案】1【详解】设等差数列的公差和等比数列的公比分别为d 和q ,则3138d q -+=-=,求得2q =-,3d =,那么221312a b -+==,故答案为1. 9.【详解】(1)数列{}n a 满足()123212=n a a n a n ++⋯+-2n ≥时,()()12132321n a a n a n ++⋯+--﹣= ∵()212n n a -= ∵221n a n =- 当1n =时,12a =,上式也成立 ∵221n a n =- (2)21121(21)(21)2121n a n n n n n ==-+-+-+ ∵数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和1111113352121n n ⎛⎫⎛⎫⎛⎫=-+-++- ⎪ ⎪ ⎪-+⎝⎭⎝⎭⎝⎭1212121n n n =-=++ 10.【详解】:(1)由所给数据计算得()11015202530205x =++++=,()1111086585y =++++=, ()()()12222221050510250i i nx x=∑-=-+-+++=,()()()()()110352005210380i i i nx x y y =∑--=-⨯+-⨯+⨯+⨯-+⨯-=-,()()()121800.32250n i i i n i i x x y y b x x==∑---===-∑- 80.322014.4ˆˆay bx =-=+⨯=.所求线性回归方程为0.3214.4y x =-+. (2)由(1)知当40x =时,0.324014.4 1.6y =-⨯+=,故当价格40x =元/kg 时,日需求量y 的预测值为1.6kg .。
新高考高三数学培优试卷

一、选择题(每题5分,共50分)1. 设函数f(x) = x^3 - 3x + 2,若f(x)在区间[1, 2]上存在极值,则f'(x) =0的解集为()A. {1, 2}B. {1}C. {2}D. {0}2. 下列命题正确的是()A. 函数y = log2(x + 1)在定义域内单调递增B. 函数y = 2^x在定义域内单调递减C. 函数y = x^2在定义域内单调递增D. 函数y = 3x + 2在定义域内单调递减3. 已知函数f(x) = x^3 - 3x + 2,若f(x)在区间[-1, 1]上存在极值,则f'(x) = 0的解集为()A. {0, 1}B. {0, -1}C. {0}D. {-1}4. 已知函数f(x) = x^3 - 3x + 2,若f(x)在区间[-2, 2]上存在极值,则f'(x) = 0的解集为()A. {-1, 1}B. {-1, 2}C. {1, 2}D. {-1, 0, 1}5. 已知函数f(x) = x^3 - 3x + 2,若f(x)在区间[-3, 3]上存在极值,则f'(x) = 0的解集为()A. {-1, 1, 2}B. {-1, 1, 0}C. {-1, 0, 2}D. {-1, 0, 1, 2}6. 已知函数f(x) = x^3 - 3x + 2,若f(x)在区间[-4, 4]上存在极值,则f'(x) = 0的解集为()A. {-1, 1, 2, 3}B. {-1, 1, 0, 3}C. {-1, 0, 2, 3}D. {-1, 0, 1, 3}7. 已知函数f(x) = x^3 - 3x + 2,若f(x)在区间[-5, 5]上存在极值,则f'(x) = 0的解集为()A. {-1, 1, 2, 3, 4}B. {-1, 1, 0, 3, 4}C. {-1, 0, 2, 3, 4}D. {-1, 0, 1, 3, 4}8. 已知函数f(x) = x^3 - 3x + 2,若f(x)在区间[-6, 6]上存在极值,则f'(x) = 0的解集为()A. {-1, 1, 2, 3, 4, 5}B. {-1, 1, 0, 3, 4, 5}C. {-1, 0, 2, 3, 4, 5}D. {-1, 0, 1, 3, 4, 5}9. 已知函数f(x) = x^3 - 3x + 2,若f(x)在区间[-7, 7]上存在极值,则f'(x) = 0的解集为()A. {-1, 1, 2, 3, 4, 5, 6}B. {-1, 1, 0, 3, 4, 5, 6}C. {-1, 0, 2, 3, 4, 5, 6}D. {-1, 0, 1, 3, 4, 5, 6}10. 已知函数f(x) = x^3 - 3x + 2,若f(x)在区间[-8, 8]上存在极值,则f'(x) = 0的解集为()A. {-1, 1, 2, 3, 4, 5, 6, 7}B. {-1, 1, 0, 3, 4, 5, 6, 7}C. {-1, 0, 2, 3, 4, 5, 6, 7}D. {-1, 0, 1, 3, 4, 5, 6, 7}二、填空题(每题5分,共25分)11. 函数f(x) = 2x^3 - 3x^2 + 2x - 1的导数为______。
