习题课_3正弦电路
习题册参考答案-《电工电子技术基础(第二版)习题册》-B01-2482

模块一电路基础及简单直流电路课题一熟悉电路基础知识填空题:(请将正确答案填在空白处)1.电源负载开关连接导线2.电荷有规则的定向移动正电荷3. 0.12 1204.电路中任意两点之间的电位差称为两点之间的电压5.导体绝缘体半导体6.通过导体的电流电压7. 越小8.标称阻值额定功率允许偏差9. 交流电压最高挡10. 含有电源的闭合电路内电路外电路11. 开路通路12.电源的电动势13. 大负载小负载14. 115.满载轻载过载16.外电阻等于电源的内阻选择题:(请在下列选项中选择一个正确答案并填在括号内)1.C2. B3. D4. A5. C判断题:(判断正误并在括号内填√或×)1.√2.√3.×4.×5. ×6.√7.×8.×9.× 10.√ 11.√ 12.× 13.√简答题:1.电路的作用主要有两个方面:一是可以进行电能的传输、分配和转换,例如供电线路可以把发电厂发出的电能传输到远处的负载,再由负载将电能转换成其他形式的能;二是可以实现电信号的产生、传递和处理。
2.(略)3.电流大小的定义:单位时间内通过导体横截面的电荷的多少。
在直流电路中,若在时间t内通过导体横截面的电量为Q,则电流的大小为:因此,电流的大小与时间和电荷量有关。
4.直流电是方向不随时间变化的电流,但大小可能会发生变化,如脉动直流电;交流电流是指大小和方向都随着时间的变化而变化的。
5.6.①电位是相对量,随着参考点的改变而改变;电压是绝对量,与参考点的选择无关。
②电压就是两点之间的电位差,所以电位相同的各点间的电位差为零,电流也为零。
7.电阻为5Ω。
8.测量时,将转换开关转到交流电压挡,测量交流电压不分正、负极,所需量程由被测电压高低来确定,如电压不知,也需从高到低逐级调到合适的挡位。
9.部分电路欧姆定律:在部分电路中,通过电阻的电流与电阻两端的电压成正比,与电阻成反比。
电工技术第3章课后习题及详细解答

第3章单相正弦电路分析已知正弦电压(V)、(V),则u1与u2的相位差为,是否正确?为什么?分析讨论相位差问题时应当注意,只有同频率正弦量才能对相位进行比较。
这是因为只有同频率正弦量在任意时刻的相位差是恒定的,能够确定超前、滞后的关系,而不同频率正弦量的相位差是随时间变化的,无法确定超前、滞后的关系,因此不能进行相位的比较。
解不正确。
因为u1的角频率为ω,而u2的角频率为2ω,两者的频率不同,相位差随时间变化,无法确定超前、滞后的关系,因此不能进行相位的比较。
已知某正弦电流的有效值为10 A,频率为50 Hz,初相为45°。
(1)写出该电流的正弦函数表达式,并画出波形图;(2)求该正弦电流在s时的相位和瞬时值。
解(1)由题设已知正弦电流的有效值A,频率Hz,初相。
由频率f可得角频率ω为:(rad/s)所以,该电流的正弦函数表达式为:(A)波形图如图所示。
(2)s时的相位为:(rad)瞬时值为:(A)已知正弦电流(A)、(A),试求i1与i2的振幅、频率、初相、有效值和相位差,并画出其波形图。
解i1与i2的振幅分别为:(A)(A)频率分别为:(Hz)初相分别为:有效值分别为:(A)(A)i1与i2的相位差为:说明i1超前i2。
波形图如图所示。
图习题解答用图图习题解答用图设,,试计算、、AB、。
分析复数可用复平面上的有向线段、代数型、三角函数型和指数型(极坐标型)等形式表示。
复数的加减运算就是将实部和虚部分别进行加减,因而采用代数型比较方便。
复数的乘法运算就是将模相乘而辐角相加,复数的除法运算就是将模相除而辐角相减,因而采用指数型(极坐标型)比较方便。
解写出下列各正弦量所对应的相量,并画出其相量图。
(1)(mA)(2)(A)(3)(V)(4)(V)分析用相量来表示正弦量,就是用一个复数来反映正弦量的振幅(或有效值)和初相,即用相量的模来代表正弦量的振幅(或有效值),用相量的辐角来代表正弦量的初相。
正弦交流电路习题课

0 由KCL, I1 I 2 I 3 j 2 1 2.263.4 A
U 40 在电压三角形中, arctg arctg 53.130 U2 30
I00 解:设 I
P 1 V1 I cos 1
Z1 Z1 1
240 171 4 cos 1
1 69.460 171 Z1 69.460 42.75 69.460 4 V V2 Z 2 2 60 2 Z1 Z 2 25 I I
提高功率因数的意义方法
• 提高功率因数能使电源设备的容量得到充 分利用; • 提高功率因数能减小线路功耗和电压损耗。 • 提高功率因数的方法通常是在感性负载 两端并联一个电容器,称之为补偿电容 器。补偿电容器的容量为:
正弦稳态电路的分析
• 用相量法分析电路时,线性电阻电路的 各种分析方法和电路定理可推广用于线 性电路的正弦稳态分析,差别仅在于所 得的电路方程是以相量形式表示的代数 方程以及用相量形式描述的电路定理, 而计算则为复数运算。
U I XC
U I XL
I CU
基尔霍夫定律的相量式
• 基尔霍夫定律的相量式与三种基本电路 元件伏安特性的相量形式,是分析正弦 交流电路的基础。 0 U
I 0
• 应用基尔霍夫定律及单一参数电路所得 出的结论,对R、L、C串联、并联电路 进行了分析,分别引出了阻抗Z和导纳Y 的概念。
正弦稳态电路的分析
习题总结课
正弦量及其三要素
1、随时间按正弦规律变化的电流、电压、 电动势等统称为正弦量。 2、正弦量的有效值(振幅)、频率(周期 或角频率)和初相是正弦量的三要素。 三要素是确定一个正弦量的充要条件。 3、直流电的大小和方向恒定不变,在直流 计算时只考虑其大小即可。而在交流电 的分析与计算时,除了考虑大小外,还 要考虑其相位。
正弦稳态电路习题课
⇒ Z1 = Z 2
2 2 2 2
Z2 = R + X
X1 = X 2
性质相反,一个 为感性,另一个 为容性
⇒
U1 = U 2 = 50 2V>U = 50V ⇒
X1 = − X 2
Z = Z1 + Z 2 = R1 + jX 1 + R2 + jX 2 = R1 + R2 = 2 R1
端口电压、电流 同相
B0 = −0.1S < 0
1 1 =− = 1H L0 = − −0.1× 10 B0ω
B0 = −0.1S < 0
⇒
5Ω
1H
正弦稳态电路习题课习题(3/8) )
图示正弦交流电路中,已知电流表的示数为2A, 3 图示正弦交流电路中,已知电流表的示数为 ,电 压表1的示数为 的示数为17V,2的示数为 的示数为10V。求电源电压 压表 的示数为 , 的示数为 。 的有效值。 的有效值。
正弦稳态电路习题课习题(6/8) )
U 图示电路中,ɺ = 50∠0o V,每一阻抗部分消耗的功 6 图示电路中, 率均为250W,且电压的峰值为 率均为 ,且电压的峰值为100V。求(1)阻抗 。 ) Z1 和 Z 2 ;( )若 ω = 800π rad/s ,求电路可能含有 ;(2) 的元件及其数值。 的元件及其数值。
jω L2
R1
ɺ Us −
+
ɺ IC
jω L1
1 jωC
ɺ IC
R2
ZL
7 解(1) 求开路电压
Z L 2 = jω L2 = j100Ω
1 ZC = = − j100Ω + jωC ɺ Us ɺ = − I R = −100 I − ɺ ɺ ⇒U
第3章 正弦交流稳态电路(1.2.3.4节)

φ 'i<0。对于同一电路中的多个相关的正弦量,只能选择一个共同的计时
零点确定各自的初相位。
3.相位差
相位差描述的是两个同频率正弦量之间的相位关系。 假设两个正弦电流
分别为
i1 i2
2 I1 sin(t 1 ) 2 I 2 sin(t 2 )
其中,设φ 1>φ 2,它们的波形如下图所示。 (两电流的相位差)
由于正弦量按周期性变化360°,所以正弦量的相量是旋转相量。 正弦电流i=Imsin(ω t+φ i)在任一时刻的值,等于对应的旋转相量该时 刻在虚轴上的投影,如图3.2-2所示。
将一个正弦量表示为相量或将一个相量表示成正弦量的过程称为相 量变换。由图3.2-2可知,该相量只表示了对应正弦量的两个特征量—
—幅值和初相位。故相量只是用于表示正弦量,并不等于正弦量。
相量在复平面上的图称为相量图。相量图可以形象地表示出各个相 量的大小和相位关系。
例3.2-1: 已知电流
i1 5 2 sin(t 30o ) A, i2 10 2 sin(t 60o ) A 试画出这
两个正弦量的相量和相量图。
2 是220V,而其幅值为
³220=311V。在我国,民用电网的供电电压为
220V,日本和美国的供电电压为110V,欧洲绝大多数国家的供电电压也为 引入有效值后,正弦电流和电压的表达式也可表示为 220V 。
i I m sin(t i ) u U m sin(t u )
弦量的初相位,计时零点在右为正,即φ i>0,如图3.1-2(a)所示初相位
为正。初相位的取值范围为|φ i|≤180°。
在电路中,初相位与计时零点的选择有关。对于同一正弦量,如果其 计时零点不同,其初相位也就不同,对于图3.1-2(a)中所示的正弦量,如 果按图3.1-2(b)所示坐标建立计时零点,则正弦量 的初相为负,即
习题课:正弦定理和余弦定理(A3)

鸡西市第十九中学学案
(2)数列:1,12,13,14,1
5
,…
n
1
2 3 4 a n 1 12
13
14
①用公式法表示:a n = . ②用列表法表示:
③用图象法表示为(在下面坐标系中绘出):
探究点三 数列的通项公式
问题 什么叫做数列的通项公式?谈谈你对数列通项公式的理解?答 如果数列{a n }的第n 项a n 与序号数列{a n }的通项公式.和函数不一定有解析式一样,并不是所有的数列都有通项公式.一个数列
的通项公式不唯一,可以有不同的表现形式,=⎩
⎪⎨⎪⎧
1(n 为奇数),-1(n 为偶数). 探究 根据所给数列的前几项求其通项公式时,需仔细观察数列的特征,并进行联想、转化、归纳,同时要熟悉一些常见数列的通项公式.下表中的一些基本数列,你能准确快速地写出它们的通项公式吗?。
电工学课后第1-6章习题答案
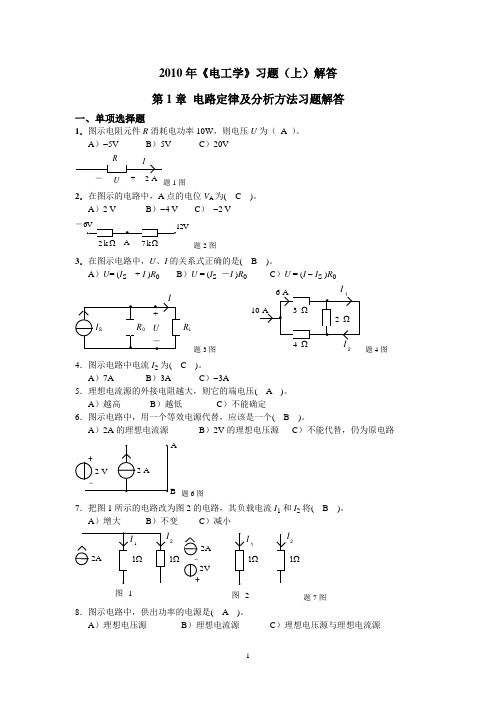
2010年《电工学》习题(上)解答 第1章 电路定律及分析方法习题解答一、单项选择题1.图示电阻元件R 消耗电功率10W ,则电压U 为( A )。
A )-5V B )5V C )20VUR 题1图2.在图示的电路中,A 点的电位V A 为( C )。
A )2 V B )-4 V C ) -2 V- 2 k 7 k ΩΩ题2图3.在图示电路中,U 、I 的关系式正确的是( B )。
A )U = (I S + I )R 0 B )U = (I S -I )R 0 C )U = (I - I S )R 0R L题3图I 2题4图4.图示电路中电流I 2为( C )。
A )7AB )3AC )-3A5.理想电流源的外接电阻越大,则它的端电压( A )。
A )越高 B )越低 C )不能确定6.图示电路中,用一个等效电源代替,应该是一个( B )。
A )2A 的理想电流源 B )2V 的理想电压源 C )不能代替,仍为原电路2 V题6图7.把图1所示的电路改为图2的电路,其负载电流I 1和I 2将( B )。
A )增大B )不变C )减小221Ω2V 2A图 1图 2+题7图8.图示电路中,供出功率的电源是( A )。
A )理想电压源 B )理想电流源C )理想电压源与理想电流源U4VS题8图S题9图9.在图示电路中,各电阻值和U S 值均已知。
欲用支路电流法求解流过电阻R G 的电流I G ,需列出独立的电流方程数和电压方程数分别为( B )。
A )4和3 B )3和3 C )3和410.在计算线性电阻电路的电压和电流时,用叠加原理。
在计算线性电阻电路的功率时,加原理( B )。
A )可以用 B )不可以用 C )有条件地使用11.在图示电路中,已知U S =12V ,I S =2A 。
A 、B 两点间的电压U AB 为( A )。
A )-18VB )18VC )-6VU I SS+题11图SA题12图12.在图示电路中,当开关S 闭合时A 点的电位V A ( C )。
2章正弦交流习题课

• IA = IAB− ICA • • • • IC • • = ICA − IBC • •
IB = IBC − IAB
◆对称负载 | ZAB| = |ZBC| = |ZCA| = | Z | ϕAB = ϕBC = ϕCA= ϕ。
IAB = IBC = ICA = Up Z ,
8. 功率因数的提高方法
P=UIcos ϕ
cos ϕ功率因数
负载并联两端并电容其大小: 负载并联两端并电容其大小:
C = P ω U
2
(tg ϕ
1
− tg ϕ
)
9. 三相电路
1 )三相电压
•
E
•
A
= E / 0° = E
1 3 E B = E / − 120° = E(− − j ) 2 2 • 1 3 E C = E / 120 ° = E ( − + j ) 2 2
A B C
解:
U2 R=3 = 806.7Ω P
•
•
I
•
B '
= 0 . 273 ∠ − 120 = 0 . 273 ∠ + 120
o
U 220∠0 IA = = 0.273 A R 806.7
• o
I
C
o
[ 例3 ] 用戴维宁定理计算下列电路中电阻RL上的电流IL。其中:R2=3 Ω , 用戴维宁定理计算下列电路中电阻 上的电流 其中: R3=4 Ω ,R4=20 Ω ,R5=8 Ω ,U=16V, I=1A。 , 。
乏
伏安( ) 伏安(VA)
注意: 、 及 三者所代表的意义 单位、功率三角形。 三者所代表的意义、 注意:P、Q及S三者所代表的意义、单位、功率三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
+
US 1 –
US 2
–
试求:两个电源各自发出的有功功率 和无功功率。
U S1 U S2 110 30 11030 j110 解: I 0.234 A jω L1 j314 1.5 j471 P U S1I cos( 30 180 ) 110 0.234 (0.866) 22.3 W(吸) 1
Uoc
U oc U oc I , I Z i R0 j1 /(ω C 0) | Z i R0 j1 /(ω C 0) |
若使 I 最大,须使|Zi+ Zi –j1/( C)|最小。
Z i R0 j1 /(ω C 0 ) 2 j1 1 j1 /(ω C 0 ) 3 j[1 1 /(ω C 0 )] Ω 若使其最小,只须使1–1/( C)=0。 1 1 1 1, C 0 0.5 F 即: ωC0 ω 2
( j L4 R5 ) I 2 U S1
is6
节点法:
us1
φ1
+ –
φ2
C2
L4 C3 is3
φ3
R5
φ 1 U S1
1 1 jω C 2 φ1 ( jω C 2 )φ 2 φ3 IS3 jω L4 jω L4 1 1 1 φ2 ( )φ 3 I S 6 jω L4 jω L4 R5
I1
+
A1
A2
七、 已知:U=220V,f=50HZ,
A3 Z3
U
–
I2
Z2 I 3
电流表A1的读数为4A, A2的读为 2A,A3 的读数为3A,且Z2 为电 阻负载,Z3为感性负载。试求: Z2和Z3。
U 220 110Ω 解:设Z2= R2, Z3 =|Z3| 3 则 R2 I2 2 求Z3. 方法一: 画相量图。以电压为参考相量 根据余弦定理: I2 U 42= 32+ 22–232cos 3 2 42 32 22 1 3 cosθ , θ 104.5o I3 232 4 4 I1 φ 3 180o θ 180o 144.5o 75.5o U 220 | Z 3 | 73.3 Ω, Z 3 73.375.5o Ω 18.4 j71Ω I3 3
Zi 1 C0
US 2
1 j5
+ –
Uoc
C0
2.5 j5 0.5 45 o o 2 j1Ω Uoc j5 0.447 18.4 V Z i 2.5 j5 2.5 j5
Zi
I
1 C0
+
–
P0 I 2 R
要使R0上功率最大,只需使电 流I 最大即可。
由上式可得:
4cos =2+3cos 3
4sin =–3sin 3
(1)
(2)
由 (1)2+(2)2 得:16 =(2+3cos 3)2+(–3sin 3)2 =4+12cos 3+9(cos 3)2+9(sin 3)2 = 4+12cos 3+9 3 1 cosφ 3 , φ 3 75.5o 12 4
设 U 2200 V, 则 I2 20 A, I3 3 φ 3 A,
求Z3, 方法二: 直接计算. Z3 模的计算同前.
I1 4φ A
I1 I2 I 3 即
4φ 20 3 φ 3
4cos +j4sin =2+3cos 3–j3sin 3
U S U 1 U 2 100 j100 U 2 100 U 2 j100
2 U S (100 U 2 ) 2 100 2 , U 2 220 2 100 2 100 96V
X 2 U 2 / I 2 96 / 30 3.2Ω, X 3 U 2 / I 3 96 / 20 4.8Ω
四、 已知:已知电流表读数为1.5A(有效值)。 求:(1)US=? (2)电路吸收的有功功率P和无功功率Q . 40Ω IR A I 24Ω j18Ω IC j30Ω + + – + U
1
US
+ –
U2
– j50Ω
U3 –
解: 设 I R 1.50 A
两个电源发出的有功功率互相抵消,而无功功率不 抵消,因为电路中的电感吸收无功。功率守恒吗?
5 + uS(t) –
六、 已知: R0 1
2.5H C0
us (t ) 2 cos(2t 45o ) V
要使R0 上获最大率, 则C0为何值?
5
解: 用戴维南等效电路: S 1 45 o V U 2.5 + –
Z3 | Z3 | φ3 73.375.5 Ω 18.4 j71Ω
o
I1
+ V –
V1
* * W
+
R
US
U1
jX 1
–
+ A2
A3
jX 2
jX 3
U2
–
I2
I3
八 . 正弦稳态电路如图示,已知电压表V读数为220V,V1 读数 为100 2 V,电流表A2读数30A,A3的读数 20A ,功率表读 数1000W(平均功率)。求各元件参数R、X1、X2和X3。
2 Q x 18 I 2 30 I C 50 I 2 18 ( 2.5) 2 30 2 2 50 ( 2.5) 2 320 Var
I
L
五、 已知: +
U S1 110 30 V, U S2 11030 V, L 1.5H, f 50Hz.
U 3 ( j50) I ( j50) 2.553.1 125 36.9 100 j75V
I
24Ω j18Ω
IR
40Ω
A
j30Ω
+ –
+
U1
–
IC
+
US
+
U2
– j50Ω
U3 –
U S U 1 U 2 U 3 j75 60 100 j75 1600 V
容性 14.14 (d)该负载是______负载, |Z|=_________, =_________. 60 比较相位必须把正弦量化为标准正弦量的形式: 1 1 i(t ) cos(400πt 150 180 ) cos(400πt 30 ) 2 2
u(t ) 10cos(400πt 30 90 ) 10cos(400πt 30 ) A
用相量法,设: U 2 U 20 V 则: I 2 j30A, I 3 j20A, I 1 I 2 I 3 j10A
P I 1 R, R P / I 1 1000 / 10 2 10 Ω
2 2
I1
*
US
V1
*
W
+ + R
+ – V
U1
jX 1
–
A1
A2
此题亦可用
jX 2
jX 3
U2
–
相量图分析。
I2
I3
设:Z1 R jX 1 Z1 φ1 则 Z 1
U 1 100 2 10 2 Ω I1 10 2 X1 2 2 2 X 1 Z 1 R (10 2 ) 10 10Ω φ 1 arctg 45 R I 1 j10 10 90 A U1 100 2 45 V
U –
(7) P I 2 R
(4) U U U U ( 6) P R R (8) | Z| R 2 (ω L) 2
2 2 L 2 2 R
2.
i
+
u
–
若 u(t ) 311cos( t 45)V, Ζ 2560 Ω u 311 cos( t 45) 311 i cos( t 45 60)A 则 Z 2560 25 311 45 o 311 / 2 Z U 2 I 15 o A Z 25 2560 o 311 i cos(t 15o ) A 25
is6 i1 + us1 –
三、电路如图所示,试列写其 相量形式的回路电流方程和节 点压程。
L4
C2
C3 is3 i2 R5
回路法:
I 1 I S6
I 2 I S3
i3
1 1 ( j j L4 R5 ) I 3 ( j j L4 ) I 1 C2 C2
正弦交流电路习题课
熟练掌握
1. 正弦量的基本概念:三要素、相位差、波形图. 2. 定量计算:相量法 3. 定性分析:相量图 4. 功率计算:有功功率、无功功率、视在功率、功 率因数、复功率等
i + u –
一、左图电路中,已知:
Z Z φ
u( t ) 10si n ( π t 60 ) V 400 1 i(t ) cos(400 t 150 ) A π 2
