2021新高考数学高中数学考点归纳(表格版)
2021版新高考数学:等差数列及其前n项和含答案

(对应学生用书第103页)考点1等差数列基本量的运算解决等差数列运算问题的思想方法(1)方程思想:等差数列的基本量为首项a1和公差d、通常利用已知条件及通项公式或前n项和公式列方程(组)求解、等差数列中包含a1、d、n、a n、S n五个量、可“知三求二”.(2)整体思想:当所给条件只有一个时、可将已知和所求都用a1、d表示、寻求两者间的联系、整体代换即可求解.(3)利用性质:运用等差数列性质可以化繁为简、优化解题过程.又零七、借问长儿多少岁、各儿岁数要详推.在这个问题中、记这位公公的第n 个儿子的年龄为a n 、则a 1=( )A .23B .32C .35D .38C [由题意可知年龄构成的数列为等差数列、其公差为-3、则9a 1+9×82×(-3)=207、解得a 1=35、故选C.]确定等差数列的关键是求出两个最基本的量、即首项a 1和公差d .考点2 等差数列的判定与证明等差数列的4个判定方法(1)定义法:证明对任意正整数n 都有a n +1-a n 等于同一个常数. (2)等差中项法:证明对任意正整数n 都有2a n +1=a n +a n +2.2.已知数列{a n}的前n项和为S n、a1=1、a n≠0、a n a n+1=λS n-1、其中λ为常数.(1)证明:a n+2-a n=λ;(2)是否存在λ、使得{a n}为等差数列?并说明理由.[解](1)证明:由题设知a n a n+1=λS n-1、a n+1a n+2=λS n+1-1、两式相减得a n+1(a n+2-a n)=λa n+1、由于a n+1≠0、所以a n+2-a n=λ.(2)由题设知a1=1、a1a2=λS1-1、可得a2=λ-1.由(1)知、a3=λ+1.令2a2=a1+a3、解得λ=4.故a n+2-a n=4、由此可得{a2n-1}是首项为1、公差为4的等差数列、a2n-1=4n-3;{a2n}是首项为3、公差为4的等差数列、a2n=4n-1.所以a n=2n-1、a n+1-a n=2、因此存在λ=4、使得数列{a n}为等差数列.考点3等差数列的性质及应用B [数列{a n }为等差数列、则a m -1+a m +1=2a m 、则a m -1+a m +1-a 2m -1=0可化为2a m -a 2m -1=0、解得a m =1.又S 2m -1=(2m -1)a m =39、则m =20.故选B.]2.设等差数列{a n }、{b n }的前n 项和分别为S n 、T n 、若对任意的n ∈N *、都有Sn Tn =2n -34n -3、则a2b3+b13+a14b5+b11的值为( ) A .2945 B .1329 C .919 D .1930C [由题意可知b 3+b 13=b 5+b 11=b 1+b 15=2b 8、∴a2b3+b13+a14b5+b11=a2+a142b8=a8b8=S15T15=2×15-34×15-3=2757=919.故选C.] 考点4 等差数列前n 项和的最值问题求等差数列前n 项和S n 最值的2种方法(1)函数法:利用等差数列前n 项和的函数表达式S n =an 2+bn 、通过配方或借助图象求二次函数最值的方法求解.(2)邻项变号法:①当a 1>0、d <0时、满足⎩⎨⎧am≥0,am +1≤0的项数m 使得S n 取得最大值为S m ; ②当a 1<0、d >0时、满足⎩⎨⎧am≤0,am +1≥0的项数m 使得S n 取得最小值为S m .。
2021高考数学475道必考题型总结(全国卷新高考)

2021 年高考数学 必考题型总结
第一章 集合与常用逻辑用语
题型 1 集合元素的“三性” (详见《专题课-集合的概念与运算》)
例 1:设集合 A={2,3,a2-3a,a+
2
+7},B={|a-2|,3},已知 4∈A,且 4∉B,则 a 的取值集合为
a
.
题型 2 集合间的关系 (详见《专题课-集合的概念与运算》)
题型 6 单调性+奇偶性解不等式 (详见《专题课-函数的单调性、奇偶性》)
1
例 9:(1)已知偶函数 f(x)在区间[0,+∞)上单调递增,则满足 f (2 x 1) f 的 x 的取值范围是________.
3
(2)已知函数 f(x-2)为奇函数,f(-2)=0 且 f(x)在区间[-2,+∞)上单调递减,则 f(3-x)>0 的解集为
A.c<b<a
B.a<b<c
C.a<c<b
例 33:设 x,y,z 为正数,且 2x=3y=5z,则 (
A.2x<3y<5z
B.5z<2x<3y
D.c<a<b
)
C.3y<5z<2x
D.3y<2x<5z
(
)
梅花香自苦寒
题型 20 构造法解抽象函数 (详见《专题课-指数、对数、幂函数》)
1
例 34:已知函数 f(x)定义域为(0,+∞),且满足 f(xy)=f(x)+f(y), f 1, 如果对于 0<x<y,都有 f(x)>f(y),则不等式
第二章 基本初等函数
“新高考”数学试卷结构、题型分析

“新高考”数学试卷结构、题型分析导读:随着新高考改革的推进,2021年又有8个省份宣布采用新高考模式。
截止目前,采用新高考模式地区暴增至14个省份!在新高考形式下,数学成为了很多同学最为关注的学科。
今天,为大家整理了2021年新高考数学全国I卷的试卷结构和分析!希望能够帮上你!新高考数学试卷结构第一大题,单项选择题,共8小题,每小题5分,共40分;第二大题,多项选择题,共4小题,每小题5分,部分选对得3分,有选错得0分,共20分;第三大题,填空题,共4小题,每小题5分,共20分;第四大题,解答题,共6小题,均为必考题,涉及的内容是高中数学的六大主干知识:三角函数,数列,统计与概率,立体几何,函数与导数,解析几何。
每小题12分,共60分。
单项选择题考点分析:多项选择题考点分析:填空题考点分析:选择填空题部分主干考点分析:从主干知识所占比重来看,新高考数学试卷与原来保持一致,主干知识的考察在60分,占整个填选题的75%,这也启示我们高中数学主干知识的稳定性与重要性,在以后的备考中要引起高度的重视。
解答题部分考点分析:全卷主干考点分析:从主干知识所占比重来看,新高考数学试卷与原来保持一致,主干知识的考察在60分,占整个填选题的75%,这也启示我们高中数学主干知识的稳定性与重要性,在以后的备考中要引起高度的重视。
六种解题技巧一、三角函数题注意归一公式、诱导公式的正确性(转化成同名同角三角函数时,套用归一公式、诱导公式(奇变、偶不变;符号看象限)时,很容易因为粗心,导致错误!一着不慎,满盘皆输!)。
二、数列题1、证明一个数列是等差(等比)数列时,最后下结论时要写上以谁为首项,谁为公差(公比)的等差(等比)数列;2、最后一问证明不等式成立时,如果一端是常数,另一端是含有n的式子时,一般考虑用放缩法;如果两端都是含n的式子,一般考虑数学归纳法(用数学归纳法时,当n=k+1时,一定利用上n=k时的假设,否则不正确。
等差、等比数列-2021届新高考数学复习知识点总结与题型归纳(原卷版)

第14讲 等差、等比数列考点1:等差数列一、等差数列的基本概念和公式1. 定义:一般地,如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列.这个常数叫做等差数列的公差,通常用字母d 表示.2. 等差中项:如果三个数x ,A ,y 组成等差数列,那么A 叫做x 和y 的等差中项,即A =x+y 2.3.通项公式:a n =a 1+(n −1)d =a m +(n −m)d ,(n ∈N ∗,m ∈N ∗,m ≤n)⇒d =a n −a m n−m(n,m ∈N ∗,n ≠m)4. 前n 项和公式:S n =n(a 1+a n )2=na 1+n(n−1)2d ,(n ∈N ∗);二、等差数列的性质:1. a m =a n +(m −n)d ,d =a m −a n m−n,(n ∈N ∗,m ∈N ∗);2. 若p +q =m +n ,则有a p +a q =a m +a n ;若2m =p +q ,则有2a m =a p +a q (p ,q ,m ,n ∈N ∗);3. {a n }为等差数列,S n 为前n 项和,则S 2n−1=(2n −1)a n ;{b n }为等差数列,S n ′为前n 项和,S 2n−1′=(2n −1)b n ;有a nb n=S 2n−1S 2n−1′.4. 若{a n },{b n }均为等差数列,且公差分别为d 1,d 2,则数列{pa n },{a n +q },{a n ±b n }也为等差数列,且公差分别为pd 1,d 1,d 1±d 2.5. 在等差数列中,等距离取出若干项也构成一个等差数列,即a n ,a n+m ,a n+2m ,....,为等差数列,公差为md .6. 等差数列的前n 项和也构成一个等差数列,即S n ,S 2n −S n ,S 3n −S 2n ,⋯⋯为等差数列,公差为n 2d ,(n ∈N ∗);三、等差数列的单调性以及前n 项和的最值探讨1. 在等差数列{a n }中,若公差d >0,则等差数列{a n }为递增数列;若公差d <0,则等差数列{a n }为递减数列;若公差d =0,则等差数列{a n }为常数列; 补充:更一般性的情况,研究任一数列的增减性可以利用逐项作差法,即构造f (n )=a n+1−a n ,然后研究自变量n 变化时函数值f (n )的符号.2. 有关等差数列{a n }的前n 项和为S n 的最值问题: 若a 1>0,d <0,则前n 项和为S n 存在最大值 若a 1<0,d >0,则前n 项和为S n 存在最小值3. 如何求最值:方法一:(任何数列都通用)通过{a n ≥0a n+1≤0解出n 可求前n 项和为S n 的最大值;通过{a n ≤0a n+1≥0解出n 可求前n 项和为S n 的最小值; 方法二:利用等差数列前n 项和S n 的表达式为关于n 的二次函数且常数项为0(若为一次函数,数列为常数列,则前n 项和S n 不存在最值),利用二次函数求最值的方法进行求解;有以下三种可能:若对称轴n 正好取得正整数,则此时n 就取对称轴;若对称轴不是正整数,而是靠近对称轴的相邻的两个整数的中点值,则n 取这两个靠近对称轴的相邻的两个整数;若对称轴即不是正整数,又不是靠近对称轴的相邻的两个整数的中点值,则n 就取靠近对称轴的那个正整数;四、等差数列的判断方法1. 定义法:a n −a n−1=d (常数)(n ∈N +,n ≥2)⇔{a n }为等差数列;2. 等差中项法:2a n =a n−1+a n+1(n ∈N +,n ≥2)⇔{a n }为等差数列;3. 通项公式法:a n =kn +b (k ,b 是常数)⇔数列{a n }是等差数列;4. 前n 项和法:数列{a n }的前n 项和S n =An 2+Bn ,(A ,B 是常数,A 2+B 2≠0) ⇔数列{a n }是等差数列;若数列{a n }的前n 项和S n =An 2+Bn +C(A ,B 是常数,C ≠0),则数列{a n }从第二项起是等差数列.典例精讲【典例1】已知数列{a n }为等差数列,S n 为其前n 项和,2+a 5=a 6+a 3,则S 7=( ) A .2 B .7 C .14 D .28【典例2】已知等差数列{a n }的公差为4,且a 2,a 3,a 6成等比数列,则a 10=( ) A .26 B .30 C .34 D .38【典例3】设等差数列{a n }的前n 项和为S n ,首项a 1>0,公差d <0,a 10•S 21<0,则S n 最大时,n 的值为( )A .11B .10C .9D .8【典例4】.已知等差数列{}n a 满足225910a a +,则12345a a a a a ++++的最大值为( ) A.B .20 C .25 D .100【典例5】.已知等差数列{}n a 满足10a >,201920200a a +>,201920200a a <.其前n 项和为n S ,则使0n S >成立时n 最大值为( ) A .2020B .2019C .4040D .4038【典例6】.等差数列{}n a 中,36a =,816a =,n S 是数列{}n a 的前n 项和,则122020111(S S S ++⋯+= ) A .20172018B .20182019C .20192020D .20202021【典例7】已知数列{}n a 是等差数列,{}n b 是等比数列,22a b m ==,33a b n ==,若m ,n 为正数,且m n ≠,则( ) A .11a b < B .11a b > C .11a b = D .1a ,1b 的大小关系不确定【典例8】已知等差数列{a n }的各项均为正数,a 1=1,且a 2+a 6=a 8.若p ﹣q =10.则a p ﹣a q =【典例9】设数列{a n }为等差数列,其前n 项和为S n ,已知a 1+a 4+a 7=60,a 2+a 5+a 8=51,若对任意n ∈N *,都有S n ≤S k 成立,则正整数k 的值为 .考点2:等比数列一、等比数列的基本概念和基本公式1. 定义:一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,通常用字母q(q ≠0)表示.等比数列中的项不为0.2. 通项公式:a n =a 1q n−1=a m q n−m (n ∈N ∗,n ≥2) ;3. 前n 项和公式:S n ={na 1 (q =1)a 1(1−q n )1−q=a 1−a n q 1−q(q ≠1).二、等比数列的性质(其中公比为q ):1. a n =a m q n−m ,q =√na mn−m(n ∈N ∗,m ∈N ∗) ; 2. 若p +q =m +n ,则有a p ⋅a q =a m ⋅a n ;若2m =p +q ,则有a m2=a p ⋅a q ; 3. 等距离取出若干项也构成一个等比数列,即a n ,a n+m ,a n+2m ,⋯⋯为等比数列,公比为q m .4. 若a ,G ,b 成等比数列,则称G 为a 、b 的等比中项,G 2=ab ,当且仅当两个数a 和b 同号 才存在等比中项.5. 若数列{a n },{b n }都是等比数列且项数相同,则c n =a n s b n t (st ≠0)仍为等比数列.三、等比数列的判断方法1.定义法:a 1≠0,a nan−1=q (常数)(n ∈N ∗,n ≥2) ⇔{a n }为等比数列.2. 等比中项法:a n 2=a n−1a n+1,(n ∈N ∗,n ≥2) ⇔{a n }为等比数列.3. 前n 项和法:数列{a n }的前n 项和S n =A −Aq n (A 是常数,A ≠0,q ≠0,q ≠1)⇔数列{a n }为等比数列;典例精讲【典例1】已知数列{a n }为等比数列,其中a 5,a 9为方程x 2+2016x +9=0的二根,则a 7的值( )A .﹣3B .3C .±3D .9【典例2】“垛积术”(隙积术)是由北宋科学家沈括在《梦溪笔谈》中首创,南宋数学家杨辉、元代数学家朱世杰丰富和发展的一类数列求和方法,有茭草垛、方垛、刍童垛、三角垛等等.某仓库中部分货物堆放成如图所示的“茭草垛”:自上而下,第一层1件,以后每一层比上一层多1件,最后一层是n 件.已知第一层货物单价1万元,从第二层起,货物的单价是上一层单价的910.若这堆货物总价是100−200(910)n 万元,则n 的值为( )A .7B .8C .9D .10【典例3】各项为正数的等比数列{a n }中,a 2与a 10的等比中项为√33,则log 3a 4+log 3a 8= .【典例4】已知公差不为0的等差数列的第2,3,6项依次构成一个等比数列,则该等比数列的公比为 .【典例5】已知正项等比数列{}n a ,向量3(a a =,8)-,7(b a =,2),若a b ⊥,则212229log log log (a a a ++⋯+= )A .12B .16C .18D .26log 5+【典例6】.在正项等比数列{}n a 中,374a a =,数列2{log }n a 的前9项之和为( ) A .11B .9C .15D .13【典例7】.已知n S 是等比数列{}n a 的前n 项和,且3S ,9S ,6S 成等差数列,256a a +=,则8a = .【典例8】.已知{}n a 为等比数列,n S 是它的前n 项和.若2312a a a =,且4a 与72a 的等差中项为34,则5S = .综合练习一.选择题(共5小题)1.设正项等差数列{a n}的前n项和为S n,若S2019=6057,则1a2+4a2018的最小值为()A.1 B.23C.136D.322.设S n为等差数列{a n}的前n项和,已知a1=S3=3,则S4的值为()A.﹣3 B.0 C.3 D.63.在等差数列{a n}中,S n表示{a n}的前n项和,若a3+a6=3,则S8的值为()A.3 B.8 C.12 D.244.已知正项等比数列{a n}满足:a7=a6+2a5,若存在两项a m、a n,使得a m a n=16a12,则1m +9n的最小值为()A.32B.83C.114D.不存在5.已知等比数列{a n}的前n项积为T n,若a1=﹣24,a4=−89,则当T n取最大值时,n的值为()A.2 B.3 C.4 D.6二.填空题(共1小题)6.已知数列1,a1,a2,9是等差数列,数列1,b1,b2,b3,9是等比数列,则b2a1+a2的值为.三.解答题(共2小题)7.已知{a n}为等差数列,且a1+a3=8,a2+a4=12.(1)求数列{a n}的通项公式;(2)记的{a n}前n项和为S n,若a1,a k,S k+2成等比数列,求正整数k的值.8.已知单调递增的等比数列{a n}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)若b n=a n log12a n,S n=b1+b2+b3+…+b n,对任意正整数n,S n+(n+m)a n+1<0恒成立,试求m的取值范围.。
2021届高考数学(新课标) 题型全归纳 数列要点讲解

数 列一、高考要求理解数列的有关概念,了解递推公式是给出数列的一种方法,并能依据递推公式写出数列的前n 项.理解等差(比)数列的概念,把握等差(比)数列的通项公式与前n 项和的公式. 并能运用这些学问来解决一些实际问题.了解数学归纳法原理,把握数学归纳法这一证题方法,把握“归纳—猜想—证明”这一思想方法. 二、热点分析1.数列在历年高考中都占有较重要的地位,一般状况下都是一个客观性试题加一个解答题,分值占整个试卷的10%左右.客观性试题主要考查等差、等比数列的概念、性质、通项公式、前n 项和公式、极限的四则运算法则、无穷递缩等比数列全部项和等内容,对基本的计算技能要求比较高,解答题大多以考查数列内容为主,并涉及到函数、方程、不等式学问的综合性试题,在解题过程中通常用到等价转化,分类争辩等数学思想方法,是属于中高档难度的题目.2.有关数列题的命题趋势 (1)数列是特殊的函数,而不等式则是深刻生疏函数和数列的重要工具,三者的综合求解题是对基础和力气的双重检验,而三者的求证题所显现出的代数推理是近年来高考命题的新热点 (2)数列推理题是新毁灭的命题热点.以往高考常使用主体几何题来考查规律推理力气,近两年在数列题中也加强了推理力气的考查。
(3)加强了数列与极限的综合考查题3.娴熟把握、机敏运用等差、等比数列的性质。
等差、等比数列的有关性质在解决数列问题时应用格外广泛,且格外机敏,主动发觉题目中隐含的相关性质,往往使运算简洁秀丽 .如243546225a a a a a a ++=,可以利用等比数列的性质进行转化:从而有223355225a a a a ++=,即235()25a a +=. 4.对客观题,应留意寻求简捷方法 解答历年有关数列的客观题,就会发觉,除了常规方法外,还可以用更简捷的方法求解.现介绍如下: ①借助特殊数列. ②机敏运用等差数列、等比数列的有关性质,可更加精确 、快速地解题,这种思路在解客观题时表现得更为突出,很多数列客观题都有机敏、简捷的解法5.在数列的学习中加强力气训练 数列问题对力气要求较高,特殊是运算力气、归纳猜想力气、转化力气、规律推理力气更为突出.一般来说,考题中选择、填空题解法机敏多变,而解答题更是考查力气的集中体现,尤其近几年高考加强了数列推理力气的考查,应引起我们足够的重视.因此,在平常要加强对力气的培育。
专题04 三角函数-2021年高考数学复习思维导图(人教版)
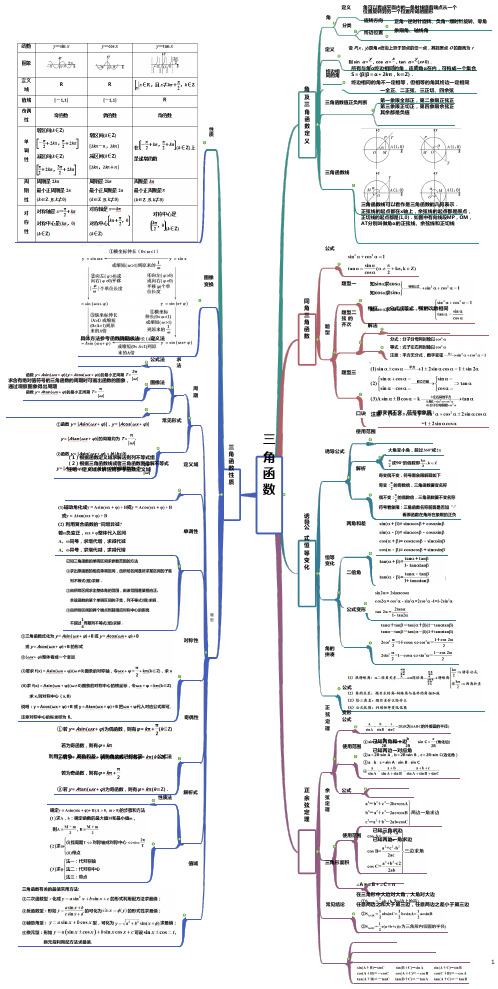
角旋转方向
分类
终边位置
正角--逆时针旋转、负角--顺时针旋转、零角象限角、轴线角
定义
终边相
同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合
S={β|β=α+2kπ,k∈Z}.
终边相同的角不一定相等,但相等的角其终边一定相同
定义域函数单调性公式恒等题
型
对称性
角的拼凑
公式
奇偶性
正
弦变形
定公式
理
利用二倍角、两角和差、辅助角公式进行化简
公式法
使用范围
已知两角和一边 已知两边一对应角
性质法
解析式
正余公式
余弦
弦定
定理
理
使用范围
已知三角求边
已知两边一角求边
值域三角形面积
常见结论
∠A+∠B+∠C=π
在三角形中大边对大角,大角对大边
任意两边之和大于第三边,任意两边之差小于第三边
图像变换
具体方法参考函数周期求法
求含有绝对值符号的三角函数的周期时可画出函数的图象,通过观察图象得出周期
定义法
公式法求法
图像法
周
期
特征分式或等式,弦的次数相同
解法
(1)根据函数定义域求解法则列不等式组
常见形式
奇变偶不变,符号看象限
(2)根据三角函数线或者三角函数图像解不等式
注明:定义域求解法则参考函数定义域
角一全正、二正弦、三正切、四余弦
及
三三角函数值正负判断
角函
性数
质定
义
第一象限全部正,第二象限正弦正第三象限正切正,第四象限余弦正其余都是负值
新高考数学高中数学考点归纳

新高考数学高中数学考点归纳新高考数学:高中数学考点归纳随着新高考改革的不断深入,高中数学的教学内容和考试重点也在不断变化。
为了更好地应对高考,我们需要对高中数学考点进行归纳和总结。
本文将针对新高考数学中高中数学考点的归纳进行探讨。
一、函数与导数函数是高中数学的重要组成部分,而导数是研究函数的重要工具。
在新高考中,函数与导数仍然是重点和难点。
考生需要掌握函数的定义域、值域、单调性、奇偶性、周期性等性质,同时还需要掌握导数的概念、运算规则和运用方法。
导数的应用在新高考中逐渐增多,如最值问题、不等式证明等。
二、三角函数与平面向量三角函数与平面向量是高中数学的基础内容,也是考试的重点。
考生需要掌握三角函数的性质、诱导公式、和差角公式等基础知识,同时还需要掌握平面向量的基本概念和运算法则。
在考试中,三角函数与平面向量常常结合其他知识点一起考查,如解三角形、数列等问题。
三、数列与不等式数列是不等式的基础,两个知识点之间有着密切的。
考生需要掌握数列的通项公式、前n项和公式等基本知识,同时还需要掌握不等式的性质和证明方法。
在考试中,数列与不等式常常结合其他知识点一起考查,如最值问题、解方程等问题。
四、解析几何与立体几何解析几何与立体几何是高中数学的两个重要分支。
考生需要掌握直线、圆、椭圆、双曲线、抛物线等图形的方程和性质,同时还需要掌握空间几何的基本概念和定理。
在考试中,解析几何与立体几何常常结合其他知识点一起考查,如面积、体积等问题。
五、统计与概率统计与概率是高中数学的两个重要分支,也是实际生活中应用广泛的领域。
考生需要掌握统计的基本概念和方法,如平均数、方差、回归分析等,同时还需要掌握概率的基本概念和计算方法。
在考试中,统计与概率常常结合其他知识点一起考查,如独立事件、互斥事件等问题。
六、复数与算法复数与算法是高中数学的进阶内容,也是部分省份高考的必考知识点。
考生需要掌握复数的概念、方程的求解方法等基础知识,同时还需要了解算法的基本思想和常见的算法类型。
2021年高考数学重要知识点大全

2021年高考数学重要知识点大全2021年高考数学重要知识点有哪些你知道吗?生活中处处会运用到数学,所以我们有了数学这门课程。
学数学是因为我们的生活离不开数学,数学是我们生活中不可缺少的一部份。
一起来看看2021年高考数学重要知识点,欢迎查阅!高考数学重要知识点(一)导数第一定义设函数y=f(x)在点x0的某个领域内有定义,当自变量x 在x0处有增量△x(x0+△x也在该邻域内)时,相应地函数取得增量△y=f(x0+△x)-f(x0);如果△y与△x之比当△x→0时极限存在,则称函数y=f(x)在点x0处可导,并称这个极限值为函数y=f(x)在点x0处的导数记为f'(x0),即导数第一定义(二)导数第二定义设函数y=f(x)在点x0的某个领域内有定义,当自变量x 在x0处有变化△x(x-x0也在该邻域内)时,相应地函数变化△y=f(x)-f(x0);如果△y与△x之比当△x→0时极限存在,则称函数y=f(x)在点x0处可导,并称这个极限值为函数y=f(x)在点x0处的导数记为f'(x0),即导数第二定义(三)导函数与导数如果函数y=f(x)在开区间I内每一点都可导,就称函数f(x)在区间I内可导。
这时函数y=f(x)对于区间I内的每一个确定的x值,都对应着一个确定的导数,这就构成一个新的函数,称这个函数为原来函数y=f(x)的导函数,记作y',f'(x),dy/dx,df(x)/dx。
导函数简称导数。
(四)单调性及其应用1.利用导数研究多项式函数单调性的一般步骤(1)求f¢(x)(2)确定f¢(x)在(a,b)内符号(3)若f¢(x)>0在(a,b)上恒成立,则f(x)在(a,b)上是增函数;若f¢(x) 2.用导数求多项式函数单调区间的一般步骤(1)求f¢(x)(2)f¢(x)>0的解集与定义域的交集的对应区间为增区间;f¢(x) 全国卷高考数学知识点必修一:1、集合与函数的概念 (这部分知识抽象,较难理解)2、基本的初等函数(指数函数、对数函数)3、函数的性质及应用 (比较抽象,较难理解)必修二:1、立体几何(1)、证明:垂直(多考查面面垂直)、平行(2)、求解:主要是夹角问题,包括线面角和面面角这部分知识是高一学生的难点,比如:一个角实际上是一个锐角,但是在图中显示的钝角等等一些问题,需要学生的立体意识较强。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x1 y1 x2 y2 0 。 a b (x1 x2 , y1 y2 ) 。 与加法运 算有同样的坐标表示。 a b (x1 x2, y1 y2 ) MN (xN xM , yN yM ) 。
a ( x, y) 。
辑
用
充要 条件
充分条件 必要条件 充要条件
p q , p 是 q 的充分条件 p q , q 是 p 的必要条件 p q , p, q 互为充要条件
若命题 p 对应集合 A ,命题 q 对应集合 B ,则 p q 等价于 A B ,p q 等 价于 A B 。
语
或命题 p q , p, q 有一为真即为真, p, q 均为假时才为假。 类比集合的并
a
b
a abb
0
。
a b 的平 行四边形 法则、三角 形法 则。
a b b a, (a b) c a (b c)
ab 的三角 形法则。
MN ON OM 。
a 为向量, 0 与 a方向相同 ,
0 与 a 方向相反, a a 。
坐标表示(向量坐标上下文理解)
复数相等
规定:i2 1 ;实数可以与它进行四则运算,并且运算时原有的加、 乘运算律仍成立。 i4k 1,i4k 1 i,i4k 2 1,i4k 3 i(k Z) 。 形如 a bi(a,b R) 的数叫做复数,a 叫做复数的实部,b 叫做复数 的虚部。 b 0 时叫虚数、 a 0,b 0 时叫纯虚数。
a,b , b cos 叫做 b 在 a 方向上的投影。【注意:投影是数量】
e1, e2 不共线,存在唯一的实数对 (, ) ,使 a e1 e2 。若 e1, e2 为 x, y 轴上
的单位正交向量, (, ) 就是向量 a 的坐标。
一般表示
a,b ( b 0 共线 存 在唯一实数 ,
平
运算 算律
面
向
减法 法则
量
运算 分解
数乘 各 运算 种 运 算
概念 算律 概念
数量 主要 积运 性质 算
算律
既有大小又有方向的量,表示向量的有向线段的长度叫做该向量的模。 长度为 0 ,方向任意的向量。【 0 与任一非零向量共线】
方向相同或者相反的两个非零向量叫做平行向量,也叫共线向量。
起点放在一点的两向量所成的角,范围是 0, 。 a, b 的夹角记为 a,b 。
a bi c di(a,b,c,d R) a c,b d
复数 运算
几何 意义
共轭复数 加减法 乘法
实部相等,虚部互为相反数。即 z a bi ,则 z a bi 。 (a bi) (c di) (a c) (b d )i , (a,b, c, d R) 。
(a bi)(c di) (ac bd ) (bc ad )i , (a,b, c, d R)
先要进行分母实数化(分母乘以自己的共轭复数),在进行四则运算时,可以把 i 看作成一个独立的 字母,按照实数的四则运算律直接进行运算,并随时把 i2 换成-1
第 2 页 共 24 页
3.平面向量
向量 重 0 向量
要 平行向量
概 向量夹角 念
投影
重 基本定理
要
法
则 定 共线条件
理 垂直条件
加法 法则
A B, B A A B
n 个元素集合子集数 2n 。
合 运算
交集
A B x | x A, 且x B CU (A B) (CU A) (CU B)
并集
A B x | x A, 或x B CU (A B) (CU A) (CU B)
集 合
补集
CU A x | x U 且x A CU (CU A) A
与
概念 能够判断真假的语句。
常
原命题:若 p ,则 q
原命题与逆命题,否命题与逆否命题互
用
命题
四种 逆命题:若 q ,则 p
逆;原命题与否命题、逆命题与逆否命
逻 辑常
命题 否命题:若 p ,则 q
题互否;原命题与逆否命题、否命题与
逆否命题:若 q ,则 p
逆命题互为逆否。互为逆否的命题等价。
用用 语逻
第 3 页 共 24 页
与上面的数量积、数乘等具有同样 的坐标表示方法。
标准方程
圆的方程 x 2+ y 2= r 2
(x – a ) 2 + ( y – b ) 2 = r 2
圆心 (0,0)
(a,b)
半径 r
r
一般方程
x 2 + y 2 +D x + E y + F = 0
D , E 2 2
1 D2 E2 4F 2
逻辑 连接词
且命题 非命题
p q , p, q 均为真时才为真, p, q 有一为假即为假。 类比集合的交
p 和 p 为一真一假两个互为对立的命题。
类比集合的补
量词
全称量词 存在量词
,含全称量词的命题叫全称命题,其否定为特称命题。 ,含存在量词的命题叫特称命题,其否定为全称命题。
2.复数
概念
虚数单位 复数
除法
(a
bi)
(c
di)
ac c2
bd d2
bc c2
da d2
i(c
di
0,
a,b, c, d
R)
复数 z a bi 一一对应 复平面内的点 Z (a,b) 一一对应 向量 OZ
向量 OZ 的模叫做复数的模, z a2 b2
大多数复数问题,主要是把复数化成标准的 z a bi 的类型来处理,若是分数形式 z= a bi ,则首 c di
(a) ( )a cos a,b
a a
a
2
,
a b
a
b
。
ab (ba)ab,(aa(bb))ca(acb)
bc
。
,
与数乘运算有同样的坐标表示。
a b
x1x2
y1 y2
。
a x2 y2 ,
x1x2 y1 y2 x12 y12 x22 y22
高 中 数 学
考点归纳表格
第 1 页 共 24 页
高中数学知识汇总
1.集合与常用逻辑用语
概念 一组对象的全体. x A, x A 。
元素特点:互异性、无序性、确定性。
子集 x A x B A B 。
A;
关系 集
真子集 相等
x A x B,x0 B, x0 A A B A B, B C A C
