数字信号处理实验答案
数字信号处理课后习题答案(全)1-7章

(5)y(n)=x2(n)
(6)y(n)=x(n2)
(7)y(n)=
n
(8)y(n)=x(n)sin(ωxn(m) )
m0
解: (1) 令输入为
输出为
x(n-n0)
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2) y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2)
所以 T[ax1(n)+bx2(n)]=aT[x1(n)]+bT[x2(n)]
第 1 章 时域离散信号和时域离散系统
(2) 令输入为
输出为
x(n-n0)
y′(n)=2x(n-n0)+3 y(n-n0)=2x(n-n0)+3=y′(n) 故该系统是非时变的。 由于
T[ax1(n)+bx2(n)]=2ax1(n)+2bx2(n)+3 T[ax1(n)]=2ax1(n)+3 T[bx2(n)]=2bx2(n)+3 T[ax1(n)+bx2(n)]≠aT[x1(n)]+bT[x2(n)] 故该系统是非线性系统。
=2x(n)+x(n-1)+ x(n-2)
将x(n)的表示式代入上式, 得到 1 y(n)=-2δ(n+2)-δ(n+1)-0.5δ(2n)+2δ(n-1)+δ(n-2)
+4.5δ(n-3)+2δ(n-4)+δ(n-5)
第 1 章 时域离散信号和时域离散系统
8. 设线性时不变系统的单位脉冲响应h(n)和输入x(n)分别有以下三种情况,
(3) 如果|x(n)|≤M, 则|y(n)|≤ nn0|x(k)|≤|2n0+1|M, 因 k nn0
数字信号处理实验答案

实验一熟悉Matlab环境一、实验目的1.熟悉MATLAB的主要操作命令。
2.学会简单的矩阵输入和数据读写。
3.掌握简单的绘图命令。
4.用MATLAB编程并学会创建函数。
5.观察离散系统的频率响应。
二、实验内容认真阅读本章附录,在MATLAB环境下重新做一遍附录中的例子,体会各条命令的含义。
在熟悉了MATLAB基本命令的基础上,完成以下实验。
上机实验内容:(1)数组的加、减、乘、除和乘方运算。
输入A=[1 2 3 4],B=[3 4 5 6],求C=A+B,D=A-B,E=A.*B,F=A./B,G=A.^B并用stem语句画出A、B、C、D、E、F、G。
clear all;a=[1 2 3 4];b=[3 4 5 6];c=a+b;d=a-b;e=a.*b;f=a./b;g=a.^b;n=1:4;subplot(4,2,1);stem(n,a);xlabel('n');xlim([0 5]);ylabel('A');subplot(4,2,2);stem(n,b);xlabel('n');xlim([0 5]);ylabel('B');subplot(4,2,3);stem(n,c);xlabel('n');xlim([0 5]);ylabel('C');subplot(4,2,4);stem(n,d);xlabel('n');xlim([0 5]);ylabel('D');subplot(4,2,5);stem(n,e);xlabel('n');xlim([0 5]);ylabel('E');subplot(4,2,6);stem(n,f);xlabel('n');xlim([0 5]);ylabel('F');subplot(4,2,7);stem(n,g);xlabel('n');xlim([0 5]);ylabel('G');(2)用MATLAB实现下列序列:a) x(n)=0.8n0≤n≤15b) x(n)=e(0.2+3j)n0≤n≤15c) x(n)=3cos(0.125πn+0.2π)+2sin(0.25πn+0.1π) 0≤n≤15d) 将c)中的x(n)扩展为以16为周期的函数x16(n)=x(n+16),绘出四个周期。
数字信号处理实验课后答案

数字信号处理实验课后答案数字信号处理实验课后答案【篇一:数字信号处理第三版课后实验程序(高西全)】txt>close all;clear all%======内容1:调用filter解差分方程,由系统对u(n)的响应判断稳定性====== a=[1,-0.9];b=[0.05,0.05]; %系统差分方程系数向量b和ax1n=[1 1 1 1 1 1 1 1 zeros(1,50)]; %产生信号x1(n)=r8(n)x2n=ones(1,128); %产生信号x2(n)=u(n)hn=impz(b,a,58); %求系统单位脉冲响应h(n)subplot(2,2,1);y=h(n);tstem(hn,y); %调用函数tstem绘图title((a) 系统单位脉冲响应h(n));box ony1n=filter(b,a,x1n); %求系统对x1(n)的响应y1(n)subplot(2,2,2);y=y1(n);tstem(y1n,y);title((b) 系统对r8(n)的响应y1(n));box ony2n=filter(b,a,x2n); %求系统对x2(n)的响应y2(n)subplot(2,2,4);y=y2(n);tstem(y2n,y);title((c) 系统对u(n)的响应y2(n));box on%===内容2:调用conv函数计算卷积============================ x1n=[1 1 1 1 1 1 1 1 ]; %产生信号x1(n)=r8(n)h1n=[ones(1,10) zeros(1,10)];h2n=[1 2.5 2.5 1 zeros(1,10)];y21n=conv(h1n,x1n);y22n=conv(h2n,x1n);figure(2)subplot(2,2,1);y=h1(n);tstem(h1n,y); %调用函数tstem绘图title((d) 系统单位脉冲响应h1(n));box onsubplot(2,2,2);y=y21(n);tstem(y21n,y);title((e) h1(n)与r8(n)的卷积y21(n));box onsubplot(2,2,3);y=h2(n);tstem(h2n,y); %调用函数tstem绘图title((f) 系统单位脉冲响应h2(n));box onsubplot(2,2,4);y=y22(n);tstem(y22n,y);title((g) h2(n)与r8(n)的卷积y22(n));box on%=========内容3:谐振器分析======================== un=ones(1,256); %产生信号u(n)n=0:255;xsin=sin(0.014*n)+sin(0.4*n); %产生正弦信号a=[1,-1.8237,0.9801];b=[1/100.49,0,-1/100.49]; %系统差分方程系数向量b和a y31n=filter(b,a,un); %谐振器对u(n)的响应y31(n) y32n=filter(b,a,xsin); %谐振器对u(n)的响应y31(n)figure(3)subplot(2,1,1);y=y31(n);tstem(y31n,y);title((h) 谐振器对u(n)的响应y31(n));box onsubplot(2,1,2);y=y32(n);tstem(y32n,y);title((i) 谐振器对正弦信号的响应y32(n));box on10.2.2 实验程序清单1 时域采样理论的验证程序清单% 时域采样理论验证程序exp2a.mtp=64/1000; %观察时间tp=64微秒%产生m长采样序列x(n)% fs=1000;t=1/fs;fs=1000;t=1/fs;m=tp*fs;n=0:m-1;a=444.128;alph=pi*50*2^0.5;omega=pi*50*2^0.5;xnt=a*exp(-alph*n*t).*sin(omega*n*t);xk=t*fft(xnt,m); %m点fft[xnt)]yn=xa(nt);subplot(3,2,1);tstem(xnt,yn); %调用自编绘图函数tstem绘制序列图box on;title((a) fs=1000hz);k=0:m-1;fk=k/tp;subplot(3,2,2);plot(fk,abs(xk));title((a) t*ft[xa(nt)],fs=1000hz);xlabel(f(hz));ylabel(幅度);axis([0,fs,0,1.2*max(abs(xk))])%===================================== ============ % fs=300hz和fs=200hz的程序与上面fs=1000hz完全相同。
数字信号处理实验五答案.doc

1・信号产生函数mstg清单function xt=xtg(N)%实验五信号x(t)产生,并显示信号的幅频特性曲线%xt=xtg产生一个长度为N,冇加性高频噪声的单频调幅信号xt,N二1000., %采样频率Fs二1000Hz%载;波频率fc=Fs/10=100Hz,调制正弦波频率f0=fc/10=10Hz.N=1000;Fs=l000;T=1/Fs;Tp=N*T;t二0:T: (N-1)*T;fc=Fs/10 ;f0=fc/10; %载波频率fc=Fs/10,单频调制信号频率为f0=Fc/10;int=cos (2*pi*f0*t) ; %产生讥频止弦波调制信号mt,频率为f0ct=cos(2*pi*fc*t) ; %产生载波iF弦波信号ct,频率为fc xt=mt. *ct; %相乘产生单频调制信号xtnt=2*rand(l, N)T; %产生随机噪声nI%=======设计高通滤波器hn,用于滤除噪声nt中的低频成分,牛成高通噪声======= fp=150;fs=200;Rp=0. l;As=70; % 滤波器指标fb=[fp, fs] ;m二[0, 1]; % 计算remezord函数所需参数f, m, devdev=[107-As/20), (10" (Rp/20)-l)/(10"(Rp/20)+l)];[n, fo, mo, W]=remezord(fb, m, dev, Fs) ; % 确定rcinezP^i数所盂参数hn=rcmcz (n, fo, mo, W) ; %调用rcme函数进行设计,用J:滤除噪声nt中的低频成分yt二f订ter (hn, 1, 10*nt) ; %滤除随机噪声中低频成分,牛成高通噪声yt%========================以下为绘图部分===================================== xt=xt+yt; %噪声加信号fst=fft(xt, N);k=0:N-l;f=k/Tp;subplot (2, 1, 1) ;plot (t, xt) ;grid;xlabel(' t/s') ;ylabel (' x(t)'); axis([0, Tp/5, min(xt), max(xt)]);titleC (a)信号加噪声波形') subplot (2, 1, 2) ;plot (f, abs(fst)/max(abs (fst))) ;grid; titleC (b)信号加噪声的频谱') axis(f0, Es/2, 0, 1. 2]) ;xlabel C f/Hz');ylabel C if®度') 2•产生FIR数字滤波器设计及软件实现clear all;%==using the function ,xtg£「to plot the picture of xt and its spectrogram==xt=xtg;N=1000;fp=120; fs=150;Rp=0.2;As=60;Fs=1000; %input the defined parameters%to design the filter using th巳Windows methodwc= (fp+fs)/Fs; Ethe cut-off frequence of the filterB=2*pi*(fs-fp)/Fs; %the width of prototype filterNb=cei丄(11*pi/B); %the length of window of blackmanhn=f ir1 (Nb-1,wc,blackman(Nb));Hw=abs(fft(hn,1024)); % the frequency characteristic of the filter ywt = f ft f i]_t (hn z xt』N);%to filter xt using fftfilt%to draw the figure using the Windows methodf=[0:1023]*Fs/1024; ~figure (2)subplot(2f1,1);plot(f,20*logl0(Hw/max (Hw)));grid;xlabel ( 1f/Hz 1);ylabel(1 Amplitude 1);title ( 1 the frequency characteristic of the low-pass filter 1); axis ( [0,Fs/2z-120, 20]);t=[0:N-1]/Fs;Tp=N/Fs;subplot (2f1,2);plot (t,ywt);grid;xlabel(1t/s1);ylabel(1y_w(t) T);title ( 1 the signal waves after filtering noises 1);axis([0,Tp/2,-1,1]);%to design the filter using the best uniform approximation method fb=[fp z fs];m=[1,0];% define the parameters of remezorddev=[ (10A (Rp/20)-1)/(10A(Rp/20)+1),10A(-As/20)];[Ne z fo, mo z W]=remezord(fb,m, dev,Fs); %define the parameters of remez hn=remez(Ne,fmo z W);Hw=abs(fft(hn z1024)); % the frequency characteristic of the filteryet=fft£i1t(hn/Xt’N);%to filter xt using filt%to draw the figure using the best uniform approximation methodf igure(3);subplot(2,1,1);f=[0:1023]*Fs/1024;plot (f, 20*logl0 (Hw/max (Hw) ) ) ; grid; xlabel ( 1 f/Hz ' ) ; ylabel ( f Amplitude 1 ); title ( 1 the frequency characteristic of the low-pass filter 1);axis([0,Fs/2,-80,10]);subplot (2, 1 z 2 ) ; plot (t, yet) ; grid; xlabel ( 11/s ' ) ; ylabel ( ' y_e (t) 1 ); title ( 1 the signal waves after filtering noises');axis([0,Tp/2,-1,1]);⑻信号加噪声波形105e oX-5-100 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2t/s(b)信号加噪声的频谱1® 0.50 50 100 150 200 250 300 350 400 450 500f/Hz-800 50 100 150 200 250 300 350400 450 500f/Hzthe signal waws after filtering noises050.5 0 0 0.05 0.1 0.15 0.2 0.250.3 0.35 0.4 0.45 0.5 t/s 0-20-40-60the frequency characteristic of the low-pass filter。
数字信号处理实验(吴镇扬)答案-2
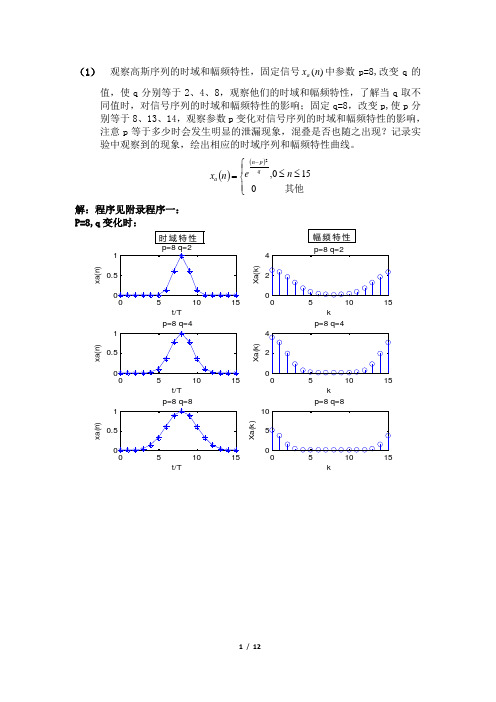
(1) 观察高斯序列的时域和幅频特性,固定信号)(n x a 中参数p=8,改变q 的值,使q 分别等于2、4、8,观察他们的时域和幅频特性,了解当q 取不同值时,对信号序列的时域和幅频特性的影响;固定q=8,改变p,使p 分别等于8、13、14,观察参数p 变化对信号序列的时域和幅频特性的影响,注意p 等于多少时会发生明显的泄漏现象,混叠是否也随之出现?记录实验中观察到的现象,绘出相应的时域序列和幅频特性曲线。
()()⎪⎩⎪⎨⎧≤≤=-其他0150,2n e n x q p n a解:程序见附录程序一:P=8,q 变化时:t/T x a (n )k X a (k )t/T x a (n )p=8 q=4k X a (k )p=8 q=4t/Tx a (n )p=8 q=8kX a (k )p=8 q=8幅频特性时域特性t/T x a (n )p=8 q=8k X a (k )p=8 q=8t/T x a (n )51015k X a (k )p=13 q=8t/Tx a (n )p=14 q=851015kX a (k )p=14 q=8时域特性幅频特性分析:由高斯序列表达式知n=p 为期对称轴; 当p 取固定值时,时域图都关于n=8对称截取长度为周期的整数倍,没有发生明显的泄漏现象;但存在混叠,当q 由2增加至8过程中,时域图形变化越来越平缓,中间包络越来越大,可能函数周期开始增加,频率降低,渐渐小于fs/2,混叠减弱;当q 值固定不变,p 变化时,时域对称中轴右移,截取的时域长度渐渐地不再是周期的整数倍,开始无法代表一个周期,泄漏现象也来越明显,因而图形越来越偏离真实值,p=14时的泄漏现象最为明显,混叠可能也随之出现;(2) 观察衰减正弦序列 的时域和幅频特性,a=0.1,f=0.0625,检查谱峰出现的位置是否正确,注意频谱的形状,绘出幅频特性曲线,改变f ,使f 分别等于0.4375和0.5625,观察这两种情况下,频谱的形状和谱峰出现的位置,有无混叠和泄漏现象?说明产生现象的原因。
数字信号处理(第三版)-课后习题答案全-(原题+答案+图)
将x(n)的表示式代入上式, 得到 1 y(n)=-2δ(n+2)-δ(n+1)-0.5δ(2n)+2δ(n-1)+δ(n-2)
+4.5δ(n-3)+2δ(n-4)+δ(n-5)
第 1 章 时域离散信号和时域离散系统
8. 设线性时不变系统的单位脉冲响应h(n)和输入x(n)分别有以下三种情况,
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
(5)y(n)=x2(n)
(6)y(n)=x(n2)
(7)y(n)=
n
(8)y(n)=x(n)sin(ωxn(m) )
m0
解: (1) 令输入为
输出为
x(n-n0)
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2) y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2)
x(m)h(n-m)
m
第 1 章 时域离散信号和时域离散系统
题7图
第 1 章 时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
数字信号处理-原理与实践(方勇)习题答案(1-2)

第一章1-1 有一个连续信号)2cos()(ψπ+=ft t x a ,式中Hz f 20=,2πψ=,(1) 求出)(t x a 的周期;(2) 用采样间隔s T 02.0=对)(t x a 进行采样,写出采样信号)(ˆt xa 的表达式; (3) 画出对应)(ˆt xa 的时域离散信号(序列))(n x 的波形,并求出)(n x 的周期。
解:(1))(t x a 的周期是s fT a 05.01==(2)∑∞-∞=-+=n a nT t fnT t x)()2cos()(ˆδψπ∑∞-∞=-+=n nT t nT )()40cos(δψπ(3))(n x 的数字频率为πω8.0=,252=ωπ周期5=N 。
)28.0cos()(ππ+=n n x ,画出其波形如题1-1图所示。
题1-1图 1-2 设)sin()(t t x a π=,()()sin()a s s x n x nT nT π==,其中s T 为采样周期。
(1))(t x a 信号的模拟频率Ω为多少? (2)Ω和ω的关系是什么?(3)当s T s 5.0=时,)(n x 的数字频率ω为多少? 解:(1))(t x a 的模拟频率s rad /π=Ω。
(2)Ω和ω的关系是:s T ⋅Ω=ω。
(3)当s T s 5.0=时,rad πω5.0=。
1-3 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1))873cos()(ππ-=n A n x ,A 为常数;(2))81()(π-=n j e n x 。
解: (1)πω73=,3142=ωπ,这是有理数,因此是周期序列,周期是14=T ; (2)81=ω,πωπ162=,这是无理数,因此是非周期序列。
1-4 研究一个线性时不变系统,其单位脉冲响应为指数序列)()(n u a n h n =,10<<a 。
对于矩阵输入序列,1,01()0N n N R n ≤≤-⎧=⎨⎩,其他 求出输出序列,并用MA TLAB 计算,比较其结果。
数字信号处理课后习题答案(吴镇扬)

习题一 (离散信号与系统)1.1周期序列,最小周期长度为5。
1.2 (1) 周期序列,最小周期长度为14。
(2) 周期序列,最小周期长度为56。
1.5()()()()()()()11s a s s s a n s s a s n X j x t p t X j ΩP j Ω2n τn τj sin j Ωjn e X 2n π2n n τj Sa X j jn e 2T 2πττ∞=-∞∞=-∞Ω==*⎡⎤⎣⎦ΩΩ⎛⎫-=-Ω ⎪⎝⎭ΩΩ⎛⎫-=Ω-Ω ⎪⎝⎭∑∑F 1.6 (1) )(ωj e kX (2) )(0ωωj n j e X e (3) )(21)(2122ωωj j e X e X -+ (4) )(2ωj e X1.7 (1)0n z -(2)5.0||,5.0111>--z z(3)5.0||,5.0111<--z z(4)0||,5.01)5.0(11101>----z zz1.8 (1) 0,)11()(211>--=---z z z z z X N (2) a z az az z X >-=--,)1()(211(3)a z az z a az z X >-+=---,)1()(311211.9 1.10(1))1(2)(1----+n u n u n (2))1(24)()5.0(6--⋅--n u n u n n (3))()sin sin cos 1(cos 000n u n n ωωωω++(4) )()()(1n u a a a n a n ---+-δ1.11 (1) )(1z c X - (2) )(2z X (3) )()1(21z X z -+ (4) -+<<x x R z R z X /1/1),/1(1.12 (1)1,11<-ab ab(2) 1 (3) 00n a n1.13 (1) 该系统不是线性系统;该系统是时不变系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f=50;Um=1;nt=2; %ÊäÈëÐźÅƵÂÊ¡¢Õñ·ùºÍÏÔʾÖÜÆÚ¸öÊý N=16;T=1/f; %TΪÐźŵÄÖÜÆÚ dt=T/N; %²ÉÑùʱ¼ä¼ä¸ôn=0:nt*N-1; %½¨Á¢ÀëÉ¢ÐźŵÄʱ¼äÐòÁÐtn=n*dt; %È·¶¨Ê±¼äÐòÁÐÑùµãÔÚʱ¼äÖáÉϵÄλÖà x=Um*sin(2*f*pi*tn)+1; %²úÉúʱÓòÐźŠsubplot(2,1,1),plot(tn,x);%Á¬ÐøÐźŠaxis([0,2*T,0,2])subplot(2,1,2),stem(tn,x); %ÀëÉ¢ÐòÁÐ1-3f=200;Um=1;nt=2; %ÊäÈëÐźÅƵÂÊ¡¢Õñ·ùºÍÏÔʾÖÜÆÚ¸öÊý Fs=4000;N=Fs/f; %²ÉÑùƵÂÊ,Çó²ÉÑùµãÊýN T=1/f;%TΪÐźŵÄÖÜÆÚ dt=T/N; %²ÉÑùʱ¼ä¼ä¸ôn=0:nt*N-1; %½¨Á¢ÀëÉ¢ÐźŵÄʱ¼äÐòÁÐtn=n*dt; %È·¶¨Ê±¼äÐòÁÐÑùµãÔÚʱ¼äÖáÉϵÄλÖà x=Um*square(2*f*pi*tn,50); %²úÉúʱÓòÐźŠsubplot(2,1,1),stairs(tn,x); %Á¬ÐøÐźŠaxis([0,nt*T,1.1*min(x),1.1*max(x)]); subplot(2,1,2),stem(tn,x); %ÀëÉ¢ÐòÁÐ axis([0,nt*T,1.1*min(x),1.1*max(x)]);n1=-5:5;n01=-3;x1=[(n1-n01)==0]; %建立x1信号 n2=n1;n02=4;x2=[(n2-n02)==0]; %建立x2信号 x=x1+2.*x2; n=-5:5;stem(n,x,'filled');ylabel('x(n)=δ(n+3)+δ(n -4)');axis([min(n),max(n),1.1*min(x),1.1*max(x)]);x (n )=δ(n +3)+δ(n -4)2-2n1=-5:5;n01=2;x1=[(n1-n01)>=0]; %建立x1信号 n2=n1;n02=-2;x2=[(n2-n02)>=0]; %建立x2信号 x=x1+x2; n=-5:5;stem(n,x,'filled','k');axis([min(n),max(n),1.1*min(x),1.1*max(x)]);2-3n=0:20;n0=3;n1=-3;x=3*cos(2*pi*n/10); %建立原信号x(n) x1=3*cos(2*pi*(n-n0)/10); %建立x(n-2)信号 x2=3*cos(2*pi*(n-n1)/10); %建立x(n+2)信号 subplot(3,1,1),stem(n,x,'filled','k'); ylabel('x(n)');subplot(3,1,2),stem(n,x1,'filled','k'); ylabel('x(n-3)');subplot(3,1,3),stem(n,x2,'filled','k'); ylabel('x(n+3)');02468101214161820x (n )x (n -3)02468101214161820x (n +3)2-4n=0:24; x1=exp(-n/16); x2=5*sin(2*pi*n/10); x=x1.*x2;subplot(3,1,1),stem(n,x1,'filled'); subplot(3,1,2),stem(n,x2,'filled'); subplot(3,1,3),stem(n,x,'filled');2-5n=0:20; x=n.*sin(n); y1=(n-3).*sin(n-3); n2=-fliplr(n); y2=fliplr(x); y3=-x;y4=(-n+3).*sin(-n+3);y5=(n/2).*sin(n/2);figure(1);subplot(3,1,1),stem(n,x,'filled'); title('x(n)');subplot(3,1,2),stem(n,y1,'filled'); title('y1(n)');axis([0,20,-20,20]);subplot(3,1,3),stem(n2,y2,'filled'); title('y2(n)');figure(2)subplot(2,2,1),stem(n,x,'filled'); title('x(n)');subplot(2,2,2),stem(n,y3,'filled'); title('y3(n)');subplot(2,2,3),stem(n,y4,'filled'); title('y4(n)');subplot(2,2,4),stem(n,y5,'filled'); title('y5(n)');x(n)y1(n)y2(n)x(n)y3(n)y4(n)y5(n)4-1%½«°ÍÌØÎÖ˹ģÄâÂ˲¨Æ÷Ô-Ðͱ任³Éʵ¼ÊÄ£Äâ¸ßͨÂ˲¨Æ÷fp=6000;wp=2*pi*fp; %ÊäÈëʵ¼ÊÂ˲¨Æ÷µÄͨ´ø½ØֹƵÂÊfs=3500;ws=2*pi*fs; %ÊäÈëʵ¼ÊÂ˲¨Æ÷µÄ×è´ø½ØֹƵÂÊRp=1;As=40; %ÊäÈëÂ˲¨Æ÷µÄͨ×è´øË¥¼õÖ¸±ê%¼ÆËãÂ˲¨Æ÷µÄ½×ÊýºÍ3dB½ØֹƵÂÊ[n,wc]=buttord(wp,ws,Rp,As,'s')%¼ÆËãn½×Ä£ÄâµÍͨÔ-ÐÍ£¬µÃµ½×ó°ëƽÃæÁ㼫µã[z0,p0,k0]=buttap(n);b0=k0*poly(z0) %Çó¹éÒ»»¯µÄÂ˲¨Æ÷ϵÊýb0a0=poly(p0) %Çó¹éÒ»»¯µÄÂ˲¨Æ÷ϵÊýa0[H,w0]=freqs(b0,a0); %Çó¹éÒ»»¯µÄÂ˲¨Æ÷ƵÂÊÌØÐÔdbH=20*log10(abs(H)/max(abs(H))); %·ù¶È»¯Îª·Ö±´Öµ%±ä»»ÎªÊµ¼ÊÄ£ÄâͨÂ˲¨Æ÷[bt,at]=lp2hp(b0,a0,wc); %´Ó¹éÒ»»¯µÍͨ±ä»»µ½Êµ¼Ê¸ßͨ[Ht,wt]=freqs(bt,at); %Çóʵ¼ÊϵͳµÄƵÂÊÌØÐÔdbHt=20*log10(abs(Ht)/max(abs(Ht))); %·ù¶È»¯Îª·Ö±´Öµsubplot(3,1,1),plot(wt/2/pi,abs(Ht));axis([0,7000,0,1.1]);ylabel('·ù¶È');xlabel('f(Hz)');gridsubplot(3,1,2),plot(wt/2/pi,dbHt);axis([0,7000,-50,1]);ylabel('dB');xlabel('f(Hz)');gridsubplot(3,1,3),plot(wt/2/pi,angle(Ht));axis([0,7000,-4,4]);gridylabel('Ïàλ');xlabel('f(Hz)');度幅f(Hz)Bdf(Hz)位相f(Hz)4-2%½«ÍÖԲģÄâÂ˲¨Æ÷Ô-Ðͱ任³Éʵ¼ÊÄ£Äâ´ø×èÂ˲¨Æ÷fp1=3.5;wp1=2*pi*fp1; %ÊäÈë´ø×èÂ˲¨Æ÷µÄͨ´ø½ØֹƵÂÊfp2=5.5;wp2=2*pi*fp2;fs1=3;ws1=2*pi*fs1; %ÊäÈë´ø×èÂ˲¨Æ÷µÄ×è´ø½ØֹƵÂÊfs2=6;ws2=2*pi*fs2;wp=[wp1,wp2];ws=[ws1,ws2];bw=wp2-wp1;w0=sqrt(wp1*wp2); %Çóͨ´ø¿í¶ÈºÍÖÐÐÄƵÂÊRp=1;As=40; %ÊäÈëÂ˲¨Æ÷µÄͨ×è´øË¥¼õÖ¸±ê%¼ÆËãÂ˲¨Æ÷µÄ½×ÊýºÍ3dB½ØֹƵÂÊ[n,wn]=ellipord(wp,ws,Rp,As,'s')%¼ÆËãn½×Ä£ÄâµÍͨÔ-ÐÍ£¬µÃµ½×ó°ëƽÃæÁ㼫µã[z0,p0,k0]=ellipap(n,Rp,As);b0=k0*poly(z0); %Çó¹éÒ»»¯µÄÂ˲¨Æ÷ϵÊýb0a0=poly(p0); %Çó¹éÒ»»¯µÄÂ˲¨Æ÷ϵÊýa0[H,w]=freqs(b0,a0); %Çó¹éÒ»»¯µÄÂ˲¨Æ÷ƵÂÊÌØÐÔdbH=20*log10(abs(H)/max(abs(H))); %·ù¶È»¯Îª·Ö±´Öµ%±ä»»ÎªÊµ¼ÊÄ£Äâ´ø×èÂ˲¨Æ÷[bt,at]=lp2bp(b0,a0,w0,bw); %´Ó¹éÒ»»¯µÍͨ±ä»»µ½Ä£Äâ´ø×è[Ht,wt]=freqs(bt,at); %Çóʵ¼Ê´ø×èÂ˲¨Æ÷µÄƵÂÊÌØÐÔdbHt=20*log10(abs(Ht)/max(abs(Ht))); %·ù¶È»¯Îª·Ö±´Öµ%ʵ¼ÊÄ£Äâ´ø×èƵÂÊÌØÐÔ×÷ͼsubplot(1,2,1),plot(wt/2/pi,abs(Ht));axis([0,8,0,1.1]);ylabel('·ù¶È');xlabel('f(kHz)');gridsubplot(1,2,2),plot(wt/2/pi,dbHt);axis([0,8,-60,1]);ylabel('dB');xlabel('f(kHz)');grid幅度f(kHz)dBf(kHz)4-3%½«ÇбÈÑ©·ò¢ñÐÍÄ£ÄâÂ˲¨Æ÷Ô-Ðͱ任³Éʵ¼ÊÄ£Äâ´øͨÂ˲¨Æ÷fp1=3;wp1=2*pi*fp1; %ÊäÈë´øͨÂ˲¨Æ÷µÄͨ´ø½ØֹƵÂÊfp2=7;wp2=2*pi*fp2;fs1=4;ws1=2*pi*fs1; %ÊäÈë´øͨÂ˲¨Æ÷µÄ×è´ø½ØֹƵÂÊfs2=6;ws2=2*pi*fs2;wp=[wp1,wp2];ws=[ws1,ws2];bw=wp2-wp1;w0=sqrt(wp1*wp2);%Çóͨ´ø¿í¶ÈºÍÖÐÐÄƵÂÊRp=1;As=35; %ÊäÈëÂ˲¨Æ÷µÄͨ×è´øË¥¼õÖ¸±ê%¼ÆËãÂ˲¨Æ÷µÄ½×ÊýºÍ3dB½ØֹƵÂÊ[n,wn]=cheb1ord(wp,ws,Rp,As,'s')%¼ÆËãn½×Ä£ÄâµÍͨÔ-ÐÍ£¬µÃµ½×ó°ëƽÃæÁ㼫µã[z0,p0,k0]=cheb1ap(n,Rp);b0=k0*poly(z0) %Çó¹éÒ»»¯µÄÂ˲¨Æ÷ϵÊýb0a0=poly(p0) %Çó¹éÒ»»¯µÄÂ˲¨Æ÷ϵÊýa0[H,w]=freqs(b0,a0); %Çó¹éÒ»»¯µÄÂ˲¨Æ÷ƵÂÊÌØÐÔdbH=20*log10(abs(H)/max(abs(H))); %·ù¶È»¯Îª·Ö±´Öµ%±ä»»ÎªÊµ¼ÊÄ£Äâ´øͨÂ˲¨Æ÷[bt,at]=lp2bs(b0,a0,w0,bw); %´Ó¹éÒ»»¯µÍͨ±ä»»µ½Ä£Äâ´øͨ[Ht,wt]=freqs(bt,at); %Çóʵ¼Ê´øͨÂ˲¨Æ÷µÄƵÂÊÌØÐÔdbHt=20*log10(abs(Ht)/max(abs(Ht))); %·ù¶È»¯Îª·Ö±´Öµsubplot(1,2,1),plot(wt/2/pi,abs(Ht));axis([0,8,0,1.1]);ylabel('dB');xlabel('f(kHz)');gridsubplot(1,2,2),plot(wt/2/pi,dbHt);axis([0,8,-60,1]);ylabel('dB');xlabel('f(kHz)');griddBf(kHz)dBf(kHz)5-1%Êý×ÖÂ˲¨Æ÷Ö¸±êwpd=0.35*pi; %Â˲¨Æ÷µÄͨ´ø½ØֹƵÂÊwsd=0.2*pi; %Â˲¨Æ÷µÄ×è´ø½ØֹƵÂÊRp=1;As=15; %ÊäÈëÂ˲¨Æ÷µÄͨ×è´øË¥¼õÖ¸±ê%ת»»ÎªÄ£ÄâÔ-ÐÍÂ˲¨Æ÷Ö¸±êFs=10;T=1/Fs;wp=(2/T)*tan(wpd/2);ws=(2/T)*tan(wsd/2);%Ä£ÄâÔ-ÐÍÂ˲¨Æ÷¼ÆËã[n,wc]=buttord(wp,ws,Rp,As,'s') %¼ÆËã½×ÊýnºÍ½ØֹƵÂÊ[z0,p0,k0]=buttap(n); %¹éÒ»»¯ÇбÈÑ©·ò1ÐÍÔ-ÐÍÉè¼Æba=k0*poly(z0); %ÇóÔ-ÐÍÂ˲¨Æ÷ϵÊýbaa=poly(p0); %ÇóÔ-ÐÍÂ˲¨Æ÷ϵÊýa[ba1,aa1]=lp2hp(ba,aa,wc);%±ä»»ÎªÄ£ÄâµÍͨÂ˲¨Æ÷ %ÓÃË«ÏßÐԱ任·¨¼ÆËãÊý×ÖÂ˲¨Æ÷ϵÊý [bd,ad]=bilinear(ba1,aa1,Fs) %Ë«ÏßÐԱ任 %ÇóÊý×ÖϵͳµÄƵÂÊÌØÐÔ [H,w]=freqz(bd,ad);dbH=20*log10(abs(H)/max(abs(H))); %»¯Îª·Ö±´Öµsubplot(2,2,1),plot(w/pi,abs(H));ylabel('|H|');title('·ù¶ÈÏìÓ¦');axis([0,1,0,1.1]);grid subplot(2,2,2),plot(w/pi,angle(H));ylabel('\phi');title('ÏàλÏìÓ¦');axis([0,1,-4,4]);grid subplot(2,2,3),plot(w/pi,dbH);title('·ù¶ÈÏìÓ¦(dB)'); ylabel('dB');xlabel('ƵÂÊ');axis([0,1,-40,5]);grid subplot(2,2,4),zplane(bd,ad);axis([-1.1,1.1,-1.1,1.1]);title('Á㼫ͼ');|H |幅度响应相位响应幅度响应(dB)d B频率Real PartI m a g i n a r y P a r t零极图5-2%Êý×ÖÂ˲¨Æ÷Ö¸±êwsd1=0.4*pi;wsd2=0.6*pi; %Êý×ÖÂ˲¨Æ÷µÄͨ´ø½ØֹƵÂÊ wpd1=0.35*pi;wpd2=0.65*pi; %Êý×ÖÂ˲¨Æ÷µÄ×è´ø½ØֹƵÂÊ Rp=1;As=20; %ÊäÈëÂ˲¨Æ÷µÄͨ×è´øË¥¼õÖ¸±ê %ת»»ÎªÄ£ÄâÂ˲¨Æ÷Ö¸±ê Fs=10;T=1/Fs;wp1=(2/T)*tan(wpd1/2);wp2=(2/T)*tan(wpd2/2); wp=[wp1,wp2]; %Ä£ÄâÂ˲¨Æ÷µÄͨ´ø½ØֹƵÂÊ ws1=(2/T)*tan(wsd1/2);ws2=(2/T)*tan(wsd2/2); ws=[ws1,ws2]; %Ä£ÄâÂ˲¨Æ÷µÄ×è´ø½ØֹƵÂÊ bw=ws2-ws1;w0=sqrt(wp1*wp2);%Ä£Äâͨ´ø´ø¿íºÍÖÐÐÄƵÂÊ %Ä£ÄâÔ-ÐÍÂ˲¨Æ÷¼ÆËã[n,wn]=ellipord(wp,ws,Rp,As,'s') %¼ÆËã½×ÊýnºÍ½ØֹƵÂÊ [z0,p0,k0]=cheb1ap(n,Rp); %Éè¼Æ¹éÒ»»¯µÄÄ£ÄâÔ-ÐÍÂ˲¨Æ÷ ba1=k0*poly(z0); %ÇóÔ-ÐÍÂ˲¨Æ÷ϵÊýbaa1=poly(p0); %ÇóÔ-ÐÍÂ˲¨Æ÷ϵÊýa[ba,aa]=lp2bs(ba1,aa1,w0,bw); %±ä»»ÎªÄ£Äâ´ø×èÂ˲¨Æ÷ %ÓÃË«ÏßÐԱ任·¨¼ÆËãÊý×ÖÂ˲¨Æ÷ϵÊý [bd,ad]=bilinear(ba,aa,Fs) %ÇóÊý×ÖϵͳµÄƵÂÊÌØÐÔ [H,w]=freqz(bd,ad);dbH=20*log10(abs(H)/max(abs(H))); %»¯Îª·Ö±´Öµ %subplot(2,2,1),plot(w/pi,abs(H),'k');ylabel('·ù¶È');xlabel('ƵÂÊ/\pi');axis([0,1,0,1.1]);grid subplot(2,2,2),plot(w/pi,angle(H)/pi,'k');ylabel('Ïàλ');xlabel('ƵÂÊ/\pi');axis([0,1,-1,1]);grid subplot(2,2,3),plot(w/pi,dbH,'k');ylabel('·ù¶È(dB)');xlabel('ƵÂÊ/\pi');axis([0,1,-30,5]);grid subplot(2,2,4),zplane(bd,ad);axis([-1.1,1.1,-1.1,1.1]);ylabel('Á㼫ͼ');0.510.51幅度频率/π0.51-1-0.500.51相位频率/π0.51-30-20-100幅度(d B )频率/π-101-1-0.500.51Real Part零极图。
