2010年数学建模D题的答案
数学建模D题

数学建模D题储药柜的优化设计摘要储药柜采用横向隔板和竖向隔板交叉的形式形成了不同类型的储药槽,用以储存各种各样的药品。
为了保证药品分拣的准确率,防止发药错误,一个储药槽内只能摆放同一种药品。
因为药品种类的复杂性,为每一种药品都设计一款匹配的储药槽基本上是不可能的,而只用类型很少的较大的药槽来储存药品的话对于小型的药品来说又是浪费储存空间。
所以本文建模的目的就是要通过数学模型来找出最适合的储药柜大小类型,一方面满足储存多种类型药品的需要,一方面节省储存空间。
本文在建模的过程中主要运用了组距分组的思想,将不同大小规格的药品按照长宽高不同的要求分成不同的组别,采用一定的标准就规格相近的药品分为一类,再按照不同的排序方法进行排序,找出每一类中需要储存空间最大的一种药品,确定一种类型的储药槽规格,则该类药品都放在这样一个储药槽中。
本建模最重要的两个方面:一是确定分组标准,将给定的药盒分为不同的组别,我们主要采用了组距分组法;二是寻找优化方法,实现目标优化,找到既适合储存药品,又节省空间的方法,我们主要采用了寻找最大面积法。
此外,在数据分组中我们利用了Excel的数据处理能力,在对分组数据进行可视化处理的时候,又用了matlab进行了图形的绘制。
关键字:目标优化组距分组最大面积法问题重述储药柜的结构类似于书橱,通常由若干个横向隔板和竖向隔板将储药柜分割成若干个储药槽。
为保证药品分拣的准确率,防止发药错误,一个储药槽内只能摆放同一种药品。
药品从后端放入,从前端取出。
为保证药品在储药槽内顺利出入,要求药盒与两侧竖向隔板之间、与上下两层横向隔板之间应留2mm的间隙,同时还要求药盒在储药槽内推送过程中不会出现并排重叠、侧翻或水平旋转。
在忽略横向和竖向隔板厚度的情况下,建立数学模型,给出下面几个问题的解决方案。
1.药房内的盒装药品种类繁多,药盒尺寸规格差异较大,附件1中给出了一些药盒的规格。
请利用附件1的数据,给出竖向隔板间距类型最少的储药柜设计方案,包括类型的数量和每种类型所对应的药盒规格。
2010全国数学建模d题

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): D我们的参赛报名号为(如果赛区设置报名号的话):20101219所属学校(请填写完整的全名):淮安信息职业技术学院参赛队员(打印并签名) :1. 王姚2. 杨彬3. 黄影影指导教师或指导教师组负责人(打印并签名):刘嘉日期: 2010 年 9月 13 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号)对学生宿舍设计方案的评价摘 要本文主要采用层次分析法对四种学生宿舍的设计进行评价。
首先,根据调查我们得到经济性、舒适性、安全性的一组正互反对比矩阵,见(矩阵一),然后可以根据这组矩阵得出特征向量w ,然后根据调查得出【建设成本、运行成本、收费标准】、【人均面积 使用方便 互不干扰 采光 通风】、【人员疏散、防盗】得出这样的3组矩阵,见(矩阵二到四),应用MATLAB 并分别可得出对应的特征向量。
然后,我们根据每种学生宿舍设计方案的楼层平面图,可以计算各个指标的数值,接着根据这些指标我们根据假设对这些指标量化。
根据量化的指标值,将每种数值归类,便可以得出一组四行十列的矩阵,根据每种方案的条件又可以得出10组四乘四的矩阵,便可以得出相应的的特征向量,以此作依据,计算出最终的权重,然后比较权重即得出最佳方案。
数学建模试卷2010(答案)

华中科技大学《数学建模》考试卷(半开卷)2010~2011学年度第一学期成绩学号专业班级姓名一、怎样解决下面的实际问题,包括需要哪些数据资料,要作些什么观察、试验以及建立什么样的数学模型等。
(10分)(1)估计一批电饭煲的寿命;(2)一高层办公楼有四部电梯,早晨上班时间非常拥挤,试制订合理的运行计划。
解:(1)从一批电饭煲中取一定数量的样本,测得其平均寿命,可作为该批电饭煲寿命的估计值。
为衡量估计的精度,需要从样本寿命确定该批电饭煲寿命的概率分布,即可得到估计值的置信区间。
还可试验用提高电压的办法加速寿命测试,以缩短测量时间。
⑤(2)统计在各层上班的人数,通过数据或计算确定电梯运行时间,以等待的人数与时间乘积为目标,建立优化模型,确定每部电梯运行的楼层(有的从大厅直接运行到高层)。
⑤二、学校共有1000名学生,235人住在A 宿舍,333人住在B 宿舍,432人住在C 宿舍。
学生们要组织一个10人的委员会,试用以下方法分别分配各宿舍的委员数。
(10分) 1.Hamilton 方法 2.Q 值方法3.其它方法或你自己提出的方法解:1.Hamilton 方法:③2.Q 值法: 先按比例计算结果将整数部分的9席分配,123n 2,n 3,n 4=== ①再用Q 值法分配第十席:()()()()()()221111222222223333p 235Q 9204.17n n 1221p 333Q 9240.75n n 1331p 432Q 9331.20n n 1441===++===++===++ ③Q 3最大,第十席分配给C 宿舍,即:123n 2,n 3,n 5===。
①3.略 ②三、人体注射葡萄糖溶液时,血液中葡萄糖浓度g (t )的增长率与注射速率r 成正比,与人体血液容积V 成反比,而由于人体组织的吸收作用,g (t )的减少率与g (t )本身成正比。
分别在以下假设下建立模型,并讨论稳定情况。
2010高教社杯全国大学生数学建模竞赛官方题目(含ABCD)
\A 题 储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
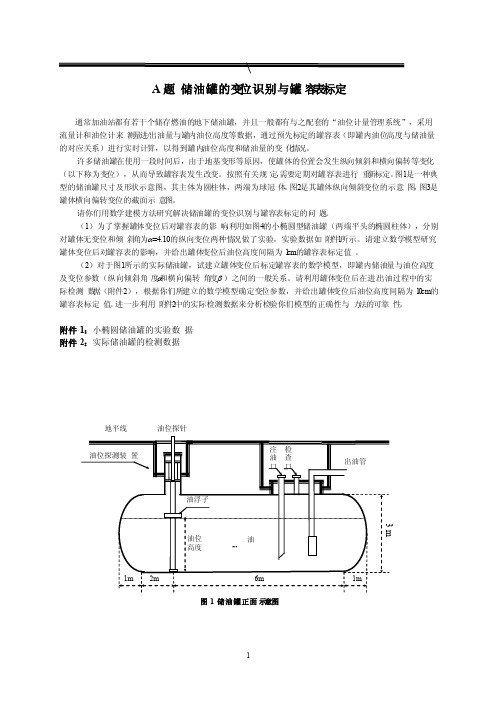
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
附件1:小椭圆储油罐的实验数据 附件2:实际储油罐的检测数据油油浮子出油管油位探测装置注油口 检查口地平线 2m6m1m1m3 m油位高度图1 储油罐正面示意图油位探针油位探针α地平线 图2 储油罐纵向倾斜变位后示意图油油浮子出油管油位探测装置注油口 检查口水平线(b) 小椭圆油罐截面示意图α油油浮子出油管油位探针注油口水平线2.05mcm 0.4m1.2m1.2m1.78m(a) 小椭圆油罐正面示意图图4 小椭圆型油罐形状及尺寸示意图图3 储油罐截面示意图(b )横向偏转倾斜后正截面图地平线β地平线垂直线油位探针(a )无偏转倾斜的正截面图油位探针油位探测装置地平线油3m油B题2010年上海世博会影响力的定量评估2010年上海世博会是首次在中国举办的世界博览会。
数学建模D题的答案

2010高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)D题对学生宿舍设计方案的评价学生宿舍事关学生在校期间的生活品质, 直接或间接地影响到学生的生活、学习和健康成长。
学生宿舍的使用面积、布局和设施配置等的设计既要让学生生活舒适,也要方便管理, 同时要考虑成本和收费的平衡, 这些还与所在城市的地域、区位、文化习俗和经济发展水平有关。
因此,学生宿舍的设计必须考虑经济性、舒适性和安全性等问题。
经济性:建设成本、运行成本和收费标准等。
舒适性:人均面积、使用方便、互不干扰、采光和通风等。
安全性:人员疏散和防盗等。
附件是四种比较典型的学生宿舍的设计方案。
请你们用数学建模的方法就它们的经济性、舒适性和安全性作出综合量化评价和比较。
对学生宿舍设计方案的评价摘要本文主要从经济性、舒适性、安全性三个方面对四种学生宿舍的设计方案做出综合量化和比较。
在评价过程中,主要运用了模糊决策和层次分析法,并利用MATLAB 软件进行求解。
由于本问题的许多条件比较模糊,具有隐藏性,我们先对附件中的数据进行预处理,从中提取与评价相关的因素,然后利用层次分析法确定各准则对目标的权重,从而建立学生宿舍设计方案的评价模型。
具体结果为:(1)经济性方面:得出四种学生宿舍设计方案在此方面的的组合权向量为: )1668.0,2265.0,5627.0,0440.0(,根据指标越小,优先选择程度越大的准则得出:方案1是经济性最优的,其次为方案4、方案3,最后为方案2。
(2)舒适性方面:得到组合权向量为:)1999.0,1576.0,5301.0,1124.0(,根据指标越大,优先选择程度越大的准则得出:方案2是舒适度最高的,其次为方案4、方案3,最后为方案1。
(3)安全性方面:得到组合权向量为:)2223.0,2684.0,4158.0,0935.0(,利用和(2)同样的准则,得出了方案2是安全性最强的,其次为方案3、方案4,最后为方案1。
2010年数学建模集训小题目解答.pdf1

生产 3 种产品的总利润为
综上所述,建立如下的线性规划模型
max
2 3 5 c x ∑ i ∑ ij − ∑∑ b j a ij xij i =1 j =1 i =1 j =1
3
s.t.
∑a
i =1
3
ij
xij ≤ d j , j = 1,2,L ,5
x11 + x12 = x13 + x14 + x15
3.某商业公司计划开办 5 家新商店。为了尽早建成营业,商业公司决定由 5 家建筑公司分
别承建。已知建筑公司 Ai ( i = 1,2,3,4,5 )对新商店 B j ( j = 1,2,3,4,5 )的建造费用的报价 , 见表 4。 商业公司应当对 5 家建筑公司怎样分配建造任务, (万元) 为 cij( i, j = 1,2,3,4,5 ) 才能使总的建造费用最少? 表 4 各建筑公司的建筑费用数据
解:用 j = 1,2,3,4 分别表示甲、乙、丙、丁四个企业, cij 表示第 i ( i = 1, L ,6 )台设备分 配给第 j 个企业创造的利润,引进 0 − 1 变量
1, 第i台设备分配给第j个企业 xij = , i = 1, L ,6 , j = 1,2,3,4 0, 第i台设备不分配给第j个企业
数学规划的 LINGO 程序:
model: sets: chanpin/1..3/:c; shebei/1..5/:b,d; link(chanpin,shebei):a,x; endsets data: c=1 1.65 2.3; a=@file('data1.txt'); b=@file('data1.txt'); d=@file('data1.txt'); enddata max=@sum(chanpin(i):c(i)*@sum(shebei(j)|j#le#2:x(i,j)))-@sum(chanpin( i):@sum(shebei(j):b(j)*a(i,j)*x(i,j))); @for(shebei(j):@sum(chanpin(i):a(i,j)*x(i,j))<d(j)); @sum(shebei(i)|i#le#2:x(1,i))=@sum(shebei(i)|i#ge#3:x(1,i)); x(2,1)+x(2,2)=x(2,3); x(3,2)=x(3,4); x(2,4)=0; x(2,5)=0; x(3,1)=0; x(3,3)=0; x(3,5)=0; end
数学与统计学学院2010年数学建模竞赛试题

数学与统计学学院2010年数学建模竞赛试题(请先仔细阅读竞赛要求)A题、武汉房地产价格问题房地产价格是一个备受关注的问题。
现在请你就以下几个方面的问题进行讨论1.给出你的房地产价格指标的定义(考虑房子所处的位置(交通,学校,医院,商场…),房子的户型,房子的楼层,房子的朝向,小区的内环境(绿化,容积率…等等),房子的开发商,物业,房子的质量,小区的大小,噪音大小,空气等等…);2.请搜集武汉近两年来的房子日销售情况表(至少搜集10天的武汉的房子日销售情况表);对你的上述房地产价格指标的定义做简化,给出一个简化的武汉的房地产价格指标的定义;并且假设:以你搜集到的10天的武汉的房子日销售情况表中时间最早的那一天武汉的房地产价格指标为100,利用你的简化的武汉的房地产价格指标的定义,计算其他天的武汉的房地产价格指标;3.请搜集相应10天的武汉(或者全国)的物价指标,请你建立武汉的房地产价格指标与武汉(或者全国)的物价指标的关系模型,并假设有一天武汉(或者全国)的物价指标,是你搜集到的10天的武汉的房子日销售情况表中时间最早的那一天的武汉(或者全国)的物价指标的100倍,请你预测那一天的武汉的房地产价格指标;4.如果某人准备在武汉买房,请你给他买房的时机的建议。
中南民族大学数学与统计学学院2010年首届数学建模竞赛要求1、参赛者为中南民族大学任意在校本科生, 以队为单位参赛。
学生自愿组队,每队有且仅有三人,鼓励学生跨院系组队。
比赛开始后不允许更换队员。
2、竞赛时间为:2010年4月9日16时至4月14日16时。
3、竞赛按照甲、乙组分别命题,甲组(参加对象为2007,2008级学生)分为A,B两题,乙组(2009级学生)分为C,D两题,每个参赛队可任选一题,4月9日16时起可在院网页上下载试题。
4、竞赛采取开放的竞赛方式,竞赛期间参赛队员可以使用各种图书资料、计算机和软件,在国际互联网上浏览,但不得与队外任何人(包括在网上)讨论。
2010数模试题与答案

华南农业大学期末考试试卷(A 卷)2010学年第二学期 考试科目: 数学建模考试类型:(闭卷) 考试时间: 120分钟学号 姓名 年级专业1、(满分10分)对下面这个众所周知的智力游戏,请按下列的要求写出该问题的状态转栘模型:人带着猫、鸡、米过河,船除需要人划之外,至多能载猫、鸡、米三者之一,而当人不在场时猫要吃鸡、鸡要吃米。
将人、猫、鸡、米分别记为i = 1,2,3,4,当i 在此岸时记x i = 1,否则为0;故此岸的状态下用s =(x 1,x 2,x 3,x 4)表示。
该问题中决策为乘船方案,记为d = (u 1, u 2, u 3, u 4),当i 在船上时记u i = 1,否则记u i = 0。
(1) 写出该问题的所有允许状态集合;(3分)解:所有允许状态集合为:S={(1,1,1,1), (1,1,1,0), (1,1,0,1), (1,0,1,1), (1,0,1,0)}及他们的5个反状态。
(2) 写出该问题的所有允许决策集合;(3分)解:允许决策集合为:D = {(1,1,0,0), (1,0,1,0), (1,0,0,1), (1,0,0,0)}(3) 写出该问题的状态转移率。
(4分)解:该问题的状态转移率为: sk+1 = s k + (-1) k d k 2、 (满分16分)根据以下的不同假设,请写出相应人口问题的微分方程模型(不用求解)。
下设x (t )表示t 时刻的人口数。
(1)假设人口的相对增长率(指dxx dt)是常数;(4分) 解:模型为:dxkx dt=, 其中k 为常数。
(2)假定人口的相对增长率是关于当时人口数的线性减函数;(4分) 解:模型为: dxdt= (r – s x)x , 其中r 与s 为常数,且s>0。
(3)假设人口的增长率与x m – x (t )成正比,其中x m 表示人口的最大数量;(4分) 解:模型为:)(x x k dtdxm -=,其中k 为常数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)D题对学生宿舍设计方案的评价学生宿舍事关学生在校期间的生活品质, 直接或间接地影响到学生的生活、学习和健康成长。
学生宿舍的使用面积、布局和设施配置等的设计既要让学生生活舒适,也要方便管理, 同时要考虑成本和收费的平衡, 这些还与所在城市的地域、区位、文化习俗和经济发展水平有关。
因此,学生宿舍的设计必须考虑经济性、舒适性和安全性等问题。
经济性:建设成本、运行成本和收费标准等。
舒适性:人均面积、使用方便、互不干扰、采光和通风等。
安全性:人员疏散和防盗等。
附件是四种比较典型的学生宿舍的设计方案。
请你们用数学建模的方法就它们的经济性、舒适性和安全性作出综合量化评价和比较。
对学生宿舍设计方案的评价摘要本文主要从经济性、舒适性、安全性三个方面对四种学生宿舍的设计方案做出综合量化和比较。
在评价过程中,主要运用了模糊决策和层次分析法,并利用MATLAB 软件进行求解。
由于本问题的许多条件比较模糊,具有隐藏性,我们先对附件中的数据进行预处理,从中提取与评价相关的因素,然后利用层次分析法确定各准则对目标的权重,从而建立学生宿舍设计方案的评价模型。
具体结果为:(1)经济性方面:得出四种学生宿舍设计方案在此方面的的组合权向量为: )1668.0,2265.0,5627.0,0440.0(,根据指标越小,优先选择程度越大的准则得出:方案1是经济性最优的,其次为方案4、方案3,最后为方案2。
(2)舒适性方面:得到组合权向量为:)1999.0,1576.0,5301.0,1124.0(,根据指标越大,优先选择程度越大的准则得出:方案2是舒适度最高的,其次为方案4、方案3,最后为方案1。
(3)安全性方面:得到组合权向量为:)2223.0,2684.0,4158.0,0935.0(,利用和(2)同样的准则,得出了方案2是安全性最强的,其次为方案3、方案4,最后为方案1。
(4)综合分析方面:得到组合权向量为:)1813.0,2111.0,5398.0,0678.0(,由此得出方案2是综合指标最高的,其次为方案3、方案4、最后为方案1。
最后,对以上建立的模型进行合理化的评价和深入的探讨,分析了模型的优缺点,并提出了进一步的改进方向。
关键词:评价模型 层次分析法 权重 MATLAB1.问题重述现如今的学生宿舍的使用面积、布局和设施配置等的设计既要让学生生活舒适,也要方便管理, 同时要考虑成本和收费的平衡, 这些还与所在城市的地域、区位、文化习俗和经济发展水平有关。
因此,学生宿舍的设计必须考虑经济性、舒适性和安全性等问题。
请用数学建模的方法,从经济性、舒适性、安全性方面对附件中给出的四种学生宿舍的设计方案作出综合量化和比较。
2.问题分析本问题要解决的问题是对四种典型的学生宿舍设计方案进行评价与比较。
题目中的数据比较模糊,具有隐藏性,而且是用图表的方式展示给我们的,因而解决这一问题的关键点有两个:(1)如何把附件中四个平面设计图中所隐藏的数据量化;(2)在建立评价比较模型时如何确定各个因素之间的权重与影响。
因而我们采用模糊决策和层次分析法相结合的方法构架评价模型,来评判各个宿舍设计方案的优劣。
3.模型假设1) 我们以附件中的四个图片作为研究的对象;2) Design1、Design2、Design3和Design4分别对应层次结构中的方案层P;3) 假设收集到的数据与理论根据是准确合理的;4) 不考虑宿舍未住满、设施损毁等情形;5) 单位面积内的建设成本我们假设为定值。
4.符号说明5.模型的建立与求解5.1经济性方面在这个层面上,把经济性设为目标层,把建设成本、运行成本、收费标准设为准则层,四种方案设为决策层,层次结构图如图2所示。
在这里我们的评价准则为:指标越小,优先选择程度越大,也就是说,所需的经费越少。
目标层1A 准则层1B 决策层1P 图2得到其相对应的成对比较矩阵如下面所示: 第二层对第一层的成对比较矩阵为:1B =⎪⎪⎪⎭⎫ ⎝⎛1464/1126/12/11 求得其最大特征根为0092.3max =λ,经一致性检验: =--=1)(n n A CI λ00458.0查找相应的平均随机一致性指标(见上表3)RI ,计算一致性比率为:=CR 1.00079.058.000458.0<==RI CI CR 说明矩阵1B 的不一致程度是可以接受的,矩阵1B 的权向量为:T W )7010.0,1929.0,1061.0(1=第三层对第二层的成对比较矩阵为:1C =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛15/15/15512/1752195/17/19/11 2C =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛13/15/15313/1753195/17/19/11 3C =⎪⎪⎪⎪⎪⎭⎫⎝⎛114/15113/1543195/15/19/11 通过MATLAB 编程计算可得两两判断矩阵在单一准则下的权向量1W 、最大特征根λ与一致性指标CR ,具体求解结果见下表4:上述一致性比率CR 均小于0.1,可以判断矩阵具有满意的一致性。
于是得出,单在经济性方面上四种设计方案的组合权向量为:T W )1668.0,2265.0,5627.0,0440.0(1=作出综合评价结论为:方案1在经济性上的权重占0.0440,方案2占0.5627,方案3占0.2265,方案4占0.1668。
因而方案1是经济性最优的,其次为方案4、方案3,最后是方案2。
5.2 舒适性方面同上面的方法,建立了舒适性方面如图3所示的层次结构图。
在这里我们的评价准则为:指标越大,优先选择程度越大,也就是说,舒适性就越好。
从而得到其相对应的成对比较矩阵如下所示: 第二层对第一层的成对比较矩阵为:2B =⎪⎪⎪⎪⎪⎭⎫⎝⎛114/15/1113/13/14312/15321第三层对第二层的成对比较矩阵为:4C =⎪⎪⎪⎪⎪⎭⎫⎝⎛12/53/12/95/214/1534179/25/17/11 目标层2A 准则层2B 决策层2P 图35C =⎪⎪⎪⎪⎪⎭⎫⎝⎛124/152/115/1345175/13/17/11 6C =⎪⎪⎪⎪⎪⎭⎫⎝⎛15/13/16/1513/52/135/314/16241 7C =⎪⎪⎪⎪⎪⎭⎫⎝⎛13/17/13/1315/17751937/19/11 通过MATLAB 编程计算可得两两判断矩阵在单一准则下的权向量2W 、最大特征根λ与一致性指标CR ,具体结果见下表:上述一致性比率CR 均小于0.1,可以判断矩阵具有满意的一致性。
于是得出,单在舒适性方面上四种设计方案的组合权向量为:T W )1999.0,1576.0,5301.0,1124.0(2=作出综合评价结论为:方案1在舒适性上的权重占0.1124,方案2占0.5301,方案3占0.1576,方案4占0.1999。
因而方案2是舒适度最高的,其次为方案4、方案3,最后是方案1。
5.3 安全性方面此方面仅考虑了人员的疏散与防盗,而不考虑其他的特殊情况。
用同5.1中的方法建立了安全性方面的层次结构图,如图4所示。
在这里我们的评价准则为:指标越大,优先选择程度越大,也就是说,安全性就越高。
经过分析我们得到了如下的成对比较矩阵: 第二层对第一层的成对比较矩阵为:3B =⎪⎪⎭⎫ ⎝⎛15/151第三层对第二层的成对比较矩阵为:8C =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛13/25/432/313/224/52/3143/12/14/119C =⎪⎪⎪⎪⎪⎭⎫⎝⎛16/17/11615/17751917/19/11 通过MATLAB 编程计算可得两两判断矩阵在单一准则下的权向量3W 、最大特征根λ与一致性指标CR ,具体结果见下表6:于是上述一致性比率CR 均小于0.1,可以判断矩阵具有满意的一致性。
目标层3A准则层3B 决策层3P图4最后得出,单在安全性方面上四种设计方案的组合权向量为:T W )2223.0,2684.0,4158.0,0935.0(3=由此可见,作出综合评价结论为:方案1在安全性上的权重占0.0935,方案2占0.4158,方案3占0.2684,方案4占0.2223。
因而方案2是安全性最强的,其次为方案3、方案4,最后是方案1。
5.4 综合分析综合考虑经济性、舒适性、安全性三个方面之间的权重,层次分析结构图见图1,我们得到了如下的成对比较矩阵为:0A =⎪⎪⎪⎭⎫ ⎝⎛14/15/1413/1531通过MATLAB 计算可得两两判断矩阵在单一准则下的权向量为:T W )0936.0,2797.0,6267.0(0=最大特征根0858.3max =λ与一致性指标CR 1.00739.0<=,则说明矩阵不一致程度是可以接受的。
于是得到最终的组合权向量为:T W )1813.0,2111.0,5398.0,0678.0(=各层的一致性检验及组合一致性检验全部通过;上面的组合权向量可以作为四个学生宿舍设计方案评价的依据。
由此得出最终的综合评价为:方案2是综合指标最高的,其次为方案3、方案4,最后是方案1。
6.模型的分析我们所建立的模型是评价模型,对四种典型宿舍设计方案作出了评价与比较。
近几年,随着我国经济的发展,人民生活水平的不断提高,学生可以根据自己的实际情况选择宿舍类型,对于不同层次的学生人群,可以根据我们的模型进行选择。
比如对于经济性要求比较高的学生来说,可以根据模型分解(经济性方面)进行评价选择;若对舒适性要求比较高的学生来说,可以根据模型分解(舒适性方面)进行择优选择。
综合三个指标,方案二是最优选择,它既在一定程度上满足学生对居住私密性的要求,又能创造一个优美舒适,富有文化气氛的学习、休息和交往的居住环境,并在一定程度上为学生对宿舍的选择提供了依据。
7.模型的评价与推广7.1 模型的评价本文主要运用模糊决策和层次分析法,对宿舍的经济性、舒适性、安全性作出科学合理的决策,克服了主观定性分析的弊端。
在建立模型时所考虑的影响因素全面且符合实际,并对各影响因素进行了合理的量化处理。
通过对已知数据的加工整合,巧妙的构建了成对比较矩阵,并用MATLAB软件求出模型的结果。
此外,模型运用大量的图表,使得到的结果非常直观,易于理解,让问题很明了,思路很清晰。
本模型的弊端是针对附件中的四个设计图之间的对比,由于受现有资料的限制,无法代表所有学生宿舍的构建情况,这样大大局限了模型的灵活性。
7.2 模型的推广本文构造的模型,能更准确的评价宿舍的优劣,该模型还可以应用到选拨决策中,在日常生活中经常会遇到各式各样的选拨,比如足球员的选拨,三好学生的选拨等等,都可以应用本模型。
在运用此模型时应结合各个有关部门的实际情况,尽量选取科学合理的指标及其权数。
