20MeV到180MeVu 16O+197Au系统的BUU计算线动量与角动量转移依赖碰撞参数与能量研究
合集下载
大学物理 动量与角动量

v2
60o
v1
6
因打击力很大,所以由碰撞引起的质点的动 量改变,基本上由打击力的冲量决定。 重
力、阻力的冲量可以忽略。
mv
2
60o
mg t
mv
打击力冲量 F t
1
Ft mv2 mv1
7
F t m v m v
2
1
F t
30o
mv
2
v v v
39
ˆ 有心力 f f (r )r 力矩为零 角动量为常矢量
角动量方向丌变:行星轨道平面方位丌变 L 角动量大小丌变: L 常数
L rm r sin t 1 r r sin m , S r r sin t 2 2m S 常数 t S 常数。 所以,面速度 t
实验表明:只要系统丌受外界影响,这 些过程的动量守恒。 5、物理学家对动量守恒定律具有充分信心。 每当出现违反动量守恒的反常现象时,总 是提出新的假设来补救,结果也总是以有 所新发现而胜利告终。 【例】在 衰变中,反中微子的发现
A Z A XZ 1Y e-
17
18
19
20
§3.4 火箭飞行原理 “神州”号飞船升空
3
§ 3.1 冲量不动量定理 力的时间积累称为冲量(impulse):
dI Fdt t I F (t )dt
t0
牛顿第二定律质点的动量定理: dI Fdt dp t I F (t )dt p p0
t0
动量定理常用于碰撞过ห้องสมุดไป่ตู้。
C
N N i 1 i 1
dvc mi ai m 4、质心的加速度 ac dt
力学3动量角动量课件

到一质量为m=2.0kg的鸟,鸟的长度为l=0.3 m。
假设鸟撞上飞机后随同飞机一起运动, 试估算 它们相撞时的平均冲力的大小。
解: 以地面为参考系,因鸟的速度远小于飞机的, 可 将它在碰撞前的速度大小近似地取为v0=0 m/s, 碰撞后的速度大小v=300m/s。
由动量定理可得 mv mv0 I Ft
LrP
dL dt
d dt
(r
P)
dr dt
P
r
dP dt
dL dt
Байду номын сангаас
r
dP dt
r
F
=
M
0 F = dP dt
质点的角动量定理:质点对任一固定点的角动量的时
间变化率,等于质点所受的合外力对该固定点的力矩。
Mdt dL (微分形式)
ot
Mdt
Lt Lo
dL
Lt
Lo
(积分形式)
注意: 冲量矩
适用于惯性系,对非惯性系,需引入“惯性力”。
3. 质点 的角动量守恒定律 若 M 0 则 Lt L0
0t Mdt Lt L0
或 L r P 恒矢量 ——角动量守恒定律
为800m/s。若每分钟发射300发子弹,求射手
肩部所受到的平均压力。
解: 根据动量定理
F
t2
t1
F (t)dt
P2
P1
t2 t1
t2 t1
射手肩部所受到的平均压力为
F FPttmtmv v
300 0.05 800 200N 60
例2.飞机以v=300m/s(即1080 km/h)的速度飞行,撞
今用手提起链的一端使之以匀速v 铅直上升。
求: 从一端离地到全链离地,手的拉力的冲量?
假设鸟撞上飞机后随同飞机一起运动, 试估算 它们相撞时的平均冲力的大小。
解: 以地面为参考系,因鸟的速度远小于飞机的, 可 将它在碰撞前的速度大小近似地取为v0=0 m/s, 碰撞后的速度大小v=300m/s。
由动量定理可得 mv mv0 I Ft
LrP
dL dt
d dt
(r
P)
dr dt
P
r
dP dt
dL dt
Байду номын сангаас
r
dP dt
r
F
=
M
0 F = dP dt
质点的角动量定理:质点对任一固定点的角动量的时
间变化率,等于质点所受的合外力对该固定点的力矩。
Mdt dL (微分形式)
ot
Mdt
Lt Lo
dL
Lt
Lo
(积分形式)
注意: 冲量矩
适用于惯性系,对非惯性系,需引入“惯性力”。
3. 质点 的角动量守恒定律 若 M 0 则 Lt L0
0t Mdt Lt L0
或 L r P 恒矢量 ——角动量守恒定律
为800m/s。若每分钟发射300发子弹,求射手
肩部所受到的平均压力。
解: 根据动量定理
F
t2
t1
F (t)dt
P2
P1
t2 t1
t2 t1
射手肩部所受到的平均压力为
F FPttmtmv v
300 0.05 800 200N 60
例2.飞机以v=300m/s(即1080 km/h)的速度飞行,撞
今用手提起链的一端使之以匀速v 铅直上升。
求: 从一端离地到全链离地,手的拉力的冲量?
大学物理角动量ppt

由于各三角形具有公共高线 OH ,
因此掠面速度相等:
dS
1 vt OH 2
1 vr sin
1 r 2
常量
dt
t
2
2
式中
v sin
r
பைடு நூலகம்
ω 相当于质点绕O点转动的角速度。
由上式可得: mvr sin 常量
写成矢量式: r p r mv 常量
②再来看有心力场的简单情形。
质点在向心力的作用下作匀速圆周运动
由: M dL dt
则有:
若 M 0 L 常矢量
若质点或质点系所受外力对某固定参照点的矩 的矢量和为零,则质点对该固定点的角动量守恒。
—角动量守恒定律
例如:质点在有心力作用下角动量守恒。
例题:质量为m的圆锥摆摆球,以速率υ运动时, 对O参考点的角动量是否守恒?对C参考点的 角动量是否守恒?
l c
星系的形状可能与此有关。
星系(银河系)的早期可能是具有动量矩的 大质量气团,在引力作用下收缩。轴向的收缩不 受什么阻碍,很快塌缩。径向却不那么容易,因 而像银河系这样的星系呈扁平状。
银河系
银河系(模拟)
5.2 刚体的定轴转动
质点的运动只代表物体的平动,物体实 际上是有形状、大小的,它可以平动、转动, 甚至更复杂的运动。因此,对于机械运动的 研究,只限于质点的情况是不够的。
刚体(rigid body)是一种特殊的质点系, 无论在多大外力作用下,系统内任意两质点 间的距离始终保持不变。即物体的形状、大 小都不变的固体称为刚体。
刚体考虑了物体的形状和大小,但不考虑它 的形变,刚体同质点一样,也是一个理想化模型。
特权福利
特权说明
VIP用户有效期内可使用VIP专享文档下载特权下载或阅读完成VIP专享文档(部分VIP专享文档由于上传者设置不可下载只能 阅读全文),每下载/读完一篇VIP专享文档消耗一个VIP专享文档下载特权。
因此掠面速度相等:
dS
1 vt OH 2
1 vr sin
1 r 2
常量
dt
t
2
2
式中
v sin
r
பைடு நூலகம்
ω 相当于质点绕O点转动的角速度。
由上式可得: mvr sin 常量
写成矢量式: r p r mv 常量
②再来看有心力场的简单情形。
质点在向心力的作用下作匀速圆周运动
由: M dL dt
则有:
若 M 0 L 常矢量
若质点或质点系所受外力对某固定参照点的矩 的矢量和为零,则质点对该固定点的角动量守恒。
—角动量守恒定律
例如:质点在有心力作用下角动量守恒。
例题:质量为m的圆锥摆摆球,以速率υ运动时, 对O参考点的角动量是否守恒?对C参考点的 角动量是否守恒?
l c
星系的形状可能与此有关。
星系(银河系)的早期可能是具有动量矩的 大质量气团,在引力作用下收缩。轴向的收缩不 受什么阻碍,很快塌缩。径向却不那么容易,因 而像银河系这样的星系呈扁平状。
银河系
银河系(模拟)
5.2 刚体的定轴转动
质点的运动只代表物体的平动,物体实 际上是有形状、大小的,它可以平动、转动, 甚至更复杂的运动。因此,对于机械运动的 研究,只限于质点的情况是不够的。
刚体(rigid body)是一种特殊的质点系, 无论在多大外力作用下,系统内任意两质点 间的距离始终保持不变。即物体的形状、大 小都不变的固体称为刚体。
刚体考虑了物体的形状和大小,但不考虑它 的形变,刚体同质点一样,也是一个理想化模型。
特权福利
特权说明
VIP用户有效期内可使用VIP专享文档下载特权下载或阅读完成VIP专享文档(部分VIP专享文档由于上传者设置不可下载只能 阅读全文),每下载/读完一篇VIP专享文档消耗一个VIP专享文档下载特权。
第四章动量和角动量概论

第四章 动量和角动量
§4.1单个质点的 动量定理
一、动量
1. 冲量
我们把 Fdt 称作冲量。
Fdt 表示力在时间上的累积,叫dt时间内合外力
F
的冲量。
2、动量定理
(1F) 微d分P形式Fdt
dP
——动量定理的微分式
dt
它表明∶一定时间内,质点所受合外力的冲量等于该时间内质
点动量的增量。
(2)积分形式 对上式作积分,即
F13 F31
F32
m3
N个质点的质点系m1、m2、......mN,第i个质点的位矢为
ri
F3
受力为 fi 即
动量为 Pi
fi fi内
mi
dri dt
fi外
,则动力学方程为
dPi dt
fi
dPi dt
对N个质点的动力学方程求和,得:
N
因为
fi内 0
N
i 1
fi内
N i 1
三、质点系的动量定理
1、动量定理
由F动力dP学 方程:
Fdt
dP
dt
——动量定理的微分式
它表明∶一定时间内,系统所受合外力的冲量等于该时间内系
统动量的增量。
对上式作积分,即
令
I
t
2
Fdt
t1t2Fdt来自d p2pt1
p1
则有 I P2 P1 ——动量定理的积分式
四、 质点系的动量守恒定律
对质点系,由
F
dP
知,当 F 0 时
dP 0
dt
P Constant
dt
N N
Pi mivi Constant
—— 动量守恒定律
§4.1单个质点的 动量定理
一、动量
1. 冲量
我们把 Fdt 称作冲量。
Fdt 表示力在时间上的累积,叫dt时间内合外力
F
的冲量。
2、动量定理
(1F) 微d分P形式Fdt
dP
——动量定理的微分式
dt
它表明∶一定时间内,质点所受合外力的冲量等于该时间内质
点动量的增量。
(2)积分形式 对上式作积分,即
F13 F31
F32
m3
N个质点的质点系m1、m2、......mN,第i个质点的位矢为
ri
F3
受力为 fi 即
动量为 Pi
fi fi内
mi
dri dt
fi外
,则动力学方程为
dPi dt
fi
dPi dt
对N个质点的动力学方程求和,得:
N
因为
fi内 0
N
i 1
fi内
N i 1
三、质点系的动量定理
1、动量定理
由F动力dP学 方程:
Fdt
dP
dt
——动量定理的微分式
它表明∶一定时间内,系统所受合外力的冲量等于该时间内系
统动量的增量。
对上式作积分,即
令
I
t
2
Fdt
t1t2Fdt来自d p2pt1
p1
则有 I P2 P1 ——动量定理的积分式
四、 质点系的动量守恒定律
对质点系,由
F
dP
知,当 F 0 时
dP 0
dt
P Constant
dt
N N
Pi mivi Constant
—— 动量守恒定律
角动量

根据,如果M=0,则dL/dt=0,因而
L=常量(M=0)
这就是说,如果作用在质点上的外力对某给定点O的力矩(r×F)为零,则质点对O的角动量在运动过程中保 持不变,这就叫做质点的角动量守恒定律。
另:某段时间内若质点所受合力对原点力矩M不为零,但是M的某分量(对某坐标轴力矩)总是零,则该段时 间内质点对原点角动量的该分量守恒,或质点对该轴角动量守恒.
质点系的总
在惯性系S系中,取某点为坐标原点O,则质点系对某点点和参考系)两个参考系中位矢和速度的变换关系是 由质心系性质得 整理得 上式右边的两项分别是质心系中质点系的总角动量L'(称为固有角动量或是自转角动量)和惯性系S系中质 量集中在质心后质心对O点的角动量Lc,于是有 L=L'+Lc
定义
质点动量p对O点之动量矩(通常称为角动量)L(O)(简记为L)为 L=r×p 其中r是质点相对O点的位矢。 角动量L的大小为L=rpsinφ(φ为r与p的夹角),方向垂直于位矢r和动量p所组成的平面,指向是由r经小 于180°的角转到p的右手螺旋前进的方向. 角动量大小的量纲[L]=[r][p]=[r][m][v]=[s]2[m][t] -1=L2MT-1, 单位有N·m·s,kg·m²/s。
感谢观看
几何意义
位矢r在单位时间内扫过的面积,称为它的掠面速度。 可以证明,掠面速度为S‘=|r×v|/2. 角动量大小L=|r×p|=|r×mv|=m|r×v|=2mS'. 角动量守恒定律指出,当合外力矩为零时,角动量守恒,物体与中心点的连线单位时间扫过的面积不变,在 天体运动中表现为开普勒第二定律。
相关定理
质点的定理
质点的守恒定 律
证明:由于L=r×p,故角动量对时间的变化率为== 在上式中,右端第一项的,,因此,矢积×p=0.这样,上式就成为. 由牛顿第二定律得,,把上式改写成. 式中的r×F是力矩的定义.(力的作用点相对给定点的位矢r与力F的矢积为力对给定点的力矩,以M表示,即 M=.) 于是有=M 即质点所受的合外力矩等于它的角动量对时间的变化率.这个结论叫做质点的角动量定理. 质点系的角动量定理也可写成同样的形式 不过M是质点系所受的总外力矩,L是质点系的总角动量. 由得dL=Mdt, 两边积分得质点角动量的积分形式
大学物理角动量 角动量守恒定律
解 小虫与细杆的碰撞视为完全非弹性碰撞,碰撞 前后系统角动量守恒
1 mv0 ml 12 4 l
2
m( ) 4 l
2
12 v 0 7 l
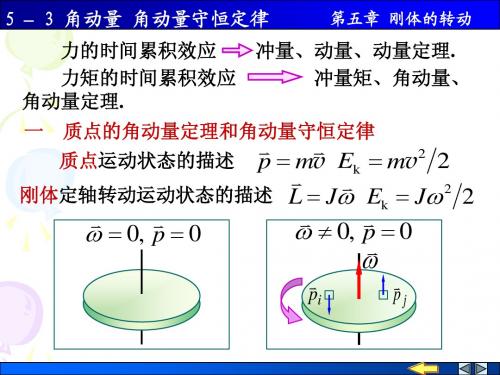
5 – 3 角动量 角动量守恒定律
12 v 0 7 l
第五章 刚体的转动
由角动量定理
M dL dt d ( J ) dt dJ dt
第五章 刚体的转动
v A (v0 v ) 1 v B 1709 m s
mM m R h
2
2
1 2
飞船在 A点喷出气体后, 在到 达月球的过程中, 机械能守恒
1 2 m v A G 1 2
2
vB
B
vA
v0
R
O h
v
u
2
A
m v B G
2
2
mM m
质点的角动量定理和角动量守恒定律
pi
pj
5 – 3 角动量 角动量守恒定律
第五章 刚体的转动
1 质点的角动量 质量为 m 的质点以速度 v 在空间运动,某时刻相对原点 O 的位矢为 r ,质点相对于原 点的角动量
L
z
v
r
o
L r p r mv 大小 L rm v sin
第五章 刚体的转动
二
刚体定轴转动的角动量定理和角动量守恒定律
1 刚体定轴转动的角动量
L
i
m i ri v i ( m i ri )
2 i
z
O ri
mi
L J
2 刚体定轴转动的角动量定理
大学物理-动量与角动量

解:以小孔O为原点,绳对小球的拉力为有心力,其力矩为零。则小球对点的角动量守恒。
因:v = rw
则小球的动能增量为:
例3.18 证明开普勒第二定律:对任一行星,它的位置矢量(以太阳中心为参考点)在相等的时间内扫过相等的面积。
太阳对行星的引力为有心力,故行星角动量守恒,即 L 为常矢量,因此有:
角动量守恒:r1mv1=r2mv2 v1=(r2/r1)v2=1.2857v2
机械能守恒:
代入数据计算时,注意长度单位要统一使用m或km。
空间累积效应
时间累积效应
瞬时效应
动量定理
角动量定理
动能定理
功能定理
质点的角动量守恒定律
力
力矩
动量
角动量
冲量
冲量矩
力与动量
力矩与角动量
动量定理(冲量与动量)
角动量定理(冲量矩与角动量)
动量守恒:某一时间间隔内,质点系所受外力矢量和始终为零,…
角动量守恒:对固定参考点而言,质点受到的合力矩始终为零,…
例2-17:将质量为m 的小球系于轻绳一端,绳的另一端穿过光滑水平面上的小孔O 用手拉住。先使小球以角速度 w1 在水平面上做半径为 r1 的圆周运动,然后慢慢将绳下拉,使半径缩小为 r2 ,求在此过程中小球的动能增量。
力矩
O
力矩的分量式:
对轴的力矩
力矩为零的情况: (1)力 F 等于零; (2)力 F 的作用线与矢径 r 共线(即 sinj = 0 )
二、角动量定理
角动量 力矩
质点对某固定点的角动量随时间的变化率,等于质点所受的合力对该点的力矩。
表示成积分形式:
冲量矩(合力矩在Δt时间内对定点的冲量矩)
由对称性分析,质心C应在x轴上。
因:v = rw
则小球的动能增量为:
例3.18 证明开普勒第二定律:对任一行星,它的位置矢量(以太阳中心为参考点)在相等的时间内扫过相等的面积。
太阳对行星的引力为有心力,故行星角动量守恒,即 L 为常矢量,因此有:
角动量守恒:r1mv1=r2mv2 v1=(r2/r1)v2=1.2857v2
机械能守恒:
代入数据计算时,注意长度单位要统一使用m或km。
空间累积效应
时间累积效应
瞬时效应
动量定理
角动量定理
动能定理
功能定理
质点的角动量守恒定律
力
力矩
动量
角动量
冲量
冲量矩
力与动量
力矩与角动量
动量定理(冲量与动量)
角动量定理(冲量矩与角动量)
动量守恒:某一时间间隔内,质点系所受外力矢量和始终为零,…
角动量守恒:对固定参考点而言,质点受到的合力矩始终为零,…
例2-17:将质量为m 的小球系于轻绳一端,绳的另一端穿过光滑水平面上的小孔O 用手拉住。先使小球以角速度 w1 在水平面上做半径为 r1 的圆周运动,然后慢慢将绳下拉,使半径缩小为 r2 ,求在此过程中小球的动能增量。
力矩
O
力矩的分量式:
对轴的力矩
力矩为零的情况: (1)力 F 等于零; (2)力 F 的作用线与矢径 r 共线(即 sinj = 0 )
二、角动量定理
角动量 力矩
质点对某固定点的角动量随时间的变化率,等于质点所受的合力对该点的力矩。
表示成积分形式:
冲量矩(合力矩在Δt时间内对定点的冲量矩)
由对称性分析,质心C应在x轴上。
大学物理角动量转动惯量及角动量的守恒定律

i
ri F i 外
质点系总角动量的时间变化率等于质点系所受 外力矩的矢量和 (合外力矩 )
dL dt
M外
i
ri F i 外
注意: 合外力矩 是质点系所受各外力矩 外 的矢量和,而非合力的力矩。 注意:质点系内力矩的作用
不能改变质点系总角动量,但是影响总角动量 在系内各质点间的分配。
i
m i ri v c M
i
m i ri M
与 i 无关
vC
由
rc
i
m i ri M
rc
i
m i ri M
i
ri m i v c M rc v c 0
质心对自己的位矢
L rc m i v i
i
L
L自 旋
L轨道
3.定轴转动刚体的角动量 转轴 z 角速度 刚体上任一质点 m i
z
转动 平面
转轴与其转动平面交点O
m i 绕O 圆周运动半径为 ri
m i 对O的角动量: L io ri m i v i
ri o
mi
vi
大小: L io ri m i v i m i ri 2 L io 方向:沿 2 即 L io m i ri
M
z
xF y yF x
力对 o 点 的力矩在 z 轴方向的分量
注意:力矩求和只能对同一参考点(或轴)进行。
M
o
M 1o M
2o
矢量和 代数和
