三角形角格点问题系列:3-2H(3-B1-H)
三角形的格点

如果三角形的三个角的度数都是10的整数倍,三角形内一点与三角形的三个顶点分别连结后,得到的所有的角也都具有这个性质,我们称这样的点为三角形中的格点.求解三角形中的格点问题,常可利用对称点.利用对称点求解三角形中的格点问题,方法简单易行,解法简洁巧妙,题面新颖有趣,是学生巩固知识,培养能力,陶冶情操,提高素质的宝贵资料.1证明对称点常用的方法大家知道,把一个图形沿着某一条直线翻折,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称.两个图形中的对应点叫做关于这条直线的对称点,这条直线叫做对称轴.Q即可.不过,在证明对称时,只须摆明条件,而不必特别指明两个三角形的全等关系.例120°.求∠MAB的度数.解:如图1,设∠MBA的平分线交AC于D,连DM.图1显然,BM平分∠DBC,而CM平分∠DCB,即M为△DBC的内心.可知∠MDB=∠MDC =60°.有∠ADB=60°=∠MDB.故点A与点M关于BD对称.则∠MAB=90°-∠DBA=70°.这里证得“点A与点M关于BD对称”是根据“角、边、角”.例2在△ABC中,∠ABC=∠ACB=40°,P为形内一点,∠PCA=∠PAC=20°.求∠PBC的度数.知PA=PC.有点A与点C关于PD对称.得∠PDA=21∠ADC=30°.由∠ACB=∠ABC=40°,可知AB=AC=AD.易知∠PAD=80°=∠PAB,可知点B与点D关于PA对称.有∠PBA=∠PDA=30°.则∠PBC=10°.这里证出“点A与点C关于PD对称”是根据“边、边、边”,证出“点B与点D关于PA对称”是根据“边、角、边”.综上可知,证明两个点关于某线段所在直线对称,是一件很容易做的事情.而且熟练以后,更可能节省些笔墨.明确了这一点,我们就要积极、主动地创造条件,注意利用对称点.2在哪些情况下应想到使用对称点三角形中的格点问题,经常会给出或求证角平分线,这是使用对称点的最方便的条件,换言之,在题目给出或求证角平分线时,要想到使用对称点例3在△ABC中,∠ABC=40°,∠ACB=30°,P为∠ABC的平分线上一点,∠PCB=10°.求∠PAB的度数.解:如图3,在BA延长线上取一点D,使BD=BC.连DP、DC.图3由BP平分∠ABC,可知点D与点C关于BP对称.有PD=PC.由∠DPC=2(∠PBC+∠PCB)=60°,可知△PCD为正三角形.有PC=DC.在△ACD中,由∠ADC=70°=∠DAC,可知AC=DC.有AC=PC.在△PCA中,由∠PCA=20°,可知∠PAC=80°.则∠PAB=30°.这里由BP平分∠ABC,想到在BA延长线上取一点D,使BD=BC,则点D为点C关于BP的对称点.这是取对称点的最简单、最基本的方法.例4在△ABC中,∠ABC=50°,∠ACB=30°,Q为形内一点,∠QBA=∠QCA=20°.求∠QAB的度数.解:如图4,设BQ交AC于D,过点D作BC的垂线交QC于E.连BE.图4由∠QBC=30°=∠ACB,可知DE为BC的中垂线.由∠QCB=10°,可知∠EBC=10°,∠QBE=20°=∠QBA.由∠EDB=60°=∠EDC,可知∠BDA=60°=∠BDE.有点A与点E关于BD对称.则∠QAB=∠QEB=∠EBC+∠ECB=20°.这里注意到BQ是∠AQC的平分线,故想到在QC上取点E,使∠EBQ=∠ABQ,则点E为点A关于BQ的对称点.为此想到满足条件的点E,恰为BC中垂线与QC的交点。
三角形角格点问题系列:B2-3A

三角形角格点问题系列:B2-3A(图中有:PB=PC,AB+AP=BC,BP平分∠ABC,AB切△BCP的外接圆于B)已知:如图,∠PBA=∠PBC=∠PCB=10°,∠PCA=30°,求∠PAC,∠PCA.解法1:(同一法)作△A'B'D',使A'B'=B'D'=AB,∠A'B'D'=∠ABC=20°,在△A'B'D'内作正△A'D'P',连B'P',延长B'D'到C',使D'C'=D'P'.则∠A'B'P'=∠P'B'C'=10°,∠B'A'P'=∠B'D'P'=20°,∠P'A'C'=100°.因为△ABC≌△A'B'C',△ABP≌△A'B'P'.所以PB=P'B',因为△BPC≌△B'P'C',所以∠PAB=∠P'A'B'=20°,故∠PAC=∠P'A'C'=100°,∠PCA=20°.解法2:如图,作正△DPC,连接DA、DB ,显然D、P关于AC对称.又PB=PC=PD,故P是△DBC的外心,∠PDB=∠PBD=20°,因此∠PBA=∠DBA=10°,则∠APB与∠ADB相等或互补.如果相等,则D、P关于AB 对称,此时△DPB是正三角形.∠BPC=120°,和已知矛盾,因此∠APB与∠ADB互补,D、B、P、A 四点共圆,∠PAB=∠PDB=20°,∠PAC=100°.解法3:(B1-2A)如图,在∠PCA内作∠PCD=20°,交AB于D,连DP,取△DBC的外心为O,连OB、OC、OD、OP.因为∠DCB=30°,所以∠DOB=60°.△DBO是正三角形,故∠OBC=∠OCB=40°,∠BOP=50°,因此∠DOP=∠DBP=10°,所以B、O关于DP对称.得∠BDP=30°=∠PCA,A、D、P、C四点共圆,∠PAC=∠PDC=100°,∠PAB=20°.解法4:(B1-2A)如图,在∠PCA内作∠PCD=20°,交AB于D,连DP,以P为圆心,PB的长为半径作圆,交CD延长线于E,连PE、BE.因为∠ECB=30°,所以∠EPB=60°,故△PBE是正三角形,∠EBA=50°,∠PEC=20°,∠BED=80°,∠BDE=50°,因此BE=ED=EP,E是△PDB的外心,∠PDB=30°=∠PCA,则A、D、P、C四点共圆,∠PAB=∠PCD=20°,∠PAC=100°.解法5:(B1-2A)如图,作正△EBC,连接EB、EC,作∠PCD=20°,交AB于D,连DE、DP.因为∠PBC=∠PCB=10°,故∠BEP=∠CEP=30°,又因为∠BCD=∠ECD=30°,所以∠DEC=∠DBC=20°,则∠DEP=10°=∠DBP,因此E、B、P、D四点共圆.∠BDP=∠BEP=30°=∠ACP,所以A、D、P、C四点共圆,∠PAB=∠PCD=20°,∠PAC=100°.解法6:(B1-2A)如图,在BC上取点D ,使∠PDB=20°,以P为圆心,PD为半径画弧交直线BA于A',联结PD、PA'、DA'.作∠PCE=20°,交AB于E,连EP,则∠PA'B=∠PDB=20°=∠PCE,A'、E、P、C四点共圆,又因为△PDA'是正三角形,所以DP=DA'=DC,则D是△PA'C的外心,因此∠PEB=∠PCA'=30°=∠PCA,故A与A'重合,∠PAB=∠PCE=20°,∠PAC=100°.解法7:如图,作正△DPC,连DA、DB,在BD上截取BE=BP,连AE.由∠ACB=40°,∠ABC=20°,可知∠CAB=120°,由∠PCB=∠PBC=10°.可知PB=PC=PD,有P为△DCB的外心,于是∠DBC=30°,∠CDB=80°,∠PDB=20°.显然∠DBA=10°=∠PBA,可知P、E关于AB对称,有AE=AP,∠APB=∠AEB,由∠PCA=30°,可知CA为DP的中垂线,有AD=AP=AE,于是∠ADB=∠AED.由∠APB+∠ADB=∠AEB+∠AED=180°,可知P、B、D、A四点共圆,有∠PAB=∠PDB=20°.所以∠PAC=∠CAB -∠PAB=100°.解法8:(2B-8)如图,△ABC的外接圆交AP的延长线于D,连接BD、CD.易知∠ADC=20°,∠ADB=40°.△BPC的外接圆交AD的延长线于E,连接BE、CE,易知∠AEC=∠AEB=∠DCE=10°,∠DBE=30°.作E关于BD的对称点F,连接FB、FC、FP、FE,因为∠DBE=30°,所以△BEF是正三角形,∠EDF=80°=∠CDF ,所以C、E关于DF对称,FE=FC=FB,故F是△BCE的外心,因此∠BCE =30°.故∠BCD=20°,∠PAB=20°,∠PAC=100°.解法9:(4B-4)如图,△ABC的外接圆交BP的延长线于D,连接AD、CD.易知∠CAD=10°,∠ADB=40°,∠BDC=120°,∠ACD=10°,∠CPD=20°.以D为圆心,CD长为半径作圆交CP于E,连EA、ED.因为∠ACP=30°,故△ADE是正三角形,所以∠DEC=40°,∠EPD=∠EDP=20°.得到EP=ED=EA,故∠APD=30°,∠PAB=20°,∠PAC=100°..解法10:(27-3)如图,△ABC的外接圆交CP的延长线于D,连接AD、BD.易知∠BAD=10°,∠ADC=20°,∠BDC=20°,∠ABD=30°,∠BPD=20°.作正△ADE,连EB、EP,因为∠ABD=30°,所以E是△ABD的外心,∠BED=20°,∠DBE=80°,∠EBP=∠EDP=40°,所以B、D、P、E四点共圆.所以PD=PE,D、E关于AP对称,所以∠DAP=30°,∠PAB=20°,∠PAC=100°.解法11:(2A-7)如图,如图,△BCP的外接圆交AP的延长线于D,连接BD、CD,易知∠ADC=∠ADB=10°.设△ABC的外接圆交AD于E,连接EB、EC.易知∠DCE=10°,∠DBE=30°.作正△DCF,联结FB,FE.因为∠EBC=∠ECB=10°,故C、D关于EF对称,因此∠DFE=∠CFE=30°,故B、E、D、F四点共圆,∠BFE=10°,∠BFC=20°=∠BDC,因此D、F关于BC 对称,所以∠BCD=30°,∠BCE=20°.故∠PAB=20°,∠PAC=100°.解法12:(B5-5A)如图,如图,△BCP的外接圆交AC的延长线于D,连接BD、DP,易知∠ADP=∠BDP=10°,∠CBD=20°.设E为B关于DP 的对称点,连EB、EP.易知E、A、D三点共线,∠ABE=40°,∠BE=50°,∠AEP=30.作正△PEF,连FA、FD,因为∠AEP=30°,所以P、F关于AE对称.AF=AP,∠APF=∠AFP ,又因为PB=PE=PF,所以P是△BEF的外心,∠EBF=30°,∠PBF=∠PFB=20°,∠ABP=∠ABF=10°,易知∠APB 与∠AFB不等,由正弦定理可得,∠APB与∠AFB互补,所以A、F、B、P 四点共圆.得到∠PAB=20°,∠PAC=100°.解法13:(27-3)如图,如图,△ABP的外接圆交CP的延长线于D,连接BD、AD,易知∠ADC=10°,∠BAD=20°.作正△ADE,连EC、EB,因为∠ACD=30°,所以E是△ACD的外心,∠AEC=20°,∠CDE=80°,∠AEB=∠ACB=40°,所以A、C、E、B四点共圆.所以BA=BE,A、E 关于DB对称,所以∠BDA=30°,∠BDC=20°.得到∠PAB=20°,∠PAC=100°.解法14:(B6-16D)如图,△ABP的外接圆交CA的延长线于D,连接BD、PD,易知∠CDP=10°.作正△DCE,连接EB、EP,显然D、E关于CP对称.得到∠CEP=∠CDP=∠CBP=10°,所以B、E、C、P四点共圆.故∠BEC=∠BCE=20°,BC=BE.得到C、E关于BD对称.∠BDC=30°,∠BDP=20°,所以∠PAB=20°,∠PAC=100°.解法15:(B4-11I)如图,△ABP的外接圆交CB于D,连接AD、PD,易知∠ADP=∠DAP=10°.△ADC的外接圆交CP的延长线于E,连接EA、ED.易知∠DAE=10°,∠ADE=30°,作正△AEF,连FD、FP,因为∠ADE=30°,故F是△ADE的外心,所以FD=FE=FA,又∠DAE=10°,故∠DFE=20°,∠AFD =80°,而PD=PA,故∠PFA=∠PAF=40°,所以A、F 关于CE对称,故∠AEC=30°=∠ADC,得∠PDC=20°.所以∠PAB=20°,∠PAC=100°.解法16:(4A-4)如图,△ACP的外接圆交BP的延长线于D,连接AD、CD,易知∠ADB=30°,∠CAD=20°.作A关于BD对称的对称点E,连接FA、FD。
正三角形黄金角格点猜想
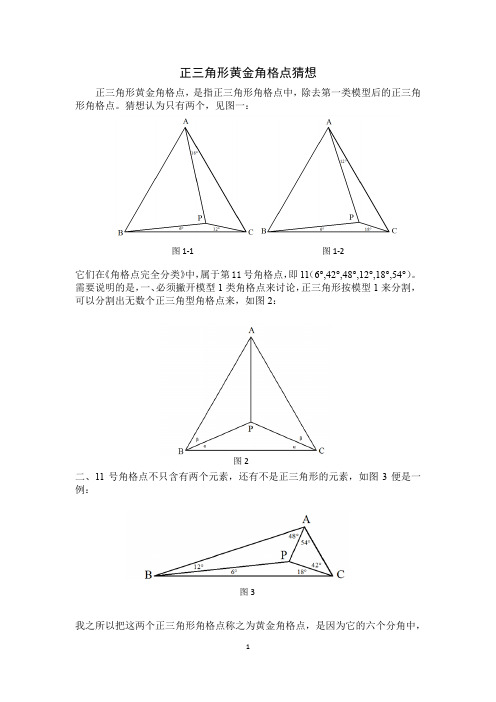
正三角形黄金角格点猜想正三角形黄金角格点,是指正三角形角格点中,除去第一类模型后的正三角形角格点。
猜想认为只有两个,见图一:它们在《角格点完全分类》中,属于第11号角格点,即11(6°,42°,48°,12°,18°,54°)。
需要说明的是,一、必须撇开模型1类角格点来讨论,正三角形按模型1来分割,可以分割出无数个正三角型角格点来,如图2:二、11号角格点不只含有两个元素,还有不是正三角形的元素,如图3便是一例:我之所以把这两个正三角形角格点称之为黄金角格点,是因为它的六个分角中,图1-1 图1-2图2 图3三个小角(6°,12°,18°)和三个大角(42°,48°,54°)刚好是两组等差数列,而且公差都是6°,在0-60°的范围内,这六个角漂亮的成对称排列,真是天合之作。
更重要的是,除了模型1包涵的正三角形角格点外,就只有这两个正三角形角格点了,再也找不出第三个了。
我们先来证明一下它的成立。
已知:△ABC是正三角形,P 是其内部一点,且∠PCA=6°∠PBA=18°∠PBC=42°∠PCB=54°作∠ACB的平分线交PB于D,连接AD,=>A、B关于CD对称∠DAB=∠DBA=18°O 是△ACD的外心,连接OA、OC、OD、OP∠ACD=30°∠AOD=60°=> △AOD是正三角形∠OAC=∠DAO-∠DAC= 60°-42°=18°∠OCA=∠OAC=18°∠PCO=6°+18°=24°∠PDA=∠DAB+ ∠DBA=18°+18°=36°∠PDO=60°-36°=24°∠PCO=∠PDO=24°=>P、O、C、D 四点共圆∠POD=∠PCD=24°=>D、O 关于AP对称=>∠PAD=30°∠PAB=30°+18°=48°∠PAC=60°-48°=12°证明的方法有很多种,这大概是最直接最简单的一种了。
利用对称点解三角形中的格点问题

利用对称点解三角形中的格点问题(本讲适合初中)如果三角形的三个角的度数都是10的整数倍,三角形内一点与三角形的三个顶点分别连结后,得到的所有的角也都具有这个性质,我们称这样的点为三角形中的格点.求解三角形中的格点问题,常可利用对称点.利用对称点求解三角形中的格点问题,方法简单易行,解法简洁巧妙,题面新颖有趣,是学生巩固知识,培养能力,陶冶情操,提高素质的宝贵资料.1证明对称点常用的方法大家知道,把一个图形沿着某一条直线翻折,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称.两个图形中的对应点叫做关于这条直线的对称点,这条直线叫做对称轴.根据对称点的定义不难知道,欲证两点M、N关于线段PQ所在的直线对称,只要证明 MPQ≌ NPQ即可.不过,在证明对称时,只须摆明条件,而不必特别指明两个三角形的全等关系.例1在 ABC中,∠ABC=60°,∠ACB=20°,M为∠ACB的平分线上一点,∠MBC=20°.求∠MAB的度数.解:如图1,设∠MBA的平分线交AC于D,连DM.图1显然,BM平分∠DBC,而CM平分∠DCB,即M为△DBC的内心.可知∠MDB=∠MDC=60°.有∠ADB=60°=∠MDB.故点A与点M关于BD对称.则∠MAB=90°-∠DBA=70°.这里证得“点A与点M关于BD对称”是根据“角、边、角”.例2 在△ABC中,∠ABC=∠ACB=40°,P为形内一点,∠PCA=∠PAC=20°.求∠PBC的度数.解:如图2,以AC为一边在△ABC外作正△DAC.连DP .由∠PCA=∠PAC=20°,可知PA=PC.有点A与点C关于PD对称.得∠PDA= 21∠ADC=30°.由∠ACB=∠ABC=40°,可知AB=AC=AD. 易知∠PAD=80°=∠PAB,可知点B与点D关于PA对称.有∠PBA=∠PDA=30°.则∠PBC=10°.这里证出“点A与点C关于PD对称”是根据“边、边、边”,证出“点B与点D关于PA对称”是根据“边、角、边”.综上可知,证明两个点关于某线段所在直线对称,是一件很容易做的事情.而且熟练以后,更可能节省些笔墨.明确了这一点,我们就要积极、主动地创造条件,注意利用对称点. 2 在哪些情况下应想到使用对称点三角形中的格点问题,经常会给出或求证角平分线,这是使用对称点的最方便的条件,换言之,在题目给出或求证角平分线时,要想到使用对称点.例3 在△ABC中,∠ABC=40°,∠ACB=30°,P为∠ABC的平分线上一点,∠PCB=10°.求∠PAB的度数.解:如图3,在BA延长线上取一点D,使BD=BC.连DP、DC.图 3由BP平分∠ABC,可知点D与点C关于BP对称.有PD=PC.由∠DPC=2(∠PBC+∠PCB)=60°,可知△PCD为正三角形.有PC=DC.在△ACD中,由∠ADC=70°=∠DAC,可知AC=DC.有AC=PC.在△PCA中,由∠PCA=20°,可知∠PAC=80°.则∠PAB=30°.这里由BP平分∠ABC,想到在BA延长线上取一点D,使BD=BC,则点D为点C关于BP的对称点.这是取对称点的最简单、最基本的方法.例4在△ABC中,∠ABC=50°,∠ACB=30°,Q为形内一点,∠QBA=∠QCA=20°.求∠QAB的度数.解:如图4,设BQ交AC于D,过点D作BC的垂线交QC于E.连BE.图4由∠QBC=30°=∠ACB,可知DE为BC的中垂线.由∠QCB=10°,可知∠EBC=10°,∠QBE=20°=∠QBA.由∠EDB=60°=∠EDC,可知∠BDA=60°=∠BDE.有点A与点E关于BD对称.则∠QAB=∠QEB=∠EBC+∠ECB=20°.这里注意到BQ是∠AQC的平分线,故想到在QC上取点E,使∠EBQ=∠ABQ,则点E为点A关于BQ的对称点.为此想到满足条件的点E,恰为BC中垂线与QC的交点。
格点三角形的专题

格点三角形的专题
1.如图,在4×4的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形.
(1)以点A为端点画一条线段AB,使它的另一个端点落在格点(即小正方形的顶点)上,且长度为5
(2)以(1)中的AB为边画一个等腰三角形ABC,使点C在格点上,且另两边的长都是无理数.
2.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画一个三角形,使它的三边长都是有理数;
(2)在图2中,画一个直角三角形,使它们的三边长都是无理数;
(3)在图3中,画一个正方形,使它的面积是10.
3.(2013•哈尔滨)如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB 和直线MN,点A,B,M,N均在小正方形的顶点上.
(1)在方格纸中画四边形ABCD(四边形的各顶点均在小正方形的顶点上),使四边形ABCD 是以直线MN为对称轴的轴对称图形,点A的对称点为点D,点B的对称点为点C;
(2)请直接写出四边形ABCD的周长.
例2:(2012•松北区二模)正方形网格中的每个小正方形边长都是1.每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形:
2、5
(1)在图1中,画△ABC,使△ABC的三边长分别为3、2
(2)在图2中,画△DEF,使△DEF为钝角三角形且面积为2.。
中考数学复习专题之格点问题

A.
B.
C.
D.
解析: 该题考查相似三角形的判断定理,利用网格长度和 勾股定理计算出各条边的长度,再利用对应边成比 例达到判断相似的目的。
【例5】三角形在正方形网格纸中的位置如图所示,则 sinα的值是( ).
3 4
A.
4
3
B. D.
3
4 5
.
C. 5
解析: 该题在网格中考查锐角的 正弦的意义,首先要用勾 股定理计算直角三角形斜 边的长.
解析该题一道人性化的操作型开放题只要理解了轴对称图形的意义选取一条适当的直线作对称轴就可以画出符合题意的图2006年江西中考题请在由边长为正三角形组成的虚线网格中画出一个所有顶点均在格点上且至少有一条边长为无理数的等腰三角形该题画法很多只要利用等腰三角形的轴对称性结合网格特点再考虑到题目中的条件即可
解析: 从题目的语气看,似乎要画直线AB与CD 夹 角的平分线,但是网格中没有画出直线AB与 CD 的夹角,图形的特殊性就在于AC//BD, 又已知AB=CD,因此四边形ABDC是等腰梯 形,线段BD的垂直平分线就是这个等腰梯形 的对称轴.如图,M、N分别为BD、AC的中 点,直线MN上的点到直线AB、CD的距离相 等.恰好点M是格点,以MB为斜边的直角三 角形的直角边长为3和1,这样,斜边在直线 MN上,直角边为3和1的格点直角三角形有3 个,符合题意的点有4个.选C.
C1 C2 C3
B
【例17】已知Rt△OAB在直角坐标系中的位置如图所 示,P(3,4)为OB的中点,点C为折线OAB上的动点, 线段PC把Rt△OAB分割成两部分. 问:点C在什么位置时,分割得到的三角形与Rt△OAB 相似? (注:在图上画出所有符合要求的线段PC,并求出相 y 应的点C的坐标)
三角形的格点公式

三角形的格点公式
(最新版)
目录
1.三角形的基本概念
2.格点公式的定义
3.三角形的格点公式
4.应用举例
正文
1.三角形的基本概念
三角形是由三条线段组成的一个闭合图形,其中任意两边之和大于第三边。
根据三角形的角度分类,可以分为锐角三角形、直角三角形和钝角三角形。
三角形在几何学中具有重要的地位,许多几何问题都与三角形有关。
2.格点公式的定义
格点公式是一种用于计算几何图形面积的公式。
在平面直角坐标系中,一个格点是指横纵坐标都是整数的点。
格点公式能够计算出一个多边形在某个方向上投影的面积。
3.三角形的格点公式
三角形的格点公式是一种计算三角形面积的公式,它可以通过三角形的三个顶点坐标来计算三角形的面积。
设三角形的三个顶点坐标分别为
A(x1, y1)、B(x2, y2) 和 C(x3, y3),那么三角形的面积 S 可以通过以下公式计算:
S = 0.5 * |(x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2))| 在这个公式中,|...|表示绝对值,保证了面积的正值。
4.应用举例
假设有一个三角形 ABC,其顶点坐标分别为 A(0, 0)、B(4, 0) 和 C(0, 3),我们可以使用三角形的格点公式来计算这个三角形的面积。
初三数学 格点问题资料
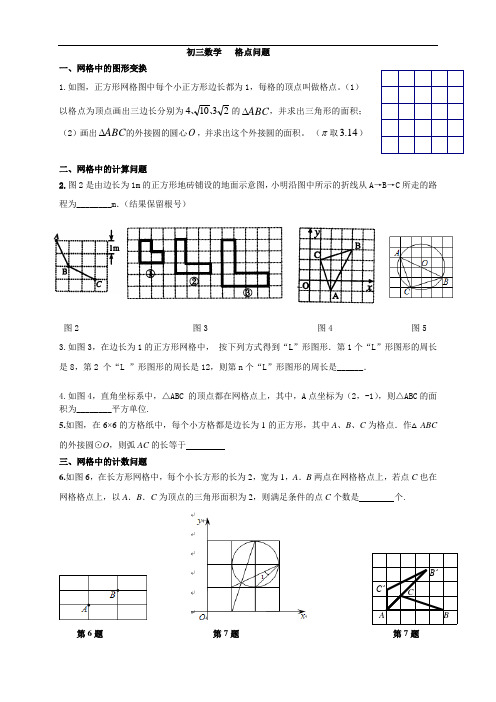
初三数学格点问题一、网格中的图形变换1.如图,正方形网格图中每个小正方形边长都为1,每格的顶点叫做格点。
(1)以格点为顶点画出三边长分别为23104、、的ABC∆,并求出三角形的面积;(2)画出ABC∆的外接圆的圆心O,并求出这个外接圆的面积。
(π取14.3)二、网格中的计算问题2.图2是由边长为1m的正方形地砖铺设的地面示意图,小明沿图中所示的折线从A→B→C所走的路程为________m.(结果保留根号)图2 图3 图4 图53.如图3,在边长为1的正方形网格中,•按下列方式得到“L”形图形.第1个“L”形图形的周长是8,第2•个“L•”形图形的周长是12,则第n个“L”形图形的周长是______.4.如图4,直角坐标系中,△ABC•的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为________平方单位.5.如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则弧AC的长等于三、网格中的计数问题6.如图6,在长方形网格中,每个小长方形的长为2,宽为1,A.B两点在网格格点上,若点C也在网格格点上,以A.B.C为顶点的三角形面积为2,则满足条件的点C个数是个.第6题第7题第7题A BCC’B’7.如图7,A 、B 、C 三点在正方形网格线的交点处,若将△ACB 绕着点A 逆时针旋转得到△AC ’B ’,则tanB ’的值为8.如第8题图,1∠的正切值等于 。
四、网格中的相似图形1. 如图2,若A 、B 、C 、P 、Q 、甲、乙、丙、丁都是方格纸中的格点,为使△ABC ∽△PQR ,则点R 应是甲、乙、丙、丁四点中的A. 甲B. 乙C. 丙D. 丁2.有一张足够大的网格图,每一小格都是边长为a 正方形,每格的顶点叫做格点。
网格上有如右图的D C B A ,,,四点,连接AD BC AC AB 、、、。
(1)请问在网格上可以找到几个格点(记这个点为E )使得以点E D A 、、为顶点的ADE ∆与ACD ∆相似;选择其中的一点,来说明ADE ∆与ACD ∆相似。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形角格点问题系列:3-2H(3-B1-H)
(图中有PB=PC)
已知:如图,∠ABP=∠CBP=10°,∠ACP=20°,∠PAC=100°,求∠PCB ,∠PAB .
解法1:如图,作∠BPD=150°,即∠BDP=20°,在BA边上作BE=BD,连接EC、ED、EP.得∠BEP=∠ACP=20°,可知A、E、C、P四点共圆.∠CEP=∠CAP=100°,因为∠ABP=∠CBP=10°,所以△DEP是正三角形,可得∠CED=40°,易知DC=DE=DF,D是△CEP的外心,则∠PCB=10°,∠PAB=30°.
解法2:如图,作△ACP的外接圆交BP延长线D,连接DA、DC.则∠ADB=20°,∠BDC=100°.作A关于BD的对称点E,连接EA、ED.易知:∠AED=∠EAD=70°,∠DEC=30°,∠ADE=40°,∠CDE=80°,作正△DEF,连接FA、FC,因为∠DEC=30°,所以D、F关于BC对称,∠CDF=∠CFD=20°,DA=DE=DF,所以D是△AEF的外心,∠DAF=∠DFA=40°,∠DCH=140°,所以A、D、C、F四点共圆.所以∠CAD=20°=∠CPD.则∠PCB=10°,∠PAB=30°.
解法3:如图,作△ABC的外接圆交BP延长线D,连接DA、DC.则∠ADB=∠BDC=10°.作正△CDE,连接EA、EP,因为DA=DC=DE,故D
是△BACE的外心,∠DAE=∠AE=40°,∠CAE=30°,∠AEC=100°,设△APE的外接圆交PC于F,连FA、FD、FE,易知∠AEF =60°,∠CEF =40°,因为∠DCP=30°,所以D、E关于PC对称,∠FDE=∠FED=20°,∠DFE=140°,所以A、D、F、E、P五点共圆,所以∠DPC=∠DEF=20°.则∠PCB=10°,∠PAB=30°.。
