2013-2014高一数学期中试题和答案
2013-2014学年高一数学上学期期中试题及答案(新人教A版 第105套)

南昌三中2013—2014学年度上学期期中考试高一数学试卷一、选择题(3'1030'⨯=)1、已知{|||}M x x x N =∈,则( )(AM (B )2M ∈(C2M M ∈且(D )以上结论都不正确 2、函数lg(1)2x y x -=-+的定义域为( ) (A )(,1)-∞(B )(,0)-∞(C )(1,)+∞(D )(0,)+∞3、函数3()4(0,1)x f x a a a -=+>≠的图像恒过定点坐标为( ) (A )(3,5)(B )(3,4)(C )(0,4)(D )(0,5)4、已知函数22,1(),12x x f x x x +≤-⎧=⎨-<<⎩,若()3f a =,则a 的取值个数为( )(A )1 (B )2 (C )3 (D )4 5、已知幂函数()f x的图像经过点(2,2,则(4)f 的值为( ) (A )16 (B )116 (C )12(D )2 6、设5.1348.020.91)21(,8,4y -===y y ,则( )(A )213y y y >>(B )312y y y >>(C )321y y y >>(D )231y y y >> 7、设x 、y 为非零实数,0,1a a >≠,则下列正确的是( ) (A )2log 2log a a x x = (B )log ||log ||log ||a a a x y x y ⋅=⋅ (C )2log 2log ||a a x x = (D )log log ()log a a a xx y y-=8、不等式2log (23)1a x x -+≤-在x R ∈时恒成立,则a 的取值范围是( ) (A )[2,)+∞ (B )(1,2] (C )1[,1)2 (D )1(0,]29、函数(10)xf x =,则(3)f 的值为( )(A )3log 10(B )lg 3(C )310(D )10310、若函数()x bf x x a-=-在区间(,4]-∞上是增函数,则有( ) (A )4a b >>(B )4a b >>(C )4a b <<(D )4a b << 二、填空题(4'520'⨯=)11、方程|lg |20x x +-=有 个实数根12、函数101()101x x f x -=+是 (填偶函数、奇函数、非奇非偶函数)13、计算:2lg 5lg2lg5lg20++=14、已知xx 1,5xx 22121+=+-则的值是 15、函数1()42(2)x x f x x -=+≤的值域是南昌三中2013—2014学年度上学期期中考试高一数学答卷一、选择题(3'1030'⨯=)二、填空题()11、 12、 13、14、 15、 三、解答题16、(8分)若全集为R ,若集合{|1},{|0}5xA x xB x x =≥=≤- (1)求A B ;(2)求U AB ð17、(10分)若函数2())f x x =-,(1)求定义域(2)求值域(3)求单调增区间18、(10分)解关于x 的不等式22231251()x x x x a a-+--+>(0,1a a >≠)19、(10分)设2221()2(log )2log f x x a b x =++,已知当12x =时,()f x 有最小值8-,(1)求,a b ;(2)满足()0f x >的x 集合20、(12分)已知定义域为R 的函数12()2x x bf x a+-+=+为奇函数(1)求,a b 的值;(2)若对任意的正数t ,不等式22(2)(2)0f t t f t k -+-<恒成立,求k 的取值范围南昌三中2013—2014学年度上学期期中考试高一数学答案二、填空题()11、1个 12、奇函数 13、2 14、23 15、(0,18] 三、解答题16、{|05}2B x x =≤<分;{|15}4A B x x =≤<分;{|1}6U A x x =<分ð;{|01}8U AB x x =≤<分ð 17、(1){|11}3x x -<<分;(2){|0}6y y ≤分; (3)(1,0]10-分((1,0)-也对)18、当1,{|23}5a x x x ><>时或分;当01,{|23}10a x x <<<<时分19、(1)246a b =-⎧⎨=-⎩分;(2)1{|02}108x x x <<>或分 20、(1)[解析] (1)∵f (x )是奇函数,∴f (0)=0,即-1+b 2+a =0,解得b =1,从而有f (x )=-2x+12x +1+a.又由f (1)=-f (-1)知-2+14+a =--12+11+a ,解得a =2.经检验a =2适合题意, ∴所求a ,b 的值为2,14分(2)由(1)知f (x )=-2x+12x +1+2=-12+12x +1.由上式易知f (x )在(-∞,+∞)上为减函数6分又因f (x )是奇函数,从而不等式f (t 2-2t )+f (2t 2-k )<0,等价于f (t 2-2t )<-f (2t 2-k )=f (-2t 2+k8分.因f (x )是减函数,由上式推得t 2-2t >-2t 2+k .即对一切0t <有3t 2-2t >k 012k ⇒<分。
2013-2014学年高一数学上学期期中试题 理 及答案(新人教A版 第15套)

长春市十一高中2013-2014学年度高一上学期期中考试数 学 试 题本试卷分第一部分(选择题)和第二部分(非选择题),满分120分,测试时间120分钟。
第一部分(选择题)一、选择题(每题4分,共48分) 1.sin 210=( )AB .C .12D .12-2.已知M ⊆{1,2,4},且M 中最多有一个偶数,这样的M 集合有( ) A.4 B.5 C.6 D.73.函数y =的定义域为 ( )A .3(,)4-∞B . 3(,1]4C . (,1]-∞D .3(,1)44.若函数2()2(1)2f x x a x =+-+在区间(],4-∞上递减,则实数a 的取值范围是( ) A. a ≤5 B. a ≥5 C. a ≥-3 D. 3a ≤-5.函数322-+=x x y 的单调递减区间为( )A .(-∞,-3]B .(-∞,-1]C .[1,+∞)D .[-3,-1] 6.y=f(x)的大体图象如下图所示,则函数y=f(|x|)的零点的个数为( )A.4B.5C.6D.77.以下四个数中最大的是( )A. (ln 2)2B. ln (ln 2)C. ln 2D. ln 28.如果方程lg 2x +(lg2+lg3)lg x +lg2·lg3=0的两根为x 1、x 2,那么x 1·x 2的值为( ) A .2lg ·3lgB .2lg +3lgC . 16D.-69.设α角属于第二象限,且2cos2cosαα-=,则2α角属于( )A 第一象限B 第二象限C 第三象限D 第四象限10.已知)2()()(2-++-=mn x n m x x f ,若a 、b 是0)(=x f 的两根,则实数m ,n ,a ,b 的大小关系可能为( )A. a <m <n <bB.m < a <b <nC.m < a <n < bD. a <m <b <n11.定义在R 上的奇函数f (x )满足:当x >0时,f (x )=x a a x log + )1(>a ,则方程f (x )=0的实根的个数为( )A .1B .2C .3D .512.已知函数x x f lg )(=,n m <<0,且)()(n f m f =,则n m 2+的取值范围是 ( )A .(22,+∞) B.(3,+∞) C .[3,+∞)D . [22,+∞)第二部分(非选择题)二、填空题(每题4分,共16分) 13.已知是第四象限角,α+-=α+-=α,53cos ,524sin m m m m 那么 αtan 的值 为________. 14.若31)3sin(=-απ,则)65cos(απ-的值为________. 15.已知函数),12lg()(2++=x ax x f若()f x 的值域是R ,则实数a 的取值范围为________.16.函数x x f a log )(=在[)+∞,2上恒有|)(x f |>1,则a 取值范围是________. 三、解答题(本大题共5小题,共56分) 17.(10分)已知2tan =x ,求xx xx sin cos sin cos -+的值。
2013-2014学年度上学期期中考试(高一数学)附答案
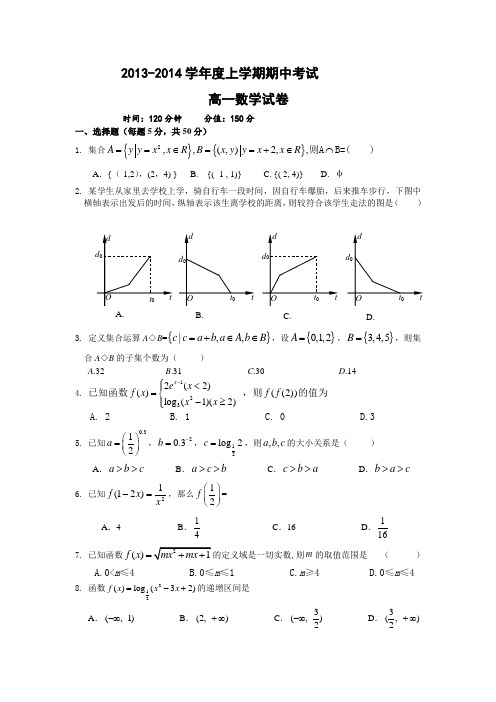
2013-2014学年度上学期期中考试高一数学试卷时间:120分钟 分值:150分一、选择题(每题5分,共50分)1. 集合{}{}2,,(,)2,,A y y x x R B x y y x x R ==∈==+∈⋂则A B=( )A .{(-1,2),(2,4) } B. {( -1 , 1)} C. {( 2, 4)} D. φ2. 某学生从家里去学校上学,骑自行车一段时间,因自行车爆胎,后来推车步行,下图中横轴表示出发后的时间,纵轴表示该生离学校的距离,则较符合该学生走法的图是( )3. 定义集合运算A ◇B =|,,c c a b a A b B =+∈∈,设0,1,2A =,3,4,5B =,则集合A ◇B 的子集个数为( )A .32B .31C .30D .144. 已知函数1232(2)()log (1)(2)x e x f x x x -⎧<⎪=⎨-≥⎪⎩ ,则))2((f f 的值为 A. 2 B. 1 C. 0 D.35. 已知0.312a ⎛⎫= ⎪⎝⎭,20.3b -=,12log 2c =,则,,a b c 的大小关系是( )A .a b c >>B .a c b >>C .c b a >>D .b a c >> 6. 已知21)21(x x f =-,那么12f ⎛⎫⎪⎝⎭= A .4 B .41 C .16 D .1617. 已知函数()=f x 的定义域是一切实数,则m 的取值范围是 ( )A.0<m ≤4B.0≤m ≤1C.m ≥4D.0≤m ≤48. 函数212()log (32)f x x x =-+的递增区间是A . (,1)-∞B . (2,)+∞C . 3(,)2-∞ D .3(,)2+∞ 9. 已知函数()f x 是定义在R 上的偶函数,在(),0-∞上单调递减,且有()3=0f ,则使得()0<f x 的x 的范围为( )A.(),3-∞B. ()3,+∞C.()(),33,-∞+∞D.()3,3-10.对实数a 和b 定义运算“⊗”:,1,,1a ab a b b a b -≤⎧⊗=⎨->⎩. 设函数22()(2)()f x x x x =-⊗-,x ∈R ,若函数()y f x c =-的图像与x 轴恰有两个公共点,则实数c 的取值范围是( )A .3(,2](1,)2-∞--B .3(,2](1,)4-∞---C .11(1,)(,)44-+∞D .31(1,)[,)44--+∞二、填空题(每题5分,共25分) 11.函数)12(log 741)(2++-=x x x f 的定义域为 .12.幂函数()22211m m y m m x--=--在()0,x ∈+∞时为减函数,则m= .13. 已知2510m n==,则11m n+= . 14. 如果函数()f x 满足:对任意实数,a b 都有()()()f a b f a f b +=,且()11f =,则()()()()()()()()()()2342011201212320102011f f f f f f f f f f +++++= _________.15. 给出下列命题:①()f x 既是奇函数,又是偶函数;②()f x x =和2()x f x x=为同一函数;③已知()f x 为定义在R 上的奇函数,且()f x 在(0,)+∞上单调递增,则()f x 在(,)-∞+∞上为增函数;④函数y =[0,4) 其中正确命题的序号是 .三、解答题(共75分)16.(本小题满分12分)⑴计算:0.25-2-25.0log 10log 2)161(85575.032----⑵已知函数)(x f 是定义域为R 的奇函数,当x ≤0时,)(x f =x(1+x).求函数)(x f 的解析式并画出函数)(x f 的图象.17.(本小题满分12分)已知集合{}|5239A x x =-≤+≤,{}|131B x m x m =+≤≤- (1)求集合A ;(2)若B A ⊆,求实数m 的取值范围.18.(本小题满分12分)某商品在近30天内每件的销售价格p (元)与时间t (天)的函数关20,025,,100,2530,.t t t N p t t t N +<<∈⎧=⎨-+≤≤∈⎩该商品的日销售量Q (件)与时间t (天)的函数关系是40+-=t Q ),300(N t t ∈≤<,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?19.(本小题满分12分)定义运算:a bad bc c d=- (1)若已知1k =,求解关于x 的不等式101x x k< -(2)若已知1()1x f x k x=- -,求函数()f x 在[1,1]-上的最大值。
2013-2014年高一上期中考试数学试卷及答案

金川公司二高2013-2014学年度第一学期高一年级期中考试数学试卷第Ⅰ卷一、选择题(本大题共12小题,每小题5分,满分60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.下列表示错误..的是().A.B.C.D.2.集合,,则().A.B.C.D.3.函数的定义域为().A.B.C.D.4.下列四组函数中,表示相同函数的一组是().A.B.C.D.5.函数的零点一定位于区间().A.B.C.D.6.设,,则().A.B.C.D.7.函数的单调增.区间是().A.B.C.D.8.在区间上的最大值是最小值的倍,则的值为().A.B.C.D.9.函数的大致图象是().A.B.C.D.10.已知函数,则().A.B.C.D.11.是定义在上递减的奇函数,当时,的取值范围是().A.B.C.D.12.若函数,实数是函数的零点,且,则的值().A.恒为正值B.等于0 C.恒为负值D.不大于0第Ⅱ卷二.填空题:(本大题共4小题,每小题5分,满分20分。
)13.若函数是定义域为的偶函数,则= .14.已知幂函数的图象经过点,那么.15.若函数是定义在上的奇函数,当时,,则时,的表达式是.16.给出下列六个结论其中正确...........)..是.(填上所有正确结论的序号..的序号①已知,,则用含,的代数式表示为:;②若函数的定义域为,则函数的定义域为;③函数恒过定点;④若,则;⑤若指数函数,则;⑥若函数,则.三.解答题:(本大题共6小题,满分70分;解答应写出文字说明,证明过程或演算步骤。
) 17.(本题满分10分)计算下列各式的值:(1); (2).18.(本题满分12分)已知函数,(1)在给定直角坐标系中画出函数的大致图象;(每个小正方形边长为一个单位长度) (2)由图象指出函数的单调递增区间(不要求证明); (3)由图象指出函数的值域(不要求证明)。
19.(本题满分12分) 已知集合,集合,若,求实数的取值范围。
2013-2014第一学期高一数学期中考试(附答案)

普宁一中2013~2014学年度第一学期期中考试高一级数学科试题注意事项:1.本试卷分试题卷和答题卷两部分,考试结束后交答题卷,总分150分,考试时间120分钟。
2.答题前,考生须将自己的姓名、班级、座位号填写在答题卡指定的位置上。
3.选择题的每小题选出答案后,用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其答案,不能答在试题卷上。
4.非选择题必须按照题号顺序在答题卡上各题目的答题区域内用黑色字迹的钢笔或签字笔作答,超出答题区域或在其它题的答题区域内书写的答案无效。
第Ⅰ卷 选择题部分(满分50分)一、单项选择题(本大题共10小题,每小题5分,共50分。
)1. 已知全集{12345}U =,,,,,集合{1,3}A =,{1,3,4}B =,则集合()U C A B =( * )A .{3}B .{4,5}C .{245},,D .{3,4,5} 2. 若全集{}{}1,2,3,41U U C A ==且,则集合A 的真子集共有( * )A. 3个B. 5个C. 7个D. 8个 3. 函数()lg(23)f x x =-的定义域是( * )A. 3[,)2+∞B. 3(,)2+∞C. 3(,]2-∞D. 3(,)2-∞4. 下列函数中,既是奇函数又是增函数的为( * )A .1y x =+B .2y x =-C .1y x=D .||y x x = 5. 三个数20.40.40.42log 2,,的大小关系为( * )A. 20.40.40.42log 2<<B. 20.40.4log 20.42<< C .20.40.40.4log 22<< D .0.420.4log 220.4<< 6. 函数1()34x f x -=-的零点所在区间为( * )A .(0, 1)B .(1,2)C .(2,3)D .(3,4)D CB A7. 定义在R 上的偶函数在[0,6]上是增函数,在[6,+∞]上是减函数,又(6)5f =, 则()f x ( * )A .在[-6,0]上是增函数,且最大值是5B .在[-6,0]上是增函数,且最小值是5C .在[-6,0]上是减函数,且最小值是5D .在[-6,0]上是减函数,且最大值是5 8. 已知幂函数()f x3),则(2)f 的值是( * )A . 4B .2C .41D .219.某同学家门前有一笔直公路直通长城,星期天,他骑自行车匀速前往旅游,他先前进了a km ,觉得有点累,就休息了一段时间,想想路途遥远,有些泄气,就沿原路返回骑了b km(b <a ), 当他记起诗句“不到长城非好汉”,便调转车头继续前进. 则该同学离起点的距离s 与时间t 的函数关系的图象大致为( * )10. 已知y =f (x )是定义在R 上的奇函数,当0x >时,()3f x x =-,那么不等式0)(<x f 的解集是( * ) A. {}03x x <<B. {}3x x <-C. {}30,03x x x -<<<<或D. {}3,03x x x <-<<或第Ⅱ卷 非选择题部分(满分100分)二、填空题(本大题共4小题,每小题5分,共20分。
2013-2014学年高一上学期期中考试数学试题 Word版含答案

2013-2014学年度第一学期期中考试高一年级数学(满分160分,考试时间120分钟)一、 填空题1、设集合}3,1{=A ,集合}5,4,2,1{=B ,则集合=B A2、若1)(+=x x f ,则(3)f =3、函数3)1()(+-=x k x f 在R 上是增函数,则k 的取值范围是4、指数函数x a y =的图像经过点(2,16)则a 的值是5、幂函数2-=x y 在区间]2,21[上的最大值是6、已知31=+aa ,则 =+aa 17、函数321)(-=x x f 的定义域是________.8、化简式子82log 9log 3的值为9、已知函数()y f x =是定义在R 上的单调减函数,且(1)(2)f a f a +>,则a 的取值范围是10、下列各个对应中, 从A 到B 构成映射的是 (填序号)A B A B A B A B(1) (2) (3) (4)11、满足82>x 的实数x 的取值范围12、设()x f 为定义在()+∞∞-,上的偶函数,且()x f 在[)+∞,0上为增函数,则()2-f ,()π-f ,()3f 的大小顺序是____________13、当0>a 且1≠a 时,函数3)(-=x a x f 的图像必过定点14、已知⎩⎨⎧≥+<-=)0(1)0(2)(2x x x x x x f 若,3)(=x f 则=x二、解答题15、全集R U =,若集合},103|{<≤=x x A }72|{≤<=x x B ,则(结果用区间表示)(1)求)()(,,B C A C B A B A U U ;(2)若集合C A a x x C ⊆>=},|{,求a 的取值范围16、对于二次函数2483y x x =-+-,(1)求函数在区间]2,2[-上的最大值和最小值;(2)指出函数的单调区间17、化简或求值:(1))3()4)(3(656131212132b a b a b a -÷-;(2)()281lg500lg lg 6450lg 2lg552+-++18、已知某皮鞋厂一天的生产成本c(元)与生产数量n(双)之间的函数关系是n=c504000+(1)求一天生产1000双皮鞋的成本;(2)如果某天的生产成本是48000元,那么这一天生产了多少双皮鞋?(3)若每双皮鞋的售价为90元,且生产的皮鞋全部售出,试写出这一天的利润P关于这一天生产数量n的函数关系式,并求出每天至少生产多少双皮鞋,才能不亏本?19、已知21()log 1xf x x+=- (1)求()f x 的定义域;(2)求证:()f x 为奇函数(3)判断()f x 的单调性,并求使()0f x >的x 的取值范围。
2013-2014学年高一数学上学期期中质量检测试题及答案(新人教A版 第112套)

高一上学期期中质量检测数学试题注:本卷中如出现A 、B 题,普通中学做A 题,重点中学做B 题.一、选择题(本大题共10小题,每小题5分,共50分,每小题四个选项中,只有一项符合题目需求)1. 设集合{}2,0,2M =-,{}N x x x ==,则MN =( )A.{}2,0,2-B.{}0,2C.{}2D.{}02. 下列函数中,与函数1y x=定义域相同的函数为( )A.y x =B.y= C.0y x =D.y =3. 设12log 3a =,0.21()3b =,132c =,则( )A.a <b <cB. c <b <aC. c <a <bD. b <a <c4. 下列函数()f x 与()g x 表示同一函数的是( )A.21()1x f x x -=-和()1g x x =+B.()1f x =和0()g x x =C.()1f x x =+和()g xD.()f x x =和()ln xg x e =5. 下列区间中,函数()lg f x x x =+的零点所在区间为( ) A.()1,2B.1,12⎛⎫ ⎪⎝⎭C.11,102⎛⎫ ⎪⎝⎭D.10,10⎛⎫ ⎪⎝⎭6. 函数2log 1y x =+的图像是()D7.设2(0)()0(0)2(0)x f x x x >⎧⎪==⎨⎪-<⎩,1()()0()x g x x ⎧=⎨⎩为有理数为无理数,则[]()f g π的值为( )A. 0B.2C.x π=D.2-8.函数y = ) A. (],3-∞ B. []0,3 C.[]0,9 D.[)0,+∞9. 已知函数253()(1)m f x m m x --=--是幂函数,且是()0,+∞上的增函数,则m 的值为( ) A.2 B. 0 C.1-或2 D. 1-10.(A 题)定义域为[]1,1-奇函数()y f x =,若1()22f =-,则1()2f -的值为( ) A.12 B.2 C.12- D.2-(B 题)奇函数()y f x =在定义域[]1,1-上是增函数,则满足(1)f m -+(21)f m -<0的m 的取值范围为( )A.[]0,1B.20,3⎡⎫⎪⎢⎣⎭ C.20,3⎡⎤⎢⎥⎣⎦D.[)0,1二、填空题(本大题共5小题,每小题5分,共25分) 11.函数31log 22y x ⎛⎫=⎪-⎝⎭的定义域为 .12.集合{}25A x R x =∈-≤的元素中最小整数为 .13.满足方程2222log log 30x x --=的x 的解集为 . 14.关于x 的方程2(1)2(1)10m x m x -++-=有且只有一个实数根,则实数m 的取值集合为 .15.(A 题)设函数()f x bx c =+,给出下列四个命题:①方程()0f x =有且只有一个实数根;②当c=0时()y f x =是奇函数;③x R ∀∈有()2()f x c f x -=-;④方程()0f x =至多有一个根。
2013-2014学年高一数学上学期期中试题及答案(新人教A版 第148套)

浙江省杭州外国语学校2013-2014学年(第一学期)高一期中考试数学试卷一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的,把答案填在答卷..相应空格中) 1.已知集合|0,1x M x x R x ⎧⎫=≥∈⎨⎬-⎩⎭,{}2|31,N y y x x R ==+∈,则M N ⋂等于( )A .φB .{}|1x x ≥C .{}|1x x >D .{}|10x x x ≥<或 2.给出下列命题:①第二象限角大于第一象限角;②三角形的内角是第一象限角或第二象限角;③不论用角度制还是用弧度制度量一个角,它们与扇形所在圆的半径的大小无关; ④若sin sin αβ=,则α与β的终边相同; ⑤若cos 0θ<,则θ是第二或第三象限的角. 其中正确..命题的个数是( )A .1B .2C .3D .43.若()f x =,则()f x 的定义域为 ( )A .1,02⎛⎫-⎪⎝⎭ B .1,02⎛⎤- ⎥⎝⎦ C .1,2⎛⎫-+∞ ⎪⎝⎭D .()0,+∞ 4.下列函数()y f x =中满足“对任意12,(0,)x x ∈+∞,当12x x <时,都有()12()f x f x <”的是 ( ) A .1()f x x= B .()2()1f x x =- C .2()f x e = D .()ln(1)f x x =+ 5.454sincos tan 363πππ⎛⎫⋅⋅- ⎪⎝⎭的值是( )A.4-B.4 C.4- D.46.定义在R 上的函数()y f x =是奇函数,且满足(1)(1)f x f x +=-.当[]1,1x ∈-时,3()f x x =,则(2013)f 的值是 ( )A .1B .2C .0D .1-7.若cos2sinαα+=tanα等于 ( ) A.12B.2 C.12-D.2-8.函数x xx xe eye e--+=-的图象大致为 ( ) 9.已知()y f x=为R上的减函数,则满足1(1)f fx⎛⎫<⎪⎝⎭的实数x的取值范围是 ( ) A.()1,1- B.()0,1 C.()()1,00,1-⋃ D.()(),11,-∞-⋃+∞10.已知函数lg,010()13,105x xf xx x⎧<≤⎪=⎨-+>⎪⎩,若,,a b c互不相等,且()()()f a f b f c==,则abc 的取值范围是 ( ) A.()1,10B.()5,10 C.()10,15D.()15,30二、填空题(本大题共7小题,每小题4分,共28分,把答案填在答卷中相应横线上)11.化简1603[(2)](1)---的值为____▲____.12.函数()f x=的单调增区间为____▲____.13.函数()2()log31xf x=+的值域为____▲____.14.已知cos63πα⎛⎫+=⎪⎝⎭,则5cos6πα⎛⎫-⎪⎝⎭的值为____ ▲____.15.已知函数()ln2f x x x=-+有一个零点所在的区间为(),1k k+ (*k N∈),则k的值为____▲____.16.已知函数())f x x=,若实数,a b满足(1)()0f a f b-+=,则a b+等于▲ .17.已知不等式2log 0a x x -<,当10,2x ⎛⎫∈ ⎪⎝⎭时恒成立,则实数a 的取值范围是▲ .三、解答题(本大题共4小题,共42分,解答应写出文字说明,证明过程或演算步骤)18.(本小题满分10分)已知集合2{310}M x x x =-≤,{121}N x a x a =+≤≤+.(Ⅰ)若2a =,求M (R N ð);(Ⅱ)若MN M =,求实数a 的取值范围.19.(本小题满分10分)已知()()sin cos 2ππαπααπ⎛⎫--+=<< ⎪⎝⎭,求下列各式的值: (Ⅰ)sin cos αα-; (Ⅱ) 33sin cos 22ππαα⎛⎫⎛⎫--+⎪ ⎪⎝⎭⎝⎭.20.(本小题满分10分)设a 为实数,函数()2()2f x x x a x a =+--.(Ⅰ)若(0)4f ≥,求a 的取值范围; (Ⅱ)求函数()f x 的最小值.21.(本小题满分12分)已知定义在D 上的函数()f x ,如果满足:对任意D x ∈,存在常数0M >, 使得|()|f x M ≤成立, 则称()f x 是D 上的有界函数, 其中M 称为函数()f x 的上界.下面我们来考虑两个函数:()421xxf x p --=+⋅+, 12()12xxq g x q -⋅=+⋅.(Ⅰ)当1p =时, 求函数()f x 在(),0-∞上的值域, 并判断函数()f x 在(),0-∞上是否为有界函数, 请说明理由;(Ⅱ)若1,22q ⎛∈⎝⎦, 函数()g x 在[]0,1上的上界是()H q , 求()H q 的取值范围;(Ⅲ)若函数()f x 在[)0,+∞上是以3为上界的有界函数, 求实数p 的取值范围.杭州外国语学校2013-1高一年级期中考试数学答题卷一、选择题:(本大题有10小题,每小题3分,共30分)二、填空题:(本大题有7小题,每小题4分,共28分)11. 3 12.[)2,+∞ 13. ()0,+∞14.1,116⎡⎫⎪⎢⎣⎭三、解答题:(本大题有4小题,共42分,请写出必要的解答过程) 18. (1) 因为a =2,所以N ={x |3≤x ≤5},∁R N ={x |x <3或x >5}. 又M ={x |-2≤x ≤5}, 所以M ∩ (∁R N )={x |x <3或x >5}∩{x |-2≤x ≤5}={x |-2≤x <3}.(2)若M ≠φ,由M N M =,得N ⊆M ,所以⎩⎪⎨⎪⎧a +1≥-22a +1≤52a +1≥a +1.解得0≤a ≤2; 当N =φ,即2a +1<a +1时,a <0,此时有N ⊆M ,所以a <0为所求.综上,实数a 的取值范围是(-∞,2].____________________________________________________________________________________19.(1)sin cos 3αα+=,所以平方可得:212sin cos 9αα+=,即:7sin cos 18αα=-所以4sin cos 3αα-===(2)原式=3322cossin (sin cos )(sin sin cos cos )αααααααα+=+-+7(1)18=+=_______________________ 姓名_____________ 试场号______________ 考号_______________…………密○………………………………………封○………………………………………○线………………………○20. (1)(0)4f ≥,即:4a a -≥,所以0a <,得到:24a ≤,所以2a ≤-(2)()()22222,()2,x x a x a f x x x a x a⎧+-≥⎪=⎨--<⎪⎩令222212()323,33g x x ax a x a a x a ⎛⎫=-+=-+≥ ⎪⎝⎭;()2222()22,h x x ax a x a a x a =+-=+-<当0a ≥时,2min ()2g g a a ==,2min ()2h h a a =-=-,所以2min 2f a =- 当0a <时,2min 1233g g a a ⎛⎫==⎪⎝⎭,2min ()2h h a a ==,所以2min 23f a =综上:2min22,02,03a a f a a ⎧-≥⎪=⎨<⎪⎩ ____________________________________________________________________________________21. (1)当p=1时,()421xx f x --=++因为)(x f 在(),0-∞上递减,所以()(0)3f x f >=,即)(x f 在(),1-∞的值域为()3,+∞故不存在常数0M >,使|()|f x M ≤成立, 所以函数()f x 在(),1-∞上不是有界函数(2)2()112xg x q =-+⋅,∵ q>0 ,[]1,0∈x ∴ ()g x 在[]0,1上递减,∴)0()()1(g x g g ≤≤ 即121()121q qg x q q--≤≤++∵1(2q ∈,∴112112q q q q --≥-++,∴1()1q g x q -≤+, ∴1()1q H q q-≥+ ,即 1[,)1qq -+∞+ (3)由题意知,3)(≤x f 在[)1,+∞上恒成立.3)(3≤≤-x f , ∴1142()22()22x x x x p -⋅-≤≤⋅- 在[)0,+∞上恒成立∴ max min 11[42()][22()]22xx x x p -⋅-≤≤⋅-设t x=2,t t t h 14)(--=,tt t p 12)(-=, 由x ∈[)0,+∞得 t ≥1,设121t t ≤<,()()2112121241()()0t t t t h t h t t t ---=>, 所以)(t h 在[)1,+∞上递减,)(t h 在[)1,+∞上的最大值为(1)5h =-, 又()()012)()(21212121<+-=-t t t t t t t p t p ,所以)(t p 在[)1,+∞上递增, )(t p 在[)1,+∞上的最小值为(1)1p =所以实数p 的取值范围为[]5,1-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013-2014学年第一学期第一学段
高一数学模块检测
命题人 李诗秀 审题人 孔祥华
第1卷(共60分)
一、选择题:本大题共l2小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}{}5,3,2,3,2==B A ,则集合B A =( )
A. {}2
B. {}3,2
C. {}5,3,2
D.{}5,3,2,3,2
2.已知集合}01|{2=-=x x A ,则下列式子表示不正确的是( )
A .A ∈1
B .A ∈-}1{
C .A ⊆φ
D .A ⊆-}1,1{
3.若14)(2+-=x x x f ,则=)2(f ( )
A. 3
B. -3
C. 6
D. -6
4.函数y x =3与x y -=3的图象关于下列那种图形对称( )
A .x 轴
B .y 轴
C .直线y x =
D .原点
5.已知奇函数()f x ,当0x >时
1
()f x x x =+,则(1)f -=( ) A.1 B.2 C.-1 D.-2
6.若二次函数y =-x 2+bx +c 的图象的对称轴是x =2,则有( ).
A .f (1)≤f (2)≤f (4)
B .f (2)>f (1)>f (4)
C .f (2)<f (4)<f (1)
D .f (4)>f (2)>f (1)
7.计算:9823log log ⋅=( )
A 12
B 10
C 8
D 6
8.函数y=x x ⋅的图象大致是( )
9.函数2(01)x y a a a =+>≠且图象一定过点( )
A (0,1)
B (0,3)
C (1,0)
D (3,0)
10.若0.52a =,πlog 3b =,2log 0.5c =,则( )
A a b c >>
B b a c >>
C c a b >> D
b c a >>
11.设()f x 是奇函数,且在(0,)+∞内是增函数,又(3)0f -=,
则()0x f x ⋅<的解集是( )
A .{}|303x x x -<<>或
B .{}|303x x x <-<<或
C .{}|33x x x <->或
D .{}|3003x x x -<<<<或
12.若方程0=--a x a x 有两个解,则a 的取值范围是( )
A ()+∞,1
B ()1,0
C ()+∞,0
D Φ
第Ⅱ卷(非选择题 共90分)
二、填空题.本大题共有4个小题,每小题4分,共16分.
13.函数2
1)(--=x x x f 的定义域为 14. 若12)1(22+=+x x f ,则)(x f =
15.
1)3()(2-++=x a x x f 在),1[+∞上是增函数,则a 的取值范围是 16. 若3632==n m ,则
=+n
m 11 三、解答题.本大题共6个小题,共74分.解答应写出文字说明、证明过程或推演
步骤. 17、(本小题满分12分)
已知集合{}|28A x x =≤≤,{}|16B x x =<<, U =R .
⑴ 求A B ⋃, (2)求(C u A)∩B ;
18、(本小题满分12分)
设函数⎪⎩
⎪⎨⎧<=>+=)0(,0)0(,)0(,1)(x x x x x f π. (1)求)0(f , (2)求)]0([f f
19、(本小题满分12分)
计算下列各式:
(1)2
1023213(2)(9.6)(3)(1.5)48
-----+; (2
)7log 23
log lg 25lg 473
+++.
20. (本小题满分12分)
我国是水资源匮乏的国家,为鼓励节约用水,某市打算出台一项水费政策措施,规定:每一季度每人用水量不超过5吨时,每吨水费收基本价1.3元;若超过5吨而不超过6吨时,超过部分水费加收200%;若超过6吨而不超过7吨时,超过部分的水费加收400%,如果某人本季度实际用水量为(07)x x ≤≤吨,应交水费为()f x 。
(1)求(4)f 、f (5.5)、f (6.5)
的值; (2)试求出函数()f x 的解析式。
21(本小题满分13分)
设函数)(x f 为定义在R 奇函数,当0>x 时,)(x f =1422++-x x ,
(1)求:当0<x 时,)(x f 的表达式;
(2)用分段函数写出)(x f 的表达式;
(3)若函数=)(x h a x f -)(恰有三个零点,求a 的取值范围(只要求写出结果). 22(本小题满分13分) 设21()12x x
a f x ∙-=+是R 上的奇函数。
(1)求实数a 的值;
(2)判定()f x 在R 上的单调性。
2013-2014学年第一学期第一学段
高一数学模块检测
命题人 李诗秀 审题人 孔祥华
参考答案
一、CBBBD BDCBA DA
二、13 {}21≠≥x x x 且 14 12-x 15 5-≥a 16
21 三、解答题
17 解(1) A B ⋃={}81≤<x x ┄┄┄┄┄┄┄┄┄┄6分
(2) C u A={}82><x x x 或┄┄┄┄ 9分,(C u A)∩B ={}
21<<x x ┄┄12分 18解: (1))0(f =π ┄┄6分 (2) )]0([f f =1+π ┄┄┄┄12分 19解.(1)原式212329373()1()()482--=--+ 2132232333()1()()222
-⨯⨯-=--+………3分 223331()()222--=--+ 12
=…………………………6分 (2)原式3433log lg(254)23
=+⨯+……………………………………9分 = 210lg 3log 241
3++- 1152244
=-++=………………………12分 20.解:(1)(4)4 1.3 5.2f =⨯=………………………………………1分
(5.5)5 1.30.5 3.98.45f =⨯+⨯=………………………………3分 (6.5)5 1.31 3.90.5 6.513.65f =⨯+⨯+⨯=……………………5分
(2)当05x ≤≤时,() 1.3 1.3f x x x =⨯=………………………………7分
当56x <≤时,() 1.35(5) 3.9 3.913f x x x =⨯+-⨯=-………………9分 当67x ≤<时,() 1.351 3.9(6) 6.5 6.528.6f x x x =⨯+⨯+-⨯=-……11分
故 1.3(05)() 3.913(56)6.528.6(67)x x f x x x x x ≤≤⎧⎪=-<≤⎨⎪-<≤⎩
………………………………………12分
21解:(1)若0<x ,0>-x ,142)(2
+--=-x x x f ,又)(x f 为定义在R 奇函数,
所以142)()(2-+=--=x x x f x f 。
………………………6分 (2)⎪⎩
⎪⎨⎧<-+=>++-=)0(,142)0(,0)0(,142)(22x x x x x x x x f ………………………10分
(3)13-<<-a 或0=a 或31<<a ………………………13分
22.(1)法一:函数定义域是R ,因为()f x 是奇函数,
所以()()f x f x -=-,即12212121212x x x
x x x
a a a ---∙∙--==+++………………2分 122x x
a a ∴-∙=-解得1a =…………………………………………6分
法二:由()f x 是奇函数,所以(0)0f =,故1a =,……………3分 再由21()12x x
f x -=+,验证()()f x f x -=-,来确定1a =的合理性…6分 (2)()f x 增函数………………………………………7分
法一:因为1
212)(+-=x x x f ,设1x ,2x R ∈,且12x x <,得122x x <2。
则12()()f x f x -=…12212(22)0(21)(21)
x x x x -=<++,即12()()f x f x < 所以()f x 说增函数。
…………………………………13分
法二:由(1)可知212()12121
x x x f x -==-++,由于2x 在R 上是增函数, 221x ∴+在R 上是减函数,221
x ∴-+在R 上是增函数,。
