数学建模第二章作业答案章绍辉
章绍辉数学建模第二章
第二章 习题二1.（1）按照“两秒准则”表明前后车距与车速成正比，这和“一车长度准则”是类似的。
在2.2节的基础上引入下面的符号: D ～前后车距（m ） v ～车速（m/s ）K ～按照“两秒准则”，D 与v 之间的比例系数（s ）,在“两秒准则”中，K=2 于是“两秒准则”的数学模型为（2）D K v K =⨯=而刹车距离的数学模型为212d kv k v =+ 要考虑“两秒准则”是否安全，即要比较D 与d 的大小212d D kv k v K v -=+-⨯（1） 代入k 1=0.75v ，k 2=0.082678，K=2，所以当d>D ，即刹车距离的理论大于前后车距时，认为不够安全；当d<D ，即刹车距离的理论小于前后车距时，认为足够安全。
计算得到当速度超过15.12 m/s 时，“两秒准则”就不安全了，也就是说“两秒准则”适用于车速不是很快的情况。
另外，还可以通过绘图直观解释为什么“两秒准则”不够安全，用以下程序把刹车距离实测数据与“两秒准则”都画在同一幅图中：v=(20:5:80).*0.44704;d2=[18,25,36,47,64,82,105,132,162,196,237,283,334 22,31,45,58,80,103,131,165,202,245,295,353,41820,28,40.5,52.5,72,92.5,118,148.5,182,220.5,266,318,376]; d2=0.3048.*d2;k1=0.75; k2=0.082678; K=2; d1=[v;v;v].*k1;d=d1+d2;plot([0,40],[0,K*40],'k')hold onplot(0:40,polyval([k2,k1,0],0:40),':k')plot([v;v;v],d,'ok')title('比较刹车距离实测数据、理论值和两秒准则')legend('两秒准则','刹车距离理论值',...'刹车距离的最小值、平均值和最大值',2)xlabel('车速v（m/s）')ylabel('距离（m）')hold off（2）“两秒准则”的不安全性在于，其刹车距离随着车速增长的速度赶不上理论刹车距离的增长速度，为此我们提出一个“t秒准则”，通过不断增加t的值使得刹车距离总是大于理论刹车距离。
数学建模章绍辉版作业
数学建模章绍辉版作业 Last revised by LE LE in 2021第四章作业第二题：针对严重的交通情况，国家质量监督检验检疫局发布的国家标准，车辆驾驶人员血液中的酒精含量大于或等于20mg/100ml,小于80mg/100ml 为饮酒驾车，血液中的酒精含量大于或等于80mg/100ml 的为醉酒驾车。
下面分别考虑大李在很短时间内和较长时间内（如2个小时）喝了三瓶啤酒，多长时间内驾车就会违反新的国家标准。
1、 问题假设大李在短时间内喝下三瓶啤酒后，酒精先从吸收室（肠胃）吸收进中心室（血液和体液），然后从中心室向体外排除，忽略喝酒的时间，根据生理学知识，假设（1） 吸收室在初始时刻t=0时，酒精量立即为032D;在任意时刻，酒精从吸收室吸收进中心室的速率（吸收室在单位时间内酒精含量的减少量）与吸收室的酒精含量成正比，比例系数为1k ；（2） 中心室的容积V 保持不变；在初始时刻t=0时，中心室的酒精含量为0；在任意时刻，酒精从中心室向体外排除的速率（中心室在单位时间内酒精含量的减少量）与中心室的酒精含量成正比，比例系数为2k ；（3） 在大李适度饮酒没有酒精中毒的前提下，假设1k 和2k 都是常量，与饮酒量无关。
2、 符号说明酒精量是指纯酒精的质量，单位是毫克；酒精含量是指纯酒精的浓度，单位是毫克/百毫升； ~t 时刻（小时）；()~x t 在时刻t 吸收室（肠胃）内的酒精量（毫克）；0~D 两瓶酒的酒精量（毫克）；(t)~c 在时刻t 吸收室（血液和体液）的酒精含量（毫克/百毫升）； 2()~c t 在时刻t 中心室（血液和体液）的酒精含量（毫克/百毫升）；~V 中心室的容积（百毫升）；1~k 酒精从吸收室吸收进中心室的速率系数（假设其为常数）；2~k 酒精从中心室向体外排除的速率系数（假设其为常数）；3~k 在短时间喝下三瓶酒的假设下是指短时间喝下的三瓶酒的酒精总量除以中心室体积，即03/2D V ；而在较长时间内（2小时内）喝下三瓶酒的假设下就特指03/4D V . 3、 模型建立和求解（1） 酒是在很短时间内喝的：记喝酒时刻为0t =（小时），设(0)0c =，可用()2113212()k t k t k k c t e e k k --=--来计算血液中的酒精含量，此时12k k 、为假设中所示的常数，而033155.792D k V ⎛⎫== ⎪⎝⎭.下面用MATLAB 程序画图展示血液中酒精含量随时间变化并且利用fzero 函数和fminbnd 函数来得到饮酒驾车醉酒驾车对应的时间段，以及血液中酒精含量最高的时刻。
【免费下载】华南师范大学参加美国数学建模竞赛获奖成绩
题号 A B B C A B B A B C A A A A A B C C
二等奖 20797 刘秀湘
二等奖
20853
二等奖 21820 刘秀湘
二等奖 23312 刘秀湘
二等奖 23232 苏洪雨
二等奖 20767
二等奖 21708
二等奖 22535
二等奖 22753
二等奖 19695 王明兰
二等奖
一等奖 22308
一等奖 20506
一等奖 22082
一等奖 20879
一等奖 22480
二等奖 20382
二等奖 20749
二等奖 21061
二等奖 21593
二等奖 21691
二等奖 22266
Hale Waihona Puke 二等奖 22398二等奖 22532
二等奖 22791
二等奖 18193
二等奖 18560
控制号 18252
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力根通保据过护生管高产线中工敷资艺设料高技试中术卷资，配料不置试仅技卷可术要以是求解指，决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资，配料而置试且时卷可，调保需控障要试各在验类最；管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下，安与要全过加，度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高；试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中，核资或对料者定试对值卷某，弯些审扁异核度常与固高校定中对盒资图位料纸置试，.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置，弯高尤曲中其半资要径料避标试免高卷错等调误，试高要方中求案资技，料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高，术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术，管以术来架及避等系免多统不项启必方动要式方高，案中为；资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资，管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装，工置合作调理并试利且技用进术管行，线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确：指灵在导活分。。线对对盒于于处调差，试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷，术调应问试采题技用，术金作是属为指隔调发板试电进人机行员一隔，变开需压处要器理在组；事在同前发一掌生线握内槽图部内 纸故，资障强料时电、，回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资，料料线试试缆卷卷敷试切设验除完报从毕告而，与采要相用进关高行技中检术资查资料和料试检，卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。
华东师大数模第2章答案02~ch2_solutions
> > > > >
dxdK1:=diff(x,K1): dydK1:=diff(y,K1): assign(K1=150000); sxK1:=dxdK1*(K1/x); syK1:=dydK1*(K1/y); sxK1 := 1.001502253 syK1 := -.01760602687
Then S(x, K_1) = +1.0015 and S(y, K_1) = -0.0176 so that if the carrying capacity for Blue whales increases by 10% then the optimal population for Blue whales increases by about 10% and the optimal population for Fin whales stays about the same. Now compute that > restart: > z:=0.05*x*(1 - x / 150000) - 10^(-8)* x* y + 0.08* y* (1 - y / K2) - 10^(-8)* x*y; 1 1 y z := .05 x x x y + .08 y 1 − − 1 − 150000 50000000 K2 > dzdx:=diff(z,x); > dzdy:=diff(z,y); dzdx := .05 − .6666666666 10-6 x − dzdy := − 1 x + .08 − 1 50000000 .16 y K2 y
{ y = 196544.8172, x = 69103.65549 }
数学建模课后习题第二章参考答案
数学建模第二章课后习题第5题参考答案5.(1)at m me w w w w w t w --+=)()(000，要使,只需。
联系：在目前的情况下，当时，两个模型中猪的体重的变化都一样，当时，新的假设中猪的体重增长的比较快，当时，新的假设猪的体重增长的比较慢。
因为，所以函数为增函数，即当t 增大时，猪的体重会随着增加，这与原来的假设是一致的。
两个假设都满足'(0)w r =，在最佳出售时机附近误差微小。
区别：150200250300当a=1/60时两个假设模型的比较由图可知，新假设是阻滞增长模型，体重w 是t 的增函数，体重增加的速率先快后慢，时间充分长后，体重趋于w m 。
而原假设w(t)=0w +rt 只假设体重匀速增加。
从长时间来看，新假设比原假设更符合实际。
(2) 则t 天之后比现在出售多赚的纯利润为：0000((0))()()()()(0)(0)(0)()matm p gt w w Q t p t w t C t p w ct p w w w w e--=--=--+- 其中p(0)=12,g=0.08, 900=w ，270=m w ,,c=3.2,代入数据并用matlab 中的fminbnd 函数运算得到： 在t=14.4336时，纯利润到达最大值：Qm =12.1513。
代码如下：Q=@(t)((12-0.08*t)*90.*270)./(90+(270-90).*exp(-(1/60)*t))-3.2*t-12*90;nQ=@(t)-Q(t);[t,Q1]=fminbnd(nQ,0,100), Qm=-Q1 t = 14.4336 Q1 = -12.1513 Qm =12.1513 （3）所以，如果生猪体重wm 增加1%，灵敏度S(tm,dwm)= 3.7669，最佳出售时间tm 就推迟0.038%。
灵敏度比较小，所以wm 对tm 不灵敏。
程序如下：Q=@(t,wm)((12-0.08*t)*90.*wm)./(90+(wm-90).*exp(-(1/60)*t))-3.2*t-12*90;数值计算W m 对t m 的灵敏度（W m =270，t m =14.4336）m m w w +∆ ()/%m m w w ∆ m m t t +∆ ()/%m m t t ∆ (,)m m S w t272.70001.000014.9773 0.0377 3.7669 283.5000 5.0000 17.0565 0.1817 3.6345 297.0000 10.0000 19.46010.34833.4825数值计算W m 对Q m 的灵敏度（W m =270，Q m =12.1513） m m w w +∆ ()/%m m w w ∆ m m Q Q +∆ ()/%m m Q Q ∆ (,)m m S w Q272.7000 1.0000 13.1078 0.0787 7.8720 283.5000 5.0000 17.1208 0.4090 8.1794 297.0000 10.0000 22.47540.84968.4963d=[.01;.05;.1];dwm=d*270;Q1=@(t)-Q(t,270+dwm(1));[t1,Q1]=fminbnd(Q1,0,30);Q2=@(t)-Q(t,270+dwm(2));[t2,Q2]=fminbnd(Q2,0,30);Q3=@(t)-Q(t,270+dwm(3));[t3,Q3]=fminbnd(Q3,0,30);Qm1=-Q1;Qm2=-Q2;Qm3=-Q3;tm=14.4336;Qm=12.1513;Sw_t=@(t,w)((t-tm)/tm)./(w/270);Sw_Q=@(Q,w)((Q-Qm)/Qm)./(w/270);t=[t1;t2;t3],Q=[Qm1;Qm2;Qm3],a=[270+d.*270,d.*100,t,(t-tm)./tm,Sw_t(t,d.*270)],b=[270+d.*270,d.*100,Q,(Q-Qm)./Qm,Sw_Q(Q,d.*270)], t =14.977317.056519.4601Q =13.107817.120822.4754a =272.7000 1.0000 14.9773 0.0377 3.7669 283.5000 5.0000 17.0565 0.1817 3.6345 297.0000 10.0000 19.4601 0.3483 3.4825b =272.7000 1.0000 13.1078 0.0787 7.8720 283.5000 5.0000 17.1208 0.4090 8.1794297.0000 10.0000 22.4754 0.8496 8.4963 (4)由图可知，新假设模型是一个阻滞增长模型，比原来的模型更符合实际，可以在较长时间内使用。
2001年度全国大学生数学建模竞赛获奖名单
张明星 姜英琼 黄志祥 周玉兰 要尉鹏 郭强辉 刘挺 李亮 林波 陈芳 徐庆新 江浩 杨涛 王瑛 刘伟 刘超慧 覃健 赵亮 程亮 杨飞锋 黄华基 李玉珍 李蓉 唐卓
陈明 黄静波 陈明生 李德 王艳辉 李胜梅 彭张节 苗宇 张晖 黄厚旗 朱亚红 陈璐 孙晓 伍微 陈爽 马熠 曾艳 方程 张丽强 徐哲晟 郑顺洪 赵大 李刚 文家新
翟冰洁 林镇伟 彭志生 张凯 李小金
李峰 廖敬青 梁祖红 郑泽伟 王茜
唐海伟 梁 斌 杨春传
秦 宇 曾 毅 李作新 许 彦 郭研研 冷建全
肖伟 魏巍 雷磊 戴帅湘
杨威 弓晨 王伟民 武胜波
涂寅辉 李艳 杜雄 刘娟
吴华玉 叶 飞 任 凯 张 杨 王慧欣 孟 超 管 立 俞一凡 高 芸
宫凤强 谷霖 李振国 谢国亮
刘则毅 李宝毅 韩家楠 教练组 郝培锋 郝培锋 薛定宇 韩莉 教师组 丁永生 杜育根 数模教练组 数模教练组 数模教练组 张耀 王兵团 邢启江 王鸣 指导小组
贺祖国 贺祖国 贺祖国 贺祖国 贺祖国 汪飞星 汪飞星 指导小组 邹述超 舒慕增 马邦勤 赵凌 数模组 欧志英等 霍海峰等 张民悦等 孙海珍 宁如云等 刘启明等 数模组 数模组 秦衍 陈荣军 梅银珍
东南大学
55
东南大学
56
东南大学
57
兰州铁道学院
58
北方交通大学
59
北京大学
60
北京大学
61
北京工业大学
62
北京邮电大学
63
北京邮电大学
64
北京邮电大学
65
北京邮电大学
66
北京邮电大学
67
北京科技大学
68
北京科技大学
69
北京理工大学
2017年广东省大学生数学建模竞赛初评结果
序号
报名号
1
20171900100
2
肖文熙
2
20171900100
5
梁智鹏
3
20171900102
4
吕坤升
Байду номын сангаас
4
20171900106
1
张丰学
5
20171900106
8
廖晨阳
6 20171900105 王昱
本科组一等奖
获奖选手
所在院校
梅洁妍 潘珏
中山大学
梁昊
祝俊浩 中山大学
陈卓晖 周斐漩 中山大学
钟钧豪 杨斌斌 中山大学
7
孙健
21
20171900117
2
黄思集
22
20171900117
5
沙钧
23
20171900118
5
王翔宇
24
20171900122
0
陈星月
25
20171900202
5
房依璐
26
20171900206
6
马一宁
27 20171900213 张浩健
获奖选手
刘俊材 史春霓
王江寅 谭有翀
陈晓聪 江俊锋
彭劲
辛弘
2017年全国大学生数学建模竞赛广东省分赛获奖名单（初稿）
根据《广东省教育厅关于做好 2017年广东省高校大学生学科竞赛工作的通知》（粤 教高函〔2017〕39号）安排，省教育厅委托中山大学组织开展 2017年全国大学生数学 建模竞赛广东省分赛。竞赛于 9月 14日至 9月 17日分本科和高职高专两个组别进行， 全省共有 88所高校 2252支代表队伍共计 6749位选手报名参赛。
数学建模第二次作业(章绍辉版)
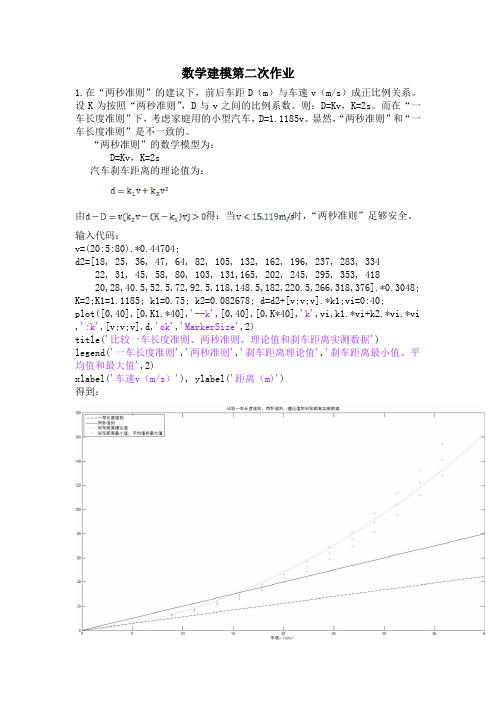
数学建模第二次作业1.在“两秒准则”的建议下，前后车距D（m）与车速v（m/s）成正比例关系。
设K为按照“两秒准则”，D与v之间的比例系数。
则：D=Kv，K=2s。
而在“一车长度准则”下，考虑家庭用的小型汽车，D=1.1185v。
显然，“两秒准则”和“一车长度准则”是不一致的。
“两秒准则”的数学模型为：D=Kv，K=2s汽车刹车距离的理论值为：由得：当时，“两秒准则”足够安全。
输入代码：v=(20:5:80).*0.44704;d2=[18, 25, 36, 47, 64, 82, 105, 132, 162, 196, 237, 283, 33422, 31, 45, 58, 80, 103, 131,165, 202, 245, 295, 353, 41820,28,40.5,52.5,72,92.5,118,148.5,182,220.5,266,318,376].*0.3048; K=2;K1=1.1185; k1=0.75; k2=0.082678; d=d2+[v;v;v].*k1;vi=0:40;plot([0,40],[0,K1.*40],'--k',[0,40],[0,K*40],'k',vi,k1.*vi+k2.*vi.*vi,':k',[v;v;v],d,'ok','MarkerSize',2)title('比较一车长度准则、两秒准则、理论值和刹车距离实测数据')legend('一车长度准则','两秒准则','刹车距离理论值','刹车距离最小值、平均值和最大值',2)xlabel('车速v（m/s）'), ylabel('距离（m)')得到：由上图也可以看出当车速超过15米每秒时，“两秒准则”不安全。
全国大学生数学建模竞赛组织委员会2.doc
深圳市科学技术协会ﻫ全国大学生数学建模竞赛组织委员会南方科技大学联系地址:北京清华大学数学科学系电话：（010）邮政编码:１0008４传真：(010)6２773４００网址：关于“2015年‘深圳杯'数学建模夏令营”的通知为了进一步促进数学建模活动的开展，培养和锻炼学生的社会实践能力和创新精神，全国大学生数学建模竞赛组委会(以下简称全国组委会)、深圳市科协和南方科技大学决定共同举办“2０1５年‘深圳杯'数学建模夏令营”,现将有关事项通知如下。
一、参加夏令营的师生名单在全国组委会和各赛区组委会推荐的基础上,经过全国组委会专家组的审核，确定了邀请参加夏令营的师生名单,见附件1 (各队的报告时间为3０分钟）。
本次夏令营原则上不接受附件1名单以外的师生参加（指导教师为集体名称或者多于１人时,每个队最多只能派一名教师参加）。
二、夏令营的时间和地点夏令营将于２0１５年8月20-25日在深圳市南方科技大学举行。
8月20日（周四)为报到时间,8月２5日(周二）为离营时间。
（具体报到地点等详细信息将于8月初发布在网站。
）营务组不负责预订火车或飞机票，请与会人员安排好行程，自行提前预订或购买返程票。
三、活动经费的分担应邀参加夏令营的学生(附件1名单中的学生)的差旅费自理,应邀参加夏令营的教师(附件１名单中的教师）的差旅费和住宿费自理,夏令营期间的其他相关费用由活动主办方承担.四、具体时间安排7月31日前,参加夏令营的师生将回执及论文摘要（见附件2,每个队填写一份)用同时发给：石瑶冰,４6４7８6７９6,电话3；;传真9蔡志杰,16３，电话不反馈或不按时反馈回执者, 视为自动放弃参加本次夏令营。
营务组收到回执后将会回复确认收到，如未收到确认邮件，请与上述联系人确认。
８月20日（周四)全天:代表报到８月２1—２４日:夏令营活动8月２5日(周二）:代表离会五、注意事项1、夏令营住宿营地不提供洗漱用品,请自备。
数学建模II第2章4-7
艇长l (米) 7.93 9.76 11.75 18.28
艇宽b (米) 0.293 0.356 0.574 0.610
l/b 27.0 27.4 21.0 30.0
空艇重w0(kg) 浆手数n 16.3 13.6 18.1 14.7
可以看出，当浆手数增加时，艇的尺寸、艇重 都随之增加，但比值l /b, w0/n 变化不大，如果假 定l /b是常数，即各种艇的形状一样，则可以得到 艇浸没面积与排水体积的关系，若假定w0/n 是常 数，则可以得到艇和浆手的总重量与浆手数之间的 关系。
乙的无差别曲线族 g(x,y)=c2具有相同性质
y
g(x,y)=c2 c2
O
x
为得到双方满意的交换方案，将双方的无 差别曲线族画在一起，其中乙的无差别曲线 族圆点在O/，且x、y轴均反向，于是当乙的 满意度c2增加时无差别曲线向下移动。
双方的交换路径 甲的无差别曲线族 f=c1 乙的无差别曲线族 g=c2 (坐标系x’O’y’, 且反向）
等价交换准则是指：两种物品用同一货币 衡量其价值，进行等价交换。
设交换前甲占有物品X（数量为x0)与乙占 有物品Y(数量为y0)具有相同的价值，则等价 交换原则下交换路径为(x0,0), (0,y0) 两点的 连线CD,于是双方满意的交换方案为CD与AB 的交点p。
y yo
.
D
B
p
0
A
.
C
xo x
实例： 设玉米的价格为每千克p元，山羊的价格 为每只q元，则有交换前甲方拥有玉米的价 值为pX, 乙方拥有山羊的价值为qY。若交换 前甲乙拥有物品的价值相同，即pX=qY。
则交换发生后，甲方拥有玉米和山羊的价 值为px+qy, 乙方拥有玉米和山羊的价值为 p(X-x)+q(Y-y)，按按等价交换的原则应该有 px+qy=p(X-x)+q(Y-y)。利用关系pX=qY， 可以得出实际交换的点（x,y）满足关系式： x/X+y/Y = 1 此曲线是一条直线，在交换路径坐标系中 画出此曲线与AB相交，就得到实际交换发生 的点。
《数学建模》(章绍辉 著)参考解答
绘得的图形：
奖 学 金 捐 款 账 户 余 额 的 演 变 ， 年 利 率 2.5% 25
20
账户余额（万元）
15
10 每 年 用 0.4万 元 每 年 用 0.5万 元 每 年 用 0.6万 元 每 年 用 1万 元 每 年 用 2万 元 0 2 4 6 8 10 第 k年 12 14 16 18 20
平衡点为 x b r . 因为 r>0，所以如果 x0 b r ，即 0 b rx0 ， xk 就会单调增 加趋于无穷大，并且增加得越来越快；如果 x0 b r ，即 b rx0 ，
xk 就会单调衰减（到零为止） ，并且减少得越来越快；如果 x0 b r ，即 b rx0 ， xk 就会保持不变，即 xk x0 .
如果养老金想用到 80 岁，即 x240 =0，那么
x0
b 1 r
240
1
r 1 r
240
170908
.
xk 0 ，可以解得只需要
k log b r log ，则 log b r log b r x0 log 1 r （上取整） 养老金在第 K 个月恰好用完. 把具体数据代入，执行以下程序， 算得 K=120，即 10 万养老金恰好 10 年用：
后第 k 月末账户总额为 xk 元， 从第一个月开始每月支取 b 元. 则 列式得
xk 1 (1 r ) xk b, k 0,1, 2, .
解得
xk (1 r )k x0 b r b r , k 0,1, 2,
依题意有 r=0.003，b=1000， x0 =100000. 因为 r>0，且 x0 b r ， 所以 xk 就会单调衰减（到零为止） ，并且减少得越来越快；若要
数学模型第二章习题答案
第二章(2)（2008年10月9日）15．速度为v 的风吹在迎风面积为s 的风车上，空气密度是ρ ，用量纲分析方法确定风车获得的功率P 与v 、S 、ρ的关系.解: 设P 、v 、S 、ρ的关系为0),,,(=ρs v P f ， 其量纲表达式为: [P]=32-T ML , [v ]=1-LT ,[s ]=2L ,[ρ]=3-ML ,这里T M L ,,是基本量纲.量纲矩阵为：A=)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---ρ()()()()()()(001310013212s v P T M L齐次线性方程组为：⎪⎩⎪⎨⎧=--=+=-++03032221414321y y y y y y y y 它的基本解为)1,1,3,1(-=y由量纲i P 定理得 1131ρπs v P -=， 113ρλs v P =∴ ， 其中λ是无量纲常数. 16．雨滴的速度v 与空气密度ρ、粘滞系数μ和重力加速度g 有关，其中粘滞系数的定义是：运动物体在流体中受的摩擦力与速度梯度和接触面积的乘积成正比，比例系数为粘滞系数，用量纲分析方法给出速度v 的表达式.解：设v ,ρ,μ,g 的关系为(f v ,ρ,μ,g )=0.其量纲表达式为[v ]=LM 0T -1，[ρ]=L -3MT 0，[μ]=MLT -2（LT -1L -1）-1L -2=MLL -2T -2T=L -1MT -1，[g ]=LM 0T -2,其中L ，M ，T 是基本量纲.量纲矩阵为A=)()()()()()()(210101101131g v T M L μρ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----- 齐次线性方程组Ay=0 ，即⎪⎩⎪⎨⎧==+=+02y -y - y -0y y 0y y -3y -y 431324321 的基本解为y=(-3 ,-1 ,1 ,1)由量纲i P 定理 得 g v μρπ13--=. 3ρμλgv =∴，其中λ是无量纲常数. 16*．雨滴的速度v 与空气密度ρ、粘滞系数μ、特征尺寸γ和重力加速度g 有关，其中粘滞系数的定义是：运动物体在流体中受的摩擦力与速度梯度和接触面积的乘积成正比，比例系数为粘滞系数，用量纲分析方法给出速度v 的表达式.解：设v ,ρ,μ,γ，g 的关系为0),,,,(=g v f μργ.其量纲表达式为[v ]=LM 0T -1，[ρ]=L -3MT 0，[μ]=MLT -2（LT -1L -1）-1L -2=MLL -2T -2T=L -1MT -1，[γ]=LM 0T 0 ，[g ]=LM 0T -2其中L ，M ，T 是基本量纲. 量纲矩阵为A=)()()()()()()()(210010110011311g v T M L μργ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----齐次线性方程组Ay=0 即⎪⎩⎪⎨⎧=---=+=+--+020035414354321y y y y y y y y y y 的基本解为⎪⎩⎪⎨⎧---=--=)21,1,1,23,0()21,0,0,21,1(21y y 得到两个相互独立的无量纲量⎩⎨⎧==-----2/112/322/12/11g g v μργπγπ 即 1212/12/31,--==πμργπγg g v . 由0),(21=Φππ , 得 )(121-=πϕπ ∴ )(12/12/3-=μργϕγυg g , 其中ϕ是未定函数.20.考察阻尼摆的周期，即在单摆运动中考虑阻力，并设阻力与摆的速度成正比.给出周期的表达式，然后讨论物理模拟的比例模型，即怎样由模型摆的周期计算原型摆的周期. 解：设阻尼摆周期t ,摆长l , 质量m ,重力加速度g ，阻力系数k 的关系为0),,,,(=k g m l t f其量纲表达式为：112120000000)(]][[][,][,][,][,][-----======LT MLT v f k T LM g MT L m T LM l T M L t 10-=MT L ， 其中L ，M ，T 是基本量纲.量纲矩阵为A=)()()()()()()()(120011010001010k g m l t T M L ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-- 齐次线性方程组⎪⎩⎪⎨⎧=--=+=+02005415342y y y y y y y 的基本解为⎪⎩⎪⎨⎧--=-=)1,21,1,21,0()0,21,0,21,1(21Y Y 得到两个相互独立的无量纲量∴g l t =1π, )(21πϕπ=, 2/12/12mg kl =π ∴)(2/12/1mgkl g l t ϕ=，其中ϕ是未定函数 . 考虑物理模拟的比例模型，设g 和k 不变，记模型和原型摆的周期、摆长、质量分别为t ,'t ；l ,'l ;m ,'m . 又)(2/12/1gm l k g l t '''='ϕ 当无量纲量l l mm '='时， 就有 ll l g g l tt '=⋅'='. 《数学模型》作业解答第三章1（2008年10月14日）⎩⎨⎧==---22/112/112/12/1ππk g m l g tl1. 在3.1节存贮模型的总费用中增加购买货物本身的费用,重新确定最优订货周期和订货批量．证明在不允许缺货模型中结果与原来的一样，而在允许缺货模型中最优订货周期和订货批量都比原来结果减少．解：设购买单位重量货物的费用为k ,其它假设及符号约定同课本．01 对于不允许缺货模型，每天平均费用为：kr rT c T c T C ++=2)(212221r c Tc dT dC+-= 令0=dTdC， 解得 r c c T 21*2= 由rT Q = ， 得212c rc rT Q ==**与不考虑购货费的结果比较，Ｔ、Ｑ的最优结果没有变．02 对于允许缺货模型，每天平均费用为：⎥⎦⎤⎢⎣⎡+-++=kQ Q rT r c r Q c c T Q T C 23221)(221),( 2223322221222TkQ rT Q c r c rT Q c T c T C--+--=∂∂Tk rT Q c c rT Qc Q C ++-=∂∂332 令⎪⎪⎩⎪⎪⎨⎧=∂∂=∂∂00QCTC， 得到驻点：⎪⎪⎩⎪⎪⎨⎧+-+-+=-+=**323222233232132233221)(22c c krc c c r k c c c c c r c Q c c k c c c rc c T与不考虑购货费的结果比较，Ｔ、Ｑ的最优结果减少．2．建立不允许缺货的生产销售存贮模型．设生产速率为常数k ，销售速率为常数r ，r k >．在每个生产周期Ｔ内，开始的一段时间()00T t <<一边生产一边销售，后来的一段时间)(0T t T <<只销售不生产，画出贮存量)(t g 的图形.设每次生产准备费为1c ，单位时间每件产品贮存费为2c ，以总费用最小为目标确定最优生产周期，讨论r k >>和r k ≈的情况.解：由题意可得贮存量)(t g 的图形如下：贮存费为 ∑⎰=→∆⋅-==∆i Ti i t TT r k c dt t g c t g c 1022022))()(limξ又 )()(00T T r T r k -=- ∴ T k r T =0 , ∴ 贮存费变为 kTT r k r c 2)(2⋅-=于是不允许缺货的情况下，生产销售的总费用（单位时间内）为kTr k r c T c kT T r k r c T c T C 2)(2)()(21221-+=-+=k r k r c Tc dT dC 2)(221-+-=. 0=dT dC令, 得)(221r k r c k c T -=* 易得函数处在*T T C )(取得最小值，即最优周期为： )(221r k r c kc T -=*rc c ，Tr k 212≈>>*时当 . 相当于不考虑生产的情况.∞→≈*，Tr k 时当 . 此时产量与销量相抵消，无法形成贮存量.第三章2（2008年10月16日）3．在3.3节森林救火模型中，如果考虑消防队员的灭火速度λ与开始救火时的火势b 有关，试假设一个合理的函数关系，重新求解模型.解：考虑灭火速度λ与火势b 有关，可知火势b 越大，灭火速度λ将减小，我们作如下假设: 1)(+=b kb λ， 分母∞→→+λ时是防止中的011b b 而加的. 总费用函数()xc b kx b x t c b kx b t c t c x C 3122121211)1()(2)1(2+--++--++=βββββββ最优解为 []k b kc b b b c kbc x ββ)1(2)1()1(223221+++++=5．在考虑最优价格问题时设销售期为T ，由于商品的损耗，成本q 随时间增长，设t q t q β+=0)(，为增长率β.又设单位时间的销售量为)(为价格p bp a x -=.今将销售期分为T t TT t <<<<220和两段，每段的价格固定，记作21,p p .求21,p p 的最优值，使销售期内的总利润最大.如果要求销售期T 内的总售量为0Q ，再求21,p p 的最优值. 解：按分段价格，单位时间内的销售量为⎪⎩⎪⎨⎧<<-<<-=T t T bp a T t bp a x 2,20,21又 t q t q β+=0)(.于是总利润为[][]⎰⎰--+--=22221121)()()()(),(TTT dt bp a t q p dt bp a t q p p p=22)(022)(20222011T Tt t q t p bp a T t t q t p bp a ⎥⎦⎤⎢⎣⎡---+⎥⎦⎤⎢⎣⎡---ββ=)8322)(()822)((20222011T t q T p bp a T T q T p bp a ββ---+---)(2)822(12011bp a TT T q T p b p -+---=∂∂β )(2)8322(22022bp a TT t q T p b p -+---=∂∂β 0,021=∂∂=∂∂p p 令, 得到最优价格为: ⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡++=)43(21)4(210201T q b a b p T q b a b p ββ 在销售期T 内的总销量为⎰⎰+-=-+-=20221210)(2)()(TTT p p bTaT dt bp a dt bp a Q 于是得到如下极值问题：)8322)(()822)((),(m ax 2022201121T t q T p bp a T T q T p bp a p p ββ---+---=t s . 021)(2Q p p bTaT =+-利用拉格朗日乘数法，解得：⎪⎩⎪⎨⎧+-=--=880201TbT Q b a p T bT Q b a p ββ 即为21,p p 的最优值.第三章3（2008年10月21日）6. 某厂每天需要角钢100吨，不允许缺货.目前每30天定购一次，每次定购的费用为2500元.每天每吨角钢的贮存费为0.18元.假设当贮存量降到零时订货立即到达.问是否应改变订货策略？改变后能节约多少费用？解：已知：每天角钢的需要量r=100(吨);每次订货费1c ＝2500（元）;每天每吨角钢的贮存费2c ＝0.18（元）.又现在的订货周期T 0＝30（天） 根据不允许缺货的贮存模型：kr rT c T c T C ++=2121)( 得：k T TT C 10092500)(++=令0=dTdC， 解得：35092500*==T 由实际意义知：当350*=T （即订货周期为350）时，总费用将最小. 又k T C 10035095025003)(*+⨯+⨯=＝300＋100kk T C 100309302500)(0+⨯+==353．33＋100k)(0T C －)(*T C ＝（353.33＋100k ）－（300＋100k ）32＝53．33.故应改变订货策略.改变后的订货策略（周期）为T *=350，能节约费用约53．33元.《数学模型》作业解答第四章（2008年10月28日）1. 某厂生产甲、乙两种产品,一件甲产品用A 原料1千克, B 原料5千克；一件乙产品用A 原料2千克,B 原料4千克.现有A 原料20千克, B 原料70千克.甲、乙产品每件售价分别为20元和30元.问如何安排生产使收入最大？ 解：设安排生产甲产品x 件,乙产品y 件，相应的利润为S 则此问题的数学模型为：max S=20x+30ys.t. ⎪⎩⎪⎨⎧∈≥≤+≤+Z y x y x y x y x ,,0,7045202这是一个整线性规划问题，现用图解法进行求解可行域为：由直线1l ：x+2y=20, 2l :5x+4y ＝702l925002+-=TdT dC以及x=0,y=0组成的凸四边形区域.直线l ：20x+30y=c 在可行域内 平行移动.易知：当l 过1l 与2l 的交点时， x S 取最大值.由⎩⎨⎧=+=+7045202y x y x 解得⎩⎨⎧==510y x此时 m ax S ＝2053010⨯+⨯＝350（元）2. 某厂拟用集装箱托运甲乙两种货物，每箱的体积、重量以及可获利润如下表：已知这两种货物托运所受限制是体积不超过24立方米，重量不超过13百斤.试问这两种货物各托运多少箱，使得所获利润最大，并求出最大利润.解:设甲货物、乙货物的托运箱数分别为1x ,2x ,所获利润为z .则问题的数学模型可表示为211020 m ax x x z +=⎪⎩⎪⎨⎧∈≥≤+≤+Z y x x x x x x x st ,,0,13522445212121这是一个整线性规划问题. 用图解法求解. 可行域为：由直线2445:211=+x x l1352:212=+x x l 及0,021==x x 组成直线 c x x l =+211020:在此凸四边形区域内平行移动.2ll1x1l2x易知：当l 过l 1与l 2的交点时，z 取最大值由⎩⎨⎧=+=+135224452121x x x x 解得 ⎩⎨⎧==1421x x90110420max =⨯+⨯=z .3．某微波炉生产企业计划在下季度生产甲、乙两种型号的微波炉.已知每台甲型、乙型微波炉的销售利润分别为3和2个单位.而生产一台甲型、乙型微波炉所耗原料分别为2和3个单位,所需工时分别为4和2个单位.若允许使用原料为100个单位,工时为120个单位,且甲型、乙型微波炉产量分别不低于6台和12台.试建立一个数学模型,确定生产甲型、乙型微波炉的台数,使获利润最大．并求出最大利润.解：设安排生产甲型微波炉x 件,乙型微波炉y 件,相应的利润为S. 则此问题的数学模型为：max S=3x +2ys.t. ⎪⎩⎪⎨⎧∈≥≥≤+≤+Z y x y x y x y x ,,12,61202410032这是一个整线性规划问题 用图解法进行求解可行域为：由直线1l ：2x+3y=100, 2l :4x+2y ＝120 及x=6,y=12组成的凸四边形区域.直线l ：3x+2y=c 在此凸四边形区域内平行移动. 易知：当l 过1l 与2l 的交点时, S 取最大值.由⎩⎨⎧=+=+1202410032y x y x 解得⎩⎨⎧==2020y x .m ax S ＝320220⨯+⨯＝100.《数学模型》作业解答第五章1（2008年11月12日）1.对于5.1节传染病的SIR 模型，证明： （1）若处最大先增加，在则σσ1)(,10=s t i s ，然后减少并趋于零；)(t s 单调减少至.∞s（2）.)()(,10∞s t s t i s 单调减少至单调减少并趋于零，则若σ解：传染病的SIR 模型（14）可写成⎪⎩⎪⎨⎧-=-=i s dtds s i dt diλσμ)1(.)(lim 0.(t) .)( .0,t 存在而单调减少知由∞∞→=∴≥-=s t s s t s dtdsi s dt ds λ.)(∞s t s 单调减少至故（1）.s s(t) .s(t) .100≤∴单调减少由若σs;)(,0 .01,10单调增加时当t i dtdis s s ∴-σσ.)(,0.01,1单调减少时当t i dtdis s ∴-σσ .0)(lim .0)18(t ==∞→∞t i i 即式知又由书上.)( .0,1m i t i dtdis 达到最大值时当∴==σ（2）().0 0.1-s ,1,10 dtdit s s σσσ从而则若()().0.0lim ==∴∞∞→i t i t i t 即单调减少且4．在5.3节正规战争模型（3）中，设乙方与甲方战斗有效系数之比为.4=ba初始兵力00y x 与相同.(1) 问乙方取胜时的剩余兵力是多少,乙方取胜的时间如何确定.(2) 若甲方在战斗开始后有后备部队以不变的速率r 增援,重新建立模型,讨论如何判断双方的胜负.解:用()()t y t x ,表示甲、乙交战双方时刻t 的士兵人数,则正规战争模型可近似表示为:()()()⎪⎪⎩⎪⎪⎨⎧==-=-=000,01 ,yy x x bx dtdyay dt dx现求(1)的解: (1)的系数矩阵为⎥⎦⎤⎢⎣⎡--=00b a Aab ab b aA E ±=∴=-==-1,22 .0λλλλλ ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛-1212,21，对应的特征向量分别为λλ ()()()tab t ab eC e C t y t x -⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛∴1212121的通解为.再由初始条件，得()()2 220000 tab tab e y x ey x t x -⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-=又由().1aybx dx dy =可得其解为 ()3 ,202022 bx ay k k bx ay -==-而(1) ()().231000202011y a b y a bx ay ak t y t x =-=-===时，当 即乙方取胜时的剩余兵力数为.230y 又令().0222,01100001=-⎪⎭⎫⎝⎛++⎪⎭⎫⎝⎛-=t ab t ab e y x e y x t x ）得由（注意到000020022,1x y y x ey x t ab -+==得. .43ln ,3121bt et ab =∴=∴ (2) 若甲方在战斗开始后有后备部队以不变的速率r 增援.则()()⎪⎪⎩⎪⎪⎨⎧==-=+-=000,)0(4 yy x x bx dtdyr ay dt dx().,4rdy aydy bxdx bxray dy dx -=-+-=即得由 相轨线为,222k bx ry ay =-- .222220.020k a r bx a r y a bx ry ay k =--⎪⎭⎫ ⎝⎛---=或 此相轨线比书图11中的轨线上移了.a r 乙方取胜的条件为.,0222020a r x a b a r y k +⎪⎭⎫ ⎝⎛- 亦即 第五章2（2008年11月14日）6. 模仿5.4节建立的二室模型来建立一室模型（只有中心室），在快速静脉注射、恒速静脉滴注（持续时间为τ）和口服或肌肉注射3种给药方式下求解血药浓度，并画出血药浓度曲线的图形.解: 设给药速率为(),0t f ()()()()().,,0/t VC t x t f t kx t x k ==+则排除速率为常数(1)快速静脉注射: 设给药量为,0D 则()()().,0,0000t k e VDt C V D C t f -===解得 (2)恒速静脉滴注(持续时间为τ): 设滴注速率为()(),00,000==C k t f k ，则解得()()()()⎪⎩⎪⎨⎧-≤≤-=----τττ t e e Vkk t e Vkk t C t k kt kt,10 ,10(3) 口服或肌肉注射: ()()，解得）式节（见134.5010010tk eD k t f -=()()()⎪⎪⎩⎪⎪⎨⎧=≠--=---010101001 ,,01k k te V kD k k e e k k V D k t C kt t k kt3种情况下的血药浓度曲线如下：第五章3（2008年11月18日）8. 在5.5节香烟过滤嘴模型中,(1) 设3.0,/50,08.0,02.0,20,80,80021=======a s mm b mm l mm l mg M νβ求./21Q Q Q 和(2) 若有一支不带过滤嘴的香烟,参数同上,比较全部吸完和只吸到1l 处的情况下，进入人体毒物量的区别.解)(857563.229102.07.050103.01508002.07.0502008.0/01/2毫克≈⎪⎪⎭⎫ ⎝⎛-⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛-=⨯⨯-⨯---e e e eba v aw Q v bl a vl β ()10/10==l M w 其中，()()97628571.0502002.008.0212===⨯----ee Q Q vl b β(2) 对于一支不带过滤嘴的香烟,全部吸完的毒物量为⎪⎪⎭⎫⎝⎛-=-vbl a e b a v aw Q '103‘ 只吸到1l 处就扔掉的情况下的毒物量为⎪⎪⎭⎫ ⎝⎛-=--vbl a v ble e b a v aw Q 1'21'04 .256531719.1110096.0032.0012.004.0508002.03.0508002.05010002.03.05010002.043111'1'≈--=--=--=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=⨯⨯⨯⨯⨯⨯--e e e e e e e e e e e e e e e e Q Q v abl v bl v abl v bl v bl a v bl v bl a vbl 44.235,84.29543≈≈ ＱQ4．在5.3节正规战争模型（3）中，设乙方与甲方战斗有效系数之比为.4=ba初始兵力00y x 与相同.(1) 问乙方取胜时的剩余兵力是多少,乙方取胜的时间如何确定.(2) 若甲方在战斗开始后有后备部队以不变的速率r 增援,重新建立模型,讨论如何判断双方的胜负.解:用()()t y t x ,表示甲、乙交战双方时刻t 的士兵人数,则正规战争模型可近似表示为:()()()⎪⎪⎩⎪⎪⎨⎧==-=-=000,01 ,yy x x bx dtdyay dt dx现求(1)的解: (1)的系数矩阵为⎥⎦⎤⎢⎣⎡--=00b a A ab ab b aA E ±=∴=-==-1,22 .0λλλλλ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛-1212,21，对应的特征向量分别为λλ ()()()tab t ab eC e C t y t x -⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛∴1212121的通解为.再由初始条件，得()()2 220000 tab tab e y x ey x t x -⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-=又由().1aybx dx dy =可得其解为 ()3 ,202022 bx ay k k bx ay -==-而(1) ()().231000202011y a b y a bx ay ak t y t x =-=-===时，当 即乙方取胜时的剩余兵力数为.230y 又令().0222,01100001=-⎪⎭⎫⎝⎛++⎪⎭⎫⎝⎛-=t ab t ab e y x e y x t x ）得由（注意到000020022,1x y y x ey x t ab -+==得. .43ln ,3121bt et ab =∴=∴ (2) 若甲方在战斗开始后有后备部队以不变的速率r 增援.则()()⎪⎪⎩⎪⎪⎨⎧==-=+-=000,)0(4 yy x x bx dtdyr ay dt dx().,4rdy aydy bxdx bxr ay dy dx -=-+-=即得由 相轨线为,222k bx ry ay =-- .222220.020k a r bx a r y a bx ry ay k =--⎪⎭⎫ ⎝⎛---=或 此相轨线比书图11中的轨线上移了.a r 乙方取胜的条件为.,0222020a r x a b a r y k +⎪⎭⎫ ⎝⎛- 亦即《数学模型》作业解答第六章（2008年11月20日）1.在6.1节捕鱼模型中，如果渔场鱼量的自然增长仍服从Logistic 规律，而单位时间捕捞量为常数h ．(1)分别就4/rN h >，4/rN h <，4/rN h =这3种情况讨论渔场鱼量方程的平衡点及其稳定状况．(2)如何获得最大持续产量，其结果与6.1节的产量模型有何不同．解：设时刻t 的渔场中鱼的数量为()t x ，则由题设条件知：()t x 变化规律的数学模型为h Nxrx dt t dx --=)1()( 记h Nxrx x F --=)1()( (1).讨论渔场鱼量的平衡点及其稳定性： 由()0=x F ，得0)1(=--h Nxrx ． 即()102=+-h rx x Nr )4(42Nhr r N rh r -=-=∆ ， (1)的解为：2412,1N rNhN x -±=①当4/rN h >，0<∆，(1)无实根，此时无平衡点；②当4/rN h =，0=∆，(1)有两个相等的实根，平衡点为20N x =. Nrxr N rx N x r x F 2)1()('-=--=，0)(0'=x F 不能断定其稳定性. 但0x x ∀ 及0x x 均有04)1()( rNN x rx x F --= ，即0 dtdx ．∴0x 不稳定；③当4/rN h <，0>∆时，得到两个平衡点：2411N rNhN x --=， 2412N rNh N x -+=易知：21N x <， 22N x > ，0)(1'>x F ，0)(2'<x F ∴平衡点1x 不稳定，平衡点2x 稳定.(2)最大持续产量的数学模型为⎩⎨⎧=0)(..max x F t s h 即 )1(max Nxrx h -=，易得 2*0N x = 此时 4rN h =， 但2*0N x =这个平衡点不稳定．这是与6.1节的产量模型不同之处．要获得最大持续产量，应使渔场鱼量2Nx >，且尽量接近2N ，但不能等于2N ．2.与Logistic 模型不同的另一种描述种群增长规律的是Gompertz 模型：()xNrx t x ln '=．其中r 和N 的意义与Logistic 模型相同．设渔场鱼量的自然增长服从这个模型，且单位时间捕捞量为Ex h =．讨论渔场鱼量的平衡点及其稳定性，求最大持续产量m h 及获得最大产量的捕捞强度m E 和渔场鱼量水平*0x ．解：()t x 变化规律的数学模型为()Ex xNrx dt t dx -=ln 记 Ex xNrx x F -=ln)( ① 令()0=x F ，得0ln =-Ex xNrx ∴r ENe x -=0，01=x ．∴平衡点为1,0x x . 又 ()E r xNr x F --=ln'，()()∞=<-=1'0',0x F r x F ． ∴ 平衡点o x 是稳定的，而平衡点1x 不稳定.②最大持续产量的数学模型为：⎪⎩⎪⎨⎧≠=-=.0,0ln ..max x Ex x N rx t s Ex h 由前面的结果可得 rE ENeh -=r Er Ee r EN Ne dE dh ---=，令.0=dEdh 得最大产量的捕捞强度r E m =．从而得到最大持续产量e rN h m /=，此时渔场鱼量水平eNx =*0． 3．设某渔场鱼量)(t x (时刻t 渔场中鱼的数量)的自然增长规律为：)1()(Nxrx dt t dx -= 其中r 为固有增长率,`N 为环境容许的最大鱼量. 而单位时间捕捞量为常数h .10．求渔场鱼量的平衡点,并讨论其稳定性;20．试确定捕捞强度m E ,使渔场单位时间内具有最大持续产量m Q ,求此时渔场鱼量水平*0x . 解：10．)(t x 变化规律的数学模型为h Nxrx dt t dx --=)1()( 记h N x rx x f --=)1()(,令 0)1(=--h N x rx ，即02=+-h rx x Nr ----（1）)4(42Nhr r N rh r -=-=∆ ， （1）的解为：2412,1N rNhN x -±=① 当0 ∆时，（1）无实根，此时无平衡点；Ex()x f② 当0=∆时，（1）有两个相等的实根，平衡点为20Nx =. Nrx r N rx N x r x f 2)1()('-=--= ，0)(0'=x f 不能断定其稳定性. 但0x x ∀ 及0x x 均有04)1()( rN N x rx x f --= ，即0 dt dx∴0x 不稳定；③ 当0 ∆时，得到两个平衡点：2411rNhN N x --=， 2412rNh N N x -+=易知 21N x， 22N x ∴0)('1 x f ， 0)('2 x f ∴平衡点1x 不稳定 ，平衡点2x 稳定.20．最大持续产量的数学模型为： ⎩⎨⎧=0)(..max x f t s h即 )1(max N x rx h -=， 易得 2*0N x = 此时 4rN h =，但2*0N x =这个平衡点不稳定. 要获得最大持续产量，应使渔场鱼量2N x ,且尽量接近2N ,但不能等于2N.《数学模型》第七章作业（2008年12月4日）1．对于7.1节蛛网模型讨论下列问题：（1）因为一个时段上市的商品不能立即售完，其数量也会影响到下一时段的价格，所以第1+k 时段的价格1+k y 由第1+k 和第k 时段的数量1+k x 和k x 决定，如果仍设1+k x 仍只取决于k y ，给出稳定平衡的条件，并与7.1节的结果进行比较.2．已知某商品在k 时段的数量和价格分别为k x 和k y ，其中1个时段相当于商品的一个生产周期.设该商品的需求函数和供应函数分别为)(k k x f y =和)2(11-++=k k k y y g x .试建立关于商品数量的差分方程模型，并讨论稳定平衡条件.3． 已知某商品在k 时段的数量和价格分别为k x 和k y ，其中1个时段相当于商品的一个生产周期.设该商品的需求函数和供应函数分别为)2(11kk k x x f y +=++和)(1k k y g x =+.试建立关于商品数量的差分方程模型，并讨论稳定平衡条件.《数学模型》作业解答第七章（2008年12月4日）2． 对于7.1节蛛网模型讨论下列问题：（1）因为一个时段上市的商品不能立即售完，其数量也会影响到下一时段的价格，所以第1+k 时段的价格1+k y 由第1+k 和第k 时段的数量1+k x 和k x 决定，如果仍设1+k x 仍只取决于k y ，给出稳定平衡的条件，并与7.1节的结果进行比较.（2）若除了1+k y 由1+k x 和k x 决定之外，1+k x 也由前两个时段的价格k y 和1-k y 确定.试分析稳定平衡的条件是否还会放宽.解：（1）由题设条件可得需求函数、供应函数分别为：⎪⎩⎪⎨⎧=+=+++)()2(111k k k k k y h x x x f y 在),(000y x P 点附近用直线来近似曲线h f ,，得到⎪⎩⎪⎨⎧>-=->-+-=-+++)2( 0, )()1( 0),2(0010101 ββααy y x x x x x y y k k k k k 由（2）得 )3( )(0102 y y x x k k -=-++β（1）代入（3）得 )2(0102x x x x x kk k -+-=-++αβ 0012222 x x x x x k k k αβαβαβ+=++∴++对应齐次方程的特征方程为 02 2=++αβαβλλ特征根为48)(22,1αβαβαβλ-±-=当8≥αβ时，则有特征根在单位圆外，设8<αβ，则248)()4(2222,1αβαβαβαβλ=+-+= 2 12,1<⇔<∴αβλ即平衡稳定的条件为2 <αβ与207P 的结果一致.（2）此时需求函数、供应函数在),(000y x P 处附近的直线近似表达式分别为：⎪⎩⎪⎨⎧>-+=->-+-=--+++)5( 0 , )2()4( 0),2(01010101 ββααy y y x x x x x y y k k k k k k 由（5）得，)( ) y y y β(y )x (x k k k 62010203 -+-=-+++ 将（4）代入（6），得 ⎥⎦⎤⎢⎣⎡-+--+-=-++++)2()2()(20101203x x x x x x x x k k k k k ααβ 001234424 x x x x x x k k k k αβαβαβαβ+=+++∴+++对应齐次方程的特征方程为(7) 024 23=+++αβαβλαβλλ 代数方程（7）无正实根，且42 ,αβαβ---, αβ不是（7）的根.设（7）的三个非零根分别为321,,λλλ，则⎪⎪⎪⎩⎪⎪⎪⎨⎧-==++-=++424321133221321αβλλλαβλλλλλλαβλλλ 对（7）作变换：,12αβμλ-=则,03=++q p μμ其中 )6128(41 ),122(412233322αββαβαβααβ+-=-=q p 用卡丹公式：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+--+++-=+--+++-=+--+++-=33233223332233223323321)3()2(2)3()2(2)3()2(2)3()2(2)3()2(2)3()2(2p q q w p q q w p q q w p q q w pq q p q q μμμ 其中,231i w +-=求出321,,μμμ，从而得到321,,λλλ，于是得到所有特征根1<λ的条件.2．已知某商品在k 时段的数量和价格分别为k x 和k y ，其中1个时段相当于商品的一个生产周期.设该商品的需求函数和供应函数分别为)(k k x f y =和)2(11-++=k k k y y g x .试建立关于商品数量的差分方程模型，并讨论稳定平衡条件.解：已知商品的需求函数和供应函数分别为)(k k x f y =和)2(11-++=k k k y y g x . 设曲线f 和g 相交于点),(000y x P ，在点0P 附近可以用直线来近似表示曲线f 和g ：0,)(00 ααx x y y k k --=- ----------------------（1）0,)2(0101 ββy y y x x k k k -+=--+ --------------------（2） 从上述两式中消去k y 可得,2,1,)1(22012=+=++++k x x x x k k k αβαβαβ， -----------（3） 上述（3）式是我们所建立的差分方程模型，且为二阶常系数线性非齐次差分方程. 为了寻求0P 点稳定平衡条件，我们考虑（3）对应的齐次差分方程的特征方程：022=++αβαβλλ容易算出其特征根为48)(22,1αβαβαβλ-±-=---------------（4） 当αβ 8时，显然有448)(22αβαβαβαβλ----= -----------（5） 从而2λ 2，2λ在单位圆外．下面设8 αβ，由(5)式可以算出 22,1αβλ=要使特征根均在单位圆内，即2,1λ1 ，必须 2 αβ．故0P 点稳定平衡条件为 2 αβ．3． 已知某商品在k 时段的数量和价格分别为k x 和k y ，其中1个时段相当于商品的一个生产周期.设该商品的需求函数和供应函数分别为)2(11kk k x x f y +=++和)(1k k y g x =+.试建立关于商品数量的差分方程模型，并讨论稳定平衡条件. 解：已知商品的需求函数和供应函数分别为)2(11kk k x x f y +=++和)(1k k y g x =+. 设曲线f 和g 相交于点),(000y x P ，在点0P 附近可以用直线来近似表示曲线f 和g ：0,)2(0101 ααx x x y y kk k -+-=-++ --------------------（1） 0,)(001 ββy y x x k k -=-+ --- ----------------（2）由（2）得 )(0102y y x x k k -=-++β --------------------（3） （1）代入（3），可得)2(0102x x x x x kk k -+-=-++αβ∴ ,2,1,2220012=+=++++k x x x x x k k k αβαβαβ， --------------（4） 上述（4）式是我们所建立的差分方程模型，且为二阶常系数线性非齐次差分方程. 为了寻求0P 点稳定平衡条件，我们考虑（4）对应的齐次差分方程的特征方程：022=++αβαβλλ容易算出其特征根为48)(22,1αβαβαβλ-±-=---------------（4） 当αβ≥8时，显然有448)(22αβαβαβαβλ-≤---= -----------（5） 从而2λ 2，2λ在单位圆外．下面设8 αβ，由(5)式可以算出 22,1αβλ=要使特征根均在单位圆内，即2,1λ1 ，必须 2 αβ．故0P 点稳定平衡条件为 2 αβ．《数学模型》作业解答第八章（2008年12月9日）1． 证明8.1节层次分析模型中定义的n 阶一致阵A 有下列性质： （1） A 的秩为1，唯一非零特征根为n ； （2） A 的任一列向量都是对应于n 的特征向量. 证明： （1）由一致阵的定义知：A 满足ik jk ij a a a =⋅，n k j i ,,2,1,, =于是对于任意两列j i ,，有ij jkika a a =，()n k ,,2,1 =.即i 列与j 列对应分量成比例. 从而对A 作初等行变换可得：∆⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡−−−→−00000011211 n b b b A 初等行变换B 这里0≠B .()1=∴B 秩，从而秩()1=A再根据初等行变换与初等矩阵的关系知：存在一个可逆阵P ，使B PA =，于是∆⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==--0000001121111 n c c c BP PAP C 易知C 的特征根为0,,0,11 c （只有一个非零特征根）.又A ～C ，A ∴与C 有相同的特征根，从而A 的非零特征根为11c ，又 对于任意矩阵有()n a a a A Tr nn n =+++=+++==+++111221121 λλλ.故A 的唯一非零特征根为n .（2）对于A 的任一列向量()Tnk k k a a a ,,,21 ，()n k ,,2,1 =有()()T nk k k nk k k n j nkn j k n j k n j jk nj n j jk j n j jk j Tnk k k a a a n na na na a a a a a a a a a a a a A ,,,,,,2121112111121121 =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=∑∑∑∑∑∑======A ∴的任一列向量()Tnk k k a a a ,,,21 都是对应于n 的特征向量.7. 右下图是5位网球选手循环赛的结果，作为竞赛图，它是双向连通的吗？找出几条完全路径，用适当方法排出5位选手的名次.解：这个5阶竞赛图是一个5阶有向Hamilton 图.其一个有向Hamilton 圈为332541→→→→→.所以此竞赛图是双向连通的.32154→→→→13542→→→→42135→→→→→→→41325→等都是完全路径.此竞赛图的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0011110100000010110001010A令()Te 1,1,1,1,1=，各级得分向量为()()TAe S 3,2,1,2,21==， ()()()TAS S 5,4,2,3,412==，()()()TAS S 9,7,4,6,723== ， ()()()TAS S 17,13,7,11,1334==由此得名次为5，1（4），2，3 （选手1和4名次相同）.注：给5位网球选手排名次也可由计算A 的最大特征根λ和对应特征向量S 得到：8393.1=λ，()TS 2769.0,2137.0,1162.0,1794.0,2137.0=数学模型作业（12月16日）解答1.基于省时、收入、岸间商业、当地商业、建筑就业等五项因素，拟用层次分析法在建桥梁、修隧道、设渡轮这三个方案中选一个，画出目标为“越海方案的最优经济效益”的层次结构图.解：目标层准则层方案层2.简述层次分析法的基本步骤. 问对于一个即将毕业的大学生选择工作岗位的决策问题要分成哪3个层次？具体内容分别是什么？答：层次分析法的基本步骤为：（1）．建立层次结构模型；（2）．构造成对比较阵；（3）．计算权向量并做一致性检验；（4）．计算组合权向量并做组合一致性检验． 对于一个即将毕业的大学生选择工作岗位的决策问题，用层次分析法一般可分解为目标层、准则层和方案层这3个层次. 目标层是选择工作岗位，方案层是工作岗位1、工作岗位2、工作岗位3等，准则层一般为贡献、收入、发展、声誉、关系、位置等.3．用层次分析法时，一般可将决策问题分解成哪3个层次？试给出一致性指标的定义以及n 阶正负反阵A 为一致阵的充要条件.答：用层次分析法时，一般可将决策问题分解为目标层、准则层和方案层这3个层次； 一致性指标的定义为：1--=n nCI λ．n 阶正互反阵A 是一致阵的充要条件为：A 的最大特征根λ=n ．第九章（2008年12月18日）1．在1.9节传送带效率模型中,设工人数n 固定不变.若想提高传送带效率D,一种简单的方法是增加一个周期内通过工作台的钩子数m ，比如增加一倍，其它条件不变．另一种方法是在原来放置一只钩子的地方放置两只钩子，其它条件不变，于是每个工人在任何时刻可以同时触到两只钩子，只要其中一只是空的，他就可以挂上产品，这种办法用的钩子数量与第一种办法一样．试推导这种情况下传送带效率的公式，从数量关系上说明这种办法比第一种办法好．解：两种情况的钩子数均为m 2．第一种办法是m 2个位置，单钩放置m 2个钩子；第二种办法是m 个位置，成对放置m 2个钩子．① 由1.9节的传送带效率公式，第一种办法的效率公式为⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--=nm n m D 21112 当mn2较小，1 n 时，有()m n m n n m n m D 41181211122--=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+--≈E D -=1 ， mnE 4≈② 下面推导第二种办法的传送带效率公式：对于m 个位置，每个位置放置的两只钩子称为一个钩对，考虑一个周期内通过的m 个钩对．任一只钩对被一名工人接触到的概率是m1； 任一只钩对不被一名工人接触到的概率是m11-；记mq m p 11,1-==．由工人生产的独立性及事件的互不相容性．得，任一钩对为空的概率为nq ，其空钩的数为m 2；任一钩对上只挂上１件产品的概率为1-n npq ，其空钩数为m ．所以一个周期内通过的m 2个钩子中，空钩的平均数为 ()1122--+=⋅+⋅n n n nnpq q m npqm q m于是带走产品的平均数是 ()122-+-n n npqq m m ， 未带走产品的平均数是 ()()122-+--n n npq q m m n ）∴此时传送带效率公式为()⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛--=+-=--1111112222'n n n n m m n m n m n npq q m m D ③ 近似效率公式：由于 ()()()321621121111m n n n m n n m n m n----+-≈⎪⎭⎫ ⎝⎛- ()()2112211111mn n m n m n --+--≈⎪⎭⎫ ⎝⎛-- ∴ ()()26211'm n n D ---≈当1 n 时，并令'1'D E -=，则 226'mn E ≈ ④ 两种办法的比较：由上知：mnE 4≈，226'm n E ≈ ∴ m n E E 32/'=，当n m 时，132 mn， ∴ E E '． 所以第二种办法比第一种办法好．《数学模型》作业解答第九章（2008年12月23日）一报童每天从邮局订购一种报纸，沿街叫卖.已知每100份报纸报童全部卖出可获利7元.如果当天卖不掉，第二天削价可以全部卖出，但报童每100份报纸要赔4元.报童每天售出的报纸数r 是一随机变量，其概率分布如下表：试问报童每天订购多少份报纸最佳(订购量必须是100的倍数)？ 解：设每天订购n 百份纸，则收益函数为⎩⎨⎧≤--+=n r n nr r n r r f 7))(4(7)( 收益的期望值为G(n) =∑=-n r r P n r 0)()411(+∑∞+=1)(7n r r P n现分别求出 n =5,4,3,2,1,0时的收益期望值. G(0)=0；G(1)=4-×0.05+7×0.1+7×（0.25+0.35+0.15+0.1）=6.45; G(2)= (05.08⨯-25.0141.03⨯+⨯+))1.015.035.0(14++⨯+8.11=; G(3)=(05.012⨯-35.02125.0101.01⨯+⨯+⨯-))1.015.0(21+⨯+4.14= G(4)=(05.016⨯-15.02835.01725.061.05⨯+⨯+⨯+⨯-)1.028⨯+15.13=G(5)=05.020⨯-1.03515.02435.01325.021.09⨯+⨯+⨯+⨯+⨯- 25.10= 当报童每天订300份时，收益的期望值最大.数模复习资料第一章1. 原型与模型原型就是实际对象.模型就是原型的替代物.所谓模型, 按北京师范大学刘来福教授的观点：模型就是人们为一定的目的对原型进行的一个抽象.如航空模型、城市交通模型等.模型⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧数学模型如地图、电路图符号模型如某一操作思维模型抽象模型如某一试验装置物理模型如玩具、照片等直观模型形象模型2. 数学模型对某一实际问题应用数学语言和方法,通过抽象、简化、假设等对这一实际问题近似刻划所得的数学结构,称为此实际问题的一个数学模型. 例如力学中著名的牛顿第二定律使用公式22dt xd mF =来描述受力物体的运动规律就是一个成功的数学模型.或又如描述人口()t N 随时间t 自由增长过程的微分方程()()t rN dtt dN =. 3. 数学建模所谓数学建模是指根据需要针对实际问题组建数学模型的过程.更具体地说,数学建模是指对于现实世界的某一特定系统或特定问题,为了一个特定的目的,运用数学的语言和方法,通过抽象和简化,建立一个近似描述这个系统或问题的数学结构(数学模型),运用适当的数学工具以及计算机技术来解模型,最后将其结果接受实际的检验,并反复修改和完善.数学建模过程流程图为：4.数学建模的步骤依次为：模型准备、模型假设、模型构成、模型求解、模型分析、模型检验、模型应用 5.数学模型的分类数学模型可以按照不同的方式分类,常见的有：。
数学建模数模第一次作业(章绍辉版)
1．（1） n=101;x1=linspace(-1,1,n); x2=linspace(-2,2,n);y1=[sqrt(1-x1.^2);-sqrt(1-x1.^2)];y2=[sqrt(4-x2.^2);-sqrt(4-x2.^2);sqrt(1-(x2.^2)/4);-sqrt(1-(x2.^2)/4)];plot(x1,y1) hold on; plot(x2,y2)title('椭圆x^2/4+y^2=1的内切圆和外切圆') axis equal-2.5-2-1.5-1-0.500.51 1.52 2.5-2-1.5-1-0.500.511.52椭圆x 2/4+y 2=1的内切圆和外切圆（2）x1=linspace(-2,2,101); x2=linspace(-2,8); axis equalplot(exp(x1),x1,x1,exp(x1),x2,x2)title('指数函数y=exp(x)和对数函数y=ln(x)关于y=x 对称')-2-112345678-2-1012345678指数函数y=exp(x)和对数函数y=ln(x)关于y=x 对称（3） hold onq=input('请输入一个正整数q;') for i=1:q for j=1:i if rem(j,i)plot(j/i,1/i) end end end0.10.20.30.40.50.60.70.80.9100.050.10.150.20.250.30.350.40.450.53．代码如下：n=input('请输入实验次数n=') k=0;for i=1:nx=ceil(rand*6)+ceil(rand*6); if x ==3|x==11 k=k+1; elseif x~=2&x~=7&x~=12y= ceil(rand*6)+ceil(rand*6); while y~=x&y~=7y=ceil(rand*6)+ceil(rand*6); end if y==7k=k+1; end end end从上表可看出打赌者赢的概率大约为。
数学建模章绍辉答案
数学建模章绍辉答案【篇一：第三次数学建模作业】数科院105 刘镜韶 20102201092 数科院105 蔡秋荣 20102201166 数科院104 梁浩坤 201022011004、不妨令第k年取出奖学金后，继续存在银行的捐款余额为xk，且银行的整存整取的利率为r，奖学金的金额为d万元，则由已知可得：xk+1 =（1+r）xk－d 故：其解为数列：xk =(x0-d/r)+d/r,且x0=20万元；①奖学金金额d0.6万元，让存在银行的捐款余额每年逐步增加；②奖学金金额d=0.6万元，让存在银行的捐款余额每年保持不变；③奖学金金额d0.6万元，让存在银行的捐款余额每年逐步减少；故对于不同的情况，不妨通过编程对比xk的变化趋势；程序：n=20;r=[0.03,0.03,0.03];x=[20,20,20];d=[0.45,0.6,0.75]; fork=1:nx(k+1,:)=x(k,:).*(1+r)-d; enddisp(本金为20万时不同的奖学金下余额的变化)disp(年 0.45万元0.6万元0.75万元) disp([(0:n),x]);plot(0:n,x(:,1),k^,0:n,x(:,2),ko,0:n,x(:,3),kv) axis([-1,n+1,14,25]) legend(d=0.45,d=0.6,d=0.75,2)title(本金为20万时不同的奖学金下余额的变化) xlabel(第k年),ylabel(余额) 其命令窗口显示结果为：年 0.45万元0.6万元0.75万元 020.000020.000020.00001.000020.150020.000019.85002.000020.304520.000019.69553.000020.463620.000019.53644.000020.627520.000019.37255.000020.796420.000019.20366.000020.970320.000019.02977.000021.149420.000018.8506 8.000021.333920.000018.66619.000021.523920.000018.4761本金为20万时不同的奖学金下余额的变化10.000021.719620.000018.2804 11.000021.921220.000018.078812.000022.128820.000017.871213.000022.342720.000017.657314.000022.562920.000017.4371 15.000022.789820.000017.210216.000023.023520.000016.976517.000023.264220.000016.735818.000023.512220.000016.4878 19.000023.767520.000016.2325 第k年20.000024.030620.000015.9694当利率r=3%时，且以整存整取一年定期的形式来存入银行时；由上述图像可知：①奖学金金额d≤0.6万元时，可以永久持续下去，实现可持续发展，即用20万元本金所得的利息作为奖学金。
数学建模第二次作业(3)(精编文档).doc
【最新整理，下载后即可编辑】数学建模任意两个城市之间的最廉价路线参与人员信息：2012 年 6 月 6 日一、问题提出某公司在六个城市C1、C2、C3、C4、C5、C6中都有分公司，从Ci到Cj的直达航班票价由下述矩阵的第i行、第j列元素给出（∞表示无直达航班），该公司想算出一张任意两个城市之间最廉价路线表，试做出这样的表来。
0 50 ∞40 25 1050 0 15 20 ∞25∞15 0 10 20 ∞40 20 10 0 10 2525 ∞20 10 0 5510 25 ∞25 55 0二、问题分析若网络中的每条边都有一个数值(长度、成本、时间等)，则找出两节点(通常是源节点和阱节点)之间总权和最小的路径就是最短路问题。
最短路问题是网络理论解决的典型问题之一，可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。
最短路问题，我们通常归属为三类：单源最短路径问题、确定起点终点的最短路径问题、全局最短路径问题———求图中所有的最短路径。
题中要求算出一张任意城市间的最廉价路线表，属于全局最短路问题，并且使得该公司总经理能够与各个子公司之间自由往返。
（此两点为主要约束条件）Floyd 算法，具体原理如下：（1） 我们确定本题为全局最短路问题，并采用求距离矩阵的方法根据路线及票价表建立带权矩阵W ，并把带权邻接矩阵我w 作为距离矩阵的初始值，即(0)(0)()ij v v D d W ⨯==（2）求路径矩阵的方法在建立距离矩阵的同时可建立路径矩阵R ，()ij v v R r ⨯=，ij r 的含义是从i v 到j v 的最短路径要经过点号为ij r 的点。
（3）查找最短路径的方法若()1v ij r p =，则点1p 是点i 到j 的最短距离的中间点，然后用同样的方法再分头查找。
三、 模型假设： 1.各城市间的飞机线路固定不变2.各城市间飞机线路的票价不改变3.忽略乘客除票价以外的各项开销费用4.不考虑雷雨云、低云、大风、雷暴、冰雹等主要天气因素对飞行的影响。
章绍辉数学建模第二章第四题解析
4.继续考虑2.3节的“生猪出手时机”案例,假设在第t 天的生猪出售的市场价格（元/公斤）为2)0()(ht gt p t p +-= （1）其中h 为价格的平稳率,取0002.0=h .其他模型假设和参数取值保持不变. （1）试比较（1）式与（2.3.1）式,解释新的假设和原来的假设的区别与联系; （2）在新的假设下求解最佳出售时机和多赚的纯利润;（3）作灵敏度分析,分别考虑h 对最佳出售时机和多赚的纯利润的影响; （4）讨论模型关于价格假设的强健性. 解:（1）两个假设的区别与联系 由课本的内容,我们有()1.3.2)0()(ΛΛgt p t p -=()1)0()(2ΛΛht gt p t p +-=这两个式子的区别与联系如下: ①区别 i ）（2.3.1）式所表示的是递减的一次函数,而（1）式所表示的则是一个开口向上的二次函数,如图1. 绘图程序：p=@(t)12-0.08*t+0.0002*t.^2; t=input('请输入t 值')plot([0,t],[12,12-0.08*t],'k:',0:.1:t,p(0:.1:t),'k') axis([0,t,0,20])title('模型假设（1）式与（2.3.1）式的比较') legend('p(0)-gt (2.3.1)式','p(0)-gt+ht^2 (1)式') xlabel('时间t （天)'),ylabel('市场价格p(元/公斤)') 图像t=400 图1ii ）（2.3.1）式表示价格匀速下降,（1）式表示价格先下降到一定程度再增加,故（2.3.1）更加符合实际的情况,如图1.iii ）（2.3.1）式中,市场价格降低的幅度为g t p -=)('错误!未找到引用源。
,而（1）式中,市场价格的降低值为ht g t p 2)('+-=错误!未找到引用源。
数学建模第二章作业答案章绍辉
习题2作业讲评1. 继续考虑2.2节的“汽车刹车距离”案例，请问“两秒准则”和“一车长度准则”一样吗？“两秒准则”是否足够安全？对于安全车距，你有没有更好的建议？（“两秒准则”，即后车司机从前车经过某一标志开始，默数2秒之后到达同一标志，而不管车速如何.刹车距离与车速的经验公式20.750.082678d v v =+，速度单位为m/s ，距离单位为m ）解答（1）“两秒准则”表明前后车距与车速成正比例关系. 引入以下符号：D ～ 前后车距（m ）；v ～ 车速（m/s ）；于是“两秒准则”的数学模型为22D K v v ==. 与“一车长度准则”相比是否一样，依赖于一车长度的选取.比较20.750.082678d v v =+与2D v =，得：()0.082678 1.25d D v v -=-所以当15.12 m/s v <（约合54.43 km/h ）时，有d<D ，即前后车距大于刹车距离的理论值，可认为足够安全；当15.12 m/s v >时，有d>D ，即前后车距小于刹车距离的理论值，不够安全. 也就是说，“两秒准则”适用于车速不算很快的情况.另外，还可以通过绘图直观的解释“两秒准则”够不够安全. 用以下MATLAB 程序把刹车距离实测数据和“两秒准则”都画在同一幅图中（图1）.v=(20:5:80).*0.44704;d2=[18,25,36,47,64,82,105,132,162,196,237,283,334 22,31,45,58,80,103,131,165,202,245,295,353,418 20,28,40.5,52.5,72,92.5,118,148.5,182,220.5,266,318,376]; d2=0.3048.*d2;k1=0.75;k2=0.082678;K2=2; d1=[v;v;v].*k1; d=d1+d2;plot([0,40],[0,K2*40],'k') hold onplot(0:40,polyval([k2,k1,0],0:40),':k') plot([v;v;v],d,'ok','MarkerSize',2)title('比较刹车距离实测数据、理论值和两秒准则') legend('两秒准则','刹车距离理论值',...'刹车距离的最小值、平均值和最大值',2) xlabel('车速v （m/s ）') ylabel('距离（m ）') hold off510152025303540020406080100120140160180比较刹车距离实测数据、理论值和两秒准则车速v （m/s ）距离（m ）图1（2）用最大刹车距离除以车速，得到最大刹车距离所需要的尾随时间（表1），并以尾随时间为依据，提出更安全的“t秒准则”（表2）——后车司机根据车速快慢的范围，从前车经过某一标志开始，默数t秒钟之后到达同一标志.v=(20:5:80).*0.44704;d2=[18,25,36,47,64,82,105,132,162,196,237,283,33422,31,45,58,80,103,131,165,202,245,295,353,41820,28,40.5,52.5,72,92.5,118,148.5,182,220.5,266,318,376];d2=0.3048.*d2;k1=0.75;k2=0.082678;d=d2+[v;v;v].*k1;vi=0:40;plot([0,10*0.44704],[0,10*0.44704],'k',...vi,k1.*vi+k2.*vi.*vi,'k:',...[v;v;v],d,'ok','MarkerSize',2)legend('t 秒准则','刹车距离理论值',...'刹车距离的最小值、平均值和最大值',2)hold onplot([10,35]*0.44704,2*[10,35]*0.44704,'k',...[35,60]*0.44704,3*[35,60]*0.44704,'k',... [60,75]*0.44704,4*[60,75]*0.44704,'k') title('t 秒准则，刹车距离的模型和数据') xlabel('车速v （m/s ）') ylabel('距离（m ）') hold off510152025303540020406080100120140160180车速v （m/s ）距离（m ）t 秒准则，刹车距离的模型和数据图24. 继续考虑2.3节“生猪出售时机”案例，假设在第t 天的生猪出售的市场价格（元/公斤）为2()(0)p t p gt ht =-+(1)其中h 为价格的平稳率，取h =0.0002. 其它模型假设和参数取值保持不变.（1） 试比较(1)式与(2.3.1)式，解释新的假设和原来的假设的区别与联系；（2）在新的假设下求解最佳出售时机和多赚的纯利润； （3）作灵敏度分析，分别考虑h 对最佳出售时机和多赚的纯利润的影响；（4）讨论模型关于价格假设的强健性. 解答一（用MATLAB 数值计算）（1）比较(1)式与(2.3.1)式，(1)式表明价格先降后升，(2.3.1)式假设价格匀速下降，(1)式更接近实际（图3）. 两个假设都满足(0)p g '=-，在最佳出售时机附近误差微小（图4）. 绘图的程序p=@(t)12-0.08*t+0.0002*t.^2; figure(1) n=400;plot([0,n],[12,12-0.08*n],'k:',... 0:.1:n,p(0:.1:n),'k') axis([0,400,0,20])title('模型假设(1)式与(2.3.1)式的比较')legend('p(0) - g t (1)式',... 'p(0) - g t + h t^2 (2.3.1)式') xlabel('t （天）')ylabel('p （元/公斤） ') figure(2) n=20;plot([0,n],[12,12-0.08*n],'k:',... 0:.1:n,p(0:.1:n),'k')title('模型假设(1)式与(2.3.1)式的比较')legend('p(0) - g t (1)式',... 'p(0) - g t + h t^2 (2.3.1)式')xlabel('t （天）'), ylabel('p （元/公斤） ')50100150200250300350400024********161820模型假设(1)式与(2.3.1)式的比较t （天）p （元/公斤）图3246810121416182010.410.610.81111.211.411.611.812模型假设(1)式与(2.3.1)式的比较t （天）p （元/公斤）图4（2）在(1)式和(2.3.1)式组成的假设下，多赚的纯利润为()()23()(0)(0)(0)Q t rp gw c t hw gr t hrt =--+-+保留h ，代入其他具体数值，得()32()900.08 1.6Q t ht h t t =+-+令()2()31800.16 1.60Q t ht h t '=+-+=解得生猪出售时机为130t =-（舍去负根）多赚的纯利润为()321111900.08 1.6Q ht h t t =+-+.代入h =0.0002，得113.829t =天，110.798Q =元.或者用MATLAB 函数fminbnd 计算，脚本如下： C=@(t)3.2*t; w=@(t)90+t;p=@(t,h)12-0.08*t+h*t.^2;Q=@(t,h)p(t,h).*w(t)-C(t)-90*12; Qh=@(t)-Q(t,0.0002); t1=fminbnd(Qh,0,30) Q1=Q(t1,0.0002)为帮助理解，可用以下脚本绘制图5： figure(2) tp=0:250;plot(tp,Q(tp,0.0002),'k') title('纯利润Q') xlabel('t （天）') ylabel('Q （元） ')050100150200250-600-500-400-300-200-100100纯利润Qt （天）Q （元）图5（3）用以下MATLAB 脚本计算灵敏度(,)t tS t h h h ∆=∆和(,)Q QS Q h h h ∆=∆，将结果列表.结论：h 的微小变化对t 和Q 的影响都很小 Qh=@(t)-Q(t,0.0002*1.01); [tn,Qn]=fminbnd(Qh,0,30); (tn-t1)/t1/0.01 (-Qn-Q1)/Q1/0.01Qh=@(t)-Q(t,0.0002*1.05); [tn,Qn]=fminbnd(Qh,0,30); (tn-t1)/t1/0.05 (-Qn-Q1)/Q1/0.05Qh=@(t)-Q(t,0.0002*1.1); [tn,Qn]=fminbnd(Qh,0,30); (tn-t1)/t1/0.1 (-Qn-Q1)/Q1/0.1表3 数值计算最佳出售时机t 对h 的灵敏度表4 数值计算多赚的纯利润Q 对h 的灵敏度（4）市场价格是经常波动的，如果价格下跌，往往会止跌回稳，模型假设(1)式以二次函数来刻画价格止跌回升的变化趋势，如果考虑的时间段长达数月，(1)式比(2.3.1)式更接近实际（见图3），但是本问题的最佳出售时机不超过20天，(1)式与(2.3.1)式在最佳出售时机附近非常近似（见图4），(1)式导致的模型解答可以由(2.3.1)式导致的解答加上灵敏度分析所代替. 所以采用更为简单的(2.3.1)式作为假设更好.具体分析如下：由12()(,)g g t p t h -+∆=，得12(,)1g p t h g gt∆-=-， 代入h =0.0002，t =13.82852279，g =0.08，得0.034571gg∆=-. 由于(,)t g S t g t g∆∆≈，根据课本2.3节，代入(,) 5.5S t g =-，t =10，算得11.901t t +∆=，与t =13.829只相差两天.用于以上分析计算的MATLAB 脚本： dg_g=(12-p(ts,0.0002))/ts/0.08-1 10+dg_g*10*(-5.5)解答二（用MATLAB 的Symbolic Math Toolbox 的MuPAD 软件符号计算）（1）运行以下MuPAD 语句，绘得图6和图7：plot(plot::Function2d(12-0.08*t+0.0002*t^2,t=0..400), plot::Function2d(12-0.08*t,t=0..150, LineStyle=Dashed));plot(plot::Function2d(12-0.08*t+0.0002*t^2,t=0..20), plot::Function2d(12-0.08*t,t=0..20, LineStyle=Dashed),#O);(1)式表明价格先降后升，在实际当中有一定道理. 而 (2.3.1)式假设价格匀速下降. 两个假设都满足(0)p g '=-，在最佳出售时机附近误差微小.图6假设(2.3.1)式与(1)式的比较图7假设(2.3.1)式与(1)式的比较(2) 在(1)式和(2.3.1)式组成的假设下，保留h，代入其他具体数值，计算多赚的纯利润. 运行以下MuPAD语句：C:=t->32/10*t:w:=t->90+t:p:=(t,h)->12-8/100*t+h*t^2:Q:=(t,h)-->expand(w(t)*p(t,h)-C(t)-90*12); plot(plot::Function2d(Q(t,0.0002),t=0..290));算得223(2)825,905ht h h t Q t t t =+-+，绘得图8.图8(,0.0002)Q t 的图像运行以下MuPAD 语句：S:=solve(diff(Q(t,h),t),t) assuming h>0; t1:=S[1];subs(t1,h=0.0002); t2:=S[2];ts:=subs(t2,h=0.0002); Q2:=Q(t2,h);Qs:=subs(Q2,h=0.0002);由方程0Qt∂=∂，解得两根：12t t ==代入h =0.0002，得12192.8381439, 13.82852279t t ==（天）. 2t 符合题意，1t 应该舍去（对应的Q 是负数）. 2t 对应的多赚的纯利润为10.79837809元.（3）接着上一小题，运行以下MuPAD 语句：subs(diff(t2,h)*h/t2,h=0.0002); //t 对h 的灵敏度利用导数算得t 对h 的灵敏度：d (,)0.4124276803d t hS t h h t=⋅=.运行以下MuPAD 语句：subs(diff(Q2,h)*h/Q2,h=0.0002); //Q 对h 的灵敏度，方法一 subs(diff(Q(t,h),h)*h/Q(t,h),t=ts,h=0.0002); //Q 对h 的灵敏度，方法二，更简单用两种方法利用导数算得Q 对h 的灵敏度：d (,)0.367739025d Q hS Q h h Q=⋅=. 结论：h 的微小变化对t 2和Q 2的影响都很小. （4）同解答一5. 继续考虑第2.3节“生猪出售时机”案例，假设在第t 天的生猪体重（公斤）为()000()mt m w w w t w w w e α-=+-(2)其中0(0)90w w ==（公斤），270m w =（公斤），其它模型假设和参数取值保持不变.（1）试比较(2)式与(2.3.2)式，解释新的假设和原来的假设的区别与联系（提示：说明当α (α>0)取何值时，在t =0时可以保持(0)1w r '==；说明当t 增大时，猪的体重会如何变化）.（2）在新的假设下求解最佳出售时机和多赚的纯利润. （3）参数m w 代表猪长成时的最终重量，对m w 做灵敏度分析，分别考虑m w 对最佳出售时机和多赚的纯利润的影响.（4）讨论模型关于生猪体重假设的强健性. 解答一（用MATLAB 数值计算）（1）在(2)式中，为使(0)w r '=，必须00()m m w w w w α-=. 当m w =270，0w =90时，有160α=.新假设(2)式是阻滞增长模型，假设生猪体重的增长率是体重的线性递减函数，于是体重增加的速率先快后慢，时间充分长后，体重趋于m w . 而(2.3.2)式0()w t w rt =+只假设体重匀速增加. 长时间来看，新假设比原假设更符合实际（图9）. 两个假设都满足(0)w r '=，在最佳出售时机附近误差微小（图10）.50100150200250300350400050100150200250300t （天）价格 p （元/公斤）模型假设(2.3.2)式与(2)式的比较图924681012141618209095100105110115t （天）价格 p （元/公斤）图10(2) 在(2.3.1)式和(2)式组成的假设下，用MATLAB 函数fminbnd 计算，可以求得生猪出售时机为t =14.434天，多赚的纯利润为Q =12.151元.(3) 编程计算(,)m m m t t S t w w w ∆=∆和(,)mm m Q QS Q w w w ∆=∆，将结果列表.表5数值计算最佳出售时机t 对m w 的灵敏性表6数值计算多赚的纯利润Q 对m w 的灵敏性结论：m w 的微小变化对t 和Q 的影响都较小.（4）模型假设(2)式导致的模型解答可以由(2.3.2)式导致的解答加上灵敏度分析所代替，所以实践中采用更为简单的(2.3.2)式作为假设即可. 具体分析过程见解答二之（4）.MATLAB 脚本： %% (1) 绘图的程序w=@(t)90*270./(90+180*exp(-t/60));figure(1)n=400;plot([0,n],[90,90+n],'k:',...0:.1:n,w(0:.1:n),'k')axis([0,400,0,300])legend('p(0) - g t (2.3.2)式',... 'p(0) - g t + h^2 (2)式',4) title('模型假设(2.3.2)式与(2)式的比较') xlabel('t（天）')ylabel('价格 p（元/公斤） ')figure(2)n=20;plot([0,n],[90,90+n],'k:',...0:.1:n,w(0:.1:n),'k')legend('p(0) - g t (2.3.2)式',... 'p(0) - g t + h^2 (2)式',2) xlabel('t（天）')ylabel('价格 p（元/公斤） ')%% (2) 最佳出售时机和多赚的纯利润C=@(t)3.2*t;w=@(t,m)90*m./(90+(m-90)*exp(-t/60));p=@(t)12-0.08*t;Q=@(t,m)p(t).*w(t,m)-C(t)-90*12;Qh=@(t)-Q(t,270);ts=fminbnd(Qh,0,30)Qs=Q(ts,270)%% (3) 灵敏度分析Qh=@(t)-Q(t,270*1.01);[tn,Qn]=fminbnd(Qh,0,30);(tn-ts)/ts/0.01(-Qn-Qs)/Qs/0.01Qh=@(t)-Q(t,270*1.05);[tn,Qn]=fminbnd(Qh,0,30);(tn-ts)/ts/0.05(-Qn-Qs)/Qs/0.05Qh=@(t)-Q(t,270*1.1);[tn,Qn]=fminbnd(Qh,0,30);(tn-ts)/ts/0.1(-Qn-Qs)/Qs/0.1%% (4) 强健性分析dr_r=(w(ts,270)-90)/ts-110+dr_r*10*6.5解答二（用MATLAB的Symbolic Math Toolbox的MuPAD软件符号计算）（1）运行以下MuPAD 语句，算得160α=：solve(subs(diff(90*270/(90+(270-90)*E^(-a*t)),t), t=0)=1,a);运行以下MuPAD 语句，绘得图11：plot(plot::Function2d(90*270/(90+180*E^(-1/60*t)), t=0..400),plot::Function2d(90+t,t=0..180,LineStyle=Dashed), plot::Line2d([0,270],[400,270],LineStyle=Dotted),#O);运行以下MuPAD 语句，绘得图12 ：plot(plot::Function2d(90*270/(90+180*E^(-1/60*t)), t=0..20),plot::Function2d(90+t,t=0..20,LineStyle=Dashed),#O);(2)式()06000()mt m w w w t w w w e -=+-是阻滞增长模型，假设生猪体重的增长率是体重的线性递减函数. 于是，体重w 是时间t 的增函数，体重增加的速率先快后慢，时间充分长后，体重趋于m w . 而(2.3.2)式0()w t w rt =+只假设体重匀速增加. 长时间来看，新假设比原假设更符合实际. 两假设都满足(0)w r '=，在最佳出售时机附近误差微小.图11假设(2.3.2)式与(2)式的比较图12假设(2.3.2)式与(2)式的比较w，代入其（2）在由(2)式和(2.3.1)式组成的假设下，保留m他具体数值，计算多赚的纯利润. 运行以下MuPAD语句：C:=t->3.2*t:w:=(t,wm)->90*wm/(90+(wm-90)*E^(-t/60)): p:=t->12-0.08*t:Q:=(t,wm)-->w(t,wm)*p(t)-C(t)-90*12;plot(plot::Function2d(Q(t,270),t=0..30));算得()()6090120.08(,) 3.210809090emm tmw tQ t w tw--=--+-，绘得图13.图13(,270)Q t的图像运行以下MuPAD语句：T:=solve(diff(Q(t,270),t),t);ts:=T[1];Qs:=Q(ts,270);可解出Q的驻点的数值解14.43357158st=（天），根据函数图像和问题的实际意义，可知这是所求的最佳出售时机，对应的多赚的纯利润为12.15129217s Q =元.（3）接着上一小题，运行以下MuPAD 语句，但是求不出当(,)m Q t w 达到最大值时t 关于m w 的函数解析式：solve(diff(Q(t,wm),t),t);运行以下MuPAD 语句：solve(diff(Q(t,wm),t),wm);可见当(,)m Q t w 达到最大值时m w 关于t 的反函数解析式却有可能求得出，只是MuPAD 给出的表达式很复杂. 其实可以按如下步骤推出m w 关于t 的反函数解析式：g1:=diff(Q(t,wm),t)=0; 算得0Q t∂=∂即： ()()260606030.0812907.2 3.209090902e 90e e m m m m t m t t w t w w w w -----=--⎛⎫++ ⎪⎝⎭观察上式，发现分母大于零，而且去分母之后，合并m w 的同类项，可以表示为m w 的二次方程：g2:=g1*((wm-90)/E^(t/60)+90)^2*25*E^(t/60); //去分母 g2:=collect(g2,wm); //合并wm 的同类项，t 当作参数2606060306060801440016200e 270327038700e e e 648000e 64800012960000e e t m m t t t t t t t w t w ⎛⎫⎛⎫--++-- ⎪ ⎪⎝⎭⎝⎭+--=运行以下MuPAD 语句，由图像（图14）可知在实际问题关心的0<t<30范围内，二次项系数608027030e tt-->：plot(plot::Function2d((270-80/E^(t/60)-3*t),t=0..100));图4 二次项系数的符号于是，运行以下MuPAD语句，解方程：S:=solve(g2,wm);MuPAD给出解的四种情况，其中第一种是二次项系数非零，正是本问题所要求的解. 但是二次方程有两个根，要检验哪一个根才是当(,)mQ t w达到最大值时mw关于t的反函数解析式.float(subs(S[1][1],t=ts));算得当st t=时，有0.8519704108mw=-，这是增根，舍去；float(subs(S[1][2],t=ts));算得当st t=时，有270mw=，这是要找的根；wms:=S[1][2]; //当Q达到最大值时wm关于t的反函数解析式float(subs(1/(diff(wms,t))*wm/t,t=ts,wm=270));//t 对wm 的灵敏度，利用反函数求导数利用反函数求导数算得t 对m w 的灵敏度：d 1(,) 3.80183985d d d m m m m m w w t S t w w w tt t=⋅=⋅=. Q 对m w 的灵敏度则比较简单，运行以下MuPAD 语句： float(subs(diff(Q(t,wm),wm)*wm/Q(t,wm),t=ts,wm=270)); //Q 对wm 的灵敏度利用导数算得Q 对m w 的灵敏度：d (,)7.786585188d m m m w Q S Q w w Q=⋅=. 结论：m w 的微小变化对t 和Q 存在一定影响，不算厉害.（4）模型假设(2)式以阻滞增长模型来刻画生猪体重的变化趋势，如果考虑的时间段长达数月，(2)式比(2.3.2)式更符合实际，但是本问题的最佳出售时机不超过20天，(2)式与(2.3.2)式在最佳出售时机附近非常近似，(2)式导致的模型解答可以由(2.3.2)式导致的解答加上灵敏度分析所代替. 所以采用更为简单的(2.3.2)式作为假设更好. 具体分析如下：由()90(,)m r r t w t w ++∆=，得(,)90m w t w r r t-∆=-， 代入270m w =，14.43357158s t t ==，r =1，得0.036565352791r r r ∆∆==. 由于(,)t r S t r t r∆∆≈，根据2.3节，代入(,) 6.5S t r =，t =10，r =1，算得12.37674793t t +∆=，与14.43357158s t =只相差两天.以上计算可以用以下MuPAD 语句实现：dr:=float((w(ts,270)-90)/ts-1);10+dr*10*6.5;。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
数学建模第二章作业答案章绍辉习题2作业讲评1. 继续考虑2.2节的“汽车刹车距离”案例，请问“两秒准则”和“一车长度准则”一样吗？“两秒准则”是否足够安全？对于安全车距，你有没有更好的建议？（“两秒准则”，即后车司机从前车经过某一标志开始，默数2秒之后到达同一标志，而不管车速如何. 刹车距离与车速的经验公式20.750.082678d v v =+，速度单位为m/s ，距离单位为m ）解答（1）“两秒准则”表明前后车距与车速成正比例关系. 引入以下符号：D ～ 前后车距（m ）；v ～ 车速（m/s ）；于是“两秒准则”的数学模型为22D K v v ==. 与“一车长度准则”相比是否一样，依赖于一车长度的选取.比较20.750.082678d v v =+与2D v =，得：()0.082678 1.25d D v v -=-所以当15.12 m/s v <（约合54.43 km/h ）时，有d<D ，即前后车距大于刹车距离的理论值，可认为足够安全；当15.12 m/s v >时，有d>D ，即前后车距小于刹车距离的理论值，不够安全. 也就是说，“两秒准则”适用于车速不算很快的情况.另外，还可以通过绘图直观的解释“两秒准则”够不够安全. 用以下MATLAB 程序把刹车距离实测数据和“两秒准则”都画在同一幅图中（图1）.v=(20:5:80).*0.44704;d2=[18,25,36,47,64,82,105,132,162,196,237,283,334 22,31,45,58,80,103,131,165,202,245,295,353,41820,28,40.5,52.5,72,92.5,118,148.5,182,220.5,266,318,376]; d2=0.3048.*d2;k1=0.75; k2=0.082678; K2=2; d1=[v;v;v].*k1; d=d1+d2;plot([0,40],[0,K2*40],'k') hold onplot(0:40,polyval([k2,k1,0],0:40),':k') plot([v;v;v],d,'ok','MarkerSize',2)title('比较刹车距离实测数据、理论值和两秒准则') legend('两秒准则','刹车距离理论值',...'刹车距离的最小值、平均值和最大值',2) xlabel('车速v （m/s ）') ylabel('距离（m ）') hold off510152025303540020406080100120140160180比较刹车距离实测数据、理论值和两秒准则车速v （m/s ）距离（m ）两秒准则刹车距离理论值刹车距离的最小值、平均值和最大值图1hold onplot([10,35]*0.44704,2*[10,35]*0.44704,'k',... [35,60]*0.44704,3*[35,60]*0.44704,'k',... [60,75]*0.44704,4*[60,75]*0.44704,'k') title('t 秒准则，刹车距离的模型和数据') xlabel('车速v （m/s ）') ylabel('距离（m ）') hold off510152025303540020406080100120140160180车速v （m/s ）距离（m ）t 秒准则，刹车距离的模型和数据t 秒准则刹车距离理论值刹车距离的最小值、平均值和最大值图24. 继续考虑2.3节“生猪出售时机”案例，假设在第t 天的生猪出售的市场价格（元/公斤）为2()(0)p t p gt ht =-+ (1)其中h 为价格的平稳率，取h =0.0002. 其它模型假设和参数取值保持不变.（1） 试比较(1)式与(2.3.1)式，解释新的假设和原来的假设的区别与联系；（2）在新的假设下求解最佳出售时机和多赚的纯利润； （3）作灵敏度分析，分别考虑h 对最佳出售时机和多赚的纯利润的影响；（4）讨论模型关于价格假设的强健性. 解答一（用MATLAB 数值计算）（1）比较(1)式与(2.3.1)式，(1)式表明价格先降后升，(2.3.1)式假设价格匀速下降，(1)式更接近实际（图3）. 两个假设都满足(0)p g '=-，在最佳出售时机附近误差微小（图4）. 绘图的程序p=@(t)12-0.08*t+0.0002*t.^2; figure(1) n=400;plot([0,n],[12,12-0.08*n],'k:',... 0:.1:n,p(0:.1:n),'k') axis([0,400,0,20])title('模型假设(1)式与(2.3.1)式的比较')legend('p(0) - g t (1)式',... 'p(0) - g t + h t^2 (2.3.1)式') xlabel('t （天）')ylabel('p （元/公斤） ') figure(2) n=20;plot([0,n],[12,12-0.08*n],'k:',... 0:.1:n,p(0:.1:n),'k')title('模型假设(1)式与(2.3.1)式的比较')legend('p(0) - g t (1)式',... 'p(0) - g t + h t^2 (2.3.1)式') xlabel('t （天）'), ylabel('p （元/公斤） ')50100150200250300350400024********161820模型假设(1)式与(2.3.1)式的比较t （天）p （元/公斤）p(0) - g t (1)式p(0) - g t + h t 2 (2.3.1)式图3246810121416182010.410.610.81111.211.411.611.812模型假设(1)式与(2.3.1)式的比较t （天）p （元/公斤）p(0) - g t (1)式p(0) - g t + h t 2 (2.3.1)式图4（2）在(1)式和(2.3.1)式组成的假设下，多赚的纯利润为()()23()(0)(0)(0)Q t rp gw c t hw gr t hrt =--+-+保留h ，代入其他具体数值，得()32()900.08 1.6Q t ht h t t =+-+令()2()31800.16 1.60Q t ht h t '=+-+=解得生猪出售时机为()210.161800.1619.230h ht ---=-（舍去负根）多赚的纯利润为()321111900.08 1.6Q ht h t t =+-+.代入h =0.0002，得113.829t =天，110.798Q =元.或者用MATLAB 函数fminbnd 计算，脚本如下： C=@(t)3.2*t; w=@(t)90+t;p=@(t,h)12-0.08*t+h*t.^2;Q=@(t,h)p(t,h).*w(t)-C(t)-90*12; Qh=@(t)-Q(t,0.0002); t1=fminbnd(Qh,0,30) Q1=Q(t1,0.0002)为帮助理解，可用以下脚本绘制图5： figure(2) tp=0:250;plot(tp,Q(tp,0.0002),'k') title('纯利润Q') xlabel('t （天）') ylabel('Q （元） ')050100150200250-600-500-400-300-200-100100纯利润Qt （天）Q （元）图5（3）用以下MATLAB 脚本计算灵敏度(,)t tS t h h h ∆=∆和(,)Q QS Q h h h ∆=∆，将结果列表.结论：h 的微小变化对t 和Q 的影响都很小 Qh=@(t)-Q(t,0.0002*1.01); [tn,Qn]=fminbnd(Qh,0,30); (tn-t1)/t1/0.01 (-Qn-Q1)/Q1/0.01Qh=@(t)-Q(t,0.0002*1.05); [tn,Qn]=fminbnd(Qh,0,30); (tn-t1)/t1/0.05 (-Qn-Q1)/Q1/0.05Qh=@(t)-Q(t,0.0002*1.1); [tn,Qn]=fminbnd(Qh,0,30); (tn-t1)/t1/0.1 (-Qn-Q1)/Q1/0.1表3 数值计算最佳出售时机t 对h 的灵敏度h h +∆h h ∆(%)t t +∆t t ∆(%)(,)t t S t h h h∆=∆0.000202 1 13.886 0.41459 0.41459 0.00021 5 14.121 2.1176 0.42352 0.000221014.431 4.35360.43536表4 数值计算多赚的纯利润Q 对h 的灵敏度h h +∆h h ∆(%)Q Q +∆Q Q ∆(%)(,)Q Q S Q h h h∆=∆ 0.000202 1 10.838 0.36936 0.36936 0.00021 5 11.001 1.8802 0.37604 0.00022 1011.2143.84790.38479（4）市场价格是经常波动的，如果价格下跌，往往会止跌回稳，模型假设(1)式以二次函数来刻画价格止跌回升的变化趋势，如果考虑的时间段长达数月，(1)式比(2.3.1)式更接近实际（见图3），但是本问题的最佳出售时机不超过20天，(1)式与(2.3.1)式在最佳出售时机附近非常近似（见图4），(1)式导致的模型解答可以由(2.3.1)式导致的解答加上灵敏度分析所代替. 所以采用更为简单的(2.3.1)式作为假设更好.具体分析如下：由12()(,)g g t p t h -+∆=，得12(,)1g p t h g gt∆-=-， 代入h =0.0002，t =13.82852279，g =0.08，得0.034571gg∆=-. 由于(,)t g S t g t g∆∆≈，根据课本2.3节，代入(,) 5.5S t g =-，t =10，算得11.901t t +∆=，与t =13.829只相差两天.用于以上分析计算的MATLAB 脚本： dg_g=(12-p(ts,0.0002))/ts/0.08-1 10+dg_g*10*(-5.5)解答二（用MATLAB 的Symbolic Math Toolbox 的MuPAD 软件符号计算）（1）运行以下MuPAD 语句，绘得图6和图7：plot(plot::Function2d(12-0.08*t+0.0002*t^2,t=0..400), plot::Function2d(12-0.08*t,t=0..150, LineStyle=Dashed));plot(plot::Function2d(12-0.08*t+0.0002*t^2,t=0..20), plot::Function2d(12-0.08*t,t=0..20, LineStyle=Dashed),#O);(1)式表明价格先降后升，在实际当中有一定道理. 而 (2.3.1)式假设价格匀速下降. 两个假设都满足(0)p g '=-，在最佳出售时机附近误差微小.图6 假设(2.3.1)式与(1)式的比较图7 假设(2.3.1)式与(1)式的比较(2) 在(1)式和(2.3.1)式组成的假设下，保留h，代入其他具体数值，计算多赚的纯利润. 运行以下MuPAD语句：C:=t->32/10*t:w:=t->90+t:p:=(t,h)->12-8/100*t+h*t^2:Q:=(t,h)-->expand(w(t)*p(t,h)-C(t)-90*12); plot(plot::Function2d(Q(t,0.0002), t=0..290));算得223(2)825,905ht h h t Q t t t =+-+，绘得图8.图8 (,0.0002)Q t 的图像运行以下MuPAD 语句：S:=solve(diff(Q(t,h),t),t) assuming h>0; t1:=S[1];subs(t1,h=0.0002); t2:=S[2];ts:=subs(t2,h=0.0002); Q2:=Q(t2,h);Qs:=subs(Q2,h=0.0002);由方程0Qt∂=∂，解得两根： 2384165625123841656252253240045004450025324004h h h t h h h t -+-+=+-+-=代入h =0.0002，得12192.8381439, 13.82852279t t ==（天）. 2t 符合题意，1t 应该舍去（对应的Q 是负数）. 2t 对应的多赚的纯利润为10.79837809元.（3）接着上一小题，运行以下MuPAD 语句：subs(diff(t2,h)*h/t2, h=0.0002); //t 对h 的灵敏度利用导数算得t 对h 的灵敏度：d (,)0.4124276803d t hS t h h t=⋅=.运行以下MuPAD 语句：subs(diff(Q2,h)*h/Q2,h=0.0002); //Q 对h 的灵敏度，方法一 subs(diff(Q(t,h),h)*h/Q(t,h),t=ts,h=0.0002); //Q 对h 的灵敏度，方法二，更简单用两种方法利用导数算得Q 对h 的灵敏度：d (,)0.367739025d Q hS Q h h Q=⋅=. 结论：h 的微小变化对t 2和Q 2的影响都很小. （4）同解答一5. 继续考虑第2.3节“生猪出售时机”案例，假设在第t 天的生猪体重（公斤）为()000()mt m w w w t w w w e α-=+- (2)其中0(0)90w w ==（公斤），270m w =（公斤），其它模型假设和参数取值保持不变.（1）试比较(2)式与(2.3.2)式，解释新的假设和原来的假设的区别与联系（提示：说明当α (α>0)取何值时，在t =0时可以保持(0)1w r '==；说明当t 增大时，猪的体重会如何变化）.（2）在新的假设下求解最佳出售时机和多赚的纯利润. （3）参数m w 代表猪长成时的最终重量，对m w 做灵敏度分析，分别考虑m w 对最佳出售时机和多赚的纯利润的影响.（4）讨论模型关于生猪体重假设的强健性. 解答一（用MATLAB 数值计算）（1）在(2)式中，为使(0)w r '=，必须00()m m w w w w α-=. 当m w =270，0w =90时，有160α=.新假设(2)式是阻滞增长模型，假设生猪体重的增长率是体重的线性递减函数，于是体重增加的速率先快后慢，时间充分长后，体重趋于m w . 而(2.3.2)式0()w t w rt =+只假设体重匀速增加. 长时间来看，新假设比原假设更符合实际（图9）. 两个假设都满足(0)w r '=，在最佳出售时机附近误差微小（图10）.50100150200250300350400050100150200250300t （天）价格 p （元/公斤）模型假设(2.3.2)式与(2)式的比较p(0) - g t (2.3.2)式p(0) - g t + h 2 (2)式图924681012141618209095100105110115t （天）价格 p （元/公斤）p(0) - g t (2.3.2)式p(0) - g t + h 2 (2)式图10(2) 在(2.3.1)式和(2)式组成的假设下，用MATLAB 函数fminbnd 计算，可以求得生猪出售时机为t =14.434天，多赚的纯利润为Q =12.151元.(3) 编程计算(,)m m m t t S t w w w ∆=∆和(,)m m mQ QS Q w w w ∆=∆，将结果列表.表5 数值计算最佳出售时机t 对m w 的灵敏性m m w w +∆m mw w ∆(%)t t +∆t t ∆(%)(,)m m mt tS t w w w ∆=∆272.7 1 14.977 3.767 3.767 283.5 5 17.057 18.173 3.6345 2971019.46 34.8253.4825表6 数值计算多赚的纯利润Q 对m w 的灵敏性m m w w +∆m m w w ∆(%)Q Q +∆Q Q ∆(%)(,)m m mQ Q S Q w w w ∆=∆272.7 1 13.108 7.872 7.872 283.5 5 17.121 40.897 8.1794 2971022.47584.9638.4963结论：m w 的微小变化对t 和Q 的影响都较小.（4）模型假设(2)式导致的模型解答可以由(2.3.2)式导致的解答加上灵敏度分析所代替，所以实践中采用更为简单的(2.3.2)式作为假设即可. 具体分析过程见解答二之（4）.MATLAB脚本：%% (1) 绘图的程序w=@(t)90*270./(90+180*exp(-t/60));figure(1)n=400;plot([0,n],[90,90+n],'k:',...0:.1:n,w(0:.1:n),'k')axis([0,400,0,300])legend('p(0) - g t (2.3.2)式',... 'p(0) - g t + h^2 (2)式',4) title('模型假设(2.3.2)式与(2)式的比较') xlabel('t（天）')ylabel('价格 p（元/公斤） ')figure(2)n=20;plot([0,n],[90,90+n],'k:',...0:.1:n,w(0:.1:n),'k')legend('p(0) - g t (2.3.2)式',... 'p(0) - g t + h^2 (2)式',2) xlabel('t（天）')ylabel('价格 p（元/公斤） ')%% (2) 最佳出售时机和多赚的纯利润C=@(t)3.2*t;w=@(t,m)90*m./(90+(m-90)*exp(-t/60)); p=@(t)12-0.08*t;Q=@(t,m)p(t).*w(t,m)-C(t)-90*12;Qh=@(t)-Q(t,270);ts=fminbnd(Qh,0,30)Qs=Q(ts,270)%% (3) 灵敏度分析Qh=@(t)-Q(t,270*1.01);[tn,Qn]=fminbnd(Qh,0,30);(tn-ts)/ts/0.01(-Qn-Qs)/Qs/0.01Qh=@(t)-Q(t,270*1.05);[tn,Qn]=fminbnd(Qh,0,30);(tn-ts)/ts/0.05(-Qn-Qs)/Qs/0.05Qh=@(t)-Q(t,270*1.1);[tn,Qn]=fminbnd(Qh,0,30);(tn-ts)/ts/0.1(-Qn-Qs)/Qs/0.1%% (4) 强健性分析dr_r=(w(ts,270)-90)/ts-110+dr_r*10*6.5解答二（用MATLAB 的Symbolic Math Toolbox 的MuPAD 软件符号计算）（1）运行以下MuPAD 语句，算得160α=：solve(subs(diff(90*270/(90+(270-90)*E^(-a*t)),t), t=0)=1, a);运行以下MuPAD 语句，绘得图11：plot(plot::Function2d(90*270/(90+180*E^(-1/60*t)), t=0..400),plot::Function2d(90+t, t=0..180, LineStyle=Dashed), plot::Line2d([0,270],[400,270],LineStyle=Dotted),#O);运行以下MuPAD 语句，绘得图12 ：plot(plot::Function2d(90*270/(90+180*E^(-1/60*t)), t=0..20),plot::Function2d(90+t,t=0..20,LineStyle=Dashed),#O);(2)式()06000()mt m w w w t w w w e -=+-是阻滞增长模型，假设生猪体重的增长率是体重的线性递减函数. 于是，体重w 是时间t 的增函数，体重增加的速率先快后慢，时间充分长后，体重趋于m w . 而(2.3.2)式0()w t w rt =+只假设体重匀速增加. 长时间来看，新假设比原假设更符合实际. 两假设都满足(0)w r '=，在最佳出售时机附近误差微小.图11 假设(2.3.2)式与(2)式的比较图12 假设(2.3.2)式与(2)式的比较w，代入其（2）在由(2)式和(2.3.1)式组成的假设下，保留m他具体数值，计算多赚的纯利润. 运行以下MuPAD语句：C:=t->3.2*t:w:=(t,wm)->90*wm/(90+(wm-90)*E^(-t/60)):p:=t->12-0.08*t:Q:=(t,wm)-->w(t,wm)*p(t)-C(t)-90*12;plot(plot::Function2d(Q(t,270),t=0..30));算得()()6090120.08(,) 3.210809090emm tmw tQ t w tw--=--+-，绘得图13.图13 (,270)Q t的图像运行以下MuPAD语句：T:=solve(diff(Q(t,270),t),t);ts:=T[1];Qs:=Q(ts,270);可解出Q的驻点的数值解14.43357158st=（天），根据函数图像和问题的实际意义，可知这是所求的最佳出售时机，对应的多赚的纯利润为12.15129217s Q =元.（3）接着上一小题，运行以下MuPAD 语句，但是求不出当(,)m Q t w 达到最大值时t 关于m w 的函数解析式：solve(diff(Q(t,wm),t),t);运行以下MuPAD 语句：solve(diff(Q(t,wm),t),wm);可见当(,)m Q t w 达到最大值时m w 关于t 的反函数解析式却有可能求得出，只是MuPAD 给出的表达式很复杂. 其实可以按如下步骤推出m w 关于t 的反函数解析式：g1:=diff(Q(t,wm),t)=0; 算得0Q t∂=∂即： ()()260606030.0812907.2 3.209090902e 90e e m m m m t m t t w t w w w w -----=--⎛⎫++ ⎪⎝⎭观察上式，发现分母大于零，而且去分母之后，合并m w 的同类项，可以表示为m w 的二次方程：g2:=g1*((wm-90)/E^(t/60)+90)^2*25*E^(t/60); //去分母 g2:=collect(g2,wm); //合并wm 的同类项，t 当作参数2606060306060801440016200e 270327038700e e e 648000e 64800012960000e e t m m t t t t t t t w t w ⎛⎫⎛⎫--++-- ⎪ ⎪⎝⎭⎝⎭+--=运行以下MuPAD 语句，由图像（图14）可知在实际问题关心的0<t <30范围内，二次项系数608027030et t -->： plot(plot::Function2d((270-80/E^(t/60)-3*t),t=0..100));图4 二次项系数的符号于是，运行以下MuPAD 语句，解方程：S:=solve(g2,wm);MuPAD 给出解的四种情况，其中第一种是二次项系数非零，正是本问题所要求的解. 但是二次方程有两个根，要检验哪一个根才是当(,)m Q t w 达到最大值时m w 关于t 的反函数解析式. float(subs(S[1][1],t=ts));算得当s t t =时，有0.8519704108m w =-，这是增根，舍去； float(subs(S[1][2],t=ts));算得当s t t =时，有270m w =，这是要找的根；wms:=S[1][2]; //当Q 达到最大值时wm 关于t 的反函数解析式 float(subs(1/(diff(wms,t))*wm/t,t=ts,wm=270));//t 对wm 的灵敏度，利用反函数求导数利用反函数求导数算得t 对m w 的灵敏度：d 1(,) 3.80183985d d d m m m m m w w t S t w w w tt t=⋅=⋅=. Q 对m w 的灵敏度则比较简单，运行以下MuPAD 语句： float(subs(diff(Q(t,wm),wm)*wm/Q(t,wm),t=ts,wm=270)); //Q 对wm 的灵敏度利用导数算得Q 对m w 的灵敏度：d (,)7.786585188d m m m w Q S Q w w Q=⋅=. 结论：m w 的微小变化对t 和Q 存在一定影响，不算厉害.（4）模型假设(2)式以阻滞增长模型来刻画生猪体重的变化趋势，如果考虑的时间段长达数月，(2)式比(2.3.2)式更符合实际，但是本问题的最佳出售时机不超过20天，(2)式与(2.3.2)式在最佳出售时机附近非常近似，(2)式导致的模型解答可以由(2.3.2)式导致的解答加上灵敏度分析所代替. 所以采用更为简单的(2.3.2)式作为假设更好. 具体分析如下：由()90(,)m r r t w t w ++∆=，得(,)90m w t w r r t-∆=-， 代入270m w =，14.43357158s t t ==，r =1，得0.036565352791r r r ∆∆==. 由于(,)t r S t r t r∆∆≈，根据2.3节，代入(,) 6.5S t r =，t =10，r =1，算得12.37674793t t +∆=，与14.43357158s t =只相差两天.以上计算可以用以下MuPAD 语句实现：dr:=float((w(ts,270)-90)/ts-1);10+dr*10*6.5;。