立体几何大二轮深刻复习的策略
高中立体几何策略

高中立体几何策略
高中立体几何是数学学习中一个重要的部分,对于这部分内容的学习和解题,可以采用以下策略:
1.掌握基础知识:
熟悉并理解立体几何的基本元素:点、线、面、体及其相互关系。
学习空间直角坐标系,能熟练运用坐标法解决立体几何问题。
掌握平面与平面、直线与直线、直线与平面的平行、垂直关系及判定定理。
2.构建图形直观:
利用模型、实物或者想象来构造立体几何图形,形成空间观念。
经常进行画图训练,通过作图理解和解决问题。
3.熟悉基本定理:
如:两直线平行、垂直的判定与性质;线面平行、垂直的判定与性质;面面平行、垂直的判定与性质等。
球体积公式、圆柱体积公式、圆锥体积公式、长方体、正方体、棱柱、棱锥等常见几何体的表面积和体积计算。
4.逻辑推理能力培养:
通过分析条件、证明结论,锻炼严谨的逻辑思维和推理能力。
学会利用公理、定理和定义进行逐步推导,写出清晰明了的证明过程。
5.解题策略:
遇到立体几何问题时,首先明确题目所求,然后分析图形特征,找出隐藏在条件中的几何关系。
根据题目的类型选择合适的方法,如向量法、综合法、解析法(坐标法)等进行解答。
对于复杂的立体几何题,尝试分解为若干个简单的几何问题,逐个击破。
6.多做练习,总结归纳:
大量做题以巩固理论知识,并通过实践提高解题速度和准确率。
做完题目后要善于总结解题思路和方法,积累经验,形成自己的解题技巧库。
7.及时复习与反思:
定期对学过的知识点进行复习,确保对立体几何的概念和定理有深刻的理解和记忆。
反思错题,找出错误的原因,避免同样的错误再次发生。
立体几何高三数学二轮复习口诀

立体几何高三数学二轮复习口诀
立体几何高三数学二轮复习口诀
关于高三数学二轮复习口诀:立体几何高中数学,高三数学二轮复习时需要大家对所有知识点进行一遍总结,立体几何是重要知识点,对于这部分知识点的学习,大家应该记住相关口诀,小编为大家提供高三数学二轮复习口诀:立体几何,供大家参考。
《立体几何》
点线面三位一体,柱锥台球为代表。
距离都从点出发,角度皆为线线成。
垂直平行是重点,证明须弄清概念。
线线线面和面面、三对之间循环现。
方程思想整体求,化归意识动割补。
计算之前须证明,画好移出的图形。
立体几何辅助线,常用垂线和平面。
射影概念很重要,对于解题最关键。
异面直线二面角,体积射影公式活。
公理性质三垂线,解决问题一大片。
上面的高三数学二轮复习口诀:立体几何,对于大家的复习非常有帮助,希望大家好好利用。
s();
【立体几何高三数学二轮复习口诀】。
立体几何大二轮复习的策略

立体几何的解题思路四川省成都第七中学 张世永 巢中俊 周建波《高中数学课程标准》建议:立体几何教学应注意引导学生通过对实际模型的认识,学会将自然语言转化为图形语言和符号语言.教师可以使用具体的长方体的点、线、面关系作为载体,使学生在直观感知的基础上,认识空间中一般的点、线、面之间的位置关系;通过对图形的观察、实验和说明,使学生进一步了解平行、垂直关系的基本性质以及判定方法,学会准确地使用数学语言表述几何对象的位置关系,并能解决一些简单的推理论证及应用问题。
理科学生不仅要掌握必修2《立体几何初步》,还要掌握选修2-1《空间中的向量与立体几何》.文科学生要求掌握必修2《立体几何初步》,为了更好地解答立体几何问题,建议教师补充讲授选修2-1《空间中的向量与立体几何》中的坐标法,让文科学生能熟练地使用坐标法,而对空间中的向量的其它知识不做介绍,以免加重文科学生的负担。
另外,文科学生不要求掌握求二面角的问题。
一.求解空间三类角:两直线所成角、直线与平面所成角、二面角,关键是转化为空间两直线所成角,常常要借助于平面的法向量.要善于一题多变.例1.(1)已知直线b a ,所成角为o 60,经过空间中一点P 作直线l ,使直线l 与a 、b 所成角均为o 60,则这样的直线l 有几条解:经过点P 作直线m n m ,o 60ο120n m ,n m ,o 60n m ,ο30n m ,o 60o 60问题的推广:已知直线b a ,所成角为o 60,经过空间中一点P 作直线l ,使直线l 与a 、b 所成角均为θ,这样的直线l 有四条,则角θ应满足什么条件有两条呢有一条呢有零条呢 答案:有四条时,o o 9060<<θ;有两条时,o o 6030<<θ;有一条时,oo 90,30=θ;有零条时,οο300<<θ.变式:(1)已知直线a 与平面α所成角的大小为o 60,经过空间中一点P 作直线l ,使直线l 与直线a 和平面α所成角均为o 45,则这样的直线l 有几条(2)已知平面α与平面β所成锐二面角的大小为o 60,经过空间中一点P 作直线l ,使直线l 与平面α和平面β所成角均为o 60,则这样的直线l 有几条(3)正三棱锥P —ABC 中,CM=2PM ,CN=2NB ,对于以下结论: ①二面角B —PA —C 大小的取值范围是(3π,π);②若MN ⊥AM ,则PC 与平面PAB 所成角的大小为2π;③过点M 与异面直线PA 和BC 都成4π的直线有3条;④若二面角B —PA —C 大小为32π,则过点N 与平面PAC 和平面PAB 都成6π的直线有3条. 正确的序号是 .解:(1) 经过点P 作平面α的法向量n ,则问题转化为 “已知直线n a ,所成角为ο30或ο150,经过点P 作直线l ,使直线l 与n a ,所成角均为ο45,则这样的直线l 有几条”由例1容易得到这样的直线l 有两条.(2) 经过点P 作平面α的法向量m ,平面β的法向量n ,则问题转化为 “已知直线n m ,所成角为ο60或ο120,经过点P 作直线l ,使直线l 与n m ,所成角均为ο30,则这样的直线l 有几条”由例1容易得到这样的直线l 有一条.(3)仿照(1)(2)可以得到答案① ② ④二.高考中有较大部分题都可以转化为以正方体为背景的问题,为此新编以正方体为背景的系列题:相同条件为“正方体1111D C B A ABCD -棱长为1”. 1. 正方体1111D C B A ABCD -棱长为1,E,F 是BD 上的动点,且BD EF 21=. (1)当E 在BD 中点时,F 恰在B 点,求二面角11C EF B --大小; (2)当EF 在BD 上运动时,该二面角是否发生变化解:(1)取11D B 中点O,易知11EFB O C 面⊥,设二面角11C EF B --大小为θ.∴==∴,36cos 1EFC EFO S S ∆∆θ二面角11C EF B --大小为36arccos(2)由(1)中求二面角的方法可知,无论EF 在BD 上的什么位置,∴==∴,36cos 1EFC EFO S S ∆∆θ二面角11C EF B --的大小不变.2. 正方体1111D C B A ABCD -棱长为1,P 为11B A 的四等分点, Q 为11C D 中点,O 为平面B B AA 11的中心. (1)求证:OC 与PQ 共面;(2)求:平面OPQC 与平面B B AA 11的夹角. (1)证明:取11B A 中点H ,连结BH,HQ.易证CQ BH //,又HB A OP 1∆为中位线,CQ OP BH OP //,//∴∴OC 与PQ 共面.(2) 连结OQ,过O 作PQ OM ⊥,连结MHMHPQ OMH PQ PQ OM PQOH PHQ OH ⊥∴⊥∴⊥⊥∴⊥,,,面又面ΘOMH ∠为面OPQC 与面B B AA 11的夹角..217arctan .217tan ,1717,21,1,41=∠∴=∠∴====OMH OMH MH OH HQ PH三.高考中有一部分题都是以三棱柱为背景的问题,为此新编以三棱柱为背景的系列题.例3.斜三棱柱111C B A ABC -的底面是等腰三角形,AB=AC ,上底面的顶点1A 在下地面的射影是ABC ∆的外心,,3,1π=∠=AB A a BC 棱柱的侧面积为232a(1) 证明:侧面B B AA 11和C C AA 11为菱形,11BCC B 是矩形; (2) 求棱柱的侧面所成的三个二面角的大小; (3) 求棱柱的体积(1)证明:BC O A ABC O A ⊥∴⊥11,面Θ, 又ΘABC ∆的外心为O,AB=AC,BC AO =∴∴⊥⊥,,11BB BC AA BC Θ四边形11BCC B 是矩形.B A AA OB A Rt OA A Rt OB OA 1111,,=∴≅∴=∆∆Θ,又AB A AB A 11,60∆∴=∠ο为正三角形.∴四边形B B AA 11为菱形,同理,可证四边形C C AA 11为菱形.(2),0)3)(23(,3260sin 2,22=+-=+===a x a x a ax x S x AC AB 即侧οa x 332=∴过B 作BD 1AA ⊥,则D 为1AA 中点,1AA CD ⊥∴ 又ΘBCD BB CC AA AA BC ∆∴⊥,////,1111的三内角即为所求BCD BC CD a BD a AD ∆∴====,,33Θ为正三角形,∴三个二面角均为ο60 31126131,1312,131232,1213213a O A S V a O A a AO a S ABC ABC =⋅=∴===∆∆)( 或32161332433131a a a AA S V BCD =⨯⨯=⋅=∆ 四.高考中有一部分题都是以三棱锥为背景的问题,为此新编以三棱锥为背景的系列题. 例4.已知三棱锥P-ABC ,PAC ∆与PBC ∆ 都是边长为2的等腰三角形,AB=2,D 为AB 中点.(1) 求证PDC AB 面⊥;(2)求三棱锥P-ABC 体积. (1)证明:,2====PB PA CB AC Θ又D 为AB 中点,AB=2..AB D,DC PD ,,1PDC AB PD AB DC 平面又⊥∴=⊥=∴I(2),2==CB AC ΘD 为AB 中点,AB=2,.1,=⊥∴DC AB DC 同理,,,90,2,2,12PD PC PDC PC PC PD ⊥=∠∴=∴==即又ο.31=+=∴---PDC B PDC A ABC P V V V五.高考中的补形问题1.将正四面体补形成正方体解析:选A2.把三条棱相互垂直的三棱锥补成长(正)方体 例2 在球面上有四点,,,P A B C ,如果,,PA PB PC 两两互相垂直,且PA PB PC a ===,那么这个 球的表面积是解析:如图,把三棱锥P ABC -补形为一个棱长为 a 的正方体,则正方体的对角线即为球的直径,因为23R a =,所以2243S R a ππ==球表面积3.把对棱相等的四面体补成长方体例3 已知四面体SABC 的三组对棱相等,依次为25,13,5,求四面体的体积.解析:如图,把四面体S ABC -补形为长方体ADBE GSHC -,设长方体的长,宽,高分别为,,a b c ,则有222222222(25),(13),5a b b c c a +=+=+=,联立以上三式并解之得:4,2,3a b c ===,故111448323S ABC S ABD V V V abc abc abc --=-=-⨯⨯==长方体4.把三棱锥补成四棱锥(或三棱柱或平行六面体) 例4 在四面体ABCD 中,设1,3AB CD ==,直线AB与CD 的距离为2,夹角为3π,则四面体的体积等于解法1 如图,将四面体ABCD 补成四棱锥A BDCE -,且//,BE CD BE CD =,则2,333ABE BE ππ∠==或, //CD ABE 平面,所以CD 与AB 的距离即为CD 到平面ABE的距离,亦即C 到平面ABE 的距离也就是三棱锥C ABE -的高2h =所以11112sin 33232A BCD A BEC C ABE ABE V V V h S AB BE π---∆===⋅=⨯⨯⨯⨯⨯=解法2 如图,把四面体ABCD 补成三棱柱ABE FCD -,则面//ABE面,//CDF AB CF ,且1CF =,则AB 与CD 的距离就是平面ABE 与 平面FCD 的距离,即三棱柱的高2h =,且233DCF ππ∠=或. 所以13sin2232FCD V S h CD CF π∆=⋅=⨯⨯⨯⨯=柱,故四面体的体积为1132V =柱解法3 如图6,把四面体ABCD 补成平行六面体, 则四面体的体积是平行六面体体积的13. 1313sin 2232V S h π=⋅=⨯⨯⨯⨯=平行六面体底,故四面体的体积为12.结论:在四面体ABCD 中,设,AB a CD b ==, 直线AB 与CD 的距离为h ,夹角为θ,则 四面体的体积为1sin 6V abh θ=5.把首尾相连两两垂直的三棱锥补成长(正)方体 例5 如图,,90PA ABC ACB ⊥∠=o平面,且PA AC BC a ===,则异面直线PB 与AC 所成角的正切值为解析:把四面体P ABC -补成正方体,//AC DB ∴设异面直线PB 与AC 所成角为θ,要求异面直线PB 与AC 所成角正切值, 即求PB 与DB 所成角的正切值,2tan 2PD aDB θ===6.把四棱锥补成长(正)方体例6 如图,四棱锥S ABCD -的底面是边长为1的正方形,SD 垂直于底面,3ABCD SB =.(1)求证:BC SC ⊥;(2)求面ASD 与面BSC 所成二面角大小.证与解:因为1AB BC ==,所以1SD =,故可把原四棱锥补成长方体111ABCD A B C S - (1)因为1BC SDCC ⊥面,所以BC SC ⊥ (2)连1A B ,则面ASD 与面BSC 所成的二面角, 即为面1ADSA 与1BCSA 所成的二面角.因为11,A S SD A S SC ⊥⊥,所以CSD ∠为所求二面角 的平面角,45CSD ∠=o,故所求二面角为45o.例7 如图,在四棱锥P ABCD -中,底面ABCD 为矩形,侧棱,PA ABCD ⊥底面3,AB =1,BC =2PA =,求直线AC 与PB 所成角的余弦值.解析:如图9所示,把四棱锥P ABCD -补成长方体111PB C D ABCD -,连结11,//,PC PC AC 所以1BPC ∠为AC 与PB 所成的角,连结1,BC 在1PBC ∆中, 由余弦定理可得:157cos BPC ∠=故直线AC 与PB 所成角的余弦值为57147.把相互垂直的两长(正)方形补成长(正)方体 例8 如图,已知正方形ABCD 和矩形ACEF 所在的 平面互相垂直,2,1,AB AF M ==是线段EF 的中点.(1)求证://AM 平面BDE ;(2)求二面角A DF B --的大小.解析:如图,将原几何体补成长方体11ABCD FB ED - (1)设AC 与BD 的交点为O ,连结OE ,则易知 //OE AM ,故//AM 平面BDE(2)由长方体的性质知,1BA ADD F ⊥面,过A 作AG DF ⊥,连BG ,则BG DF ⊥,所以AGB ∠为所求二面角的平面角,在Rt AGB ∆中,易求60AGB ∠=o8.把三棱柱补成四棱柱例9 如图,在直三棱柱111ABC A B C -中,3,4,AC BC ==15,4AB AA ==,求异面直线1AC 与1B C 所成角的余弦值.解:由条件知AC CB ⊥,如图,把直三棱柱111ABC A B C -补成长方体1111ABCD A B C D -,连结1B D ,则11//B D AC , 且11B D AC =,所以1DB C ∠为1AC 与1B C 所成角(或其补角), 连结CD ,在1B CD ∆中,115,5,42CD B D BC ===, 由余弦定理得122cos 5DB C ∠=六.考试模式例1.(理科)已知正四棱锥S ABCD -所有棱长为4,E 是侧棱SC 上一点,且1SE =,过点E 垂直于SC 的平面截该正四棱锥,则该平面与这个正四棱锥的截面面积为( )(A )82 (B )2 (C )52 (D )42答案 C(文科)已知正三棱锥S ABC -所有棱长为4,E 是侧棱SC 上一点,且1SE =,过点E 垂直于SC 的平面截该正三棱锥,则该平面与这个正三棱锥的截面面积为( ) (A )22 (B )322(C )2 (D )2 答案 C例 2..某三棱锥的三视图如图所示,则该三棱锥的表面积是( )A 25+B 5C 45+D 225+ 答案 D例3. 具有公共y 轴的两个直角坐标平面α和β所成的二面角βα轴-y -等于︒60,已知β内的曲线C '的方程是24y x '=,曲线C '在α内的射影在平面α内的曲线方程为22y px =,则p =_____________答案 4例4.如图,直角三角形ABC 中,60,BAC ∠=o点F 在斜边AB 上,且4,,AB AF D E =是平面ABC 同一侧的两点,AD ⊥平面,ABC BE ⊥平面,ABC 3, 4.AD AC BE ===⑴ 求证:平面CDF ⊥平面;CEF⑵(理科) 点M 在线段BC 上,且二面角F DM C --的余弦值为25,求CM 的长度.⑵ (文科)点M 在线段BC 上,异面直线CF 与EM 所成角的余弦值为1,4求CM 的长.证明:(Ⅰ)∵直角三角形ABC 中,∠BAC=60°,AC=4, ∴AB=8,AF=AB=2,由余弦定理得CF=2且CF ⊥AB .∵AD ⊥平面ABC ,CF ⊂平面ABC ,∴AD ⊥CF ,又AD∩AB=A ,∴CF ⊥平面DABE , ∴CF ⊥DF ,CF ⊥EF .∴∠DFE 为二面角D ﹣CF ﹣E 的平面角. 又AF=2,AD=3,BE=4,BF=6,故Rt △ADF ∽Rt △BFE .∴∠ADF=∠BFE ,∴∠AFD+∠BFE=∠AFD+∠ADF=90°, ∴∠DFE=90°,D ﹣CF ﹣E 为直二面角.∴平面CDF ⊥平面CEF . (建系求解,只要答案正确,也给分)解:(2)(理科)以C 为坐标原点,建立如图所示的空间直角坐标系C ﹣xyz ,设CM x =(0,0,0),(0,,0),(4,0,3),(3,3,0)C M x D F ∴(4,,3);(1,3,3)DM x DF =--=--u u u u r u u u r则面DMF 的法向量:43(3,3,)3x m x -=-u r同理可知:面CDM 的法向量(3,0,4)n =-r由2|cos ,|5m n <>=u r r ,则139343x = 或3x =经检验,3x =时二面角F DM C --的余弦值为25-不合题意 所以139343CM =(2)(文科)以C 为坐标原点,建立如图所示的空间直角坐标系C ﹣xyz , 则C (0,0,0),B (0,4,0),E (0,4,4),F (3,,0),M (0,a ,0),(0≤a≤4) ∴=(3,,0),=(0,a ﹣4,﹣4),∵异面直线CF 与EM 所成角的余弦值为,∴cos ,CF EM =u u u r u u u u r=,解得83163()a a ==或舍 故83.3CM =例5.(理科)如图,矩形ABEF 所在的平面与等边ABC ∆所在的平面垂直,22AB AF ==,O 为AB 的中点.(1)求证:OE FC ⊥;(2)求二面角F CE B --的余弦值.(I )证:连接OC ,OF ,因为AC BC =,O 是AB 的中点,故OC AB ⊥. …1分 又因为平面ABEF ⊥平面ABC ,面ABEF ⋂面ABC AB =,OC ⊂面ABC ,故OC ⊥平面ABEF . …………………2分 因为OE ⊂面ABEF ,于是OC OE ⊥. ……………………3分又矩形ABEF ,22AB AF ==,所以OF OE ⊥. ……………4分 又因为OF OC O ⋂=,故OE ⊥平面OFC , ………………5分所以OE FC ⊥. ………………6分(Ⅱ)由(I )得,22AB AF ==,取EF 的中点D ,以O 为原点,,,OC OB OD 所在的直线分别为,,x y z 轴,建立空间直角坐标系。
高三数学二轮专题复习教案――立体几何
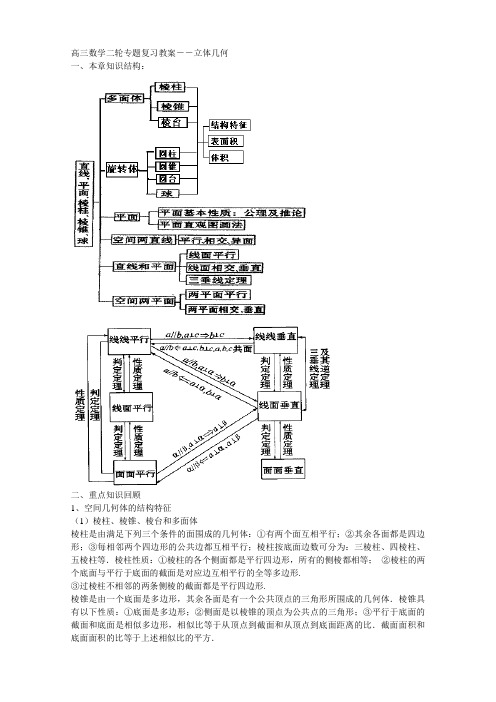
高三数学二轮专题复习教案――立体几何一、本章知识结构:二、重点知识回顾1、空间几何体的结构特征(1)棱柱、棱锥、棱台和多面体棱柱是由满足下列三个条件的面围成的几何体:①有两个面互相平行;②其余各面都是四边形;③每相邻两个四边形的公共边都互相平行;棱柱按底面边数可分为:三棱柱、四棱柱、五棱柱等.棱柱性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等;②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等多边形.③过棱柱不相邻的两条侧棱的截面都是平行四边形.棱锥是由一个底面是多边形,其余各面是有一个公共顶点的三角形所围成的几何体.棱锥具有以下性质:①底面是多边形;②侧面是以棱锥的顶点为公共点的三角形;③平行于底面的截面和底面是相似多边形,相似比等于从顶点到截面和从顶点到底面距离的比.截面面积和底面面积的比等于上述相似比的平方.棱台是棱锥被平行于底面的一个平面所截后,截面和底面之间的部分.由棱台定义可知,所有侧棱的延长线交于一点,继而将棱台还原成棱锥.多面体是由若干个多边形围成的几何体.多面体有几个面就称为几面体,如三棱锥是四面体.(2)圆柱、圆锥、圆台、球分别以矩形的一边,直角三角形的一直角边,直角梯形垂直于底边的腰所在的直线,半圆以它的直径所在直线为旋转轴,旋转一周而形成的几何体叫做圆柱、圆锥、圆台、球圆柱、圆锥和圆台的性质主要有:①平行于底面的截面都是圆;②过轴的截面(轴截面)分别是全等的矩形、等腰三角形、等腰梯形;③圆台的上底变大到与下底相同时,可以得到圆柱;圆台的上底变小为一点时,可以得到圆锥.2、空间几何体的侧面积、表面积(1)棱柱侧面展开图的面积就是棱柱的侧面积,棱柱的表面积就是它的侧面积与两底面面积的和.因为直棱柱的各个侧面都是等高的矩形,所以它的展开图是以棱柱的底面周长与高分别为长和宽的矩形.如果设直棱柱底面周长为c,高为h,则侧面积S ch=侧.若长方体的长、宽、高分别是a、b、c,则其表面积2() S ab bc ca=++表.(2)圆柱的侧面展开图是一个矩形.矩形的宽是圆柱母线的长,矩形的长为圆柱底面周长.如果设圆柱母线的长为l,底面半径为r,那么圆柱的侧面积2πS rl=侧,此时圆柱底面面积2πS r=底.所以圆柱的表面积222π2π2π()S S S rl r r r l=+=+=+侧底.(3)圆锥的侧面展开图是以其母线为半径的扇形.如果设圆锥底面半径为r,母线长为l,则侧面积πS rl=侧,那么圆锥的表面积是由其侧面积与底面面积的和构成,即为2πππ()S S S rl r r r l=+=+=+侧底.(4)正棱锥的侧面展开图是n个全等的等腰三角形.如果正棱锥的周长为c,斜高为h',则它的侧面积12S ch'=侧.(5)正棱台的侧面积就是它各个侧面积的和.如果设正棱台的上、下底面的周长是c c',,斜高是h',那么它的侧面积是12S ch'=侧.(6)圆台侧面展开图是以截得该圆台的圆锥母线为大圆半径,圆锥与圆台的母线之差为小圆半径的一个扇环.如果设圆台的上、下底面半径分别为r r',,母线长为l,那么它的侧面积是π()S r r l'=+侧.圆台的表面积等于它的侧面积与上、下底面积的和,即2222π()πππ() S S S S r r l r r r r r l rl''''=++=+++=+++侧上底下底.(7)球的表面积24πS R =,即球的表面积等于其大圆面积的四倍.3、空间几何体的体积(1)柱体(棱柱、圆柱)的体积等于它的底面积S 和高h 的积,即V Sh=柱体.其中底面半径是r ,高是h 的圆柱的体积是2πV r h=圆柱.(2)如果一个锥体(棱锥、圆锥)的底面积是S ,高是h ,那么它的体积是13V Sh=锥体.其中底面半径是r ,高是h 的圆锥的体积是21π3V r h=圆锥,就是说,锥体的体积是与其同底等高柱体体积的13.(3)如果台体(棱台、圆台)的上、下底面积分别是S S ',,高是h,那么它的体积是1()3V S S h=+台体.其中上、下底半径分别是r R ,,高是h 的圆台的体积是221π()3V r Rr R h=++圆台.(4)球的体积公式:334R V π=.4、中心投影和平行投影(1)中心投影:投射线均通过投影中心的投影。
关于立体几何复习的几点建议
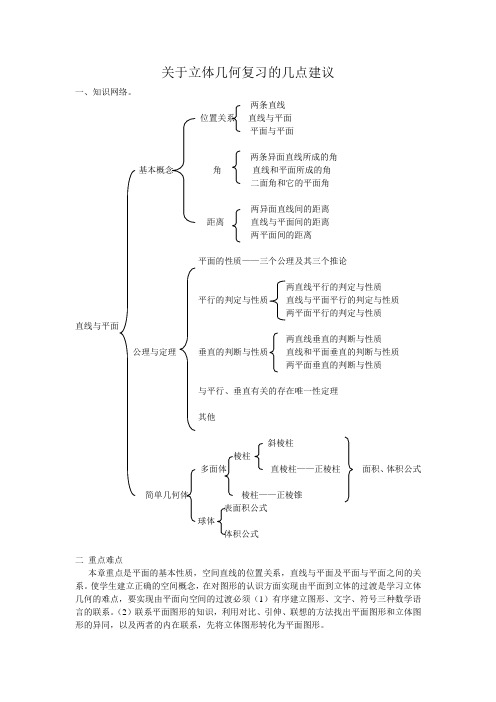
关于立体几何复习的几点建议一、知识网络。
两条直线位置关系直线与平面平面与平面两条异面直线所成的角基本概念角直线和平面所成的角二面角和它的平面角两异面直线间的距离距离直线与平面间的距离两平面间的距离平面的性质——三个公理及其三个推论两直线平行的判定与性质平行的判定与性质直线与平面平行的判定与性质两平面平行的判定与性质直线与平面两直线垂直的判断与性质公理与定理垂直的判断与性质直线和平面垂直的判断与性质两平面垂直的判断与性质与平行、垂直有关的存在唯一性定理其他斜棱柱棱柱多面体直棱柱——正棱柱面积、体积公式简单几何体棱柱——正棱锥表面积公式球体体积公式二重点难点本章重点是平面的基本性质,空间直线的位置关系,直线与平面及平面与平面之间的关系。
使学生建立正确的空间概念,在对图形的认识方面实现由平面到立体的过渡是学习立体几何的难点,要实现由平面向空间的过渡必须(1)有序建立图形、文字、符号三种数学语言的联系。
(2)联系平面图形的知识,利用对比、引伸、联想的方法找出平面图形和立体图形的异同,以及两者的内在联系,先将立体图形转化为平面图形。
三 命题研究本章高考命题形式比较稳定,主要考查线线、线面、面面的平行与垂直,及空间角和距离的计算,及面积、体积的计算,着重考查学生的空间想象能力,近年来在传统题型的基础上,进行了一些改革,出现了开放题型及探索性题型,考查了学生综合运用知识的能力。
四 复习建议(一)、立足课本,重点突出在复习中,首先要夯实概念,弄清概念的内含和外延,其次定理的内容是什么及怎样运用这些定理,再把这些知识网络化,把知识转化为能力。
在高考试题中,常出现考查学生对概念及定理的理解和运用。
例1(05全国Ⅰ)在正方形''''D C B A ABCD 中,过对角线'BD 的一个平面交'AA 于E ,交'CC 于F ,则① 四边形E BFD '一定是平行四边形 ② 四边形E BFD '有可能是正方形③ 四边形E BFD '在底面ABCD 内的投影一定是正方形 ④ 四边形E BFD '有可能垂直于平面D BB '以上结论正确的为 ①③④ 。
2022年高考数学第二轮几何复习建议

所以 VA BCD
VABEC
VC ABE
1 3
h
SABE
1 2 1 AB BE sin
32
3
1 2
解法 2 如图,把四面体 ABCD补成三棱柱 ABE FCD ,则面 ABE / /
面 CDF, AB / /CF ,且 CF 1,则 AB 与 CD 的距离就是平面 ABE 与
平面 FCD的距离,即三棱柱的高 h 2 ,且 DCF 或 2 .
二. 加强对三视图、体积和表面积的复习 在立体几何中,几何体的表面积和体积是几何问题中两个最
基本的量,常常会结合三视图考查,比如说给出三视图求体积或 表面积,如果学生不能够根据三视图想象出该几何体的实际形状, 那么也很难求出体积和表面积。有时也会有根据几何体得出三视 图的题型。学生在平时的学习中就要注重几何体的空间与平面三 视图的不同表示方法,增强空间想象能力。
BGHC B1G1H1C1 ,在 GH 上取一点 F1 ,使 GF1 1 ,
连结 EF1, C1F1 ,则 D1F / /C1F1, EC1F1 为 EC1 与 FD1 所成角(或其补角)
在 EC1F1 中,由余弦定理易得 cos EC1F1
21 14
例 13 在梯形 ABCD 中, ABC , AD / /BC, BC 2AD 2AB 2 ,
直线 AB 与 CD 的距离为 h ,夹角为 ,则
四面体的体积为V 1 abh sin
6
5.把首尾相连两两垂直的三棱锥补成长(正)方体
例 5 如图, PA 平面ABC, ACB 90 ,且
PA AC BC a ,则异面直线 PB 与 AC 所
成角的正切值为 解析:把四面体 P ABC 补成正方体,
高考数学冲刺复习立体几何考点攻略

高考数学冲刺复习立体几何考点攻略高考数学中,立体几何一直是重要的考点之一,也是许多同学感到棘手的部分。
在冲刺复习阶段,掌握立体几何的核心考点和解题方法,对于提高成绩至关重要。
接下来,就让我们一起深入探讨立体几何的考点攻略。
一、空间几何体的结构特征首先,要清晰地理解常见空间几何体的结构特征,如棱柱、棱锥、棱台、圆柱、圆锥、圆台和球。
了解它们的定义、性质以及图形特点。
棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行。
棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形。
棱台:用一个平行于棱锥底面的平面去截棱锥,截面与底面之间的部分。
圆柱:以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体。
圆锥:以直角三角形的一条直角边为旋转轴,旋转一周所形成的曲面所围成的几何体。
圆台:用一个平行于圆锥底面的平面去截圆锥,截面与底面之间的部分。
球:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体。
对于这些几何体,要能够通过直观图和三视图准确判断其结构特征,并且能够计算它们的表面积和体积。
二、空间点、线、面的位置关系这是立体几何的基础,包括线线、线面、面面的位置关系。
线线位置关系:平行、相交、异面。
线面位置关系:线在面内、线面平行、线面相交。
面面位置关系:平行、相交。
要熟练掌握这些位置关系的判定定理和性质定理,例如线面平行的判定定理、面面垂直的性质定理等。
同时,要能够运用这些定理进行推理和证明。
三、直线与平面平行、垂直的判定与性质直线与平面平行的判定方法:(1)利用定义:直线与平面没有公共点。
(2)判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
(3)平面与平面平行的性质:如果两个平面平行,那么一个平面内的任意一条直线都平行于另一个平面。
直线与平面平行的性质:(1)一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
浅谈立体几何教学的复习策略探究

浅谈立体几何教学的复习策略探究
立体几何是数学中的一个重要分支,它是指研究立体几何形体
的属性和关系,并通过数学语言来表示和计算。
在立体几何教学中,复习角度有很多,可以从以下几个方面入手。
一、基础概念回顾
立体几何的基本概念包括立体图形的构成要素、几何体的公式
和性质、空间平面的性质等。
在复习时,可以通过做练习题的方式
来回顾这些知识点,并注意理解其中的关系和联系。
二、立体几何证明方法和技巧
在立体几何的证明过程中,往往需要运用相关的证明方法和技巧,如勾股定理、相似三角形的性质、平行直线截立体的性质等。
复习时可以针对这些内容进行系统、全面的梳理,同时结合实际例
题进行讲解和分析。
三、应用题练习
在课程中,应用题占据了很大的比重。
因此,复习时需要重点
关注应用题。
对于不熟悉的应用题,建议先分析题目,找到解题方法,并且在熟悉之后要多做类似题目进行练习。
四、思维拓展
从立体几何的角度出发,可以帮助学生开拓思维,具体包括建模、推导和综合运用等。
在复习时,可以针对这些内容进行较为深
入的思考,探究如何运用立体几何的知识去解决实际问题。
总之,立体几何的复习策略应该是多维度、多方面的。
只有全
面系统、深入地理解了相关知识点,才能更好地解决应用问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何的解题思路四川省成都第七中学 张世永 巢中俊 周建波《高中数学课程标准》建议:立体几何教学应注意引导学生通过对实际模型的认识,学会将自然语言转化为图形语言和符号语言.教师可以使用具体的长方体的点、线、面关系作为载体,使学生在直观感知的基础上,认识空间中一般的点、线、面之间的位置关系;通过对图形的观察、实验和说明,使学生进一步了解平行、垂直关系的基本性质以及判定方法,学会准确地使用数学语言表述几何对象的位置关系,并能解决一些简单的推理论证及应用问题。
理科学生不仅要掌握必修2《立体几何初步》,还要掌握选修2-1《空间中的向量与立体几何》.文科学生要求掌握必修2《立体几何初步》,为了更好地解答立体几何问题,建议教师补充讲授选修2-1《空间中的向量与立体几何》中的坐标法,让文科学生能熟练地使用坐标法,而对空间中的向量的其它知识不做介绍,以免加重文科学生的负担。
另外,文科学生不要求掌握求二面角的问题。
一.求解空间三类角:两直线所成角、直线与平面所成角、二面角,关键是转化为空间两直线所成角,常常要借助于平面的法向量.要善于一题多变.例1.(1)已知直线b a ,所成角为o 60,经过空间中一点P 作直线l ,使直线l 与a 、b 所成角均为o 60,则这样的直线l 有几条?解:经过点P 作直线m//a, n//b, 则直线n m ,所成角为o 60或 120, 点P 作直线n m ,的两条角平分线,其中有一条与n m ,所成角均为o 60,另一条与n m ,所成角均为 30,把这条角平分线沿着点P 旋转可以得到两条直线与n m ,所成角均为o 60,从而与a 、b 所成角均为o 60的直线有三条.问题的推广:已知直线b a ,所成角为o 60,经过空间中一点P 作直线l ,使直线l 与a 、b 所成角均为θ,这样的直线l 有四条,则角θ应满足什么条件?有两条呢?有一条呢?有零条呢?答案:有四条时,o o 9060<<θ;有两条时,o o 6030<<θ;有一条时,oo90,30=θ;有零条时, 300<<θ.变式:(1)已知直线a 与平面α所成角的大小为o 60,经过空间中一点P 作直线l ,使直线l 与直线a 和平面α所成角均为o 45,则这样的直线l 有几条?(2)已知平面α与平面β所成锐二面角的大小为o 60,经过空间中一点P 作直线l ,使直线l 与平面α和平面β所成角均为o 60,则这样的直线l 有几条?(3)正三棱锥P —ABC 中,CM=2PM ,CN=2NB ,对于以下结论: ①二面角B —PA —C 大小的取值范围是(3π,π);②若MN ⊥AM ,则PC 与平面PAB 所成角的大小为2π;③过点M 与异面直线PA 和BC 都成4π的直线有3条;④若二面角B —PA —C 大小为32π,则过点N 与平面PAC 和平面PAB 都成6π的直线有3条. 正确的序号是 .解:(1) 经过点P 作平面α的法向量n ,则问题转化为 “已知直线n a ,所成角为 30或150,经过点P 作直线l ,使直线l 与n a ,所成角均为 45,则这样的直线l 有几条?”由例1容易得到这样的直线l 有两条.(2) 经过点P 作平面α的法向量m ,平面β的法向量n ,则问题转化为 “已知直线n m ,所成角为 60或 120,经过点P 作直线l ,使直线l 与n m ,所成角均为 30,则这样的直线l 有几条?”由例1容易得到这样的直线l 有一条.(3)仿照(1)(2)可以得到答案① ② ④二.高考中有较大部分题都可以转化为以正方体为背景的问题,为此新编以正方体为背景的系列题:相同条件为“正方体1111D C B A ABCD -棱长为1”. 1. 正方体1111D C B A ABCD -棱长为1,E,F 是BD 上的动点,且BD EF 21=. (1)当E 在BD 中点时,F 恰在B 点,求二面角11C EF B --大小; (2)当EF 在BD 上运动时,该二面角是否发生变化?解:(1)取11D B 中点O,易知11EFB O C 面⊥,设二面角11C EF B --大小为θ.∴==∴,36cos 1EFC EFO S S ∆∆θ二面角11C EF B --大小为36arccos(2)由(1)中求二面角的方法可知,无论EF 在BD 上的什么位置,∴==∴,36cos 1EFC EFO S S ∆∆θ二面角11C EF B --的大小不变.2. 正方体1111D C B A ABCD -棱长为1,P 为11B A 的四等分点, Q 为11C D 中点,O 为平面B B AA 11的中心.(1)求证:OC 与PQ 共面;(2)求:平面OPQC 与平面B B AA 11的夹角. (1)证明:取11B A 中点H ,连结BH,HQ.易证CQ BH //,又HB A OP 1∆为中位线,CQ OP BH OP //,//∴∴OC 与PQ 共面.(2) 连结OQ,过O 作PQ OM ⊥,连结MHMHPQ OMH PQ PQ OM PQOH PHQ OH ⊥∴⊥∴⊥⊥∴⊥,,,面又面OMH ∠为面OPQC 与面B B AA 11的夹角..217arctan .217tan ,1717,21,1,41=∠∴=∠∴====OMH OMH MH OH HQ PH三.高考中有一部分题都是以三棱柱为背景的问题,为此新编以三棱柱为背景的系列题.例3.斜三棱柱111C B A ABC -的底面是等腰三角形,AB=AC ,上底面的顶点1A 在下地面的射影是ABC ∆的外心,,3,1π=∠=AB A a BC 棱柱的侧面积为232a(1) 证明:侧面B B AA 11和C C AA 11为菱形,11BCC B 是矩形; (2) 求棱柱的侧面所成的三个二面角的大小; (3) 求棱柱的体积(1)证明:BC O A ABC O A ⊥∴⊥11,面 , 又 ABC ∆的外心为O,AB=AC,BC AO =∴∴⊥⊥,,11BB BC AA BC 四边形11BCC B 是矩形.B A AA OB A Rt OA A Rt OB OA 1111,,=∴≅∴=∆∆ ,又AB A AB A 11,60∆∴=∠ 为正三角形.∴四边形B B AA 11为菱形,同理,可证四边形C C AA 11为菱形.(2),0)3)(23(,3260sin 2,22=+-=+===a x a x a ax x S x AC AB 即侧a x 332=∴ 过B 作BD 1AA ⊥,则D 为1AA 中点,1AA CD ⊥∴ 又 BCD BB CC AA AA BC ∆∴⊥,////,1111的三内角即为所求BCD BC CD a BD a AD ∆∴====,,33为正三角形,∴三个二面角均为 60 31126131,1312,131232,1213213a O A S V a O A a AO a S ABC ABC =⋅=∴===∆∆)( 或32161332433131a a a AA S V BCD =⨯⨯=⋅=∆ 四.高考中有一部分题都是以三棱锥为背景的问题,为此新编以三棱锥为背景的系列题. 例4.已知三棱锥P-ABC ,PAC ∆与PBC ∆ 都是边长为2的等腰三角形,AB=2,D 为AB 中点.(1) 求证PDC AB 面⊥;(2)求三棱锥P-ABC 体积. (1)证明:,2====PB PA CB AC 又D 为AB 中点,AB=2..AB D,DC PD ,,1PDC AB PD AB DC 平面又⊥∴=⊥=∴(2),2==CB AC D 为AB 中点,AB=2,.1,=⊥∴DC AB DC 同理,,,90,2,2,12PD PC PDC PC PC PD ⊥=∠∴=∴==即又.31=+=∴---PDC B PDC A ABC P V V V五.高考中的补形问题1.将正四面体补形成正方体解析:选A2.把三条棱相互垂直的三棱锥补成长(正)方体例2 在球面上有四点,,,P A B C,如果,,PA PB PC两两互相垂直,且PA PB PC a===,那么这个球的表面积是解析:如图,把三棱锥P ABC-补形为一个棱长为a的正方体,则正方体的对角线即为球的直径,因为23R a=,所以2243S R aππ==球表面积3.把对棱相等的四面体补成长方体例3 已知四面体SABC的三组对棱相等,依次为25,13,5,求四面体的体积.解析:如图,把四面体S ABC-补形为长方体ADBE GSHC-,设长方体的长,宽,高分别为,,a b c,则有222222222(25),(13),5a b b c c a+=+=+=,联立以上三式并解之得:4,2,3a b c===,故111448323 S ABC S ABDV V V abc abc abc --=-=-⨯⨯==长方体4.把三棱锥补成四棱锥(或三棱柱或平行六面体) 例4 在四面体ABCD中,设1,AB CD ==AB与CD 的距离为2,夹角为3π,则四面体的体积等于解法1 如图,将四面体ABCD 补成四棱锥A BDCE -,且//,BE CD BE CD =,则2,33ABE BE ππ∠==或//CD ABE 平面,所以CD 与AB 的距离即为CD 到平面ABE的距离,亦即C 到平面ABE 的距离也就是三棱锥C ABE -的高2h =所以11112sin 33232A BCD A BEC C ABE ABE V V V h S AB BE π---∆===⋅=⨯⨯⨯⨯⨯= 解法2 如图,把四面体ABCD 补成三棱柱ABE FCD -,则面//ABE面,//CDF AB CF ,且1CF =,则AB 与CD 的距离就是平面ABE 与 平面FCD 的距离,即三棱柱的高2h =,且233DCF ππ∠=或. 所以13sin2232FCD V S h CD CF π∆=⋅=⨯⨯⨯⨯=柱,故四面体的体积为1132V =柱解法3 如图6,把四面体ABCD 补成平行六面体, 则四面体的体积是平行六面体体积的13. 131sin 2232V S h π=⋅=⨯⨯=平行六面体底,故四面体的体积为12.结论:在四面体ABCD 中,设,AB a CD b ==, 直线AB 与CD 的距离为h ,夹角为θ,则 四面体的体积为1sin 6V abh θ=5.把首尾相连两两垂直的三棱锥补成长(正)方体 例5 如图,,90PA ABC ACB ⊥∠=平面,且PA AC BC a ===,则异面直线PB 与AC 所成角的正切值为解析:把四面体P ABC -补成正方体, //AC DB ∴设异面直线PB 与AC 所成角为θ,要求异面直线PB 与AC 所成角正切值, 即求PB 与DB 所成角的正切值,tan PD DB θ== 6.把四棱锥补成长(正)方体例6 如图,四棱锥S ABCD -的底面是边长为1的正方形,SD垂直于底面,ABCD SB =.(1)求证:BC SC ⊥;(2)求面ASD 与面BSC 所成二面角大小. 证与解:因为1AB BC ==,所以1SD =,故可把原四棱锥补成长方体111ABCD A B C S - (1)因为1BC SDCC ⊥面,所以BC SC ⊥ (2)连1A B ,则面ASD 与面BSC 所成的二面角, 即为面1ADSA 与1BCSA 所成的二面角.因为11,A S SD A S SC ⊥⊥,所以CSD ∠为所求二面角 的平面角,45CSD ∠=,故所求二面角为45.例7 如图,在四棱锥P ABCD -中,底面ABCD 为矩形,侧棱,PA ABCD ⊥底面AB =1,BC =2PA =,求直线AC 与PB 所成角的余弦值.解析:如图9所示,把四棱锥P ABCD -补成长方体111PB C D ABCD -,连结11,//,PC PC AC 所以1BPC ∠为AC 与PB 所成的角,连结1,BC 在1PBC ∆中,由余弦定理可得:1cos 14BPC ∠=故直线AC 与PB7.把相互垂直的两长(正)方形补成长(正)方体 例8 如图,已知正方形ABCD 和矩形ACEF 所在的平面互相垂直,1,AB AF M ==是线段EF 的中点.(1)求证://AM 平面BDE ;(2)求二面角A DF B --的大小.解析:如图,将原几何体补成长方体11ABCD FB ED - (1)设AC 与BD 的交点为O ,连结OE ,则易知 //OE AM ,故//AM 平面BDE(2)由长方体的性质知,1BA ADD F ⊥面,过A 作AG DF ⊥,连BG ,则BG DF ⊥,所以AGB ∠为所求二面角的平面角,在Rt AGB ∆中,易求60AGB ∠=8.把三棱柱补成四棱柱例9 如图,在直三棱柱111ABC A B C -中,3,4,AC BC ==15,4AB AA ==,求异面直线1AC 与1B C 所成角的余弦值.解:由条件知AC CB ⊥,如图,把直三棱柱111ABC A B C -补成长方体1111ABCD A B C D -,连结1B D ,则11//B D AC , 且11B D AC =,所以1DB C ∠为1AC 与1B C 所成角(或其补角), 连结CD ,在1B CD ∆中,115,5,CD B D BC ===由余弦定理得1cos 5DB C ∠=六.考试模式例1.(理科)已知正四棱锥S ABCD -所有棱长为4,E 是侧棱SC 上一点,且1SE =,过点E 垂直于SC 的平面截该正四棱锥,则该平面与这个正四棱锥的截面面积为( )(A )82 (B )62 (C )52 (D )42 答案 C(文科)已知正三棱锥S ABC -所有棱长为4,E 是侧棱SC 上一点,且1SE =,过点E 垂直于SC 的平面截该正三棱锥,则该平面与这个正三棱锥的截面面积为( ) (A )22 (B )322(C )2 (D )22 答案 C例2..某三棱锥的三视图如图所示,则该三棱锥的表面积是( )A 25+B 5C 45+D 225+ 答案 D例3. 具有公共y 轴的两个直角坐标平面α和β所成的二面角βα轴-y -等于︒60,已知β内的曲线C '的方程是24y x '=,曲线C '在α内的射影在平面α内的曲线方程为22y px =,则p =_____________答案 4例4.如图,直角三角形ABC 中,60,BAC ∠=点F 在斜边AB 上,且4,,AB AF D E =是平面ABC 同一侧的两点,AD ⊥平面,ABC BE ⊥平面,ABC 3, 4.AD AC BE ===⑴ 求证:平面CDF ⊥平面;CEF⑵(理科) 点M 在线段BC 上,且二面角F DM C --的余弦值为25,求CM 的长度. ⑵ (文科)点M 在线段BC 上,异面直线CF 与EM 所成角的余弦值为1,4求CM 的长.证明:(Ⅰ)∵直角三角形ABC 中,∠BAC=60°,AC=4, ∴AB=8,AF=AB=2,由余弦定理得CF=2且CF ⊥AB .∵AD ⊥平面ABC ,CF ⊂平面ABC ,∴AD ⊥CF ,又AD ∩AB=A ,∴CF ⊥平面DABE , ∴CF ⊥DF ,CF ⊥EF .∴∠DFE 为二面角D ﹣CF ﹣E 的平面角. 又AF=2,AD=3,BE=4,BF=6,故Rt △ADF ∽Rt △BFE .∴∠ADF=∠BFE ,∴∠AFD+∠BFE=∠AFD+∠ADF=90°, ∴∠DFE=90°,D ﹣CF ﹣E 为直二面角.∴平面CDF ⊥平面CEF . (建系求解,只要答案正确,也给分)解:(2)(理科)以C 为坐标原点,建立如图所示的空间直角坐标系C ﹣xyz ,设CM x =(0,0,0),(0,,0),(4,0,3),(3,3,0)C M x D F ∴(4,,3);(1,3,3)DM x DF =--=--则面DMF 的法向量:43(3,3,)x m x -=-同理可知:面CDM 的法向量(3,0,4)n =- 由2|cos ,|5m n <>=,则139343x = 或3x =经检验,3x =时二面角F DM C --的余弦值为25-不合题意 所以139343CM =(2)(文科)以C 为坐标原点,建立如图所示的空间直角坐标系C ﹣xyz , 则C (0,0,0),B (0,4,0),E (0,4,4),F (3,,0),M (0,a ,0),(0≤a ≤4) ∴=(3,,0),=(0,a ﹣4,﹣4),∵异面直线CF 与EM 所成角的余弦值为,∴cos ,CF EM ==,解得83163()33a a ==或舍 故CM =例5.(理科)如图,矩形ABEF 所在的平面与等边ABC ∆所在的平面垂直,22AB AF ==,O 为AB 的中点. (1)求证:OE FC ⊥;(2)求二面角F CE B --的余弦值.(I )证:连接,OF ,因为,是的中点,故. …1分 又因为平面平面,面面,面,故平面. …………………2分 因为OE ⊂面,于是OC OE ⊥. ……………………3分又矩形ABEF ,22AB AF ==,所以. ……………4分又因为,故平面, ………………5分所以. ………………6分(Ⅱ)由(I )得,22AB AF ==,取的中点,以为原点,所在的直线分别为轴,建立空间直角坐标系。
