2014年学生中考成绩证明
初中毕业证明模板

初中毕业证明模板
初中毕业证明。
尊敬的有关部门:
兹证明,本人XXX,系我校20XX届初中毕业生,于20XX年X月X日顺利
完成了学业,取得了初中毕业证书。
在此,特向有关部门提供如下证明:
一、学籍信息。
本人XXX,性别XX,出生年月XX年XX月XX日,身份证号码XXXXXXXXXXXXXXXXXX。
在我校就读期间,本人品学兼优,积极参加各项学校活动,表现优异,受到老师和同学的一致好评。
二、学业成绩。
在学业方面,本人努力学习,认真对待每一门课程,成绩优异。
在期末考试中,各科成绩均名列前茅,获得了优异的成绩。
在学校的各项考核评比中,本人也取得了突出的成绩,充分展现了自己的学习潜力和能力。
三、品德表现。
在品德方面,本人遵守校纪校规,积极参加社会实践活动,乐于助人,乐于奉献,受到老师和同学的一致好评。
在学校的各项评比中,本人也多次获得了先进个人、优秀学生干部等荣誉称号。
四、综合素质。
在校期间,本人不仅在学业上取得了优异的成绩,在各项综合素质方面也有所
突出。
积极参加各类文体活动,善于团结同学,勇于担当,是一名优秀的学生代表。
五、其他事项。
特此证明,本人为我校20XX届初中毕业生,学业成绩优异,品德表现良好,已取得初中毕业证书。
在此,恳请有关部门给予认可,并提供相关的证明文件。
谨此证明!
申请人,XXX。
XX年XX月XX日。
黄山区2014年初中毕业学业考试
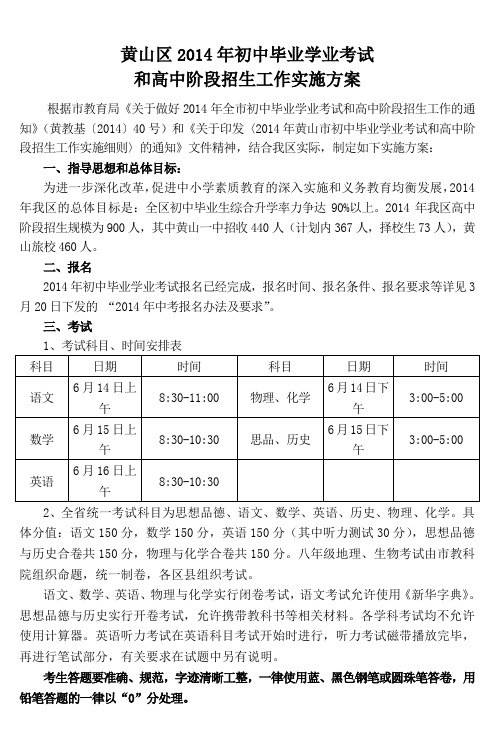
黄山区2014年初中毕业学业考试和高中阶段招生工作实施方案根据市教育局•关于做好2014年全市初中毕业学业考试和高中阶段招生工作的通知‣(黄教基…2014‟40号)和•关于印发†2014年黄山市初中毕业学业考试和高中阶段招生工作实施细则‡的通知‣文件精神,结合我区实际,制定如下实施方案:一、指导思想和总体目标:为进一步深化改革,促进中小学素质教育的深入实施和义务教育均衡发展,2014年我区的总体目标是:全区初中毕业生综合升学率力争达90%以上。
2014年我区高中阶段招生规模为900人,其中黄山一中招收440人(计划内367人,择校生73人),黄山旅校460人。
二、报名2014年初中毕业学业考试报名已经完成,报名时间、报名条件、报名要求等详见3月20日下发的“2014年中考报名办法及要求”。
三、考试1、考试科目、时间安排表2、全省统一考试科目为思想品德、语文、数学、英语、历史、物理、化学。
具体分值:语文150分,数学150分,英语150分(其中听力测试30分),思想品德与历史合卷共150分,物理与化学合卷共150分。
八年级地理、生物考试由市教科院组织命题,统一制卷,各区县组织考试。
语文、数学、英语、物理与化学实行闭卷考试,语文考试允许使用•新华字典‣。
思想品德与历史实行开卷考试,允许携带教科书等相关材料。
各学科考试均不允许使用计算器。
英语听力考试在英语科目考试开始时进行,听力考试磁带播放完毕,再进行笔试部分,有关要求在试题中另有说明。
考生答题要准确、规范,字迹清晰工整,一律使用蓝、黑色钢笔或圆珠笔答卷,用铅笔答题的一律以“0”分处理。
3、体育考试和物理、化学的实验操作考试由市教育局统一命题,由区教育局招考办负责组织考试。
凡回户籍所在地报考的应届毕业生,回报考地参加体育和理化实验操作考试。
体育总分值为40分;物理、化学实验操作考试由考生抽签考一科,总分值为15分。
4、听力残障学生(500HZ、1000HZ、2000HZ、4000HZ的纯音听力检测结果为每侧耳的平均听力损失均等于或大于40分贝<HL>),凭医院证明材料,学校审核并报招生主管部门批准后可免试英语听力。
四川省成都市嘉祥外国语学校2024年九年级数学第一学期开学达标测试试题【含答案】

四川省成都市嘉祥外国语学校2024年九年级数学第一学期开学达标测试试题题号一二三四五总分得分A 卷(100分)一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、(4分)下列函数中,y 随x 的增大而减小的函数是()A . 3 y x=B .41y x =-C .2y x =--D .31y x =-2、(4分)下面有四个定理:①平行四边形的两组对边分别相等;②平行四边形的两组对角分别相等;③平行四边形的两组对边分别平行;④平行四边形的对角线互相平分;其逆命题正确的有()A .1个B .2个C .3个D .4个3、(4分)有一组数据7、11、12、7、7、8、11,下列说法错误的是()A .中位数是7B .平均数是9C .众数是7D .极差为54、(4分)在2(1)1y k x k =++-中,若y 是x 的正比例函数,则k 值为()A .1B .1-C .±1D .无法确定5、(4分)如图,一根木棍斜靠在与地面OM 垂直的墙面ON 上,设木棍中点为P ,若木棍A 端沿墙下滑,且B 沿地面向右滑行.在此滑动过程中,点P 到墙角点O 的距离()A .不变B .变小C .变大D .先变大后变小6、(4分)2014年4月13日,某中学初三650名学生参加了中考体育测试,为了了解这些学生的体考成绩,现从中抽取了50名学生的体考成绩进行了分析,以下说法正确的是()A .这50名学生是总体的一个样本B .每位学生的体考成绩是个体C .50名学生是样本容量D .650名学生是总体7、(4分)长春市某服装店销售夏季T 恤衫,试销期间对4种款式T 恤衫的销售量统计如下表:款式A B C D 销售量/件1851该店老板如果想要了解哪种款式的销售量最大,那么他应关注的统计量是()A .平均数B .众数C .中位数D .方差8、(4分)甲、乙是两个不透明的纸箱,甲中有三张标有数字14,12,1的卡片,乙中有三张标有数字1,2,3的卡片,卡片除所标数字外无其他差别,现制定一个游戏规则:从甲中任取一张卡片,将其数字记为a ,从乙中任取一张卡片,将其数字记为b .若a ,b 能使关于x 的一元二次方程210ax bx ++=有两个不相等的实数根,则甲获胜;否则乙获胜.则乙获胜的概率为()A .23B .59C .49D .13二、填空题(本大题共5个小题,每小题4分,共20分)9、(4分)某种细菌病毒的直径为0.00005米,0.00005米用科学记数法表示为______米.10、(4分)在平面直角坐标系中,已知坐标()3, 1B ,将线段AB (第一象限)绕点O (坐标原点)按逆时针方向旋转90︒后,得到线段''A B ,则点'B 的坐标为____.11、(4分)如图,在△ABC 中,BC 的垂直平分线MN 交AB 于点D ,CD 平分∠ACB .若AD =2,BD =3,则AC 的长为_____.12、(4分)点P 在第四象限内,P 到轴的距离是3,到轴的距离是5,那么点P 的坐标为.13、(4分)分解因式:225ax a -=____________三、解答题(本大题共5个小题,共48分)14、(12分)在开任公路改建工程中,某工程段将由甲,乙两个工程队共同施工完成,据调查得知,甲,乙两队单独完成这项工程所需天数之比为2:3,若先由甲,乙两队合作30天,剩下的工程再由乙队做15天完成.(1)求甲、乙两队单独完成这项工程各需多少天?(2)此项工程由两队合作施工,甲队共做了m 天,乙队共做了n 天完成.已知甲队每天的施工费为15万元,乙队每天的施工费用为8万元,若工程预算的总费用不超过840万元,甲队工作的天数与乙队工作的天数之和不超过80天,请问甲、乙两队各工作多少天,完成此项工程总费用最少?最少费用是多少?15、(8分)某人购进一批琼中绿橙到市场上零售,已知卖出的绿橙数量x(千克)与售价y(元)的关系如下表:数量x(千克)12345…售价y(元)2+0.14+0.26+0.38+0.410+0.5…(1)写出售价y(元)与绿橙数量x(千克)之间的函数关系式;(2)这个人若卖出50千克的绿橙,售价为多少元?16、(8分)如图,在▱ABCD 中,E 、F 分别是BC 、AD 边上的点,且∠1=∠1.求证:四边形AECF 是平行四边形.17、(10分)如图,AB 是⊙O 的直径,AC ⊥AB ,E 为⊙O 上的一点,AC =EC ,延长CE 交AB 的延长线于点D .(1)求证:CE 为⊙O 的切线;(2)若OF ⊥AE ,OF =1,∠OAF =30°,求图中阴影部分的面积.(结果保留π)18、(10分)一水果店主分两批购进某一种水果,第一批所用资金为2400元,因天气原因,水果涨价,第二批所用资金是2700元,但由于第二批单价比第一批单价每箱多10元,以致购买的数量比第一批少25%.(1)该水果店主购进第一批这种水果的单价是多少元?(2)该水果店主计两批水果的售价均定为每箱40元,实际销售时按计划无损耗售完第一批后,发现第二批水果品质不如第一批,于是该店主将售价下降a %销售,结果还是出现了20%的损耗,但这两批水果销售完后仍赚了不低于1716元,求a 的最大值.B 卷(50分)一、填空题(本大题共5个小题,每小题4分,共20分)19、(4分)在比例尺为1∶100000的地图上,量得甲、乙两地的距离是15cm ,则两地的实际距离▲km.20、(4分)如图,△ABC 中,已知AB=8,∠C=90°,∠A=30°,DE 是中位线,则DE 的长为_____.21、(4分)若某组数据的方差计算公式是S 2=14[(7-x )+(4-x )2+(3-x )2+(6-x )2],则公式中x =______.22、(4分)在平面直角坐标系xoy 中,将点N ()1,2--绕点O 旋转180,得到的对应点的坐标是__________.23、(4分)已知关于x 的方程x 2-2ax +1=0有两个相等的实数根,则a =____.二、解答题(本大题共3个小题,共30分)24、(8分)如图,矩形ABCD 中,AB=2,BC=5,E 、P 分别在AD .BC 上,且DE=BP=1.连接BE,EC,AP,DP,PD 与CE 交于点F,AP 与BE 交于点H .(1)判断△BEC 的形状,并说明理由;(2)判断四边形EFPH 是什么特殊四边形,并证明你的判断;(3)求四边形EFPH 的面积.25、(10分)已知:直线l :y =2kx ﹣4k +3(k ≠0)恒过某一定点P .(1)求该定点P 的坐标;(2)已知点A 、B 坐标分别为(0,1)、(2,1),若直线l 与线段AB 相交,求k 的取值范围;(3)在0≤x ≤2范围内,任取3个自变量x 1,x 2、x 3,它们对应的函数值分别为y 1、y 2、y 3,若以y 1、y 2、y 3为长度的3条线段能围成三角形,求k 的取值范围.26、(12分)今年水果大丰收,A ,B 两个水果基地分别收获水果380件、320件,现需把这些水果全部运往甲、乙两销售点,从A 基地运往甲、乙两销售点的费用分别为每件40元和20元,从B 基地运往甲、乙两销售点的费用分别为每件15元和30元,现甲销售点需要水果400件,乙销售点需要水果300件.(1)设从A 基地运往甲销售点水果x 件,总运费为W 元,请用含x 的代数式表示W ,并写出x 的取值范围;(2)若总运费不超过18300元,且A 地运往甲销售点的水果不低于200件,试确定运费最低的运输方案,并求出最低运费.一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、C【解析】根据一次函数的性质,k<0,y随x的增大而减小,找出各选项中k值小于0的选项即可.【详解】解:A、B、D选项中的函数解析式k值都是正数,y随x的增大而增大,=--中,k=1-<0,y随x的增大而减少.C选项y x2故选:C.本题考查了一次函数的性质,主要利用了当k>0时,y随x的增大而增大;当k<0时,y 随x的增大而减小.2、D【解析】分别写出各个命题的逆命题,根据平行四边形的判定定理判断即可.【详解】解:平行四边形的两组对边分别相等的逆命题是两组对边分别相等的四边形是平行四边形,是真命题;平行四边形的两组对角分别相等的逆命题是两组对角分别相等的四边形是平行四边形,是真命题;平行四边形的两组对边分别平行的逆命题是两组对边分别平行的四边形是平行四边形,是真命题;平行四边形的对角线互相平分的逆命题是对角线互相平分的四边形是平行四边形,是真命题。
初中毕业证证明

初中毕业证证明初中毕业证证明(1)尊敬的有关部门:我谨向贵部门申请初中毕业证明。
我是XXX,于XXXX年在XXX学校完成了我的初中学业。
在我就读初中期间,我积极参与各项学习和活动。
我努力学习各门课程,并取得了良好的成绩。
同时,我也积极参与学校组织的各种社团和俱乐部活动,如学生会、篮球队等。
这些经历不仅让我获得了丰富的知识,还培养了我的领导能力和团队合作精神。
我还拥有良好的品德和行为表现。
我始终遵守学校的规章制度,尊敬师长,团结同学。
在班级中,我积极参与集体活动,为班级争光。
我也热心公益事业,曾参加过多次社区志愿者活动,为社会做出一份微薄的贡献。
通过这封申请信,我希望能够获得初中毕业证明。
这将是我进入高中的重要凭证,也是我人生中的重要里程碑。
我相信,拥有初中毕业证明将为我未来的学习和就业提供良好的基础。
再次感谢贵部门对我的关注和支持。
我期待着能够尽快获得初中毕业证明,并继续追求更高的学业成就。
此致敬礼!XXX初中毕业证证明(2)致 XXX 学校:本人系XXX学校的一名学生,现已顺利完成初中学业。
在此,我诚挚地请求贵校为我开具初中毕业证明,以备后续升学和就业之需。
我在初中阶段刻苦学习,全面发展。
我尊重师长,严守校规,努力完成各项学业任务。
同时,我也积极参与校内外的各种活动,包括文体比赛、社会实践等,不仅锻炼了自己的身心素质,还培养了团队协作精神和领导才能。
在学习方面,我始终保持良好的学习态度和学习成绩。
我努力掌握各门学科的知识,通过努力学习,取得了优异的成绩。
我也积极参加各类学科竞赛,并在其中获得了一些奖项。
这些成就是我努力学习和勤奋付出的结果。
我相信初中毕业证明将成为我未来升学和就业的重要凭据。
它将证明我已经完成了初中阶段的学业,具备了一定的学术水平和综合素质。
同时,它也将是我人生中的一个重要里程碑,标志着我即将迈入新的学习阶段。
再次感谢贵校对我教育的培养和关心。
我真诚希望能够尽快获得初中毕业证明,为我的未来铺就坚实的基础。
湖南省郴州市中考数学试卷含答案

湖南省郴州市中考数学试卷一、选择题(共8小题,每小题3分,满分24分)1.(2014年湖南郴州)﹣2的绝对值是()A.B.﹣C.2D.﹣2分析:根据负数的绝对值等于它的相反数解答.解:﹣2的绝对值是2,即|﹣2|=2.故选:C.点评:本题考查了绝对值的性质,一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.2.(2014年湖南郴州)下列实数属于无理数的是()A.0 B.πC.D.﹣分析:无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.解:A、是整数,是有理数,选项错误;B、正确;C、=3是整数,是有理数,选项错误;D、是分数,是有理数,选项错误.故选:B.点评:此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.3.(3分)(2014年湖南郴州)下列运算正确的是()A.3x﹣x=3 B.x2•x3=x5C.(x2)3=x5D.(2x)2=2x2考点:幂的乘方与积的乘方;合并同类项;同底数幂的乘法.分析:根据合并同类项,可判断A;根据同底数幂的乘法,可判断B;根据幂的乘方,可判断C;根据积的乘方,可判断D.解答:解:A、系数相减字母部分不变,故A错误;B、底数不变指数相加,故B正确;C、底数不变指数相乘,故C错误;D、积得乘方等于每个因式分别乘方,再把所得的幂相乘,故D错误;故选:B.点评:本题考查了幂的乘方与积的乘方,幂的乘方底数不变指数相乘.4.(3分)(2014年湖南郴州)已知圆锥的母线长为3,底面的半径为2,则圆锥的侧面积是()A.4πB.6πC.10π D.12π考点:圆锥的计算.专题:计算题.分析:根据锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算即可.解答:解:圆锥的侧面积=•2π•2•3=6π.故选:B.点评:本题考查了圆锥的计算:锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.5.(3分)(2014年湖南郴州)以下图形既是轴对称图形,又是中心对称图形的是()A.等腰三角形B.平行四边形C.矩形D.等腰梯形考点:中心对称图形;轴对称图形.分析:根据轴对称图形与中心对称图形的概念求解.解答:解:A、是轴对称图形,不是中心对称图形;B、是中心对称图形,不是轴对称图形;C、是中心对称图形,也是轴对称图形;D、不是中心对称图形,是轴对称图形.故选:C.点评:掌握好中心对称图形与轴对称图形的概念.判断轴对称图形的关键是寻找对称轴,图形两部分沿对称折叠后可重合,判断中心对称图形的关键是要寻找对称中心,旋转180度后与原图重合.6.(3分)(2014年湖南郴州)下列说法错误的是()A.抛物线y=﹣x2+x的开口向下B.两点之间线段最短C.角平分线上的点到角两边的距离相等D.一次函数y=﹣x+1的函数值随自变量的增大而增大考点:二次函数的性质;一次函数的性质;线段的性质:两点之间线段最短;角的概念.分析:根据二次函数的性质对A进行判断;根据线段公理对B进行判断;根据角平分线的性质对C进行判断;根据一次函数的性质对D进行判断.解答:解:A、由于a=﹣1<0,则抛物线开口向下,所以A选项的说法正确;B、两点之间线段最短,所以B选项的说法正确;C、角平分线上的点到角两边的距离相等,所以C选项的说法正确;D、当k=﹣1,y随x的增大而减小,所以D选项的说法错误.故选:D.点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(﹣,),对称轴直线x=﹣,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上;当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下.也考查了一次函数的性质、角平分线的性质和线段的性质.7.(3分)(2014年湖南郴州)平行四边形、矩形、菱形、正方形都具有的是()A.对角线互相平分B.对角线互相垂直C.对角线相等D.对角线互相垂直且相等考点:正方形的性质;平行四边形的性质;菱形的性质;矩形的性质.专题:证明题.分析:本题主要依据平行四边形、矩形、菱形、正方形都具有对角线相互平分的性质来判断.解答:解:A、对角线相等是平行四边形、矩形、菱形、正方形都具有的性质;B、对角线互相垂直是菱形、正方形具有的性质;C、对角线相等是矩形和正方形具有的性质;D、对角线互相垂直且相等是正方形具有的性质.故选:A.点评:本题主要考查平行四边形、矩形、菱形、正方形的性质定理.8.(3分)(2014年湖南郴州)我市某中学举办了一次以“我的中国梦”为主题的演讲比赛,最后确定7名同学参加决赛,他们的决赛成绩各不相同,其中李华已经知道自己的成绩,但能否进前四名,他还必须清楚这七名同学成绩的()A.众数B.平均数C.中位数D.方差考点:统计量的选择.分析:7人成绩的中位数是第4名的成绩.参赛选手要想知道自己是否能进入前4名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.解答:解:由于总共有7个人,且他们的分数互不相同,第5的成绩是中位数,要判断是否进入前4名,故应知道中位数的多少.故选:C.点评:此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.二、填空题(共8小题,每小题3分,满分24分)9.(3分)(2014年湖南郴州)根据相关部门统计,2014年我国共有9390000名学生参加高考,9390000用科学记数法表示为9.39×106.考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:解:9390000用科学记数法表示为9.39×106,故答案为:9.39×106.点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.10.(3分)(2014年湖南郴州)数据0、1、1、2、3、5的平均数是2.考点:算术平均数.分析:根据算术平均数的计算公式列出算式,再求出结果即可.解答:解:数据0、1、1、2、3、5的平均数是(0+1+1+2+3+5)÷6=12÷6=2;故答案为:2.点评:此题考查了算术平均数,用到的知识点是算术平均数的计算公式,关键是根据题意列出算式.11.(3分)(2014年湖南郴州)不等式组的解集是﹣1<x<5.考点:解一元一次不等式组.分析:先求出不等式组中每一个不等式的解集,再求出它们的公共部分就是不等式组的解集.解答:解:,解①得:x>﹣1,解②得:x<5,则不等式组的解集是:﹣1<x<5.点评:本题主要考查了一元一次不等式解集的求法,其简便求法就是用口诀求解,求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).12.(3分)(2014年湖南郴州)如图,已知A、B、C三点都在⊙O上,∠AOB=60°,∠ACB= 30°.考点:圆周角定理.分析:由∠ACB是⊙O的圆周角,∠AOB是圆心角,且∠AOB=60°,根据圆周角定理,即可求得圆周角∠ACB的度数.解答:解:如图,∵∠AOB=60°,∴∠ACB=∠AOB=30°.故答案是:30°.点评:此题考查了圆周角定理.此题比较简单,注意掌握数形结合思想的应用.13.(3分)(2014年湖南郴州)函数的自变量x的取值范围是x≥6.考点:函数自变量的取值范围;二次根式有意义的条件.分析:二次根式有意义的条件是被开方数是非负数,列不等式求解.解答:解:根据题意得:x﹣6≥0,解得x≥6.点评:本题考查的知识点为:二次根式的被开方数是非负数.14.(3分)(2014年湖南郴州)如图,在△ABC中,若E是AB的中点,F是AC的中点,∠B=50°,则∠AEF=50°.考点:三角形中位线定理.分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC,再根据两直线平行,同位角相等可得∠AEF=∠B.解答:解:∵E是AB的中点,F是AC的中点,∴EF是△ABC的中位线,∴EF∥BC,∴∠AEF=∠B=50°.故答案为:50°.点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行线的性质,熟记定理与性质并准确识图是解题的关键.15.(3分)(2014年湖南郴州)若,则=.考点:比例的性质.分析:先用b表示出a,然后代入比例式进行计算即可得解.解答:解:∵=,∴a=,∴=.故答案为:.点评:本题考查了比例的性质,用b表示出a是解题的关键,也是本题的难点.16.(3分)(2014年湖南郴州)如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点上,则DF的长为6.考点:翻折变换(折叠问题).分析:根据矩形的性质得出CD=AB=8,∠D=90°,根据折叠性质得出CF=BC=10,根据勾股定理求出即可.解答:解:∵四边形ABCD是矩形,∴AB=DC=8,∠D=90°,∵将矩形ABCD沿CE折叠后,点B落在AD边的F点上,∴CF=BC=10,在Rt△CDF中,由勾股定理得:DF===6,故答案为:6.点评:本题考查了勾股定理,折叠的性质,矩形的性质的应用,解此题的关键是求出CF 和DC的长,题目比较典型,难度适中.三、解答题(共6小题,满分36分)17.(6分)(2014年湖南郴州)计算:(1﹣)0+(﹣1)2014﹣tan30°+()﹣2.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:原式第一项利用零指数幂法则计算,第二项利用乘方的意义化简,第三项利用特殊角的三角函数值计算,最后一项利用负指数幂法则计算即可得到结果.解答:解:原式=1+1﹣×+9=10.点评:此题考查了实数的运算,熟练掌握运算法则是解本题的关键.18.(6分)(2014年湖南郴州)先化简,再求值:(﹣),其中x=2.考点:分式的化简求值.分析:先将括号内的部分因式分解,约分后再将除法转化为乘法,然后代入求值.解答:解:原式=[﹣]•=(+)•=•=.当x=2时,原式==1.点评:本题考查了分式的化简求值,熟悉约分、通分因式分解是解题的关键.19.(6分)(2014年湖南郴州)在13×13的网格图中,已知△ABC和点M(1,2).(1)以点M为位似中心,位似比为2,画出△ABC的位似图形△A′B′C′;(2)写出△A′B′C′的各顶点坐标.考点:作图-位似变换.分析:(1)利用位似图形的性质即可位似比为2,进而得出各对应点位置;(2)利用所画图形得出对应点坐标即可.解答:解:(1)如图所示:△A′B′C′即为所求;(2)△A′B′C′的各顶点坐标分别为:A′(3,6),B′(5,2),C′(11,4).点评:此题主要考查了位似图形的性质,利用位似图形的性质得出对应点坐标是解题关键.20.(6分)(2014年湖南郴州)已知直线l平行于直线y=2x+1,并与反比例函数y=的图象相交于点A(a,1),求直线l的解析式.考点:反比例函数与一次函数的交点问题.专题:计算题.分析:先根据反比例函数图象上点的坐标特征确定A(1,1),再设直线l的解析式为y=kx+b,利用两直线平行得到k=2,然后把A点坐标代入y=2x+b求出b,即可得到直线l 的解析式.解答:解:把A(a,1)代入y=得a=1,则A点坐标为(1,1)设直线l的解析式为y=kx+b,∵直线l平行于直线y=2x+1,∴k=2,把A(1,1)代入y=2x+b得2+b=1,解得b=﹣1,∴直线l的解析式为y=2x﹣1.点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式.21.(6分)(2014年湖南郴州)我市党的群众路线教育实践活动不断推进并初见成效.某县督导小组为了解群众对党员干部下基层、查民情、办实事的满意度(满意度分为四个等级:A、非常满意;B、满意;C、基本满意;D、不满意),在某社区随机抽样调查了若干户居民,并根据调查数据绘制成下面两个不完整的统计图.请你结合图中提供的信息解答下列问题.(1)这次被调查的居民共有200户;(2)请将条形统计图补充完整.(3)若该社区有2000户居民,请你估计这个社区大约有多少户居民对党员干部的满意度是“非常满意”.根据统计结果,对党员干部今后的工作有何建议?考点:条形统计图;用样本估计总体;扇形统计图.分析:(1)利用“非常满意”的人数除以它所占的百分比即可得这次被调查的居民户数;(2)这次被调查的居民总户数减去非常满意、基本满意、不满意的人数求得满意的人数,再补全条形统计图即可;(3)用该社区的居民总户数乘以“非常满意”人数占的百分比即可得这个社区对党员干部的满意度是“非常满意”的人数.建议答案不唯一.解答:解:(1)50÷25%=200(户),答:这次被调查的居民共有200户,故答案为:200;(2)200﹣50﹣20﹣10=120(户),条形统计图如下:(3)2000×25%=500(户),答:估计这个社区大约有500户居民对党员干部的满意度是“非常满意”.根据统计结果,看出本社区党员干部下基层、察民情、办实事情况不错,要继续保持.点评:本题考查扇形统计图与条形统计图的综合能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.22.(6分)(2014年湖南郴州)某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)考点:解直角三角形的应用-仰角俯角问题.专题:应用题.分析:在Rt△CDB中求出BD,在Rt△CDA中求出AD,继而可得AB,也即此时渔政船和渔船的距离.解答:解:在Rt△CDA中,∠ACD=30°,CD=3000米,∴AD=CDtan∠ACD=1000米,在Rt△CDB中,∠BCD=60°,∴BD=CDtan∠BCD=3000米,∴AB=BD﹣AD=2000米.答:此时渔政船和渔船相距2000米.点评:本题考查了解直角三角形的应用,解答本题的关键是熟练锐角三角函数的定义,能利用已知线段及锐角三角函数值表示未知线段.四、证明题(共1小题,满分8分)23.(8分)(2014年湖南郴州)如图,已知四边形ABCD是平行四边形,点E、B、D、F 在同一直线上,且BE=DF.求证:AE=CF.考点:全等三角形的判定与性质;平行四边形的性质.专题:证明题.分析:根据平行四边形的对边相等可得AB=CD,AB∥CD,再根据两直线平行,内错角相等可得∠ABD=∠CDB,然后求出∠ABE=∠CDF,再利用“边角边”证明△ABE和△CDF 全等,根据全等三角形对应边相等证明即可.解答:证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABD=∠CDB,∴180°﹣∠ABD=180°﹣∠CDB,即∠ABE=∠CDF,在△ABE和△CDF中,,∴△ABE≌△CDF(SAS),∴AE=CF.点评:本题考查了全等三角形的判定与性质,平行四边形的性质,熟记性质与三角形全等的判定方法求出全等的条件是解题的关键.五。
2014年中考百日动员“杰出学子”颁奖词

2014年中考百日动员“杰出学子”颁奖词1、“杰出学子”——崔书源他,自信乐观,面对困难,勇往直前,面对挫折,永不言弃;怀揣着对知识的渴望,不懈努力,成绩卓著,众人瞩目。
他——就是三年五班——崔书源。
2、“杰出学子”——郭茜在校园这片圣洁的土地上,她用执着和勤奋,诠释着什么是青春,她将天真编织成美丽,将智慧化作一身的光辉。
她刻苦努力,勤奋踏实,是学习上的巨人,她团结同学,真诚善良,是生活中的强者,她在充满希望的土地上播撒汗水,收获的定是累累硕果。
她——就是三年二班这个雁群的领头雁——郭茜。
3、“杰出学子”——段宁一脸阳光,绽放着对同学的友爱、对教师的尊敬;一往无前,凝聚着奋进的执著和孝亲的热血。
正义面前他当先,邪恶来临他无惧。
劳动中落不下他的身影,小组讨论中少不了他的踊跃。
乐观,笑对生活;坚韧,直面困难;博学,徜徉书海;友善,帮助同学。
她——就是三年一班——段宁。
4、“杰出学子”——朱丽莹她,如同春天的一株小草,吸收着知识的甘霖,蓬勃向上;她,如同夏天里的一缕清风,驱散同学们心头失意的阴霾;她,如同秋天里的一株野菊,外表柔弱,内心顽强;她,如同冬日里挺拔的青松,风雪压不垮她的身躯,更摧残不了她的意志。
学习上,不服输,敢拼搏,爱思考;生活上,节俭为美,穿着整洁,从不攀比;工作上,以集体为重,心中装着同学,装着班级。
她是新一代中学生的楷模。
她——就是三年一班——朱丽莹。
5、“杰出学子”——张富媛舞台上的她,落落大方,毫无怯意;生活中的她,开朗爱笑,不吝施与。
学校的每次活动,她是必不可少的一抹风景,生活中的每件小事,她用细心热情打理得有条不紊。
回首过往,她的形象如涓涓清泉沁入人心,往昔峥嵘,她用出色的成绩与多才多艺的表现赢得了大家的好评。
她——就是三年一班——张富媛。
6、“杰出学子”——侯佳悦她,静静学习,悄悄绽放,散发出独特的芬芳。
课堂上,她总是深入思考,不急不躁;休闲时,她经常一卷在手,多读多思。
校级教学能力考核优秀证明【范本模板】

校级教学能力考核优秀证明
我校张三同志多年来担任初中英语教学工作。
从教以来曾获得**县初中英语优质课评比二等奖3次;指导青年教师李四参加玉林市青年教师教学技能大赛获二等奖,指导青年教师王五参加广西教育学会英语教学专业委员会组织的全区英语教师说课比赛获一等奖;2013年中考该同志任教班级的英语成绩优秀率在本县同类学校排名是第二名,平均分排名是第一名;指导学生参加自治区专业部门组织的学科比赛共有*人次获一等奖,*人次获二等奖,*人次获三等奖,参加玉林市教育学会组织的学科比赛,共有*人次获一等奖,*人次获二等奖,*人次获三等奖;该同志2012年被评为玉林市优秀教师,2014年被评为玉林市骨干教师,2015年被玉林市教科所评为玉林市初中英语学科带头人。
我校参考张三同志以上情况及日常课堂教学水平与教学成绩等,认为该同志教学能力达到优秀水平。
此材料已于2017年*月*日—*日在本校公示,群众无异议。
**县**中学
经办人:
2017年*月*日。
青岛中考自招材料

青岛中考自招材料一、学生基本信息表基本信息表是申请自招的基本材料,需要填写的内容包括学生的姓名、性别、出生日期、身份证号码、联系电话、电子邮箱等基本信息。
这些信息需要真实准确,以便学校对学生的基本情况进行了解。
二、成绩单及证明成绩单及证明是申请自招的重要材料之一,需要提供初中三年的学习成绩单,以及相关的考试证明,如英语等级考试、数学竞赛等。
这些材料可以充分反映学生的学习情况,对申请自招有一定的帮助。
三、获奖及荣誉证书获奖及荣誉证书可以充分反映学生在各方面的表现和能力,包括学科竞赛、文艺比赛、社会实践等方面的荣誉和奖项。
这些证书和奖项可以为学生的自招申请增添亮点。
四、特长及才艺证明特长及才艺证明也是申请自招的重要材料之一,可以反映学生的个性和特长。
如果学生在音乐、舞蹈、美术、体育等方面有特长或才艺,可以提供相关的证书或证明材料。
这些证明材料可以为学生的自招申请增加竞争力。
五、推荐信及评价表推荐信及评价表可以反映学生的人际关系和社交能力,以及教师和同学对学生的评价。
如果可能的话,可以请初中班主任或任课老师撰写推荐信,或者填写相关的评价表。
这些材料可以为学生的自招申请提供一定的参考。
六、社会实践及志愿者服务证明社会实践及志愿者服务证明可以反映学生的社会实践能力和公益精神。
如果学生在社会实践或志愿者服务方面有表现和经历,可以提供相关的证明或证书。
这些证明材料可以为学生自招申请加分。
七、学生个人陈述及自荐信学生个人陈述及自荐信是学生自我介绍和展示个人特色的重要材料,需要结合自己的学习和生活经历,表述自己的特点、特长和优势等。
