材料力学期末考试复习题及答案 2
材料力学I期末考试题及答案
材料力学I期末考试题及答案一、选择题（每题2分，共20分）1. 材料力学中，下列哪一项不是基本假设？A. 均匀性假设B. 连续性假设C. 各向同性假设D. 各向异性假设答案：D2. 在拉伸试验中，材料的屈服强度是指：A. 弹性极限B. 屈服极限C. 强度极限D. 断裂强度答案：B3. 影响材料弹性模量的因素不包括：A. 材料种类B. 温度C. 材料的几何形状D. 加载速度答案：C4. 梁的弯曲应力公式为：A. σ = My/IB. σ = Mx/IC. σ = VQ/ID. σ = Vx/I答案：A5. 材料力学中，下列哪一项不是应力状态的描述？A. 正应力B. 剪应力C. 应力集中D. 应力梯度答案：D6. 材料的疲劳破坏通常发生在：A. 最大应力处B. 最小应力处C. 应力集中处D. 应力均匀处答案：C7. 根据材料力学理论，下列哪一项不是材料的强度理论？A. 最大正应力理论B. 最大剪应力理论C. 最大应变理论D. 能量理论答案：D8. 梁的弯曲变形公式为：A. v = (Mx/EI)(1 - x^2/L^2)B. v = (Mx/EI)(1 - x^3/L^3)C. v = (Mx/EI)(1 - x/L)D. v = (Mx/EI)(1 - x^2/L^3)答案：B9. 材料的塑性变形是指：A. 弹性变形B. 永久变形C. 可逆变形D. 弹性和塑性变形的总和答案：B10. 在拉伸试验中，材料的弹性模量可以通过下列哪一项来确定？A. 弹性阶段的斜率B. 屈服阶段的斜率C. 断裂阶段的斜率D. 塑性变形阶段的斜率答案：A二、填空题（每题2分，共20分）1. 材料力学中，__________是指材料在外力作用下发生形变，但当外力移除后，形变能够完全恢复的性质。
答案：弹性2. 当材料受到拉伸时，其内部产生的__________应力称为正应力。
答案：垂直3. 材料力学中，__________是指材料在外力作用下发生形变，但当外力移除后，形变不能完全恢复的性质。
材料力学期末试卷(含答案)
满足强度条件。（5分）
六．一根圆截面压杆两端固定，工作压力F=1.7KN，直径为d=8mm，材料为A3钢，其性能参数为： ， ， ， ， 。杆的长度为 ，规定的稳定安全系数是 。试校核压杆的稳定性。（15分）
解：（1） ，
（2分）
而 （2分）
，欧拉公式不成立（1分）
A.强度低，对应力集中不敏感；
B.相同拉力作用下变形小；
C.断裂前几乎没有塑性变形；
D.应力-应变关系严格遵循胡克定律。
2.在美国“9.11”事件中，恐怖分子的飞机撞击国贸大厦后，该大厦起火燃烧，然后坍塌。该大厦的破坏属于（A）
A．强度坏；B．刚度坏；C．稳定性破坏；D．化学破坏。
3.细长柱子的破坏一般是（C）
C． ；D． 。
10.长度和横截面面积均相同的两杆，一为钢杆，一为铝杆，在相同的拉力用下（A）
A.铝杆的应力和钢杆相同，而变形大于钢杆
B.铝杆的应力和钢杆相同，而变形小于钢杆
C.铝杆的应力和变形都大于钢杆
D.铝杆的应力和变形都小于钢杆
三、阶梯形钢杆的两端在 时被固定，杆件上下两段的面积分别是 ， ，见图1。当温度升高至 时，试求杆件各部分的温度应力。钢材的 ， 。（15分）
解：用支反力 代替支座B（见图2），则B端在 和 的作用下挠度为零，即：
（8分）
（5分）
（2分）
五．一铸铁圆柱的直径为40mm，其一端固定，另一端受到315 N.m的力偶矩作用。若该铸铁材料的许用拉应力为 ，试根据强度理论对圆柱进行强度校核。（15分）
解：圆柱表面的切应力最大，即：
（5分）
圆柱表面首先破坏，其上任一点的应力状态为纯剪切，见图3。
一、填空（每题2分，共20分）
材料力学期末考试复习题及答案(2)
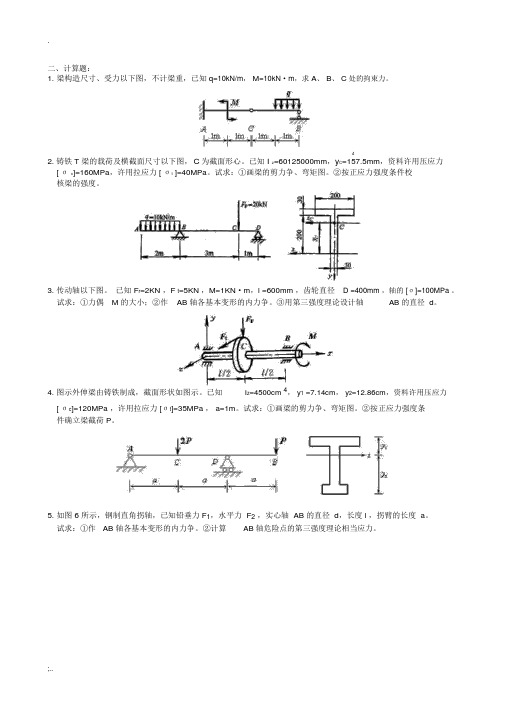
.二、计算题：1.梁构造尺寸、受力以下图，不计梁重，已知q=10kN/m， M=10kN·m，求 A、 B、 C处的拘束力。
42. 铸铁 T 梁的载荷及横截面尺寸以下图，C为截面形心。
已知 I z=60125000mm，y C=157.5mm，资料许用压应力[ σc]=160MPa，许用拉应力 [ σt ]=40MPa。
试求：①画梁的剪力争、弯矩图。
②按正应力强度条件校核梁的强度。
3. 传动轴以下图。
已知 F r=2KN ，F t=5KN ，M=1KN·m，l =600mm ，齿轮直径 D =400mm ，轴的 [σ]=100MPa 。
试求：①力偶M 的大小；②作AB 轴各基本变形的内力争。
③用第三强度理论设计轴AB 的直径 d。
4. 图示外伸梁由铸铁制成，截面形状如图示。
已知I z=4500cm 4， y1 =7.14cm， y2=12.86cm，资料许用压应力[ σc]=120MPa ，许用拉应力 [σt]=35MPa ， a=1m。
试求：①画梁的剪力争、弯矩图。
②按正应力强度条件确立梁截荷 P。
5.如图 6 所示，钢制直角拐轴，已知铅垂力F1，水平力 F2，实心轴 AB 的直径 d，长度 l ，拐臂的长度 a。
试求：①作AB 轴各基本变形的内力争。
②计算AB 轴危险点的第三强度理论相当应力。
6. 图所示构造，载荷 P=50KkN ，AB 杆的直径 d=40mm ，长度 l=1000mm ，两头铰支。
已知资料E=200GPa，σ，σs=235MPa，a=304MPa， b=1.12MPa ，稳固安全系数n st=2.0， [ σ]=140MPa 。
试校核 AB 杆p=200MPa能否安全。
7. 铸铁梁如图 5，单位为 mm，已知 Iz=10180cm 4，资料许用压应力 [σ，许用拉应力 [σt]=40MPa，c]=160MPa试求：①画梁的剪力争、弯矩图。
②按正应力强度条件确立梁截荷P。
1《材料力学》试卷答案2
***学院期末考试试卷一、 填空题（总分20分，每题2分）1、求杆件任一截面上的内力时，通常采用 法。
2、工程中常以伸长率将材料分为两大类：伸长率大于5%的材料称为 材料。
3、梁截面上剪力正负号规定，当截面上的剪力使其所在的分离体有 时针方向转动趋势时为负。
4、虎克定律可以写成/N l F l E A∆=，其中E 称为材料的 ，EA 称为材料的 。
5、材料力学在研究变形固体时作了连续性假设、 假设、 假设。
6、在常温、静载情况下，材料的强度失效主要有两种形式：一种是 ，一种是 。
7、在设计中通常由梁的 条件选择截面，然后再进行 校核。
8、外力的作用平面不与梁的形心主惯性平面重合或平行，梁弯曲后的扰曲轴不在外力作用平 面内，通常把这种弯曲称为 。
9、在工程实际中常见的组合变形形式有斜弯曲、 ， 。
10、当材料一定时，压杆的柔度λ越大，则其稳定系数ϕ值越 。
二、 单项选择(总分20分，每题2分)1、构件的刚度是指( )A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持原有平衡态的能力C. 在外力作用下构件抵抗破坏的能力D. 在外力作用下构件保持原有平稳态的能力2、轴向拉伸细长杆件如图所示，则正确的说法应是( )A 1-1、2-2面上应力皆均匀分布B 1-1面上应力非均匀分布，2-2面上应力均匀分布C 1-1面上应力均匀分布，2-2面上应力非均匀分布D 1-1、2-2面上应力皆非均匀分布4、单位长度扭转角 与（ ）无关。
A 杆的长度；B 扭矩C 材料性质；D 截面几何性质。
5、当梁的某段上作用均布荷载时。
该段梁上的（ ）。
A. 剪力图为水平直线 B 弯矩图为斜直线。
C. 剪力图为斜直线 D 弯矩图为水平直线6、应用叠加原理求梁横截面的挠度、转角时，需要满足的条件是（ ）。
A 梁必须是等截面的B 梁必须是静定的C 变形必须是小变形；D 梁的弯曲必须是平面弯曲7.若某轴通过截面的形心，则（ ）A ．该轴一定为主轴， B. 该轴一定是形心轴C ．在所有轴中，截面对该轴的惯性矩最小。
《材料力学》期末考试试卷A、B卷及答案 (2)
***学院期末考试试卷一、填空题（总分20分，每题2分）1、杆件在外力作用下，其内部各部分间产生的，称为内力。
2、杆件在轴向拉压时强度条件的表达式是。
3、低碳钢拉伸时，其应力与应变曲线的四个特征阶段为阶段，阶段，阶段，阶段。
4、线应变指的是的改变，而切应变指的是的改变。
5•梁截面上弯矩正负号规定，当截面上的弯矩使其所在的微段梁凹向下时为。
6•梁必须满足强度和刚度条件。
在建筑中，起控制做用的一般是条件。
7、第一和第二强度理论适用于材料，第三和第四强度理论适用于材料。
8、求解组合变形的基本方法是。
9、力作用于杆端方式的不同，只会使与杆端距离在较小的范围内受到影响，该原理被称为O10、欧拉公式是用来计算拉（压）杆的，它只适用于杆。
二、单项选择（总分20分，每题2分）1、用截面法可求出图示轴向拉压杆a-a截面的内力N二P-P，下面说法正确的是（）12A.N其实是应力B.N是拉力C.N是压力D.N的作用线与杆件轴线重合2、构件的强度是指（）A.在外力作用下构件抵抗变形的能力B.在外力作用下构件保持原有平衡态的能力C.在外力作用下构件抵抗破坏的能力D.在外力作用下构件保持原有平稳态的能力3、现有钢、铸铁两种杆材，其直径相同。
从承载能力与经济效益两个方面考虑，图示结构中两种合理选择方案是（）A.1杆为钢，2杆为铸铁B.1杆为铸铁，2杆为钢C.2杆均为钢D.2杆均为铸铁4、从拉压杆轴向伸长（缩短）量的计算公式A l =可以看出，E 和A 值越大，A l 越小，故（）。
EAA.E 为杆的抗拉（压）刚度。
B •乘积EA 表示材料抵抗拉伸（压缩）变形的能力。
C.乘积EA 为杆的抗拉（压）刚度D.以上说法都不正确。
5、空心圆轴的外径为D ,内径为d ,«二d/D 。
其抗扭截面系数为（）。
兀D 3冗D 3A W P =-D-(1-a )B W P =-D-(1-a 2)C W P (1-a 3)D W P (1-a 4)P16(P 166、在没有荷载作用的一段梁上，（）A.剪力图为一水平直线B.剪力图为一斜直线C.没有内力D.内力不确定7、在平行移轴公式I 二I +a 2A 中，其中Z 轴和轴Z 轴互相平行，则（）。
材料力学期末试卷(含答案)
11．圆轴扭转时的强度条件为 ，刚度条件为 。
13．莫尔强度理论的强度条件为 。
14．进行应力分析时，单元体上切应力等于零的面称为主平面，其上应力称为主应力。
二、单项选择题(每题2分，共20分)
1.所有脆性材料，它与塑性材料相比，其拉伸力学性能的最大特点是（C）。
（2） （2分）
即有 ，宜采用经验公式（3分）
（2分）
（3） 工作安全系数：
（3分）
压杆稳定性满足。
A.强度低，对应力集中不敏感；
B.相同拉力作用下变形小；
C.断裂前几乎没有塑性变形；
D.应力-应变关系严格遵循胡克定律。
2.在美国“9.11”事件中，恐怖分子的飞机撞击国贸大厦后，该大厦起火燃烧，然后坍塌。该大厦的破坏属于（A）
A．强度坏；B．刚度坏；C．稳定性破坏；D．化学破坏。
3.细长柱子的破坏一般是（C）
C． ；D．为铝杆，在相同的拉力用下（A）
A.铝杆的应力和钢杆相同，而变形大于钢杆
B.铝杆的应力和钢杆相同，而变形小于钢杆
C.铝杆的应力和变形都大于钢杆
D.铝杆的应力和变形都小于钢杆
三、阶梯形钢杆的两端在 时被固定，杆件上下两段的面积分别是 ， ，见图1。当温度升高至 时，试求杆件各部分的温度应力。钢材的 ， 。（15分）
A．强度坏；B．刚度坏；C．稳定性破坏；D．物理破坏。
4.不会引起静定结构产生内力的因素是（D）
A．集中力；B．集中力偶；C．分布力；D．温度变化。
5.“顺正逆负”的正负规定适用于（A）。
A．剪力；B．弯矩；C．轴力；D．扭矩。
6.多余约束出现在（B）中。
A．静定结构；B．超静定结构；C．框架结构；D．桁架。
《材料力学》期末考试试卷A、B卷及答案 (2)
***学院期末考试试卷一、填空题（总分20分，每题2分）1、杆件在外力作用下，其内部各部分间产生的，称为内力。
2、杆件在轴向拉压时强度条件的表达式是。
3阶段，阶段。
45.6.789。
10分)1截面的内力12N P P=-，下面说法正确的是（）C.N是压力D.N的作用线与杆件轴线重合2、构件的强度是指()A.在外力作用下构件抵抗变形的能力B.在外力作用下构件保持原有平衡态的能力C.在外力作用下构件抵抗破坏的能力D.在外力作用下构件保持原有平稳态的能力3、现有钢、铸铁两种杆材，其直径相同。
从承载能力与经济效益两个方面考虑，图示结构中两种合理选择方案是()A.1杆为钢，2杆为铸铁B.1杆为铸铁，2杆为钢C.2杆均为钢D.2杆均为铸铁4、从拉压杆轴向伸长（缩短）量的计算公式EANll=∆可以看出，E和A值越大，l∆越小，故（）。
A.E为杆的抗拉（压）刚度。
B.乘积EA表示材料抵抗拉伸（压缩）变形的能力。
C.乘积EA为杆的抗拉（压）刚度D.以上说法都不正确。
5、空心圆轴的外径为D，内径为d，α=d/D。
其抗扭截面系数为（）。
A)1(163απ-=DW P B)1(1623απ-=DW PC)1(1633απ-=DW P D)1(1643απ-=DW P6、在没有荷载作用的一段梁上，（）A.剪力图为一水平直线B.C．没有内力D.内力不确定7C.Z8A.C.9。
A.C.冰的温度较铸铁高；D.冰的应力等于零。
10、设ϕ和λ分别是压杆的稳定系数和柔度系数，（）。
A．对同一种材料制成的压杆，ϕ值较大则λ值就越小；B．ϕ值越大，λ值就越小，这与压杆所用材料无关；C．当ϕ〉1时，压杆肯定是稳定的，不必对其进行稳定计算；D．ϕ值与压杆杆端的约束情况无关。
三、简答题（总分24分，每题6分）1、拉（压）杆通过铆钉连接在一起时，连接处的强度计算包括哪些计算？2、在梁横截面的中性轴上，其正应力和切应力的值如何？3、梁的变形用什么来度量的？这些量的几何意义各是什么？4、工程中提高压杆稳定性的措施主要从哪几个方面入手？四、画出下列梁的剪力图和弯矩图。
材料力学期末考试复习题与答案
材料力学期末考试复习题与答案work Information Technology Company.2020YEAR二、计算题：1.梁结构尺寸、受力如图所示，不计梁重，已知q=10kN/m，M=10kN·m，求A、B、C处的约束力。
2.铸铁T梁的载荷及横截面尺寸如图所示，C为截面形心。
已知I z=60125000mm4，y C=157.5mm，材料许用压应力[σc]=160MPa，许用拉应力[σt]=40MPa。
试求：①画梁的剪力图、弯矩图。
②按正应力强度条件校核梁的强度。
3.传动轴如图所示。
已知F r=2KN，F t=5KN，M=1KN·m，l=600mm，齿轮直径D=400mm，轴的[σ]=100MPa。
试求：①力偶M的大小；②作AB轴各基本变形的内力图。
③用第三强度理论设计轴AB的直径d。
4.图示外伸梁由铸铁制成，截面形状如图示。
已知I z=4500cm4，y1=7.14cm，y2=12.86cm，材料许用压应力[σc]=120MPa，许用拉应力[σt]=35MPa，a=1m。
试求：①画梁的剪力图、弯矩图。
②按正应力强度条件确定梁截荷P。
5.如图6所示，钢制直角拐轴，已知铅垂力F1，水平力F2，实心轴AB的直径d，长度l，拐臂的长度a。
试求：①作AB轴各基本变形的内力图。
②计算AB轴危险点的第三强度理论相当应力。
6.图所示结构，载荷P=50KkN，AB杆的直径d=40mm，长度l=1000mm，两端铰支。
已知材料E=200GPa，σp=200MPa，σs=235MPa，a=304MPa，b=1.12MPa，稳定安全系数n st=2.0，[σ]=140MPa。
试校核AB杆是否安全。
7.铸铁梁如图5，单位为mm，已知I z=10180cm4，材料许用压应力[σc]=160MPa，许用拉应力[σt]=40MPa，试求：①画梁的剪力图、弯矩图。
②按正应力强度条件确定梁截荷P。
8.图所示直径d=100mm的圆轴受轴向力F=700kN与力偶M=6kN·m的作用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
材料力学期末考试复习题及答案配高等教育出版社第五版一、填空题：1.受力后几何形状和尺寸均保持不变的物体称为。
2.构件抵抗的能力称为强度。
3.圆轴扭转时，横截面上各点的切应力与其到圆心的距离成比。
4.梁上作用着均布载荷，该段梁上的弯矩图为。
5.偏心压缩为的组合变形。
6.柔索的约束反力沿离开物体。
7.构件保持的能力称为稳定性。
8.力对轴之矩在情况下为零。
9.梁的中性层与横截面的交线称为。
10.图所示点的应力状态，其最大切应力是。
11.物体在外力作用下产生两种效应分别是。
12.外力解除后可消失的变形，称为。
13.力偶对任意点之矩都。
14.阶梯杆受力如图所示，设AB和BC段的横截面面积分别为2A和A，弹性模量为E，则杆中最大正应力为。
15.梁上作用集中力处，其剪力图在该位置有。
16.光滑接触面约束的约束力沿指向物体。
17.外力解除后不能消失的变形，称为。
18.平面任意力系平衡方程的三矩式，只有满足三个矩心的条件时，才能成为力系平衡的充要条件。
19.图所示，梁最大拉应力的位置在点处。
20.图所示点的应力状态，已知材料的许用正应力[σ]，其第三强度理论的强度条件是。
21.物体相对于地球处于静止或匀速直线运动状态，称为。
22.在截面突变的位置存在集中现象。
23.梁上作用集中力偶位置处，其弯矩图在该位置有。
24.图所示点的应力状态，已知材料的许用正应力[σ]，其第三强度理论的强度条件是。
25.临界应力的欧拉公式只适用于杆。
26.只受两个力作用而处于平衡状态的构件，称为。
27.作用力与反作用力的关系是。
28.平面任意力系向一点简化的结果的三种情形是。
29.阶梯杆受力如图所示，设AB和BC段的横截面面积分别为2A和A，弹性模量为E，则截面C的位移为。
30.若一段梁上作用着均布载荷，则这段梁上的剪力图为。
二、计算题：1.梁结构尺寸、受力如图所示，不计梁重，已知q=10kN/m，M=10kN·m，求A、B、C处的约束力。
2.铸铁T梁的载荷及横截面尺寸如图所示，C为截面形心。
已知I z=60125000mm4，y C=157.5mm，材料许用压应力[σc]=160MPa，许用拉应力[σt]=40MPa。
试求：①画梁的剪力图、弯矩图。
②按正应力强度条件校核梁的强度。
3.传动轴如图所示。
已知F r=2KN，F t=5KN，M=1KN·m，l=600mm，齿轮直径D=400mm，轴的[σ]=100MPa。
试求：①力偶M的大小；②作AB轴各基本变形的内力图。
③用第三强度理论设计轴AB的直径d。
4.图示外伸梁由铸铁制成，截面形状如图示。
已知I z=4500cm4，y1=7.14cm，y2=12.86cm，材料许用压应力[σc]=120MPa，许用拉应力[σt]=35MPa，a=1m。
试求：①画梁的剪力图、弯矩图。
②按正应力强度条件确定梁截荷P。
5.如图6所示，钢制直角拐轴，已知铅垂力F1，水平力F2，实心轴AB的直径d，长度l，拐臂的长度a。
试求：①作AB轴各基本变形的内力图。
②计算AB轴危险点的第三强度理论相当应力。
6.图所示结构，载荷P=50KkN，AB杆的直径d=40mm，长度l=1000mm，两端铰支。
已知材料E=200GPa，σp=200MPa，σs=235MPa，a=304MPa，b=1.12MPa，稳定安全系数n st=2.0，[σ]=140MPa。
试校核AB杆是否安全。
7.铸铁梁如图5，单位为mm，已知I z=10180cm4，材料许用压应力[σc]=160MPa，许用拉应力[σt]=40MPa，试求：①画梁的剪力图、弯矩图。
②按正应力强度条件确定梁截荷P。
8.图所示直径d=100mm的圆轴受轴向力F=700kN与力偶M=6kN·m的作用。
已知M=200GPa，μ=0.3，[σ]=140MPa。
试求：①作图示圆轴表面点的应力状态图。
②求圆轴表面点图示方向的正应变。
③按第四强度理论校核圆轴强度。
9.图所示结构中，q=20kN/m，柱的截面为圆形d=80mm，材料为Q235钢。
已知材料E=200GPa，σp=200MPa，σs=235MPa，a=304MPa，b=1.12MPa，稳定安全系数n st=3.0，[σ]=140MPa。
试校核柱BC是否安全。
10.如图所示的平面桁架，在铰链H处作用了一个20kN的水平力，在铰链D处作用了一个60kN的垂直力。
求A、E处的约束力和FH杆的内力。
11.图所示圆截面杆件d=80mm，长度l=1000mm，承受轴向力F1=30kN，横向力F2=1.2kN，外力偶M=700N·m的作用，材料的许用应力[σ]=40MPa，试求：①作杆件内力图。
②按第三强度理论校核杆的强度。
12.图所示三角桁架由Q235钢制成，已知AB、AC、BC为1m，杆直径均为d=20mm，已知材料E=200GPa，σp=200MPa，σs=235MPa，a=304MPa，b=1.12MPa，稳定安全系数n st=3.0。
试由BC杆的稳定性求这个三角架所能承受的外载F。
13.槽形截面梁尺寸及受力图如图所示，AB=3m，BC=1m，z轴为截面形心轴，I z=1.73×108mm4，q=15kN/m。
材料许用压应力[σc]=160MPa，许用拉应力[σt]=80MPa。
试求：①画梁的剪力图、弯矩图。
②按正应力强度条件校核梁的强度。
14.图所示平面直角刚架ABC在水平面xz内，AB段为直径d=20mm的圆截面杆。
在垂直平面内F1=0.4kN，在水平面内沿z轴方向F2=0.5kN，材料的[σ]=140MPa。
试求：①作AB段各基本变形的内力图。
②按第三强度理论校核刚架AB段强度。
15.图所示由5根圆钢组成正方形结构，载荷P=50KkN，l=1000mm，杆的直径d=40mm，联结处均为铰链。
已知材料E=200GPa，σp=200MPa，σs=235MPa，a=304MPa，b=1.12MPa，稳定安全系数n st=2.5，[σ]=140MPa。
试校核1杆是否安全。
（15分）16.图所示为一连续梁，已知q、a及θ，不计梁的自重，求A、B、C三处的约束力。
17.图所示直径为d的实心圆轴，受力如图示，试求：①作轴各基本变形的内力图。
②用第三强度理论导出此轴危险点相当应力的表达式。
18.如图所示，AB=800mm，AC=600mm，BC=1000mm，杆件均为等直圆杆，直径d=20mm，材料为Q235钢。
已知材料的弹性模量E=200GPa，σp=200MPa，σs=235MPa，a=304MPa，b=1.12MPa。
压杆的稳定安全系数n st=3，试由CB杆的稳定性求这个三角架所能承受的外载F。
参考答案一、填空题：1.刚体2.破坏3.正4.二次抛物线5.轴向压缩与弯曲6.柔索轴线7.原有平衡状态8.力与轴相交或平行9.中性轴 10.100MPa 11.变形效应（内效应）与运动效应（外效应） 12.弹性变形 13.相等 14.5F /2A 15.突变 16.接触面的公法线 17.塑性变形 18.不共线 19.C 20.2τx ≤[σ] 22.平衡 22.应力 23.突变 24.224[]στσ+≤ 25.大柔度（细长） 26.二力构件 27.等值、反向、共线 28.力、力偶、平衡 29.7Fa /2EA 30.斜直线 二、计算题：1.解：以CB 为研究对象，建立平衡方程B()0:=∑M F C 1010.520⨯⨯-⨯=F:0=∑yFB C 1010+-⨯=F F解得： B 7.5kN =F C 2.5kN =F 以AC 为研究对象，建立平衡方程:0=∑yFA C 0-=y F FA()0:=∑MF A C 1020M F +-⨯=解得： A 2.5kN =y F A 5kN m =-⋅M 2.解：①求支座约束力，作剪力图、弯矩图B()0:=∑M F D 102120340⨯⨯-⨯+⨯=F:0=∑yFB D 102200+-⨯-=F F解得： B 30kN =F D 10kN =F②梁的强度校核1157.5mm =y 2230157.572.5mm =-=y拉应力强度校核 B 截面33B 2tmaxt 12201072.51024.1MPa []6012500010--⨯⨯⨯σ===≤σ⨯z M y I C 截面33C 1tmaxt 121010157.51026.2MPa []6012500010--⨯⨯⨯σ===≤σ⨯z M y I 压应力强度校核（经分析最大压应力在B 截面）33B 1cmaxc 122010157.51052.4MPa []6012500010--⨯⨯⨯σ===≤σ⨯z M y I 所以梁的强度满足要求3.解：①以整个系统为为研究对象，建立平衡方程()0:=∑x M F t 02⨯-=DF M 解得：1kN m =⋅M （3分）②求支座约束力，作内力图 由题可得：A B 1kN ==y y F F A B 2.5kN ==z z F F③由内力图可判断危险截面在C 处22222r332()[]σσ+++==≤y z M M T M T W 222332() 5.1mm []πσ++∴≥=y z M M T d4.解：①求支座约束力，作剪力图、弯矩图A()0:M F =∑ D 22130y F P P ⨯-⨯-⨯=:0=∑yFA D 20y y F F P P +--= 解得：A 12y F P =D 52y F P =②梁的强度校核拉应力强度校核 C 截面C 22tmax t 0.5[]z zM y Pa y I I ⋅σ==≤σ 24.5kN P ∴≤ D 截面D 11tmax t []z zM y Pa y I I ⋅σ==≤σ 22.1kN P ∴≤压应力强度校核（经分析最大压应力在D 截面）D 22cmax c []z zM y Pa y I I ⋅σ==≤σ 42.0kN P ∴≤所以梁载荷22.1kN P ≤5.解：①② 由内力图可判断危险截面在A 处，该截面危险点在横截面上的正应力、切应力为2221N 2232()()4F a Fl F F M A W d σπ+=+=13p 16F aT W dτπ== 2221222221r323332()()4164()4()F a Fl F F a d d d σστπππ+∴=+++6.解：以CD 杆为研究对象，建立平衡方程C()0:MF =∑ AB 0.80.6500.90F ⨯⨯-⨯=解得：AB 93.75kN F =AB 杆柔度1100010040/4liμλ⨯===229p 6p 2001099.320010ππλσ⨯⨯===⨯E由于p λλ>，所以压杆AB 属于大柔度杆222926cr cr 22200104010248.1kN 41004E dF A ππππσλ-⨯⨯⨯⨯===⨯=工作安全因数cr st AB 248.1 2.6593.75F n n F ===> 所以AB 杆安全 7.解：①②梁的强度校核196.4mm y = 225096.4153.6mm y =-=拉应力强度校核A 截面 A 11tmax t 0.8[]z zM y P y I I ⋅σ==≤σ 52.8kN P ∴≤C 截面C 22tmax t 0.6[]z zM y P y I I ⋅σ==≤σ 44.2kN P ∴≤压应力强度校核（经分析最大压应力在A 截面）A 22cmax c 0.8[]z zM y P y I I ⋅σ==≤σ 132.6kN P ∴≤所以梁载荷44.2kN P ≤8.解：①点在横截面上正应力、切应力3N 247001089.1MPa 0.1F A σπ⨯⨯===⨯ 33P 1661030.6MPa 0.1T W τπ⨯⨯===⨯ 点的应力状态图如下图：②由应力状态图可知σx =89.1MPa ，σy =0，τx =30.6MPacos 2sin 222x yx yx ασσσσσατα+-=+-o 4513.95MPa σ∴= o 4575.15MPa σ-=由广义胡克定律o o o 65945454511139503751510429751020010()(...).E εσμσ--=-=⨯-⨯⨯=-⨯⨯ ③强度校核r41037MPa [].σσ===≤所以圆轴强度满足要求9.解：以梁AD 为研究对象，建立平衡方程A ()0:MF =∑ AB 4205 2.50F ⨯-⨯⨯=解得： BC 62.5kN F =BC 杆柔度1400020080/4li μλ⨯===p 99.3λ=== 由于p λλ>，所以压杆BC 属于大柔度杆222926cr cr 22200108010248.1kN 42004E dF A ππππσλ-⨯⨯⨯⨯===⨯= 工作安全因数cr st AB 248.1 3.9762.5F n n F ===> 所以柱BC 安全10.解：以整个系统为研究对象，建立平衡方程:=∑0x FE 200xF -= :0=∑yF A E 600y y F F +-= A ()0:M F =∑ E 82036060y F ⨯-⨯-⨯=解得：E 20kN xF = E 52.5kN y F = A 7.5kN y F =过杆FH 、FC 、BC 作截面，取左半部分为研究对象，建立平衡方程C ()0:M F =∑ A HF12405y F F -⨯-⨯= 解得：HF 12.5kN F =-11.解：①②由内力图可判断危险截面在固定端处，该截面危险点在横截面上的正应力、切应力为33N 234301032 1.21029.84MPa 0.080.08z z F M A W σππ⨯⨯⨯⨯=+=+=⨯⨯ 3p 16700 6.96MPa 0.08T W τπ⨯===⨯ 2222r3429.844 6.9632.9MPa []σστσ∴=++⨯=≤所以杆的强度满足要求12.解：以节点C 为研究对象，由平衡条件可求BC F F =BC 杆柔度1100020020/4li μλ⨯=== 229p 6p 2001099.320010ππλσ⨯⨯===⨯E 由于p λλ>，所以压杆BC 属于大柔度杆222926cr cr 2220010201015.5kN 42004E dF A ππππσλ-⨯⨯⨯⨯===⨯= cr st AB 15.5 3.0F n n F F∴==≥=解得： 5.17kN F ≤13.解：①求支座约束力，作剪力图、弯矩图A ()0:MF =∑ B 315420y F ⨯-⨯⨯= :0=∑y F A B 1540y y F F +-⨯=解得：A 20kN y F =B 40kN y F =②梁的强度校核拉应力强度校核D 截面33D 1tmax t 81240/3101831014.1MPa []1.731010z M y I --⨯⨯⨯σ===≤σ⨯⨯ B 截面 33B 2tmax t 8127.5104001017.3MPa []1.731010z M y I --⨯⨯⨯σ===≤σ⨯⨯ 压应力强度校核（经分析最大压应力在D 截面）33D 2tmax c 81240/3104001030.8MPa []1.731010z M y I --⨯⨯⨯σ===≤σ⨯⨯ 所以梁的强度满足要求14.解：①②由内力图可判断危险截面在A 处，该截面危险点在横截面上的正应力、切应力为97.8MPa M W σ=== 3p 166038.2MPa 0.02T W τπ⨯===⨯r3124.1MPa []σσ∴===≤所以刚架AB 段的强度满足要求15.解：以节点为研究对象，由平衡条件可求135.36kN F P == 1杆柔度1100010040/4li μλ⨯===p 99.3λ=== 由于p λλ>，所以压杆AB 属于大柔度杆222926cr cr 22200104010248.1kN 41004E dF A ππππσλ-⨯⨯⨯⨯===⨯=工作安全因数cr st 1248.1735.36F n n F ===> 所以1杆安全16.解：以BC 为研究对象，建立平衡方程B ()0:=∑M FC cos 02a F a q a θ⨯-⨯⨯= 0:x F =∑ B C sin 0x F F θ-=C ()0:MF =∑ B 02y a q a F a ⨯⨯-⨯= 解得： B tan 2x qa F θ= B 2y qa F = C 2cos qa F θ= 以AB 为研究对象，建立平衡方程0:x F=∑ A B 0x x F F -= :0=∑yFA B 0y y F F -=A ()0:=∑M F AB 0y M F a -⨯=解得： A tan 2xqa F θ= A 2y qa F = 2A 2qa M = 17.解：①② 由内力图可判断危险截面在固定端处，该截面危险点在横截面上的正应力、切应力为2223N 1232(2)()4F l F l F F M A W d σπ+=+= 3p 16e M T W dτπ== 222322221r323332(2)()1644()4()e F l F l M F d d d σστπππ+∴=+++18.解：以节点B 为研究对象，由平衡条件可求BC 53F F = BC 杆柔度1100020020/4li μλ⨯=== 229p 6p 2001099.320010ππλσ⨯⨯===⨯E 由于p λλ>，所以压杆AB 属于大柔度杆222926cr cr 2220010201015.5kN 42004E dF A ππππσλ-⨯⨯⨯⨯===⨯=cr st BC 15.535/3F n n F F ∴==≥= 解得： 3.1kN F ≤。