三角形四心的向量性质
三角形四心的向量性质及应用 学生版
---1---
五．欧拉线： △ABC 的外心 O ，重心 G ，垂心 H 三点共线(欧拉线)，且 OG 1 GH ． 2
测试题
一．选择题
1． O 是 ABC 所在平面上一定点，动点 P 满足 OP OA ( AB AC) ， 0, ，
则点 P 的轨迹一定通过 ABC 的( )
A．外心
B．内心
8．在 △ABC 中，动点
P
2
满足： CA
2
CB
2 AB
CP
，则
P
点轨迹一定通过△ABC
的(
)
Ａ．外心 Ｂ．内心 C．重心 D．垂心
9．已知 ABC 三个顶点 A、B、C 及平面内一点 P ，满足 PA PB PC 0 ，若实数 满足： AB AC AP ，
则 的值为(
A．2
)
B． 3 2
，若
2
AB
AB
AC
AB CB
BC CA ，则 ABC 为(
)
A．等腰三角形 二．填空题
C．重心
D．垂心
2．(03 全国理 4) O 是 ABC 所在平面上一定点，动点 P 满足 OP OA ( AB AC ) ， 0, ，
AB AC
则点 P 的轨迹一定通过 ABC 的(
)
A．外心
B．内心
C．重心
D．垂心
3． O 是 ABC 所在平面上一定点，动点 P 满足 OP OA ( AB AC ) ， R ， AB cosB AC cosC
变式：已知 D，E，F 分别为 △ABC 的边 BC，AC，AB 的中点．则 AD BE CF 0 ．
二、三角形的外心的向量表示及应用
2
2
三角形四心与向量的关系
三角形四心与向量的关系三角形是几何学中的基本图形之一，它有许多重要的性质和特点。
在三角形中，有四个特殊的点，它们被称为三角形的四心，分别是重心、外心、垂心和内心。
本文将探讨这四个特殊点与向量之间的关系。
我们来介绍一下三角形的四心。
重心是三角形三条中线交于一点的点，它被定义为三角形三个顶点的坐标的平均值。
外心是三角形外接圆的圆心，它被定义为三角形三个顶点和三个外接圆弧的交点之一。
垂心是三角形三个高线交于一点的点，它被定义为三角形三个顶点和三个高线的交点之一。
内心是三角形的内切圆的圆心，它被定义为三角形三条边的垂直平分线的交点之一。
接下来，我们来研究这些四心与向量之间的关系。
首先，我们来看重心。
重心可以表示为三个顶点向量的平均值。
设三角形的三个顶点分别为A、B、C，对应的向量为a、b、c，则重心G可以表示为G=(a+b+c)/3。
这个公式说明了重心与向量之间的关系，即重心是三个顶点向量的平均值。
然后，我们来看外心。
外心可以表示为三个顶点向量的线性组合。
设三角形的三个顶点分别为A、B、C，对应的向量为a、b、c，则外心O可以表示为O=(a+b+c)/2。
这个公式说明了外心与向量之间的关系，即外心是三个顶点向量的线性组合。
接下来，我们来看垂心。
垂心可以表示为三个顶点向量的和的负数。
设三角形的三个顶点分别为A、B、C，对应的向量为a、b、c，则垂心H可以表示为H=-(a+b+c)。
这个公式说明了垂心与向量之间的关系，即垂心是三个顶点向量的和的负数。
我们来看内心。
内心可以表示为三条边的单位法向量的线性组合。
设三角形的三个顶点分别为A、B、C，对应的边向量为AB、BC、CA，单位法向量为n1、n2、n3，则内心I可以表示为I=(n1+n2+n3)/(|n1|+|n2|+|n3|)。
这个公式说明了内心与向量之间的关系，即内心是三条边的单位法向量的线性组合。
我们可以得出结论：三角形的四心与向量之间有着紧密的关系。
三角形“四心”定义与性质
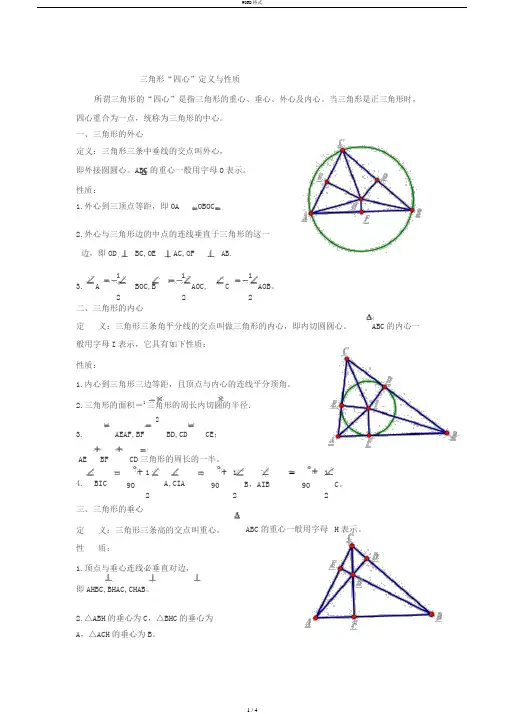
三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时，四心重合为一点，统称为三角形的中心。
一、三角形的外心定义：三角形三条中垂线的交点叫外心，即外接圆圆心。
ABC的重心一般用字母O表示。
性质：1.外心到三顶点等距，即OA OB OC。
2.外心与三角形边的中点的连线垂直于三角形的这一边，即OD BC,OE AC,OF AB.3. A 1BOC,B1AOC,C1AOB。
2 2 2二、三角形的内心定义：三角形三条角平分线的交点叫做三角形的内心，即内切圆圆心。
ABC的内心一般用字母I表示，它具有如下性质：性质：1.内心到三角形三边等距，且顶点与内心的连线平分顶角。
2.三角形的面积＝1三角形的周长内切圆的半径．23. AEAF,BF BD,CD CE；AE BF CD三角形的周长的一半。
4. BIC1A,CIA1B，AIB1C。
90 90 902 2 2三、三角形的垂心定义：三角形三条高的交点叫重心。
ABC的重心一般用字母H表示。
性质：1.顶点与垂心连线必垂直对边，即AHBC,BHAC,CH AB。
2.△ABH的垂心为C，△BHC的垂心为A，△ACH的垂心为B。
四、三角形的“重心”：定义：三角形三条中线的交点叫重心。
ABC 的重心一般用字母G 表示。
性质：1. 顶点与重心G 的连线必平分对边。
2. 重心定理：三角形重心与顶点的距离等于它与对边中点的距离的2倍。
即GA2GD,GB2GE,GC2GF3.重心的坐标是三顶点坐标的平均值．即x G x A x B xC,y Gy A y B yC .334.向量性质：（1）GAGB GC0 ；（2）PG 1(PAPB PC)，31S5.S BGC SCGASAGBABC 。
3五、三角形“四心”的向量形式：结论1：若点O 为 ABC 所在的平面内一点，满足OAOB OBOC OCOA ，则点O 为 ABC 的垂心。
三角形重心外心垂心内心的向量表示及其性质
三角形“四心”向量形式的充要条件应用知识点总结1.0是的重心；若0是的重心，则故；为的重心.2.0是的垂心；若0是（非直角三角形）的垂心，则故3.0是的外心（或）若0是的外心则故4. 0是内心的充要条件是引进单位向量，使条件变得更简洁。
如果记的单位向量为，则刚才0是内心的充要条件可以写成，0是内心的充要条件也可以是。
若0是的内心，则故；是的内心；向量所在直线过的内心（是的角平分线所在直线）；xx 例（一）将平面向量与三角形内心结合考查例1. O是平面上的一定点，A,B,C是平面上不共线的三个点，动点P满足，则P 点的轨迹一定通过的（）（A）外心（B）内心（C）重心（D）垂心解析：因为是向量的单位向量设与方向上的单位向量分别为，又，则原式可化为，由菱形的基本性质知AP平分，那么在xx，AP平分，贝卩知选B.（二）将平面向量与三角形垂心结合考查“垂心定理”例2. H是厶ABC所在平面内任一点，点H是厶ABC的垂心.由,同理，.故H是厶ABC的垂心.（反之亦然（证略））例3.（xx）P 是厶ABC所在平面上一点，若，则P是厶ABCF（D ）A.外心B.内心C.重心D.垂心解析: 由. 即贝S所以P为的垂心.故选D.（三）将平面向量与三角形重心结合考查“重心定理”例4. G是厶ABC所在平面内一点，=0点G是厶ABC的重心.证明作图如右，图中连结BE和CE贝S CE=GB BE=GCBGCE平行四边形D是BC的中点，AD为BC边上的中线.将代入=0，得=0,故G是厶ABC的重心.（反之亦然（证略））例5. P是厶ABC所在平面内任一点.G是厶ABC的重心.证明••*是厶ABC的重心/• =0=0,即由此可得. （反之亦然（证略））例6 若为内一点, ,则是的（）A.内心B.外心C.垂心D.重心解析：由得，如图以OB OC为相邻两边构作平行四边形，贝卩，由平行四边形性质知,,同理可证其它两边上的这个性质,所以是重心,选D。
三角形四心的向量性质及证明
三角形四心的向量性质及证明符号说明：“AB”表示向量，“|AB|”表示向量的模【一些结论】：以下皆是向量1 若P是△ABC的重心PA+PB+PC=02 若P是△ABC的垂心PA*PB=PB*PC=PA*PC(内积）3 若P是△ABC的内心aPA+bPB+cPC=0(abc是三边）4 若P是△ABC的外心|PA|=|PB|=|PC|（AP就表示AP向量 |AP|就是它的模）5 AP=λ（AB/|AB|+AC/|AC|),λ∈[0,+∞) 则直线AP经过△ABC内心6 AP=λ（AB/|AB|cosB+AC/|AC|cosC),λ∈[0,+∞) 经过垂心7 AP=λ（AB/|AB|sinB+AC/|AC|sinC),λ∈[0,+∞）或AP=λ(AB+AC),λ∈[0,+∞) 经过重心8.若aOA=bOB+cOC,则0为∠A的旁心,∠A及∠B,∠C的外角平分线的交点【以下是一些结论的有关证明】1.O是三角形内心的充要条件是aOA向量+bOB向量+cOC向量=0向量充分性：已知aOA向量+bOB向量+cOC向量=0向量，延长CO交AB于D，根据向量加法得：OA=OD+DA,OB=OD+DB,代入已知得：a(OD+DA)+b(OD+DB)+cOC=0,因为OD与OC共线，所以可设OD=kOC,上式可化为(ka+kb+c) OC+(aDA+bDB)=0向量,向量DA与DB共线，向量OC与向量DA、DB不共线，所以只能有：ka+kb+c=0，aDA+bDB=0向量,由aDA+bDB=0向量可知：DA与DB的长度之比为b/a,所以CD为∠ACB的平分线，同理可证其它的两条也是角平分线。
必要性：已知O是三角形内心,设BO与AC相交于E，CO与AB相交于F，∵O是内心∴b/a=AF/BF，c/a=AE/CE过A作CO的平行线，与BO的延长线相交于N，过A作BO的平行线，与CO的延长线相交于M，所以四边形OMAN是平行四边形根据平行四边形法则，得向量OA=向量OM+向量ON=(OM/CO)*向量CO+(ON/BO)*向量BO=(AE/CE)*向量CO+(AF/BF)*向量BO=(c/a)*向量CO+(b/a)*向量BO∴a*向量OA=b*向量BO+c*向量CO∴a*向量OA+b*向量OB+c*向量OC=向量02.已知△ABC 为斜三角形,且O是△ABC所在平面上的一个定点,动点P满足向量OP=OA+入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)}, 求证P点轨迹过三角形的垂心OP=OA+入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)},OP-OA=入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)},AP=入{(AB /|AB|＾2*sin2B)+AC /(|AC|＾2*sin2C)},AP*BC=入{(AB*BC /|AB|＾2*sin2B)+AC*BC /(|AC|＾2*sin2C)}, AP*BC=入{|AB|*|BC|cos(180° -B) /(|AB|＾2*sin2B) +|AC|*|BC| cosC/(|AC|＾2*sin2C)},AP*BC=入{-|AB|*|BC| cos B/(|AB|＾2*2sinB cos B) +|AC|*|BC| cosC/(|AC|＾2*2sinC cosC)},AP*BC=入{-|BC|/ (|AB|*2sinB) +|BC|/(|AC|*2sinC )},根据正弦定理得：|AB|/sinC=|AC|/ sinB,所以|AB|*sinB=|AC|*sinC ∴-|BC|/ (|AB|*2sinB ) +|BC|/(|AC|*2sinC )=0，即AP*BC=0，P点轨迹过三角形的垂心3. OP=OA+λ(AB/(|AB|sinB)+AC/(|AC|sinC))OP-OA=λ(AB/(|AB|sinB)+AC/(|AC|sinC))AP=λ(AB/(|AB|sinB)+AC/(|AC|sinC))AP与AB/|AB|sinB+AC/|AC|sinC共线根据正弦定理：|AB|/sinC=|AC|/sinB,所以|AB|sinB=|AC|sinC,所以AP与AB+AC共线 AB+AC过BC中点D，所以P点的轨迹也过中点D，∴点P过三角形重心。
三角形重心、垂心、内心、外心的向量性质及简单应用
中学数学研究
41
三角形重心、垂心、内心、外心的向量性质及简单应用
广东省珠海市斗门区第一中学 (519100) 陈水松
一、三角形四心的表述与性质
(一) 重心——三角形三条边上的中线的交点叫做三角
形的重心. 重心将中线长度分成 2: 1 的两部分. 1. −O→A + −O−→B + −O−→C = −→0 ⇔O 是 △ABC 的重心.
AC BC −→ + −−→
.
|AC| |BC|
|−B−B+−−→ →CCb| −B)−→C, 所
= 以
4.
−−→ PO
=
−→ aP A
−−→ + bP B + a+b+c
−−→ cP C
⇔
O
为
△ABC
的内心,
P 为平面上任意点.
(二) 垂心——三角形三条高线的交点叫做三角形的垂
证明
因为
O
为
△ABC
证 法 1 设 O(x, y), A(x1, y1), B(x2, y2), C(x3, y3),
−→ −−→ −−→ OA+OB+OC
=
−→0
⇔
x=
x1 + x2 + x3
(x1 − x) + (x2 − x) + (x3 − x) = 0 (y1 − y) + (y2 − y) + (y3 − y) = 0
=
−→0 ,
所以
−→ AO
=
2−O−→D,
所以
A、O、D
三点共线,
三角形四心的向量性质及应用（详细答案版）
三角形“四心”的向量性质及其应用三角形“四心”的概念介绍(1)重心—三条中线的交点：重心将中线长度分成2：1；(2)外心—三边中垂线的交点(外接圆的圆心)：外心到三角形各顶点的距离相等；(3)垂心—三条高线的交点：高线与对应边垂直；(4)内心—三条内角平分线的交点(内切圆的圆心)：角平分线上的任意点到角两边的距离相等．工具：O 为ABC △内一点，则有：0+⋅+⋅∆∆∆OC S OB S OA S O O CA O BC 证明：作：OA S OA OCB ⋅=∆'，OB S OB OCA ⋅=∆'，S OC OAB =∆'不难得知：AOB COA BOC OC B S S OC OC OB OB S S ∆∆∆∆⋅=⋅=''''即BO C AO B CO A O C B S S S S ∆∆∆∆⋅⋅=''；同理==∆∆''''O B A O A C S S ''O C B BO C AO B CO A S S S S ∆∆∆∆=⋅⋅ 从而：O 为'''C B A ∆的重心，则+'OA +'OB 0'=OC ， 得：0=⋅+⋅+⋅∆∆∆OC S OB S OA S O AB O CA O BC .一、三角形的重心的向量表示及应用知识：G 是ABC △的重心⇔)(31AC AB AG +=⇔0=++GC GB GA ⇔)(31OC OB OA OG ++= (O 为该平面上任意一点)变式：已知D E F ，，分别为ABC △的边BC AC AB ，，的中点．则0=++CF BE AD ． 二、三角形的外心的向量表示及应用知识：O 是ABC △的外心⇔222||||||OC OB OA OC OB OA ==⇔== 02sin 2sin 2sin =⋅+⋅+⋅⇔OC C OB B OA A略证：C B A S S S O AB O CA O BC 2sin :2sin :2sin ::=∆∆∆，得：02sin 2sin 2sin =⋅+⋅+⋅OC C OB B OA A ;常用结论：O 是ABC △的外心⇒.2|| ;2||22AC AO AC AB AO AB =⋅=⋅ 三、三角形的垂心的向量表示及应用知识：H 是ABC △的垂心⇔HA HC HC HB HB HA ⋅=⋅=⋅⇔222222||||||||||||AB HC CA HB BC HA +=+=+0tan tan tan =⋅+⋅+⋅⇔HC C HB B HA A略证：C B A S S S H AB H CA H BC tan :tan :tan ::=∆∆∆，得：0tan tan tan =⋅+⋅+⋅HC C HB B HA A ； 扩展：若O 是ABC △的外心，点H 满足：OC OB OA OH ++=，则H 是ABC △的垂心． 证明：如图：BE 为直径，H 为垂心，O 为外心，D 为BC 中点；'有：为平行四边形AHCE EA CH AB EA AB CH EC AH BC EC BC AH ⇒⎪⎪⎭⎪⎪⎬⎫⇒⎭⎬⎫⊥⊥⇒⎭⎬⎫⊥⊥////进而得到：,//EC AH 且EC AH =，即：EC AH =； 又易知：OC OB OD EC +==2；故：OA OH OC OB AH -=+=，即：OC OB OA OH ++=又：OG OC OB OA ⋅=++3（G 为重心），故：OG OH ⋅=3；故：得到欧拉线：ABC △的外心O ，重心G ，垂心H 三点共线(欧拉线)，且GH OG 21=．证毕． 四、三角形的内心的向量表示及应用知识：I 是ABC △的内心⇔⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⎭⎫⎝⎛-⋅=⎭⎫⎝⎛-⋅=⎭⎫⎝⎛-⋅0||||0||||0||||CB CB CA CA CI BC BC BA BA BI AC AC AB AB AI ⇔⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⎭⎫⎝⎛+⋅=⎭⎫⎝⎛+⋅=⎭⎫⎝⎛+⋅0||||0||||0||||CA CA BC BC CI BA BA CB CB BI AC AC BA BA AI 0=⋅+⋅+⋅⇔IC c IB b IA a c b a OCc OB b OA a OI ++⋅+⋅+⋅=⇔cb a ACc AB b AI ++⋅+⋅=⇔ 0sin sin sin =⋅+⋅+⋅⇔IC C IB B IA A 注：式子中|||,||,|AB c CA b BC a ===，O 为任一点．略证：C B A c b a S S S IAB ICA IBC sin :sin :sin ::::==∆∆∆，得之． 五．欧拉线：ABC △的外心O ，重心G ，垂心H 三点共线(欧拉线)，且GH OG 21=．（前已证） 测试题一．选择题1．O 是ABC ∆所在平面上一定点，动点P 满足)(AC AB OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ∆的( )A ．外心B ．内心C ．重心D ．垂心 解析：点P 的轨迹为BC 边的中线（射线），选C2．(03全国理4)O 是ABC ∆所在平面上一定点，动点P 满足AC AB OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ∆的( )A ．外心B ．内心C ．重心D ．垂心 解析：AC AB OA OP ++=λ⇔AC AB AP +=λAC AB +必平分BAC ∠，理由如下：ADACABACACABAB=+==1111,1==，故四边形11DCAB为菱形，对角线AD平分一组对角，ADACAB=+必定平分11ACB∠，即BAC∠，从而ACABAP+=λ也平分BAC∠.故知点P的轨迹为A∠的内角平分线（射线），选 B3．O是ABC∆所在平面上一定点，动点P满足ACABOAOP++=λ，R∈λ，则点P的轨迹一定通过ABC∆的( )A．外心B．内心C．重心D．垂心解析：ACABOAOP++=λ⇔ACABAP+=λ由BCACBCABBCACBCABBCAP+=+=⋅λλ得：0|)|||(=+-=⋅BCBCBCAPλ，得BCAP⊥点P的轨迹为BC边的高线所在直线. 选D4．O是ABC∆所在平面上一定点，动点P满足ACABOAOP+=λ，[)+∞∈,0λ，则点P的轨迹一定通过ABC∆的( )A．外心B．内心C．重心D．垂心解析：由于CACCbBcBAB sin||sinsinsin||=⋅=⋅=，知点P的轨迹为BC边的中线（射线）,选C5．O是ABC∆所在平面上一定点，动点P满足2cos cosOB OC AB ACOPAB B AC Cλ⎛⎫+ ⎪=++⎪⎝⎭，R∈λ，则点P的轨迹一定通过ABC△的( )．A．外心B．内心C．重心D．垂心解析：0||||=+-=+=⋅+BCBCBCACBCABBCACAB知点P的轨迹为BC边的中垂线, 选A6．O是ABC∆所在平面上一定点，动点P满足])21()1()1[(31OCOBOAOPλλλ++-+-=，*R∈λ，则点P的轨迹一定通过ABC△的( )．A．内心B．垂心C．重心D．AB边的中点解析：])21()1()1[(31OCOBOAOPλλλ++-+-=OCOD3)21(3)22(λλ++-=（D为AB边的中点）知CDP,,三点共线（因1321322=++-λλ），故知点P 的轨迹为AB 边的中线所在直线，但是0≠λ，故除去重心. 选D 7．已知O 是ABC ∆的重心，动点P 满足)22121(31OC OB OA OP ++=,则点P 一定为ABC △的( ) A ．AB 边中线的中点 B ．AB 边中线的三等分点(非重心)C ．重心D ．AB 边的中点解析：)22121(31OC OB OA OP ++=OC OD 3231+=（D 为AB 边的中点） 进而有：PC DP 2=，故为AB 边中线的三等分点(非重心), 选B8．在ABC △中，动点P 满足：CP AB CB CA ⋅-=222，则P 点轨迹一定通过△ABC 的( )Ａ．外心 Ｂ．内心 C ．重心 D ．垂心解析：CP AB CB CA ⋅-=222⇔02))((222=⋅-+-=⋅--CP AB CA CB CA CB CP AB CA CB 进而有：02=⋅PD AB （D 为AB 边的中点），故知点P 的轨迹为AB 边的中垂线, 选A9．已知ABC ∆三个顶点C B A 、、及平面内一点P ，满足0=++PC PB PA ，若实数λ满足：AP AC AB λ=+，则λ的值为( )A ．2B ．23C ．3D ．6 解析：P 为重心，得)(31AC AB AP +=，故AP AC AB ⋅=+3,选C10．设点P 是ABC ∆内一点，用ABC S ∆表示ABC ∆的面积，令ABC PBC S S ∆∆=1λ，ABCPCA S S∆∆=2λ，ABC PAB S S ∆∆=3λ．定义),,()(321λλλ=P f ，若)61,31,21()(),31,31,31()(==Q f G f 则( )A ．点Q 在ABG ∆内B ．点Q 在BCG ∆内C ．点Q 在CAG ∆内D ．以上皆不对 解析：G 为重心，画图得知, 选A11．若ABC ∆的外接圆的圆心为O ，半径为1，0=++OC OB OA ，则=⋅OB OA ( )A ．21 B ．0 C ．1 D ．21- 解析：由OC OB OA -=+，平方得知, 选D12．O 是平面上一定点，C B A 、、是平面上不共线的三个点，若222OB BC OA =+222AB OC CA +=+，则O 是ABC ∆的( )A ．外心B ．内心C ．重心D ．垂心 解析：由2222CA OB BC OA +=+⇔2222BC CA OB OA -=-BA BC CA OB OA BA BC CA BC CA OB OA OB OA ⋅-=+⋅⇔+-=+-⇔)()())(())(( 0)2()(=⋅=-++⋅⇔OC BA CA BC OB OA BA ，得AB OC ⊥；同理得：AC OB ⊥,BC OA ⊥，故为垂心, 选D 13．(06陕西)已知非零向量AB 与AC 满足0||||=⋅⎭⎫⎝⎛+BC AC AC AB AB 21||||=AC AC AB AB , 则ABC ∆为( ) A ．三边均不相等的三角形 B ．直角三角形 C ．等腰非等边三角形 D ．等边三角形解析：21||||=AC AC AB AB 0||||=⋅⎭⎫⎝⎛+BC AC AC AB AB ：表明A ∠的内平分线也垂直于BC （三线合一）， 知ABC ∆等腰；21||||=AC AC AB AB ：得到︒=∠60A ；两者结合得到ABC ∆为等边三角形. 选D 14．已知ABC ∆三个顶点C B A 、、，若CA BC CB AB AC AB AB ⋅+⋅+⋅=2，则ABC ∆为( )A ．等腰三角形B ．等腰直角三角形C ．直角三角形D ．既非等腰又非直角三角形 解析：CA BC CB AB AC AB AB ⋅+⋅+⋅=2CA BC AB CA BC CB AC AB ⋅+=⋅++⋅=2)( 得到：0=⋅CA BC ，得：︒=∠90C ,选C 二．填空题15．ABC ∆的外接圆的圆心为O ，两条边上的高的交点为H ，)(OC OB OA m OH ++=，则实数m = 1 ． 解析：直接用结论16．ABC ∆中，7,3,1===BC AC AB ，O 为重心，则=⋅AC AO27． 解析：)9(31)(31)(312+⋅=+⋅=+=⋅AC AB AC AC AB AC AC AB AC AO 利用：CB AC AB =-，两边平方得.23=⋅AC AB 故27)923(31=+=⋅AC AO17．点O 在ABC ∆内部且满足032=++OC OB OA ，则:ABC S ∆=∆AOC S 3 ．解析：法1：利用工具结论易知：AOB COA BOC S S S ∆∆∆=::3:2:1，得:ABC S ∆=∆AOC S 32:6= 法2：0422232=+=+++=++OD OE OC OB OC OA OC OB OA （E 为AC 的中点，D 为BC 的中点）易得：D O E ,,三点共线，且OD EO 2=，从而得到：ABC ADC AOC S S S ∆∆∆==3132. 法3：作：OA OA ='，OB OB 2'=，OC OC 3'=则+'OA +'OB 0'=OC ，则O 为'''C B A ∆的重心，则：''''''O B A O A C O C B S S S ∆∆∆==.设为S又⎪⎩⎪⎨⎧======∆∆∆∆∆∆SS SS S S S S S AOB OB A COA OA C BOC OC B 236'''''' 从而得：331:13:)236(:==++=∆∆S S S S S S COA ABC ． 18．点O 在ABC ∆内部且满足AC AB AO 5152+=，则:ABC S ∆=∆AOB S 5 ． 解析：法1：AC AB AO 5152+=，用O 拆开得：022=+⋅+⋅OC OB OA ， 'A 'B 'C O)(A BC利用工具结论易知：AO B CO A BO C S S S ∆∆∆=::1:2:2，则:ABC S ∆51:5==∆AO B S 法2：AC AD AC AB AO 51545152+=+=，（D 为AB 边的中点），得到：C O D ,,共线，且OD CO 4=， 则:ABC S ∆5:==∆OD CD S AO B . 法3：同上题中法3，此处略.19．已知ABC ∆中，6,5===BC AC AB ，I 为ABC ∆的内心，且BC AB AI μλ+=，则=+μλ1615. 解析：法1：由BC AB BC AB AB AC AB c b a AC c AB b AI ⋅+⋅=+⋅+⋅=++⋅+⋅=++⋅+⋅=165161016)(5555655法2：如图，线长易知，角平分线分线段成比例，得：3:5:=ID AI ， 故)21(8585BC AB AD AI ⋅+⋅=⋅=AB +⋅=1658520．已知ABC ∆中，1,1,2-=⋅==AC AB AC AB ，O 为ABC ∆的外心，且BC y AB x AO +=，则=+y x 27． 解析：法1：由BC y AB x AO +=AC y AB y x +-=)(，由AC AB y AB y x ABBC y AB y x AB AO AB ⋅+-=⇒+-⋅=⋅22)(2))((，得：y y x --=)(42；同理22)(2))((AC y AC AB y x ACBC y AB y x AC AO AC +⋅-=⇒+-⋅=⋅，得：y y x +--=)(21；易得：34,613==y x ，得27=+y x . 法2：以},{AC AB 为基底，表示：CO BO AO ,,，利用222CO BO AO ==，得之BC y AB x AO +=AC y AB y x +-=)(，y y x y y x AO )(2)(4222--+-=； AC y AB y x AB AO BO +--=-=)1(，y y x y y x BO )1(2)1(4222---+--=； AC y AB y x AC AO CO )1()(-+-=-=，)1)((2)1()(4222----+-=y y x y y x CO ；由22BO AO =0254=--⇒⇒y x 移项做差； 由22CO AO =0142=+-⇒⇒y x 移项做差； 联立方程解得：34,613==y x ，得27=+y x .BCA MNG21．已知O 为锐角ABC ∆的外心，︒=∠30A ，若AO m B C AC C B AB 2sin cos sin cos =⋅+⋅，则=m 21． 解析：由AO m AB B CAC C B AB AB 2)sin cos sin cos (⋅=⋅+⋅⋅ 得：22||sin cos cos ||||sin cos ||AB m B CA AC ABC B AB =⋅⋅⋅+⋅得：C m C A B mc BCA b c CB c sin cos cos cos sin cos cos sin cos 22⋅=+⇒=⋅⋅⋅+⋅得到：C A C A C A C A B C m sin sin cos cos )cos(cos cos cos sin =++-=+=⋅ 得：.2130sin sin =︒==A m 22．在ABC∆中，1,==⊥AD BC AB AD ，则⋅AD AC解析：.33)(2===⋅=⋅+=⋅AD AD AD BC AD BC AB AD AC 三．解答题23． 如图，已知点G 是ABC ∆的重心，过G 作直线与AC AB ,两边分别交于N M ,两点，且AM xAB = ，AN yAC = ，求证：113x y+=．解：由N G M ,,三点共线， 得：AN t AM t AG ⋅+⋅-=)1(AC ty AB x t ⋅+⋅-=)1(--------①又G 是ABC ∆的重心得：AC AB AG ⋅+⋅=3131 ---------② 由①②得：⎪⎪⎩⎪⎪⎨⎧==-3131)1(ty x t ，消去t 得：113x y +=.24．设O 在ABC ∆的内部，若有正实数321,,λλλ满足：0321=⋅+⋅+⋅OC OB OA λλλ， 求证：AO B CO A BO C S S S ∆∆∆=::::321λλλ．证明：作：OA OA ⋅=1'λ，OB OB ⋅=2'λ，OC OC ⋅=3'λ 则+'OA +'OB 0'=OC ，则O 为'''C B A ∆的重心，则：''''''O B A O A C O C B S S S ∆∆∆==.设为S又⎪⎩⎪⎨⎧=⋅==⋅==⋅=∆∆∆∆∆∆SS SS S S S S S AOB OB A COA OA C BOC OC B 2!''13''32''λλλλλλ 从而得：AOB COA BOC S S S SSS∆∆∆==::::::211332321λλλλλλλλλ25．已知向量1OP ，2OP ，3OP 满足条件1OP +2OP +3OP =0，|1OP |=|2OP |=|3OP |=1，求证：321P P P ∆为正三角形． 证明：由1OP +2OP +3OP =0⇒1OP +2OP =3OP -平方得：1212112121-=⋅⇒=⋅++OP OP OP OP'A 'B 'C OABC从而得：3||21====P P同理可得：3||||1332==P P P P ，即321P P P ∆为正三角形． 26．在ABC ∆中，︒===60,5,2A AC AB ，求从顶点B A ,出发的两条中线BE AD ,的夹角的余弦值．解：设b AB a AC ==,，则,560cos 25,4,2522=︒⨯⨯=⋅==b a b a且b a BE b a AD -=+=21),(21； 则,3)8525(41)2(41)21()(2122=--=-⋅-=-⋅+=⋅b b a a b a b a BE AD2394102521|)(|21||=++==+=b a AD22116202521|)2(|21||=+-==-=b a BE 故：.919149142212393||||,cos ==⋅=>=<BE AD BEAD BE AD27．已知H 是ABC △的垂心，且||||BC AH =，试求∠A 的度数．解：设ABC △的外接圆半径为R ，点O 是ABC △的外心。
向量中三角形四心的结论和推导
向量中三角形四心的结论和推导一、引言在平面几何中，一个三角形有四个特殊的点，它们分别是三角形的重心、外心、内心和垂心。
这些点被称为三角形的四心。
在向量中，我们也可以推导出三角形的四心的坐标。
二、定义1. 向量向量是一个有大小和方向的量，通常用箭头表示。
在平面直角坐标系中，一个向量可以表示为(x, y)，其中x和y分别是向量在x轴和y轴上的投影长度。
2. 三角形三角形是由三条线段连接而成的图形。
它有三个顶点和三条边。
3. 重心重心是连接三角形每个顶点与对边中点所得线段交于一点的点。
4. 外心外接圆是通过三角形每个顶点并且垂直于对边所得圆。
外接圆圆心就是外心。
5. 内心内切圆是切于三角形每一条边并且内部没有其他点在其内部所得圆。
内切圆圆心就是内心。
6. 垂心垂足分别位于每条高线上，高线即从某个顶点垂直于对边所得线段。
7. 四边形四边形是由四条线段连接而成的图形。
它有四个顶点和四条边。
8. 向量的运算向量的加法：向量相加就是将它们的坐标对应位相加。
向量的减法：向量相减就是将它们的坐标对应位相减。
向量的数量积：两个向量之间的数量积等于这两个向量模长之积与这两个向量夹角余弦值之积。
三、结论1. 重心三角形ABC三个顶点坐标分别为A(x1, y1), B(x2, y2), C(x3, y3)。
则重心G坐标为：G = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3)2. 外心三角形ABC三个顶点坐标分别为A(x1, y1), B(x2, y2), C(x3, y3)。
则外心O坐标为：OA = OB = OC = R其中R为外接圆半径，有以下公式：R = a/(2sinA) = b/(2sinB) = c/(2sinC)其中a、b、c分别为三角形ABC三条边长度，A、B、C分别为对应角度。
O = ((x1^2+y1^2)(y2-y3)+(x2^2+y2^2)(y3-y1)+(x3^2+y3^2)(y1-y2))/(2(x1(y2-y3)+x2(y3-y1)+x3(y1-y2))), ((x1^2+y1^2)(x3-x2)+(x2^2+y2^2)(x1-x3)+(x3^2+y3^2)(x2-x1))/(2(y1(x3-x2)+y2(x1-x3)+y3(x2-x1)))其中，(x,y)为向量的坐标。
三角形“四心”向量形式的结论及证明
三角形“四心”向量形式的结论及证明三角形的“四心”是指三角形的重心、外心、内心和垂心。
它们的位置可以用向量的形式来描述。
本文将分别介绍三角形“四心”的向量形式以及其证明。
1.重心:重心是指三角形三个顶点的中线交点所在的点，用G表示。
假设三角形的三个顶点分别为A(x1,y1)、B(x2,y2)和C(x3,y3)，则重心G的坐标可以通过以下公式得到：G=(A+B+C)/3其向量形式为：OG=(OA+OB+OC)/3其中O为坐标原点。
证明：由定义可知，重心是三角形三个顶点的中线交点所在的点。
而中线的坐标可以通过两个顶点的坐标的平均值得到。
因此，重心的坐标是三个顶点坐标的平均值。
根据向量加法的性质，可以得到上述结论。
2.外心:外心是指可以通过三角形的三个顶点作为圆心，找到一个圆使得三条边都是这个圆的切线。
用O表示外心。
假设三角形的三个顶点分别为A(x1,y1)、B(x2,y2)和C(x3,y3)，则外心O的坐标可以通过以下公式得到：O=(a^2*A+b^2*B+c^2*C)/(a^2+b^2+c^2)其中a、b、c分别表示三角形的边长BC、AC和AB的长度。
其向量形式为：OO=(a^2*OA+b^2*OB+c^2*OC)/(a^2+b^2+c^2)其中O为坐标原点。
证明：设外心为O，连接OA、OB、OC，并设AO的长度为R，BO的长度为R'，CO的长度为R''。
根据定义可知，OA，OB，OC都是截圆半径，可以得到以下关系：OA⊥BC，OB⊥AC，OC⊥AB由于OA、OB、OC是向量，因此上述关系可以写为：OA·BC=0，OB·AC=0，OC·AB=0其中“·”表示点乘。
根据向量的点乘性质可知：OA·(B-C)=0，OB·(C-A)=0，OC·(A-B)=0将向量差展开得：OA·B-OA·C=0，OB·C-OB·A=0，OC·A-OC·B=0进一步展开可得：R^2-R'^2=0，R'^2-R''^2=0，R''^2-R^2=0整理得：R^2-R'^2=R''^2-R^2移项得：2R^2=R'^2+R''^2根据圆的定义可知，外心到三角形的每个顶点的距离都相等，因此R=R'=R''。
三角形重心、外心、垂心、内心的向量表示及其性质
三角形“四心”向量形式的充要条件应用知识点总结1．O是的重心;若O是的重心，则故;为的重心.2．O是的垂心;若O是(非直角三角形)的垂心，则故3．O是的外心(或)若O是的外心则故4．O是内心的充要条件是引进单位向量，使条件变得更简洁。
如果记的单位向量为，则刚才O是内心的充要条件可以写成，O是内心的充要条件也可以是。
若O是的内心，则故;是的内心;向量所在直线过的内心(是的角平分线所在直线)；xx 例(一)将平面向量与三角形内心结合考查例1．O是平面上的一定点，A,B,C是平面上不共线的三个点，动点P满足，则P点的轨迹一定通过的（）（A）外心（B）内心（C）重心（D）垂心解析：因为是向量的单位向量设与方向上的单位向量分别为，又，则原式可化为，由菱形的基本性质知AP平分，那么在xx，AP平分，则知选B.(二)将平面向量与三角形垂心结合考查“垂心定理”例2． H是△ABC所在平面内任一点，点H是△ABC的垂心.由,同理，.故H是△ABC的垂心. （反之亦然（证略））例3.(xx)P是△ABC所在平面上一点，若，则P是△ABC的（D ）A．外心B．内心C．重心D．垂心解析:由.即则所以P为的垂心. 故选D.(三)将平面向量与三角形重心结合考查“重心定理”例4． G是△ABC所在平面内一点，=0点G是△ABC的重心.证明作图如右，图中连结BE和CE，则CE=GB，BE=GCBGCE为平行四边形D是BC的中点，AD为BC边上的中线.将代入=0，得=0，故G是△ABC的重心.（反之亦然（证略））例5． P是△ABC所在平面内任一点.G是△ABC的重心.证明∵G是△ABC的重心∴=0=0，即由此可得.（反之亦然（证略））例6 若为内一点，，则是的（）A．内心B．外心C．垂心D．重心解析：由得，如图以OB、OC为相邻两边构作平行四边形，则，由平行四边形性质知，，同理可证其它两边上的这个性质，所以是重心，选D。
(四) 将平面向量与三角形外心结合考查例7若为内一点，，则是的（）A．内心B．外心C．垂心D．重心解析：由向量模的定义知到的三顶点距离相等。
向量与三角形内心、外心、重心、垂心
向量与三角形的重心、垂心、内心、外心的关系一、四心的概念介绍、（1）重心——中线的交点：重心将中线长度分成2：1； （2）垂心——高线的交点：高线与对应边垂直； （3）内心——角平分线的交点（内切圆的圆心）：角平分线上的任意点到角两边的距离相等；（4）外心——中垂线的交点（外接圆的圆心）：外心到三角形各顶点的距离相等。
二、四线与向量的结合121212,PA =1=,=.ABOA OB PB AB l l l l l l =++1.1.定理：如图，设定理：如图，设定理：如图，设OP OP 则则，且 (记忆:交叉分配系数) =()OA OBAP BP l +2.2.若若M 是OP OP上的任意一点，则上的任意一点，则上的任意一点，则OM OM (记忆:分母对应分配系数) 应用1: （1）中线: （2）高线: （3）角平分线: （4）中垂线: 应用2.四线上的动点表示: (1)中线上的动点: ()AB AC l +或()||sin ||sin AB AC AB B AC Cl +(2)高线上的动点:()cos cos AB AC AB BAC C l +, (3)角平分线上的动点:()AB ACABACl +(4)中垂线上的动点: ()2||cos ||cos OB OCAB AC OP AB B AC Cl +=++,O ABC OA S OB S OC D 定理：设是内任意一点，b a SAOBAOC：：：=D =1:1:1Û0OA OB OC ++=B tan A tan S AOB AOC ：：：=D 0OC OB OA 0aOA bOB cOC 1()3PO PA PB PC =++OA OB OB OC OC OA ×=×=× )))AB AC BC BA CA OC OB OA 已知O 是平面上一定点，||||AB AC AB AC l æö=++ç÷, l 题2：已知O 是平面上一定点，()OP OA AB AC l =++, l ÎO 是平面上的一定点，A ()||sin ||sin AB AC OP OA AB B AC Cl =++是平面上的一定点，A 、B ()||cos ||cos AB AC AB B AC Cl +题5：已知O 是平面上的一定点，A 、B 、C 是平面上不共线的三个点，动点()OB OCABAC++D. 内心,,OA OB OC 满足()||||AB CA OA AB CA ×+=(||BA OB BA ×+||CB CB ) ()||||BC CAOC BC CA ×+= 0内心 D. 外心OA OB OC ++= 0, 1()PO PA PB PC D. 垂心OA OB OB OC OC OA ×=×=×，则 D. 垂心 2222|||||||OA BC OB CA +=+=22|||OC AB +，则 D. 外心题11：已知O 是△ABC )OA OB AB +×()OB OC BC +×()OC OA CA +×= 0，则 D. 垂心aOA bOB cOC ++= = 00，则D. 垂心aPA bPB cPC =题14：△ABC 的外OH =()m OA OB OC ++，则实数二、与三角形形状相关的向量问题题15：已知||||ABACAB AC 12||||AB AC AB AC ×=，则△等边三角形|||2|OB OC OB OC OA -=+-，则等边三角形||BA tBC -≥||AC ，则△题18：已知a , b, c 分别为△GA b GB c GC ×+×+×= = 00, 则△内一点，23OA OB OC ++= 0, 则：题20：如图，已知点是△ABC 的重心，若PQ 过△ABC 的重心，记CA = a ,则11m n +=_____.|(sin AB OP OA C ABl =++sin )AC B ACG C P Q 。
与三角形四心相关的向量结论
与三角形四心相关的向量结论.doc
下面是一些与三角形的四个特殊点（重心、外心、内心和垂心）相关的向量结论：
1. 重心：三角形的重心是三条中线的交点，表示为G，并且满足以下向量等式：
AG + BG + CG = 0
2. 外心：三角形的外心是三角形外接圆的圆心，表示为O，并且满足以下向量等式：
AO = BO = CO = R（半径）
3. 内心：三角形的内心是三角形内切圆的圆心，表示为I，并
且满足以下向量等式：
AI = BI = CI = r（半径）
4. 垂心：三角形的垂心是三条高线（从顶点到对边垂直的线段）的交点，表示为H，并且满足以下向量等式：
AH + BH + CH = 0。
空间向量的四心公式
空间向量的四心公式空间向量的四心公式是空间解析几何中的一个重要定理，它描述了一个三角形的四个特殊点。
在本文中，我们将介绍四心公式的定义、性质和应用。
让我们来看一下四心公式的定义。
对于一个三角形ABC，它的四心分别是外心O、垂心H、重心G和内心I。
外心是三角形外接圆的圆心，垂心是三角形三条高的交点，重心是三角形三条中线的交点，内心是三角形内切圆的圆心。
四心公式给出了这四个点的坐标关系。
接下来，我们来看一下四心公式的性质。
首先，外心O是三角形三个顶点的中垂线的交点，即OA⊥BC，OB⊥AC，OC⊥AB。
其次，垂心H是三角形三个顶点的垂线的交点，即AH⊥BC，BH⊥AC，CH⊥AB。
再次，重心G是三角形三个顶点的中线的交点，即AG=2GM，BG=2GN，CG=2GL，其中M、N、L分别是BC、AC、AB的中点。
最后，内心I是三角形三条边的角平分线的交点，即∠BAI=∠CAI，∠ABI=∠CBI，∠BCI=∠ACI。
四心公式的应用非常广泛。
首先，它可以用于计算三角形的各种特征，如面积、周长、角度等。
例如，可以利用四心公式计算三角形的外接圆半径、内切圆半径和面积。
其次，四心公式还可以用于解决一些几何问题，如判断三角形的类型（锐角、直角、钝角）、判断四点是否共面等。
此外，四心公式还有一些拓展应用，如用于求解平面内的最小包围圆、最小包围球等。
在实际应用中，四心公式还可以与其他数学知识相结合，解决更复杂的问题。
例如，可以利用向量运算和线性代数的知识，推导出四心公式的几何解释和向量形式。
同时，四心公式也可以与三角函数、三角恒等式等知识相结合，推导出更深入的结论和定理。
空间向量的四心公式是空间解析几何中的一个重要定理，它描述了一个三角形的四个特殊点。
四心公式具有一些重要的性质和应用，可以用于计算三角形的各种特征和解决几何问题。
在实际应用中，四心公式还可以与其他数学知识相结合，解决更复杂的问题。
因此，掌握四心公式对于深入理解和应用空间解析几何非常重要。
妙用三角形“四心”的性质解答向量问题
四、妙用三角形垂心的性质
三角形的垂心是三角形三条边上的高的交点.其
性质有：（1）若 O、H 分别为 △ABC 的外心和垂心，则
O∠AB∙AOOB==∠OHB∙AOCC，=∠OACB∙OHA=.∠在O解BC答，向∠量BC问O题= ∠时H，C可A ；以（根2）
据三角形垂心的定义推断出垂心的位置，也可以通过 关 系 式 OA∙OB = OB∙OC = OC∙OA 来 判 定 三 角 形 的 垂
意确定三角形的外心，然后根据题意明确外心与三角
形三个顶点、三个角之间的关系，灵活运用三角形外
心的性质来解题.
共
例 2. 线的
已知 O 是平 三 点. 若 动
面内一点 点P满
，A,B,C 是平 足 OP = OB
面内不
+ 2
O C
+
| | | | æ
λçç è
ABAcBos B +
ACAcCos
C
ö ÷ ÷ ø
三角形边的AB距C离的相外等心，，则都等aO于A 内+ b切OB圆 +的cO半C径= 0；（；（3）4）若∠OBO为C三=
90°+
∠
A 2
，∠BOA
=90°+
∠
C 2
，∠AOC
=90°+
∠
B 2
.在解
答向量问题时，需根据三角形内心的定义确定内心的
位置及其与三条角平分线之间的关系，便可根据三角
形内心的性质来解题.
，λμ A=P45=.m
AD
，
∴
AD
=
λ m
AB
+
μ m
AC
，
∵
高一三角形“四心”的向量性质及其应用(含解析)
1 1 1 1 1 定义 f ( P) = (λ , λ , λ ) ，若 f (G) = ( 1 , , ), f (Q) = ( , , ) 则( ) 3 3 3 2 3 6 A．点 Q 在 ∆ABG 内 B．点 Q 在 ∆BCG 内 C．点 Q 在 ∆CAG 内 D．以上皆不对 解析： G 为重心，画图得知 例 8． 如图，已知点 G 是 ∆ABC 的重心，过 G 作直线与 AB, AC 两边分别交于 M , N 两点，
=
1 5
2 1 AB + AC ，用 O 拆开得： 2 ⋅ OA + 2⋅ OB + OC = 0 ， 法 2： AO = 5 5
由奔驰定理可得： S
∆BOC
: S ∆COA : S ∆AOB = 2 : 2 : 1
，则 S
∆ABC
: S ∆AOB = (2 + 2 + 1) : 1 = 5 .
A
2 1 4 1 AB + AC = AD + AC ， 法 3： AO = 5 （取 D 为 AB 边的中点） ， 5 5 5
∆ABC ∆ABC
∆AOC ∆ABC
⋅ AB +
S ∆AOB ⋅ AC S ∆ABC
A
O B C
两边乘以 S 整理可得： − S 移项整理为 (S − S − S 即得 S ⋅ OA + S ⋅ OB + S 注：若简记三个面积： S = S ， S
∆ABC ∆AOC ∆OBC ∆OCA ∆OBC A
A
=λ
，S S
∆AOB ∆ABC
=µ
，S S
三角形四心向量公式
三角形四心向量公式在我们学习数学的奇妙旅程中，三角形的四心向量公式就像是隐藏在数学城堡中的神秘宝藏，等待着我们去探索和发现。
先来说说什么是三角形的四心吧。
这四心分别是重心、垂心、内心和外心。
它们在三角形中有着独特的地位和重要的性质。
咱们先聊聊重心。
重心可是三角形三条中线的交点哦。
那重心的向量公式是什么呢？设三角形三个顶点的坐标分别为 A(x₁, y₁)、B(x₂,y₂)、C(x₃, y₃)，那么重心 G 的坐标就是((x₁ + x₂ + x₃)/3, (y₁ + y₂+ y₃)/3)。
我记得有一次给学生们讲这个知识点的时候，有个小调皮鬼一脸茫然地问我：“老师，这重心到底有啥用啊？”我笑着回答他：“你想想啊，如果我们要做一个三角形的跷跷板，那重心的位置是不是就特别重要啦？它得在正中间，不然跷跷板可就不平衡咯！”同学们听了都哈哈大笑，一下子就记住了重心的重要性。
再来说说垂心。
垂心是三角形三条高的交点。
对于垂心的向量公式，那可有点复杂啦，不过别担心，咱们慢慢理解。
内心呢，是三角形三条内角平分线的交点。
它到三角形三边的距离相等。
内心的向量公式理解起来也需要花点心思。
最后是外心，外心是三角形三边中垂线的交点，也就是三角形外接圆的圆心。
在解决与三角形四心相关的问题时，这些向量公式可真是我们的得力助手。
比如，在一些几何证明题中，巧妙地运用这些公式，就能让复杂的问题变得简单明了。
记得有一次考试，有一道关于三角形重心的题目，很多同学都没有做对。
我在讲解的时候，一步一步地引导他们运用重心的向量公式，看着他们恍然大悟的表情，我心里别提多有成就感了。
学习三角形四心向量公式，就像是在数学的海洋中驾驭一艘小船，虽然有时会遇到风浪，但只要我们掌握好方向，就能顺利前行。
希望同学们在面对这些公式的时候，不要害怕，多做练习，多思考，相信大家一定能够熟练掌握，在数学的世界里畅游无阻！。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三角形“四心”的向量性质及其应用一、三角形的重心的向量表示及应用命题一 已知A B C ，，是不共线的三点，G 是ABC △内一点，若GA GB GC ++=0．则G 是ABC △的重心．证明：如图1所示，因为GA GB GC ++=0，所以 ()GA GB GC =-+．以GB ，GC 为邻边作平行四边形BGCD ， 则有GD GB GC =+，所以GD GA =-．又因为在平行四边形BGCD 中，BC 交GD 于点E ， 所以BE EC =，GE ED =．所以AE 是ABC △的边BC 的中线． 故G 是ABC △的重心．点评：①解此题要联系重心的定义和向量加法的意义；②把平面几何知识和向量知识结合起来解决问题是解此类问题的常用方法．例1 如图2所示，ABC △的重心为G O ，为坐标原点，OA =a ，=OB b ，=OC c ，试用a b c ，，表示OG ．解：设AG 交BC 于点M ，则M 是BC 的中点，⎪⎩⎪⎨⎧=-=-=-GC OG c GB OG b GA OG a GC GB GA OG c b a ++=-++∴而03=-++∴OG c b a图23cb a OG ++=∴ 点评：重心问题是三角形的一个重要知识点，充分利用重心性质及向量加、减运算的几何意义是解决此类题的关键．变式：已知D E F ，，分别为ABC △的边BCAC AB ，，的中点．则AD BE CF ++=0．证明：如图的所示，⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-=-=GCCF GBBE GA AD 232323 )(23GC GB GA CF BE AD ++-=++∴0=++GC GB GA AD BE CF ∴++=0．．变式引申：如图4，平行四边形ABCD 的中心为O ，P 为该平面上任意一点， 则1()4PO PA PB PC PD =+++．证明：1()2PO PA PC =+，1()2PO PB PD =+， 1()4PO PA PB PC PD ∴=+++．点评：（1）证法运用了向量加法的三角形法则，证法2运用了向量加法的平行四边形法则．（2）若P 与O 重合，则上式变为OA OB OC OD +++=0．二、三角形的外心的向量表示及应用命题二：已知G 是ABC △内一点，满足MC MB MA ==，则点M 为△ABC 的外心。
例2 已知G 、M 分别为不等边△ABC 的重心与外心，点A ，B 的坐标分别为A （-1，0），B （1，0），且GM ∥AB ，（1）求点C 的轨迹方程；（2）若直线l 过图3点（0，1），并与曲线交于P 、Q 两点，且满足0=OP ，求直线l 的方程。
解 （1）设C （x,y ），则G （3,3y x ），图5其中0,≠y x ， 由于GM ∥， 故my m =， 外心M （0，3y ）， 为外心M∴MC MA =，得222)3(1)3()0(yy y x +=-+-∴轨迹E 的方程是3322=+y x )0(≠xy（2）略。
三、三角形的垂心的向量表示及应用命题三：已知G 是ABC △内一点，满足⋅=⋅=⋅，则点G 为垂心。
（2005全国文12）证明:由0=⋅-⋅⋅=⋅PC PB PB PA PC PB PB PA 得. 即0,0)(=⋅=-⋅即 则AB PC BC PA CA PB ⊥⊥⊥,,同理所以P 为ABC∆的垂心.点评：本题将平面向量有关运算、“数量积为零，则两向量所在直线垂直”、三角形垂心定义等相关知识巧妙结合。
变式：若H为△ABC所在平面内一点，==则点H 是△ABC 的垂心证明: 2222BC CA HB HA -=-BA CB CA BA HB HA •+=•+∴)()( =•--+BA CB CA HB HA )(得0即=•+BA HC HC )(0HC AB ⊥∴同理HB AC ⊥，HA BC ⊥ 故H 是△ABC 的垂心四、三角形的内心的向量表示及应用 命题四：O 是内心ABC ∆的充要条件是|CB ||CA ||BC ||BA |(AC|AB |=-⋅=-⋅=-⋅变式1：如果记CA ,BC ,AB 的单位向量为321e ,e ,e ，则O 是ABC ∆内心的充要条件是0)e e ()e e ()e e (322131=+⋅=+⋅=+⋅变式2：如果记,,的单位向量为321e ,e ,e ，则O 是ABC ∆内心的充要条件也可以是c b a =++。
例4（2003江苏）已知O 是平面上一定点，A、B 、C是平面上不共线的三个点，满足++=λ，[)+∞∈,0λ，则P 的轨迹一定通过△ABC的内心 。
解： 如图AP OA OP +=由已知OA OP ++=λ，+=λ ，[)+∞∈,0λ∴[)+∞∈,0λ设=λ，=λ，∴D 、E 在射线AB 和AC 上。
∴AE AD AP +=∴AP 是平行四边行的对角线。
又= ，∴ADPE 是菱形。
∴点P 在EAD ∠ 即CAD ∠ 的平分线上。
故P 点的轨迹一定通过△ABC 的内心。
五、三角形外心与重心的向量关系及应用命题五：设△ABC 的外心为O ，则点G 为△ABC 重心的充要条件为：)(31OC OB OA OG ++=证明：如图8，设G 为重心，连结AG 并延长，交BC 于D ，则D 为BC的中点。
∴ )(3132AC AB OA AD OA AG OA OG ++=+=+=)(31)(31OC OB OA OA OC OA OB OA ++=-+-+=反之，若)(31++=， 则由上面的证明可知：)(31AC AB AG +=设D 为BC 的中点，则)(21AC AB AD +=， 图8从而AD AG 32=， ∴G 在中线AD 上且AG=32AD ，即G 为重心。
六、三角形外心与垂心的向量关系及应用命题六：设△ABC 的外心为O ，则点H 为△ABC 的垂心的充要条件是OC OB OA OH ++=。
证明：如图2，若H 为垂心，以OB 、OC 为邻边作平行四边形OBDC ， 则 OC OB OD +=∵O 为外心， ∴OB=OC ，∴平行四边形OBDC 为菱形 ∴ OD ⊥BC ，而AH ⊥BC ， ∴ AH ∥OD ，∴存在实数λ，使得OC OB OD AH λλλ+== ∴ OC OB OA AH OA OH λλ++=+=①。
同理，存在实数μ，ω，使得μμ++=+= ②OB OA OC CH OC OH ωω++=+=③ 比较①、②、③可得，1===ωμλ， ∴ OC OB OA OH ++=反之，若OC OB OA OH ++=，则OC OB AH +=，∵ O 为外心，∴OB=OC∴0||||)()(22=-=-•+=•OC OB OC OB OC OB CB AH ∴AH ⊥CB ，同理，BH ⊥AC 。
∴ H 为垂心。
图9例6、已知H 是△ABC 的垂心，且AH=BC ，试求∠A 的度数 解：设△ABC 的外接圆半径为R ，点O 是外心。
∵ H 是△ABC 的垂心 ∴OC OB OA OH ++= ∴OC OB OA OH AH +=-=∴)2cos 21(2)(||2222A R OC OB AH AH +=+== ∵OB OC BC -= ，∴)2cos 21(2)(||2222A R OB OC BC BC -=-==∵AH=BC ，∴ A A 2cos 212cos 21-=+ ∴ 02cos =A而∠A 为△ABC 的内角，∴ 0＜2A ＜360° 从而2A=90°或270° ∴ ∠A 的度数为45°或135°。
七、三角形的外心、重心、垂心的向量关系及应用命题七：△ABC 的外心、重心、垂心分别为O 、G 、H ，则O 、G 、H 三点共线（O 、G 、H 三点连线称为欧拉线），且OG=21GH 。
证明：如图10，由命题五、六知，连结AG 并延长，交BC 于D ，则D 为BC 的中点。
)(31OC OB OA OG ++=，OC OB OA OH ++=，∴OG OH 3= ∴O 、G 、H 三点共线，且OG=21GH 。
例7、已知O （0，0），B （1，0），C （b ，c ），是OBC 的三个顶点。
试写出OBC 的重心G ，外心F ，垂心H 的坐标，并证明G 、F 、H 三点共线。
（2002年全国）解：重心G 为)3,31(c b +，设H 点的坐标为),(0y bDGH O A图10OCBAP图11∵BC OH ⊥，BC =(b-1，c )，0)1(0=++cy b b ，故cb b y )1(0-=H 点的坐标为))1(,(c b b b -设外心F 的坐标为),21(1y 由|FO |=|FC |，得c c b b y 2)1(21+-=，所以F 点的坐标为（，）。
从而可得出GH =（，），FH =（，）FH 32 GH =，GH ∥FH ，F 、G 、H 三点共线。
点评：向量不仅是平面解析几何入门内容，而且是解在关数形结合问题的重要工具。
它一般通过概念的移植、转化，将坐标与向量结合起来，从而使一些难题在思路上获得新的突破。
例8、已知P 是非等边△ABC 外接圆上任意一点，问当P 位于何处时，PA 2+PB 2+PC 2取得最大值和最小值。
解：如图11，设外接圆半径为R ，点O 是外心，则 PA 2+PB 2+PC 2=222)()()(OC PO OB PO OA PO +++++)(262OC PO OB PO OA PO R ⋅+⋅+⋅+= )(262OC OB OA PO R ++⋅+=OH PO R ⋅+=262（由命题六知：H 为垂心，） ∴当P 为OH 的反向延长线与外接圆的交点时，有最大值6R 2+2R ·OH当P 为OH 的延长线与外接圆的交点时，有最小值6R 2－2R ·OH。