平移与旋转练习题
三年级数学-平移和旋转练习(含答案)

平移和旋转一、单选题1.平移是沿着()移动A. 直线B. 曲线C. 某个点2.下面哪些图案不能通过平移得到?()A. B. C.3.分针围绕钟面中心顺时针旋转3圈后,时针围绕钟面中心顺时针旋转了()A. 60°B. 90°C. 180°D. 360°4.如图:在三角形ABC中∠ACB=90°, ∠A=40°,以C为旋转中心,将三角形ABC旋转到三角形A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边C′A′交AB于D,则旋转角等于()A. 70°B. 80°C. 60°二、判断题5.杂技演员连续后空翻是旋转现象。
( )6.滑梯是平移现象,风扇是旋转现象。
7.旋转中,对应点划过的痕迹是一条圆弧。
8.判断对错.找出下面图形的变化规律,然后根据这个规律在最后一个图的空格里画上相关的图形.三、填空题9.不倒翁的摆动是________现象。
10.写出分针从12旋转到下面各个位置所经过的时间________分________分________分11.小船向________平移了________格;小鱼向________平移了________格.12.分针和时针的转速比是________。
四、解答题13.把平移前后两幅图中的平行线涂上相同的颜色。
14.下面哪幅图是由图①旋转得到的?圈出来五、综合题15.左边的图形是如何变成右边的图形的?(1)红色三角形:________(2)蓝色三角形:________(3)黄色三角形:________(4)绿色三角形:________六、应用题16.将图先向右平移6格,再向上平移4格,并画出平移后的图形.参考答案一、单选题1.【答案】A【解析】【解答】平移是沿着直线移动【分析】考查了平移的相关知识2.【答案】B【解析】【解答】解:A、一个小三角形平移后得到整个图形;B、曲线所指的方向变化了,不是平移得到的;C、一个五边形平移后得到整个图形.故答案为:B【分析】平移后的图形的形状、大小、方向都不变,位置发生了变化,由此根据平移的特征判断哪些图形是通过平移得到的即可.3.【答案】B【解析】4.【答案】B【解析】【解答】解:图中BC绕C点旋转后得到B′C,CB=CB′,又因为∠A′B′C是∠ABC旋转后的角,因此两角相等都是50度,经过计算得到∠B′CB=80°,故∠ACD=80°.故答案为:B【分析】旋转后的图形的大小不变,各个角的度数也不变,这样∠B′就是50度,三角形BB′C是等腰三角形,所以能计算出∠B′CB的度数,然后就能确定旋转角的大小.二、判断题5.【答案】错误【解析】【解答】杂技演员连续后空翻是平移现象,原题说法错误.故答案为:错误.【分析】杂技演员后空翻是旋转现象,杂技演员连续后空翻是平移现象,据此判断.6.【答案】正确【解析】【解答】解:根据平移、旋转的意义可得滑梯是平移现象,风扇是旋转现象,可见原题说法正确. 故答案为:正确.【分析】平移是水平或竖直或其他方向的平行移动;在平面内将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转,根据平移和旋转的定义进行分析即可解答.7.【答案】正确【解析】【解答】解:旋转中,对应点划过的痕迹是一条圆弧,原题说法正确.故答案为:正确【分析】旋转中,对应的点划过的痕迹是一条圆弧,圆弧的圆心角就是旋转的度数.8.【答案】错误【解析】【解答】正确解答:如下图所示。
平移与旋转的练习题

平移与旋转的练习题一、选择题1. 平移变换不改变图形的:A. 形状B. 大小C. 位置D. 颜色2. 下列哪个不是平移的特点:A. 改变图形的位置B. 改变图形的形状C. 图形各部分平移距离相等D. 方向相同3. 旋转变换不改变图形的:A. 形状B. 大小C. 位置D. 颜色4. 旋转中心是旋转变换中:A. 旋转的起始点B. 旋转的终止点C. 不旋转的点D. 旋转的方向5. 旋转角度为负值时,表示:A. 顺时针旋转B. 逆时针旋转C. 没有旋转D. 旋转的方向不确定二、填空题6. 平移变换中,图形的____和____不变,只有____发生变化。
7. 旋转变换中,图形的____和____不变,只有____发生变化。
8. 如果一个图形绕某一点旋转90°,则该点是图形的____。
9. 平移向量可以用____个坐标来表示。
10. 旋转变换可以用____和____来描述。
三、判断题11. 平移变换可以改变图形的形状。
()12. 旋转变换可以改变图形的大小。
()13. 平移向量的方向和大小决定了图形平移后的位置。
()14. 旋转变换中,所有点的旋转角度相同。
()15. 旋转变换中,图形的旋转方向可以是任意的。
()四、简答题16. 描述平移变换和旋转变换的基本概念,并说明它们的区别。
17. 解释为什么平移向量可以唯一确定一个平移变换。
18. 举例说明旋转变换在日常生活中的应用。
五、计算题19. 给定一个点A(3,4),若该点向右平移5个单位,求平移后点A'的坐标。
20. 若一个图形绕原点O(0,0)顺时针旋转30°,求旋转后图形上任意一点P(x,y)的新坐标。
六、应用题21. 一个正方形的边长为4,其顶点坐标分别为A(1,1), B(5,1),C(5,5), D(1,5)。
若正方形绕点A顺时针旋转45°,求旋转后各顶点的新坐标。
22. 在平面直角坐标系中,有一个矩形,其顶点坐标为E(0,0),F(0,6), G(8,6), H(8,0)。
平移与旋转练习题精选(有答案)

第10章轴对称、平移、旋转练习题一、选择题1、下列说法正确的是()A.平移不改变图形的形状和大小,而旋转则改变图形的形状和大小B.平移和旋转的共同点是改变图形的位置C.图形可以向某方向平移一定距离,也可以向某方向旋转一定距离D.在平移和旋转图形中,对应角相等,对应线段相等且平行2、.轴对称与平移、旋转的关系不正确的是( )A.经过两次翻折(对称轴平行)后的图形可以看作是原图形经过—次平移得到的B.经过两次翻折(对称轴不平行)后的图形可以看作是原图形经过—次平移得到的C.经过两次翻折(对称轴不平行)后的图形可以看作是原图形经过旋转得到的3、如图,将图(1)中的正方形图案绕中心旋转180°后,得到的图案是()4、如图,已知△OAB绕点O到△OCD的位置,且∠A=110°,∠D=第4题图ODCBA∠AOD 的度数为 . A. 30° B. 40° C. 50° D. 60°5、如图(1)中的图形N 平移后的位置如图6(2)中所示,那么正确的平移方法是( )A.先向下移动1格,再向左移动1格B.先向下移动1格,再向左移动2格C.先向下移动2格,再向左移动1格D.先向下移动2格,再向左移动2格7题图6、国旗上的五角星是旋转对称图形,它需要旋转( )后,才能与自身重合。
A. 36°B. 45°C. 60°D. 72°7、如图,把直角三角形ABC 绕直角顶点顺时针方向旋转90°后到达C B A ''∆,延长AB 交''B A 于D ,则'ADA ∠的度数是( ) A. 30° B. 60° C. 75° D. 90°8、如图,P 是正△ABC 内的一点,若将△PBC 绕点B 旋转到△P ’BA ,则∠PBP’的度数是 ( )A .45° B.60° C.90° D.120° 9、如图,该图形围绕旋转中心,按下列角度旋转后,不能..与其自身重合的是( )A、72 B、108 C、144 D、21610、如图,在正方形ABCD 中,E 为DC 边上的点,连接BE ,将A CB ’△BCE 绕点C 顺时针方向旋转90°得到△DCE ,连结EF ,若∠BEC=60°,则∠EFD 的度数为( )A 、10° B 、15° C 、20° D 、25°8题图 9题图10题图二、 填空题11、如图,四边形OACB 绕点O 旋转到四边形DOEF ,在这个旋转过程中,旋转中心是_________,旋转角是_________,AO 与DO 的关系是_______,AOD ∠与BOE ∠的关系是___________。
【小学】小学三年级数学(下)《平移与旋转现象》练习题(含答案)
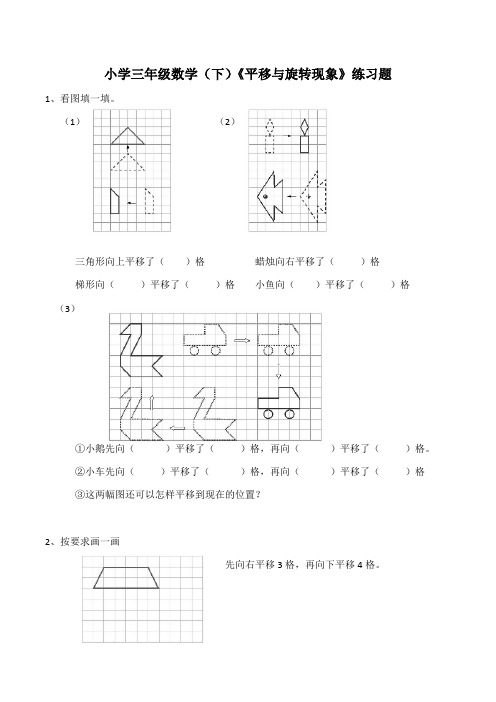
小学三年级数学(下)《平移与旋转现象》练习题1、看图填一填。
(1)(2)三角形向上平移了()格蜡烛向右平移了()格梯形向()平移了()格小鱼向()平移了()格(3)①小鹅先向()平移了()格,再向()平移了()格。
②小车先向()平移了()格,再向()平移了()格③这两幅图还可以怎样平移到现在的位置?2、按要求画一画先向右平移3格,再向下平移4格。
3、说一说,填一填。
分针顺时针旋转了()度。
逆时针旋转了()度。
4、下列图形中,不能由左图经过一次平移或亩得到的是()。
5、画一画。
(1)把图①绕O点顺时针旋转90°(2)把图②绕O点逆时针旋转90°。
6、旗帜上的图案哪些可以通过旋转得到,哪些可能通过平移得到?7、请你利用平衡或旋转的方法,将图2恢复到图一的样子。
说出变化的过程。
8、哪两个图形通过平移或旋转能够完全重合?(连一连)9、(1)上面的的哪些标志是轴对称的?(2)用旋转或平移的方法设计一个漂亮的标志。
附参考答案1、看图填一填。
(1)3格,左4格,(2)4格,左,5格。
(3)①左,7格,上,6格,②右,7格,下,6格,③小鹅向先上平移6格,再向左平移7格。
小车先向下平移6格,再向右平移7格。
2、画图。
略3、说、填。
图1:90°,图2:90°4、不能一次由旋转或平移得到的图形是②5、略6、由平移得到的是①④⑥,由旋转得到的是②③⑤7、把左下图向右平移1格,再向上平移格。
把右下图逆时针90°就恢复了原图。
8、通过平移重合的有:①和⑤,通过旋转重合的有:④和⑥,①和⑧,④和⑫,③和⑪,9、(1)轴对称图形有:上1,上2,上4,上5,下1,下3,下10;(2)略。
初二平移与旋转练习题

初二平移与旋转练习题题目一:平移练习题1. 在平面直角坐标系中,顶点坐标分别是 (2,4)、(4,4)、(4,6)、(2,6)的正方形ABCD,向右平移3 个单位,求平移后的正方形的顶点坐标。
2. 在平面直角坐标系中,顶点坐标分别是 (-3,1)、(-2,5)、(-5,6)、(-6,2) 的四边形 EFGH,向下平移 4 个单位,求平移后的四边形的顶点坐标。
3. 在平面直角坐标系中,点 P 的坐标为 (1,3),将点 P 向右平移 2 个单位、向上平移 5 个单位,求平移后点 P 的坐标。
题目二:旋转练习题1. 将直角坐标系中的点 A(2,3) 逆时针旋转 90 度,求旋转后点的坐标。
2. 将直角坐标系中的点 B(-5,2) 顺时针旋转 180 度,求旋转后点的坐标。
3. 将直角坐标系中的点 C(-1,4) 逆时针旋转 270 度,求旋转后点的坐标。
题目三:平移与旋转综合练习题1. 以直角坐标系中的点 D(3,2) 为中心,将正方形 ABCD 逆时针旋转 90 度并向上平移 4 个单位,求旋转和平移后正方形的顶点坐标。
2. 以直角坐标系中的点 E(-2,5) 为中心,将四边形 EFGH 顺时针旋转 180 度并向右平移 3 个单位,求旋转和平移后四边形的顶点坐标。
3. 以直角坐标系中的点 F(0,-3) 为中心,将点 P(1,1) 逆时针旋转 120 度并向上平移 2 个单位,求旋转和平移后点 P 的坐标。
以上为初二平移与旋转练习题。
通过解答这些练习题,可以帮助你巩固平移与旋转的知识,提升解题能力。
希望你能认真思考并准确回答每个问题,加深对这两个概念的理解。
祝你学习进步!。
平移与旋转练习题

平移与旋转练习题一、平移题1. 平面上有一个点P(2, 5),要将点P向右平移4个单位和向上平移3个单位,请求出平移后点的坐标。
解析:根据平移的性质,点向右平移4个单位等价于在横坐标上加4,点向上平移3个单位等价于在纵坐标上加3。
所以,平移后点的坐标为(2 + 4, 5 + 3),即(6, 8)。
2. 平面上有一个点Q(-3, 1),要将点Q向左平移2个单位和向下平移6个单位,请求出平移后点的坐标。
解析:根据平移的性质,点向左平移2个单位等价于在横坐标上减2,点向下平移6个单位等价于在纵坐标上减6。
所以,平移后点的坐标为(-3 - 2, 1 - 6),即(-5, -5)。
二、旋转题1. 平面上有一条线段AB,其中A的坐标为(-1, 3),B的坐标为(2, 6)。
以原点为中心,逆时针旋转30度,请求出旋转后线段AB的新坐标。
解析:以原点为中心逆时针旋转30度,相当于对每个点进行坐标变换。
设点A'和点B'是旋转后的点,根据旋转公式可以得到:A'的横坐标 = A的横坐标 * cos(30度) - A的纵坐标 * sin(30度)A'的纵坐标 = A的横坐标 * sin(30度) + A的纵坐标 * cos(30度)B'的横坐标 = B的横坐标 * cos(30度) - B的纵坐标 * sin(30度)B'的纵坐标 = B的横坐标 * sin(30度) + B的纵坐标 * cos(30度)代入A(-1, 3)和B(2, 6)的坐标,计算得到:A'的横坐标 = (-1) * cos(30度) - 3 * sin(30度) ≈ -0.134A'的纵坐标 = (-1) * sin(30度) + 3 * cos(30度) ≈ 2.732B'的横坐标 = 2 * cos(30度) - 6 * sin(30度) ≈ 2.598B'的纵坐标 = 2 * sin(30度) + 6 * cos(30度) ≈ 6.732所以,旋转后线段AB的新坐标为A'(-0.134, 2.732)和B'(2.598, 6.732)。
(完整版)平移与旋转练习题精选(有答案)

22 、如下图, E 是正方形 ABCD 中 CD 边上任一点,以点 A 为中心,把△ ADE 顺时针旋转 90°,在给出图
形中画出旋转后的图形,并完成下列填空. ( 1)因为点 A 是对称中心,所以它的对应点是 (
);
( 2 )正方形 ABCD 中, AD=AB ,∠ DAB=90° ,所以旋转后点 D 与点 (
)重合.
23 、如图所示, E、 F 分别是△ ABC 的边 AB 、 AC 的两定点,在 BC 上求一点 M ,使△ MEF 的周长最短。
26、如图:若∠ AOD= ∠ BOC=60 °,A 、O、C 三点在同一条线上,△
求:( 1)旋转中心, ( 2)旋转角度数,
( 3)图中经过旋转后能重合的三角形共有几对?若
( 3)∵∠ FDE=45° ,∠ ADC=9°0 ,∴∠ ADF+ ∠ EDC=9°0 -45°=45°,∵∠ GDF= ∠ GDA+ ∠ADF,∠ GDA= ∠EDC, ∴∠ GDF= ∠EDC+ ∠ADF=45° .
26 、( 1) .O 点 (2).60 度 (3).3 对,成立,因为角 AOD为 60 度,角 DOC为 120 度,向加 180 度,所以成立 (4).90 因为角 BOC=角 AOD=45度,所以应旋转 90 度 (5).120 度
二、填空题
11、 O 12 、C
∠ EOB 顺时针
AO=DO 90°
∠ AOD= ∠BOE .
13 、由图可知, OB 、OD 是对应边,∠ BOD 是旋转角,所以,旋转角∠ BOD= ∠AOD- ∠AOB=127° -90 °=37 度
14 、解:∵ AD∥ BC,∠ EFB=65°,∴ DEF=65° ,又∵∠ DEF= ∠ D′ EF,∴∠ D′ EF=65°,∴∠ AED′ =50°
旋转与平移练习题

旋转与平移练习题一、选择题1. 平移变换不改变图形的:A. 形状B. 大小C. 颜色D. 位置2. 下列哪个图形是经过旋转变换后的图形?A. 正方形B. 长方形C. 圆形D. 等边三角形3. 一个图形经过旋转变换后,其:A. 形状会改变B. 大小会改变C. 位置会改变D. 颜色会改变4. 平移变换是指图形在平面内:A. 沿直线移动B. 沿曲线移动C. 沿圆周移动D. 不移动5. 旋转变换是指图形绕着某一点或直线:A. 沿直线移动B. 沿曲线移动C. 旋转一定角度D. 旋转任意角度二、填空题6. 平移变换的性质包括:图形的________、________和________不变。
7. 旋转变换的性质包括:图形的________、________和________不变,但________发生了变化。
8. 如果一个图形绕着原点顺时针旋转90度,则该图形的坐标变化规律为:(x, y)变为(-y, x)。
9. 平移变换中,若图形向右平移a个单位,则图形的坐标变化规律为:(x, y)变为(x+a, y)。
10. 旋转变换中,若图形绕着原点逆时针旋转90度,则图形的坐标变化规律为:(x, y)变为(y, -x)。
三、判断题11. 平移变换可以改变图形的形状。
(对/错)12. 旋转变换可以改变图形的大小。
(对/错)13. 一个图形经过旋转变换后,其位置一定会发生变化。
(对/错)14. 平移变换和旋转变换都不会改变图形的面积。
(对/错)15. 一个图形绕着原点顺时针旋转180度后,其坐标变为(-x, -y)。
(对/错)四、简答题16. 描述一个图形经过平移变换后,其形状、大小和位置的变化情况。
17. 解释旋转变换中,图形绕着某一点旋转90度、180度、270度和360度时,图形的变化规律。
18. 举例说明一个图形经过平移变换后,其坐标如何变化。
19. 举例说明一个图形经过旋转变换后,其坐标如何变化。
20. 阐述平移变换和旋转变换在实际生活中的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年11月27日数学周测试卷一、选择题(共10小题;共50分)1. 如图,将绕点旋转后得到,则旋转方式是A. 顺时针旋转B. 逆时针旋转C. 顺时针旋转D. 逆时针旋转2. 下列说法正确的是A. 平移不改变图形的形状和大小,而旋转则改变图形的形状和大小B. 平移和旋转的共同点是改变了图形的位置,而图形的形状大小没有变化C. 图形可以向某方向平移一定距离,也可以向某方向旋转一定距离D. 在平移和旋转图形中,对应角相等,对应线段相等且平行3. 如图,点,,,,都在方格纸的格点上,若绕点按逆时针方向旋转到的位置,则旋转的角度为A. B. C. D.4. 如图,在的网格中,每个小方格的边长都是个单位长度,将平移到的位置,下面正确的平移步骤是A. 先向左平移个单位长度,再向下平移个单位长度B. 先向右平移个单位长度,再向下平移个单位长度C. 先向左平移个单位长度,再向上平移个单位长度D. 先向右平移个单位长度,再向上平移个单位长度5. 如图,是等边三角形,为边上的点,,经旋转后到达的位置,那么旋转了A. B. C. D.6. 如图,在中,,,,现将绕点逆时针旋转至,使得点恰好落在上,连接,则的长度是A. B. C. D.7. 如图,在方格中有两个涂有阴影的图形,,图1 中图形平移后位置如图2所示,以下对图形的平移方法叙述正确的是A. 向右平移个单位,向下平移个单位B. 向右平移个单位,向下平移个单位C. 向右平移个单位,向下平移个单位D. 向右平移个单位,向下平移个单位8. 如图,在中,,,,将沿射线的方向平移,得到′′′,再将′′绕点逆时针旋转一定角度后,点恰好与点重合,则平移的距离和旋转角的度数分别A. ,B. ,C. ,D. ,9. 如图,在方格纸上,经过变换得到,下列对变换过程的叙述正确的是A. 绕着点顺时针旋转,再向右平移格B. 向右平移格,再向上平移格C. 绕着点逆时针旋转,再向右平移格D. 向右平移格,再绕着点逆时针旋转10. 下列图形中,由如图经过一次平移得到的图形是A. B.C. D.二、填空题(共10小题;共52分)11. 图形的旋转(1)旋转:在平面内,将一个图形绕一个 ? 按某个方向转动一个角度,这样的图形运动称为旋转.这个定点称为 ?,转动的角称为 ?.(2)旋转的性质①旋转不改变图形的形状和大小;②对应点到旋转中心的距离 ?;③任意一组对应点与 ? 的连线所成的角都等于旋转角;④对应线段 ?,对应角 ?.12. 如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“”平移到刻度“”,则顶点平移的距离 ?.13. 如图,把绕点按顺时针方向旋转,得到,交于点.若,则 ?.14. 如图,将沿方向向右平移得到,连接,若的周长为,则四边形的周长为 ?.15. 如图是一块电脑主板的示意图,每一转角处都是直角.数据如图(单位:),则该主板的周长是 ?.16. 如图,是等边内的一点,若将绕点逆时针旋转到,则的度数为 ? 度.17. 如图,将一块斜边长为,的直角三角板,绕点逆时针方向旋转至的位置,再沿向右平移,使点刚好落在斜边上,则此三角板向右平移的距离为 ?.18. 如图是一块从一个边长为的正方形材料中剪出的垫片,现测得,则这个剪出的图形的周长是 ?.19. 如图,把放在直角坐标系内,其中,,点,的坐标分别为,,将沿轴向右平移,当点落在直线上时,线段扫过的面积为 ?.20. 如图,中,,,,绕顶点逆时针旋转到处,此时线段与的交点为的中点,则线段的长度为 ?.三、解答题(共10小题;共130分)21. (1)按要求在网格中画图:如图,画出图形关于直线的对称图形,再将所画图形与原图形组成的图案向右平移格.(2)根据以上构成的图案,请写一句简短、贴切的解说词 ?.22. 如图,在平面上,七个边长为个单位的等边三角形,分别用①至⑦表示.从④⑤⑥⑦组成的图形中,取出一个三角形,使剩下的图形经过一次平移,①②③组成的图形拼成一个正六边形.你取出的是哪个三角形?写出平移的方向和平移的距离.23. 在正方形中,,绕点顺时针旋转,它的两边分别交,(或它们的延长线)于点,.当绕点旋转到时(如图甲所示),易证.(1)当绕点旋转到时(如图乙所示),线段,和之间有怎样的数量关系?写出猜想,并加以证明.(2)当绕点旋转到如图丙所示的位置时,线段,和之间有怎样的数量关系?请直接写出你的猜想.24. 在学习了图形的旋转知识后,数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究.如图1,在四边形中,,,,点,分别在线段,上,,连接.(1)如图2,将绕点逆时针旋转后得到(与重合),请直接写出? 度,线段,,之间的数量关系为 ?;(2)如图3,当点,分别在线段,的延长线上时,其他条件不变,请探究线段,,之间的数量关系,并说明理由.25. 如图,将沿直角边向右平移个单位长度至,如果,,且的面积为,试求图中阴影部分的面积.26. 如图1,在中,,,,点为射线上任意一点(不与重合),连接,将线段绕点按顺时针方向旋转得到线段,直线分别交直线,射线于点,.(1)直接写出的度数;(2)如图2,图3,当为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由.27. 如图,已知的面积为,将沿平移得到,使点和点重合,连接,交于点.(1)求证: .(2)求的面积.28. 如图,已知在中,,先把绕点顺时针旋转后至,再把沿射线平移至,,相交于点.(1)判断线段,的位置关系,并说明理由;(2)连接,求证:四边形是正方形.29. 已知矩形中,,,将绕点顺时针旋转得到,使点的对应点落在延长线上,点对应点为点,点对应点为点,点与点重合(如图),此时将以每秒个单位长度的速度沿直线向左平移,直至点与点重合时停止运动,设运动的时间为.(1)当为何值时,点落在线段上?(2)设在平移过程中与矩形重叠部分的面积为,请直接写出与之间的函数关系式,并写出相应的的取值范围;(3)在平移过程中,当点与点重合时(如图),将绕点逆时针旋转得到,直线与所在直线交于点,与所在直线交于点.在旋转过程中,的旋转角为,是否存在这样的,使得为等腰三角形?若存在,请写出的度数,若不存在,请说明理由.30. 有两张完全重合的矩形纸片,小亮将其中一张绕点顺时针旋转后得到矩形(如图1),连接,,此时他测得,.(1)在图1中,请你判断直线和是否垂直?并证明你的结论;(2)小红同学用剪刀将与剪去,与小亮同学继续探究.他们将绕点顺时针旋转得,交于点(如图2),设旋转角为,当为等腰三角形时,请直接写出旋转角的度数;(3)若将沿方向平移得到(如图3),与交于点,与交于点,当时,求平移的距离是多少.答案第一部分1. B2. B3. C4. A5. B【解析】是等边三角形,,,经旋转后到达的位置,等于旋转角,即旋转角等于.6. B 【解析】因为,,所以,因为绕点逆时针旋转至,所以,,,因为,,所以为等边三角形,所以,所以,所以为等边三角形,所以.7. B 8. B 【解析】由平移的性质可得,,.由旋转的性质可得,是等边三角形,.,即平移的距离为 .是等边三角形,,即旋转角的度数为.9. C 10. C第二部分11. (1)定点,旋转中心,旋转角,(2)②相等,③旋转中心,④相等,相等12.13.14.15.16.17.18.19.20.【解析】因为,,,所以 . 因为绕顶点逆时针旋转到处,所以, . 因为点为的中点,所以 .所以 .过点作于 ..解得 .在中,. 因为,,所以(等腰三角形三线合一).所以.第三部分21. (1)如图??????(2)解说词合理即可,如“爱心传递”或“我们心连心”等.22. 答案不唯一,如:取出⑦,④⑤⑥向上平移个单位.23. (1)成立.如图所示,把绕点顺时针旋转,得到则可证得,,三点共线.易得,证得..,.??????(2).24. (1);【解析】由旋转的性质知,,,.,,,,.在和中,,,即.,.??????(2)如图,在上截取,连接,在和中,,,.,.,,.在和中,,.,,.即线段,,之间的数量关系为.25. 由平移知,.的面积为,.设交于点,连接.易知,,,,,.阴影部分的面积为.26. (1),,.在和中,,.又,,.??????(2)不变.选取图 2,证明如下:,,即.在和中,,.又,,即.27. (1)沿平移得到,,,.又,.??????(2)沿平移得到,,与的面积相等,等于.,与的面积相等,等于 .28. (1).理由如下:由题意,得,,.,,即.??????(2)沿射线平移至.,.四边形是平行四边形.,四边形是矩形.,四边形是正方形.29. (1)因为,,所以 .延长交于点 .因为绕点顺时针旋转得到,所以 .所以 .因为以每秒个单位长度的速度沿直线向左平移,秒,所以当时,点落在线段上.??????(2)当时,;当时,;当时,;当时,;当时,.??????(3)因为为等腰三角形,当时, .所以 .因为,所以,所以.同理:当时,;当时,.所以为等腰三角形,旋转角为、、.30. (1)垂直.证明:延长交于点.由题意得..,...??????(2)的度数为或.【解析】根据旋转的性质知,.当时,.则,即;②当时,.,即;的度数为或.??????(3)由题意知四边形为矩形.设,则.在中,,.,..在中,...,,,解得.即平移的距离是.。
