高中物理一轮复习课件:选修3-4.1.1机械振动
合集下载
高中物理选修3-4机械振动ppt课件

由牛顿第三定律知,物体对弹簧的最小压力: FN′=FN=12mg。 由以上可以得出振幅为 A 时最大回复力为 0.5mg, 所以有 kA=0.5mg ③, 欲使物体在振动中不离开弹簧,则最大回复力可为 mg, 所以有 kA′=mg ④, 由③和④两式联立解得 A′=2A。
[解题反思] 解决此类问题,首先要确定对称点,认识到在 这一对称点时速度大小相等,加速度大小相等,回复力大小相等, 最后根据题目要求来确定所需要的物理量。
3.时间的对称性:系统在通过关于平衡位置对称的两段位 移的时间相等。振动过程中通过任意两点 A、B 的时间间隔与逆 向通过的时间间隔相等。
[典例指津] 如图所示,质量为 m 的物体放在弹簧上,与弹簧一起在竖 直方向上做简谐运动,当振幅为 A 时,物体对弹簧的最大压力 是物重的 1.5 倍,则物体对弹簧的最小压力是多少?要使物体在 振动中不离开弹簧,振幅不能超过多大?
(3)确定振动的周期和频率。振动图象上一个完整的正弦(或 余弦)函数图形在时间轴上拉开的“长度”表示周期。
由下图可知,OD、AE、BF 的时间间隔都等于振动周期,T =0.2 s,频率 f=T1=5 Hz。
(4)确定各时刻质点的振动方向。例如下图中的 t1 时刻,质 点正远离平衡位置向位移的正方向运动;在 t3 时刻,质点正向着 平衡位置运动。
[解题反思] 在利用图象解决问题时,首先要明确图象的物 理含义,根据图象的特点做出振动过程;然后分析各物理量的变 化规律,包括大小和方向,利用所提供的信息进行分析问题。
[变式训练] 一质点简谐运动的振动图象如图所示。 (1)该质点振动的振幅是________cm;周期是________s;初 相是________。 (2)写出该质点简谐运动的表达式,并求出当 t=1 s 时质点的 位移。
教科版选修3-4 1 《机械振动》复习课件

R R L T T0 2π Rh R h g0
(3)小球在光滑圆弧上的往复 滚动,和单摆完全等同。只要摆 角足够小,这个振动就是简谐运 动。这时周期公式中的l应该是圆 弧半径R
例1. 一质点在平衡位置O点附近作简谐运动,它离
开O点经2.5s第一次通过M点,再经过1s第二次通过
11s或3 点的振动周期为 12s或4
一、简谐运动 1、定义:如果质点的位移与时 间的关系遵从正弦函数的规律, 即它的振动图象是一条正弦曲线, 这样的振动叫简谐运动. 注:简谐运动是最简单最基本的 振动。
2、简谐运动的描述 (1)描述简谐运动的物理量 ①位移x:由平衡位置指向质点 所在位置的有向线段,是矢量。 注:位移的参考点是平衡位置 ②振幅A:振动物体离开平衡位 置的最大距离,是标量,表示振 动的强弱.
②从平衡位置开始计时,函数表 达式为x=Asin ωt,图象如图1 -1所示.从最大位移处开始计 时,函数表达式为x=Acos ωt, 图象如图1-2所示.
3.简谐运动的回复力和能量 (1)简谐运动回复力的特点:回复力 的大小跟偏离平衡位置的位移大小 成正比,回复力的方向总指向平衡 位置 即:F= -kx 注:①回复力时刻指向平衡位置;②可 由F= -kx 判定一个振动是否是简谐 运动。③回复力是按效果命名的, 可 由任意性质的力提供.可以是几个 力的合力也可以是一个力的分力;
A. 1/3 s
B. 8/15s
C. 1.4s
D. 1.6s
答案:AC
受迫振动与共振 1. 受迫振动 物体在驱动力(即周期性外力)作用下的振动叫 受迫振动. 受 ⑴物体做受迫振动的频 迫 A 振 率等于驱动力的频率, 动 的 与物体的固有频率无关。 振 幅 ⑵物体做受迫振动的振幅由 驱动力频率和物体的固有频 0 f′ 率共同决定:两者越接近, 共振曲线 受迫振动的振幅越大,两者 相差越大受迫振动的振幅越 小。
高考物理总复习 1机械振动课件 新人教版选修34
第16页
选修3-4 机械振动与机械波 光 电磁波与相对论
高考调研
高三物理 (新课标版)
• 【答案】 < <
• 【学法指导】 本题关于周期的判断,也可定性说明,到 平衡位置分开,说明a的速度大小在平衡位置仍是原来的 值,到达最大位置时的速度为零,从速度的平均作用效果 上看与原来一样,但是振幅减小,故所用的时间减小.
• (1)使物体回到平衡位置,方向跟离开平衡位置的位移方向 相反的力,叫回复力.
• (2)表达式:F=-kx.
第5页
选修3-4 机械振动与机械波 光 电磁波与相对论
高考调研
高三物理 (新课标版)
• 【名师点拨】 ①回复力是从力的作用效果命名的.对做 简谐运动的物体进行受力分析时,千万不能加上回复力, 要始终牢记受力分析,分析的是性质力.
第12页
选修3-4 机械振动与机械波 光 电磁波与相对论
高考调研
高三物理 (新课标版)
• 2.周期和频率
• (1)定义:周期指振动物体完成一次全振动所需时间;符号: T;单位:秒(s).
• 频率指单位时间内完成全振动的次数;符号:f;单位:赫 兹(Hz).
• (2)物理意义:都是表征振动快慢的物理量.
高考调研
高三物理 (新课标版)
• 【例3】 (2013·课标全国)如图所示,一轻弹簧一端固定, 另一端连接一物块构成弹簧振子,该物块是由a、b两个小 物块粘在一起组成的.物块在光滑水平面上左右振动,振 幅为A0,周期为T0.当物块向右通过平衡位置时,a、b之间 的粘胶脱开;以后小物块a振动的振幅和周期分别为A和T, 则A________A0(填“>”“<”或“=”), T________T0(填“>”“<”或“=”).
教科版高中物理选修3-4全套PPT课件

5.简谐运动的加速度 (1)计算方法:a=-kx/m ,式中m表示振子的质量,k
表示比例系数,x表示振子距平衡位置的位移。
(2)特点:加速度大小随位移呈线性变化,方向只在平 衡位置发生改变。
典题强化
1.下列说法正确的是( )
A.弹簧振子的运动是简谐运动 B.简谐运动是机械运动中最简单、最基本的一种 C.做简谐运动的物体每次经过同一位置时,其速度、位移 都相同
D.做简谐运动的物体在平衡位置两侧对称的位置上,其速 度、位移都反向
三、 振幅、周期和频率
1.振幅(A)
(1)定义:振动物体离开平衡位置的
。
(2)物理意义:表示
,是
。
2.全振动
简谐运动的物体完成一个完整的振动过程。
3.周期(T)和频率(f)
重点诠释
1.振幅与振动中几个常见量的关系 (1)振幅与位移的关系:
(2)位移的表示方法:以平衡位置为坐标原点,以振动 所在的直线为坐标轴,规定正方向,则某时刻振子偏离平衡 位置的位移可用该时刻振子所在位置的坐标来表示。
3.简谐运动的回复力
(1)由F=-kx知,简谐运动的回复力大小与振子的位移 大小成正比,回复力的方向与位移的方向相反,即回复力的 方向总是指向平衡位置。
四、 简谐运动的能量
1.弹簧振子振动过程中的能量转化
如图所示,弹簧振子以O为平衡位置,在BC间振
动,则在从B到O过程中,动能 ,弹性势
能 ,当运动到O时,动能
,弹性势
能
。
2.简谐运动的能量
简谐运动的能量是指振动系统的
,振动
的过程就是 和
相互转化的过程,在简谐
运动中,振动系统的机械能 。
重点诠释
(1)如图所示,一弹簧振子在B 、 C之间振动,O点为 平衡位置。
表示比例系数,x表示振子距平衡位置的位移。
(2)特点:加速度大小随位移呈线性变化,方向只在平 衡位置发生改变。
典题强化
1.下列说法正确的是( )
A.弹簧振子的运动是简谐运动 B.简谐运动是机械运动中最简单、最基本的一种 C.做简谐运动的物体每次经过同一位置时,其速度、位移 都相同
D.做简谐运动的物体在平衡位置两侧对称的位置上,其速 度、位移都反向
三、 振幅、周期和频率
1.振幅(A)
(1)定义:振动物体离开平衡位置的
。
(2)物理意义:表示
,是
。
2.全振动
简谐运动的物体完成一个完整的振动过程。
3.周期(T)和频率(f)
重点诠释
1.振幅与振动中几个常见量的关系 (1)振幅与位移的关系:
(2)位移的表示方法:以平衡位置为坐标原点,以振动 所在的直线为坐标轴,规定正方向,则某时刻振子偏离平衡 位置的位移可用该时刻振子所在位置的坐标来表示。
3.简谐运动的回复力
(1)由F=-kx知,简谐运动的回复力大小与振子的位移 大小成正比,回复力的方向与位移的方向相反,即回复力的 方向总是指向平衡位置。
四、 简谐运动的能量
1.弹簧振子振动过程中的能量转化
如图所示,弹簧振子以O为平衡位置,在BC间振
动,则在从B到O过程中,动能 ,弹性势
能 ,当运动到O时,动能
,弹性势
能
。
2.简谐运动的能量
简谐运动的能量是指振动系统的
,振动
的过程就是 和
相互转化的过程,在简谐
运动中,振动系统的机械能 。
重点诠释
(1)如图所示,一弹簧振子在B 、 C之间振动,O点为 平衡位置。
高考备考指南物理课件选修3-4第1讲机械振动和振动图像
选修3-4 机械振动和光学(选考)
高考备考指南
理科综合 物理
例1 (多选)(2018年济宁期末)关于水平放置的弹簧振子的简谐运动,下列说法
正确的是( )
A.加速度的方向总是由振子所在处指向平衡位置
B.位移的方向总是由振子所在处指向平衡位置
C.经过半个周期振子经过的路程一定为振幅的2倍
D.若两时刻相差半个周期,弹簧在这两个时刻的形变量一定相等
选修3-4
机械振动和光学(选考)
第1讲 机械振动和振动图像
高考备考指南
理科综合 物理
【考纲解读】 1.知道简谐运动的概念,理解简谐运动的表达式和图像.2.知道什 么是单摆,知道在摆角较小的情况下单摆的运动是简谐运动,熟记单摆的周期公 式.3.理解受迫振动和共振的概念,掌握产生共振的条件.
栏目索引
选修3-4 机械振动和光学(选考)
栏目索引
选修3-4 机械振动和光学(选考)
高考备考指南
7.简谐运动的两种基本模型
项目
弹簧振子(水平)
理科综合 物理 单摆
模型 示意图
条件
忽略弹簧质量、无摩擦阻力 细线不可伸长,质量忽略,无空气阻
栏目索引
等
力等,摆角很小
选修3-4 机械振动和光学(选考)
高考备考指南
理科综合 物理
项目 平衡位置
回复力
E.振子的动能相等时,弹簧的长度不一定相等
栏目索引
【答案】ACE
选修3-4 机械振动和光学(选考)
高考备考指南
理科综合 物理
【解析】弹簧振子的振动周期 T=2π mk ,振子质量越大,振动系统的周期越
长,选项 A 正确.振幅越大则机械能越大.而能量与周期、振子质量及频率等均无
高三物理一轮复习人教版优质课件选修3-4第1章第1讲机械振动
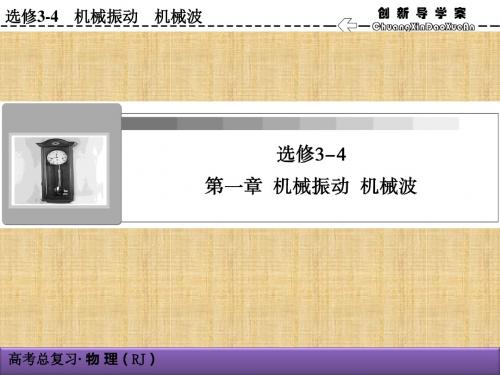
4.对称性特征 T 2n+1T (1)相隔2或 (n 为正整数)的两个时刻,振子位置关于 2 平衡位置对称,位移、速度、加速度大小相等,方向相反。
(2)如图所示,振子经过关于平衡位置 O 对称的两点 P、 P′(OP=OP′)时,速度的大小、动能、势能相等,相对于平衡 位置的位移大小相等。 (3)振子由 P 到 O 所用时间等于由 O 到 P′所用时间, 即 tPO =tOP′。
高考总复习· 物 理(RJ)
选修3-4 机械振动 机械波
第 1讲
机械振动
1.概念:质点的位移与时间的关系遵从 正弦函数 的规 律,即它的振动图象(x -t图象)是一条 正弦函数 。
2.简谐运动的表达式
-kx (1)动力学表达式:F= 位移 与
高考总复习· 物 理(RJ)
,其中“-”表示回复力
的方向相反。
选修3-4 机械振动 机械波
(2)从正的最大位移处开始计时,函数表达式为x= Acos ωt , 图象如图乙所示。
2.一质点做简谐运动的振动图象如下图所示。
高考总复习· 物 理(RJ)
选修3-4 机械振动 机械波
(1)该质点振动的振幅是________cm。周期是________s, 初相是________。 (2)写出该质点做简Hale Waihona Puke 运动的表达式,并求出当t=1 s时质
高考总复习· 物 理(RJ)
选修3-4 机械振动 机械波
(4)振子往复过程中通过同一段路程 (如 OP段) 所用时间相 等,即tOP=tPO。 5.能量特征:振动的能量包括动能Ek和势能Ep,简谐运
动过程中,系统动能与势能相互转化,系统的机械能守恒。
1.关于简谐振动,以下说法中正确的是( A.回复力总指向平衡位置 B.加速度、速度方向永远一致
(2)如图所示,振子经过关于平衡位置 O 对称的两点 P、 P′(OP=OP′)时,速度的大小、动能、势能相等,相对于平衡 位置的位移大小相等。 (3)振子由 P 到 O 所用时间等于由 O 到 P′所用时间, 即 tPO =tOP′。
高考总复习· 物 理(RJ)
选修3-4 机械振动 机械波
第 1讲
机械振动
1.概念:质点的位移与时间的关系遵从 正弦函数 的规 律,即它的振动图象(x -t图象)是一条 正弦函数 。
2.简谐运动的表达式
-kx (1)动力学表达式:F= 位移 与
高考总复习· 物 理(RJ)
,其中“-”表示回复力
的方向相反。
选修3-4 机械振动 机械波
(2)从正的最大位移处开始计时,函数表达式为x= Acos ωt , 图象如图乙所示。
2.一质点做简谐运动的振动图象如下图所示。
高考总复习· 物 理(RJ)
选修3-4 机械振动 机械波
(1)该质点振动的振幅是________cm。周期是________s, 初相是________。 (2)写出该质点做简Hale Waihona Puke 运动的表达式,并求出当t=1 s时质
高考总复习· 物 理(RJ)
选修3-4 机械振动 机械波
(4)振子往复过程中通过同一段路程 (如 OP段) 所用时间相 等,即tOP=tPO。 5.能量特征:振动的能量包括动能Ek和势能Ep,简谐运
动过程中,系统动能与势能相互转化,系统的机械能守恒。
1.关于简谐振动,以下说法中正确的是( A.回复力总指向平衡位置 B.加速度、速度方向永远一致
高考物理一轮复习选修34第1讲机械振动课件高三选修34物理课件

周期
与_振__幅__无关
T=_2___gl__
_弹__性__势__能__与_动__能__ _重__力__势__能__与_动__能__
能量转化 的相互转化,机械 的相互转化,机械
能守恒
能守恒
知识点4:受迫振动和共振(b) 1.三种振动形式的比较:
振动类型 自由
比较项目
振动
受迫振动
受力情况
仅受 回复 力
比较项目
受迫振动
共振
振动能量
振动物体 由产生驱动 振动物体获
的机械能 力的物体提 得的能量
_不__变__ 供
_最__大__
2.受迫振动中系统能量的变化:受迫振动系统机械能 _不__守__恒__,系统与外界时刻进行能量交换。
【秒判正误】 (1)简谐运动是匀变速运动。 ( × ) (2)简谐运动的平衡位置就是质点所受合力为零的位 置。 ( × ) (3)简谐运动的周期与振幅成正比,振幅就是简谐运动 物体的位移。 ( × ) (4)简谐运动的回复力可以是恒力。 ( × )
4.描述简谐运动的物理量:
物理量
定义
意义
由_平__衡__位__置__指向质 描述质点振动中某
位 移 点_所__在__位__置__的有向 时刻的位置相对于
线段
_平__衡__位__置__的位移
振动物体离开平衡 描述振动的_强__弱__和 振 幅 位置的_最__大__距__离__ 能量
物理量
定义
意义
振动物体完成一次
2.图象: (1)从平衡位置开始计时,函数表达式为x=_A_s_i_n_ω__t_,图 象如图甲所示。
(2)从最大位移处开始计时,函数表达式为x=_A_c_o_s_ω__t_, 图象如图乙所示。
沪科版物理选修3-4课件:第1章1.1

置 D.简谐运动中位移方向总与速度方向相反
栏目 导引
第1章
机械振动
解析:选A.弹簧振子的运动就是简谐运动,
但简谐运动有许多种,如水中浮标上下微小 的浮动,后面将要学习的单摆在空气中小角 度摆动都是简谐运动,它是机械振动中最基 本、最简单的一种,而机械运动中最基本、
最简单的一种是匀速直线运动,因此A正确,
栏目 导引
第1章
机械振动
【精讲精析】
振动物体的位移是从平衡位
置O到振子所在位置的有向线段,所以振子
在OB之间运动时,位移为正,在AO间运动 时,其位移为负,而加速度总与位移方向相 反,在O右侧时为负,在O左侧时为正.在C 处时,振子运动方向不定,其速度可能为正
值,也可能为负值.
栏目 导引
第1章
机械振动
栏目 导引
第1章
机械振动
(3)周期与频率的关系:周期和频率都是表示 振动快慢 物体____________的物理量.它们的关系是
T=1/f ________.在国际单位制中,周期的单位是
秒 赫兹 ____.频率的单位是______,1 Hz=1 s-1. 2.振幅:振动物体在振动过程中离开平衡位 最大位移 置的____________叫做振动的振幅.振幅是 标量 __________,用A表示,单位是米(m).
栏目 导引
第1章
机械振动
热点示例创新拓展
简Hale Waihona Puke 运动的对称性 [经典案例] (8分)一个做简
谐运动的质点,先后以同样的速度通过相距
10 cm的A、B两点,历时0.5 s(如图所示),
过B点后再经过t=0.5 s,质点以大小相等、 方向相反的速度再次通过B点.试求:质点 振动的周期是多少?
栏目 导引
第1章
机械振动
解析:选A.弹簧振子的运动就是简谐运动,
但简谐运动有许多种,如水中浮标上下微小 的浮动,后面将要学习的单摆在空气中小角 度摆动都是简谐运动,它是机械振动中最基 本、最简单的一种,而机械运动中最基本、
最简单的一种是匀速直线运动,因此A正确,
栏目 导引
第1章
机械振动
【精讲精析】
振动物体的位移是从平衡位
置O到振子所在位置的有向线段,所以振子
在OB之间运动时,位移为正,在AO间运动 时,其位移为负,而加速度总与位移方向相 反,在O右侧时为负,在O左侧时为正.在C 处时,振子运动方向不定,其速度可能为正
值,也可能为负值.
栏目 导引
第1章
机械振动
栏目 导引
第1章
机械振动
(3)周期与频率的关系:周期和频率都是表示 振动快慢 物体____________的物理量.它们的关系是
T=1/f ________.在国际单位制中,周期的单位是
秒 赫兹 ____.频率的单位是______,1 Hz=1 s-1. 2.振幅:振动物体在振动过程中离开平衡位 最大位移 置的____________叫做振动的振幅.振幅是 标量 __________,用A表示,单位是米(m).
栏目 导引
第1章
机械振动
热点示例创新拓展
简Hale Waihona Puke 运动的对称性 [经典案例] (8分)一个做简
谐运动的质点,先后以同样的速度通过相距
10 cm的A、B两点,历时0.5 s(如图所示),
过B点后再经过t=0.5 s,质点以大小相等、 方向相反的速度再次通过B点.试求:质点 振动的周期是多少?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
做初相.
3.回复力 (1)定义:使物体返回到__平__衡__位__置____的力. (2)方向:时刻指向__平__衡__位__置___. (3)来源:振动物体所受的沿__振__动__方__向____的合力.
4.描述简谐运动的物理量
物理量 位移
定义
由__平__衡___位__置指向质点 _所___在__位___置的有向线段
(4分)
(3)振子经过一个周期位移为零,路程为5×4 cm=20 cm,前100 s
刚好经过了25个周期,所以前100 s振子位移x=0, (1分)
振子路程s=20×25 cm=500 cm=5 m. 答案:(1)x=5sin t(cm) (2)见规范解答
2
(3)0 5 m
(1分)
【总结提升】简谐运动问题的求解思路
(1)应用简谐运动的表达式x=Asin(ωt+φ)解决简谐运动问题,
首先要明确表达式中各物理量的意义,找到各物理量对应的数值, 根据ω= 2=2πf确定此三个描述振动快慢的物理量间的关系.
T
对于同一质点的振动,不同形式的简谐运动位移表达式初相位并
不相同. (2)求解简谐运动问题的有效方法就是紧紧抓住一个模型——水
(2)平衡位置是回复力等于零的位置,但合力不等于零.
(3)公式T=2π l ,可以把l理解为等效摆长L′并不一定是绳
g
长,其大小等于悬点到球心的距离;把g理解为等效重力加速度
g′,其值等于单摆所处的相应的平衡位置且不摆动时(即摆球
相对悬点静止,不管悬点如何运动还是受别的力作用)摆线的拉
力F与摆球质量的比值,即g′= F .这样,等效单摆的周期公式
单摆
摆球_重__力___沿与摆
线垂直方向的分力
不作要求
T=
2 l g
弹性势能与动能相
互转化,机___械__能_守
恒
重力势能与动能相互
转化,_机__械___能_守恒
1.弹簧振子(是一种理想化的模型)的理解 (1)水平方向的弹簧振子,回复力是弹簧的弹力,振动过程中动 能和弹性势能间相互转化. (2)竖直方向的弹簧振子,回复力是弹簧的弹力和重力的合力, 振动过程中动能、弹性势能以及重力势能间相互转化. 2.单摆的理解 (1)回复力由重力的切向分力提供,在偏角最大时,回复力也可 以说成拉力和重力的合力.
由驱动力的周期 或频率决定,即 T=T驱或f=f驱
T驱=T固或f驱=f固
振动类型 比较项目
自由振动
振动能量
振动物体的 机械能不变
受迫振动
共振
由产生驱动力 的物体提供
振动物体获得 的能量最大
常见例子
弹簧振子或单摆 (θ<10°)
机械工作时底座 发生的振动
共振筛、转速 计等
考点5 实验:用单摆测定重力加速度
2.图象信息 (1)由图象可以得出质点做简谐运动的振幅、周期. (2)可以确定某时刻质点离开平衡位置的位移. (3)可以根据图象确定某时刻质点回复力、加速度和速度的方向. ①回复力和加速度的方向:因回复力总是指向平衡位置,故回 复力和加速度在图象上总是指向t轴. ②速度的方向:速度的方向可以通过下一时刻位移的变化来判 定,下一时刻位移如增加,振动质点的速度方向就是远离t轴, 下一时刻位移如减小,振动质点的速度方向就是指向t轴.
第1讲 机械振动
考点1 简谐运动
1.概念:质点的位移与时间的关系遵从__正__弦__函__数___的规律,即 它的振动图象(x-t图象)是一条__正__弦__曲__线__ 2.简谐运动的表达式 (1)动力学表达式:F=____-_k_x___,其中“-”表示回复力与_位__移__ 的方向相反.
(2)运动学表达式:x=Asin(ωt+φ),其中A代表振幅,ω=__2_π__f_ 表示简谐运动的快慢,(ωt+φ)代表简谐运动的__相__位___,φ叫
意义 描述质点振动中某时刻的位置相对
于__________平的衡位移位置
振幅 周期 频率 相位
振动物体离开平衡位置的
______最___大_ 距离
描述振动的__强__弱__和能量
振动物体完成一次
__全__振___动_所需时间
振动物体___单___位__时_内间完成
全振动的次数
描述振动的_____快__,慢两者互为倒
(4)摆球振动时,要使之保持在同一个竖直平面内,不要形成圆 锥摆. (5)计算单摆的振动次数时,应从摆球通过最低位置时开始计时, 为便于计时,可在摆球平衡位置的正下方作一标记.以后摆球每 次从同一方向通过最低位置时进行计数,且在数“零”的同时 按下秒表,开始计时计数.
简谐运动的特征 【例证1】(多选)如图所示,一轻弹簧与质量为m的物体组成弹 簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡 位置,C为AO的中点,已知CO=h,弹簧的劲度系数为k.某时刻物 体恰好以大小为v的速度经过C点并向上运动.则以此时刻开始半 个周期的时间内,对质量为m的物体,下列说法正确的是( )
则圆频率ω= 2 =rad/s,
(1分)
T2
故该振子做简谐运动的表达式为:x=5
sin
t(cm)(2分)
2
(2)由图可知,在t=2 s时振子恰好通过平衡位置,此时加速度为
零,随着时间的延续,位移值不断加大,加速度的值也变大,速度
值不断变小,动能不断减小,弹性势能逐渐增大.当t=3 s时,加速
度的值达到最大,速度等于零,动能等于零,弹性势能达到最大值.
数:
T= 1
f
ωt+φ
描述周期性运动在各个时刻所处的
_________不_ 同状态
简谐运动的五个特征 1.动力学特征:F=-kx,“-”表示回复力的方向与位移方向相反, k是比例系数,不一定是弹簧的劲度系数. 2.运动学特征:简谐运动的加速度与物体偏离平衡位置的位移成 正比而方向相反,为变加速运动,远离平衡位置时,x、F、a、 Ep均增大,v、Ek均减小,靠近平衡位置时则相反. 3.运动的周期性特征:相隔T或nT的两个时刻振子处于同一位置 且振动状态相同.
tOP=tPO. 5.能量特征:振动的能量包括动能Ek和势能Ep,简谐运动过程中, 系统动能与势能相互转化,系统的机械能守恒.
考点2 简谐运动的图象
1.物理意义:表示振子的_位__移___随时间变化的规律,为正弦(或 余弦)曲线 2.简谐运动的图象 (1)从平衡位置开始计时,把开始运动的方向规定为正方向,函 数表达式为x=__A_s_i_n_ω__t_,图象如图甲所示.
【总结提升】解答本题的关键是要明确简谐运动具有对称性的 特点,竖直方向的弹簧振子做简谐运动的回复力是重力和弹簧 弹力的合力,以及重力做功与路径无关的特点.对易错选项及错 误原因具体分析如下:
易错角度
错误原因
易错选B
在确定A项正确的基础上,与水平放置的弹簧振子类比,认为 回复力是弹簧的弹力,弹簧振子受到重力和回复力两个力, 半个周期内振子动能的变化为零,由动能定理知回复力做的 功与重力做的功的代数和为零,即W-2mgh=0,因此错选B 项.实际上竖直方向的弹簧振子的回复力是重力和弹簧弹力的 合力提供的
.
2.注意事项 (1)选择材料时应选择细、轻又不易伸长的线,长度一般在1 m 左右,小球应选用密度较大的金属球,直径应较小,最好不超 过2 cm. (2)单摆悬线的上端不可随意卷在铁夹的杆上,应夹紧在铁夹中, 以免摆动时发生摆线下滑、摆长改变的现象. (3)摆动时注意控制摆线偏离竖直方向不超过10°.可通过估算 振幅的办法掌握.
易错角度 易漏选C
错误原因
忽视了速度是矢量,误将速度作为标量,求速度 的变化量应按照矢量运算法则,即平行四边形定 则来计算
易错选D
审题不仔细,误将C点当做振动的平衡位置,而 实际上O点才是振动的平衡位置
简谐运动的公式与图象 【例证2】(12分)如图所示为一弹簧振子的振动图象,试完成以 下问题:
(1)写出该振子简谐运动的表达式. (2)在第2 s末到第3 s末这段时间内,弹簧振子的加速度、速度、 动能和弹性势能各是怎样变化的? (3)该振子在前100 s的总位移是多少?路程是多少?
42l
g
T2
中算出重力加速度g的值,再算出g的平均值,即为
T2
当地的重力加速度的值.
方法二:图象法
由单摆的周期公式T=2π
l g
可得l=
g 42
T2
,
因此以摆长l为纵轴,以T2为横轴作出的
l-T2图象是一条过原点的直线,如图所
示,求出图线的斜率k,即可求出g值.
g=4π2k,
k=
l T2
=
l T2
平方向振动的弹簧振子,熟练掌握振子的振动过程以及振子振动
过程中各量的变化规律,遇到简谐运动问题,头脑中立即呈现出
考点3 简谐运动的两种模型
名称 项目 模型示意图
做简谐运动 的条件
平衡位置
水平弹簧振子
①忽略弹簧质量
②无__摩__擦___③在弹簧弹
性限度内
弹簧处于_原___长_处
单摆
①细线不可伸缩②摆球
足ቤተ መጻሕፍቲ ባይዱ小且密___度__大_③摆角
很小 小球运动轨迹的最低点
名称 项目
回复力
周期公式
能量转化
水平弹簧振子
弹簧的_弹__力__提供
m
变为T=2π L .
g
考点4 受迫振动和共振
1.受迫振动 (1)概念:振动系统在周期性__驱__动__力___作用下的振动. (2)特点:受迫振动的频率等于__驱__动__力___的频率,跟系统的固 有频率__无__关____. 2.共振 (1)现象:当驱动力的频率等于系统的__固__有__频__率__时,受迫振动 的振幅最大.
(2)从正的最大位移处开始计时,函数表达式为x=__A_c_o_s_ω__t__,图 象如图乙所示.
3.回复力 (1)定义:使物体返回到__平__衡__位__置____的力. (2)方向:时刻指向__平__衡__位__置___. (3)来源:振动物体所受的沿__振__动__方__向____的合力.
4.描述简谐运动的物理量
物理量 位移
定义
由__平__衡___位__置指向质点 _所___在__位___置的有向线段
(4分)
(3)振子经过一个周期位移为零,路程为5×4 cm=20 cm,前100 s
刚好经过了25个周期,所以前100 s振子位移x=0, (1分)
振子路程s=20×25 cm=500 cm=5 m. 答案:(1)x=5sin t(cm) (2)见规范解答
2
(3)0 5 m
(1分)
【总结提升】简谐运动问题的求解思路
(1)应用简谐运动的表达式x=Asin(ωt+φ)解决简谐运动问题,
首先要明确表达式中各物理量的意义,找到各物理量对应的数值, 根据ω= 2=2πf确定此三个描述振动快慢的物理量间的关系.
T
对于同一质点的振动,不同形式的简谐运动位移表达式初相位并
不相同. (2)求解简谐运动问题的有效方法就是紧紧抓住一个模型——水
(2)平衡位置是回复力等于零的位置,但合力不等于零.
(3)公式T=2π l ,可以把l理解为等效摆长L′并不一定是绳
g
长,其大小等于悬点到球心的距离;把g理解为等效重力加速度
g′,其值等于单摆所处的相应的平衡位置且不摆动时(即摆球
相对悬点静止,不管悬点如何运动还是受别的力作用)摆线的拉
力F与摆球质量的比值,即g′= F .这样,等效单摆的周期公式
单摆
摆球_重__力___沿与摆
线垂直方向的分力
不作要求
T=
2 l g
弹性势能与动能相
互转化,机___械__能_守
恒
重力势能与动能相互
转化,_机__械___能_守恒
1.弹簧振子(是一种理想化的模型)的理解 (1)水平方向的弹簧振子,回复力是弹簧的弹力,振动过程中动 能和弹性势能间相互转化. (2)竖直方向的弹簧振子,回复力是弹簧的弹力和重力的合力, 振动过程中动能、弹性势能以及重力势能间相互转化. 2.单摆的理解 (1)回复力由重力的切向分力提供,在偏角最大时,回复力也可 以说成拉力和重力的合力.
由驱动力的周期 或频率决定,即 T=T驱或f=f驱
T驱=T固或f驱=f固
振动类型 比较项目
自由振动
振动能量
振动物体的 机械能不变
受迫振动
共振
由产生驱动力 的物体提供
振动物体获得 的能量最大
常见例子
弹簧振子或单摆 (θ<10°)
机械工作时底座 发生的振动
共振筛、转速 计等
考点5 实验:用单摆测定重力加速度
2.图象信息 (1)由图象可以得出质点做简谐运动的振幅、周期. (2)可以确定某时刻质点离开平衡位置的位移. (3)可以根据图象确定某时刻质点回复力、加速度和速度的方向. ①回复力和加速度的方向:因回复力总是指向平衡位置,故回 复力和加速度在图象上总是指向t轴. ②速度的方向:速度的方向可以通过下一时刻位移的变化来判 定,下一时刻位移如增加,振动质点的速度方向就是远离t轴, 下一时刻位移如减小,振动质点的速度方向就是指向t轴.
第1讲 机械振动
考点1 简谐运动
1.概念:质点的位移与时间的关系遵从__正__弦__函__数___的规律,即 它的振动图象(x-t图象)是一条__正__弦__曲__线__ 2.简谐运动的表达式 (1)动力学表达式:F=____-_k_x___,其中“-”表示回复力与_位__移__ 的方向相反.
(2)运动学表达式:x=Asin(ωt+φ),其中A代表振幅,ω=__2_π__f_ 表示简谐运动的快慢,(ωt+φ)代表简谐运动的__相__位___,φ叫
意义 描述质点振动中某时刻的位置相对
于__________平的衡位移位置
振幅 周期 频率 相位
振动物体离开平衡位置的
______最___大_ 距离
描述振动的__强__弱__和能量
振动物体完成一次
__全__振___动_所需时间
振动物体___单___位__时_内间完成
全振动的次数
描述振动的_____快__,慢两者互为倒
(4)摆球振动时,要使之保持在同一个竖直平面内,不要形成圆 锥摆. (5)计算单摆的振动次数时,应从摆球通过最低位置时开始计时, 为便于计时,可在摆球平衡位置的正下方作一标记.以后摆球每 次从同一方向通过最低位置时进行计数,且在数“零”的同时 按下秒表,开始计时计数.
简谐运动的特征 【例证1】(多选)如图所示,一轻弹簧与质量为m的物体组成弹 簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡 位置,C为AO的中点,已知CO=h,弹簧的劲度系数为k.某时刻物 体恰好以大小为v的速度经过C点并向上运动.则以此时刻开始半 个周期的时间内,对质量为m的物体,下列说法正确的是( )
则圆频率ω= 2 =rad/s,
(1分)
T2
故该振子做简谐运动的表达式为:x=5
sin
t(cm)(2分)
2
(2)由图可知,在t=2 s时振子恰好通过平衡位置,此时加速度为
零,随着时间的延续,位移值不断加大,加速度的值也变大,速度
值不断变小,动能不断减小,弹性势能逐渐增大.当t=3 s时,加速
度的值达到最大,速度等于零,动能等于零,弹性势能达到最大值.
数:
T= 1
f
ωt+φ
描述周期性运动在各个时刻所处的
_________不_ 同状态
简谐运动的五个特征 1.动力学特征:F=-kx,“-”表示回复力的方向与位移方向相反, k是比例系数,不一定是弹簧的劲度系数. 2.运动学特征:简谐运动的加速度与物体偏离平衡位置的位移成 正比而方向相反,为变加速运动,远离平衡位置时,x、F、a、 Ep均增大,v、Ek均减小,靠近平衡位置时则相反. 3.运动的周期性特征:相隔T或nT的两个时刻振子处于同一位置 且振动状态相同.
tOP=tPO. 5.能量特征:振动的能量包括动能Ek和势能Ep,简谐运动过程中, 系统动能与势能相互转化,系统的机械能守恒.
考点2 简谐运动的图象
1.物理意义:表示振子的_位__移___随时间变化的规律,为正弦(或 余弦)曲线 2.简谐运动的图象 (1)从平衡位置开始计时,把开始运动的方向规定为正方向,函 数表达式为x=__A_s_i_n_ω__t_,图象如图甲所示.
【总结提升】解答本题的关键是要明确简谐运动具有对称性的 特点,竖直方向的弹簧振子做简谐运动的回复力是重力和弹簧 弹力的合力,以及重力做功与路径无关的特点.对易错选项及错 误原因具体分析如下:
易错角度
错误原因
易错选B
在确定A项正确的基础上,与水平放置的弹簧振子类比,认为 回复力是弹簧的弹力,弹簧振子受到重力和回复力两个力, 半个周期内振子动能的变化为零,由动能定理知回复力做的 功与重力做的功的代数和为零,即W-2mgh=0,因此错选B 项.实际上竖直方向的弹簧振子的回复力是重力和弹簧弹力的 合力提供的
.
2.注意事项 (1)选择材料时应选择细、轻又不易伸长的线,长度一般在1 m 左右,小球应选用密度较大的金属球,直径应较小,最好不超 过2 cm. (2)单摆悬线的上端不可随意卷在铁夹的杆上,应夹紧在铁夹中, 以免摆动时发生摆线下滑、摆长改变的现象. (3)摆动时注意控制摆线偏离竖直方向不超过10°.可通过估算 振幅的办法掌握.
易错角度 易漏选C
错误原因
忽视了速度是矢量,误将速度作为标量,求速度 的变化量应按照矢量运算法则,即平行四边形定 则来计算
易错选D
审题不仔细,误将C点当做振动的平衡位置,而 实际上O点才是振动的平衡位置
简谐运动的公式与图象 【例证2】(12分)如图所示为一弹簧振子的振动图象,试完成以 下问题:
(1)写出该振子简谐运动的表达式. (2)在第2 s末到第3 s末这段时间内,弹簧振子的加速度、速度、 动能和弹性势能各是怎样变化的? (3)该振子在前100 s的总位移是多少?路程是多少?
42l
g
T2
中算出重力加速度g的值,再算出g的平均值,即为
T2
当地的重力加速度的值.
方法二:图象法
由单摆的周期公式T=2π
l g
可得l=
g 42
T2
,
因此以摆长l为纵轴,以T2为横轴作出的
l-T2图象是一条过原点的直线,如图所
示,求出图线的斜率k,即可求出g值.
g=4π2k,
k=
l T2
=
l T2
平方向振动的弹簧振子,熟练掌握振子的振动过程以及振子振动
过程中各量的变化规律,遇到简谐运动问题,头脑中立即呈现出
考点3 简谐运动的两种模型
名称 项目 模型示意图
做简谐运动 的条件
平衡位置
水平弹簧振子
①忽略弹簧质量
②无__摩__擦___③在弹簧弹
性限度内
弹簧处于_原___长_处
单摆
①细线不可伸缩②摆球
足ቤተ መጻሕፍቲ ባይዱ小且密___度__大_③摆角
很小 小球运动轨迹的最低点
名称 项目
回复力
周期公式
能量转化
水平弹簧振子
弹簧的_弹__力__提供
m
变为T=2π L .
g
考点4 受迫振动和共振
1.受迫振动 (1)概念:振动系统在周期性__驱__动__力___作用下的振动. (2)特点:受迫振动的频率等于__驱__动__力___的频率,跟系统的固 有频率__无__关____. 2.共振 (1)现象:当驱动力的频率等于系统的__固__有__频__率__时,受迫振动 的振幅最大.
(2)从正的最大位移处开始计时,函数表达式为x=__A_c_o_s_ω__t__,图 象如图乙所示.
