七年级11.14
2014.11.14七年级期中考试试卷分析
Friend ’s name Alice Miller
第2页,共7页。
单项选择
21 22 23 24 25 26 27 28 29 30 AC C AB AC C B C 31 32 33 34 35 BBCCA
词语填空
36 37 38 39 40 41 42 43 44 45 C AAAB C C B C B
第3页,共7页。
阅读选择A
50 Mary(09:45:10a.m.)
Hi, Jim. Nice to meet you! I’m a girl. My name is Mar4y7Green4.6My favorite color is red. My telephone number is 873-3516.
阅读选择B
52
Good afternoon, boys and girls. I’m Li Hong. I’m an E5n1glish boy. Li Hong is my Chinese name. Look, this
is a picture of my family. The tall man is my father.
53
His
name
is
Ken
Martin5. 4Thisismymother,
Sandy
Jordan. Who’s that little girl? She is my sister, Lucy. Can you find me in the picture5?5I’m the boy in blue.
总体分析
及格人数 及格率 优秀人数 优秀率
C151
48
97.96 %
42
85.71 %
七年级11月份数学训练课(一)
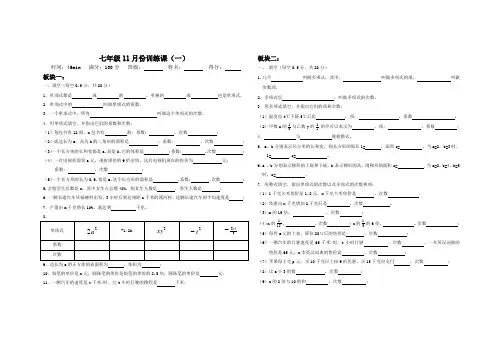
七年级11月份训练课(一)时间:45min 满分:100分班级:姓名:得分:板块一:一、填空(每空0.5分,共20分)1.单项式都是或的,单独的或也是单项式。
2.单项式中的叫做单项式的系数。
3.一个单项式中,所有叫做这个单项式的次数。
4.用单项式填空,并指出它们的系数和次数:(1)每包书有12册,n包书有册;系数:,次数;(2)底边长为a,高为h的三角形的面积是;系数:,次数;(3)一个长方体的长和宽都是a,高是h,它的体积是;系数:,次数;(4)一台电视机原价a元,现按原价的9折出售,这台电视机现在的售价为元;系数:,次数;(5)一个长方形的长为0.9,宽是a,这个长方形的面积是。
系数:,次数;5.全校学生总数是x,其中女生占总数48%,则女生人数是,男生人数是;6.一辆长途汽车从杨柳村出发,3小时后到达相距s千米的溪河村,这辆长途汽车的平均速度是;7.产量由m千克增长10%,就达到千克。
8.9.边长为a的正方体的表面积为,体积为;10.铅笔的单价是x元,圆珠笔的单价是铅笔的单价的2.5倍,圆珠笔的单价是元;11.一辆汽车的速度是v千米/时,它t小时行驶的路程是千米;板块二:一、填空(每空0.5分,共20分)1.几个叫做多项式,其中,叫做多项式的项,叫做常数项。
2.多项式里,叫做多项式的次数。
3.用多项式填空,并指出它们的项和次数:(1)温度由t℃下降5℃后是,项:,系数;(2)甲数x的31与乙数y的21的差可以表示为,项:,系数;4.与统称整式。
5.a、b分别表示长方形的长和宽,则长方形的周长l= ,面积s= ,当a=2,b=3时,l= ,s= 。
6.a 、b分别表示梯形的上底和下底,h表示梯形的高,则梯形的面积s= ,当a=2,b=4,h=5时,s= 。
7.用整式填空,指出单项式的次数以及多项式的次数和项:(1)1千克大米售价是1.2元,x千克大米售价是,次数;(2)体重由x千克增加2千克后是,次数。
七年级期中考试具体安排
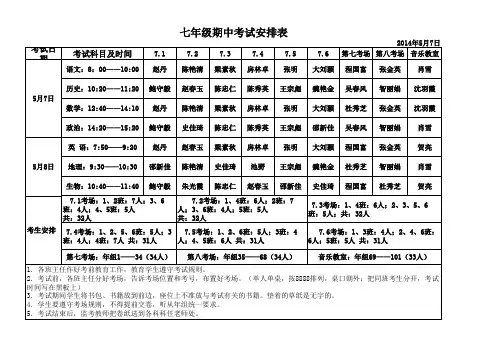
考试日期 考试科目及时间
语文:8:00——10:00 历史:10:20——11:20 5月7日 数学:12:40——14:10 政治:14:20——15:20 英 语:7:50——9:20 5月8日 地理:9:30——10:30 生物:10:40——11:40 赵丹 鲍守毅 赵丹 邵新佳 鲍守毅 陈艳清 史佳琦 赵春玉 陈艳清 朱光霞 梁素秋 陈忠仁 梁素秋 史佳琦 陈忠仁 房林卓 陈秀英 房林卓 池野 赵春玉 张明 王宗彪 张明 王宗彪 邵新佳 大刘颖 邵新佳 大刘颖 魏艳金 史佳琦 杜秀芝 吴春风 程国富 杜秀芝 程国富 张金英 智丽娟 张金英 智丽娟 杜秀芝 沈羽霞 肖雪 贺亮 肖雪 贺亮 7.1 赵丹 鲍守毅 7.2 陈艳清 赵春玉 7.3 梁素秋 陈忠仁 7.4 房林卓 陈秀英 7.5 张明 王宗彪 7.6 大刘颖 魏艳金 2014年5月7日 第七考场 第八考场 音乐教室 程国富 吴春风 张金英 智丽娟 肖雪 沈羽霞
Hale Waihona Puke 7.1考场:1、2班:7人;3、6 班:4人;4、5班:5人 共:32人 考生安排
7.2考场:1、4班:6人;2班:7 人;3、6班:4人;5班:5人 共:32人
7.3考场:1、4班:6人;2、3、5、6 班:5人;共:32人 7.6考场:1、3班:4人;2、4、6班: 6人;5班:5人 共:31人 音乐教室:年组69——101(33人)
7.4考场:1、2、5、6班:5人;3 7.5考场:1、2、6班:5人;3班:4 班:4人;4班:7人 共:31人 人;4、5班:6人 共:31人 第七考场:年组1——34(34人) 第八考场:年组35——68(34人)
1.各班主任作好考前教育工作,教育学生遵守考试规则。 2.考试前,各班主任分好考场,告诉考场位置和考号,布置好考场。(单人单桌,按8888排列,桌口朝外;把同班考生分开,考试 时间写在黑板上) 3.考试期间学生将书包、书籍放到前边,座位上不准放与考试有关的书籍。垫着的草纸是无字的。 4.学生要遵守考场规则,不得提前交卷,听从年组统一要求。 5.考试结束后,监考教师把卷纸送到各科科任老师处。
部编版道德与法治七年级上册教学计划

部编版道德与法治七年级上册教学计划一、教学目标课程标准明确规定:“道德与法治课是一门综合课程,教材体现了综合性、过程性、实践性特点。
”据此,以初中学生生活经验为依据,以青春生命在与他人、与集体、与社会、与国家以及全球关系中的自我发展为线索,以培养社会主义合格公民为中心,遵循生活逻辑,整合道德、心理、法律及国情方面的知识领域,凝练三年六册教材各个单元的学习主题,统筹安排各年级教育。
二、教材分析第一单元:第一单元作为对初中生活开端的理性阐述,具有统领全套教材的意义,既是学生整个初中道德与法治课程的学习起点,也是全套教材建构的逻辑起点。
对于刚刚步入中学校门的学生而言,中学时代是一个全新的人生阶段的开始。
面对生活和学习的变化,学生会有各种感受,也可能有各种困惑和问题。
教材不是让学生被动去适应这些变化,而是把变化看成是生命成长馈赠给自己的礼物,认识到新的阶段意味着新的机会和可能,接纳变化,在积极面对中学学习、自我探索等课题中中成长。
本单元以“成长的节拍”为主题,体现了学生初中生活的基调,映射出全套教材的青春文化底色。
第二单元:学会交往,处理交友中的问题既是学生道德和心理发展在本阶段的核心任务,也是初中生活逐步展开后学生实际的需要,在学生生命成长中具在重要的意义。
2016年 2月,《中国学生发展核心素养(征求意见稿)》出台,“积极交往,有效互动,建立和维良好的人际关系”被作为中国学生发展应具备的核心素养提出。
青少年期的同伴关系,不仅活动范围进一步扩大,朋友之间亲密感也进一步增加。
这一方面提高了中学生友谊的质量,另一方面,也对学生的交友态度和能力提出了更高的要求。
第三单元:过富有情趣的生活。
承接上一单元学会与同伴交往,本单元则是帮助学生正确处理师生关系、亲子关系和家庭关系,是人际交往的继续与延伸。
师长是中学生成长中的“重要他人”,学生和师长的关系如何,直接影响到学习和生活质量。
到了青春期以后,随着青少年自我意识的凸显,他们要求摆脱依赖、走向独立的愿望和行动增强,有时会和师长产生冲突。
七年级传统文化教案3篇

七年级传统文化教案3篇七年级传统文化教案1一、学生分析:学生经过小学六年的学习,对我国博大精深的传统文化有了初步的了解。
在七年级语文课本中有《论语·十则》,学生对《论语》的内容有了初步的背诵基础,大多数学生对祖国的文化表现出较浓郁的兴趣,借此时机,将传统文化精髓灌输课堂中,培养学生的学习兴趣,立志继承和发扬传统文化,让学生做个具有传统文化素养的中国人。
二、教材分析:(一)、教学目的要求:本套教材以齐鲁文化为主,反应中华传统文化精髓。
以诵读原创经典、感怀名人志士、游历名山胜水、品味艺术之乐为基本活动内容,旨在使民族文化得以血脉相承,使少年儿童受到中华传统文化的滋养,从而陶冶情操,开启心智,提升智趣,提高综合文化素养,激发爱国情感,培养民族气节。
(二)、教材结构:本册教材包括“经典驿站”“名人长廊”“文艺园林”“风土画卷”四个单元。
“经典驿站”:学习、谅解中华民族传统原创经典,受益于千古美文的文化滋养,培养对传统文化精髓的喜爱之情。
“名人长廊”:学习屈原、王羲之、魏征、文天祥等人的高xx质,学习他们的爱国精神。
教材基本呈现形式为:“经典回放”(呈现原创经典中精华部分);“”();“”()(三)教材编排原则:本教材突出了原典性、知识性、情感性、趣味性、实践性和地方特色,通过诵读、感悟、熏陶、探究、交流、合作等基本活动方式,达到提高学生综合文化素养的目的。
具体体现在以下三方面:1.坚持以人为本的原则,充分考虑到学生的年龄特点和兴趣特点,营造浓厚的探索实践氛围。
2.以提升学生素养为目的,逐步培养其良好得到人文素养,塑造其诚信向上的民族气节和人生信念。
3.注重培养学生的探究学习能力,培养其初步的探究学习能力,形成其积极的人生观和价值观。
三、教学中应注意的问题:1.要关注学生的主体性。
本教材形式多样活泼,遵循学生的认知规律,符合学生的心理体验,教学中要培养学生良好的品德。
2.要尊重学生的主动性。
教学要以“活”为基础,以“动”为特征,旨在倡导研究性学习方式。
上海市罗泾中学七年级数学上册 114 中心对称教案 沪教版五四制

(定义得出后点击幻灯片三的空白处,不要点练习或超链接)左图是一 幅中心对称图形,O是对称中心,你还可以怎么看?
[说明]问这个问题再次说明中心对称图形与中心对称这两者之间的联系。
请 你找出点 A绕点O旋转180°后的对应点B;
点C的对应点D在哪里?怎么找得?
你能很快的找到点E的对应点F吗?
3、画出四边形ABCD关于点O的中心对称的图形。
4、如图所示的两个图形成中心对称,你能找到对称 中心吗?
11.4中心对称
教学目标:
1、知道中心对称的意义及与中心对称图形的区别;
2.知道成中心对称的两个图形的性质,会判断两个图形是否成中心对称;
3.会画已知图形关于已知点成中心对称的图形;
教学重称与中心对称图形的区别与联系.
教学用具准备
多媒体课件
二、新课讲授
1、中心对称的意义
1、中心对称的概念:把一个图 形绕着某一点旋转180°,如果它能够和另一个图形重合,我们就说这两个图形成中心对称,这个点叫做对称中心,中心对称是旋转角为180°的旋转对称。
[ 说明]强调中心对称图形只是一个图形本身的性质,而中心对称是指两个图形之间的关系。
2、指出上图中的对应点、对应线段、 对应角。
3、总结概括
中心对称的特征:在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分。
中心对称的识别:如果两个图形的对应点连成的线段都经过某一点,并且被平分,那么这两个图形一定关于这点成中心对称.
作图题:
1、已知点A和点O,画出点B,使点A和点B关于点O成中心对称。
2、已知线段AB和点O,画出线段CD,使线段AB和线段CD关于点O成中心对称。
探究应用新思维数学7年级1140教学内容
当A 、B 两点中有一点在原点时,不妨设点A 在原点,如图①,AB OB b a b ==--|;当A 、B 两点都不在原点时,(1)如图②,点A 、B 都在原点的右边,AB OB OA b a b a a b =-=-=-=-;(2)如图③,点A 、B 都在原点的左边,()AB OB OA b a b a a b =-=-=---=- (3)如图④,点A 、B 在原点的两边,()AB OA OB a b a b a b =+=+=+-=-; 综上,数轴上A 、B 两点之间的距离AB a b =-.请回答:①数轴上表示2和5的两点之间的距离是_______,数轴上表示2-和5-的两点之间的距离是_______,数轴上表示1和3-的两点之间的距离是________;②数轴上表示x 和1-的两点A 和B 之间的距离是_______,如果2AB =,那么x 为_______; ③当代数式12x x ++-取最小值时,相应的x 的取值范围是_______.(南京市中考题)思维方法天地11.已知1a =,2b =,3c =,且a b c >>,那么a b c +-=________.(北京市“迎春杯”竞赛题)12.在数轴上,点A 表示的数是3x +,点B 表示的数是3x -,且A 、B 两点的距离为8,则x =________.(“五羊杯”竞赛题)13.已知5x =,1y =那么x y x y --+=________.(北京市“迎春杯”竞赛题)14.(1)11x x ++-的最小值为__________.(“希望杯”邀请赛试题)(2)111213x x x ++-++的最小值为________.(北京市“迎春杯”竞赛题)15.有理数a 、b 在数轴上对应的位置如图所示:,则代数式1111a ab a ba a ab b +---+-+--的值为( ). A.1-B.0C.1D.2 (“希望杯”邀请赛试题)16.若()2210m n ++-=,则2m n +的值为( ).A.4-B.1-C.0D.4(北京市中考题)17.如图,已知数轴上点A 、B 、C 所对应的数a 、b 、c 都不为0,且C 是AB 的中点.如果2220a b a c b c a b c +--+--+-=,那么原点O 的位置在( ).A.线段AC 上B.线段CA 的延长线上.iC.线段BC 上D.线段CB 的延长线上!(江苏省竞赛题)18.设1m x x =+-,则m 的最小值为( ). A.0B.1C.1-D.2(重庆市竞赛题)19.已知点A 在数轴上对应的数为a ,点B 对应的数为b ,且()2410a b ++-=,A 、B 之间的距离记作AB . (1)求线段的长AB ;(2)设点P 在数轴上对应的数为x ,当2PA PB -=时,求x 的值;(3)若点P 在A 的左侧,M 、N 分别是的中点,当点P 在A 的左侧移动时,式子PN PM -的值是否发生改变?若不变,请求其值;若发生变化,请说明理由. 20.已知a b c abcx a b c abc=+++,且a 、b 、c 都不等于0,求1的所有可能值.; (“华罗庚杯”香港中学竞赛题)应用探究乐园21.绝对值性质(1)设a 、b 为有理数,比较a b +与a b +的大小.(2)已知a 、b 、c 、d 是有理数,9a b -≤,16c d -≤,且25a b c d --+=,求b a dc ---的值.(“希望杯”邀请赛试题)22.已知数轴上两点A 、B 对应的数分别为1-,3,点P 为数轴上一动点,其对应的数为x . (1)若点P 到点A 、点B 的距离相等,求点P 对应的数.:(2)数轴上是否存在点P ,使点P 到点A 、点B 的距离之和为5?若存在,请求出x 的值;若不存在,请说明理由.(3)当点P 以每分钟1个单位长的速度从O 点向左运动时,点A 以每分钟5个单位长的速度向左运动,点B 以每分钟20个单位长的速度向左运动,问它们同时出发,几分钟后P 点到点A 、点B 的距离相等?3.有理数的运算解读课标有理数及其运算是整个数与代数的基础,有关式的所有运算都是建立在数的运算基础上.深刻理解有理数相关概念,掌握一定的有理数运算技能是数与代数学习的基础.有理数的运算不同于算术数的运算:这是因为有理数的运算每一步要确定符号,有理数的运算很多是字母运算,也就是常说的符号演算.运算能力是运算技能与推理能力的结合.这就要求我们既能正确地算出结果,又善于观察问题的结构特点,选择合理的运算路径,提高运算的速度.有理数运算常用的技巧与方法有: 利用运算律;以符代数;恰当分组;裂项相消;分解相约;错位相减等. 问题解决 例1(1)已知()()211,2,3,1n a n n ==+L ,记()1121b a =-,()()()()()21212211,,b 2111n n b a a a a a =--=---L L ,则通过计算推测n b 的表达式n b =_________.(用含n 的代数式表示)(成都市中考题)(2)若a 、b 是互为相反数,c 、d 是互为倒数,x 的绝对值等于2,则42x cdx a b +--的值是______.(“希望杯”邀请赛试题)试一试 对于(2),运用相关概念的特征解题.例2 已知整数a 、b 、c 、d 满足25abcd =,且a b c d >>>,那么a b c d +++等于( ).: A.0B.10C.2D.12(江苏省竞赛题)试一试 解题的关键是把25表示成4个不同整数的积的形式. 例3 计算: (1)1121231259233444606060⎛⎫⎛⎫⎛⎫++++++++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭L L ; (广西竞赛题)(2)111112123123100+++++++++++L L ; (“祖冲之杯”邀请赛试题)(3)77371217381727111385271739172739⎛⎫⎛⎫+-÷+- ⎪ ⎪⎝⎭⎝⎭. (“五羊杯”竞赛题)试一试 对于(1),设原式S =,将各括号反序相加;对于(2),若计算每个分母值,则易掩盖问题的实质,不妨先从考察一般情形入手;对于(3),视除数为一整体,从寻找被除数与除数的关系入手.例4 在数学活动中,小明为了求2341111122222n +++++L 的值(结果用n 表示),设计了如图所示的几何图形.图①图②(1)请你用这个几何图形求2341111122222n +++++L 的值; (2)请你用图②,再设计一个能求2341111122222n +++++L 的值的几何图形.(辽宁省大连市中考题)试一试 求原式的值有不同的解题方法,而剖分图形面积是构造图形的关键. 例5 在1,2,,2002L 前面任意添上正号和负号,求其非负和的最小值.分析与解 首先确定非负代数和的最小值的下限,然后通过构造法证明这个下限可以达到即可.整数的和差仍是整数,而最小的非负整数是0.代数和的最小值能是0吗?能是1吗?由于任意添“+”号或“-”号,形式多样,因此,不可能一一尝试再作解答,从奇数、偶数的性质入手. 因a b +与a b -的奇偶性相同,故所求代数和的奇偶性与()20021200212320012002100120032⨯++++++==⨯L 的奇偶性相同,即为奇数.因此,所求非负代数和不会小于1. 又()()()()1234567891011121314-++--++--++--+++Q L ()19992000200120021--+=,∴所求非负代数和的最小值为1.类比类比是一种推理方法,根据两#事物在某些特征上的相似,作出它们在其他特征上也可能相似的结论.触类旁通,即用类比的方法提出问题及寻求解决问题的途径和方法. 例6 观察下面的计算过程111111111111141122334451223344555⎛⎫⎛⎫⎛⎫⎛⎫+++=-+-+-+-=-= ⎪ ⎪ ⎪ ⎪⨯⨯⨯⨯⎝⎭⎝⎭⎝⎭⎝⎭. 问:(1)从上面的解题方法中,你发现了什么?用字母表示这一规律. (2)“学问”,既要学会解答,又要学会发问.爱因斯坦曾说:“提出问题比解决问题更重要”. 请用类比的方法尽可能多地提出类似的问题. 分析与解 (1)()11111n n n n =-++.(2)从连续自然数到连续偶数,从2个到3个,从分数到整数,类比可提出下列计算问题:①111244620122014+++⨯⨯⨯L ; ②111123234201220132014+++⨯⨯⨯⨯⨯⨯L ; ③12233420122013⨯+⨯+⨯++⨯L ;④22221232012++++L .数学冲浪知识技能广场1.如图,每一个小方格的面积为1,则可根据面积计算得到如下算式:()135721n +++++-=L _______.(用n 表示,n 是正整数).(第1题)(2012年潍坊市中考题)2.某数学活动小组的20位同学站成一列做报数游戏,规则是:从前面第一位同学开始,每位同学依次报自己顺序数的倒数加1,第1位同学报111⎛⎫+ ⎪⎝⎭,第2位同学报112⎛⎫+⎪⎝⎭,第3位同学报113⎛⎫+ ⎪⎝⎭……这样得到的20个数的积为________. (2012年河北省中考题)3.计算:(1)()211455365455211545545365⨯-+⨯-⨯+⨯=______.(“希望杯”邀请赛试题)(2)23181920223222-----+=L _______.(广西桂林市中考题)4.“数学王子”高斯从小就善于观察和思考,在他读小学时就能在课堂上快速地计算出12398991005050++++++=L ,今天我们可以将高斯的做法归纳如下: 1239899100S =++++++L ① 1009998321S =++++++L ② ①+②有()21100100S =+⨯,5050S =. 请类比以上做法,回答下列问题:若n 为正整数,()35721168n +++++=L ,则n =_______.(2012年湖北省黄石市中考题)5.设0a <,在代数式|a ,a -,2009a ,2010a,a -,2a a a ⎛⎫+ ⎪⎝⎭,2a a a ⎛⎫- ⎪⎝⎭中负数的个数是( ). A.1B.2C.3D.4(“希望杯”邀请赛试题)6.我国邮政国内外埠邮寄印刷品邮资标准如下:100克以内0.7元,每增加100克(不足100克按100克计)0.4元.某人从成都邮寄一本书到上海,书的质量为470克,则他应付邮资( )元.A.2.3B.2.6C.3D.3.5(2012年四川省竞赛题)7.为了求23200812222+++++L 的值,可令23200812222S +=++++L ,则2342009222222S ++++=+L ,,因此2009221S S -=-所以23200820091222221+++++=-L .仿照上面推理计算出23200915555+++++L 的值是( ). A.200951-B.201051-C.2009514-D.2010514-(湖北省鄂州市中考题)8.下面是按一定规律排列的一列数: 第1个数:11122-⎛⎫-+ ⎪⎝⎭; 第2个数:()()2311111113234⎛⎫⎛⎫---⎛⎫-+++ ⎪⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭; 第3个数:()()()()234511111111111423456⎛⎫⎛⎫⎛⎫⎛⎫-----⎛⎫-+++++ ⎪⎪⎪⎪ ⎪ ⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭; ……第n 个数:()()()232111111111112242n n n -⎛⎫⎛⎫⎛⎫----⎛⎫-++++ ⎪⎪ ⎪ ⎪ ⎪⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭L . 那么,在第10个数、第11个数、第12个数、第13个数中,最大的数是( ).A.第10个数B.第11个数C.第12个数D.第13个数(江苏省中考题)观察图形,解答问题:(1)按下表已填写的形式填写表中的空格:(2012年益阳市中考题)10.观察下列等式: 第1个等式:111111323a ⎛⎫==⨯- ⎪⨯⎝⎭; 第2个等式:2111135235a ⎛⎫==⨯- ⎪⨯⎝⎭ 第3个等式:3111157257a ⎛⎫==⨯- ⎪⨯⎝⎭ 第4个等式:4111179279a ⎛⎫==⨯- ⎪⨯⎝⎭; ……请解答下列问题:(1)按以上规律列出第5个等式:5a =______=_______;(2)用含n 的代数式表示第n 个等式n a =______=_______;(n 为正整数); (3)求1234100a a a a a +++++L 的值.(2012年广东省中考题)思维方法天地 11.计算: (1)11111111111113243546979998100⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+⨯+⨯+⨯+⨯⨯+⨯+= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⨯⨯⨯⨯⨯⨯⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭L ______.(“华罗庚杯”邀请赛试题)(2)1511914117111234567892612203042567290-+-+-+-+=_____. (“希望杯”邀请赛试题)(3)555111139139993311993311⎛⎫⎛⎫++÷++= ⎪ ⎪⎝⎭⎝⎭_____.(江苏省竞赛题)12.设三个互不相等的有理数,既可分别表示为1,a b +,a 的形式,又可分别表示为0,ab,b 的形式,则20042001a b +=______. 13.已知31x x =+,则()2005264489x x ++=______.(“五羊杯”竞赛题)14.已知a 、b 、c 满足()()()0a b b c c a +++=且0abc <,则代数式的a b ca b c++值是________.(四川省竞赛题)15.11111161111161621212626313136+++++⨯⨯⨯⨯⨯⨯的值是( ). A.118 B.136 C.133 D.166(北京市竞赛题)16.如果4个不同的正整数m 、n 、p 、q 满足()()()()77774m n p q ----=,那么m n p q +++等于( ). A.10 B.21C.24D.26E.2817.如果3121231t t t t t t ++=,那么123123t t t t t t 的值为( ). A.1-B.1C.1±D.不确定(河北省竞赛题)18.观察下列各式: (1)211=; (2)32343++=; (3)2345675++++=; (4)2456789107++++++=;……请你根据观察得到的规律判断下列各式正确的是( ).A.210051006100730162011++++=L 2B.210051006100730172011++++=LC.210061007100830162011++++=LD.210071008100930172011++++=L(济南市中考题)19.观察下面的等式:224⨯=,224+=; 313422⨯=,313422+=; 414533⨯=,414533+=; 515644⨯=,515644+=. (1)小明归纳上面各式得出一个猜想:“两个有理数的积等于这两个有理数的和”,小明的猜想正确吗?为什么?(2)请你观察上面各式的结构特点,归纳出一个猜想,并证明你的猜想.(“希望杯”邀请赛试题)20.同学们,我们曾经研究过n n ⨯的正方形网格,得到了网格中正方形的总数的表达式为2222123n ++++L .但n 为100时,应如何计算正方形的具体个数呢?下面我们就一起来研究并解决这个问题.首先,通过探究我们已经知道()()()10112231113n n n n n ⨯+⨯+⨯++-⨯=+-L 时,我们可以这样做:(1)观察并猜想:()()()()2212101112101212120112+=+⨯++⨯=+⨯++⨯=++⨯+⨯, ()()()2221231011121231012123++=+⨯++⨯++⨯=+⨯++⨯++ ()()23123011223⨯=+++⨯+⨯+⨯,()()()22221134101112123+++=+⨯++⨯++⨯+_______101=+⨯+212323+⨯++⨯+______()()1234_______________=++++;……(2)归纳结论:()()()()222212310111212311n n n ++++=+⨯++⨯++⨯+++-⎡⎤⎣⎦L L()1012123231n n n =+⨯++⨯++⨯+++-⨯L=(_________________)+(_______________________) =____________+______________ 16=_____________;(3)实践应用::通过以上探究过程,我们就可以算出当n 为100时,正方形网格中正方形的总个数是________.(四川省内江市中考题)应用探究乐园21.我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”.数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透.数形结合的基本思想,就是在研究问题的过程中,注意把数和形结合起来考察,斟酌问题的具体情形,把图形性质的问题转化为数量关系问题,或者把数量关系的问题转化为图形性质的问题,使复杂问题简单化,抽象问题具体化,化难为易,获得简便易行的成功方案.例如,求1234n +++++L 的值,其中n 是正整数.对于这个求和问题,如果采用纯代数的方法(首尾两头加),问题虽然可以解决,但在求和过程中,需对n 的奇偶性进行讨论.如果采用数形结合的方法,即用图形的性质来说明数量关系的事实,那就非常的直观.现利用图形的性质来求1234n +++++L 的值,方案如下:如图,斜线左边的三角形图案是由上到下每层依次分别为1,2,3,,n L 个小圆圈排列组成的,而组成整个三角形小圆圈的个数恰为所求式子1234n +++++L 的值.为求式子的值,现把左边三角形倒放于斜线右边,与原三角形组成一个平行四边形.此时,组成平行四边形的小圆圈共有n 行,每行有()1n +个小圆圈,所以组成平行四边形小圆圈的总个数为()1n n +个,因此,组成一个三角形小圆圈的个数为()12n n +,即()112342n n n ++++++=L .(1)仿照上述数形结合的思想方法,设计相关图形,求()135721n +++++-L 的值,其中n 是正整数.(要求:画出图形,并利用图形作必要的推理说明).(2)试设计另外一种图形,求()135721n +++++-L 的值,其中n 是正整数.(要求:画出图形,并利用图形作必要的推理说明)(山东省青岛市中考题)22.在“123456789□□□□□□□□□”的小方格中填上“+”、“-”号,如果可以使其代数和为n ,就称数n 是“可被表出的数”(如1是可被表出的数,这是因为123456789++--++--+是1的一种可被表出的方法). (1)求证:7是可被表出的数,而8是不可被表出的数; (2)求25可被表出的不同方法的种数.(四川省竞赛题)4.信息技术中的数学问题解读课标伴随着计算机和网络技术的迅猛发展,人类社会已步入信息时代,并将迈入后信息化时代:IT 技术、赛伯空间、数字化技术、智能通讯等信息技术彻底改变着我们的生活方式与思维方式. 计算器、计算机正深刻影响着数学学习内容和方式,现代信息技术是学习数学和解决问题的有力工具.近年出现的以信息技术为背景的问题是中考竞赛试卷一道靓丽的风景,这类问题将信息技术与数学知识有机融合和渗透,构思巧妙、立意新颖,其托容涉及计算机常识(数制、字节等)、计算机的数据输出、计算机中的数据处理、计算机运算程序、网络与通讯等. 解决这类问题的关键是找到数学知识与其内在的联系,将其转化为数学问题. ——问题解决——例1 给出下列程序x k −−→−−→⨯−−→立方输入输出,且已知当输入的x 值为1时,输出值为1;输入的x 值为1-时,输出值为3-,则当输入的x 值为12时,输出值为____. (广西竞赛题)试一试 把程序流程图用代数式表示,由条件先求出k 、b 的值.例2 计算机利用的是二进制数,它共有两个数码0、1,将一个十进制数转化为二进制数,只需把该数写成若干个2n 数的和,依次写出1或0即可.如()()4321219162112020212110011=++=⨯+⨯+⨯+⨯+=十.为二进制下的5位数,则十进制数2004是二进制下的( ). A.10位数 B.11位数 C.12位数D.13位数(湖北省荆门市中考题)试一试本例渗透了计算机的基本知识—“二进制计算”,无论何种进制的数都可表示为与数位上的数字、进制值有关联的和的形式.例3 一条信息可通过如图所示的网络线由上(A 点)往下向各站点传送.例如信息到2b 点可由经1a 的站点送达,也可由经2a 的站点送达,共有两条途径传送,那么信息由A 点到达3d 的不同途径共有多少条.(第17届“希望杯”邀请赛试题)试一试 在阅读理解的基础上,画出路线示意图,穷举得出结论.例4 你觉得手机很神奇吗?它能在瞬间清晰地传递声音、文字、图像等信号,据说以后还能发送味道、触觉信息呢!这里都有手机中电脑芯片的功劳.其实,这些信号在电脑芯片中都是以二进制数的形式给出的.每个二进制数都由0和1构成,电脑芯片上电子元件的“开”、“关”分别代表“1”和“0”.一组电子元件的“开”“关”状态就表示相应的二进制数.例如“开”“开”“关”表示“110”.如图,电脑芯片的某段电路上分布着一组电子元件(假设它们首尾不相连),且相邻的两个元件不能同时是关的.(以下各小题要求写出解答过程)(1)若此电路上有4个元件,则这4个元件所有不同的“开”“关”状态共有多少种?(请一一列出);(2)若用k a 表示电路上()1k k ≥只电子元件所有不同的“开”“关”状态数,试探索k a 、1k a +、2k a +之间的关系式(不要求论证);(3)试用(2)中探索出的递推关系式,计算10a 的值.(《时间学习报》数学文化节试题)试一试对于(1),通过穷举,得出答案值;对于(2),从特例入手,归纳出相应关系式. 例5 先阅读下面的材料,再解答后面各题.现代社会对保密要求越来越高,密码正在成为人们生活的一部分.有一种密码的明文(真实文)按计算机键盘字母排列分解,其中Q 、W 、E 、…、N 、M 这26个字母依次对应1、2、给出一个变换公式:()()(),126,3,126,,3217,331,126,318,23xx x x x x x x x x x x x x x ⎧'=⎪⎪+⎪'=+⎨⎪+⎪≤≤≤≤≤≤'=+⎪⎩是正整数被整除是正整数被整除余是正整数被整除余 将明文转换成密文,如:42417193+→+=,即R 变为L ; 111118123+→+=,即A 变为S .将密文转换成明文,如:()2132117210→⨯--=,即X 变为P ; ()133138114→⨯--=,即D 变为F .(1)按上述方法将明文NET 译为密文;(2)若按上述方法将明文译成的密文为DWN ,请找出它的明文.(湖北省十堰市中考题)试一试对于(1),由明文选择变换公式,求得相应整数,推出密文;对于(2),逆用变换公式,即由x'导出x值,推出明文,解题的关键是确定变换公式中x'的取值范围.电话号码的破译例6同学们看电影、看电视时,经常遇到破译密码的故事情节.在军事上、商业上,为了保密,都采用密码.破译密码需要有解密的“钥匙”.下面我们也来破译一个电话号码:一名间谍在他所追踪的人拨打电话时(话机是拨盘式的,如图,话机上的数字排列顺序是1,2,3,4,5,6,7,8,9,0,图中画出了拨数字5时相应的小孔转过的路线),随着拨号盘转回的声音,用铅笔以同样的速度在纸上画线,他画出的6条线如下:他很快就知道了那人拨的电话号码,这个号码是多少?(《时代学习报》数学文化节试题)分析与解从电话拨盘上可以看出,拨1时,画出的线段最短,拨0时,画出的线段最长,由于画线速度相同,所以,每个数字所对应的线段应比它下一个数所对应的线段增加一个固定的长度.间谍所画下的这6条线段的长度互不相等,所表示的6个数字当然也不一样,在0~9这10个数字的6个数字中至少有2个数字是相邻的(想一想为什么),因此,长度最接近的两条线段的长度差,就一定是上面所谈到的那个固定长度.通过对这6条线段进行度量,可以发现第一条线段与第二条线段最为接近,它们相差0.6厘米(相当于1个格子的宽度).由于最长的线段与最短的线段相差5.4厘米(相当于9个格子的宽度),因此可以断定最长的线段代表数字0,而最短的线段则代表1.+=,同样可推知第六条线段代第一条线段比第三条线段长3厘米,因此第一条线段代表156表3,第四条线段代表8,第二条线段代表5,所以这个电话号码是651803.数学冲浪知识技能广场1.二进制数为法国数学家莱布尼兹所创,例如二进制数1101表示十进制数3211212021⨯+⨯+⨯+,即相当于十进制数13,试将二进制数1101化为十进制数________.二进制数是现代计算机理论的基础.2.如图,是一个简单的数值运算程序,当输入x的值为1-时,则输出的数值为_____.()32x−−→⨯-−−→-−−→输入输出(江苏省南通市中考题)那么,当输入数据是时,输出的数据是_______.(广东省深圳市中考题)4.在计算器上按照下面的程序进行操作:下表中的x 与y 分别是输入的6个数及相应的计算结果:(浙江省台州市中考题)5.在计算机程序中,二叉树是一种表示数据结构的方法.如图,一层二叉树的结点总数为1,二层二叉树的结点总数为3,三层二叉树的结点总数为7……照此规律,七层二叉树的结点总数为( ).(第5题)A.63B.64C.127D.128(呼和浩特市中考题)6.如图所示的运算程序中,若开始输入的x 值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,……,则第2010次输出的结果为( ). A.6 B.3C.200632 D.100332(山东省淄博市中考题)7.计算机是将信息换成二进制数进行处理的,二进制即“逢2进1”,如()21101表示二进制数,将它转换成十进制形式是321121202113⨯+⨯+⨯+=,那么将二进制数()21101转换成十进制形式是数( ).A.8B.15C.20D.308.按下列程序计算,把答案写在表格内:n n n n −−→−−→+−−→÷−−→-−−→平方答案(1)填写表格:(2)请将题中计算程序用代数式表达出来,并给予化简.(广东省中考题)9.密码在通信安全技术、国防军事中扮演着重要角色,下面6道算式,乍看真是莫名其妙! ①8762+=;②535+=;③12823+=;④50954+=;⑤11155⨯=;⑥091-=. 当你知道这只是密码算式,各个密码数字各自对应另一个不同数字时,算式就合理了. 请根据算式,写出表中密码所对应的数字.密).已知有一种密码,将英文26个小写字母,,,,a b c z L 依次对应0,1,2,3,,25L 这26个自然数(见表格).当明文中的字母对应的序号为β时,将10β+除以26后所得的余数作为密s c按上述规定,将明文“”译成密文.(广州市中考题)思维方法天地11.我们知道在十进制加法中,逢十进一,如9817+=,也可写成()()()1010109817+=;在四进制加法中,逢四进一,如()()()4443711+=,那么在n 进制中有等式()()()5543142n n n +=,则n =______.(深圳市“启智杯”数学思维能力竞赛题)12.某综合性大学拟建校园局域网络,将大学本部A 和所属专业学院B 、C 、D 、E 、F 、G 之间用网线连接起来.经过测算,网线费用如图所示(单位:万元),每个数字表示对应网线(线段)的费用,实际建网时,部分网线可以省略不建,但本部及所属专业学院之间可以传递信息,那么建网所需的最少网线费用为_________万元.(第12题) (第13题)13.计算机中的堆栈是一些连续的存储单元,在每个堆栈中数据的存入、取出,按照“先进后出”的原则.如图堆栈(1)的2个连续存储单元已依次存入数据b ,a ,取出数据的顺序是a ,b ;堆栈(2)的3个连续存储单元已依次存入数据e ,d ,c ,取出数据的顺序则是c ,d ,e 现在要从这两个堆栈中取出这5个数据(每次取出1个数据),则不同顺序的取法的种数有( ).A.5种B.6种C.10种D.12种(江苏省竞赛题)14.如图,小圆圈表示网络的结点,结点之间的连线表示它们之间有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量.现从结点A 向结点B 传递信息,信息可以分开沿不同的路线同时传递,由单位时间内传递的最大信息量为( ). A.19 B.20 C.24 D.26(第14题) (第16题)15.写出一个四位数,它的各个数位上的数字都不相等(如6847),用这个四位数各个数位上的数字组成一个最大的数和一个最小的数,并用最大数减去最小数,得到一个新的四位数,对于新得到的四位数,重复上面过程,又得到一个新的四位数,一直重复下去,你发现了什么?请你用计算器,帮助你进行探索.16.某人租用一辆汽车由A 城前往B 城,沿途可能经过的城市以及通过两城市之间所需的时间(单位:小时)如图所示.若汽车行驶的平均速度为80千米/时,而汽车每行驶1千米需要的平均费用为1.2元,试指出此人从A 城出发到B 城的最短路线,并求出所需费用最少为多少元?(全国初中数学竞赛题)17.按下面的程序计算,若开始输入的值为正数x ,最后输出的结果为656,那么满足条件的x 的不同值最多有多少个?(浙江省中考题)18.在密码学中,你直接可以看到的内容为明码,对明码进行某种处理后得到的内容为密码.对于英文,人们将26个字母按顺序分别对应整数0到25,现有4个字母构成的密码单词,记4个字母对应的数字分别为1x ,2x ,3x ,4x .已知整数122x x +,23x ,342x x +,43x ,除以26的余数分别是9,16,23,12,请你通过推理计算破译此密码,写出这个单词,并写出此单词的汉语词意.(新疆建设兵团中考题)5.整式的加减解读课标代数式是用加、减、乘、除等运算符号把数或表示数的字母连接而成的式子,是后续学习中进行运算、解决问题的基础.在代数式中,我们把那些含相同的字母,并且相同字母的次数也分别相同的单项式看作一类—称为同类项,一个多项式中的同类项可以合聚在一起——称为合并同类项,整式的加减就是合并同类项.代数式的化简求值是代数式研究的一个重要课题,解这类问题的基本方法有:将字母的值代人或字母间的关系整体代人,而关键是对代数式进行恰当变形,其中去括号、添括号能改变代数式的结构,是变形求解的常用工具. ——问题解决——例1 平、乙、丙三家超市为了促销一种定价为m 元的商品,甲超市连续两次降价20%;乙超市一次性降价40%;丙超市第一次降价30%,第二次降价10%,此时顾客要购买这种商品,最划算的超市是_______.(2012年黑龙江省绥化市中考题)试一试 用m 的式子分别表示三家超市降价后的价格.例2 下列四个数中可以写成100个连续自然数之和的是( ). A.1627384950 B.2345678910 C.3579111300 D.4692581470(江苏省竞赛题)试一试 用字母表示数,从揭示100个连续自然数之和的规律入手.例3 已知关于x 的二次多项式()()3223325a x x x b x x x -++++-,当2x =时的值为17-,求当2x =-时该多项式的值.(北京市“迎春杯”竞赛题)试一试 设法求出a 、b 的值,解题的突破口是根据多项式降幂排列、多项式次数等概念挖掘隐含的关于a 、b 的等式.例4 有这样的两位数,交换该数数码所得到的两位数与原数的和是一个完全平方数.例如,29就是这样的两位数,因为2299212111+==,请你找出所有这样的两位数.(江苏省竞赛题)试一试 设原数为发现的特点是解本例的出发点.例5 如图,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第6个图案需要________枚棋子,摆第n 个图案需要_______枚棋子.(山东省青岛市中考题)1716116a ==+=+⨯;()21916121126a ==++=++⨯; ()33716121811236a ==+++=+++⨯;……猜想()2112346331n a n n n =++++++⨯=++L ,再将6n =代入该代数式得127.解法二 数形结合,分解图形,感悟从部分研究整体的思想.问题中“按照这样的方式摆下去”,何种方式并没有明确的界定,我们可以有不同的理解,如从平行四边形角度看,把图形分成三个平行四边形. 如图,图的序列号:1,2,3,4,5,L 图中的点的数目:7,19,37,61,91,L()171123a ==+⨯⨯; ()2191233a ==+⨯⨯; ()3371343a ==+⨯⨯; ()4611453a ==+⨯⨯; ()5911563a ==+⨯⨯;……猜想()2113331n a n n n n =++⨯=++⎡⎤⎣⎦.整体思考整体思考是将问题看成一个完整的整体,从大处着眼,由整体入手,突出对问题的整体结构的分析与改造,从整体上把握问题的特征和解题方向.例6(1)已知当1x =时,226ax x +的值为3,则当2x =时,268ax x +-的值为_______.(2012年成都市中考题)(2)把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为mcm ,宽为ncm )的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,。
2020年秋人教版七年级数学上册暑期课程跟踪——1.2.3相反数学情评价
3.下列说法中,正确的有( )
①-x 一定是负数;②任何一个有理数都有相反数;③只有正数和负数才能
构成相反数;④互为相反数的数是指两个不同的数;⑤符号不同的两个数互
为相反数.
A.1 个
B.2 个
C.3 个
D.4 个
4.下列各数互为相反数的是( )
1 A.-6 与6
4 B.-1.25 与5
1 C.0.01 与-100
16.若 −x = 2 ,则 −−(−x) = _____.
2/6
17.化简下列各数:-[-(+2)]=________;-[-(-2)]=________. 18.当+2 前面有 2 020 个负号时,化简的结果是________;当+2 前面有 2 021 个负号时,化简的结果是________. 三、解答题 19.如图,数轴上 A 点表示的数是﹣2,B 点表示的数是 5,C 点表示的数是 10.
②小猫逮住老鼠时的“位置”恰好在
,求时间 t.
20. 化简下列各数:-(-68),-(+0.75),--35,-(+3.8).
21. 如图是一个正方体纸盒的平面展开图.若在其中三个正方形 A,B,C
内分别填入适当的数,使得折成正方体后相对面上的两个数互为相反数,则
填入正方形 A,B,C 内的数分别是多少?
1.2.3 相反数学情评价
一、选择题
1. 在-1,+(-2),-(-3),-(+4)中,负数的个数是( )
A.1 B.2 C.3 D.4
2.下列各对数:-1 与+(-1),+(+1)与-1,-(-2)与+(-2),-(-12)
与+(+12),-(+3)与-(-3),其中互为相反数的有( )
A.1 对 B.2 对 C.3 对 D.4 对
浙教版七年级数学上册知识点汇总
七年级(上册)1. 有理数1.1. 从自然数到有理数分数都可以化为小数。
分数在化成小数时, 结果可能是有限小数, 也可能是无限循环小数。
大于0的数, 叫正数;小于0的数, 叫负数;0既不是正数也不是负数。
整数和分数统称为有理数。
⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧⎭⎬⎫负分数正分数分数负整数自然数零正整数整数有理数 ⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 1.2. 数轴像这样规定了原点、单位长度和正方向的直线叫做数轴。
任何一个有理数都可以用数轴上的点表示。
如果两个数只有符号不同, 那么我们称其中一个数为另一个数的相反数, 也称这两个数互为相反数。
0的相反数是0。
1.3. 在数轴上, 表示互为相反数(0除外)的两个点, 位于原点的两侧, 并且到原点的距离相等。
1.4. 绝对值我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值。
一个数a 的绝对值表示为|a|。
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0。
互为相反数的两个数的绝对值相等。
1.5. 有理数的大小比较在数轴上表示的两个数, 右边的数总比左边的数大。
2. 正数都大于0, 负数都小于0, 正数大于负数。
3. 两个正数比较大小, 绝对值大的数大;两个负数比较大小, 绝对值大的数反而小。
4. 有理数的运算4.1. 有理数的加法同号两数相加, 取与加数相同的符号, 并把绝对值相加。
异号两数相加, 取绝对值较大的加数的符号, 并用较大的绝对值减去较小的绝对值。
互为相反数的两个数相加得0;一个数同0相加, 仍得这个数。
加法交换律:两个数相加, 交换加数的位置, 和不变。
a +b = b + a加法结合律: 三个数相加, 先把前面两个数相加, 或者先把后两个数相加, 和不变。
( a + b ) + c = a + ( b + c )4.2.有理数的减法减去一个数, 等于加上这个数的相反数。
最新2022-2021年七年级(上)月考数学试卷(11月份)
七年级(上)月考数学试卷(11月份)一、选择题1.若a>b,则下列结论正确的是()A.a2>b2B.a2<b2C.a2≥b2D.a2与b2的大小关系不能确定2.对于有理数a、b,如果ab<0,a+b<0.则下列各式成立的是()A.a<0,b<0 B.a>0,b<0且|b|<a C.a<0,b>0且|a|<b D.a>0,b<0且|b|>a3.下列四个运算中,结果最小的是()A.﹣1+(﹣2)B.1﹣(﹣2)C.1×(﹣2)D.1÷(﹣2)4.如果a+b<0,a>b,ab<0,则()A.a<0,b>0 B.|a|<|b|C.|a|>|b|D.a<0,b<05.两个数的和为正数,那么这两个数是()A.正数B.负数C.一正一负D.至少一个为正数6.有理数a、b在数轴上的位置如图所示,则下列正确的是()A.a+b<0 B.a+b>0 C.ab>0 D.a﹣b>07.下列各组数中,数值相等的一组是()A.2 3和3 2 B.﹣2 3和(﹣2)3C.﹣3 2和(﹣3)2 D.(﹣3×2)2和﹣3 2×2 28.哈市某天的最高气温为28℃,最低气温为21℃,则这一天的最高气温与最低气温的差为()A.5℃B.6℃C.7℃D.8℃9.刘谦的魔术表演风靡全国,小明同学也学起了刘谦发明了一个魔术盒,当任意有理数对(a,b)进入其中时,会得到一个新的有理数:a2+b﹣1.例如把(3,﹣2)放入其中,就会得到32+(﹣2)﹣1=6.现将有理数对(﹣1,﹣2)放入其中,则会得到()A.﹣1 B.﹣2 C.﹣3 D.210.一对小兔子从出生到第三个月就可以长大,并且生一对小兔子,以后每个月可以生一对小兔子,新生的小兔子三个月后又可以生小兔子.如果你也有一对刚出生的小兔子,那么到第10个月你所有的兔子的对数是()A.9 B.89 C.21 D.2811.若一个正整数能表示为两个正整数的平方差,则称这个正整数为“智慧数”(如3=22﹣12,16=52﹣32).已知智慧数按从小到大顺序构成如下数列:3,5,7,8,9,11,12,13,15,16,17,19,20,21,23,24,25,….则第2006个智慧数是()A.2672 B.2675 C.2677 D.268012.如图是中国古代著名的“杨辉三角形”的示意图.图中填入的所有数的总和等于()A.126 B.127 C.128 D.129二、填空题13.若表示a,b的点在数轴上的位置如图所示,则ab2a2b.(填“>”“<”“=”)14.用字母表示有理数的加法运算律.(1)交换律:;(2)结合律:.15.定义一种新运算:,那么4⊗(﹣1)=.16.现有四个有理数3,4,﹣6,10,将这四个数(每个数用且只能用一次)进行加减乘除四则运算,使其运算的结果是24,请你写出一个符合条件的算式.17.计算:(1)(﹣25)+(﹣35)=;(2)(﹣12)+(+3)=;(3)(+8)+(﹣7)=;(4)0+(﹣7)=.三、计算题18.观察下列各式:13+23=×4×9=×22×32;13+23+33=36=×9×16=×32×42;13+23+33+43=100=×16×25=×42×52;(1)计算:13+23+33+43+53的值;(2)计算:13+23+33+43+…+103的值;(3)猜想:13+23+33+43+…+n3的值.19.计算:|﹣2|+﹣(﹣1)2.20.计算:3+|﹣|﹣2cos60°+.21.计算下式的值:211×555+445×789+555×789+211×445.22.计算:0+﹣2cos30°+()﹣1.七年级(上)月考数学试卷(11月份)参考答案与试题解析一、选择题1.若a>b,则下列结论正确的是()A.a2>b2B.a2<b2C.a2≥b2D.a2与b2的大小关系不能确定【考点】有理数的乘方;有理数大小比较.【分析】分0>a>b和a>b>0两种情况,根据乘方法则计算即可.【解答】解:当0>a>b时,a2<b2,A不符合题意;当a>b>0时,a2>b2,B不符合题意;a2≠b2,C不符合题意;a2与b2的大小关系不能确定,D符合题意,故选:D.2.对于有理数a、b,如果ab<0,a+b<0.则下列各式成立的是()A.a<0,b<0 B.a>0,b<0且|b|<a C.a<0,b>0且|a|<b D.a>0,b<0且|b|>a【考点】有理数的乘法;有理数的加法.【分析】根据有理数的乘法法则,由ab<0,得a,b异号;根据有理数的加法法则,由a+b<0,得a、b同负或异号,且负数的绝对值较大,综合两者,得出结论.【解答】解:∵ab<0,∴a,b异号.∵a+b<0,∴a、b同负或异号,且负数的绝对值较大.综上所述,知a、b异号,且负数的绝对值较大.故选D.3.下列四个运算中,结果最小的是()A.﹣1+(﹣2)B.1﹣(﹣2)C.1×(﹣2)D.1÷(﹣2)【考点】有理数大小比较;有理数的混合运算.【分析】本题是对有理数的大小比较和混合运算的法则的综合考查,减去一个数等于加上这个数的相反数.除以一个数等于乘以一个数的倒数.【解答】解:A、原式=﹣1﹣2=﹣3;B、原式=1+2=3;C、原式=﹣2;D、原式=1×(﹣)=﹣;∵﹣3<﹣2<﹣<3,∴在上面四个数中,最小的数是﹣3;故选A.4.如果a+b<0,a>b,ab<0,则()A.a<0,b>0 B.|a|<|b|C.|a|>|b|D.a<0,b<0【考点】有理数的乘法;有理数的加法.【分析】根据异号得负判断出a、b异号,再根据有理数的加法运算法则解答.【解答】解:∵ab<0,∴a、b异号,∵a+b<0,a>b,∴a>0,b<0,且|a|<|b|.故选B.5.两个数的和为正数,那么这两个数是()A.正数B.负数C.一正一负D.至少一个为正数【考点】有理数的加法.【分析】根据有理数的加法法则进行逐一分析即可.【解答】解:A、不一定,例如:﹣1+2=1,错误;B、错误,两负数相加和必为负数;C、不一定,例如:2与6的和8为正数,但是2与6都是正数,并不是一正一负,错误;D、正确.故选D.6.有理数a、b在数轴上的位置如图所示,则下列正确的是()A.a+b<0 B.a+b>0 C.ab>0 D.a﹣b>0【考点】数轴.【分析】根据绝对值的性质确定出a、b,再根据有理数的加法和乘法运算法则对各选项分析判断利用排除法求解.【解答】解:由图可知,﹣1<a<0,1<b<2,A、a+b>0,故本选项错误;B、a+b>0,故本选项正确;C、ab<0,故本选项错误;D、a﹣b<0,本选项错误.故选B.7.下列各组数中,数值相等的一组是()A.2 3和3 2 B.﹣2 3和(﹣2)3C.﹣3 2和(﹣3)2 D.(﹣3×2)2和﹣3 2×2 2【考点】有理数的乘方;有理数的乘法.【分析】原式各项计算得到结果,比较即可.【解答】解:A、23=8,32=9,不相等;B、﹣23=(﹣2)3=﹣8,相等;C、﹣32=﹣9,(﹣3)2=9,不相等;D、(﹣3×2)2=36,﹣32×22=﹣36,不相等,故选B8.哈市某天的最高气温为28℃,最低气温为21℃,则这一天的最高气温与最低气温的差为()A.5℃B.6℃C.7℃D.8℃【考点】有理数的减法.【分析】根据有理数的减法,减去一个数等于加上这个数的相反数,可得答案.【解答】解:28﹣21=28+(﹣21)=7,故选:C.9.刘谦的魔术表演风靡全国,小明同学也学起了刘谦发明了一个魔术盒,当任意有理数对(a,b)进入其中时,会得到一个新的有理数:a2+b﹣1.例如把(3,﹣2)放入其中,就会得到32+(﹣2)﹣1=6.现将有理数对(﹣1,﹣2)放入其中,则会得到()A.﹣1 B.﹣2 C.﹣3 D.2【考点】有理数的混合运算.【分析】此题根据题意,把实数对(﹣1,﹣2)代入a2+b﹣1=2中,即可求出结果.【解答】解:把实数对(﹣1,﹣2)代入a2+b﹣1=2中得:(﹣1)2﹣2﹣1=1﹣2﹣1=﹣2.故选B.10.一对小兔子从出生到第三个月就可以长大,并且生一对小兔子,以后每个月可以生一对小兔子,新生的小兔子三个月后又可以生小兔子.如果你也有一对刚出生的小兔子,那么到第10个月你所有的兔子的对数是()A.9 B.89 C.21 D.28【考点】规律型:数字的变化类.【分析】首先审清题意,理解题目中的关系:开始有兔子的对数是1,第10个月以后可以生10﹣3+1=8对;3个月以后新生的小兔子可以生10﹣6+1=5对兔子;4个月以后新生的小兔子可以生10﹣7+1=4对兔子;5个月以后新生的小兔子可以生10﹣8+1=3对兔子;6个月以后新生的小兔子可以生(10﹣9+1)×2=4对兔子;7个月以后新生的小兔子可以生(10﹣10+1)×3=3对兔子.再把它们相加即可.【解答】解:1+(10﹣3+1)+(10﹣6+1)+(10﹣7+1)+(10﹣8+1)+(10﹣9+1)×2+(10﹣10+1)×3=1+8+5+4+3+4+3=28对.故选D.11.若一个正整数能表示为两个正整数的平方差,则称这个正整数为“智慧数”(如3=22﹣12,16=52﹣32).已知智慧数按从小到大顺序构成如下数列:3,5,7,8,9,11,12,13,15,16,17,19,20,21,23,24,25,….则第2006个智慧数是()A.2672 B.2675 C.2677 D.2680【考点】整数问题的综合运用.【分析】根据题意观察探索规律,知全部智慧数从小到大可按每三个数分一组,从第2组开始每组的第一个数都是4的倍数.归纳可得第n组的第一个数为4n (n≥2),又因为2006=3×668+2,所以第2006个智慧数是第669组中的第2个数,从而得到4×669+1=2677.【解答】解:观察探索规律,知全部智慧数从小到大可按每三个数分一组,从第2组开始每组的第一个数都是4的倍数,归纳可得第n组的第一个数为4n(n≥2).因2006=3×668+2,所以第2006个智慧数是第669组中的第2个数,即为4×669+1=2677.故选C.12.如图是中国古代著名的“杨辉三角形”的示意图.图中填入的所有数的总和等于()A.126 B.127 C.128 D.129【考点】规律型:数字的变化类.【分析】第一行有1个数,和为1=20,第二行有2个数,和为2=21,第3行有3个数,和为4=22,…那么图中所有数的总和为20+21+22+…+26,计算即可.【解答】解:第1行只有1=20,第2行1+1=2=21,第3行1+2+1=4=22,第4行1+3+3+1=8=23,第5行1+4+6+4+1=16=24,第6行1+5+10+10+5+1=32=25第7行1+6+15+20+15+6+1=64=26图中填入所有数之和为1+2+4+8+16+32+64=127,故选B.二、填空题13.若表示a,b的点在数轴上的位置如图所示,则ab2>a2b.(填“>”“<”“=”)【考点】数轴.【分析】根据数轴可得a>0,b<0,从而可以推得ab<0,从而得到ab2与a2b 的关系,从而可以解答本题.【解答】解:由数轴可得,a>0,b<0,∴ab<0,∴ab•b>0,ab•a<0,∴ab•b>ab•a,即ab2>a2b故答案为:>.14.用字母表示有理数的加法运算律.(1)交换律:a+b=b+a;(2)结合律:(a+b)+c=a+(b+c).【考点】列代数式.【分析】(1)加法交换律:两个数相加,交换加数的位置,它们的和不变;(2)加法结合律:三个数相加,可以先把前两个数相加,再和第三个数相加,也可以先把后两个数相加,再和第一个数相加,结果不变;据此分别用字母表示出来即可.【解答】解:(1)交换律:a+b=b+a;(2)结合律:(a+b)+c=a+(b+c).故答案为:a+b=b+a;(a+b)+c=a+(b+c).15.定义一种新运算:,那么4⊗(﹣1)=2.【考点】代数式求值.【分析】根据题意可知,该运算是a的与b的差.【解答】解:根据新运算,4*(﹣1)=×4﹣(﹣1)=2.故答案为:2.16.现有四个有理数3,4,﹣6,10,将这四个数(每个数用且只能用一次)进行加减乘除四则运算,使其运算的结果是24,请你写出一个符合条件的算式答案不惟一,如:3×(﹣6+4+10)=24.【考点】有理数的混合运算.【分析】首先认真分析找出规律,然后根据有理数的运算法则列式.【解答】解:例如:3×[(﹣6)+4+10]=24;4﹣(﹣6)÷3×10=24;3×(10﹣4)﹣(﹣6)=24.17.计算:(1)(﹣25)+(﹣35)=﹣60;(2)(﹣12)+(+3)=﹣9;(3)(+8)+(﹣7)=1;(4)0+(﹣7)=﹣7.【考点】有理数的加法.【分析】(1)为同号(两负数)相加;(2)、(3)为异号两数相加;(4)为0加上一个有理数,然后根据法则先确定和的符号,后计算绝对值,即“先符号,后绝对值”.【解答】解:(1)(﹣25)+(﹣35)=﹣(25+35)=﹣60;(2)(﹣12)+(+3)=﹣(12﹣3)=﹣9;(3)(+8)+(﹣7)=+(8﹣7)=1;(4)0+(﹣7)=﹣7.故答案为﹣60,﹣9,1,﹣7.三、计算题18.观察下列各式:13+23=×4×9=×22×32;13+23+33=36=×9×16=×32×42;13+23+33+43=100=×16×25=×42×52;(1)计算:13+23+33+43+53的值;(2)计算:13+23+33+43+…+103的值;(3)猜想:13+23+33+43+…+n3的值.【考点】规律型:数字的变化类.【分析】(1)根据已知得出规律,连续自然数的立方等于末位数与下一个自然数的平方的积的进而分别求出即可;(2)利用13+23+33+43+…+103=×102×112求出即可;(3)利用(1)中分析得出即可.【解答】解:∵;;;∴(1)13+23+33+43+53=×52×62=225;(2)13+23+33+43+…+103=×102×112=×121×100=3025;(3)13+23+33+43+…+n3=×n2×(n+1)2.19.计算:|﹣2|+﹣(﹣1)2.【考点】实数的运算.【分析】本题涉及绝对值、乘方、二次根式化简3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.【解答】解:原式=2+2﹣1=3.20.计算:3+|﹣|﹣2cos60°+.【考点】实数的运算;负整数指数幂;特殊角的三角函数值.【分析】原式第一项化为最简二次根式,第二项利用绝对值的代数意义化简,第三项利用特殊角的三角函数值计算,最后一项利用负指数幂法则计算即可得到结果.【解答】解:原式=6+﹣2×+4=6+4.21.计算下式的值:211×555+445×789+555×789+211×445.【考点】因式分解的应用;有理数的混合运算.【分析】直接计算很麻烦,根据运算规则,添加括号改变运算次序,可使计算简单.本题可将第一、第四项和第二、第三项分别结合起来计算.【解答】解:原式=+,=211×+×789,=211×1000+1000×789,=1000×,=1 000 000.22.计算:0+﹣2cos30°+()﹣1.【考点】实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.【分析】原式第一项利用零指数幂法则计算,第二项化为最简二次根式,第三项利用特殊角的三角函数值计算,最后一项利用负指数幂法则计算即可得到结果.【解答】解:原式=1+2﹣2×+2=3+.2022年2月26日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级提高练习 11月14日一.根据括号里的要求或句意填空:(15分)1. often(同义词)2.goose (复数)3. two (序数词)4.finish(第三人称单数)5.behind(反义词)6.We all learn English wish great i7.A g is a place for parking cars.8.Wha t’s the m ?9.What do they do in their s time ?10. It’s 9:30 now ,that is h _ past nine.11.I like swimming best. Swimming is my sport.12.Mr. Wang is (friend) to me.13.How many (sheep) are there in the field ?14.There is a stamp (collect) in our school hall.15.I have a house .(let)二、词组互译1.存钱 6.a map of China .2.擅长 7.be different from3.弹钢琴 8.put the books away4.在椅子下面 9.three times a week5.在右边 10.at the foot of the hill 三.选择填空(20分)( )1. do you usually get to school ? -----By bus.A. WhatB. What timeC. HowD. When( )2.Lucy sits between Lily andA. meB.IC. myD. mine( )3.He usually football after school.A. playB. playsC. is playingD. played( )4.May I ask you questions?A. anyB. some.C. aD. an( )5.There some water in the bottleA. isB. areC. beD. am( )6.There are hundreds birds in the sky.A. ofB. toC. aboutD. with( )7.Some of us enjoy books in the reading-room.A. readB. readsC. reading D .to read( )8.If the road is , you cross the road .A. busy, canB. free, canC. clear, canD. crowed, may( )9. It’s 5:00, It’s time .A. goes homeB. to go to homeC. to go homeD. go home( )10.The cakes taste .A. very muchB. badlyC. deliciousD. nicely( )11.There a pen ,two pencils and some pictures in the box.A. amB. isC. areD. have( )12. is he late for school? ----Never.A. HowB. How oftenC. How longD. What time( )13.How does Jim get to school? He the school bus.A. takesB. byC. getsD. on( )14.Is there behind the door ?A. other anythingB. else anythingC. anything elseD. other( )15.If everybody the rulers, the roads will be safer.A. obeys, muchB. obey, muchC. obeys, manyD. obey, many( )16.The two girls rent house.A. an one-bedroomB. two-bedroomsC .a one-bedroom D. two-bedroom( )17.How many are there in the supermarkets.A. peopleB. peoplesC. personD. child( )18.We usually ______in the supermarkets.A. eat mealsB. buy thingsC. mail thingsD. read( )19.I will try to play the piano more_______A. quiteB. quietC. quietlyD. quitely( )20.We hear ______in the next room.A. someone readingB. someone to readC. someone readsD. someone are reading四、用所给动词的正确形式填空。
(15分)1.The kitchen fan_____(not work)very well today.2.The traffic in the cities______(be)too heavy.3.There_____(be)a lot of tall buildings in the city.4.______(not put)your things here. boys and girls.5.Can you______(see)crayons, newspapers and a lamp on the desk?6.I want_______(tell)you something about my new house.7.Look! Lucy______(run)on the playground.8.Sometimes my mother________(have)lunch at school.9.Thank you for_______(teach)us so well.10.They love________(watch)TV in the living-room.11.Why not________(play)basketball after class?12.I often go ________(swim)with my parents.13.We______(let)you know if we find your purse.14.I’d like_______(have)a look at your new book.15.Le t’s _______(go)upstairs.五、句型转换(15分)1.There are some keys in my purse(变为一般疑问句)___________ ___________ ___________keys in _________purse?2.Is there a present for your school?(作否定回答)________, ___________ ____________3.There is a soccer behind the door(就划线部分提问)___________ ___________behind the door?4. I usually go to work by bike(就划线部分提问)___________ ____________you usually go to work?5.My mother is watching TV(就划线部分提问)__________is your mother___________?6.She always watches TV on Sundays(就划线部分提问)__________ __________ _________she watch TV on Sundays. 7.—Happy New Year, Mr. John.(写出答语)---__________ ___________ ___________ ___________。
8.Mr. Wang drives a car everyday(用now 替换everyday)Mr. Wang __________ ____________a car now.9. What else can you see?(同义句替换)What__________ __________can you see?10.Could you tell me how to get to your school(同义句替换)Could you tell me_________ _________ _________your school.11.There is a key on the desk (改成复数形式)There_________ _________ _________on the desk.六、完成句子(15分)1.有许多孩子住在那里吗?_________there many__________ __________there?2.这本书我能借多久?_________ _________can I _________the book?3.很高兴收到你的来信。
I’m very _________to_________ __________you.4.他们从下午4:15开始做户外活动?They begin to do_________ ____________from a__________ _________four in the afternoon.5.政治和历史也很难。
___________ and history__________ __________,too.6.我们喜欢在音乐课上唱歌跳舞。
We like _________ ___________ __________in music lesson.7.我很少看小说。
She ________ __________ ___________.8.一直往向前走,在第二个路口向右拐。
Go straight___________, ___________ __________at the second turning.9.我们必须遵守交通规则。
