2015广1模分数线
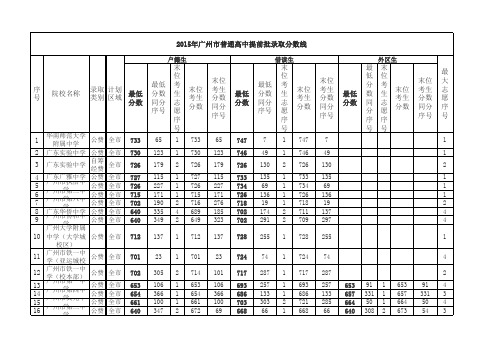
2015年广州中考录取分数线(最全)
625 149 1 625 149 683 230 1 683 230
4
6
广州市第十七 中学
公办
老三 区
630 131 1 630 131 662 245 1 662 245
4
7
广州市第二十 一中学
公办
老三 区
640 250 3 674 113 680 311 1 680 311
3
8
广州市培正中 学
702
313
4
702
259
651 40 1 651
40
4
34
广州市禺山高 级中学
公费 全市
613
253
4
625
38
679 315 1 679 315 613 251 4 625
38
4
35
广东第二师范 学院番禺附属
公费 全市
600
273
4
623
85
672 244 1 672 244 600 225 4 623
公办
老三 区
621
36 1 621
36 676 207 1 676 207
4
3
广州市西关外 国语学校
公办
老三 区
640 119 2 690
63 689
90 1 689
90
2
4
广州市真光中 学
公办
老三 区
682 346 1 682 346 698 352 1 698 352
1
5
广州市第十三 中学
公办
老三 区
最末
低位
分 数 同 分
考 生 志 愿
末位 考生 分数
序序
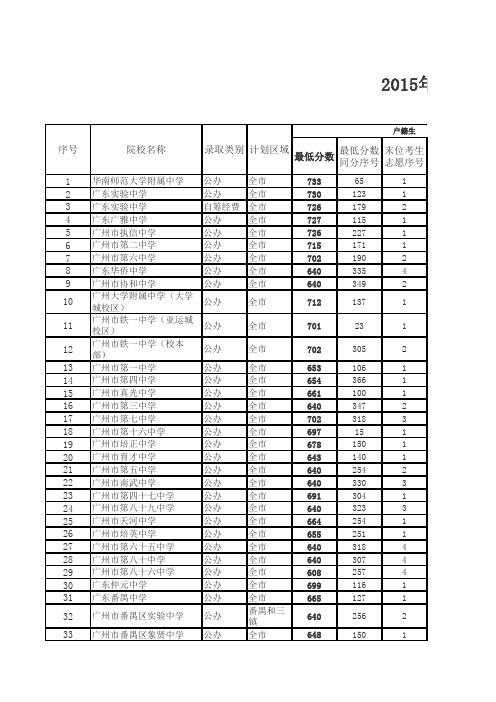
2015年广州中考录取分数线(最全)

34级中学公费全市6132534625386793151679315613251462538435广东第二师范学院番禺附属公费全市6002734623856722441672244600225462385436广州市花都区秀全中学公费全市6557016557069625816962586691961669196437广州市花都区邝维煜纪念中公费全市605299363311467531516753156061703636265438广州市花都区新华中学公费全市5772382577197652921652925772382578206339广州市南沙第一中学公费全市640337464715268895168895644394654190440广州市玉岩中学公费全市62614336381268415816841586542331654233341增城市增城中学公费全市6581701658170679161679166882611688261342增城市新塘中学公费全市569238460724464032126635057174608204443从化市从化中学公费全市622308262545627234162723462545262545444从化市第六中学公费全市59625825991575961492618133596245260314445华师附中南海实验高中民办全市6488316488364128716412874说明:3.“最低分数同分序号”是指向该校投档考生最低分数的同分最大排位序号。
4.“末位考生分数同分序号”是指向该校投档最后一名考生分数的同分最大排位序号。
5.“末位考生志愿序号”是指向该校投档最后一名考生的志愿序号。
6.“最大志愿序号”是指向该校投档考生中最大的志愿序号。
1.表中“户籍生”是指我市户籍的考生,政策性照顾借读生与户籍生报考和录取资格相同;“借读生”是指具有我市初中三年完整学籍的非政策性照顾借读生;“外区生”是指区属示范性高中录取的非本区考生。
2015年广州一模文科数学试题及参考答案(纯word版)

图17432109878试卷类型:A2015年广州市普通高中毕业班综合测试(一)数学(文科)2015.3 本试卷共4页,21小题, 满分150分.考试用时120分钟. 注意事项:1.答卷前,考生务必用2B 铅笔在“考生号”处填涂考生号。
用黑色字迹钢笔或签字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B 铅笔填涂选做题题号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式:锥体的体积公式Sh V 31=,其中S 是锥体的底面积,h 是锥体的高. 一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知全集{}1,2,3,4,5U =, 集合{}3,4,5M =,{}1,2,5N =, 则集合{}1,2可以表示为 A .MN B .()U M N ð C .()U MN ð D .()()U U M N 痧 2.已知向量()3,4a =,若5λ=a ,则实数λ的值为A .15 B .1 C .15± D .1± 3. 若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,叶为个位数,则这组数据的中位数是 A. 91 B. 91.5 C. 92 D. 92.54.已知i 为虚数单位,复数i z a b =+(),a b ∈R 的虚部b 记作Im ()z ,则Im 11i ⎛⎫=⎪+⎝⎭A .12- B .1- C .12D .1侧视图正视图5. 设抛物线:C24y x=上一点P到y轴的距离为4,则点P到抛物线C的焦点的距离是A.4B.5C.6D.76. 已知△ABC的三边,,a b c所对的角分别为,,A B C,且sinsin2BAa b=, 则cos B的值为A. B.12C.12-D.7. 已知数列{}n a为等比数列,若4610a a+=,则()713392a a a a a++的值为A.10B. 20C.100D. 2008. 若直线3y x=上存在点(),x y满足约束条件40,280,,x yx yx m++≥⎧⎪-+≥⎨⎪≤⎩则实数m的取值范围是A. [)1,-+∞ B. ()1,-+∞C. (],1-∞- D. (),1-∞-9. 已知某锥体的正视图和侧视图如图2,图2A. B. D.10.已知圆O的圆心为坐标原点,半径为1,直线:(l y kx t k=+为常数,0)t≠与圆O 相交于,M N两点,记△MON的面积为S,则函数()S f t=的奇偶性为A.偶函数B.奇函数C.既不是偶函数,也不是奇函数D.奇偶性与k的取值有关二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.(一)必做题(11~13题)11. 函数()()ln2f x x=-的定义域为.图312. 已知e 为自然对数的底数,则曲线2y =e x在点()1,2e 处的切线斜率为 .13. 已知函数()11f x x =+,点O 为坐标原点, 点()(),(n A n f n n ∈N *), 向量()0,1=i ,n θ是向量n OA 与i 的夹角,则201512122015cos cos cos sin sin sin θθθθθθ+++的值为 .(二)选做题(14~15题,考生只能从中选做一题) 14. (坐标系与参数方程选做题)在直角坐标系xOy 中,曲线1C 和2C 的参数方程分别为cos sin ,(cos sin x y θθθθθ=+⎧⎨=-⎩为参数)和2,(x t t y t =-⎧⎨=⎩为参数).以原点O 为极点,x 轴正半轴为极轴,建立极坐标系,则曲线1C 与2C 的交点的极坐标...为 . 15. (几何证明选讲选做题)如图3,BC 是圆O 的一条弦,延长BC 至点E ,使得22BC CE ==,过E 作圆O 的切线,A BAC ∠的平分线AD 交BC 于点D ,则DE三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分) 已知函数()sin cos 6f x x x π⎛⎫=-+ ⎪⎝⎭. (1)求函数()f x 的最小正周期; (2)若α是第一象限角,且435f πα⎛⎫+= ⎪⎝⎭,求tan 4πα⎛⎫- ⎪⎝⎭的值.图4O F EDC B A 图5FE PODB A从广州某高校男生中随机抽取100名学生,测得他们的身高(单位: cm)情况如表1:表1 (1)求,,a b c 的值;(2)按表1的身高组别进行分层抽样, 从这100名学生中抽取20名担任广州国际马拉松 志愿者, 再从身高不低于175cm 的志愿者中随机选出2名担任迎宾工作, 求这2名 担任迎宾工作的志愿者中至少有1名的身高不低于180cm 的概率.18.(本小题满分14分) 如图4,在边长为4的菱形ABCD 中,60DAB ︒∠=,点E ,F 分别是边CD ,CB 的中点,ACEF O =.沿EF 将△CEF 翻折到△PEF ,连接PA,PB,PD ,得到如图5的五棱锥P ABFED -,且PB =(1)求证:BD ⊥平面POA ; (2)求四棱锥P BFED -的体积.已知数列{}n a 的前n 项和为n S ,且满足11a =, ()()1112n n n n nS n S ++-+=, n ∈N *. (1)求2a 的值;(2)求数列{}n a 的通项公式;(3)是否存在正整数k ,使k a ,2k S , 4k a 成等比数列? 若存在,求k 的值; 若不存在,请说明理由.20.(本小题满分14分)已知椭圆1C 的中心在坐标原点,两焦点分别为双曲线222:12x C y -=的顶点,直线0=x 与椭圆1C 交于A ,B 两点,且点A 的坐标为(1),点P 是椭圆1C 上异于点A ,B 的任意一点,点Q 满足0AQ AP ⋅=,0BQ BP ⋅=,且A ,B ,Q 三点不共线.(1) 求椭圆1C 的方程; (2) 求点Q 的轨迹方程;(3) 求ABQ ∆面积的最大值及此时点Q 的坐标.21.(本小题满分14分)已知t 为常数,且01t <<,函数()()1102t g x x x x -⎛⎫=+> ⎪⎝⎭的最小值和函数()h x =()32f x x ax bx =-++(,a b ∈R )的零点.(1)用含a 的式子表示b ,并求出a 的取值范围; (2)求函数()f x 在区间[]1,2上的最大值和最小值.2015年广州市普通高中毕业班综合测试(一)数学(文科)试题参考答案及评分标准说明:1.参考答案与评分标准给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分. 一、选择题:本大题考查基本知识和基本运算.共10小题,每小题5分,满分50分.二、填空题:本大题考查基本知识和基本运算,体现选择性.共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题. 11. ()2,+∞ 12. 2e 13.2015201614. 4π⎫⎪⎭15. 说明: 第14题答案可以是2,4k k ππ⎫+∈⎪⎭Z . 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)(本小题主要考查三角函数图象的周期性、同角三角函数的基本关系、三角恒等变换等知识,考查化归与转化的数学思想方法,以及运算求解能力) (1)解:()sin cos 6f x x x π⎛⎫=-+ ⎪⎝⎭sin coscos sincos 66x x x ππ=-+ …………………………1分1sin cos 22x x =+ …………………………2分 sin cos cos sin66x x ππ=+ …………………………3分sin 6x π⎛⎫=+⎪⎝⎭. …………………………4分∴ 函数()f x 的最小正周期为2π. …………………………5分(2)解:∵435f πα⎛⎫+= ⎪⎝⎭, ∴ 4sin 365ππα⎛⎫++= ⎪⎝⎭. …………………………6分 ∴ 4sin 25πα⎛⎫+= ⎪⎝⎭. ∴ 4cos 5α=. …………………………7分 ∵α是第一象限角,∴3sin 5α==. …………………………8分 ∴ sin 3tan cos 4ααα==. …………………………9分 ∴ tan tan4tan 41tan tan 4παπαπα-⎛⎫-=⎪⎝⎭+⋅ …………………………10分3143114-=+⨯ …………………………11分17=-. …………………………12分17. (本小题满分12分)(本小题主要考查古典概型、分层抽样等基础知识,考查化归与转化的数学思想方法,以及数据处理能力与应用意识)(1)解: 由0.050.350.200.10 1.00c ++++=,得0.30c =. …………………………1分由0.30100a=,得30a =, …………………………2分 由5303510100b ++++=,得20b =. …………………………3分(2)解:依据分层抽样的方法,抽取的20名志愿者中身高在区间[)175,180上的有0.20204⨯=名,记为,,,A B C D ; …………………………………………5分而身高在区间[)180,185上的有0.10202⨯=名,记为,E F . ……………………7分 记“这2名担任迎宾工作的志愿者中至少有1名的身高不低于180cm ”为事件M , 从身高不低于175cm 的志愿者中随机选出2名担任迎宾工作,共有15种不同取法:{,},{,},{,},{,},{,}A B A C A D A E A F ,{,},{,},{,},{,}B C B D B E B F ,{,},{,},{,}C D C E C F ,{,},{,}D E D F ,{,}E F . …………………………9分H F EPODBA事件M 包含的基本事件有9种:{,},{,}A E A F ,{,},{,}B E B F ,{,},{,}C E C F{,},{,}D E D F ,{,}E F . …………………………11分∴()P M =93155=为所求. …………………………12分 18.(本小题满分14分)(本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力) (1)证明:∵点E ,F 分别是边CD ,CB 的中点,∴BD ∥EF . …………………………1分 ∵菱形ABCD 的对角线互相垂直,∴BD AC ⊥. …………………………2分 ∴EF AC ⊥. …………………………3分 ∴EF AO ⊥,EF PO ⊥. …………………………4分 ∵AO ⊂平面POA ,PO ⊂平面POA ,AO PO O =, ∴EF ⊥平面POA . …………………………5分 ∴BD ⊥平面POA . …………………………6分 (2)解:设AO BD H =,连接BO , ∵60DAB ︒∠=,∴△ABD 为等边三角形. …………………………7分∴4BD =,2BH =,HA =HO PO == ……………………8分 在R t △BHO中,BO …………………………9分在△PBO 中,22210+==BO PO PB , …………………………10分 ∴PO BO ⊥. …………………………11分 ∵PO EF ⊥,EF BO O =,EF ⊂平面BFED ,BO ⊂平面BFED , ∴PO ⊥平面BFED . …………………………12分梯形BFED 的面积为()12S EF BD HO =+⋅=,………………………13分 ∴四棱锥P BFED -的体积11333V S PO =⋅=⨯=.………………14分19.(本小题满分14分)(本小题主要考查等差数列、等比数列等知识,考查化归与转化的数学思想方法,以及运算求解能力和创新意识)(1)解:∵11a =, ()()1112n n n n nS n S ++-+=, ∴2112212S S ⨯-==. …………………………1分∴ 21112123S S a =+=+=. …………………………2分 ∴ 2212a S a =-=. …………………………3分(2)解法1: 由()()1112n n n n nS n S ++-+=, 得1112n n S S n n +-=+. ……………………4分∴ 数列n S n ⎧⎫⎨⎬⎩⎭是首项为111S =, 公差为12的等差数列. ∴()()1111122n S n n n =+-=+. …………………………5分 ∴ ()12n n n S +=. …………………………6分 当2n ≥时, 1n n n a S S -=- …………………………7分 ()()1122n n n n+-=- n =. …………………………8分而11=a 适合上式,∴ n a n =. …………………………9分解法2: 由()()1112n n n n nS n S ++-+=, 得()()112n n n n n n S S S ++--=, ∴()112n n n n na S ++-=. ① …………………………4分 当2n ≥时,()()1112n n n n n a S ----=,② ①-②得()()()()1111122n n n n n n n n na n a S S +-+-----=-, ∴1n n na na n +-=. …………………………5分 ∴11n n a a +-=. …………………………6分 ∴ 数列{}n a 从第2项开始是以22a =为首项, 公差为1的等差数列. ………7分 ∴ ()22n a n n =+-=. …………………………8分而11=a 适合上式,∴ n a n =. …………………………9分(3)解:由(2)知n a n =, ()12n n n S +=. 假设存在正整数k , 使k a , 2k S , 4k a 成等比数列,则224k k k S a a =⋅. …………………………10分即()222142k k k k +⎡⎤=⋅⎢⎥⎣⎦. …………………………11分∵ k 为正整数, ∴()2214k +=.得212k +=或212k +=-, …………………………12分 解得12k =或32k =-, 与k 为正整数矛盾. …………………………13分 ∴ 不存在正整数k , 使k a , 2k S , 4k a 成等比数列. …………………………14分20.(本小题满分14分)(本小题主要考查椭圆的方程、双曲线的方程、直线与圆锥曲线的位置关系等知识,考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力和运算求解能力)(1)解法1: ∵ 双曲线222:12x C y -=的顶点为1(0)F ,20)F , …………1分∴ 椭圆1C 两焦点分别为1(0)F ,20)F .设椭圆1C 方程为12222=+by a x ()0a b >>,∵ 椭圆1C 过点A (1),∴ 1224a AF AF =+=,得2a =. ………………………2分∴ 2222b a =-=. ………………………3分∴ 椭圆1C 的方程为 22142x y +=. ………………………4分解法2: ∵ 双曲线222:12x C y -=的顶点为1(0)F ,20)F , …………………1分∴ 椭圆1C 两焦点分别为1(0)F ,20)F .设椭圆1C 方程为12222=+by a x ()0a b >>,∵ 椭圆1C 过点A (1), ∴22211a b+=. ① ………………………2分 . ∵ 222a b =+, ② ………………………3分 由①②解得24a =, 22b =.∴ 椭圆1C 的方程为 22142x y +=. ………………………4分 (2)解法1:设点),(y x Q ,点),(11y x P ,由A (1)及椭圆1C 关于原点对称可得B 1)-,∴(1)AQ x y =-,11(1)AP x y =-,(1)BQ x y =+,11(1)BP x y =+.由 0AQ AP ⋅=, 得 11((1)(1)0x x y y +--=, ……………………5分即 11((1)(1)x x y y =---. ①同理, 由0BQ BP ⋅=, 得 11((1)(1)x x y y =-++. ② ……………6分①⨯②得 222211(2)(2)(1)(1)x x y y --=--. ③ ………………………7分由于点P 在椭圆1C 上, 则2211142x y +=,得221142x y =-, 代入③式得 2222112(1)(2)(1)(1)y x y y ---=--.当2110y -≠时,有2225x y +=,当2110y -=,则点(1)P -或P ,此时点Q 对应的坐标分别为或当点P 与点A 重合时,即点P (1),由②得3y -,解方程组2225,3,x y y ⎧+=⎪⎨=-⎪⎩ 得点Q的坐标为)1-或22⎛⎫- ⎪ ⎪⎝⎭.同理, 当点P 与点B 重合时,可得点Q的坐标为()或2⎛⎫⎪⎪⎝⎭. ∴点Q 的轨迹方程为 2225x y +=,除去四个点)1-,2⎫-⎪⎪⎝⎭, (),22⎛⎫- ⎪ ⎪⎝⎭. ………………………9分 解法2:设点),(y x Q ,点),(11y x P ,由A (1)及椭圆1C 关于原点对称可得B 1)-, ∵0AQ AP ⋅=,0BQ BP ⋅=, ∴AQ AP ⊥,BQ BP ⊥.1=-(1x ≠,① ……………………5分1=-(1x ≠. ② ……………………6分①⨯② 得 12222111122y y x x --⨯=--. (*) ………………………7分 ∵ 点P 在椭圆1C 上, ∴ 2211142x y +=,得221122x y =-, 代入(*)式得2212211112122x y x x --⨯=--,即2211122y x --⨯=-, 化简得 2225x y +=.若点(1)P -或P , 此时点Q对应的坐标分别为或当点P 与点A 重合时,即点P (1),由②得3y -,解方程组2225,3,x y y ⎧+=⎪⎨=-⎪⎩ 得点Q的坐标为)1-或22⎛⎫- ⎪ ⎪⎝⎭.同理, 当点P 与点B 重合时,可得点Q的坐标为()或2⎛⎫⎪⎪⎝⎭. ∴点Q 的轨迹方程为 2225x y +=,除去四个点)1-,2⎫-⎪⎪⎝⎭, (),22⎛⎫- ⎪ ⎪⎝⎭. ………………………9分 (3) 解法1:点Q (),x y 到直线:AB 0x =.△ABQ的面积为S =10分x ==………………………11分而222(2)42y x x =⨯⨯≤+(当且仅当2x =∴S =≤=2=. ……12分当且仅当2x =, 等号成立.由22225,x x y ⎧=⎪⎨⎪+=⎩解得2,x y ⎧=⎪⎨⎪=⎩或 2.x y ⎧=⎪⎨⎪=-⎩………………………13分 ∴△ABQ此时,点Q的坐标为2⎫⎪⎪⎝⎭或2⎛⎫- ⎪ ⎪⎝⎭.…14分 解法2:由于AB =,故当点Q 到直线AB 的距离最大时,△ABQ 的面积最大. ………………………10分设与直线AB平行的直线为0x m +=,由220,25,x m x y ⎧++=⎪⎨+=⎪⎩消去x,得225250y c ++-=, 由()223220250m m ∆=--=,解得2m =±. ………………………11分若2m =,则2y =-,2x =-;若2m =-,则2y =,2x =. …12分 故当点Q的坐标为22⎛⎫ ⎪ ⎪⎝⎭或22⎛⎫-- ⎪ ⎪⎝⎭时,△ABQ 的面积最大,其值为122S AB ==. ………………………14分21. (本小题满分14分)(本小题主要考查函数的最值、函数的导数、函数的零点与单调性等知识,考查数形结合、化归与转化、分类与讨论的数学思想方法,以及运算求解能力、抽象概括能力与创新意识)(1)解: 由于01t <<,0x >,则()11122t g x x x -⎛⎫=+≥⨯= ⎪⎝⎭ 当且仅当1tx x-=,即x =()min g x =⎡⎤⎣⎦. …………………1分()h x ==1x=时,()min h x =⎡⎤⎣⎦.………………………2分∵01t <<,∴1<<01<.由于()32f x x ax bx =-++()2x x ax b =-++,结合题意,可知,方程20x ax b -++=, ………………………3分a=b =-. ………………………4分∴2222a b =+=-. ∴2112b a =-. ………………………5分而方程20x ax b -++=的一个根在区间(上,另一个根在区间()0,1上.令()2x x ax b ϕ=-++,则()()00,110,20.b a b b ϕϕϕ⎧=<⎪⎪=-++>⎨⎪=-+<⎪⎩………………………6分即222110,21110,21210.2a a a a ⎧-<⎪⎪⎪-++->⎨⎪⎪-++-<⎪⎩解得02,a a a a ⎧<>⎪<<⎨⎪≠⎩ ………………………7分2a <<. ………………………8分 ∴2112b a =-2a <<. 求a 的取值范围的其它解法:另法1:由a =22a =+ ………………………6分 ∵01t <<,∴224a <<. ………………………7分∵a =0>,2a <<. ………………………8分 另法2:设()t ϕ=01t <<, 则()0t ϕ'==<,………………………6分 故函数()t ϕ在区间()0,1上单调递减. ∴())2t ϕ∈. ………………………7分2a <<. ………………………8分 (2)解:由(1)得()322112f x x ax a x ⎛⎫=-++-⎪⎝⎭,则()2213212f x x ax a '=-++-. ………………………9分2a <<,∴二次函数()2213212f x x ax a '=-++-的开口向下,对称轴233a x =<. 故函数()f x '在区间[]1,2上单调递减. ………………………10分 又()()221113212022f a a a '=-++-=--<, ………………………11分 ∴当[]1,2x ∈时,()()10f x f ''≤<.∴函数()f x 在区间[]1,2上单调递减. ………………………12分 ∴函数()f x 的最大值为()2112f a a =-,最小值为()2246f a a =-+-. ………………………14分。
2015年茂名市一模分数线与统计

46.08
5087
64.90
7022
89.59
茂南
2473
7
0.28
67
2.71
175
7.08
499
20.18
1506
60.90
滨海
315
0.00
7
2.22
15
4.76
49
15.56
140
44.44
电白
11946
308
2.58
1323
11.07
2646
22.15
5137
43.00
9424
78.89
31.85
7600
55.81
12667
83.11
化州
12072
733
6.07
2522
15.84
4367
28.23
7011
52.45
10458
82.20
信宜
13450
580
4.31
2204
16.57
3819
29.15
6514
52.40
10946
81.53
合计
市直
7838
829
10.58
2374
30.29
56.65
25077
81.25
合计
40639
3311
8.15
11731
28.87
17266
42.49
25900
63.73
34601
85.14
文科类
往届
5100
322
6.31
1565
2015广州一测预测分数线公告

2015年广州市普通高中毕业班综合测试(一)预测分数线公告根据广州市普通高中毕业班综合测试(一)(以下简称广州一测)成绩进行预测,主要是为了在备考复习的第二阶段更好找准工作方向,明确备考策略。
我们的预测使用了五种不同方法进行。
其中运用到的主要数据有:广州应届考生总数、全省招生计划数、去年实绩、历年上线和录取比例常模、广州一测考生上线比例常模、广州占全省录取数百分比常模、增幅比例常模、文理科原始分录取比例常模。
经验校正系数主要综合下列数据形成:今年工作要求、本届学生现状(如广州一测成绩、学业水平测试成绩、调研模拟测试成绩等)、实考考生中应届生比例、各批次应届生累计上线占全地区累计上线比例、我市历年高考成绩、我市历年广州一测预测与高考实绩相关分析及回归分析等。
根据以上数据,结合我市多年预测经验常模、本届高中毕业年级三年来的教学状况、我市各类学校加工能力常模、全省各地高中办学的发展,综合分析得出今年广州一测上线预测如下:注:①总分上线人数只包含文科类、理科类考生,不含体艺类。
②所有成绩数据均按四舍五入原则取整数。
③英语成绩包括听说和笔试成绩。
为了在备考复习的下一阶段更好地找准工作方向,我们在去年的成功经验基础上,划出考生总分上线临界范围。
根据经典教育测量理论(CTT),考试分数(x)=真分数(t)+偶然误差(e)。
其中,偶然误差包括:考试内容抽样、考生心理、考试过程、阅卷过程等多种因素的干扰所造成的误差,该误差一般是随机的,呈正态分布的。
为避免上述误差带来的误判,根据理论模型和多年实践常模,我们尝试在划出各层次分数线的基础上,再划出临界值(x±ZSe),以便学校估计各层次总分上线临界学生的范围。
同时,为反映考生各学科成绩与总分之间相互配合的情况,根据本次测试划定的总分各条分数线,权衡各学科的平均分、标准差、考生排位、单科满分值与总分满分值之间的关系等诸多因素的影响,运用教育测量学的等值计算技术,通过特定的数学模型,确定学科上线有效分的预测分数线如下:注:①所有成绩数据均按四舍五入原则取整数。
2015年广一模广州市一测理科数学(广州一模理数)试题及参考答案

图17432109878试卷类型:A2015年广州市普通高中毕业班综合测试(一)数学(理科)2015.3 本试卷共4页,21小题, 满分150分.考试用时120分钟. 注意事项:1.答卷前,考生务必用2B 铅笔在“考生号”处填涂考生号。
用黑色字迹钢笔或签字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B 铅笔填涂选做题题号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式:锥体的体积公式Sh V 31=,其中S 是锥体的底面积,h 是锥体的高. ()()22221211236n n n n ++++++=()*n ∈N . 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知全集{}1,2,3,4,5U =, 集合{}3,4,5M =, {}1,2,5N =, 则集合{}1,2可以表示为 A .M N B .()U M N ð C .()U MN ð D .()()U U M N 痧2.已知向量()3,4a =,若5λ=a ,则实数λ的值为A .15 B .1 C .15± D .1± 3. 若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,叶为个位数,则这组数据的中位数和平均数分别是 A. 91, 91.5 B. 91, 92 C. 91.5, 91.5 D. 91.5, 924. 直线10x ay ++=与圆()2214x y +-=的位置关系是A. 相交B. 相切C. 相离D. 不能确定侧视图正视图5. 若直线3y x=上存在点(),x y满足约束条件40,280,,x yx yx m++>⎧⎪-+≥⎨⎪≤⎩则实数m的取值范围是A. ()1,-+∞ B. [)1,-+∞C. (),1-∞- D. (],1-∞-6. 已知某锥体的正视图和侧视图如图2,图2A. B. D.7. 已知a为实数,则1a≥是关于x的绝对值不等式1x x a+-≤有解的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件8. 已知i是虚数单位,C是全体复数构成的集合,若映射:f C→R满足: 对任意12,z z C∈,以及任意λ∈R , 都有()()()()()121211f z z f z f zλλλλ+-=+-, 则称映射f具有性质P. 给出如下映射:①1:f C→R , ()1f z x y=-, z x y=+i(,x y∈R);②2:f C→R , ()22f z x y=-, z x y=+i(,x y∈R);③3:f C→R , ()32f z x y=+, z x y=+i(,x y∈R);其中, 具有性质P的映射的序号为A. ①②B. ①③C. ②③D. ①②③二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.(一)必做题(9~13题)9. 已知tan2α=,则tan2α的值为.10. 已知e为自然对数的底数,若曲线y x=e x在点()1,e处的切线斜率为.11. 已知随机变量X服从正态分布()2,1N. 若()130.6826P X≤≤=,则()3P X>图3等于 . 12. 已知幂函数()223(m m f x xm --+=∈Z )为偶函数,且在区间()0,+∞上是单调增函数,则()2f 的值为 .13.已知,n k ∈N *,且k n ≤,k C k n n =C 11k n --,则可推出C 12n +C 23n +C 3n k ++C k n n ++C (n n n =C 01n -+C 11n -++C 11k n --++C 11)n n --12n n -=⋅, 由此,可推出C 122n +C 223n +C 32n k ++C 2k n n ++C n n = .(二)选做题(14~15题,考生只能从中选做一题) 14. (坐标系与参数方程选做题)在直角坐标系xOy 中,曲线1C 和2C 的参数方程分别为cos sin ,(cos sin x y θθθθθ=+⎧⎨=-⎩为参数)和2,(x t t y t=-⎧⎨=⎩为参数).以原点O 为极点,x 轴正半轴为极轴,建立极坐标系,则曲线1C 与2C 的交点的极坐标...为 . 15. (几何证明选讲选做题)如图3,BC 是圆O 的一条弦,延长BC 至点E , 使得22BC CE ==,过E 作圆O 的切线,A 为切点,BAC ∠的平分线AD 交BC 于点D , 则DE 的长为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数()()sin 0,06f x A x A πωω⎛⎫=+>> ⎪⎝⎭的图象在y 轴右侧的第一个最高点和第一个最低点的坐标分别为()02x ,和022x ,π⎛⎫+- ⎪⎝⎭. (1)求函数()f x 的解析式; (2)求0sin 4x π⎛⎫+ ⎪⎝⎭的值.图4OF ED C B A 图5FE PODB A袋子中装有大小相同的白球和红球共7个,从袋子中任取2个球都是白球的概率为17,每个球被取到的机会均等. 现从袋子中每次取1个球,如果取出的是白球则不再放回,设在取得红球之前已取出的白球个数为X . (1)求袋子中白球的个数; (2)求X 的分布列和数学期望.18. (本小题满分14分)如图4,在边长为4的菱形ABCD 中,60DAB ︒∠=,点E ,F 分别是边CD ,CB 的 中点,ACEF O =,沿EF 将△CEF 翻折到△PEF ,连接PA,PB,PD ,得到如图5的五棱锥P ABFED -,且PB =(1)求证:BD ⊥平面POA ;(2)求二面角--B AP O 的正切值.19. (本小题满分14分)已知数列{}n a 的各项均为正数,其前n 项和为n S ,且满足111,1n a a +==,n ∈N *.(1)求2a 的值;(2)求数列{}n a 的通项公式;(3)是否存在正整数k , 使k a , 21k S -, 4k a 成等比数列? 若存在, 求k 的值; 若不存在, 请说明理由.已知椭圆1C 的中心在坐标原点,两焦点分别为双曲线222:12x C y -=的顶点,直线0=x 与椭圆1C 交于A ,B 两点,且点A 的坐标为(1),点P 是椭圆1C 上异于点A ,B 的任意一点,点Q 满足0AQ AP ⋅=,0BQ BP ⋅=,且A ,B ,Q 三点不共线.(1) 求椭圆1C 的方程; (2) 求点Q 的轨迹方程;(3) 求ABQ ∆面积的最大值及此时点Q 的坐标.21. (本小题满分14分) 已知函数()()2ln 12a f x x x x =++-()0a ≥. (1)若()0f x >对()0,x ∈+∞都成立,求a 的取值范围;(2)已知e 为自然对数的底数,证明:∀n ∈N *22212111n n n n ⎛⎫⎛⎫⎛⎫<++⋅⋅⋅+ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭e <.2015年广州市普通高中毕业班综合测试(一)数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题考查基本知识和基本运算.共8小题,每小题5分,满分40分.二、填空题:本大题考查基本知识和基本运算,体现选择性.共7小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题. 9. 43-10. 2e 11. 0.1587 12. 16 13. ()212n n n -+⋅14. 4π⎫⎪⎭15. 说明: 第14题答案可以是2,4k k ππ⎫+∈⎪⎭Z . 三、解答题:本大题共6小题,满分80分.16.(本小题满分12分)(本小题主要考查三角函数的图象与性质、三角两角和公式等等知识,考查化归与转化的数学思想方法,以及运算求解能力)(1)解:由题意可得2,A =, …………………………1分00222T x x ππ⎛⎫=+-= ⎪⎝⎭, …………………………3分 ∴.T π= …………………………4分 由,2πωπ=得2=ω, …………………………5分∴()2sin 26f x x π⎛⎫=+⎪⎝⎭. …………………………6分(2)解: ∵ 点()0,2x 是函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭在y 轴右侧的第一个最高点, ∴ 0262x ππ+=. …………………………7分∴ 06x π=. …………………………8分 ∴0sin 4x π⎛⎫+⎪⎝⎭sin 64ππ⎛⎫=+ ⎪⎝⎭…………………………9分 sincoscossin6464ππππ=+ …………………………10分12222=⨯+ …………………………11分4=. …………………………12分 17.(本小题满分12分)(本小题主要考查古典概型、解方程、随机变量的分布列与均值(数学期望)等知识,考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识)(1)解:设袋子中有n (n ∈N *)个白球,依题意得,22717n C C =,………………………1分即()1127672n n -=⨯, 化简得,260n n --=, …………………………2分解得,3n =或2n =-(舍去). …………………………3分 ∴袋子中有3个白球. …………………………4分 (2)解:由(1)得,袋子中有4个红球,3个白球. …………………………5分X 的可能取值为0,1,2,3, …………………………6分()407P X ==, ()3421767P X ==⨯=, ()3244276535P X ==⨯⨯=,()321413765435P X ==⨯⨯⨯=. ………………10分∴X 的分布列为:…………………………11分GH F EPODBA∴4241301237735355EX =⨯+⨯+⨯+⨯=. …………………………12分 18.(本小题满分14分)(本小题主要考查空间线面关系、二面角、空间向量及坐标运算等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力) (1)证明:∵点E ,F 分别是边CD ,CB 的中点,∴BD ∥EF . …………………………1分 ∵菱形ABCD 的对角线互相垂直,∴BD AC ⊥. ∴EF AC ⊥. ∴EF AO ⊥,EF PO ⊥. …………………………2分 ∵AO ⊂平面POA ,PO ⊂平面POA ,AO PO O =, ∴EF ⊥平面POA . …………………………3分∴BD ⊥平面POA . …………………………4分 (2)解法1:设AO BD H =,连接BO , ∵60DAB ︒∠=, ∴△ABD 为等边三角形.∴4BD =,2BH =,HA =HO PO ==……5分 在R t △BHO中,BO在△PBO 中,22210+==BO PO PB ,∴PO BO ⊥. …………………………6分 ∵PO EF ⊥,EF BO O =,EF ⊂平面BFED ,BO ⊂平面BFED , ∴PO ⊥平面BFED . …………………………7分 过H 作⊥HG AP ,垂足为G ,连接BG ,由(1)知⊥BH 平面POA ,且⊂AP 平面POA , ∴⊥BH AP .∵=HG BH H ,⊂HG 平面BHG ,⊂BH 平面BHG ,∴⊥AP 平面BHG . …………………………8分 ∵⊂BG 平面BHG ,∴⊥AP BG . …………………………9分 ∴∠BGH 为二面角--B AP O 的平面角. …………………………10分 在Rt △POA中,AP在Rt △POA 和Rt △HGA 中,90,︒∠=∠=∠=∠POA HGA PAO HAG , ∴Rt △POA ~Rt △HGA . …………………………11分 ∴=PO PAHG HA.∴⋅===PO HA HG PA …………………………12分A在Rt △BHG中,tan ∠===BH BGH HG . ……………………13分 ∴二面角--B AP O…………………………14分 解法2:设AOBD H =,连接BO ,∵60DAB ︒∠=, ∴△ABD 为等边三角形.∴4BD =,2BH =,HA =HO PO ==………………………5分 在R t △BHO中,BO在△PBO 中,22210+==BO PO PB ,∴PO BO ⊥. …………………………6分 ∵PO EF ⊥,EF BO O =,EF ⊂平面BFED ,BO ⊂平面BFED , ∴PO ⊥平面BFED . …………………………7分 以O 为原点,OF 所在直线为x 轴,AO 所在直线为y 轴,OP 所在直线为z 轴, 建立空间直角坐标系-O xyz ,则()0,-A,()2,B,(P,()0,H .…………8分∴(=AP,()=AB . 设平面PAB 的法向量为=n (),,x y z ,由⊥n AP ,⊥n AB ,得0,20.⎧+=⎪⎨+=⎪⎩x 令1=y ,得3=-z,=x ∴平面PAB 的一个法向量为=n ()3-. 由(1)知平面PAO 的一个法向量为()2,0,0=-BH , ……………………11分 设二面角--B AP O 的平面角为θ, 则cos θ=cos ,n BH⋅=n BH nBH==………………………12分∴sin 13θ==sin tan cos 3θθθ==.………………………13分∴二面角--B AP O 的正切值为3…………………………14分 19.(本小题满分14分)(本小题主要考查等差数列、数列的前n 项和等知识,考查化归与转化的数学思想方法,以及运算求解能力和创新意识)(1)解:∵111,1n a a +==,∴2113a ===. …………………………1分(2)解法1:由11n a +=,得11n n S S +-=, …………………………2分故)211n S +=. …………………………3分∵0n a >,∴0n S >.1=. …………………………4分∴数列1=,公差为1的等差数列.()11n n =+-=. …………………………5分 ∴2n S n =. …………………………6分当2n ≥时,()221121n n n a S S n n n -=-=--=-, …………………………8分又11a =适合上式,∴21n a n =-. …………………………9分解法2:由11n a +=,得()2114n n a S +-=, …………………………2分 当2n ≥时,()2114n n a S --=, …………………………3分 ∴()()()22111144n n n n n a a S S a +----=-=. …………………………4分∴2211220n n n n a a a a ++---=.∴()()1120n n n n a a a a +++--=. …………………………5分 ∵ 0n a >,∴12n n a a +-=. …………………………6分 ∴数列{}n a 从第2项开始是以23a =为首项,公差为2的等差数列.……………7分 ∴()()322212n a n n n =+-=-≥. …………………………8分 ∵11a =适合上式,∴21n a n =-. …………………………9分 解法3:由已知及(1)得11a =,23a =,猜想21n a n =-. …………………………2分 下面用数学归纳法证明.① 当1n =,2时,由已知11211a ==⨯-,23a ==221⨯-,猜想成立. ………3分 ② 假设n k =()2k ≥时,猜想成立,即21k a k =-, …………………………4分由已知11k a +=,得()2114k k a S +-=, 故()2114k k a S --=.∴()()()22111144k k k k k a a S S a +----=-=. …………………………5分∴22211220k k k k a a a a ++---=.∴()()1120k kk k a a aa +++--=. …………………………6分∵10,0k k a a +>>,∴120k k a a +--=. …………………………7分 ∴()12212211k k a a k k +=+=-+=+-. …………………………8分 故当1n k =+时,猜想也成立.由①②知,猜想成立,即21n a n =-. …………………………9分 (3)解:由(2)知21n a n =-, ()21212n n n S n +-==.假设存在正整数k , 使k a , 21k S -, 4k a 成等比数列,则2214k k k S a a -=⋅. …………………………10分即()()()4212181k k k -=-⋅-. …………………………11分 ∵ k 为正整数, ∴ 210k -≠. ∴ ()32181k k -=-.∴ 328126181k k k k -+-=-.化简得 32460k k k --=. …………………………12分 ∵ 0k ≠,∴ 24610k k --=.解得6384k ±==, 与k 为正整数矛盾. ……………………13分 ∴ 不存在正整数k , 使k a , 21k S -, 4k a 成等比数列. …………………………14分20.(本小题满分14分)(本小题主要考查椭圆的方程、双曲线的方程、直线与圆锥曲线的位置关系等知识,考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力和运算求解能力)(1)解法1: ∵ 双曲线222:12x C y -=的顶点为1(0)F ,20)F , …………1分∴ 椭圆1C 两焦点分别为1(0)F ,20)F .设椭圆1C 方程为12222=+by a x ()0a b >>,∵ 椭圆1C 过点A (1),∴ 1224a AF AF =+=,得2a =. ………………………2分∴ 2222b a =-=. ………………………3分∴ 椭圆1C 的方程为 22142x y +=. ………………………4分解法2: ∵ 双曲线222:12x C y -=的顶点为1(0)F ,20)F , ……………………1分∴ 椭圆1C 两焦点分别为1(0)F ,20)F .设椭圆1C 方程为12222=+by a x ()0a b >>,∵ 椭圆1C 过点A (1), ∴22211a b +=. ① ………………………2分 . ∵ 222a b =+, ② ………………………3分 由①②解得24a =, 22b =.∴ 椭圆1C 的方程为 22142x y +=. ………………………4分 (2)解法1:设点),(y x Q ,点),(11y x P ,由A (1)及椭圆1C 关于原点对称可得B 1)-,∴(1)AQ x y =-,11(1)AP x y =-,(1)BQ x y =+,11(1)BP x y =+.由 0AQ AP ⋅=, 得 11((1)(1)0x x y y +--=, ……………………5分即 11((1)(1)x x y y =---. ①同理, 由0BQ BP ⋅=, 得 11((1)(1)x x y y =-++. ② ……………6分①⨯②得 222211(2)(2)(1)(1)x x y y --=--. ③ ………………………7分由于点P 在椭圆1C 上, 则2211142x y +=,得221142x y =-, 代入③式得 2222112(1)(2)(1)(1)y x y y ---=--.当2110y -≠时,有2225x y +=,当2110y -=,则点(1)P -或P ,此时点Q 对应的坐标分别为或(1)- ,其坐标也满足方程2225x y +=. ………………………8分当点P 与点A 重合时,即点P (1),由②得 3y -,解方程组2225,3,x y y ⎧+=⎪⎨=-⎪⎩ 得点Q的坐标为)1-或2⎫-⎪⎪⎝⎭. 同理, 当点P 与点B 重合时,可得点Q的坐标为()或22⎛⎫- ⎪ ⎪⎝⎭.∴点Q 的轨迹方程为 2225x y +=,除去四个点)1-,22⎛⎫- ⎪ ⎪⎝⎭, (), 22⎛⎫- ⎪ ⎪⎝⎭. ………………………9分 解法2:设点),(y x Q ,点),(11y x P ,由A (1)及椭圆1C 关于原点对称可得B 1)-, ∵0AQ AP ⋅=,0BQ BP ⋅=, ∴AQ AP ⊥,BQ BP ⊥.1=-(1x ≠,① ……………………5分1=-(1x ≠. ② ……………………6分①⨯② 得 12222111122y y x x --⨯=--. (*) ………………………7分 ∵ 点P 在椭圆1C 上, ∴ 2211142x y +=,得221122x y =-, 代入(*)式得2212211112122x y x x --⨯=--,即2211122y x --⨯=-, 化简得 2225x y +=.若点(1)P -或P , 此时点Q对应的坐标分别为或(1)- ,其坐标也满足方程2225x y +=. ………………………8分当点P 与点A 重合时,即点P (1),由②得3y -,解方程组2225,3,x y y ⎧+=⎪⎨=-⎪⎩ 得点Q的坐标为)1-或2⎫-⎪⎪⎝⎭.同理, 当点P 与点B 重合时,可得点Q的坐标为()或2⎛⎫⎪⎪⎝⎭. ∴点Q 的轨迹方程为 2225x y +=,除去四个点)1-,22⎛⎫- ⎪ ⎪⎝⎭, (),22⎛⎫- ⎪ ⎪⎝⎭. ………………………9分 (3) 解法1:点Q (),x y 到直线:AB 0x =.△ABQ的面积为S =10分x ==………………………11分而222(2)42y x x =⨯⨯≤+(当且仅当2x =∴S =≤=2=. ……12分当且仅当2x =, 等号成立.由22225,x x y ⎧=⎪⎨⎪+=⎩解得,22,x y ⎧=⎪⎨⎪=⎩或22.x y ⎧=-⎪⎨⎪=-⎩………………………13分 ∴△ABQ的面积最大值为2, 此时,点Q的坐标为2⎫⎪⎪⎝⎭或2⎛⎫- ⎪ ⎪⎝⎭.…14分 解法2:由于AB =,故当点Q 到直线AB 的距离最大时,△ABQ 的面积最大. (1)0分 设与直线AB 平行的直线为0x m +=,由220,25,x m x y ⎧++=⎪⎨+=⎪⎩消去x ,得225250y c ++-=, 由()223220250m m ∆=--=,解得m =. ………………………11分若2m =,则2y =-,2x =-;若2m =-,则2y =,2x =.…12分 故当点Q的坐标为22⎛⎫ ⎪ ⎪⎝⎭或22⎛⎫-- ⎪ ⎪⎝⎭时,△ABQ 的面积最大,其值为122S AB ==. ………………………14分 21.(本小题满分14分)(本小题主要考查函数的导数、不等式等知识,考查数形结合、化归与转化、分类与讨论的数学思想方法,以及运算求解能力、抽象概括能力与创新意识) (1)解:∵()()2ln 12a f x x x x =++-,其定义域为()1,-+∞, ∴()()11111x ax a f x ax x x+-'=+-=++. …………………………1分 ① 当0a =时,()1xf x x'=-+,当x ∈()0,+∞时,()0f x '<, 则()f x 在区间()0,+∞上单调递减,此时,()()00f x f <=,不符合题意. …2分 ② 当01a <<时,令()0f x '=,得10x =,210ax a-=>, 当x ∈10a ,a -⎛⎫ ⎪⎝⎭时,()0f x '<,则()f x 在区间10a ,a -⎛⎫⎪⎝⎭上单调递减,此时,()()00f x f <=,不符合题意. …………………………3分③ 当1a =时,()21x f x x'=+,当x ∈()0,+∞时,()0f x '>,则()f x 在区间()0,+∞上单调递增,此时,()()00f x f >=,符合题意. ……4分 ④ 当1a >时,令()0f x '=,得10x =,210ax a-=<,当x ∈()0,+∞时,()0f x '>, 则()f x 在区间()0,+∞上单调递增,此时,()()00f x f >=,符合题意. ……5分 综上所述,a 的取值范围为[)1,+∞. …………………………6分 (2)证明:由(1)可知,当0a =时,()0f x <对()0,x ∈+∞都成立,即()ln 1x x +<对()0,x ∈+∞都成立. …………………………7分∴2222221212ln 1ln 1ln 1n nn n n n nn⎛⎫⎛⎫⎛⎫++++++<+++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.………………8分 即ln 2222121211112n n n n n n n n ⎡⎤++++⎛⎫⎛⎫⎛⎫+++<= ⎪⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦. 由于n ∈N *,则111111222221n n n +=+≤+=⨯. …………………………9分 ∴ln 222121111n n n n ⎡⎤⎛⎫⎛⎫⎛⎫+++< ⎪⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦. ∴ 22212111n n n n ⎛⎫⎛⎫⎛⎫+++ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭e <. …………………………10分 由(1)可知,当1a =时,()0f x >对()0,x ∈+∞都成立, 即()21ln 12x x x -<+对()0,x ∈+∞都成立. …………………………11分 ∴2222224442221211212ln 1ln 1ln 12n n n n nn n nn n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++-+++<++++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭.…………………………12分即()()()2422212111126ln 11122n n n n n n n n n n n ++⎡⎤⎢⎥+⎡⎤⎛⎫⎛⎫⎛⎫-<+++⎢⎥ ⎪⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎢⎥⎢⎥⎣⎦. 得323222643112ln 11112n n n n n n n n +--⎡⎤⎛⎫⎛⎫⎛⎫<+++ ⎪⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦由于n ∈N *,则()()32232333363316431611212122n n n n n n n n n n n+-+-+--=≥=. …………………………13分∴12<ln 22212111n n n n ⎡⎤⎛⎫⎛⎫⎛⎫+++ ⎪⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.∴22212111n n n n ⎛⎫⎛⎫⎛⎫<+++ ⎪⎪⎪⎝⎭⎝⎭⎝⎭. …………………………14分 22212111n n n n ⎛⎫⎛⎫⎛⎫<+++ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭e <.。
2015年广州一模文数部分答案

n n 1 , 2
„„„„„„„„„„1 分
3
1 2 1. 2
∴ S 2 1 2 S1 1 2a1 3 . ∴ a2 S 2 a1 2 . (2)解法 1: 由 nSn 1 n 1 Sn
„„„„„„„„„„2 分 „„„„„„„„„„3 分
tan tan
„„„„„„„„„„10 分
„„„„„„„„„„11 分
„„„„„„„„„„12 分
17. (本小题满分 12 分) (本小题主要考查古典概型、分层抽样等基础知识,考查化归与转化的数学思想方法,以 及数据处理能力与应用意识) (1)解: 由 0.05 c 0.35 0.20 0.10 1.00 ,得 c 0.30 . „„„„„„„„„„1 分 由
2
„„„„„„„„„„10 分
2
2k 2k 1 即 k 4k . 2
∵ k 为正整数, ∴ 2k 1 4 .
2
„„„„„„„„„„11 分
得 2k 1 2 或 2k 1 2 , 解得 k
„„„„„„„„„„12 分 „„„„„„„„„„13 分 „„„„„„„„„„14 分
二、填空题:本大题考查基本知识和基本运算,体现选择性.共 5 小题,每小题 5 分,满 分 20 分.其中 14~15 题是选做题,考生只能选做一题. 11.
2,
12. 2e
13.
2015 2016
14. 2,
4
15.
3
说明: 第 14 题答案可以是 2, 2k
1 3 或 k , 与 k 为正整数矛盾. 2 2
2015广州市普通高中学校录取分数(全)
最低分数最低分数同分序号末位考生志愿序号1华南师范大学附属中学公办全市7336512广东实验中学公办全市73012313广东实验中学自筹经费全市72617924广东广雅中学公办全市72711515广州市执信中学公办全市72622716广州市第二中学公办全市71517117广州市第六中学公办全市70219028广东华侨中学公办全市64033549广州市协和中学公办全市640349210广州大学附属中学(大学城校区)公办全市712137111广州市铁一中学(亚运城校区)公办全市70123112广州市铁一中学(校本部)公办全市702305213广州市第一中学公办全市653106114广州市第四中学公办全市654366115广州市真光中学公办全市661100116广州市第三中学公办全市640347217广州市第七中学公办全市702318318广州市第十六中学公办全市69715119广州市培正中学公办全市678150120广州市育才中学公办全市643140121广州市第五中学公办全市640254222广州市南武中学公办全市640330323广州市第四十七中学公办全市691304124广州市第八十九中学公办全市640323325广州市天河中学公办全市664254126广州市培英中学公办全市655251127广州市第六十五中学公办全市640318428广州市第八十中学公办全市640307429广州市第八十六中学公办全市608257430广东仲元中学公办全市699116131广东番禺中学公办全市665127132广州市番禺区实验中学公办番禺和三镇640256233广州市番禺区象贤中学公办全市6481501序号院校名称录取类别计划区域2015年广户籍生34广州市禺山高级中学公办全市613253435广东第二师范学院番禺附属中学公办全市600273436广州市花都区秀全中学公办全市65570137广州市花都区邝维煜纪念中学公办全市605299338广州市花都区新华中学公办全市577238239广州市南沙第一中学公办全市640337440广州市玉岩中学公办全市626143341增城市增城中学公办全市658170142增城市新塘中学公办全市569238443从化市从化中学公办全市622308244从化市第六中学公办全市596258245华师附中南海实验高中民办全市648831一、面向老三区或本区招生的普通高中学校最低分数最低分数同分序号末位考生志愿序号1广州市第一中学公办老三区65427512广州市南海中学公办老三区6213613广州市西关外国语学校公办老三区64011924广州市真光中学公办老三区68234615广州市第十三中学公办老三区62514916广州市第十七中学公办老三区63013117广州市第二十一中学公办老三区64025038广州市培正中学公办老三区69310819广州市育才中学公办老三区676340110广州市恒福中学公办老三区600265211广州市知用中学公办老三区605205112广州市第九十七中学公办老三区601135113广州市第四十一中学公办老三区600248214广州市海珠外国语实验中学公办老三区627259115广州市第七十五中学公办天河区603219116广州市第一一三中学公办天河区636129117广州市东圃中学公办天河区60615118广州市天河外国语学校公办天河区69970119广州市第六十五中学公办白云区612222120广州市第八十中学公办白云区572204121广州市白云中学公办白云区525186222广州彭加木纪念中学公办白云区525165523广州市第六十六中学公办白云区52995序号学校名称录取类别计划区域户籍生第一批24广州市第二外国语学校公办白云区5361471 25广州市白云艺术中学公办白云区5291335 26广州市第七十一中学公办白云区4801705 27广州市第八十一中学公办白云区5291585 28同德中学公办白云区5251202 29广州石化中学公办黄埔区549104130广州市番禺区实验中学公办番禺和三镇635141131广州市番禺区石碁中学公办番禺和三镇514169332广州市番禺区洛溪新城中学公办番禺和三镇54075133广州市番禺区石北中学公办番禺和三镇520158434广州市番禺区石楼中学公办番禺和三镇480106435广州市番禺区南村中学公办番禺和三镇496140436广州市番禺区石碁第三中学公办番禺和三镇531171137广州市花都区第一中学公办花都区4801663 38广州市花都区第二中学公办花都区563101 39广州市花都区花东中学公办花都区5651301 40广州市花都区狮岭中学公办花都区629111 41花都区实验中学公办花都区489913 42花都区圆玄中学公办花都区49742143广州市南沙第一中学公办南沙和三镇526100144广州市南沙东涌中学公办番禺和南沙576178145广州市南沙大岗中学公办番禺和南沙506177246广州科学城中学公办萝岗区490421 47广州开发区外国语学校公办萝岗区480892 48增城市郑中钧中学公办增城市4801004 49增城市第一中学公办增城市5411131 50增城市高级中学公办增城市5201722 51增城市新塘中学北校区公办增城市5221473 52增城市荔城中学公办增城市5201783 53从化市第二中学公办从化市5141592 54从化市第五中学公办从化市527471二、面向全市招生的普通高中学校序号学校名称录取类别计划区域最低分数最低分数同分序号末位考生志愿序号老三区6831881天河区683121白云区6833101黄埔区6843511番禺区6832041花都区6951671南沙区——萝岗区——增城区6831301从化区——老三区6402583天河区6411662白云区6383153黄埔区6272672番禺区6471182花都区653952南沙区——萝岗区——增城区6291892从化区64742老三区6411212天河区640902白云区6381552黄埔区——番禺区6421592花都区——南沙区——萝岗区631291增城区——从化区——老三区6002092天河区6062162白云区5611471黄埔区646312番禺区5961531花都区561631南沙区——萝岗区529201增城区——从化区——老三区6002453天河区60016431中山大学附属中学民办2广州市北大附中为明广州实验学校民办3广州市海珠中学民办4广州市培才高级中学民办白云区5311343黄埔区5741622番禺区5311943花都区539103南沙区——萝岗区5211902增城区573443从化区601513老三区600212天河区602842白云区529582黄埔区60972番禺区531412花都区587941南沙区5321201萝岗区5521251增城区527901从化区——老三区7092171天河区7061361白云区7061681黄埔区7132411番禺区7111811花都区7102851南沙区——萝岗区——增城区7212171从化区7122211老三区688371天河区6882001白云区687621黄埔区7123121番禺区6912591花都区6893751南沙区——萝岗区——增城区——从化区——老三区660451天河区6601491白云区6581511黄埔区6901791番禺区663541花都区6593511南沙区6892715广州思源学校民办6广州市华美英语实验学校民办7广东实验中学附属天河学校民办8广州大学附属实验学校民办9广州市广外附设外语学校民办萝岗区——增城区6581581从化区682281老三区65391天河区6752531白云区——黄埔区——番禺区646791花都区——南沙区——萝岗区——增城区——从化区669591老三区6412882天河区6401072白云区639212黄埔区6301332番禺区6352082花都区637972南沙区6663482萝岗区627231增城区621822从化区6143001老三区712161天河区7051591白云区7072461黄埔区——番禺区7231691花都区7052661南沙区——萝岗区——增城区7102091从化区712361老三区6102172天河区600282白云区528362黄埔区5701452番禺区5411542花都区5791792南沙区——萝岗区6381911增城区54321从化区57231老三区644952天河区6401882校10广州市番禺区祈福英语实验学校民办11广州市华师附中番禺学校民办12黄冈中学广州学校民办13广州市香江中学民办白云区6352132黄埔区640802番禺区638862花都区6261761南沙区——萝岗区643722增城区6392192从化区6382481老三区6403242天河区640572白云区6362982黄埔区6292901番禺区6362852花都区6141022南沙区6392471萝岗区6413131增城区6111341从化区——一、第二批提前录取计划区域最低分数最低分数同分序号最低分数1广州市美术中学公办全市5552668二、面向老三区或本区招生的普通高中学校15华师附中南海实验高中民办14南海执信中学民办借读生序号学校名称录取类别户籍生户籍生第二批最低分数最低分数同分序号末位考生志愿序号1广州市西关培英中学公办老三区6071312广州市荔湾区汾水中学公办老三区60023333广州市越秀外国语学校公办老三区61416014广州市海珠外国语实验中学公办老三区62011915广州市岭南画派纪念中学公办老三区59521916广州市第四十四中学公办天河区5984917广州彭加木纪念中学公办白云区4804118广州市第六十六中学公办白云区48218119广州市白云艺术中学公办白云区48189110广州市第八十一中学公办白云区480173111广州市第八十七中学公办黄埔区49089112广州市番禺区石北中学公办番禺和三镇480145113广州市花都区第二中学公办花都区48370214广州市花都区花东中学公办花都区48085215广州市花都区狮岭中学公办花都区521187116广州市南沙鱼窝头中学公办番禺和南沙480133117广州市南沙区麒麟中学公办南沙和三镇480161118增城市高级中学公办增城区48962119增城市派潭中学公办增城区490167120增城市中新中学公办增城区491181121增城市仙村中学公办增城区49068122增城市新塘中学北校区公办增城区480154423增城市荔城中学公办增城区480163324从化市第三中学公办从化区480129125从化市第四中学公办从化区4801721三、面向全市招生的普通高中学校招生最低区域分数序号学校名称录取类别计划区域序号学校名称录取类别最低分数同分序号末位考生志愿序号老三区643201天河区6451771白云区6461081黄埔区6761061番禺区6431691花都区648671南沙区——萝岗区——增城区6651771从化区——老三区6413031天河区6512291白云区6411641黄埔区6411491番禺区642331花都区——南沙区——萝岗区——增城区——从化区——老三区612761天河区6131431白云区6131981黄埔区6191361番禺区6232581花都区——南沙区665191萝岗区638281增城区——从化区——老三区600842天河区6002462白云区551152黄埔区553252番禺区544322花都区55022南沙区60142萝岗区570872增城区564332从化区——老三区6951451天河区6953091白云区6953041黄埔区——番禺区69519011广州市北大附中为明广州实验学校民办2广州市海珠中学民办3广州市培才高级中学民办4广州市华美英语实验学校民办5广东实验中学附属天河学校民办花都区6962611南沙区——萝岗区——增城区7011851从化区7021161老三区667691天河区671631白云区6682071黄埔区6752981番禺区668801花都区6813161南沙区677201萝岗区——增城区6732171从化区——老三区6011691天河区603551白云区6021311黄埔区6041731番禺区6001271花都区597611南沙区6221001萝岗区6312241增城区603911从化区——老三区5801053天河区5811362白云区492923黄埔区490822番禺区4901322花都区514631南沙区55583萝岗区5361321增城区5051102从化区503811广州英豪学校民办5广东实验中学附属天河学校民办6广州大学附属实验学校民办7广州中大附属雅宝学校民办8第三批一、面向增城区招生的普通高中学校二、面向全市招生的普通高中学校序号学校名称录取类别计划区域最低分数最低分数同分序号末位考生志愿序号1广州思源学校民办全市6259012广州中大附属雅宝学校民办全市62713913黄冈中学广州学校民办全市68818814广州市香江中学民办全市5948915广州南洋英文学校民办全市579416广州英豪学校民办全市5944413.“末位考生分数同分序号”是指向该校投档最后一名考生分数的同分最大排位序号。
