《图形的认识初步》水平测试(A)

合集下载

冀教版七年级上《第1章+图形的初步认识》2013年单元测试卷a

冀教版七年级上《第1章图形的初步认识》2013年单元测试卷A一、选择题（每小题3分，共30分）1．（3分）（2005•宜昌）图中物体的形状类似于（）．C D．3．（3分）图中的几何体有（）个面．4．（3分）将下列哪个图形绕直线l旋转一周，可以得到图所示立体图形（）．C D．．C D．6．（3分）（2005•深圳）我们从不同的方向观察同一物体时，可以看到不同的平面图形，如图，从图的左面看这个几何体的左视图是（）．CD ．．CD ．8．（3分）桌上摆满了朋友们送来的礼物，小狗贝贝好奇地想看个究竟．①小狗先是站在地面上看，②然后抬起了前腿看，③唉，还是站到凳子上看吧，④最后，它终于爬上了桌子…按小狗四9．（3分）给出以下四个几何体，其中能截出长方形的几何体共有（）二、填空题（每小题3分，共24分） 11．（3分）如图，这个几何体的名称是 _________ ；它有 _________ 个面组成；它有 _________ 个顶点；经过每个顶点有 _________ 条边．12．（3分）点动成 _________ ，线动成 _________ ，面动成 _________ ．面面相交得到 _________ ，线线相交得到 _________ ． 13．（3分）薄薄的硬币在桌面上转动时，看上去象球，这说明了 _________ ． 14．（3分）一个直角三角形绕其中一条直角边旋转一周所形成的几何体是 _________ ．15．（3分）水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示下图是一个正方体的平面展示图，若图中的“似”表示正方体的前面，“锦”表示右面，“程”表示下面，则“祝”、“你”、“前”分别表示正方体的_________．16．（3分）根据下列多面体的平面展开图，填写多面体的名称：（1）_________，（2）_________，（3）_________．17．（3分）指出图（1）、图（2）、图（3）是几何体从哪个方向看到的图形．（1）_________（2）_________（3）_________．18．（3分）若一个几何体的截面是圆，则该几何体可能是_________．三、作图题（每小题7分，共14分）19．（7分）如图分别从正面、左面、上面看下面几何体，画出所得到的平面图形．20．（7分）如图所示，它是由什么图形旋转而成的？请你画出来．四、解答题（每小题8分，共16分）21．（8分）如图所示的八棱柱，它的底面边长都是5厘米，侧棱长都是6厘米，回答下列问题：（1）这个八棱柱一共有多少个面？它们的形状分别是什么？图形哪些面的形状、面积完全相同？（2）这个八棱柱一共有多少条棱？它们的长度分别是多少？（3）沿一条侧棱将其侧面全部展成一个平面图形，这个图形是什么形状？面积是多少？22．（8分）如图，图（1）是正方体木块，把它切去一块，可能得到（2）、（3）、（4）、（5）所示的图形，问（2）、（3）、（4）、（5）图中切掉的部分可能是其他几块中的哪一块？五、应用题（每小题8分，共16分）23．（8分）现有4枚相同的骰子，骰子的展开图如图所示，这4枚骰子摞在一起后，如图，相互接触的两个面点数之和都是8，这4个骰子每个骰子都有一个面被遮住了，你能说出每个被遮住的面各是几个点吗？24．（8分）正方体的每一面不同的颜色，对应着不同的数字，将四个这样的正方体如图拼成一个水平放置的长方体，冀教版七年级上《第1章图形的初步认识》2013年单元测试卷A参考答案与试题解析一、选择题（每小题3分，共30分）1．（3分）（2005•宜昌）图中物体的形状类似于（）．C D．3．（3分）图中的几何体有（）个面．4．（3分）将下列哪个图形绕直线l旋转一周，可以得到图所示立体图形（）．C D．．C D．6．（3分）（2005•深圳）我们从不同的方向观察同一物体时，可以看到不同的平面图形，如图，从图的左面看这个几何体的左视图是（）．C D．．C D．8．（3分）桌上摆满了朋友们送来的礼物，小狗贝贝好奇地想看个究竟．①小狗先是站在地面上看，②然后抬起了前腿看，③唉，还是站到凳子上看吧，④最后，它终于爬上了桌子…按小狗四9．（3分）给出以下四个几何体，其中能截出长方形的几何体共有（）二、填空题（每小题3分，共24分）11．（3分）如图，这个几何体的名称是五棱柱；它有7个面组成；它有10个顶点；经过每个顶点有3条边．12．（3分）点动成线，线动成面，面动成体．面面相交得到线，线线相交得到点．13．（3分）薄薄的硬币在桌面上转动时，看上去象球，这说明了面动成体．14．（3分）一个直角三角形绕其中一条直角边旋转一周所形成的几何体是圆锥体．15．（3分）水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示下图是一个正方体的平面展示图，若图中的“似”表示正方体的前面，“锦”表示右面，“程”表示下面，则“祝”、“你”、“前”分别表示正方体的后面、上面、左面．16．（3分）根据下列多面体的平面展开图，填写多面体的名称：（1）长方体，（2）三棱柱，（3）三棱锥．17．（3分）指出图（1）、图（2）、图（3）是几何体从哪个方向看到的图形．（1）正面（2）上面（3）左面．18．（3分）若一个几何体的截面是圆，则该几何体可能是圆锥、球、圆台、圆柱等．三、作图题（每小题7分，共14分）19．（7分）如图分别从正面、左面、上面看下面几何体，画出所得到的平面图形．20．（7分）如图所示，它是由什么图形旋转而成的？请你画出来．四、解答题（每小题8分，共16分）21．（8分）如图所示的八棱柱，它的底面边长都是5厘米，侧棱长都是6厘米，回答下列问题：（1）这个八棱柱一共有多少个面？它们的形状分别是什么？图形哪些面的形状、面积完全相同？（2）这个八棱柱一共有多少条棱？它们的长度分别是多少？（3）沿一条侧棱将其侧面全部展成一个平面图形，这个图形是什么形状？面积是多少？22．（8分）如图，图（1）是正方体木块，把它切去一块，可能得到（2）、（3）、（4）、（5）所示的图形，问（2）、（3）、（4）、（5）图中切掉的部分可能是其他几块中的哪一块？五、应用题（每小题8分，共16分）23．（8分）现有4枚相同的骰子，骰子的展开图如图所示，这4枚骰子摞在一起后，如图，相互接触的两个面点数之和都是8，这4个骰子每个骰子都有一个面被遮住了，你能说出每个被遮住的面各是几个点吗？24．（8分）正方体的每一面不同的颜色，对应着不同的数字，将四个这样的正方体如图拼成一个水平放置的长方体，。

第四章《几何图形初步》测验题4页

七年级第四章《几何图形初步》测验题姓名一、选择题（本大题共8个小题，每小题3分，满分24分） 1、如果与互补，与互余，则与的关系是（）A=BC D 以上都不对2、对于直线，线段，射线，在下列各图中能相交的是（）3、下列四个图中，能用∠1、∠AOB 、∠O 三种方法表示同一个的是（）4、已知线段AB ，延长A B 至C ，使AC=2BC ，反向延长AB 至D ，使AD=21BC ，那么线段AD 是线段AC 的（）A ．31B ．72C ．51D ．415、把一张报纸的一角斜折过去，使A 点落在E 点处，BC 为折痕，BD 是∠EBM 的平分线，则∠CBD ＝（）A .85°B .80°C .75°D .90°6、将下列图形绕直线l 旋转一周,可以得到右图所示的立体图形的是( )7、时间5点整时,时钟上时针与分钟之间的夹角是( ) A.210° B.30° C.150° D.60° 8、下列语句中，正确的个数是（）个①两条直线相交,只有一个交点. ②在∠ABC 的边BC 的延长线上取一点D .③若∠1+∠2+∠3=90°,则∠1、∠2、∠3互余. ④一个角的余角比这个角的补角小. A.1 B.2 C.3 D.4 二、填空题（本大题共7个小题，每小题3分，满分21分）9、若∠1∶∠2∶∠3∶∠4=1∶2∶3∶4，四个角的和为180°，则∠2=______; ∠3=______;∠1与∠4互为角。

10、不在同一直线上的四点最多能确定条直线。

11、已知α∠与β∠互余，且40α=∠15’，则α∠的余角为 .12、如图，若是中点，是中点，若，，_______。

13、如图，从学校A 到书店B 最近的线路是（1）号线，其道理用几何知识解释应是 .CBAEODF14、已知线段AB ，在BA 的延长线上取一点C, 使CA=3AB ，则CB= AB15、如图2，OA 、OB 是两条射线，C 是OA 上一点， D 、E 分别是OB 上两点，则图中共有__________条线段,共有___________射线. 三、解答题：16、（1）76O35/ +69O65/ （2）180O- 23O17/ 57// （3）19O37/ 26//×917、（本题10分）A 、B 、C 三点在一直线上，已知AB=8cm ，BC=3cm ，求AC 的长。

《图形认识初步》综合测试题(A)

，，／
不论什么时候．只要你有一个目标，就得牺牲一定的自由去实现它。—— Ｗ．．姆你Ｓ毛
，，／
，
４７
２．案不唯一．如６答例问：车相向而行．时相遇？两何解：设小时后相遇，由题意，（５＋４＝４，得３５０
Ｇｏｌｅｅｍｉａｓｄｔｒｎｅｗｈａｏｒｏｎｇｔｅｔｕ’ｅｇｉｂ．ｙｏ
一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
１
２．七年级共有名学生。３设则根据题意有＋２＝．得＝３０解６．
６０４５
解得＝．
２
答：年级共有３０名学生．七６
答：相向两车而行， ÷小时后相遇．
二
２改：一）（一）７４为２２３ｘ导：，．（一２
１．图中几何体，正面看能得到（２下从
）．
日］］
第ｌ２题图ＡＤ
１．３同时经过平面内的三点可以作直线（Ａ一条．Ｂｊ条．
）．
）．Ｃ０条．Ｄ０条或一条．
１．图，４如它需再添 …个面，叠后才能围成一个正方体，图中的黑色小正方形分别由四名同折下

《图形认识初步》综合测试题(A)

所示，Ｂ平分厶４，Ｃ平分ＬＢＤ，ＬＢＣ＝２。则ＯＯＯＣＯＯ且Ｏ５，Ｄ＝
／Ｄ
１
／
Ｃ
Ａ产
。
．
｜Ｂ／
第６题图第８题图
．
…
第５题图
果两个角互补，并且它们的差是３。那么较大的角等于０，
，
从地到曰地有三条路 ① 、、可走， ② ③ 每条路长分别为ｚｎ图中“广、Ｊ，（ｍ， ”“ －
体块．
ｃ
。
日日
’
— ］Ｉ — ］＿１Ｊｌ图题
ｆｆＩＩＪＩｌｌｆ
知两根木条，一根长６０厘米，根长１０厘米，它们的一端重合，在同一条直一０将放两根木条中点的距离是厘米．
＼
西５。０
Ｅ１／、。＼
／
Ｄ
南
第２图９题
３０
分）１图是棱长为口的小正方体，２图３是由这样的小正方体摆放而的图形．照这图、戈按
拘方法继续摆放，自上而下分别叫做第ｌ、２层、 … 、ｎ层，ｎ层的小正方体的层第 … 第第毁记做５请解答下列问题．。Ｉ按要求填表：
４４
、一一一．、一一
人生的奋斗目标决定你将成为什么样的人。— — 华盛顿・文欧
ｔｒａｈｏｅｍａｅｒａｅｔｐｋｓｇｅｔｍｅｎ．
．

2021-2022学年浙教版七年级数学上册《第6章图形的初步认识》单元综合测试题(附答案)

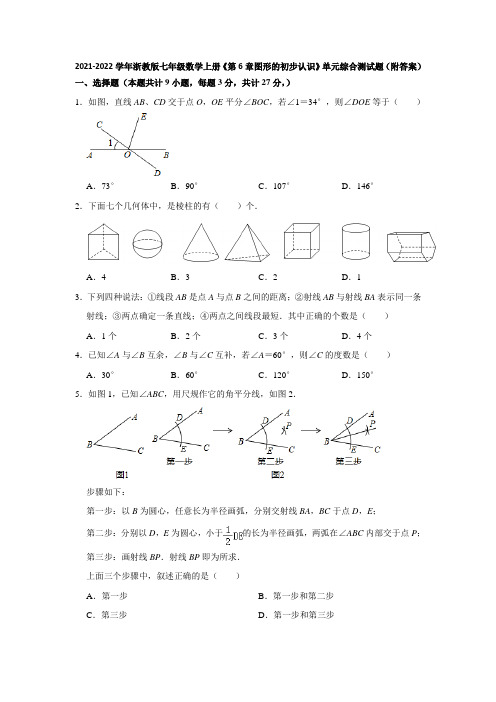
2021-2022学年浙教版七年级数学上册《第6章图形的初步认识》单元综合测试题（附答案）一、选择题（本题共计9小题，每题3分，共计27分，）1．如图，直线AB、CD交于点O，OE平分∠BOC，若∠1＝34°，则∠DOE等于（）A．73°B．90°C．107°D．146°2．下面七个几何体中，是棱柱的有（）个．A．4B．3C．2D．13．下列四种说法：①线段AB是点A与点B之间的距离；②射线AB与射线BA表示同一条射线；③两点确定一条直线；④两点之间线段最短．其中正确的个数是（）A．1个B．2个C．3个D．4个4．已知∠A与∠B互余，∠B与∠C互补，若∠A＝60°，则∠C的度数是（）A．30°B．60°C．120°D．150°5．如图1，已知∠ABC，用尺规作它的角平分线，如图2．步骤如下：第一步：以B为圆心，任意长为半径画弧，分别交射线BA，BC于点D，E；第二步：分别以D，E为圆心，小于的长为半径画弧，两弧在∠ABC内部交于点P；第三步：画射线BP．射线BP即为所求．上面三个步骤中，叙述正确的是（）A．第一步B．第一步和第二步C．第三步D．第一步和第三步6．如图，三条直线相交于点O，若∠AOC＝∠BOC＝90°，∠1＝56°，则∠2＝（）A．30°B．34°C．45°D．56°7．下列语句中正确的是（）A．在所有连接两点的线中，直线最短B．∠AOB与∠BOA表示相同的角C．一个锐角与一个钝角的和是一个平角D．两点之间的线段是两点之间的距离8．平面内三条不同直线相交最多能构成对顶角的对数是（）A．4对B．5对C．6对D．7对9．如图，建筑工人砌墙时，经常在两个墙脚的位置分别插一根木桩，然后拉一条直的参照线，这种做法用几何知识解释应是（）A．两点之间，线段最短B．射线只有一个端点C．两直线相交只有一个交点D．两点确定一条直线二、填空题（本题共计8小题，每题3分，共计24分，）10．已知A、B、C三点在一条直线上，且线段AB＝15cm，BC＝5cm，则线段AC ＝．11．如果线段AB＝CB，那么C是线段AB的中点．．12．如图，有一个与地面成30°角的斜坡，现要在斜坡上竖起一根电线杆，设电线杆与斜坡所夹的角为∠1，当∠1的度数为时，电线杆与地面垂直．13．某小区A自来水供水路线为AB，现进行改造，沿路线AO铺设管道，并与主管道BO连接（AO⊥BO），这样路线AO最短，工程造价最低，根据是．14．如图，点C在线段AB的延长线上，BC＝2AB，点D是线段AC的中点，AB＝2cm，则BD的长度是．15．如图是由、长方体、圆柱三种几何体组成的物体．16．当时针指向11：10时，时针与分针的夹角是度．17．如图，AC⊥BC，C为垂足，CD⊥AB，D为垂足，BC＝8，CD＝4.8，BD＝6.4，AD＝3.6，AC＝6，那么点C到AB的距离是，点A到BC的距离是，点B到CD的距离是，A，B两点间的距离是．三、解答题（本题共计7小题，共计69分，）18．一辆汽车从A点出发向北偏西25°方向行120千米到达B点，一辆货车同时从A点出发向南偏东25°方向行200千米到达C点，这两辆汽车现在相距多少千米？19．如图，已知线段AB，请用尺规按下列要求作图．（1）延长线段AB到C，使BC＝AB；（2）延长线段BC到D，使CD＝AC．20．如图，汽车站、码头分别位于A，B两点，直线b和波浪线分别表示公路与河流．（1）从汽车站A到码头B怎样走最近？画出最近路线，并说明理由；（2）从码头B到公路b怎样走最近？画出最近路线BC，并说明理由．21．如图，已知线段AB，延长AB到C，使得BC＝AB，D为AC中点且AC＝30，求线段BD的长．22．如图，AB⊥CD，垂足为O．（1）比较∠AOD，∠EOB，∠AOE的大小，并用“＜”号连接．（2）若∠EOC＝28°，求∠EOB和∠EOD的度数．23．如图，A、O、B在一条直线上，∠AOC＝∠BOC+30°，OE平分∠BOC，求∠BOE 的度数．24．已知：0为直线AB上的一点，射线OA表示正北方向，射线OC在北偏东m°的方向，射线OE在南偏东n°的方向，射线OF平分∠AOE，且2m+2n＝180．（1）如图，∠COE＝°，∠COF和∠BOE之间的数量关系为．（2）若将∠COE绕点O旋转至图2的位置，射线OF仍然平分∠AOE时，试问（1）中∠COF和∠BOE之间的数量关系是否发生变化？若不发生变化，请你加以证明，若发生变化，请你说明理由；（3）若将∠COE绕点O旋转至图3的位置，射线OF仍然平分∠AOE时，则2∠COF+∠BOE＝°．参考答案一、选择题（本题共计9小题，每题3分，共计27分，）1．解：如图，∵∠1＝34°，∴∠2＝∠1＝34°，∠BOC＝180°﹣∠1＝146°．又∵OE平分∠BOC，∴∠BOE＝∠BOC＝73°．∴∠DOE＝∠BOE+∠2＝73°+34°＝107°．故选：C．2．解：如图，根据棱柱的特征可得，①是三棱柱，②是球，③圆锥，④三棱锥，⑤正方体，⑥圆柱体，⑦六棱柱，因此棱柱有：①⑤⑦，故选：B．3．解：①线段AB是点A与点B之间的距离，说法错误，应是线段AB的长度是点A与点B 之间的距离；②射线AB与射线BA表示同一条射线，说法错误，端点字母不一样；③两点确定一条直线，说法正确；④两点之间线段最短，说法正确．说法正确的有2个．故选：B．4．解：∵∠A＝60°，∠A与∠B互余，∴∠B＝90°﹣∠A＝90°﹣60°＝30°，∵∠B与∠C互补，∴∠C＝180°﹣∠B＝180°﹣30°＝150°．故选：D．5．解：第二步为：分别以D，E为圆心，大于的长为半径画弧，两弧在∠ABC内部交于点P．故选：D．6．解：∵∠BOC＝90°，∠1＝56°，∴∠3＝90°﹣∠1＝90°﹣56°＝34°，∴∠2＝∠3＝34°故选：B．7．解：A、在所有连接两点的线中，线段最短，故本选项错误；B、∠AOB与∠BOA表示相同的角，故本选项正确；C、一个锐角与一个钝角的和不一定是平角，故本选项错误；D、两点之间的线段的长度是两点之间的距离，故本选项错误．故选：B．8．解：如图，单个的角是对顶角有3对，两个角的复合角是对顶角有3对，所以，对顶角的对数是3+3＝6对．故选：C．9．解：建筑工人砌墙时，经常在两个墙脚的位置分别插一根木桩，然后拉一条直的参照线，这种做法用几何知识解释应是：两点确定一条直线．故选：D．二、填空题（本题共计8小题，每题3分，共计24分，）10．解：当点C在线段AB的延长线上时，AC＝AB+BC＝20cm，当点C在线段AB上时，AC＝AB﹣BC＝10cm，故答案为：20cm或10cm．11．解：AB＝CB不能确定C是线段AB的中点，例如中就不能是线段AB的中点．故答案为错误．12．解：如图，要使CB⊥AB，则在△ABC中，∠CBA＝90°，∴∠1＝∠ACB＝90°﹣30°＝60°．故答案为：60°．13．解：沿路线AO铺设管道，并与主管道BO连接（AO⊥BO），这样路线AO最短，工程造价最低，根据是垂线段最短．故答案为：垂线段最短．14．解：∵AB＝2cm，BC＝2AB，∴BC＝4cm．∴AC＝AB+BC＝6cm．∵D是AC的中点，∴AD＝AC＝3cm．∴BD＝AD﹣AB＝1cm．故答案为：1cm．15．解：如图是由三棱柱、长方体、圆柱三种几何体组成的物体．故答案是：三棱柱．16．解：30＝85°故答案为：85°．17．解：点C到直线AB的垂线段是CD，所以线段CD的长是点C到直线AB的距离，即点C到AB的距离是4.8；点A到直线BC的垂线段是AC，所以线段AC的长是点A到直线BC的距离，即点A到BC的距离是6；点B到直线CD的垂线段是BD，所以线段BD的长是点B到直线CD的距离，即点B到CD的距离是6.4；点B到点A的距离是线段AB的长，即点B到点A的距离是10．故填4.8，6，6.4，10．三、解答题（本题共计7小题，共计69分，）18．解：如图，以点A为中心，建立方位图，由图可得点A，点B，点C在一条直线上，所以BC＝AB+AC＝120+200＝320（米）．所以这两辆汽车现在相距320千米．19．解：如图所示：．20．解：（1）如图，线段AB即为所求作．（2）如图，线段BC即为所求作．21．解：∵BC＝AB，∴AC＝3BC，∵AC＝30，∴BC＝AC＝×30＝10，∵D为AC中点且AC＝30，∴CD＝AC＝15，∴BD＝CD﹣BC＝5．22．解：∠AOD＝90°，∠EOB＝90°+∠EOC，∠AOE＝90°﹣∠EOC ∴∠AOE＜∠AOD＜∠EOB（2）∠EOB＝∠EOC+90°＝118°∠AOE＝90°﹣∠EOC＝62°23．解：∵OE为∠BOC的平分线，∴∠BOE＝∠COE＝x，∴∠AOC＝180°﹣2x，根据题意得：180°﹣2x＝x+30°，解得：x＝50°，则∠BOE＝50°．24．解：（1）∵2m+2n＝180∴m+n＝90∠COE＝180﹣m﹣n＝90°，∠BOE＝2∠COF；（2）不发生变化．证明如下：∵∠COE＝90°∴∠COF＝90°﹣∠EOF＝90°﹣∠AOE＝90°﹣（180°﹣∠BOE）＝90°﹣90°+∠BOE＝∠BOE∴∠BOE＝2∠COF（3）360°．故答案是：（1）90°，∠BOE＝2∠COF （3）360°。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《图形的认识初步》水平测试（A ）
一、耐心填一填，一锤定音！（每小题4分，共32分） 1．计算：984536712234''''''+= ___________________．
2．如图1，90AOD = ∠，90COE = ∠，则图中相等的锐角有_________对．
3．一个角等于它的余角的
13
，这个角是_________度，这个角的补无须是
_________度．
4．如图2所示，射线O A 表示_________方向，射线O B 表示_________方向． 5．若平面内有A ，B ，C 三点，过其中任意两点画直线，最多可以画_________条直线，最少可以画_________条直线． 6．将两块直角三角板的直角顶点重合，如图3所示，若128AOD = ∠，则
B O
C =∠_________．
7．把一个圆形的蛋糕按如图4分成n 份，如果每份中的角是15 ，那么n 的值是_________．
图
1
图2
图
3
图4
8．如图5的线段m 和n ，用眼睛看，m ，n 的大小关系是m n >，而度量后才发现实际上是m n =，这一现象说明：_________（用一句话说出你的感想）．
二、精心选一选，慧眼识金（每小题3分，共24分） 1．下列图形中，1∠和2∠互为余角的是（）
2．如果要在一条直线上得到6条不同的线段，那么在这条直线上应选几个不同的点（）
Ａ．3个Ｂ．4个Ｃ．5个Ｄ．6个 3．圆锥的侧面展开图是（）
Ａ．三角形Ｂ．扇形Ｃ．长方形Ｄ．圆
4．已知直线A B 上有两点M ，N ，且8cm M N =，再找一点P ，使10c m M P P N +=，则P 点的位置（）
Ａ．只在直线A B 上Ｂ．只在直线A B 外Ｃ．在直线A B 上或在直线A B 外Ｄ．不存在
5．图6为正方体的一种平面展开图，各面都标有数字，则数字为4-的面与其对面上的数字之积是（）
Ａ．4 Ｂ．12 Ｃ．4- Ｄ．0
6．两条相等线段A B ，C D 有三分之一重合，M ，N 分别是A B ，C D 的中点，且12cm M N =，则A B 的长度是（）
Ａ．12cm Ｂ．14cm Ｃ．16cm Ｄ．18cm
7．我们从不同的方向观察同一物体时，可以看到不同的平面图形，如图7，从图的左面看这个几何体得到的图形是（）
m n 图
4 Ａ．Ｂ．Ｃ．Ｄ．
图6
8．观察下列各正方形图案，每条边上有()n n 2≥个圆点，每个图案中圆点的总数是S ．
按此规律推断出S 与n 的关系式为（）Ａ．4S n =
Ｂ．4(1)S n =+
Ｃ．4(1)S n =-
Ｄ．2S n =
三、用心做一做，马到成功！（本大题共64分）
1．（本题8分）一个角的补角是1232416''' ，则这个角的余角是多少？
2．（本题10分）图8中正方形的边长为4cm ，求出图案中所有线的总长．
3．（本题10分）如图9，AB ，C D 交于O 点．
（1）如果3A O D B O D =∠∠，那么B O D =∠_________度，C O B =∠_________度；
（2）如果2AOC x = ∠，(90)BO C x =+ ∠，(4)BO D y =+ ∠，求x ，y 的值．
图
7
Ａ．Ｂ．Ｃ．Ｄ．
2n =，4S = 3n =，8S = 4n =，12S =
图8
4．（本题11分）如图10，已知直线A B 和C D 相交于O 点，C O E ∠是直角，O F
平分A O E ∠，34COF = ∠，求B O D ∠的度数．
5．（本题12分）如图11，将其画在一张纸上．（1）将它折叠能得到什么同何体？
（2）要把这个几何体重新展开，最少需要剪开几条棱？
6．（本题13分）α为锐角，β为钝角，甲、乙、丙、丁四人在计算1
()
6
αβ+时，结果依次为10 ，23 ，46 ，51 ，其中只有一个是正确的，你知道四人中谁的结果正确吗？
参考答案
一、1．170810''' 2．2 3．22.5，157.5 4．北偏西65 ；南偏东15
5．3，1 6．52 7．24 8．答案不唯一
A C F
E
B D O
图10
A
C
O
D
B
图
9
图11
二、1．Ｄ 2．Ｂ 3．Ｂ 4．Ｃ 5．Ｂ 6．Ｄ 7．Ｂ 8．Ｃ
三、1．332416''' 2．168π+ 3．（1）45 ，135
；
（2）30，56． 4．22 5．（1）三棱柱；（2）5条． 6．乙。