2014-2015学年四川省成都市都江堰中学高一(上)期末数学模拟试卷含参考答案
四川省成都市高中高一上期末数学试卷习题

2015-2016 学年四川省成都市高一(上)期末数学试卷一、选择题 :本大题共 12 小题,每题 5 分,共 60 分。
在每题给出的四个选项中,只有一项为哪一项吻合题目要求的1.( 5 分)已知会集 A={ ﹣ 1,0, 1, 2} ,B={ x| x < 2} ,则 A ∩B=( )A . { ﹣1,0, 1}B .{ ﹣ 1,0,2}C . { ﹣ 1 , 0}D . { 0, 1}12.(5 分)已知函数 (f x )=,其中 [ x] 表示不高出 x 的最大整数,如, [ ﹣ 3?5] =﹣4, [ 1?2] =1,设 n ∈N * ,定义函数 f n (x )为: f 1( x ) =f ( x ),且 f n ( x )=f[ f n﹣1 ( x ) ] (n ≥ 2),有以下说法:①函数 y=的定义域为 { x|≤x ≤ 2} ;2.( 5 分) sin150 的°值等于( )②设会集 A={ 0,1,2} , B={ x| f 3( x )=x ,x ∈ A} ,则 A=B ; A . B . C . D .③ f2015()+f2016()= ;3.( 5 分)以下函数中, f (x )与 g ( x )相等的是()④若会集 M={ x| f 12(x ) =x , x ∈[ 0,2]} ,则 M 中最少包含有 8 A . f (x ) =x , g ( x ) =2,g (x ) =() 4个元素.B . f ( x ) =x其中说法正确的个数是()C .f ( x )=x 2, g ( x ) =D .f ( x )=1,g (x )=x 0A .1 个B . 2 个C . 3 个D . 4 个a) 二、填空题:本大题共 4 小题,每题 5 分,共 20 分。
4.( 5 分)幂函数 y=x(α是常数)的图象(A .必然经过点( 0,0)B .必然经过点( 1,1)13.( 5 分)函数 y= 的定义域是.C .必然经过点(﹣ 1,1)D .必然经过点( 1,﹣ 1)5.(5 分)以下函数中,图象关于点(,0)对称的是() 14.( 5 分)已知 α是第三象限角, tan α= ,则 sin α= .A . y=sin ( x+) B .y=cos ( x ﹣ ) C . y=sin ( x+)15.( 5 分)已知函数 f ( x )(对应的曲线连续不断)在区间 [ 0,2] 上的部分对应值如表: D . y=tan ( x+)6.( 5 分)已知 a=log 32, b=(log 32) 2, c=log4 ,则()A . a < c <bB . c <b < aC .a <b < cD . b <a <c7.(5 分)若角 α =2rad ( rad 为弧度制单位),则以下说法错误的 是()A .角 α为第二象限角B . α=C .sin α> 0D . sin α<cos α8.(5 分)以下函数中,是奇函数且在( 0,1] 上单调递减的函数 是()2B . y=x+ x﹣xD .y=1﹣ A . y=﹣x+2xC . y=2 ﹣ 2 9.( 5 分)已知关于 x 的方程 x 2﹣kx+k+3=0,的两个不相等的实数根都大于 2,则实数 k 的取值范围是( )A . k >6B .4< k <7C . 6<k < 7D .k > 6 或 k >﹣ 210.( 5 分)已知函数 f ( x ) =2log 22x ﹣4λ log 2x ﹣ 1 在 x ∈[ 1,2] 上 的最小值是﹣,则实数 λ的值为()A . λ=﹣1B .λ=C .λ=D .λ=11.(5 分)定义在 R 上的偶函数 f (x )满足 f (x+2) =f ( x ),当2+4x+3,则 y=f[ f (x ) ]+ 1 在区间 [ ﹣ x ∈ [ ﹣3,﹣ 2] 时, f (x ) =x 3, 3] 上的零点个数为()A . 1 个B .2 个C .4 个D .6 个由此可判断:当精确度为 0.1 时,方程 f (x )=0 的一个近似解为(精确到 0.01)x0.881.301.4061.4311.521.621.7 1.8 275 f ( x ) ﹣ ﹣ ﹣﹣ 0.1450.62 1.97 2.5 4.0 5 2 0.96 0.3400.05355455316.( 5 分)已知函数 f ( x )=tan ,x ∈(﹣ 4, 4),则满足不等式( a ﹣ 1) log [ f ( a ﹣1) + ] ≤ 2的实数 a 的取值范围是.三、解答题:本大题共 6 小题,共 70 分。
四川省某重点中学2014—2015学年高一下学期期末模拟考试数学版含答案

n cos n 2
1 , 前 n 项和为 Sn , 则 s13
19.
③ 若数列 an n2 n(n N ) 为单调递增数列,则 取值范围是
2;
3
④ 已知数列 { an} 的通项 an
2n
,其前
11
n 项和为
Sn ,则使
Sn
0 的 n 的最小值为 12 .
⑤1
1
2
1
2
23
1
2
2 1 (n 2)
n
n
其中正确结论的序号为 _____________(写出所有正确的序号) .
三、解答题:本大题共 6 小题,共 74 分。解答应写出必要的文字说明,证明过程或演算步
骤。
17.( 本题满分 12 分 ) 已知向量 a =e1- 2e2 , b = 3e1 +e2 , 其中 e1 =( 1,0 ), e2 =( 0,1 ) , 求:
(1) a b ;
( 2) a 与 b 夹角的余弦值。
13.U>V. 14. 等边三角形 . 15.(-
5
,0)
(0,+ ).
16.
3
②, ⑤.
17.(1) a b =1
(2)
2
;
10
18.(1) a=- 1 或 a=-2 8
1
(2)当 a=-2 ,则 {x|- <x<1}
2
:当 a=- 1 ,则 {x|-1<x<7} 8
10
19. (1)-
;
10
2 33
12.对于一个有限数列 p ( p1, p2 , , pn ) , p 的蔡查罗和(蔡查罗是一位数学家)定义为
中学2014-2015学年高一上学期期末考试数学试卷word版含答案

D.无论 为何值,均有4个零点
9.已知直角梯形ABCD中,AD∥BC, ∠ADC=90°,AD=2,BC=1,P是腰DC上的动点,
则 的最小值为 ()
A.4B.5C. D.2
10.
A. B. C. D.
二、填空题: 本大题共5小题, 每小题5分, 共25分. 请将答案填在答题卡对应题号的位置上. 答错位置, 书写不清, 模棱两可均不得分
(1)当9天购买一次配料时, 求该食堂用于配料的保管费用 是多少元?
(2)设该食堂 天购买一次配料, 求该食堂在这 天中用于配料的总费用 (元)关于 的函数关系式, 并求该食堂多少天购买一次配料才能使平均每天支付的费用最少?
20.对于函数 , 如果存在实数 使得 , 那么称 为 的线性函数.
(1)下面给出两组函数, 是否分别为 的线性函数?并说明理由;
19.
已知武汉二中食堂需要定期购买食品配料, 该食堂每天需要食品配料200千克, 配料的价格为 元/千克, 每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若 天购买一次, 需要支付 天的保管费). 其标准如下: 7天以内(含7天), 无论重量多少, 均按10元/天支付; 超出7天以外的天数, 根据实际剩余配料的重量, 以每天0.03元/千克支付.
第一组: ;
第二组: ;
(2)设 , 线性函数 .若不等式
在 上有解, 求实数 的取值范围;
21.(1)有时一个式子可以分拆成两个式子, 求和时可以达到相消化简的目的, 如我们初中曾学
过: = =
请用上面的数学思维来证明如下:
11.已知弧度数为2的圆心角所对的弦长为2, 则这个圆心角所对的弧长是.
12.已知 ,则 =. (用t表示)
四川省成都市2015_2016学年高一数学上学期期末试卷(含解析)

2015-2016学年四川省成都市高一(上)期末数学试卷一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的1.已知集合A={﹣1,0,1,2},B={x|x<2},则A∩B=()A.{﹣1,0,1} B.{﹣1,0,2} C.{﹣1,0} D.{0,1}2.sin150°的值等于()A.B. C.D.3.下列函数中,f(x)与g(x)相等的是()A.f(x)=x,g(x)=B.f(x)=x2,g(x)=()4C.f(x)=x2,g(x)=D.f(x)=1,g(x)=x04.幂函数y=x a(α是常数)的图象()A.一定经过点(0,0)B.一定经过点(1,1)C.一定经过点(﹣1,1) D.一定经过点(1,﹣1)5.下列函数中,图象关于点(,0)对称的是()A.y=sin(x+)B.y=cos(x﹣)C.y=sin(x+)D.y=tan(x+)6.已知a=log32,b=(log32)2,c=log4,则()A.a<c<b B.c<b<a C.a<b<c D.b<a<c7.若角α=2rad(rad为弧度制单位),则下列说法错误的是()A.角α为第二象限角B.α=()°C.sinα>0 D.sinα<cosα8.下列函数中,是奇函数且在(0,1]上单调递减的函数是()A.y=﹣x2+2x B.y=x+C.y=2x﹣2﹣x D.y=1﹣9.已知关于x的方程x2﹣kx+k+3=0,的两个不相等的实数根都大于2,则实数k的取值范围是()A.k>6 B.4<k<7 C.6<k<7 D.k>6或k>﹣210.已知函数f(x)=2log22x﹣4λlog2x﹣1在x∈[1,2]上的最小值是﹣,则实数λ的值为()A.λ=﹣1 B.λ=C.λ=D.λ=11.定义在R上的偶函数f(x)满足f(x+2)=f(x),当x∈[﹣3,﹣2]时,f(x)=x2+4x+3,则y=f[f(x)]+1在区间[﹣3,3]上的零点个数为()A.1个B.2个C.4个D.6个12.已知函数f(x)=,其中[x]表示不超过x的最大整数,如,[﹣3•5]=﹣4,[1•2]=1,设n∈N*,定义函数f n(x)为:f1(x)=f(x),且f n(x)=f[f n﹣1(x)](n≥2),有以下说法:①函数y=的定义域为{x|≤x≤2};②设集合A={0,1,2},B={x|f3(x)=x,x∈A},则A=B;③f2015()+f2016()=;④若集合M={x|f12(x)=x,x∈[0,2]},则M中至少包含有8个元素.其中说法正确的个数是()A.1个B.2个C.3个D.4个二、填空题:本大题共4小题,每小题5分,共20分。
成都市重点中学2014-2015学年度高一(下)期期末考试数学模拟试题
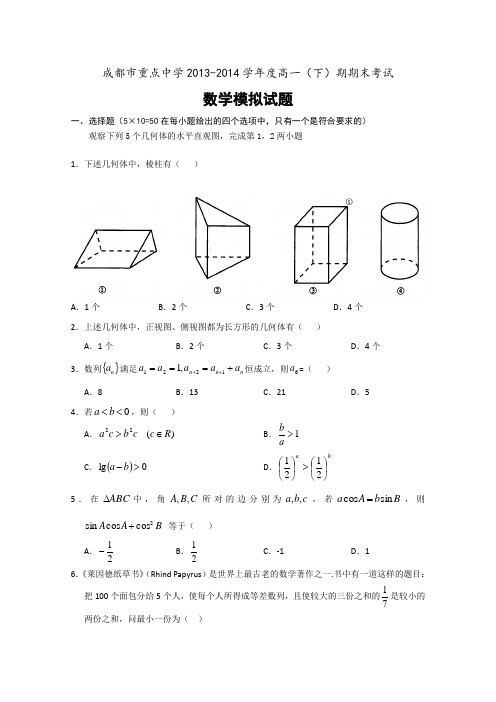
成都市重点中学2013-2014学年度高一(下)期期末考试数学模拟试题一、选择题(5×10=50在每小题给出的四个选项中,只有一个是符合要求的)观察下列5个几何体的水平直观图,完成第1,2两小题1.下述几何体中,棱柱有( )A .1个B .2个C .3个D .4个2.上述几何体中,正视图、侧视图都为长方形的几何体有( ) A .1个B .2个C .3个D .4个3.数列{}n a 满足n n n a a a a a +===++1221,1恒成立,则6a =( ) A .8B .13C .21D .54.若0<<b a ,则( ) A .c b c a 22> )(R c ∈ B .1>abC .()0lg >-b aD .ba⎪⎭⎫ ⎝⎛>⎪⎭⎫ ⎝⎛21215.在A B C ∆中,角C B A ,,所对的边分别为c b a ,,,若B b A a s i n c o s=,则B A A 2c o s c o s s i n + 等于( )A .21-B .21 C .-1 D .16.《莱因德纸草书》(Rhind Papyrus )是世界上最古老的数学著作之一.书中有一道这样的题目:把100个面包分给5个人,使每个人所得成等差数列,且使较大的三份之和的71是较小的两份之和,问最小一份为( )○5A .35 B .310 C .65 D .611 7.数列{}n a 满足()12+=n n a n ,若前n 相和35>n S ,则n 的最小值是( )A .4B .5C .6D .78.已知1,0,0=+>>b a b a 则ba 221--的最大值为( ) A .-3B .-4C 41-D .29-9.已知点()y x ,M 满足⎪⎩⎪⎨⎧≤--≥+-≥.022,01,1y x y x x 若y ax +的最小值为3,则a 的值为( )A .1B .2C .3D .410.两次购买同一种物品,可以用两种不同的策略,第一种是不考虑物品价格的升降,每次购买这种物品数量一定;第二种是不考虑物品价格的升降,每次购买这种物品所花的钱数一定,哪种购物方式比较经济( ) A .第一种B .第二种C .都一样D .不确定二、填空题(5×5=25请将答案写在答题卡中对应的横线上) 11.数列{}n a 是等比数列8,141==a a 则公比q =_____________. 12.锐角三角形的三边分别为3,5,x ,则x 的范围是___________. 13.关于x 的不等式mx x x >+-2212的解集为(0,2)则m =____________. 14.y x ,满足⎪⎩⎪⎨⎧≥+-≥+≤04422y x y x x 则22y x +的最小值是___________.15.ABC ∆中角C B A ,,的对边分别为c b a ,,,已知.,3,60x b a A ==︒=∠若满足条件的三角形有两个.则x 的范围是___________.三、解答题(12×4+13+14=75解答应写出文字说明,证明过程或演算步骤,解答写在答题卡对应的题号处)16.(1)当1>x 时,比较3x 与12+-x x 的大小(2)已知:ba b a 11,<<.判定b a , 的符号.17.已知ABC ∆的三个内角C B A ,,所对的边分别为A c b a ,,,是锐角,且B a b sin 23⋅=. (1)求A ;(2)若ABC a ∆=,7的面积为310,求22c b +的值.18.数列{}n a 为等差数列,13853a a =,前n 项和为n S . (1)若391=a ,求n a .(2)若01>a ,求n S 最大时n 的值.19.某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按40个工时计算)生产空调器、彩电、冰箱共120台,且冰箱至少生产20台.已知生产这些家电产品每台所需工时和每台产值如下表:问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)20.北京、张家港2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估。
20142015高一上学期数学期末试题有答案 副本

密云县2014―2015 学年度第一学期期末考试高一数学试卷2015.1 第一部分(选择题共40分)一、选择题 . 共 8 小题,每题 5 分,共 40分.在每题列出的四个选项中,选出吻合题目要求的一项. 1 .已知集合,,则A.B.C.D.2.A.B.C.D. 3.已知△ 三个极点的坐标分别为,,,若,那么的值是 A. B.3 C. D.4 4.在下列函数中,既是偶函数又在区间上单调递减的函数为 A. B. C. D. 5 .函数的一个对称中心 A. B. C. D. 6.函数(且)的图象经过点,函数(且)的图象经过点,则以下关系式中正确的选项是A. B. C. D. 7.如图,点在边长为的正方形的边上运动,设是的中点,则当沿着路径运动时,点经过的行程与△ 的面积的函数关系为,则的图象是8.已知函数,在下列结论中:①是的一个周期 ;②的图象关于直线对称 ;③在上单调递减.正确结论的个数为第二部分(非选择题共 110分)二、填空题共6小题,每题5分,共30分.9. 假如向量,,且,共线,那么实数 . 10.已知集合,则. 11.sin15osin75o的值是____________. 12.已知函数且,则的值为.13.已知是正三角形,若与向量的夹角大于,则实数的取值范围是__________. 14. 给出定义:若(此中为整数),则叫做离实数近来的整数,记作,即 .在此基础上给出以下关于函数的四个判断:①的定义域是,值域是;② 点是的图象的对称中心,此中;③函数的最小正周期为;④函数在上是增函数.则上述判断中正确的序号是.(填上全部正确的序号)三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题满分13分)已知函数.(I)求函数的定义域;(II)求的值;(III)求函数的零点.16.(本小题满分14分)已知.其中是第三象限角.(Ⅰ)求的值;(Ⅱ)求的值;(III)求的值.17.(本小题满分13分)已知向量,,其中 .(Ⅰ)当时,求的值;(Ⅱ)当时,求的最大值.18.(本小题满分14分)函数f(x)=Asin( ω x +φ) (A>0,ω >0,| φ|< π 2)的部分图象如图所示.(Ⅰ)求函数的分析式;(Ⅱ)将y=f(x)的图象向右平移π6 个单位后得到新函数的图象,求函数的分析式;(Ⅲ)求函数的单调增区间.19.(本小题满分13分)设二次函数满足条件:①,②;③在上的最小值为.( I)求的值;( II)求的分析式;(III)求最大值,使得存在,只要,都有成立.20.(本小题满的,均有判断下边两个由.①;②.(),求证(Ⅱ)的条件给出证明,若密云县2014―2015数学试卷参考择题共8小题12345678答题,每题5分13分)若函数对任意,则称函数拥有性质.(Ⅰ )函数能否拥有性质,并说明理(Ⅱ)若函数拥有性质,且:对任意有;(Ⅲ)在下,能否对任意均有 .若成立不成立给出反例.学年度第一学期期末考试高一答案及评分参照2015 . 01一、选,每题5分,共40分.题号案 DADCBCAC二、填空题共6小分,共30分.9. -210 .11.12.13. 14.①③④三、解答题共 6 小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题满分13分)解:( I)由题:, ----------------2分函数的定义域 . ----------------4分( II)----------------8分( III)令,函数的零点为----------------13分16.(本小题满分14分)解:(Ⅰ)且是第三象限角, ----------------2分----------------4分(Ⅱ)由(Ⅰ),----------------6分----------------9分(III) ----------------12分----------------14分 17.(本小题满分13分)解:(Ⅰ)当时,,---------------2分----------------5分(Ⅱ)由题: . ----------------10分, .当即时,----------------11分的最大值为 .-------------------13分18.(本小题满分14分)解:(Ⅰ)由所给图象知A=1,---------------1分34T= 11π 12-π6 =3π4 , T=π,所以ω= 2π T=2分由sin2 ×π6+φ = 1 ,| φ|< π 2得π3+φ=π2 ,解得φ=π6,-------4分所以f(x)=sin2x +π6.----------------5分(Ⅱ )f(x)=sin2x +π6的图象向右平移π 6个单位后得到的图象对应的函数解析式为= sin2x-π6+π6----------------7分=sin2x-π6.--------------9分(Ⅲ)由题: .----------------12分----------------13分 .------------14分19.(本小题满分13分)解:(I) ∵在上恒成立,∴即 . ---------------------------2分(II)∵,∴函数象关于直称,∴∵,∴4分又∵ 在上的最小---------------------------,∴,即,由解得,∴;-------------7分( III)∵ 当,恒成立,∴且,由得,解得---------------9分由得:,解得,⋯⋯⋯⋯⋯(10分)∵,∴,---------------11分当,于任意,恒有,∴的最大. -------------------12分另解:(酌情分)且在上恒成立∵在上减,∴,∵在上减,∴∴,∴,,∵,∴,∴,∴的最大20.(本小分13分)(Ⅰ)明:①函数拥有性.,⋯⋯⋯⋯⋯1 分即,此函数具有性. ⋯⋯⋯⋯⋯2分② 函数不具有性.⋯⋯⋯⋯⋯3 分例如,当,,,所以,,⋯⋯⋯⋯⋯4分此函数不拥有性.(Ⅱ)假中第一个大于的,,因函数具有性,所以,于任意,均有,所以,所以,与矛盾,所以,任意的有 .⋯⋯⋯⋯⋯9 分(Ⅲ)不成立.例如⋯⋯⋯⋯⋯ 10 分明:当有理数,均有理数,,当无理数,均无理数,因此,函数任意的,均有,即函数具有性.⋯⋯⋯⋯⋯ 12 分而当()且当无理数,.因此,在(Ⅱ)的条件下,“任意均有” 不成立 . ⋯⋯⋯⋯⋯ 13分(其余反例仿此分,如等 .)。
历年高一数学期末试题】四川省成都市2014-2015学年高一上学期期末考试数学试题 Word版含答案

历年高一数学期末试题】四川省成都市2014-2015学年高一上学期期末考试数学试题 Word版含答案成都市2014-2015年度高一上期末考试-数学一、选择题21、已知集合A={x|x-2x>0},B={x|-1<x<1},则A∩B=∅。
2、函数y=|x|的图像与函数y=2-x的图像所有交点的横坐标之和等于6.3、已知函数y=sin(πx),最小正周期为2,则该函数的图象关于点x=1对称。
4、当x=1时,函数y=1/(x-1)的最小值为无穷大。
5、已知f(x)=a cos(πx)+b sin(πx)+c,是定义在R上的周期为2的偶函数,且f(0)=2,f(1)=1,设a>b>c,则a>b>c。
6、已知点A(1,0),B(-1,0),C(0,2),是△ABC的重心,若P为△ABC内部一点,则AP+BP+CP的最小值是2.7、如图,在△ABC中,D、E、F分别为BC、CA、AB 上的一点,若.8、设Q为有理数集,函数f(x)=x-1,g(x)=x+1/x,则函数h(x)=f(x)·g(x)是奇函数但不是偶函数。
9、已知函数f(x)=x^2-2x+1,点A(1,0),B(2,1)。
对应于区间[1,2]内的实数x上均有意义,且f(x)在区间[1,2]内单调递增,取函数g(x)=f(x-1),h(x)=g(x)/x,则h(1)=0,h(2)=2,且在[1,2]上恒有h(x)≤2x-2.那么就称函数h(x)在[1,2]上“2阶线性近似”。
若函数h(x)在[1,2]上“3阶线性近似”,则实数k的取值范围为-1<k<3.10、函数f(x)=x^3-3x^2+3x在[-1,3]上存在闭区间[0,1],使得函数f(x)在[0,1]的“4倍值区间”内是单调函数;且f(x)在[1,3]上恒有f(x)>f(1)。
满足:①在[-1,3]上f(x)有3个驻点,分别为x=-1,x=1,x=2;②f(x)在[-1,1)上单调递减,在(1,3]上单调递增。
成都市20142015学年度上期期末学业质量监测模拟一高二数学

成都市2014-2015学年度上期期末学业质量检测模拟一高二数学一.选择题(本题共10小题,每题5分,共计50分) 1.点在空间直角坐标系的位置是(▲)A. y 轴上B. 平面上C.平面上 D.平面上2.以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测 试中的成绩(单位:分)已知甲组数据的中位数为15,乙组数 据的平均数为16.8,则x ,y 的值分别为(▲) A .2,5 B .5,5 C .5,8 D .8,83.已知βα,是两个不同的平面,n m ,是两条不同的直线,则下列命题不.正确..的是(▲) A .若α⊥m n m ,//,则α⊥n B .若n m =⋂βαα,//,则n m // C .若αβ⊥⊥m m ,,则βα// D .若βα⊂⊥m m ,,则βα⊥ 4.已知x ,y 之间的数据如表所示,则回归直线过点(▲)A.(2,1.8) B .(4,3.2) C .(3,2.5)D .(5,3.8)5.已知程序框图如右图所示,则输出的i =(▲)A .5B .7C .9D .11 6.如图,直三棱柱111ABC A B C -,AC BC ⊥,且12C A C C C B ==,则直线1BC 与直线1AB所成角的余弦值为(▲) A .55 B .53C .255D .357.右图的平行六面体ABCD-A 1B 1C 1D 1中,点M 在BB 1上,点N 在 DD 1上,且BM =12BB 1,D 1N=13D 1D ,若1MN AB AD AA x y z =++, 则=++z y x (▲)甲组乙组9 0 9x 2 1 5 y 8 7 4 2 4x 1 2 3 4 5 y1.21.82.53.23.8C 1B 1A 1CABA .17 B .16 C .23 D .328.已知()0,12,1--=t t a ,()t t b ,,2=,则a b -的最小值为(▲) A.2 B. 6 C. 5 D. 39.已知点),(y x P 满足2284160x x y y -+-+≤,则xy的取值范围(▲) A.40,3⎡⎤⎢⎥⎣⎦ B. ⎥⎦⎤⎢⎣⎡43,0 C. ⎥⎦⎤⎢⎣⎡1,43 D.⎥⎦⎤⎢⎣⎡34,110.三棱锥P-ABC 中,PA 、PB 、PC 两两垂直,且PA=3,PB=2,PC=1,设M 是底面△ABC 内一点,定义()()p n m M f ,,=,其中p n m ,,分别是三棱锥M-PAB ,三棱锥M-PBC ,三棱锥M-PCA 的体积;若()⎪⎭⎫⎝⎛=y x M f ,,21,且81≥+y a x 恒成立,则正实数a 的最小值为(▲)A.1B. 3413-C. 249-D. 2二.填空题(本题共5小题,每题5分,共25分)11.一个容量为100的样本,其数据的分组与各组的频数如下: 组别(]10,0 (]20,10 (]30,20 (]40,30 (]50,40 (]60,50 (]70,60频数 12 13241516137则样本落在(]40,10上的频率是 ▲ .12.直线013=+-y x 的倾斜角为______▲_______.13.从点)5,4(P 向圆C :4)2(22=+-y x 引切线,则该切线方程是_______▲___________. 14.四棱锥P-ABCD 的底面ABCD 是正方形,且顶点P 在底面ABCD 的射影为底面的中心,若AB a =,棱锥体积为366a ,则侧棱AP 与底面ABCD 所成的角是_____▲___________. 15.如图,将∠B =π3,边长为1的菱形ABCD 沿对角线AC 折成大小等于θ的二面角B -AC -D ,若DABC MNθ∈[π3,2π3 ],M 、N 分别为AC 、BD 的中点,则下面的四种说法:①AC ⊥MN ; ②DM 与平面ABC 所成的角是θ; ③线段MN 的最大值是34,最小值是34; ④当θ=π2时,BC 与AD 所成的角等于π2.其中正确的说法有 ▲_ (填上所有正确说法的序号).三.解答题(本题共6小题,共计75分)16.(本题满分12分)已知点P (2,-1)(1)求过P 点且与直线012:1=+-y x l 垂直的直线l 的方程; (2)求过P 点且与原点距离为2的直线l 的方程;17.(本题满分12分)某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取 部分高一女生测量身高,所得数据整理后列出频率分布表如下: (1)求出表中字母m 、n 、M 、N 所对应的数值; (2)在给出的直角坐标系中画出频率分布直方图; (3)估计该校高一女生身高在149.5~165.5 cm 范围内有多少人?18.(本题满分12分)如图所示,已知空间四边形ABCD 的每条边和对角线AC 、BD 长都等于1,点E ,F ,G 分别是AB 、AD 、CD 的中点,计算: (1)EF →·BA →; (2)EG 的长;(3)异面直线AG 与CE 所成角的余弦值.组别 频数 频率 145.5~149.5 8 0.16 149.5~153.5 6 0.12 153.5~157.5 14 0.28 157.5~161.5 10 0.20 161.5~165.5 8 0.16 165.5~169.5m n 合计MN19.(本题满分12分)已知圆C: 2220x x y -+=,直线l :40x y +-=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014-2015学年四川省成都市都江堰中学高一(上)期末数学模拟试卷(1)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5.00分)已知集合A={﹣1,2},B={x∈Z|0≤x≤2},则A∩B等于()A.{0}B.{2}C.{0,1,2}D.∅2.(5.00分)函数f(x)=+lg(x+1)的定义域为()A.[﹣1,3)B.(﹣1,3)C.(﹣1,3]D.[﹣1,3]3.(5.00分)已知向量,,若,则实数x的值为()A.9 B.﹣9 C.1 D.﹣14.(5.00分)当时,幂函数y=xα的图象不可能经过()A.第一象限B.第二象限C.第三象限D.第四象限5.(5.00分)如图所示,角θ的终边与单位圆交于点,则cos(π﹣θ)的值为()A.B.C.D.6.(5.00分)函数y=sin2x的图象经过变换得到y=sin(2x+)的图象,则该变换可以是()A.所有点向右平移个单位B.所有点向左平移个单位C.所有点向左平移个单位D.所有点向右平移个单位7.(5.00分)定义在R上的偶函数f(x),在(0,+∞)上是增函数,则()A.f(3)<f(﹣4)<f(﹣π)B.f(﹣π)<f(﹣4)<f(3)C.f(3)<f(﹣π)<f(﹣4)D.f(﹣4)<f(﹣π)<f(3)8.(5.00分)在平行四边形ABCD中,点E为CD中点,=,=,则等于()A.﹣B.﹣C.D.9.(5.00分)若奇函数f(x)=ka x﹣a﹣x(a>0且a≠1)在R上是增函数,那么的g(x)=log a(x+k)大致图象是()A.B.C.D.10.(5.00分)如图,半径为1的圆M,切直线AB于点O,射线OC从OA出发,绕O点顺时针方向旋转到OB,旋转过程中OC交⊙M于P,记∠PMO为x,弓形PNO的面积S=f(x),那么f (x)的图象是()A.B.C.D.二、填空题:本大共5小题,每小题5分,满分25分)11.(5.00分)计算:=.12.(5.00分)已知α∈(,π),且sinα=,则tanα的值为.13.(5.00分)函数f(x)=|x2﹣1|的单调递减区间为.14.(5.00分)在边长为3的等边三角形ABC中,=2,则•等于.15.(5.00分)若函数f(x)的图象在区间[a,b]上连续不断,给定下列的命题:①若f(a)•f(b)<0,则f(x)在区间[a,b]上恰有1个零点;②若f(a)•f(b)<0,则f(x)在区间[a,b]上至少有1个零点;③若f(a)•f(b)>0,则f(x)在区间[a,b]上没有零点;④若f(a)•f(b)>0,则f(x)在区间[a,b]上可能有零点.其中正确的命题有(填写正确命题的序号).三、解答题:本大题共6小题,满分75分,解答须写出文字说明、证明过程或演算步骤.16.(12.00分)已知向量和满足=(2,0),||=1,与的夹角为120°,求|+2|.17.(12.00分)已知函数f(x)=Asin(2ωx+φ)(其中A>0,ω>0,0<φ<)的周期为π,其图象上一个最高点为M(,2).(Ⅰ)求f(x)的解析式,并求其单调减区间;(Ⅱ)当x∈[0,]时,求f(x)的最值及相应的x的取值,并求出函数f(x)的值域.18.(12.00分)已知函数.(Ⅰ)讨论f(x)的奇偶性;(Ⅱ)判断f(x)在(﹣∞,0)上的单调性并用定义证明.19.(12.00分)医学上为研究某种传染病传播中病毒细胞的发展规律及其预防,将病毒细胞注入一只小白鼠体内进行实验,经检测,病毒细胞的增长数与天数的关系记录如下表.已知该种病毒细胞在小白鼠体内的个数超过108的时候小白鼠将死亡.但注射某种药物,将可杀死其体内该病毒细胞的98%.(Ⅰ)为了使小白鼠在实验过程中不死亡,第一次最迟应在何时注射该种药物?(精确到天)(Ⅱ)第二次最迟应在何时注射该种药物,才能维持小白鼠的生命?(精确到天)(参考数据:lg2=0.3010,lg3=0.4771)20.(13.00分)已知二次函数f(x)=ax2+bx+c(a≠0)的图象过点(0,1),且有唯一的零点﹣1.(Ⅰ)求f(x)的表达式;(Ⅱ)当x∈[﹣2,2]时,求函数F(x)=f(x)﹣kx的最小值g(k).21.(14.00分)已知集合M是满足下列性质的函数f(x)的全体:在定义域D 内存在x0,使得f(x0+1)=f(x0)+f(1)成立.(1)函数f(x)=是否属于集合M?说明理由;(2)若函数f(x)=k•2x+b属于集合M,试求实数k和b满足的条件;(3)设函数f(x)=lg属于集合M,求实数a的取值范围.2014-2015学年四川省成都市都江堰中学高一(上)期末数学模拟试卷(1)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5.00分)已知集合A={﹣1,2},B={x∈Z|0≤x≤2},则A∩B等于()A.{0}B.{2}C.{0,1,2}D.∅【解答】解:∵集合A={﹣1,2},B={x∈Z|0≤x≤2}={0,1,2},∴A∩B={2}.故选:B.2.(5.00分)函数f(x)=+lg(x+1)的定义域为()A.[﹣1,3)B.(﹣1,3)C.(﹣1,3]D.[﹣1,3]【解答】解:根据题意,得;,解得﹣1<x≤3;∴f(x)的定义域为(﹣1,3].故选:C.3.(5.00分)已知向量,,若,则实数x的值为()A.9 B.﹣9 C.1 D.﹣1【解答】解:∵∴=1×3+3x=0∴x=﹣1故选:D.4.(5.00分)当时,幂函数y=xα的图象不可能经过()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:当α=、1、2、3 时,y=xα是定义域内的增函数,图象过原点,当α=﹣1 时,幂函数即y=,图象在第一、第三象限,故图象一定不在第四象限.∴答案选D.5.(5.00分)如图所示,角θ的终边与单位圆交于点,则cos(π﹣θ)的值为()A.B.C.D.【解答】解:∵|OP|==1(O为单位圆的圆心),∴cosθ==﹣,∴cos(π﹣θ)=﹣cosθ=.故选:C.6.(5.00分)函数y=sin2x的图象经过变换得到y=sin(2x+)的图象,则该变换可以是()A.所有点向右平移个单位B.所有点向左平移个单位C.所有点向左平移个单位D.所有点向右平移个单位【解答】解:∵y=sin(2x+)=sin[2(x+)],∴函数y=sin2x的图象经过所有点向左平移个单位.故选:C.7.(5.00分)定义在R上的偶函数f(x),在(0,+∞)上是增函数,则()A.f(3)<f(﹣4)<f(﹣π)B.f(﹣π)<f(﹣4)<f(3)C.f(3)<f(﹣π)<f(﹣4)D.f(﹣4)<f(﹣π)<f(3)【解答】解:∵定义在R上的偶函数f(x),在(0,+∞)上是增函数,且3<π<4,∴f(3)<f(π)<f(4)即:f(3)<f(﹣π)<f(﹣4).故选:C.8.(5.00分)在平行四边形ABCD中,点E为CD中点,=,=,则等于()A.﹣B.﹣C.D.【解答】解:由题意可得,=++=﹣++=﹣,故选:B.9.(5.00分)若奇函数f(x)=ka x﹣a﹣x(a>0且a≠1)在R上是增函数,那么的g(x)=log a(x+k)大致图象是()A.B.C.D.【解答】解:∵函数f(x)=ka x﹣a﹣x,(a>0,a≠1)在(﹣∞,+∞)上是奇函数,则f(﹣x)+f(x)=0.即(k﹣1)a x+(k﹣1)a﹣x=0,解之得k=1.又∵函数f(x)=ka x﹣a﹣x,(a>0,a≠1)在(﹣∞,+∞)上是增函数,∴a>1,可得g(x)=log a(x+k)=log a(x+1).函数图象必过原点,且为增函数.故选:C.10.(5.00分)如图,半径为1的圆M,切直线AB于点O,射线OC从OA出发,绕O点顺时针方向旋转到OB,旋转过程中OC交⊙M于P,记∠PMO为x,弓形PNO的面积S=f(x),那么f (x)的图象是()A.B.C.D.【解答】解:由题意得S=f (x )=x﹣f′(x)=≥0当x=0和x=2π时,f′(x)=0,取得极值.则函数S=f (x )在[0,2π]上为增函数,当x=0和x=2π时,取得极值.结合选项,A正确.故选:A.二、填空题:本大共5小题,每小题5分,满分25分)11.(5.00分)计算:=3.【解答】解:=1+4﹣4+2(lg5+lg2)=3.故答案为:3.12.(5.00分)已知α∈(,π),且sinα=,则tanα的值为﹣.【解答】解:∵α∈(,π),且sinα=,∴cosα=﹣=﹣,则tanα==﹣.故答案为:﹣13.(5.00分)函数f(x)=|x2﹣1|的单调递减区间为(﹣∞﹣1)和(0,1).【解答】解:函数f(x)=|x2﹣1|=,如图所示:故函数f(x)的减区间为(﹣∞﹣1)和(0,1),故答案为(﹣∞﹣1)和(0,1).14.(5.00分)在边长为3的等边三角形ABC中,=2,则•等于3.【解答】解:由题意可得,||=3,|=2,∴=|=3×2×=3,故选C.15.(5.00分)若函数f(x)的图象在区间[a,b]上连续不断,给定下列的命题:①若f(a)•f(b)<0,则f(x)在区间[a,b]上恰有1个零点;②若f(a)•f(b)<0,则f(x)在区间[a,b]上至少有1个零点;③若f(a)•f(b)>0,则f(x)在区间[a,b]上没有零点;④若f(a)•f(b)>0,则f(x)在区间[a,b]上可能有零点.其中正确的命题有②④(填写正确命题的序号).【解答】解:若函数f(x)的图象在区间[a,b]上连续不断,①若f(a)•f(b)<0,则f(x)在区间[a,b]上至少有1个零点,故不正确;②若f(a)•f(b)<0,则f(x)在区间[a,b]上至少有1个零点,正确;③若f(a)•f(b)>0,则f(x)在区间[a,b]上没有零点,不正确,可以二次函数为反例;④若f(a)•f(b)>0,则f(x)在区间[a,b]上可能有零点,正确.故答案为:②④.三、解答题:本大题共6小题,满分75分,解答须写出文字说明、证明过程或演算步骤.16.(12.00分)已知向量和满足=(2,0),||=1,与的夹角为120°,求|+2|.【解答】解:由于=(2,0),则||=2,又||=1,与的夹角为120°,则=||•||•cos120°=2×=﹣1,则有|+2|===2.17.(12.00分)已知函数f(x)=Asin(2ωx+φ)(其中A>0,ω>0,0<φ<)的周期为π,其图象上一个最高点为M(,2).(Ⅰ)求f(x)的解析式,并求其单调减区间;(Ⅱ)当x∈[0,]时,求f(x)的最值及相应的x的取值,并求出函数f(x)的值域.【解答】(Ⅰ)解:由题意可得A=2,T==π,∴ω=1,∴f(x)=2sin(2x+φ).由题意当x=时,2×+φ=,求得φ=,故f(x)=2sin(2x+).令2kπ+≤2x+≤2kπ+,k∈z,求得[kπ+,kπ+],k∈z.(Ⅱ)当x∈[0,]时,2x+∈[,],故当2x+=时,函数f(x)取得最小值为1,当2x+=时,函数f(x)取得最大值为2.故f(x)值域为[1,2].18.(12.00分)已知函数.(Ⅰ)讨论f(x)的奇偶性;(Ⅱ)判断f(x)在(﹣∞,0)上的单调性并用定义证明.【解答】解:(Ⅰ)由题意可得≠0,解得x≠0,故函数f(x)的定义域为{x|x ≠0}关于原点对称.由,可得,若f(x)=f(﹣x),则,无解,故f(x)不是偶函数.若f(﹣x)=﹣f(x),则a=0,显然a=0时,f(x)为奇函数.综上,当a=0时,f(x)为奇函数;当a≠0时,f(x)不具备奇偶性(Ⅱ)函数f(x)在(﹣∞,0)上单调递增;证明:设x1<x2<0,则,由x1<x2<0,可得x1x2>0,x2 ﹣x1>0,从而,故f(x2)>f(x1),∴f(x)在(﹣∞,0)上单调递增.19.(12.00分)医学上为研究某种传染病传播中病毒细胞的发展规律及其预防,将病毒细胞注入一只小白鼠体内进行实验,经检测,病毒细胞的增长数与天数的关系记录如下表.已知该种病毒细胞在小白鼠体内的个数超过108的时候小白鼠将死亡.但注射某种药物,将可杀死其体内该病毒细胞的98%.(Ⅰ)为了使小白鼠在实验过程中不死亡,第一次最迟应在何时注射该种药物?(精确到天)(Ⅱ)第二次最迟应在何时注射该种药物,才能维持小白鼠的生命?(精确到天)(参考数据:lg2=0.3010,lg3=0.4771)【解答】解:(Ⅰ)由题意病毒细胞总数y关于时间x的函数关系式为y=2x﹣1(其中x∈N*),(3分)则由2x﹣1≤108,两边取常用对数得(x﹣1)lg2≤8,从而(6分)即第一次最迟应在第27天注射该种药物.(7分)(Ⅱ)由题意注入药物后小白鼠体内剩余的病毒细胞为226×2%,(8分)再经过x天后小白鼠体内病毒细胞为226×2%×2x,(10分)由题意226×2%×2x≤108,(11分)两边取常用对数得26lg2+lg2﹣2+xlg2≤8,解得x≤6.2(13分)故再经过6天必须注射药物,即第二次应在第33天注射药物.(14分)20.(13.00分)已知二次函数f(x)=ax2+bx+c(a≠0)的图象过点(0,1),且有唯一的零点﹣1.(Ⅰ)求f(x)的表达式;(Ⅱ)当x∈[﹣2,2]时,求函数F(x)=f(x)﹣kx的最小值g(k).【解答】解:(Ⅰ)依题意得c=1,,b2﹣4ac=0解得a=1,b=2,c=1,从而f(x)=x2+2x+1;…(3分)(Ⅱ)F(x)=x2+(2﹣k)x+1,对称轴为,图象开口向上当即k≤﹣2时,F(x)在[﹣2,2]上单调递增,此时函数F(x)的最小值g(k)=F(﹣2)=k+3;…(5分)当即﹣2<k≤6时,F(x)在上递减,在上递增,此时函数F(x)的最小值;…(7分)当即k>6时,F(x)在[﹣2,2]上单调递减,此时函数F(x)的最小值g(k)=F(2)=9﹣2k;…(9分)综上,函数F(x)的最小值;…(10分)21.(14.00分)已知集合M是满足下列性质的函数f(x)的全体:在定义域D 内存在x0,使得f(x0+1)=f(x0)+f(1)成立.(1)函数f(x)=是否属于集合M?说明理由;(2)若函数f(x)=k•2x+b属于集合M,试求实数k和b满足的条件;(3)设函数f(x)=lg属于集合M,求实数a的取值范围.【解答】解:(1)D=(﹣∞,0)∪(0,+∞),若f(x)=∈M,则存在非零实数x0,使得=+1,即x02+x0+1=0,因为此方程无实数解,所以函数(x)=∉M.(2)D=R,由f(x)=k•2x+b∈M,存在实数x0,使得k•2x0+1+b=k•2x0+b+2k+b,k•2x0=2k+b,若k=0,则b=0,k≠0有>0,所以,k和b满足的条件是k=0,b=0或>0.(3)由题意,a>0,D=R.由f(x)=lg∈M,存在实数x0,使得lg=lg+lg,所以,=•,化简得(a﹣3)x02+2ax0+3a﹣6=0,当a=3时,x0=﹣,符合题意.当a>0且a≠3时,由△≥0得4a2﹣18(a﹣3)(a﹣2)≥0,化简得2a2﹣15a+18≤0解得a≤6且a≠3综上,实数a的取值范围是a≤6.。
