桥梁工程第12讲第五章横向分布系数计算GM法
桥梁工程荷载横向分布

其中:
tan
ai I i e
n
得:
e
n i 1
i 1
a I
Ri ' '
2 i i .
a I
i 1
2 i i
二、偏心压力法(刚性横梁法)
ii)偏心力矩M=1·e的作用
Ri ' '
ai I i e
a I
i 1
n
2 i i
Ri " 的正负:
ai与e在中心线同侧时为正,异侧时为负。
它是反映荷载横向分布程度的参数,表示某根主梁 所承担的最大荷载是轴重的倍数。
荷载横向分布系数的影响因素:
梁位 荷载类型 荷载位置 梁的横向刚度
荷载横向分布系数的影响因素:
桥梁横向刚度对荷载横向分布系数的影响:
荷载横向分布系数的计算方法:
横向分布的规律与结构横向连结刚度关系密切, 目前常用的荷载横向分布计算方法主要有: 梁格系模型 : ( 1 )杠杆原理法 ( 2 )偏心压力法(修正的偏心压力法) ( 3 )铰接板(梁)法 ( 4 )刚接梁法
i 1
ak ai I k
n 2 i i
二、偏心压力法(刚性横梁法)
典型例题分析:一座计算跨径为19.5m的钢筋 混凝土简支梁桥,跨度内设有 5 道横隔梁,横 截面布置如图所示,试求荷载位于跨中时, 1 号边梁相对应于汽车荷载和人群荷载的横向分 布系数。
二、偏心压力法(刚性横梁法)
解:此桥具有很大的横向连接刚性,且长宽 比大于2,故可按偏心压力法绘制荷载横 向分布影响线。
三、铰接板法
基本假定 : 1.竖向荷载作用下,结合缝内只传递竖向剪力 g(x) ;
三、铰接板法
横向分布系数计算

其中, 数。
48E l3
为常
w1’
精品课件
由竖向静力平衡条件:
5
5
Ri i Ii 1
i1
i1
i
1
5
Ii
i1
P=1
w1’ w2’ R1’ R2’ R3’ R4’ R5’
R
i
Ii
5
Ii
i1
………………………………………(a)
精品课件
(2) 偏心力矩 M=e 作用
1
2
+1
图 双主梁桥
精品课件
人群
por
1
2
3
4
pr
汽车
a
Pq Pq
22
1
r
1号梁
1
2号梁
图 杠杆原理法计算横向分布系数
➢假定荷载横向分布影响线的 坐标为η ,车辆荷载轴重为 P ,轮重为 P/2,按最不利情 况布载,则分布到某主梁的最 大荷载为:
Pm ax P 212P
➢则汽车荷载横向分布系数为:
某梁上某截面的内力(弯矩、剪力)影响面:η=ηx, y
精品课件
梁桥由承重结构(主梁)及传力结构(横隔梁、 桥面板)两大部分组成。多片主梁依靠横隔梁和 桥面板连成空间整体结构。公路桥梁桥面较宽, 主梁的片数往往较多,当桥上的车辆处于横向不 同位置时,各主梁不同程度的要参与受力,精确 求解这种结构的受力和变形,需要借助空间计算 理论。但由于实际结构的复杂性,完全精确的计 算较难实现 ,目前通用的方法是引入横向分布 系数,将复杂的空间问题合理的简化为平面问题 来求解—空间理论的实用计算方法。
分担的荷载比值变化曲线,也称为该主梁的荷 载横向分布影响线。
横向分布系数

横向分布系数荷载横向分布系数:表示某根主梁所承担的最大荷载占各个轴重的倍数。
为使荷载横向分布的计算能更好地适应各种类型的结构特性,就需要按不同的横向结构简化计算模型拟定出相应的计算方法。
目前最常用的几种方法:杠杆原理法:把横向结构(桥面板和横隔梁)视作在主梁上断开而简支在其上的简支梁。
适用于双主梁桥、荷载位于靠近主梁支点处。
偏心压力法:把横隔梁视作刚性极大的梁,故又称刚性横梁法。
当计及主梁抗扭刚度影响时此法又称为修正偏心压力法(修正刚性横梁法)。
适用于窄桥(宽跨比B /l 小于或接近0.5的情况)。
G-M 法:由比拟正交异性板法发展而来,能利用计算机工具或编就的计算图表得出相对来说比较精确的结果。
此法概念明确,计算简捷,对于各种桥面净空宽度和多种荷载组合的情况,可以很快的求出各片主梁的相应内力值。
例:如图所示桥梁横断面,在公路-Ⅰ级荷载作用下,分别用杠杆原理法和偏心压力法求①和②号梁的荷载横向分布系数。
杠杆原理法:首先在①号梁和②号梁横向影响线上,按最不利方式布载,如图所示:①号梁:11900180011219002m −=×+× 11110.0530.521922=×+≈×+ 0.5265= ②号梁:1190018001119001300121900221900m −−=×+×+× 1111611 10.0530.50.316219221922=×+×+×≈×++× 0.6845=偏心压力法:首先画①号梁和②号梁横向影响线,那就要先找到其影响线的两个控制竖标值,由于各主梁的截面均相同,故可按下式计算:()()()()()()422222212341122222221112122114212121 1.5 1.90.5 1.90.5 1.9 1.5 1.918.05m 1.5 1.911=0.250.450.7418.051.5 1.911=0.250.450.2418.051=n ii i i n ii n i i i a a a a a a a n a a n a a a n a ηηη=====+++=×+×+−×+−×=×+=+=+=×−=−=−=−×+∑∑∑∑()()()()212424210.5 1.9 1.5 1.910.250.150.4418.050.5 1.9 1.5 1.911=0.250.150.1418.05n i ni i a a n aη==×××=+=+=××××−=−=−=∑∑然后在①号梁和②号梁横向影响线上,按最不利方式布载,如图所示:①号梁:()10.7160.4320.2260.508=0.6582m =×++− ②号梁:()10.4050.3110.2420.147=0.55252m =×+++ 荷载横向分布系数延桥垮的变化:通常用“杠杆原理法”来计算荷载位于支点处的横向分布系数m 0,其他方法均适用于计算荷载位于跨中的横向分布系数m c 。
桥梁上部计算教程--横向力分布系数计算

桥梁上部计算教程--横向力分布系数计算(转)总的来说,横向力分布系数计算归结为两大类(对于新手能够遇到的):1、预制梁(板梁、T梁、箱梁)这一类也可分为简支梁和简支转连续2、现浇梁(主要是箱梁)首先我们来讲一下现浇箱梁(上次lee_2007兄弟问了,所以先讲这个吧)在计算之前,请大家先看一下截面这是一个单箱三室跨径27+34+27米的连续梁,梁高1.55米,桥宽12.95米!!支点采用计算方法为为偏压法(刚性横梁法)mi=P/n±P×e×ai/(∑ai x ai)跨中采用计算方法为修正偏压法(大家注意两者的公式,只不过多了一个β)mi=P/n±P×e×ai×β/(∑ai x ai)β---抗扭修正系数β=1/(1+L^2×G×∑It/(12×E×∑ai^2 Ii)其中:∑It---全截面抗扭惯距Ii ---主梁抗弯惯距 Ii=K Ii` K为抗弯刚度修正系数,见后L---计算跨径G---剪切模量 G=0.4E 旧规范为0.43EP---外荷载之合力e---P对桥轴线的偏心距ai--主梁I至桥轴线的距离在计算β值的时候,用到了上次课程/thread-54712-1-1.html我们讲到的计算截面几何性质中的抗弯惯矩和抗扭惯矩,可以采用midas计算抗弯和抗扭,也可以采用桥博计算抗弯,或者采用简化截面计算界面的抗扭,下面就介绍一下这种大箱梁是如何简化截面的:简化后箱梁高度按边肋中线处截面高度(1.55m)计算,悬臂比拟为等厚度板。
①矩形部分(不计中肋):计算公式:It1=4×b^2×h1^2/(2×h/t+b/t1+b/t2)其中:t,t1,t2为各板厚度h,b为板沿中心线长度h为上下板中心线距离It1=4×((8.096+7.281)/2)^2×1.34^2/(2×1.401/0.603+8.097/0 .22+7.281/0.2)=5.454 m4②悬臂部分计算公式: It2=∑Cibiti3其中:ti,bi为单个矩形截面宽度、厚度Ci为矩形截面抗扭刚度系数,按下式计算:Ci=1/3×(1-0.63×ti/bi + 0.052×(ti/bi)^5)=1/3×(1-0.63×0.26/2.2+0.052×(0.26/2.2)^5)=0.309It2=2×0.309×2.2×0.26^3=0.0239 m4③截面总的抗扭惯距It= It1+ It2=5.454+0.0239=5.4779 m4大家可以用midas计算对比一下看看简化计算和实际能差多少??先计算一下全截面的抗弯和中性轴,下面拆分主梁需要用的到采用<<桥梁博士>>V2.9版中的截面设计模块计算全截面抗弯惯距,输出结果如下:<<桥梁博士>>---截面设计系统输出文档文件: D: \27+34+27.sds文档描述: 桥梁博士截面设计调试任务标识: 组合截面几何特征任务类型: 截面几何特征计算------------------------------------------------------------截面高度: 1.55 m------------------------------------------------------------计算结果:基准材料: JTJ023-85: 50号混凝土基准弹性模量: 3.5e+04 MPa换算面积: 7.37 m2换算惯矩: 2.24 m4中性轴高度: 0.913 m沿截面高度方向 5 点换算静矩(自上而下):主截面:点号: 高度(m): 静矩(m××3):1 1.55 0.02 1.16 1.773 0.775 1.834 0.388 1.585 0.0 0.0------------------------------------------------------------计算成功完成结果:I全= 2.24 m4 中性轴高度H=0.913m下面来讲一下主梁拆分的原则:将截面划分为τ梁和I梁,保持将两截面中性轴与全截面中性轴位置一致。
桥梁工程荷载横向分布计算简介

2、横向分布系数(m)的概念:
• 多片式梁桥,在横向分布影响线上用规范规定的车轮 横向间距按最不利位置加载
说明:1)近似计算方法,但对直线梁桥,误差不大
2)不同梁,不同荷载类型,不同荷载纵向位置, 不同横向连接刚度,m不同。
3、横向连结刚度对荷载横向分布的影响
结论:横向分布的规律与结构横向连结刚度关系密切,
根据表中的横向影响线坐 标值绘制影响线图
公路-I级
七、横向分布系数沿桥纵向的变化
•对于弯矩
由于跨中截面车轮加载值占总荷载的绝大多数,近 似认为其它截面的横向分布系数与跨中相同
•对于剪力
从影响线看跨中与支点均占较大比例 从影响面看近似影响面与实际情况相差较大
计算剪力时横向分布沿桥纵向的变化
横向分布系数
横向分布系数 :在横向分布影响线上加载
3. 铰接梁法
假定各主梁除刚体 位移外,还存在截 面本身的变形
与铰接板法的区别:变位系数中增加桥面板变形项
4.刚接梁法
假定各主梁间除传递剪力外,还传递弯矩
与铰接板、梁的区别: 未知数增加一倍,力法方程数增加一倍
5 .铰接板桥计算m举例:
如图所示,l=12.60m的铰接空心板桥横截面布置。 桥面净空为净-7+2x0.75m人行道。全桥由9块预应力混凝 土空心板组成,欲求1、3、5号板的公路-I级和人群荷载作用 的跨中横向分布系数?
值(ki)
1 ai ak 若各梁截面尺寸相同: ki Rki Rik n n 2 ai
i 1
(三) 计算举例
例2-5-3: 已知:l=19.50m,荷载位于跨中 试求:1#边梁,2#中梁的mcq,mcr
作业
已知:l=29.16m, 38.88m,荷载位于跨中时 试求:2#中梁的mcq,mcr
桥梁工程设计 GM法

广西大学 土木建筑工程学院 土木工程专业(交通土建方向)
《桥梁工程》课程设计
姓 名:浦远鹏 班 级:交建061 学 号:0603110337 指导老师:林春姣 广西大学土木建筑工程学院课程设计
- 1 - 钢筋混凝土T形梁桥设计 一.设计资料与结构布置 (一) 设计资料 1、 桥面跨径及桥宽
主梁:
标准跨径Lb=25m(墩中心距离); 计算跨径L=24.50m(支座中心距离); 预制长度L’=24.95m(主梁预制长度);
横隔梁5根,肋宽15cm; 桥面净宽:净-7(车行道)+2×1.0(人行道)+2×0.25(栏杆)。 2、 设计荷载
公路-II级,人群3.5kN/m2。 3、 材料初步选定 材料 规格 内容
钢筋
HRB335(原Ⅱ级) 主梁主筋、弯起钢筋和架立钢筋
R235(原Ⅰ级) 箍筋 混凝土
C25 主梁
C30防水 桥面铺装
4、 设计依据 1)中华人民共和国行业标准《公路桥涵设计通用规范》JTG D60-2004,
人民交通出版社,2004年9月; 2)中华人民共和国行业标准《公路钢筋混凝土及预应力混凝土桥涵设计规范》 JTG D62-2004,人民交通出版社,2004年9月; 3)公路桥涵设计手册《梁桥》,1994年6月,人民交通出版社; 4)桥梁计算示例集,2000年10月,人民交通出版社; 5)本课程教材《桥梁工程》,人民交通出版社; 6)《桥梁工程设计计算方法及应用》,2003年10月,中国建筑工业出版社; 7)有关梁桥设计图纸。 (二) 结构布置 1、 主梁高:钢筋混凝土T形简支梁高跨比的经济范围大约在111~161,根据跨度广西大学土木建筑工程学院课程设计 - 2 - 大者取较小值的原则,本设计取用161,则梁高为1.5625m。实际设计取1.6m; 2、 主梁间距:装配式钢筋混凝土T形简支梁的主梁间距一般选在1.5~2.2m之间,本设计采用1.9m; 3、 主梁梁肋宽:为保证主梁的抗剪需要,梁肋受压时的稳定,以及混凝土的振捣质量,通常梁肋宽度取在15~18cm,鉴于本设计的跨度为25m,纵向钢筋数量较多,故按较大值取为18cm; 4、 翼缘板尺寸:由于桥面宽度是给定的,主梁间距确定后,翼缘板的宽度即可得到为1.9m。因为翼缘板同时又是桥面板,根据其受力特点,一般设计成变厚度
荷载横向分布系数的计算比拟法实用课件
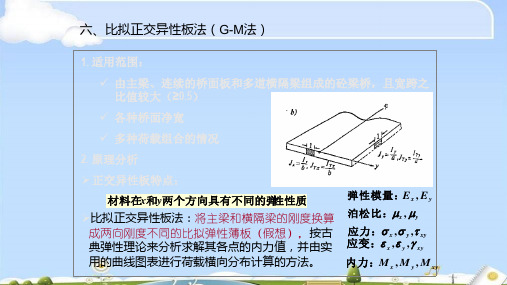
1. 适用范围:
✓ 由主梁、连续的桥面板和多道横隔梁组成的砼梁桥,且宽跨之
比值较大(≥0.5)
✓ 各种桥面净宽
✓ 多种荷载组合的情况
2. 原理分析
➢ 正交异性板特点:
材料在x和y两个方向具有不同的弹性性质
➢比拟正交异性板法:将主梁和横隔梁的刚度换算 成两向刚度不同的比拟弹性薄板(假想),按古 典弹性理论来分析求解其各点的内力值,并由实 用的曲线图表进行荷载横向分布计算的方法。
换算后的比拟异性板-假想的板
2E JxJ y
换算后的比拟异性板-假想的板
截面抗弯和抗扭刚度的计算 代数平均值与单宽抗弯刚度几何平均值之比。对于常用的T形和工字型梁
在0 46年 法 国 的 居 翁 (Guyon) 引 用 正 交 异 性 板 的论理解 决 了 无 扭 梁 格
可见,任何纵横梁格系结构比拟成的异性板,可以完全仿照真正 实际结构:
梁肋间距 a 和 b 相比桥跨结构的长度或宽度很小,并且桥面板与梁肋具有完善的结合。
比拟正交异性板法:将主梁和横隔梁的刚度换算成两向刚度不同的比拟弹性薄板(假想),按古典弹性理论来分析求解其各点的内力值,并由实用的曲线图表进行荷载横向分布计
2. 原理分析
实际结构纵横向构 造
换算后的比拟异性板-假想的 板
J x , JTx
J y , JTy
实际结构:(如果) 梁肋间距 a 和 b 相比桥跨结构的长度或宽度很 小,并且桥面板与梁肋具有完善的结合。
纵向主
梁:间距b,每根主
梁的
截面抗
弯惯矩I
、抗
x
扭惯矩ITx
横隔梁:间距a,截面抗弯惯矩I y、抗扭惯矩ITy
《桥梁工程》荷载横向分布计算(偏心压力法)

3.偏心压力法 Method based on stiffness transverse connection
3)原理 Theory
P
Pe
L P Pe
w φ
P w
φ
Pe
3.偏心压力法 Method based on stiffness transverse connection
3)原理 Theory
当荷载P=1作用于第i号梁上时,
各主梁的荷载分布:
P=1
a1
ki Rik Rik ……(5)
R51
当各主梁截面尺寸相同时,
R11
ik
1 n
ai ak
5
ai2
……(6) η11
η15
i 1
3.偏心压力法 Method based on stiffness transverse connection
1)基本假设 横梁刚性极大,刚性横梁的微小变形可以忽略不计
PP
P/2
P/2
L
B
f
f
f’
f >>f’
3.偏心压力法 Method based on stiffness transverse connection
3.偏心压力法 Method based on stiffness transverse connection
i 1
i 1
ai wi’’
φ
MT1 R1’’
R2’’ MT2 MT3
R4’’ R5’’ MT4 MT5
4.修正偏心压力法
Modified method of the stiffness transverse connection
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年3月22日
土木与建筑工程学院
总结
1、GM法:√ 2、铰接板法 3、铰接梁法 4、刚接梁法
2013年3月22日
土木与建筑工程学院
下次课再见! 作业!!!
2013年3月22日
土木与建筑工程学院
2013年3月22日
土木与建筑工程学院
0.56 J X
扭弯参数α 纵、横向截面抗弯刚度之比
2013年3月22日
土木与建筑工程学院
(3)查表
将桥全宽分八等分九个点,对称。 表中只有9点值,必须通过内插计算实际位置值。
RkiK 2Bki
2BKki nn
b 2B n
2013年3月22日
No mage
2013年3月22日
土木与建筑工程学院
总结
• 1、计算原理 • 2、好处 • 3、步骤
• (1)计算几何特性。J X 、JTX 、J Y 、JTY
• JTY (2)计算参数α、。 • (3)计算各主梁横向影响线竖标。
2013年3月22日
土木与建筑工程学院
作业
• 书上例题。 • 扭弯参数 J X
JX
2013年3月22日
土木与建筑工程学院
(2)比拟正交异性板挠曲微分方程
正交异性定义:结构材料两个方向弹性性质不同 桥跨结构纵横向构造不同
内力与位移关系方程:Dx4xw42Hx24wy2Dy4yw4P(x,y)
2013年3月22日
土木与建筑工程学院
比拟原理实质
任何纵横梁格系结构比拟成的异性板,可以 完全仿照真正的材料异性板来求解,只是方程中的 刚度常数不同。
2013年3月22日
土木与建筑工程学院
B 4
l
Jx Jy
• 四阶非齐次偏微分方程:求解难!
• 实际:编制计算图表,查表求解。
• 作者:居翁(G)
•
麦桑纳特(M)
2013年3月22日
土木与建筑工程学院
优点:
• 1、结果比较精确。 • 2、适用于各种桥面净空宽度和多种荷载组合。 • 3、宽窄桥全适用。
2013年3月22日
土木与建筑工程学院
三、比拟正交异性板法
1、计算原理 (1)将由主梁、连续的桥面板和多横隔梁所组成 的梁桥,比拟简化为一块矩形的平板; (2)求解板在半波正弦荷载下的挠度; (3)利用挠度比与内力比、荷载比相同的关系计 算横向分布影响线。
2013年3月22日
土木与建筑工程学院
(1)比拟
土木与建筑工程学院
ki
w ki 2Bw
位移互等定理
பைடு நூலகம்
K ki
w ki w
引入影响系数
ki
K ki 2B
RkikibK2Bkib
2013年3月22日
土木与建筑工程学院
(2)Kki影响系数
Kki影响系数,是欲计算的板条位置k、荷 载位置i、扭弯参数α以及纵、横向截面抗弯刚 度之比的函数,为弹性力学挠曲微分方程, 初等数学无法求解。已经被制成图表,为α、 、 i、 k的函数。制表人居翁Guyon、麦桑纳 特Massonnet,本方法称G-M法。给出α=1 、 α=0的曲线图表,其余内插。
桥梁工程
2007年5月7日
土木与建筑工程学院 2013年3月22日
黑龙江公程学院土木工程系 主讲人 : 王丽荣
活载(汽车、人群)特点:横向分布
J
X
桥上的荷载→某梁的某截面内力←→ 空间问题→多个车辆纵横向移动→
难
实用:平面化
①横桥向上,荷载分配至各梁→ 横向分布问题。
②某梁在分得荷载的作用下,内力计算问题。
2013年3月22日
= C w n k n 土木与建筑工程学院
• 根据内、外力的平衡:等代
n
(C1 w C2 w C3 w Cn )w 1C w i1C(w )A i 1
C
1 A( w )
X
2013年3月22日
A(w)2Bw
C
1
2 Bw
ik
Cwik
wik 2Bw
规律:不同结构→ 不同刚度→不同的算法
方法:杠杆法适用:支点
偏心压力法(刚性横梁法)适用:跨中窄桥
GM法适用:跨中宽桥√
铰接板(梁)法
刚接梁法
2013年3月22日
土木与建筑工程学院
第12讲 第五章 混凝土简支梁桥的计算-荷载横向分布系数
• 学教内容: • 1、掌握GM法计算横向分布系数的特点、定义 • 2、掌握GM法计算横向分布系数的方法。 • 重 点: • 1、 GM法的特点、定义。 • 2、 GM法计算横向分布系数的方法。 • 难 点: • 1、 GM法计算横向分布系数的方法。 •
土木与建筑工程学院
K值
2013年3月22日
土木与建筑工程学院
主梁荷载横向影响线
J
2013年3月22日
土木与建筑工程学院
X
4、弯扭参数α计算
(1)抗弯惯矩计算 纵: 横:必须考虑受压翼板有效工作宽度。
No
Image
2013年3月22日
土木与建筑工程学院
(2)抗扭惯矩计算 必须区分连续宽板与独立主梁翼板。
2013年3月22日
土木与建筑工程学院
好处:
• (1)其他方法主要在横向联结方式不同假 定不同平面问题。
• (2)实际空间结构非精确解。 • (3)弹性薄板用弹性理论分析,简化为计
算图表求解实际问题。
2013年3月22日
土木与建筑工程学院
2、求解板在半波正弦荷载下的挠度
• (1)弹性板的挠曲面微分方程:正交均质
2013年3月22日
土木与建筑工程学院
3、横向分布系数计算
(1)绘制影响线的原理
1 k = C w 1
A、根据荷载、挠度、内力的关系。
= C w 2 k 2
= C w (1 k2 k3 k 3 k 3 n)k
… … C、为与跨度和截面刚度相关的常数。
B、外载为单位正弦荷载。
纵、横向截面抗弯刚度之比 G(JTx JTy) E Jx Jy
2013年3月22日
土木与建筑工程学院
JX
活载(汽车、人群)特点:空间问题 实用:平面化 ①横桥向上,荷载分配至各梁→ 横向分布问题。 ②某梁在分得荷载的作用下,内力计算问题。 规律:不同结构→ 不同刚度→不同的算法 方法:杠杆法:多适用于荷载位于支点
