[拉压、扭转作业解答
拉伸与扭转实验

圆筒形薄壁压力容器, 圆筒形薄壁压力容器,内径为 D、壁厚为 t,承 、 , 受内力p作用 受内力 作用
p
周向 轴向 径向
p
重要应用实例
σm σt
p
l
D
pDl
σm
σm(π D)δ
D δ
pπ D 2 4
p
σm
σt
σt (2 δ l )
σt
重要应用实例
σm
σm(π D)δ
D δ
pπ d 2 4
α
τx
σy
τy
n
τα σα
α A Acosα
Asinα
σ:拉应力为正 : τ:顺时针转动为正 : α:逆时针转动为正
平衡原理的应用——微元局部 微元局部 平衡原理的应用 的平衡方程
平衡对象——用α斜截面截取 用 平衡对象 的微元局部 参加平衡的量——应力乘以 应力乘以 参加平衡的量 其作用的面积 平衡方程—— 平衡方程
3
Mz σx = − Wz
3
圆杆受扭转和拉伸共同作用
m
P P m
τ
σ
N 4P σ= = A πd2
16 m T τ= = Wt π d 3
§8-2
y σ y
平面应力状态下的应力分析
y
τ yx τ xy
σy τy
σx
x
τx σx x
一、解析法
y
σy
τx σx
τy
n
α
τx σx x
τy σy
σx
cos 2α − τ x sin 2α
x
y
sin 2α + τ x cos 2α
σ α 和τ α 都是α的函数。利用上式便可确
第02章拉压题解
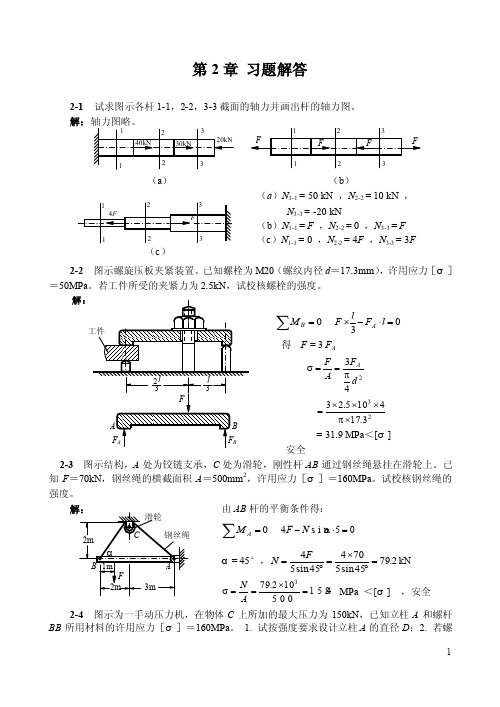
第2章 习题解答2-1 试求图示各杆1-1,2-2,3-3截面的轴力并画出杆的轴力图。
解:(a )N 1-1 = 50 kN ,N 2-2 = 10 kN ,N 3-3 = -20 kN(b )N 1-1 = F ,N 2-2 = 0 ,N 3-3 = F(c )N 1-1 = 0 ,N 2-2 = 4F ,N 3-3 = 3F2-2 图示螺旋压板夹紧装置。
已知螺栓为M20(螺纹内径d =17.3mm ),许用应力[ζ]=50MPa 。
若工件所受的夹紧力为2.5kN ,试校核螺栓的强度。
∑=0BM03=⋅-⨯l F lF A得F = 3 F A243dF A F Aπ==σ233.174105.23⨯π⨯⨯⨯== 31.9 MPa <[ζ]安全2-3 图示结构,A 处为铰链支承,C 处为滑轮,刚性杆AB 通过钢丝绳悬挂在滑轮上。
已知F =70kN ,钢丝绳的横截面积A =500mm 2,许用应力[ζ]=160MPa 。
试校核钢丝绳的强度。
由AB 杆的平衡条件得:∑=0A M 05s i n 4=⋅α-N F α= 45°,2.7945sin 570445sin 54=︒⨯=︒=F N kN4.158500102.793=⨯==σA N MPa <[ζ] ,安全 2-4 图示为一手动压力机,在物体C 上所加的最大压力为150kN ,已知立柱A 和螺杆BB 所用材料的许用应力[ζ]=160MPa 。
1. 试按强度要求设计立柱A 的直径D ;2. 若螺(a )(b )杆BB 的内径d =40mm ,试校核其强度。
解:由平衡条件得 752150==A N kN 1. 由立柱的强度条件 24DN A N AA A π==σ≤[ζ] 得 D ≥4.2416010754][43=⨯π⨯⨯=πζA N mm2. 螺杆的应力1194010150423=⨯π⨯⨯==σBB BB A N MPa <[ζ] 螺杆强度足够。
[拉压、扭转作业解答

材料力学习题详解第二章拉伸、压缩与剪切题图(a)所示结构中,若钢拉杆BC的横截面直径为10mm,试求拉杆内应力。
设BC连接的1和2两部分均为刚体。
解:首先根据刚体系的平衡条件,求出BC杆的内力。
刚体1受力图如题图(b)所示,平衡条件为DM=∑, 1.5 4.530N AF F F⨯+⨯-⨯=①刚体2受力图如题图(c)所示,平衡条件为EM=∑, 1.50.750A NF F⨯-⨯=②解①、②式得BC杆的内力为6NF kN=故拉杆BC杆内的应力为()32361076.410104NFPa MPaAσπ-⨯===⨯⨯题图(a)所示结构中,1、2两杆的横截面直径分别为10mm和20mm。
试求两杆内的应力。
设两根横梁皆为刚体。
解:先求1、2杆的轴向内力,选取AB 杆为受力体,其受力图如题图(b)所示,由平衡条件有0yF=∑, 10NA NC F F += ①0AM=∑, 10210NC F ⨯-⨯= ②解①、②式,得 10NA F kN =, 20NC F kN = 故1、2杆内的应力分别为()3123101012710104Pa MPa σπ-⨯==⨯⨯()3223201063.720104Pa MPa σπ-⨯==⨯⨯如题图所示,直径为10mm 的圆杆,在拉应力F =10kN 的作用下,试求最大切应力,并求与木杆的横截面夹角为30α=︒的斜截面上正应力及切应力。
解:受轴向载荷杆,斜截面上的应力公式为2cos N F A ασα=, sin 22N FAατα=当45α=︒时,杆内切应力达到最大值,所以3max21010sin 2sin 9063.72220.014N F F Pa MPa A A ταπ⨯==︒==⨯在与木杆的横截面夹角为30︒的斜截面上,正应力及切应力分别为3230210103cos3095.50.0144FPa MPaAσπ︒⎛⎫⨯=︒=⨯=⎪⨯⎝⎭()330210103sin23055.120.014FPa MPaAτπ︒⎛⎫⨯=⨯︒=⨯=⎪⎪⨯⎝⎭题图(a)所示的双杠杆夹紧机构,需产生一对20kN的夹紧力,试求水平连杆AB 及二斜连杆BC和BD的横截面直径。
第一部分-拉压及扭转

应力应变关系如图(B为常数),
推导轴横截面上的剪应力公式(设 平截面假设仍成立),并画出横截 面上的剪应力分布图。
T
T
2R
B
d 解: 1、几何关系参考教材,为: = dx
d 2、由物理关系得: B = B dx
3、静力学关系:
M x dA
T
I
II
d
T
D
T
MxI
轴I
+
T
轴II
MxII MxII
+
MxI
T
轴II 受力
几何性质
0
b
z
h
y=zn
y
(n>1)
思考题:试计算图 示图形的面积和形 心位置。
答案:
n 1 zc b n2 n 1 n yc b 2n 1
梁的内力
a
l
a
思考题:利用弯曲内力知识,分析图 示标准双杠为什么将尺寸设计为a=l/4? (提示:假设运动员在杠上运动时,每根 横梁上只有一个力的作用点,力的作用线 垂直于横梁,而且力的大小与作用点的位 置无关,条件是使横梁重量为最轻。)
D
d
图示一等强度杆(每 一横截面上的应力都 同时达到许用应力), 杆顶端有轴向外力F 作用,杆的重度为γ, 材料的许用应力为[ζ], 试求杆的横截面面积 A(x)的表达式及轴向 变形△l。
F
A(x)
l
A
30
C
0
F
B
思考题:在小变形条件下,节点B的位移与杆BC 的变形之间的大小关系为:δ B= △lBC。(要 求计算过程)
A R 0 2 d B d d 0 dx
04、基本知识 怎样推导轴向拉压和扭转的应力公式、变形公式(供参考)

04、基本知识 怎样推导轴向拉压和扭转的应力公式、变形公式(供参考)同学们学习下面内容后,一定要向老师回信(****************),说出你对本资料的看法(收获、不懂的地方、资料有错的地方),以便考核你的平时成绩和改进我的工作。
回信请注明班级和学号的后面三位数。
1 * 问题的提出 ........................................................................................................................... 1 2 下面就用统一的步骤,研究轴向拉压和扭转的应力公式和变形公式。
........................... 2 3 1.1 轴向拉压杆的应力公式推导 ............................................................................................ 2 4 1.2 轴向拉压杆的变形公式推导 ............................................................................................ 4 5 1.3 轴向拉压杆应力公式和变形公式的简要推导 ................................................................ 4 6 1.4 轴向拉压杆的强度条件、刚度条件的建立 .................................................................... 4 7 2.1 扭转轴的应力公式推导 .................................................................................................... 5 8 2.2 扭转轴的变形公式推导 .................................................................................................... 7 9 2.3 扭转轴应力公式和变形公式的简要推导 ........................................................................ 7 10 2.4 扭转的强度条件、刚度条件的建立 ............................................................................ 8 11 3. 轴向拉压、扭转、梁的弯曲剪切,应力公式和变形公式推导汇总表 .. (9)1* 问题的提出在材料力学里,分析杆件的强度和刚度是十分重要的,它们是材料力学的核心内容。
习题解答1(轴向拉压)

3
初始应力对杆件稳定性的影响
初始应力会降低杆件的稳定性,使杆件在受载时 更容易发生失稳现象。
06
典型例题解析与讨论
简单载荷作用下杆件问题解析
轴向拉伸与压缩基本概念
通过例题解析,阐述轴向拉伸与压缩的基本概念,包括受力特点、 变形特点等。
截面法求内力
通过具体例题,讲解如何利用截面法求解杆件在简单载荷作用下的 内力,包括轴力和轴力图。
02
轴向拉压杆件内力分析
内力计算方法
截面法
通过截取杆件的一部分,分析截面上的 内力和外力平衡关系,从而求得杆件的 内力。
VS
节点法
对于由多个杆件组成的结构,可以通过分 析节点处的平衡关系,求得各杆件的内力 。
截面法求内力
截开杆件
在需要求内力的截面处,假想地将杆件截开, 取其中一部分为研究对象。
01
轴向变形与位移是密切相关的,轴向变形是引起位移的主要 因素之一。
02
在小变形条件下,轴向变形与位移成正比关系;而在大变形 条件下,由于材料非线性等因素的影响,两者之间的进一步研究轴向变形与位移 之间的关系,为工程应用提供更为准确的理论依据。
04
轴向拉压杆件强度条件与 刚度条件
超静定问题解析
通过具体例题,讲解超静定问题的求解方法,包括力法和 位移法。讨论超静定结构的特点及在工程中的应用。
特殊情况下杆件问题解析
温度变化对杆件的
影响
解析温度变化对杆件内力和变形 的影响,以及如何处理由此产生 的附加应力和变形。结合例题进 行讨论。
初始应力对杆件的
影响
阐述初始应力对杆件承载能力和 稳定性的影响,以及如何在设计 和分析中考虑初始应力的影响。 通过具体例题进行解析。
材料力学拉伸与扭转题目答案

75
2
3
1
A
B
C
P
40
80
80
变形相容条件 变形后三根杆与梁 仍绞接在一起。 变形几何方程
2 l2 l1 l3
2
3
1
A
B
C
l1
P
l2
l3
40
80
80
75
2 l2 l1 l3
补充方程
2 N 2 l2 N1l1 N3l3 EA EA EA
静力平衡方程
N1 N2 N3 P 0 2N2 4N3 P 0
2
3
1
A
B
C
P
40
80
80
N1
N2
N3
P
75
3、阶梯形圆杆AE段为空心,外径 D =140mm,内径 d=100mm。BC段为实心,直径 d=100mm。外力偶矩 mA=18KN.m,mB=32KN.m,mC=14KN.m。已知许用切应力 []=80MPa 。试校核轴的强度。
mA
D
d
A
E
mB mC
二、计算题
1:悬臂吊车如图所示。G=20KN,许用应力 []=120MPa,弹性模量E=200GPa。AB杆为圆钢。试设计 AB杆的直径并计算其伸长量l
A
C
300
3m
D B
2m
G
1、解:计算AB杆的轴力
A
mc 0
3N AB sin300 5G 0
C
300
D
NAB=66.7KN (1) 设计AB杆的直径
d
C B
mAB =18KN.m ,mBD =14KN.m
BC
M nBC Wn
材料力学拉伸压缩剪切扭转名称公式判别及汇总

一、拉(压)杆强度条件:--------(1)二、(剪切)切应力条件和挤压强度条件1.切应力强度条件:τ --------(2)2.挤压强度条件:--------(3)三、圆轴扭转时的强度和刚度条件资料个人收集整理,勿做商业用途1.扭转强度条件:-----------(4)----------------(5)2.扭转刚度条件:-----------(6)----------------(7)四:弯曲正应力强度条件:------(8)符号释义:1.:正应力2. τ:切应力3.T:扭矩4.:轴力5.:剪切力6.7.A:剪切截面面积8.:抗扭截面系数9.:横截面对圆心的极惯性矩10.y: 正应力到中性轴的距离11.ε:正应变(线应变) 三个弹性材料的关系:1.E:弹性模量(GN/m²)2. μ:为泊松比(钢材的μ为0.25-0.33)3.G:剪切弹性模量(GN/m²)剪切胡可定律:τ=Gγ16.E:抗拉刚度17.胡可定律:σ=Eεσ=E18.ρ:曲率半径19.:梁弯曲变形后的曲率20.M:弯矩轴力、剪切力、均为内力求内力的方法-截面法:1.假想沿m-m横截面将杆件切开2.留下左半端或右半段3.将弃去部分对留下部分的作用(力)用内力代替4.对留下部分写平衡方程,求出内力的值。
当你选择好研究对象时,建立坐标系,这个对象的所有受力的x方向的代数和,和y方向的代数和为零,这就建立平衡方程,【me=o】,就是你在研究对象上选取一个点作为支点,然后所有力对这个点取矩,顺时针和逆时针方向的代数和为零,这样就分别建立三个平衡方程,可以联立接触其中未知数,这种情况只是用于解决静定结构的。
12.γ:切应变(角应变)21.:外力偶矩13.EA:抗拉强度(钢材的EA约为200GPa)14.δ:断后伸长率15.ψ:断面收缩率/相对扭转角梁受力有:轴力、剪切力和弯矩M。
一、材料力学的几个基本感念1.构件:工程结构或机械的每一组成部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学习题详解第二章 拉伸、压缩与剪切2.4 题2.4图(a)所示结构中,若钢拉杆BC 的横截面直径为10mm ,试求拉杆内应力。
设BC 连接的1和2两部分均为刚体。
解:首先根据刚体系的平衡条件,求出BC 杆的内力。
刚体1受力图如题2.4图(b)所示,平衡条件为0DM =∑, 1.5 4.530N A F F F ⨯+⨯-⨯= ①刚体2受力图如题2.4图(c)所示,平衡条件为0EM=∑, 1.50.750A N F F ⨯-⨯= ②解①、②式得BC 杆的内力为 6N F kN = 故拉杆BC 杆内的应力为()32361076.410104N F Pa MPa A σπ-⨯===⨯⨯2.5 题2.5图(a)所示结构中,1、2两杆的横截面直径分别为10mm 和20mm 。
试求两杆内的应力。
设两根横梁皆为刚体。
解:先求1、2杆的轴向内力,选取AB 杆为受力体,其受力图如题2.5图(b)所示,由平衡条件有0yF=∑, 10NA NC F F += ①0AM=∑, 10210NC F ⨯-⨯= ②解①、②式,得 10NA F kN =, 20NC F kN = 故1、2杆内的应力分别为()3123101012710104Pa MPa σπ-⨯==⨯⨯()3223201063.720104Pa MPa σπ-⨯==⨯⨯2.6 如题2.6图所示,直径为10mm 的圆杆,在拉应力F =10kN 的作用下,试求最大切应力,并求与木杆的横截面夹角为30α=︒的斜截面上正应力及切应力。
解:受轴向载荷杆,斜截面上的应力公式为2cos N F A ασα=, sin 22N FAατα=当45α=︒时,杆内切应力达到最大值,所以3max21010sin 2sin 9063.72220.014N F F Pa MPa A A ταπ⨯==︒==⨯在与木杆的横截面夹角为30︒的斜截面上,正应力及切应力分别为3230210103cos 3095.50.0144F Pa MPa A σπ︒⎛⎫⨯=︒=⨯= ⎪⨯⎝⎭()33021010sin 23055.120.014F Pa MPa A τπ︒⎛⨯=⨯︒== ⨯⎝⎭2.10 题2.10图(a)所示的双杠杆夹紧机构,需产生一对20kN 的夹紧力,试求水平连杆AB 及二斜连杆BC 和BD 的横截面直径。
已知:该三杆的材料相同,[]100,30MPa σα==︒。
解:欲确定AB 、BC 和BD 三杆的直径,首先要求出三杆的内力,从而计算出三杆的工作应力,再根据强度条件,确定它们的直径。
因AB 、BC 、BD 三杆都是二力杆,所以三杆都只受轴向力,取CE 杆为受力体,受力图如题2.10图(b)所示,由平衡条件0M=∑, cos NBC E F l F l α=得BC 杆的轴力为 2023.1cos30NBC F kN kN ==根据强度条件,BC 杆的工作应力不应超过许用应力,即[]24NBC NBC BC BC BC F FA d σσπ==≤由上式可确定BC 杆的直径为17.2BC d mm ≥== 由于结构对称,所以 17.2BD BC d d mm ==B 铰链的受力图如题2.10图(c)所示,由平衡条件0xF=∑, 2cos60NBC NAB F F =解得 23.1NAB F kN = 根据强度条件 []24NAB NAB AB AB AB F FA d σσπ==≤ 可确定AB 杆的直径为17.2AB d mm ≥==2.11 如题 2.11图(a)所示,卧式拉床的油缸内径D =186mm ,活塞杆直径165d mm =,材料为20Cr 并经过热处理, []130MPa σ杆=。
缸盖由6个M20的螺栓与缸体连接,M20螺栓的内径d =17.3mm ,材料为35钢,经热处理后[]110MPa σ螺=。
试按塞杆和螺栓强度确定最大油压p 。
解:(1)按活塞杆的强度要求确定最大油压p 。
活塞杆的受力如题2.11图(b)所示,由平衡条件可得活塞杆的轴力为()221N F p D d π-杆=4根据活塞杆的强度条件()[]222144N F p D d d A ππσσ⎡⎤⎫-≤ ⎪⎢⎥⎣⎦⎝⎭杆杆杆杆== 解上式得最大油压力为[]26212222130100.06518.10.1860.065d p Pa MPa D d σ⨯⨯≤==--杆(2)按螺栓的强度要求确定最大油压p 。
设缸盖所受的压力由6个螺栓平均分担,每个螺栓所承受的轴力为()22164N F p D d π⎡⎤-⎢⎥⎣⎦螺=根据螺栓的强度条件()[]2221644N F p D d d A ππσσ⎛⎫==-⨯≤ ⎪⎝⎭螺螺螺螺解上式得最大油压为[]2622222166110100.0173 6.50.1860.065d p Pa MPa D d σ⨯⨯⨯≤==--螺 比较由以上两种强度条件所确定的许用油压值,可知最大油压力为6.5p MPa =2.15 题2.15图所示的拉杆沿斜截面m-m 由两部分胶合而成。
设在胶合面上许用拉应力[]100MPa σ=,许用切应力[]50MPa τ=。
设由胶合面的强度控制杆件的拉力。
试问:为使杆件承受最大拉应力F ,α角的值应为多少?若杆件横截面面积为24A cm =,并规定60α≤︒,试确定许可载荷F 。
解:拉杆的任一斜截面上的应力为2cos a F A σα=, sin cos a FAταα=既然由胶合面的强度来控制杆件的拉力大小,那么最合适的状态是胶合面上的正应力和切应力同时达到各自的许用应力,这时杆件承受的拉力F 最大。
因此有[]2cos a FA σασ== ①[]sin cos a FA ταατ== ②比较①、②式得 [][]50tan 0.5100τασ=== 由上式得26.6α=︒,所以26.6α=︒时,杆件承受的拉力最大[]46max224101001050cos cos 26.6A F N kN σα-⨯⨯⨯===︒ 2.20 设题2.20图(a)中CG 杆为刚体(即CG 杆的弯曲变形可以忽略),BC 杆为铜杆,DG 杆为钢杆,两杆的横截面面积分别为1A 和2A ,弹性模量分别为1E 和2E 。
如要求CG杆始终保持水平位置,试求x 。
解: CG 杆的受力图如题2.20图(b)所示,其平衡条件为0cM =∑, 2N Fx F l = ①0yF=∑, 12N N F F F += ②由拉压胡克定律得二杆的轴向变形11111N F l l E A ∆=, 22222N F ll E A ∆= 欲使CG 杆始终保持水平状态,必须12l l ∆=∆,即11221122N N F l F l E A E A =③ 联立①、②、③式,解得 122211122ll E A x l E A l E A =+2.26 木桩打入粘土的部分长为L ,顶上荷载为F (题2.26图(a))。
设载荷全由摩擦力承担,且沿木桩单位长度内的摩擦力f 按抛物线2f Ky =变化,这里K 为常数。
若2420,12,640,10F kN L m A cm E MPa ====,试确定常数K ,并求木桩的缩短量。
解:木桩受力如题2.26图(b)所示,根据平衡条件0y F =∑, 0Lfdy F =⎰将2f Ky =代入上式,得 20Lf Ky dy F ==⎰由上式可确定K 值33333334201072912F K N m N m L⨯⨯=== 距下端面为y 处的轴力为(题2.26图(b))()32003yyN Ky F y fdy Ky dy ===⎰⎰杆的总变形为()34494072912 1.9731212101064010LL N F y Ky dy KL l dy m mm EA EA EA -⨯∆=====⨯⨯⨯⨯⎰⎰木桩缩短了1.97mm 。
2.30 钢制受拉杆件如题2.30图(a)所示,横截面面积2200A mm =,5l m =,单位体积的质量为337.810/kg m ρ=⨯。
如不计自身影响,试计算杆件的应变能V ε和应变能密度v ε。
如考虑自重影响,试计算杆件的应变能,并求应变能密度的最大值。
设200E GPa =。
解:应变能和应变能密度的计算公式分别为22N LF dxV EAε=⎰, dV v dV εε=当不考虑自重时,轴力为常数,如题2.30图(b)所示,N F F =,所以()23229632105642222001020010NF l F lV J J EA EA ε-⨯⨯====⨯⨯⨯⨯ 因 22N F dxdV EAε=, dV Adx = 所以()()23234322963210 6.410222*********NdV F v J m J m dV EA εε-⨯====⨯⨯⨯⨯⨯ 当考虑自重时(题2.30图(c))()22222322032222l N LAx g F dx F dx A g l F l A gl FV EA EA EA EAερρρ++===+⎰⎰()()()()222633629696200107.8109.815332000520010765005320002200102001022001020010J ----⎡⎤⨯⨯⨯⨯+⨯⨯⨯⨯⨯⎢⎥=+⎢⎥⨯⨯⨯⨯⨯⨯⨯⨯⎣⎦64.2J =()222A gx F dV v dV EAεερ+== 当x l =时,比能取最大值()()2633333max 296200107.8109.815321064.31022001020010v J m J m ε--⨯⨯⨯⨯⨯+⨯==⨯⨯⨯⨯⨯2.39 如题2.39图(a)所示,水柱短柱的四角用四个40404mm mm mm ⨯⨯的等边角钢加固。
已知角钢的许用应力[]160MPa σ=钢,=200GPa E 钢。
木材许用应力[]12MPa σ=木, =10GPa E 木,试求许可载荷F 。
解:查附录三型钢表得2=308.6mm A 钢,受力图如题2.39图(b)所示。
这是一个超静定问题,先用平衡条件确定木柱及角钢的轴力,再用强度条件确定许可载荷。
平衡条件为0yF=∑, N N F F F +=钢木 ①方程①不能解出两个未知力,须利用木柱与角钢的变形协调条件l l ∆∆钢木= ②再应用胡克定律,将未知力N N 钢木、与变形联系起来,即l N F lE A ∆钢钢钢钢=, N F l l E A ∆=木木木木③ 将③式代入②式,得补充方程96921200104308.61010100.25N N F F -⨯⨯⨯⨯⨯⨯⨯木钢= ④ 联立①、④二式,解得0.283N F F 钢=, 0.717N F F 木=由角钢的强度条件60.2831604308.610N F FMPa A σ-==≤⨯⨯钢钢钢 得 []1698F kN ≤ 由木柱的强度条件 20.717120.25N F FMPa A σ≤木木木==得 []21046F kN ≤故许可载荷为 698F kN =2.44 如题2.44图(a)所示,钢杆AB 悬挂于1、2两杆上,杆1的横截面面积为260mm ,杆2的为2120mm ,且两杆材料相同。
