组合数学(西安电子科技大学(第二版))第二章母函数_版24样版
组合数学(2)

S1<S2<…<S100,且 S100 = (a1 + … +a10) + (a11 + … +a20)+… + (a91 + … +a100)
根据假定有 S100≤10×16 = 160
作序列S1 , S2 , … , S100 , S1 +39, … , S100+39 . 共200项.其中最大项 S100+39≤160+39=199 由鸽巢原理,必有两项相等.而且必是前段中 某项与后段中某项相等.设 Sk = Sh + 39,
1j 1 j n
2j
amj ( ai j )
1 j n 1i m 1 j n
4. 给定数42的所有因子之和: 因为 42 =2×21=2×3×7=6×7=1×42=….
所以42的所有因子为:1,2,3,6,7,14,21,42
5
1+2+3+6+7+14+21+42=
至少有一个盒子里放的物件数不少于2个。
29
推论3若q1, q2, …, qn是n个正整数,而且 qi / n r 1
i 1
n
则qi(i=1, 2, …, n)中至少有一个不小于r。
推论 2 、 3 是说明平均放置物品的情况,在下
面的例题中我们会多次使用。
22
0m+a, 1m+a, 2m+a, ….., (n-1)m+a;
这些整数中每个除以m都余a。假设其中的 两个除以n有相同的余数r。令这两个数表示形 式为im+a和jm+a,其中0≤i<j≤n-1。因此,存 在两个整数qi和qj,使得:
攻略高中数学联赛赛程、时间安排、25本数竞书单

攻略⾼中数学联赛赛程、时间安排、25本数竞书单挤进清北等优质名校是众多⾼中⽣的梦想,有梦想是好的,但现实很残酷,这些⾼校招⽣名额有限!尤其在招⽣⽅式改⾰后,⾼考裸分被录取的可能性更⼩。
因此,通过学科竞赛拿奖牌获得降分优惠或直接被保送,成为许多考⽣的必然选择。
但你知道,学科竞赛应该如何备考才能拿到⾼含⾦量的奖牌吗?学科竞赛⽹(jingsai985)根据多年经验,总结出⼀份⾼含⾦量的数学竞赛备考秘籍。
我们从不轻易告诉外⼈,但今天很⾼兴与你分享,因为我们是⾃家⼈!(⼀)先看赛程数学预选赛(初赛)在各地市学校举⾏,评选出的奖项分为市⼀、市⼆、市三,考核优秀的学⽣晋级参加数学联赛。
数学联赛(⼀试、⼆试)全省在指定的⼀个或⼏个地⽅进⾏选拔考试,评选出的奖项分为省⼀(含省队)、省⼆、省三,考核优秀的学⽣晋级参加全国数学决赛,即冬令营(CMO)。
冬令营全国统⼀指定⼀个地⽅进⾏选拔考核,评选出的奖项分为国⼀(含集训队)、国⼆、国三,考核优秀的学⽣晋级参加国家集训队。
最终选出6名优秀选⼿代表中国参加IMO。
IMO全世界在指定的⼀个地⽅进⾏选拔考核,评选出国际⾦牌,国际银牌,国际铜牌。
(⼆)重点看时间安排和阶段备考内容⾼中学业较之前本来就繁重,还要挤出时间备战数竞,因此,进⾏科学规划显得尤为重要。
从初赛到国决⼤略可分为以下五个阶段:1、第⼀阶段:初三暑假到⾼⼀上学期⼤部分学⽣的竞赛之路是从初三毕业那个暑假开始的,虽然某些省份呈低龄化趋势,但并⾮主流。
这个阶段多数竞赛⽣学习必备知识,由于预选赛(初赛)和⼀试的内容均是⾼中知识,且初赛难度较⼩,所以,⽆需单独备考初赛,准备⼀试即可。
此阶段,你需要配合⽼师的课堂教学,以最短时间尽可能⾃学完成⾼考要求掌握的数学知识,同时要注意做题训练。
可以从数学53(五年⾼考三年模拟)【⽂末附详细书单】开始练习,若做起来⽐较顺⼿,就跳过直接刷浙⼤版《⾼中数学竞赛培优教程:⼀试》(第四版),偶尔选53重要题型练⼿感;若做起来有难度,还是要坚持先把53弄懂吃透,奠定⾼考基础。
工学硕士研究生课程教学大纲

工学硕士研究生课程教学大纲1、课程编号:063301 课程中文名称:组合数学32学时/ 2学分英文译名:Combinatorics适用领域:计算机应用技术、计算机软件理论、计算机系统结构及通信、交通运输、实验设计、排程等方面任课教师:钱真、沈晶教学目的:组合数学是现代数学中发展最快的数学分支。
组合数学的研究对象是排列、模式、设计、调度和布局等。
高速计算机使得各领域中实际组合问题的求解成为可能,而计算机科学的发展本身有带来了大量具有挑战性的组合问题。
本课程的教学目的是:1.使学生掌握计数的基本原理和方法。
2.使学生了解组合设计的基础知识。
3.使学生了解一些优化问题和模型。
4.培养学生的组合思维方法和组合技巧。
教学方式及学时分配:1.教学方式为课堂授课。
2.学时分配:第一章排列与组合,8学时第二章母函数与递推关系,8学时第三章容错原理和鸽巢原理,8学时第四章Polya定理,4学时第五章组合设计,2学时第六章线性规划,2学时教学主要内容及对学生的要求:1.教学主要内容:介绍组合数学的基本工具;围绕组合数学的基本问题,重点介绍组合计数问题、简介组合数学求解中的存在问题和组合优化问题。
2.要求:学生学习本课程应具备的先修知识是高等数学(I)、(II)、离散数学。
内容摘要:在第一章中主要介绍组合数学的基本工具,包括加法规则、乘法规则、一一对应规则;线排列和圆排列、不可重组合与可重组合、二项式及多项式定理、排列和组合的生成算法;在第二章至第四章中重点介绍组合计数问题,包括递推关系及其求解;用母函数求解递推关系,母函数在排列组合中的应用;物件性质的组合,特定、全非、恰K性质型容斥原理;鸽巢原理,Ramsey原理;Burnside引理,polya定理,母函数型的Polya定理;在第五章中简介存在问题,包括拉丁方设计,均衡不完全的区组设计,Hadamard矩阵;第六章简介组合优化问题,包括搜索与优化,动态规划法,分支定界法,背包问题、调度问题、最大流量问题的求解,匹配问题。
《组合数学》教案 2章(母函数)《组合数学》教案 2章(母函数)
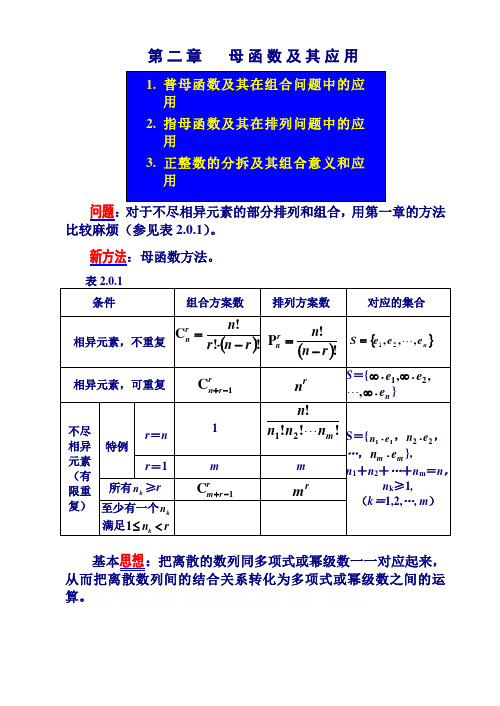
第二章母函数及其应用问题:对于不尽相异元素的部分排列和组合,用第一章的方法比较麻烦(参见表2.0.1)。
新方法:母函数方法。
基本思想:把离散的数列同多项式或幂级数一一对应起来,从而把离散数列间的结合关系转化为多项式或幂级数之间的运算。
2.1 母函数(一) 母函数 (1)定义【定义2.1.1】对于数列{}n a ,称无穷级数()∑∞=≡n n n x a x G 为该数列的(普通型)母函数,简称普母函数或母函数。
(2)例【例2.1.1】有限数列rn C (r =0, 1, 2, …, n )的普母函数是:()x G =nn n n n n x C x C x C C ++++ 2210=()nx +1【例2.1.2】无限数列{1, 1. …, 1, …}的普母函数是()x G = +++++n x x x 21=x-11(3)说明● n a 可以为有限个或无限个。
● 数列{}n a 与母函数一一对应。
{0, 1, 1, …, 1, …}↔ +++++nx x x 20=xx-1● 将母函数视为形式函数,目的是利用其有关运算性质完成计数问题,故不考虑“收敛问题”,而且始终认为它是可“逐项微分”和“逐项积分”的。
(4)常用母函数(二) 组合问题 (1)组合的母函数【定理2.1.1】组合的母函数:设{}m m e n e n e n S ⋅⋅⋅=,,,2211 ,且n 1+n 2+…+n m =n ,则S 的r 可重组合的母函数为()x G =∏∑==⎪⎪⎭⎫ ⎝⎛mi n j j i x 10=∑=n r rr x a 0其中,r 可重组合数为rx 之系数r a ,r =0, 1, 2, …, n 。
理论依据:多项式的任何一项与组合结果一一对应。
优点:● 将无重组合与重复组合统一起来处理; ● 使处理可重组合的枚举问题变得非常简单。
(2)特例【推论1】{}n e e e S ,,,21 =,则r 无重组合的母函数为G (x )= (1+x )n组合数为r x 之系数rn C 。
组合数学第二章二章六节

应用举例:斐波那契数列求解
• 斐波那契数列定义:$F_0 = 0, F_1 = 1, Fn = F{n-1} + F_{n-2} (n \geq 2)$
应用举例:斐波那契数列求解
生成函数求解
设斐波那契数列的生成函数为$F(x) = sum_{n=0}^{infty} F_n x^n$
根据递推关系和初始条件,得到$F(x) = x + x^2 + 2x^3 + 3x^4 + 5x^5 + cdots$
05
生成函数与递推关系
生成函数定义及性质
乘积性质
两个生成函数的乘积对应于序列 的卷积。
线性性质
生成函数的线性组合对应于序列 的线性组合。
微分性质
生成函数的微分对应于序列的差 分。
定义
生成函数是一种将离散数学中的 序列通过幂级数形式表示出来的 函数,常用于组合数学中的计数
问题。
积分性质
生成函数的积分对应于序列的部 分和。
04
容斥原理与错排问题
容斥原理表述与证明
容斥原理的表述
对于两个集合A和B,它们的并集元素个数等于各自元素个数之和减去它们的交 集元素个数,即∣A∪B∣=∣A∣+∣B∣−∣A∩B∣。
容斥原理的证明
通过分类讨论和数学归纳法可以证明容斥原理的正确性。
应用举例:错排问题求解
错排问题的定义
在n个元素的全排列中,不是其自然排列(即每个元 素都不在其原来的位置上)的排列称为错排。
递推关系建立与求解方法
02
01
03
建立递推关系 通过组合问题的具体背景,分析问题的递推结构。 利用已知的初始条件和边界条件,建 Nhomakorabea递推关系式。
组合数学第二章课后习题答案

2.1题(陈兴)求序列{ 0,1,8,27,3n }的母函数。
解:由序列可得到32333()23n G x x x x n x =+++++因为23111n x x x x x =++++++- 2311()'12341n x x x nx x-=++++++-设 2311()()'23(1)1n np x x x x x n x nx x-==++++-+-2222221[()]'123(1)n n p x x x x n x n x --=+++++-+设 2223212()[()]'23(1)n nq x x p x x x x n x n x -==++++-+3323231[()]'123(1)n n q x x x n x n x --=++++-+ 3233313[()]'23(1)n n x q x x x x n x n x -=+++-+ 由以上推理可知[()]'x q x =,[7*94*(6)],n n +-所以可通过求得[()]'x q x 得到序列的母函数:32()4G x x x x =++2321()()[34(3)]6n H x F x dx x x n x +==++++⎰2.2题(陈兴)已知序列343,,,,333n ⎧+⎛⎫⎛⎫⎛⎫⎫⎨⎬ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎭⎩,求母函数 解: 3*2*14*3*2(3)*(2)*(1)()3*2*13*2*13*2*1nn n n G x x +++=+++=1[3.2.1 4.3.2(3)(2)(1)]6n x n n n x ++++++211()()[3.2 4.3(3)(2)]6n F x G x dx x x n n x +==+++++⎰ 2321()()[34(3)]6n H x F x dx x x n x +==++++⎰3431()()[]6n I x H x dx x X x ++==++⎰因为23111n x x x x+=+++++-所以211()(1)61I x x x x=----所以31()[]'''61x G x x=-就是所求序列的母函数。
组合数学(西安电子科技大学(第二版))习题3

习题三(递推关系)1.解下列递推关系:(1)120171000,1n n n a a a a a ---+=⎧⎨==⎩ (2)12016900,1n n n a a a a a --++=⎧⎨==⎩ (3)20100,2n n a a a a -+=⎧⎨==⎩ (4)120121n n n a a a a a --=-⎧⎨==⎩ (5)123012990,1,2n n n n a a a a a a a ---=+-⎧⎨===⎩ 解:(1)对应的特征方程为:27100x x -+=,解得122,5x x ==。
所以齐次递推方程的通解为:25n n n a A B =+,代入初始条件,得:00a A B =+=,1251a A B =+=,解得:11,33A B =-=, 故 112533n n n a =-+。
(2)对应的特征方程为:2690x x ++=,解得:123x x ==-,所以,齐次递推方程的通解为:()(3)n n a A Bn =+-,代入初始条件,00a A ==,1()(3)1a A B =+-=,解得:10,3A B ==-,故1(3)3n n a n =--。
(3)对应的特征方程为:210x +=,解得:12,x i x i ==-,所以,齐次递推方程的通解为:()()n n n a A i B i =+-,代入初始条件,00a A B =+=,12a A i B i =-=,解得:,A i B i =-=,故 11()()n n n a i i --=+-。
(4)对应的特征方程为:2210x x -+=,解得:121x x ==,所以,齐次递推方程的通解为:n a A Bn =+,代入初始条件,01a A ==,11a A B =+=,解得:1,0A B ==,故 1n a =。
(5)对应的特征方程为:32990x x x --+=,解得:1231,3,3x x x ===-,所以,齐次递推方程的通解为:3(3)n n n a A B C =++-,代入初始条件,00a A B C =++=,1331a A B C =+-=,2992a A B C =++=, 解得,111,,4312A B C =-==-,故 1113(3)412n n n a -=-+--2.求由A ,B ,C ,D 组成的允许重复的排列中AB 至少出现一次的排列数。
组合数学_绪论

(1,1)( 2,2)(3,3) 1 2 3 1 2 3 (3,2)(1,3)( 2,1) 3 1 2 2 3 1 2 3 1 3 1 2 ( 2 , 3 )( 3 , 1 )( 1 , 2 )
m
x a b
j 1 i 1 j 1
绪 论 组态的存在性、分类计数及构造,一般都不是互相独立 的, 它们常集中在同一组合问题中。一般而言,若一组合问题 的存在性需要大量研究时,则其计数问题的难度将难以想象。 但若一组合问题已有一特定的解,则还是有机会计算其解的个 数或对其进行分类。
1 n ( n 1) / 2
C
n ( n 1) / 2 n ( n 1) / 2
2
n ( n 1) / 2
2 2
n
n ( n 1) / 2
对 n=5 , 5 元集上自反关系的数目为 25×(5-1)=220=10242 ; 5 元 集上对称关系的数目为25×(5+1)/2=215=32×1024。
绪 论 组合数学研究的核心问题是“把有限个离散对象按一定规则 或模式进行安排”,这种安排被考究地称为组态 (Configuration)。关于幻方的几个问题也正是组合数学要解决 的问题, 即组态的存在性问题、 组态的计数问题和组态的构造 问题。 此外, 还涉及组态的优化问题。
绪 论 1. 组态的存在性 组合数学中解决组态存在性的方法很巧妙,其构思过程往 往出人意料, 让人拍案叫绝。其中,著名的例子就是众所周知 的哥尼斯堡七桥问题。 1736年,年轻的大数学家Euler将人们在 娱乐中提出的一个数学难题抽象为点线构成的图及寻找走边的 一笔画问题, 并给出了精巧的解答, 即七桥问题无解。 由此 引出了一门新型数学学科——图论。Euler也被后人誉为图论之父。
