常州外国语学校2007—2008学年第一学期高二年级阶段质量调研
2023-2024学年江苏省常州高级中学高二上学期期中质量检查物理试题

2023-2024学年江苏省常州高级中学高二上学期期中质量检查物理试题1.某同学在实验室利用发波水槽演示了波的衍射现象,调整缝的宽度为PQ=5cm,M、N为挡板后放置的两个浮球,实验时发现两浮球始终静止不动,则下列说法正确的是()A.适当增大振源的振幅,两球一定能上下浮动B.适当增大振源的频率,两浮球一定能上下浮动C.将缝的宽度适当调小,则两浮球可能上下浮动D.无论如何调节振源的频率,两浮球始终静止2.如图所示,以频率f上下振动的振针沿水平方向移动,移动过程中在水面上形成了如图所示的水波图形,下列说法正确的是()A.振针在向左移动B.如果A处的观察者保持静止,接收到的水波频率大于fC.如果A处的观察者水平向左移动,接收到的水波频率可能大于fD.如果A处的观察者水平向右移动,接收到的水波频率可能小于f3.在做“验证动量守恒定律”实验时,入射球a的质量为m1,被碰球b的质量为m2,两小球的半径均为r,各小球的落地点如图所示,下列关于这个实验的说法正确的是()A.斜面要选择尽可能光滑的材料B.入射球与被碰球最好采用大小相同、质量相等的小球C.要用秒表记录小球在空中运动的时间D.多次重复实验,落点可以不同4.如图所示,甲、乙两同学用插针法测量梯形玻璃砖的折射率,P1、P2、P3和P4是实验中甲同学插的大头针,P1'、P2'是乙同学插的大头针。
下列说法正确的是()A.甲同学利用大头针P1、P2及P3、P4作图,测出入射角和折射角,用角度比值即可求出折射率B.甲同学插好大头针P1、P2并画好两平行边界后,不小心将玻璃砖向上平推了一下,则实验测得的折射率不变C.沿P1、P2方向的入射光线,经AB面折射到达CD面时,在CD面可能发生全反射D.乙同学在界面BD观察到大头针P1 '、P2 '的像,不可以测量玻璃砖的折射率5.在短道速滑比赛中,“接棒”的运动员甲提前站在“交棒”的运动员乙前面,并且开始向前滑行,待乙追上甲时,乙猛推甲一把,使甲获得更大的速度向前冲出。
2008~2009学年第一学期

2008~2009学年第一学期学校工作计划海门市三厂中学2008年8月24日一、指导思想以坚持科学发展和构建和谐校园统领全局,以提高质量和创新管理为学校发展的两大主题,按照“勤业、精艺、认真、缜密”的工作要求,围绕“抓实教学、放大德育、投资教师、聚焦课堂、规范后勤”的总体思路,通过教学常规检查、德育主题活动、后勤岗位考核等措施,在执行力、思想力和沟通力上下功夫,不断加强质量管理和行政管理,努力提高教师专业水平、班主任班级管理水平和后勤服务水平,促使学生行为习惯和学习习惯逐渐改善,努力确保实现“综合考评第五”的目标。
二、工作目标1.高三年级要确保在全市综合考评中前五位,高二年级、高一年级整体实力要确保全市第五。
2.创造条件,搭建平台,促使班主任队伍和青年教师队伍建设再上一个台阶。
要加强校本培训,每月集中培训至少一次,并结合教学实际积极开展教学研究和教学反思。
在教师各类竞赛和09高考中,获奖人数、受表彰的备课组、受表彰的班级要确保有所增加。
要壮大校内骨干教师群体队伍,并能充分发挥示范作用。
3.积极探索符合学科特点的一体化讲义和有效课堂教学模式,不断提高课堂教学质量。
4.积极开展南通市级课题研究,确保100%的教师参与科研。
5.挖掘德育资源,整合德育力量,充分引爆学生潜能,提高内驱力,增强学生学习动力。
6.全面加强综治安全管理,确保师德合格率100%,师生违法犯罪率0%,学校无重大安全责任事故发生。
7.后勤工作进一步规范,做到定人,定岗,定责任,过程有考核,有督查。
8.确保年度预算按计划完成,确保教职工福利稳中有升。
三、重点工作1.研究教学管理。
构建高三年级教学质量管理组和基础年级教学质量管理组,实行班级、学科联系制,质管组的同志要走近教师,走进课堂,走访学生,加强调研,及时了解教师教的效果和学生学的状态,适时反馈存在问题。
进一步发挥年级组职能,加大管理力度,由组内实施决策、执行和检查。
加强教师管理和学生管理,增强团队意识,加重群体考核,着底抓起,关注、关爱学困生、问题生,大力开展帮扶工程,增添学习信心和动力。
常州市20082009学年度第一学期期末质量调研高二历史

常州市2008—2009学年度第一学期期末质量调研高二历史试题命题单位:常州市教育教研室2009年1月说明:考试形式为闭卷考试,考试时间100分钟,满分120分。
题号 1 2 3 4 5 6 7 8 9 10 答案题号11 12 13 14 15 16 17 18 19 20 答案一、选择题:本大题共20小题。
每小题3分。
共计60分。
在每小题列出的四个选项中,只有一项是最符合题目要求的。
1.史书记载,有一次孔子家的马棚失火,孔子退朝回家,看着焦土断垣,急切地问:“伤人了没有”?而对财产却只字未提。
这体现了孔子A.以人为本的思想B.反对苛政的思想C.“人无有不善”的思想D.为政以德的思想2.从战国时期“百家争鸣”到西汉时期“独尊儒术”的转变中,我们能够看到①大一统局面的形成②古代学术思想的自由发展受到扼制③中国传统文化主流思想的确立④中央集权的加强和自然经济的鼎盛A.①②③B.②③④C.①②④D.①③④3.中国封建时代的正统人士、近代资产阶级某些革命家们在监狱苦刑中以宋明理学自恃自乐。
这是因为宋明理学①重视主观意志力量②注重气节、品德③讲求以理统情④批判君主专制A.①②B.①②③C.②③D.①②③④4.明清之际三位进步思想家的思想产生,是多种因素综合作用的结果。
这些因素不包括A.商品经济、资本主义萌芽的发展B.市民工商业者成为不可忽视的力量C.封建专制统治出现危机D.儒家思想受到西方思想冲击,地位动摇5.文艺复兴时期,人文主义者从古典文化中汲取精神力量,铸成了反对神学桎梏的武器。
能反映这个时期最符合人文主义核心内涵的古希腊名言是A.求知是人类的本性B.心灵美比形体美更珍贵C.人的出类拔萃为城邦增加的荣耀可以超过神D.健康和聪明是人生的两大幸福6.《金史》记载:“声如雷震,热力达半亩之上,人与牛皮皆碎进无迹,甲铁皆透。
”这段材料描述的科技成就是A.指南针B.印刷术C.火药D.造纸术7.辛弃疾和陆游相同,总有壮志未酬、英雄无用武之地的感慨。
常州高中高三英语第二次调研试卷及答案

江苏省常州高级中学2008~2009学年高三年级第二次阶段教学质量调研英语试卷2008.10 说明:1. 以下题目的答案全部做在答卷纸上。
2. 本试卷分第Ⅰ卷和第Ⅱ卷两部分.考试时间为120 分钟,满分为120分.第I 卷(选择题共85 分)第一部分:听力(共两节,满分20 分)第一节(共5 小题;每小题1 分,满分5 分)听下面5 段对话。
每段对话后有一个小题,从题中所给的A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What does the man suggest doing ?A.Rearranging some furniture.B. Selling the old table.C. Buying another bookshelf.2.How will the woman travel to New York?A.By car.B. By .trainC.By plane.3.What does the woman mean?A.She will go shopping.B.She will work with the man.C.She cannot go with the man.4.How does the man think the woman plays the guitar?A.Worse than he.B. Better than he.C. As well as he.5.Why is the climate getting warmer?A.Pollution is stopping the sun’s heat leaving the atmosphereB.The ice at the Poles is beginning to melt.C.The sun’s heat is getting stronger.第二节(共15 小题;每小题1 分,满分15 分)听下面5 段对话。
2023-2024学年江苏省常州市高二上学期10月阶段调研数学质量检测模拟试题(含解析)

2023-2024学年江苏省常州市高二上册10月阶段调研数学模拟试题一、单选题1.焦点在x 轴的椭圆2214x y m +=的焦距是4,则m 的值为()A .8B .3C .5或3D .20【正确答案】A【分析】根据焦点的位置可得m 的取值范围,结合焦距可求m 的值.【详解】因为焦点在x 轴,故4m >,而焦距是42=即8m =,故选:A.2.设a ∈R ,则“1a =”是“直线20ax y +=与直线(1)20x a y +++=平行”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【正确答案】A【分析】根据两直线平行列出方程,求出:2a =-或1,验证后均符合要求,从而得到“1a =”是“直线20ax y +=与直线(1)20x a y +++=平行”的充分不必要条件.【详解】当1a =时,20x y +=与220x y ++=的斜率相等,故平行,充分性成立,若“直线20ax y +=与直线(1)20x a y +++=平行”,则满足()120a a +-=,解得:2a =-或1,经验证,:2a =-或1时,两直线不重合,故:2a =-或1,两直线平行,故必要性不成立.故选:A3.过点A (1,2)的直线在两坐标轴上的截距之和为零,则该直线方程为()A .x-y +1=0B .x+y-3=0C .y =2x 或x+y-3=0D .y =2x 或x-y+1=0【正确答案】D【分析】考虑直线是否过坐标原点,设出直线方程,分别求解出直线方程.【详解】当直线过原点时,其斜率为20210-=-,故直线方程为y =2x ;当直线不过原点时,设直线方程为1x y a a+=-,代入点(1,2)可得121a a +=-,解得a =-1,故直线方程为x-y+1=0.综上,可知所求直线方程为y =2x 或x-y+1=0,故选:D.本题主要考查直线方程的截距式以及分类讨论思想的应用,考查逻辑推理和数学运算.在利用直线方程的截距式解题时,一定要注意讨论直线的截距是否为零.4.已知直线20l x y -+=:与圆22:220C x y y m +--=相离,则实数m 的取值范围是()A .(),0∞-B .1,2⎛⎫-+∞ ⎪⎝⎭C .1,4⎛⎫-∞- ⎪⎝⎭D .11,24⎛⎫-- ⎪⎝⎭【正确答案】D【分析】由圆心到直线的距离大于半径即可求解.【详解】由22220x y y m +--=,得()22121x y m +-=+,∵直线20l x y -+=:与圆22:220C x y y m +--=相离,∴210,m +>⎧1124m -<<-.∴实数m 的取值范围是11,24⎛⎫-- ⎪⎝⎭,故选:D .5.我们把离心率为2的椭圆称为“最美椭圆”.已知椭圆C 为“最美椭圆”,焦点在x 轴上,且以椭圆C 上一点P 和椭圆两焦点1F 和2F 为顶点的三角形的面积最大值为4,则椭圆C 的方程为()A .2212x y +=B .22142x y +=C .22163x y +=D .22184x y +=【正确答案】D 【分析】先由2e =得到2c =与2b =,再由12PF F S 的最大值得4bc =,进而求得28a =,24b =,故可得到椭圆C 的方程.【详解】由已知2c e a ==,得2c =,故2b a =,∵121211222PF F P P S F F y c y bc ==⨯≤ ,即()12max 4PF F S bc == ,4=,得28a =,故22142b a ==,所以椭圆C 的方程为22184x y +=.故选:D.6.如图,已知1F ,2F 分别是椭圆的左、右焦点,现以2F 为圆心作一个圆恰好经过椭圆的中心并且交椭圆于点M ,N .若过点1F 的直线1MF 是圆2F 的切线,则椭圆的离心率为()A1-B .2C .2D 【正确答案】A【分析】由切线的性质,可得2MF c =,1MF =,再结合椭圆定义122+=MF MF a ,即得解【详解】因为过点1F 的直线1MF 圆2F 的切线,2MF c =,122F F c =,所以1MF =.由椭圆定义可得122MF MF c a +=+=,可得椭圆的离心率1c e a =-.故选:A7.设m ∈R ,过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(,)P x y ,则PA PB ⋅的最大值是()A .4B .10C .5D【正确答案】C【分析】由题意可知两条动直线经过定点(0,0)A 、()1,3B ,且始终垂直,有PA PB ⊥,利用勾股定理求出||AB ,再利用基本不等式求得答案.【详解】由题意可知,动直线0x my +=经过定点(0,0)A ,动直线30mx y m --+=即(1)30m x y --+=,经过定点()1,3B ,因为110⨯-⨯=m m ,所以动直线0x my +=和动直线30mx y m --+=始终垂直,P 又是两条直线的交点,则有PA PB ⊥,222||||||10PA PB AB ∴+==,故22||||||||52PA PB PA PB +⋅≤=(当且仅当||||PA PB ==时取“=”),故选:C .8.在平面直角坐标系xOy 中,已知圆()22:29C x y -+=,,E F 是直线:2l y x =+上的两点,若对线段EF 上任意一点P ,圆C 上均存在两点,A B ,使得cos 0APB ∠≤,则线段EF 长度的最大值为()A .2BC .D .4【正确答案】C【分析】设圆的切线为PM 、PN ,由cos 0APB ∠≤得90APB ∠≥ ,即90MPN ∠≥ ,再求得PC 的取值范围,求得点P 的坐标,即可求得EF 的最大值.【详解】由题意,圆心到直线:2l y x =+的距离为3d ==<(半径)故直线l 和圆相交;当点P 在圆外时,从直线上的点向圆上的点连线成角,当且仅当两条线均为切线时,APB ∠才是最大的角,不妨设切线为PM ,PN ,则由cos 0APB ∠≤,得90APB ∠≥ ,90MPN ∴∠≥ ;当90MPN ∠= 时,3sin sin 452MPC PC ∠===,PC ∴=设()00,2P x x +,PC ==,解得:0x =设())2,2E F,如图,EF 之间的任何一个点P ,圆C 上均存在两点,A B ,使得90APB ∠≥ ,线段EF 长度的最大值为EF ==故选:C 二、多选题9.下列说法中正确的是A .若两条直线互相平行,那么它们的斜率相等B .方程()()()()211211x x y y y y x x --=--能表示平面内的任何直线C .圆22240x y x y ++-=的圆心为()1,2-5D .若直线()2320t x y t -++=不经过第二象限,则t 的取值范围是30,2⎡⎤⎢⎥⎣⎦【正确答案】BD【分析】由两直线平行于y 轴排除A ;根据直线平行或不平行于坐标轴,可确定方程均可以表示出来,知B 正确;整理得到圆的标准方程,进而确定圆心和半径,排除C ;由直线不过第二象限可构造不等式组求得结果,知D 正确.【详解】对于A ,若两条直线均平行于y 轴,则两条直线斜率都不存在,A 错误;对于B ,若直线不平行于坐标轴,则原方程可化为112121y y x x y y x x --=--,为直线两点式方程;当直线平行于x 轴,则原方程可化为1y y =;当直线平行于y 轴,则原方程可化为1x x =;综上所述:方程()()()()211211x x y y y y x x --=--能表示平面内的任何直线,B 正确;对于C ,圆的方程可整理为()()22125x y ++-=,则圆心为()1,2-,C 错误;对于D ,若直线不经过第二象限,则23022t t -⎧-≥⎪⎪⎨⎪-≤⎪⎩,解得:302t ≤≤,D 正确.故选.BD本题考查直线和圆部分相关命题的辨析,涉及到直线方程的应用、根据直线所过象限求解参数范围、由圆的方程确定圆心和半径等知识,属于基础知识的综合考查.10.已知222212:220,:2410O x y mx y O x y x my +-+=+--+= .则下列说法中,正确的有()A .若(1,1)-在1O 内,则0m B .当1m =时,1O 与2O 共有两条公切线C .若1O 与2O 存在公共弦,则公共弦所在直线过定点11,36⎛⎫ ⎪⎝⎭D .m ∃∈R ,使得1O 与2O 公共弦的斜率为12【正确答案】BC【分析】根据点与圆的位置关系判断方法判断A ,通过判断圆与圆的位置关系确定1O 与2O 的公切线的条数,通过将两圆方程相减确定两圆的公共弦的方程,判断C ,D.【详解】因为222212:220,:2410O x y mx y O x y x my +-+=+--+= ,所以1O :222()(1)1x m y m -++=+,2O :222(1)(2)4x y m m -+-=,则1(1)O m -,,1r =2(12)O m ,,22||r m =,则0m ≠,由(11)-,在1O 内,可得221(1)220m +---<,即0m >,A 错误;当1m =时,1(11)O -,,1r 2(12)O ,,22r =,所以12||3O O =∈(22,所以两圆相交,共两条公切线,B 正确;12O O - ,得(22)(24)10m x m y -+++-=,即(24)(221)0m x y x y -+++-=,令2402210x y x y -+=⎧⎨+-=⎩,,解得1316x y ⎧=⎪⎪⎨⎪=⎪⎩,,所以定点为1136⎛⎫ ⎪⎝⎭,,C 正确;公共弦所在直线的斜率为2224m m -+,令221242m m -=+,无解,所以D 错误,故选:BC .11.已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ,长轴长为4,点P 在椭圆C 外,点Q 在椭圆C 上,则()A .椭圆C的离心率的取值范围是⎛ ⎝⎭B .当椭圆C的离心率为2时,1QF的取值范围是[2-+C .存在点Q 使得120QF QF ⋅=D .1211QF QF +的最小值为1【正确答案】BCD【分析】根据点)P在椭圆C 外,即可求出b 的取值范围,即可求出离心率的取值范围,从而判断A ,根据离心率求出c ,则[]1,QF a c a c ∈-+,即可判断B ,设上顶点A ,得到120AF AF <,即可判断C ,利用基本不等式判断D.【详解】解:由题意得2a =,又点)P在椭圆C 外,则22114b+>,解得b <所以椭圆C的离心率2c e a ==>,即椭圆C的离心率的取值范围是,12⎫⎪⎪⎝⎭,故A 不正确;当2e =时,c =1b ==,所以1QF 的取值范围是[],a c a c -+,即22⎡⎣,故B 正确;设椭圆的上顶点为()0,A b ,()1,0F c -,()2,0F c ,由于222212·20AF AF b c b a =-=-<,所以存在点Q 使得120QF QF ⋅= ,故C 正确;()21121212112224QF QF QF QF QF QF QF QF ⎛⎫++=++≥+= ⎪ ⎪⎝⎭,当且仅当122QF QF ==时,等号成立,又124QF QF +=,所以12111QF QF +≥,故D 正确.故选:BCD12.法国数学家加斯帕·蒙日被称为“画法几何创始人”、“微分几何之父”.他发现与椭圆相切的两条互相垂直的切线的交点的轨迹是以该椭圆中心为圆心的圆,这个圆称为该椭圆的蒙日圆.若椭圆()2222:10x y a b a bΓ+=>>的蒙日圆为2223:2C x y a +=,过C 上的动点M 作Γ的两条切线,分别与C 交于P ,Q 两点,直线PQ 交Γ于A ,B 两点,则()A .椭圆Γ的离心率为2B .MPQ 面积的最大值为232aC .M 到Γ的左焦点的距离的最小值为(2aD .若动点D 在Γ上,将直线DA ,DB 的斜率分别记为1k ,2k ,则1212k k =-【正确答案】ABD【分析】由条件可得222a b =,由此可求椭圆Γ的离心率,由此判断A ,由条件可得PQ 为圆C 的直径,确定MPQ 面积的表达式求其最值,由此判断B ,由条件确定2MF 的表达式求其范围,由此判断C ,结合点差法判断D.【详解】依题意,过椭圆Γ的上顶点作y 轴的垂线,过椭圆Γ的右顶点作x 轴的垂线,则这两条垂线的交点在圆C 上,所以22232a b a +=,得222a b =,所以椭圆Γ的离心率2c e a ==,故A 正确;因为点M ,P ,Q 都在圆C 上,且90PMQ ∠=︒,所以PQ 为圆C 的直径,所以2PQ =,所以MPQ面积的最大值为21322PQ a ==,故B 正确;设00(,)M x y ,Γ的左焦点为(),0F c -,连接MF ,因为222212c a b a =-=,所以()222222222000000031222222MF x c y x y x c c a x a a a =++=+++=+⨯+=,又0x ≤≤,所以(222MF a ≥-,则M 到Γ的左焦点的距离的最小值为2a ,故C 不正确;由直线PQ 经过坐标原点,易得点A ,B 关于原点对称,设()11,A x y ,()22,D x y ,则()11,B x y --,12112y y k x x -=-,12212y y k x x +=+,又2211222222221212x y b b x y b b ⎧+=⎪⎪⎨⎪+=⎪⎩,所以222212122202x x y y b b --+=,所以221212122212121212y y y y y y x x x x x x --+=⋅=---+,所以1212k k =-,故D 正确故选:ABD .椭圆的蒙日圆及其几何性质过椭圆()222210x y a b a b+=>>上任意不同两点M ,N 作椭圆的切线,若两切线垂直且相交于P ,则动点P 的轨迹为圆2222:O x y a b +=+,此圆即椭圆的蒙日圆.椭圆的蒙日圆有如下性质:性质1:PM PN ⊥.性质2:PO 平分切点弦MN .性质3:MON S 的最大值为2ab ,MON S 的最小值为2222a ba b +.三、填空题13.已知点(1,3)A 关于直线l 的对称点为(5,1)B -,则直线l 的方程为______________________________【正确答案】340x y ++=【分析】求出线段AB 的中垂线方程即可.【详解】131513AB k -==--,其中垂线的斜率为3-,又AB 中点为(2,2)-,∴直线方程为23(2)y x -=-+,即340x y ++=.故340x y ++=.本题考查点的对称性,考查求两点的对称轴方程.掌握对称的性质即可求解.14.已知()P ,a b 为圆C :222440x y x y +--+=上任意一点,则-12b a +的取值范围为________【正确答案】304⎡⎤⎢⎥⎣⎦,【分析】求12b a -+的取值范围表示圆上的点()P a b ,与点()21Q -,连线的斜率的取值范围,画出图形,可知当直线与圆相切时斜率取到最值,利用点到直线的距离公式计算即可.【详解】由题意,12b a -+表示圆C 上的点()P a b ,与圆外的点()21Q -,连线的斜率.把圆22:2440C x y x y +--+=化为标准式()()22121x y -+-=,圆心()12C ,,半径1r =.设过点()21Q -,的直线方程为()12y k x -=+,即210kx y k -++=.当直线210kx y k -++=与圆C 相切时,斜率k 取得最值.由222111k k k -++=+,解得0k =或34k =.所以12b a -+的取值范围为3[0]4,.故答案为.3[0]4,15.如图,设椭圆221167x y +=的左右焦点分别为12F F 、,过焦点1F 的直线交椭圆于A B 、两点,若2ABF ∆的内切圆的面积为π,设A B 、两点的坐标分别为1122(,)(,)A x y B x y 、,则12||y y -值为_____【正确答案】83【分析】由已知2ABF ∆的内切圆的面积为π得出半径1r =,从而求出2ABF ∆的面积,再由2ABF ∆面积12122y y c =-⨯,即可求出12||y y -.【详解】因为2ABF ∆的内切圆的面积为π,所以2ABF ∆的内切圆半径1r =,2ABF ∆面积()2211282S AB AF BF a =⨯⨯++==所以2ABF ∆面积121211223822y y c y y =-⨯=-⨯⨯=,所以128||3y y -=故答案为83本题主要考查了椭圆的定义,三角形内切圆的性质,三角形的面积公式,属于中档题.16.把椭圆2212516x y +=的长轴AB 分成2018等份,过每个等分点作x 轴的垂线交椭圆的上半部分于2017个点,F 是椭圆的一个焦点,则这2017个点到F 的距离之和为______.【正确答案】10085【分析】若设过2017等分点作x 轴的垂线交椭圆的上半部分于2017个点分别为12320162017,,,,,P P P P P ⋅⋅⋅,由椭圆的定义与椭圆的对称性,得到1201722016100810102PF P F P F P F P F P F a +=+=⋅⋅⋅=+=,结合1009P F a =和题中的数据,可得答案.【详解】解:由题意可知5a =,若设过2017等分点作x 轴的垂线交椭圆的上半部分于2017个点分别为12320162017,,,,,P P P P P ⋅⋅⋅,F 是椭圆的一个焦点,设椭圆的另一个焦点为'F ,则根据椭圆的对称性,得'12017112PF P F PF PF a +=+=,同理'22016222P F P F P F P F a +=+=,……,'10081010100810082P F P F P F P F a +=+=,又因为1009P F a ==,所以12320162017210082017=20175=10085PF P F P F P F P F a a a +++⋅⋅⋅++=⨯+=⨯故10085此题考查了椭圆的标准方程、椭圆的定义与简单几何性质等知识,属于中档题.四、解答题17.已知圆C 的圆心在x 轴上,且经过点1,0,()(,2)1A B -.(1)求圆C 的标准方程;(2)过点(0,2)P 的直线l 与圆C 相交于,M N 两点,且||MN =l 的方程.【正确答案】(1)22(1)4x y -+=(2)0x =或3480x y +-=【分析】(1)根据题意,设AB 的中点为D ,求出D 的坐标,求出直线CD 的斜率,由直线的点斜式方程分析可得答案,设圆C 的标准方程为222()x a y r -+=,由圆心的位置分析可得a 的值,进而计算可得r 的值,据此分析可得答案;(2)设F 为MN 的中点,结合直线与圆的位置关系,分直线l 的斜率是否存在两种情况讨论,综合即可得答案.【详解】解:(1)设AB 的中点为D ,则(0,1)D ,由圆的性质得CD AB ⊥,所以1CD AB K K ⨯=-,得1CD K =-,所以线段AB 的垂直平分线方程是1y x =-+,设圆C 的标准方程为222()x a y r -+=,其中(,0)C a ,半径为()0r r >,由圆的性质,圆心(,0)C a 在直线CD 上,化简得1a =,所以圆心()1,0C ,||2r CA ==,所以圆C 的标准方程为22(1)4x y -+=;(2)由(1)设F 为MN 中点,则CF l ⊥,得||||FM FN =圆心C 到直线l 的距离||1d CF ===,当直线l 的斜率不存在时,l 的方程0x =,此时||1CF =,符合题意;当直线l 的斜率存在时,设l 的方程2y kx =+,即20kx y -+=,由题意得d =,解得34k =-;故直线l 的方程为324y x =-+,即3480x y +-=;综上直线l 的方程为0x =或3480x y +-=.本题考查直线与圆的位置关系,涉及直线与圆方程的综合应用,属于基础题.18.已知ABC 的顶点()5,1A ,边AB 上的中线CM 所在直线方程为250x y --=,边AC 上的高BH 所在直线方程为250x y --=,(1)求顶点C 的坐标;(2)求ABC 的面积.【正确答案】(1)()4,3C ;(2)8.【分析】(1)首先设(),C m n ,根据题意得到125250n m m n -⎧=-⎪-⎨⎪--=⎩,再解方程组即可.(2)首先设(),B a b ,得到51,22a b M ++⎛⎫ ⎪⎝⎭,从而得到15502250b a a b +⎧+--=⎪⎨⎪--=⎩,解方程得到()1,3B --,再求出BC 和点A 到直线BC 的距离,即可得到答案.【详解】(1)设(),C m n ,因为直线AC 与直线BH 垂直,且C 点在直线250x y --=上,所以125250n m m n -⎧=-⎪-⎨⎪--=⎩,解得43m n =⎧⎨=⎩,故()4,3C .(2)设(),B a b 由题知:51,22a b M ++⎛⎫ ⎪⎝⎭,所以15502250b a a b +⎧+--=⎪⎨⎪--=⎩,解得13a b =-⎧⎨=-⎩,即()1,3B --.336415BC k +==+,直线()6:345BC y x -=-,即.6590x y --=BC ==点A 到直线BC的距离d所以182ABC S == .本题主要考查直线的方程,同时考查点到直线的距离公式,属于中档题.19.圆1C :222280x y x y +++-=与2C :22210240x y x y +-+-=相交于A 、B 两点.(1)求圆心在直线y =-x 上,且经过A 、B 两点的圆的方程;(2)求经过A 、B 两点且面积最小的圆的方程.【正确答案】(1)226680x y x y ++-+=(2)()()22215x y ++-=【分析】(1)首先设圆系方程()2222210240228x y x y x y x y λ+++-+-+-=+(λ为常数),根据圆心在直线y x =-上,求λ,即可求得圆的方程;(2)面积最小的圆,就是以线段AB 为直径的圆,求出该圆的圆心和半径可得圆的方程.【详解】(1)因为圆2C 的圆心25(1,)C -不在直线y x =-上,所以所求圆不是圆2C ,故可设经过A 、B 两点的圆的方程为()2222210240228x y x y x y x y λ+++-+-+-=+(λ为常数),即22222108240111x y x λλλλλλ-+++++-=+++,则圆心坐标为115,11λλλλ---⎛⎫ ⎪++⎝⎭;又圆心在直线y =-x 上,故115011λλλλ---+=++,解得12λ=-,故所求方程为226680x y x y ++-+=.(2)因为圆1C 的圆心1(1,1)C --,半径1r ,圆2C 的圆心25(1,)C -,半径2r =,所以直线12C C 的方程为115111y x ++=-++,即230x y ++=,由题意可知以线段AB 为直径的圆的面积最小,由两个圆的方程相减可得直线AB 的方程为240x y -+=,联立230240x y x y ++=⎧⎨-+=⎩,解得21x y =-⎧⎨=⎩,则所求圆的圆心为(2,1)-,圆心1(1,1)C --到直线:240AB x y -+=的距离d ==所以||AB ===故面积最小的圆的方程为()()22215x y ++-=.20.如图,已知C 的圆心在原点,且与直线30x y ++=相切.点P 在直线8x =上,过点P 引C的两条切线PA 、PB ,切点为A 、B .(1)求四边形OAPB 面积的最小值;(2)求证:直线AB 过定点.【正确答案】(1)5;(2)证明见解析.【分析】(1)连接OA ,OB ,求出圆C 的方程和2OAPB OAP S S =!=(2)求出以OP 为直径的圆的方程,再求出两圆的公共弦方程即得证.【详解】(1)解:依题意得:圆心(0,0)到直线x +3y=0的距离d =r ,∴5r d ===,∴圆C 的方程为x2+y2165=.如图,连接OA ,OB ,∵PA ,PB 是圆C 的两条切线,∴OA ⊥AP ,OB ⊥BP ,∴112||||22OAPB OAP S S OA PA ==⋅=⨯!=∴当PO 取最小值为8时,min ()OAPB S =(2)证明:由①得,A ,B 在以OP 为直径的圆上,设点P 的坐标为(8,b ),R b ∈,则线段OP 的中点坐标为(4,2b ),∴以OP 为直径的圆方程为222(4)()1624b b x y -+-=+,即x2+y2﹣8x ﹣by =0.∵AB 为两圆的公共弦,∴由222216580x y x y x by ⎧+=⎪⎨⎪+--=⎩得直线AB 的方程为8x by +=165,b ∈R ,即8(x 25-)+by =0,则直线AB 恒过定点(25,0).21.已知动圆M 经过定点1(1,0)F -,且与圆222:(1)8F x y -+=相内切.(1)求动圆圆心M 的轨迹C 的方程;(2)设点T 在2x =上,过点T 的两条直线分别交轨迹C 于A ,B 和P ,Q 两点,且TA TB TP TQ ⋅=⋅,求直线AB 的斜率和直线PQ 的斜率之和.【正确答案】(1)2212x y +=(2)0【分析】(1)设动圆圆心(),M x y ,半径为r ,利用椭圆的定义可得到动圆圆心M 的轨迹方程.(2)设出AB 直线方程和PQ 直线方程,分别与椭圆方程联立,写出韦达定理,利用弦长公式表示出TA TB TP TQ ⋅=⋅,即可得到斜率之和.【详解】(1)设动圆圆心(),M x y ,半径为r ,由题意得:12MF r MF r⎧=⎪⎨=-⎪⎩得12122MF MF F F +=>=.所以圆心M 的轨迹是以1F ,2F为焦点的椭圆,且1a cb ===故轨迹C 方程为2212x y +=.(2)设(2,)T t ,11(,)A x y ,22(,)B x y ,AB 直线方程为1(2)y t k x -=-,33(,)P x y ,44(,)Q x y ,PQ 直线方程为2(2)y t k x -=-,()221122x y y t k x ⎧+=⎪⎨⎪-=-⎩联立相消得2221111(21)4(2)2(2)20k x k t k x t k ++-+--=,()2111221211221842122221k k t x x k t k x x k ⎧-+=⎪+⎪⎨--⎪=⎪+⎩()22121212222121t TA TB x x k k +⋅--=++同理()2222222121t TP TQ k k +⋅=++,又TA TB TP TQ ⋅=⋅,2222121222121102121k k k k k k ++=⇒-=++,又12k k ≠,120k k +=.22.在平面直角坐标系xoy 中,已知圆22:4O x y +=,椭圆22:14x C y +=,A 为椭圆的右顶点,过原点O 且异于坐标轴的直线与椭圆C 交于,B C 两点,直线AB 与圆O 的另一个交点为P ,直线AC 与圆O 的另一个交为Q ,设直线,AB AC 的斜率分别为12,k k,(1)求椭圆的离心率;(2)求12k k 的值;(3)求证:AB AC AP AQ+为定值.【正确答案】(1(2)14-;(3)证明见解析.【分析】(1)根据椭圆离心率的公式直接求解即可;(2)设()00,B x y ,则()00,C x y --,然后根据两点间的斜率公式表示出12k k ,进一步化简整理即可求出结果;(3)分别将直线,AB AC 与椭圆联立,依次表示出点,,,B C P Q 的横坐标,然后根据线段的比与横坐标的关系转换为关于12,k k 的关系,进一步化简即可求出结果.【详解】(1)2c e a ==;(2)设()00,B x y ,则()00,C x y --,220014x y +=,因此()22200011444x y x =-=-,且()2,0A ,所以200012200012244y y y k k x x x =⋅==--+-;(3)设直线()1:2AB y k x =-,联立()()122222111221416164014y k x k x k x k x y ⎧=-⎪⇒+-+-=⎨+=⎪⎩,则221122111648221414B B k k x x k k --=⇒=++联立()()22221111222144404y k x k x k x k x y ⎧=-⇒+-+-=⎨+=⎩,则221122114422211P P k k x x k k --=⇒=++而21212814C k x k -=+,设直线()2:2AC y k x =-,联立()()222222222221416164014y k x k x k x k x y ⎧=-⎪⇒+-+-=⎨+=⎪⎩,则22212221222321116Q k k x k k --==++,22112211221122118228222214142223222221116C B P Q k k AB AC x x k k k k AP AQ x x k k ------+++=+=+------++()()()()222211112222111151411165205144414414414k k k k k k k k ++++=+===++++,解决直线与椭圆的综合问题时,要注意:(1)注意观察应用题设中的每一个条件,明确确定直线、椭圆的条件;(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.。
江苏省常州市2023_2024学年高二生物上学期10月阶段调研试题含解析

B、ce段动作电位的下降:Na+通道关闭,K+通道大量打开,K+大量外流,膜电位恢复为外正内负的静息电位,B正确;
C、动作电位的峰值与 Na+内流最后达到 Na+平衡电位有关(膜内外钠离子浓度差有关)。在有效刺激的基础上加大刺激,不会提高动作电位的峰值,C错误;
A.d点达到静息电位的最大值
B.ce时间段内发生钾离子的外流
C. 如果增大刺激强度,动作电位的峰值将会增大
D.ac段钠离子进入细胞和ce段钾离子流出细胞的方式不同
【答案】B
【解析】
【分析】静息电位与动作电位过程中膜电位变化曲线解读:a点之前,静息电位;神经细胞膜对K+的通透性大,对Na+的通透性小,主要表现为 K+外流,使膜电位表现为外正内负。ac段动作电位的上升:与 Na+大量内流有关,神经细胞接受一定刺激时,Na+通道打开,Na+大量内流导致膜电位迅速逆转,表现为外负内正。ce段动作电位的下降:Na+通道关闭,K+通道大量打开,K+大量外流,膜电位恢复为外正内负的静息电位。ef段:一次兴奋完成后,通过钠钾泵将动作电位产生过程中流入胞内的 Na+泵出膜外,将流出的 K+泵入膜内,以维持细胞外 Na+浓度高和细胞内 K+浓度高的状态,为下一次兴奋做好准备。
【详解】A、摄入过咸的食物后,细胞外液渗透压升高,引起下丘脑渗透压感受器兴奋,A正确;
B、血红蛋白存在与红细胞内,不存在于内环境中,B错误;
C、内环境稳态的实质是内环境的渗透压,温度和pH等理化性质保持动态平衡,C错误;
D、小肠绒毛上皮细胞生活的内环境为组织液,D错误。
故选A。
3. 下图是某反射弧的结构示意图,图中字母代表组成反射弧的神经元或其他结构,神经元与肌肉细胞之间也是通过突触联系的。下列相关叙述正确的是()
江苏省常州市2023_2024学年高二地理上学期10月阶段调研试题(含答案)

7. 该日0时甲地的风向最可能是( )
A. 西南风B. 西北风C. 东南风D. 东北风
降水相态与温度存在密切关系,700hPa以下温度均高于0℃时为雨,700hPa以下温度均低于0℃时为雪。近地层温度(1000hPa以下)在1~2℃时,且750hPa附近有高于2℃的暖温层时,降水相态为雨,若低于2℃则为雨夹雪或雪。下图示意我国大致在113°E上的四城市2017年2月21日8时温度垂直剖面。完成下面小题。
3. 从图中可知( )
A. 图中山峰海拔可能为1075mB. 两处养殖场直线距离约2km
C. ①处陡崖相对高度可达40mD. ①③两处不适宜发展种植业
4. ①③④⑤四地中,在②地一定可以看到的是( )
A. ①⑤B. ③⑤C. ①④D. ③④
5. 图中建有一小型水库,甲养殖场濒临水库最高水位,则( )
A. 水坝最低处可至1025mB. 水库水深最深20~30m
C. 水坝的长度约为380mD. 两养殖场不会污染水库
月牙泉位于我国甘肃省敦煌市城南,四周沙漠环抱。左图为月牙泉位置示意图,右图为夏季某日月牙泉与周边沙漠近地面气温日变化统计图。据此完成下面小题。
6. 该日气温日变化状况产生的主要原因( )
D. ②③两地的图上距离为1厘米,则甲图的比例尺约为1:666000000
2. 与甲图相比,乙图( )
A. 比例尺较大,表示的范围较小B. 比例尺较小,表示的范围较小
C. 比例尺较小,表示 范围较大D. 比例尺较大,表示的范围较大
下图为某区域等高线(单位:m)地形图,甲、乙两地建有养殖场,读图,完成下面小题。
17. 若甲处河流补给方式如图b所示,则甲河流域此季节( )
常州市教育教研室2007—2008学年度第一学期第三周教研活动安排
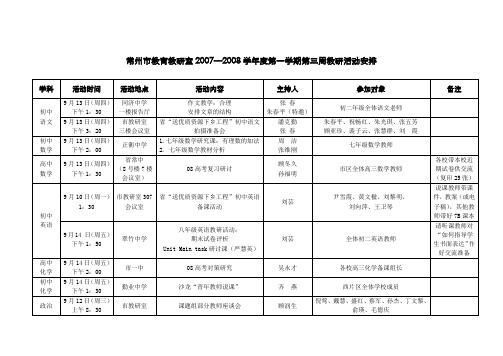
初中课题组活动
封晶晶
有意参加初中课题组的教师
音乐
9月13日(周四)
上午8:30
市一中
高中音乐模块教学研究课
洪毅
市区(含天宁、新北、戚区)全体高中音乐教师
美术
9月13日(周四)
上午8:30
市一中
高中美术模块教学研讨
朱丹
市区(含新北、天宁区、戚区)全体高中美术教师
品德
9月13日
(周四全天)
上午9:00
顾润生
倪莺、戴慧、盛红、蔡军、孙杰、丁文黎、俞瑛、毛德庆
历史
9月12日(周
闵晓弘
市区全体高一历史教师
事先备好课
9月14日(周五)
下午3:00
孝都中学
省教育科学“十一五”规划课题结题
王俊
闵晓弘
全体课题组成员
在市二中门口乘车前往
初中
生物
9月14日(周五)
上午9:00
常州市教育教研室2007—2008学年度第一学期第三周教研活动安排
学科
活动时间
活动地点
活动内容
主持人
参加对象
备注
初中
语文
9月13日(周四)
下午1:30
同济中学
一楼报告厅
作文教学:合理
安排文章的结构
张春
朱春平(特邀)
初二年级全体语文老师
9月13日(周四)
下午3:20
市教研室
三楼会议室
省“送优质资源下乡工程”初中语文拍摄准备会
耿群志
徐婉玉
任雄伟
陆伟
常州科学教师
附:局属各学校,优秀教研组评选已结束,请各校于本周到教研室领回评选材料。
初三英语伴你学已到,请订书的学校到教研室领取。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常州外国语学校2007—2008学年第一学期高二年级阶段质量调研语文试题2007年10月一、课内文言语段阅读(8分)阅读下面的文言文,完成1—4题。
古者富贵而名摩灭,不可胜记,唯倜傥非常之人称焉。
盖文王拘而演《周易》;仲尼厄而作《春秋》;屈原放逐,乃赋《离骚》;左丘失明,厥有国语;孙子膑脚,《兵法》修列;不韦迁蜀,世传《吕览》;韩非囚秦,《说难》《孤愤》;《诗》三百篇,大底圣贤发愤之所为作也。
此人皆意有郁结,不得通其道,故述往事,思来者。
乃如左丘无目,孙子断足,终不可用,退而论书策,以舒其愤,思垂空文以自见。
仆窃不逊,近自托于无能之辞,网罗天下放失旧闻,略考其行事,综其终始,稽其成败兴坏之纪,上计轩辕,下至于兹,为十表,本纪十二,书八章,世家三十,列传七十,凡百三十篇。
亦欲以究天人之际,通古今之变,成一家之言。
草创未就,会遭此祸,惜其不成,是以就极刑而无愠色。
仆诚以著此书,藏之名山,传之其人,通邑大都,则仆偿前辱之责,虽万被戮,岂有悔哉!然此可为智者道,难为俗人言也。
1.对下列各句中加点的词解释有误的一项是()A.古者富贵而名摩.灭摩:通“磨”B.唯倜傥非常之人称.焉称:被称道C.仲尼厄.而作《春秋》厄:困穷D.则仆偿前辱之责.责:责罚2.下列各组句子中,加点的词的意义和用法相同的一组是()A.盖文王拘而.演《周易》摇尾而.求食,积威约之渐也B.然.此可为智者道,难为俗人言也阙然.久不报,幸勿为过!C.退论书策,以.舒其愤可以.濯吾缨D.至激于.义理者则不然圣人不凝滞于.物3.句式与“文王拘而演《周易》”相同的一项是()A.安能以身之察察,受物之汶汶者乎?B.洎牧以谗诛C.又杂植兰桂竹木于庭D.楚左尹项伯者,项羽季父也4.下列叙述不符合文意的一项是()A.文中谈到孔子等人郁郁不得志,而发愤著述的事例,意在自况。
B.作者身受“腐刑”却不以为辱,反而把它作为著书立说的动力。
C.在作者看来富贵顺达者难成大事,唯有历经磨难、卓越非常之人常能发愤而有所成就。
D.司马迁著史记的目的在于研究历史,借鉴前人而不拘泥于前人,力求有自己的见解。
二、课内现代文阅读(8分)南州六月荔枝丹(节选)荔枝不耐贮藏,正如白居易说的:“一日而色变,二日而香变,三日而味变,四五日外,色香味尽去矣。
”在21摄氏度的环境里,可贮藏一二星期。
人们一直在设法延长贮藏期,以利于长途运输……唐代杜牧诗云:“长安回望绣成堆,山顶千门次第开。
一骑红尘妃子笑,无人知是荔枝来。
”当时是“昼夜奔腾,有毒虫猛兽之害”,“颠坑仆谷相枕藉”,“惊尘溅血流千载”。
为了封建统治者个人口腹之好,竟如此劳民伤财!但也足见当时荔枝贮藏与运输的不易。
荔枝的核就是种子,长圆形,表面光滑而色棕褐,少数品种为绿色。
优良的荔枝,种子发育不全,形状很小,有似丁香,也叫焦核。
现在海南岛有无核荔枝,核就更加退化了。
荔枝花期是二月初到四月初,早晚随品种而不同。
广东有双季荔枝,一年开花两次。
又有四季荔枝,一年开花四次之多。
花形小,绿白色或淡黄色。
花分雌雄,仅极少数品种有完全花……雌雄花往往不同时开放,宜选择适当的品种混栽在一起,以增加受粉的机会。
一个荔枝花序,生花可有一二千朵,但结实总在数百以下,所以俗有“荔枝十花一子”的谚语。
5.分点概括以上语段所介绍的内容。
(3分)6.以上语段除了引用说明外,还用了什么说明方法,请举例加以说明。
(2分)7.文中划线处引用了诗歌和谚语,试分析它们的具体作用....。
(3分)三、古代诗文阅读(32分)(一)阅读下面的文言文,完成8-12题。
(16分)韦丹字文明,京兆万年人。
新罗国君死,诏拜侍封郎中往吊。
故事,使外国,赐州县十官,卖以取费,号“私觌官”。
丹曰:“使外国,不足于资,宜上请,安有贸官受钱?”即具疏所宜费,帝命有司与之,因著令。
未行,而新罗立君死,还为容州刺史。
教民耕织,止惰游,兴学校,民贫自鬻者,赎归之,禁吏不得掠为隶。
始城州,周十三里,屯田二十四所,教种茶、麦、仁化大行。
以谏议大夫召,有直名。
刘辟反,议者欲释不诛,丹上疏,以为“孝文世,法废人慢,当济以威,今不诛辟,则可使者惟两京耳”。
宪宗褒美。
徙为江南西道观察使。
始,民不知为瓦屋,草茨竹椽,久燥则戛而焚。
丹召工教为陶,聚材于场,度其费为估,不取赢利。
人能为屋者,受材瓦于官,免半赋,徐取其偿;贫不能者,畀(bì,给与)以财;身往劝督。
置南北市,为营以舍军,岁中旱,募人就功,厚与直,给其食。
有吏主仓十年,丹覆其粮,亡三千斛,丹曰:“吏岂自费邪?”籍其家,尽得文记,乃权吏所夺。
召诸吏曰:“若恃权取于仓,罪也,与若期一月还之。
”皆顿首谢,及期无敢违。
有卒违令当死,释不诛,去,上书告丹不法,诏丹解官待辨。
会卒,年五十八。
验卒所告,皆不实,丹治状愈明。
宣宗读《元和实录》,见丹政事卓然,它日与宰相语:“元和时治民孰第一?”周墀对曰:“臣尝守江西,韦丹有大功,德被八州,殁四十年,老幼思之不忘。
”(《新唐书·循吏列伟》)8.对下列句子中加点的词语的解释,不正确的一项是()A.故事..,使外国,赐州县十官故事:旧日的典章制度B.则可使者..惟两京耳使者:出使的人C.度其费为估,不取赢利..赢利:获得的利润D.吏岂自费..邪自费:自己耗费9.下列各组句子中,加点的词意义和用法相同的一组是()A.受材瓦于.官冰,水为之,而寒于.水B.及其所.之既倦师之所.为,郑必知之C.帝命有司与之,因.著令因.人之力而敝之,不仁D.今不诛辟,则.可使者惟两京耳于其身也,则.耻师焉10.下列句子分别编为四组,全都表明韦丹“仁化大行”(仁政教化得以广泛实行)的一组是①具疏所宜费,帝命有司与之,因著令②民贫自鬻者,赎归之,禁使不得掠为隶③丹召不教为陶④贫不能者,畀以财⑤岁中旱,募人就功,厚与直,给其食⑥籍其家,尽得文记A.①③④B.①⑤⑥C.②③⑥D.②④⑤()11.下列叙述不符合原文意思的一项是()A.韦丹力主某除陈规旧法。
他认为出使外国所用的资费,应该由朝廷拨付,不应该沿袭陈规卖官筹款。
皇帝听从了他的意见,修改了法令制度。
B.韦丹担任言官以正直闻名。
他认为如不以强力威慑,人们就会轻忽法令;刘辟反叛如不加讨伐,朝廷就无法统辖全国。
为此他得到了皇帝的赞扬。
C.韦丹执法宽厚仁慈。
对于依仗权势从官仓强取粮食的主仓吏,他只是责令限期归还。
对于违犯法令被判死刑的兵卒,他也没有执行,而是将这个兵卒释放了。
D.韦丹为政功绩显著。
他担任地方官以仁化为本,多方造福地方百姓。
他被诬告的罪名经查也尽属不实,这更显现出他的功绩。
12.把文言文阅读材料中画线的句子翻译成现代汉语。
(1)使外国,不足于资,宜上请,安有贸官受钱?(3分)译文______________________________________________________(2)籍其家,尽得文记,乃权吏所夺。
(3分)译文______________________________________________________(3)皆顿首谢,及期无敢违。
(2分)译文______________________________________________________(二)诗歌阅读(8分)阅读下面这首唐诗,完成13-14题。
(8分)章台夜思韦庄清瑟怨遥夜,绕弦风雨哀。
孤灯闻楚角,残月下章台。
芳草已云暮,故人殊未来。
家书不可寄,秋雁又南回。
【注】章台:即楚灵王行宫章华台,故址在今湖北省监利县西南。
瑟:琴瑟。
13.“清瑟怨遥夜,绕弦风雨哀”运用了什么修辞手法?请赏析其作用。
(4分)答:14.本诗的题目为《章台夜思》,有人认为这首诗全篇未现一个“思”,却“秋思”不断,令人回味,你同意这种看法吗?请结合具体的内容进行阐述。
(4分)答:(三)名句名篇默写(8分)15.补写出下列名句名篇中的空缺部分。
(8分)(1),内无应门五尺之僮;,形影相吊。
(李密《陈情表》)(2)_______________,_______________。
臣不胜犬马怖惧之情,谨拜表以闻。
(李密《陈情表》)(3)四周山色中,一鞭残照里,,量这些大小车儿如何载得起?(王实甫《长亭送别》)(4)青山隔送行,疏林不做美,。
(5)亦欲以,通古今之变,成一家之言。
(司马迁《报任安书》)(6)屈原曰:“举世皆浊我独清,。
是以见放。
”四、文学文本的阅读(18分)阅读下面的散文,完成16—19题。
读荷吴长忠(1)世人皆爱荷,叹其美艳,赞其高洁。
常常地、细细地品味荷花,我感觉荷花、也许只有荷花,达到了美而至圣的境界。
(2)圣和美无疑是人类所追求的价值体系中的两个核心概念。
在人类感知自身及外部世界的过程中,形成了人类的意识形态。
在意识形态的主要形式中,每一种形式都对应着一个核心概念,或曰核心价值。
正如哲学之对应真,道德伦理学之对应善,法律之对应安,体育之对应力,圣和美则分别是宗教与艺术的核心概念。
这个价值体系中的诸核心价值,在其最高境界则是相通的。
其一例是高水平的体育竞赛不仅能引起人们对“更高、更快、更强”之趋于力的极限的赞叹,也能同时给人们以美的享受,即由核心价值“力”至核心价值“美”的渡溢。
其另例如古希腊雕塑“断臂的维纳斯”,千百年来,面对这尊美得令人炫目的人体,没有人想过触摸或占有,她在人们的心底激起的是神圣的感觉,因为她的美而使人找到了一种近平神圣的自信,这是由核心价值“美”至核心价值“圣”的升华。
(3)观诸四季花卉,或暗香清芳,明媚娇艳,或姹紫嫣红,百态千姿,实乃自然造化之精华。
若自然界亦有核心价值体系,我相信“花”应居于体系之高端,正如“美”居于人类社会核心价值体系之顶层。
(4)然因四时花卉生长特征自然品性之差异,给予欣赏主体的感觉也是不同的,更何况欣赏主体亦有千差万别,作为同一个体的欣赏者在不同时空环境下的感受也是不同的。
(5)秋天品味菊花,我为其风节而感动,“宁肯枝头抱香死,何曾吹落北风中”,伟丈夫也。
冬天品味梅花,我为其勇毅而击节。
自知风寒侵凌,依然前行报春,真勇士也。
春天品味牡丹,我为其气韵而赞叹。
看那姚黄魏紫在春阳下绽放,在春风中摇曳,似将日月精华集于一身,纵情恣肆地展示着生命的高贵与艳丽。
(6)此花中三品,可赞可叹。
然而细品其生命过程,止于在自然形态之荚艳中展示其节其气,而未入由美至圣之境界。
入此境者,唯有荷花。
你看她自盈盈清水中拔节而出,在纤尘不染的绿叶间绽放,在暖暖夏晖中凋谢,生来默默,归去静静,不争不嚣,无艾无怨。
在转瞬间开放,为夏晨染一片亮丽,又在转瞬间逝去,为午后添一层静穆。
我曾多次守候荷塘,却从未见一片荷花落下,似乎她特意选择人们不经意时归去。
那不知什么时候洒落在荷叶上的花瓣,却片片鲜嫩,似从清水中绽出的新的花朵。
你再看那未曾落下的残荷,却依然在惠风中、在清水上、在绿叶间摇曳着,绽放着妩媚。
