第四章 相图
第四章 二元相图

铁碳相图和铁碳合金
铁-石墨相图:Fe-C; 铁-渗碳体相图:Fe-Fe3C。
1 铁碳合金中的组元和相 L, δ, A(γ), F(α), Fe3C(渗碳体)
46
2 Fe-Fe3C相图分析
点:16个。 线:两条磁性转变线;三条等温转变线; 其余三条线: GS,ES,PQ。
区:5个单相区,7个两相区,3个三相区。
5
4.1.4 二元相图的几何规律 (1)相区接触法则:两个单相区之间必定有一个由这两个相 组成的两相区,而不能以一条线接界。两个两相区必须以单 相区或三相水平线隔开。由此可以看出二元相图中相邻相区 的相数差一个(点接触除外)。 (2)在二元相图中,若是三相平衡,则三相区必为一水平 线.这条水平线与三个单相区的接触点确定了三个平衡相及 相浓度。每条水平线必与三个两相区相邻。 (3)如果两个恒温转变中有两个相同的相,则这两条水平 线之间一定是由这两个相组成的两相区。
39
2、 组元间形成化合物的相图 稳定化合物:具有一定熔点,在熔点以下不分 解的化合物。 3、具有异晶转变的相图 一个固相转变为另一个固相的转变称为异晶转 变也称同素异构转变。 4、具有固溶体形成中间相转变的相图 5、具有有序---无序转变的相图 6、具有磁性转变的相图
40
38
4.3二元相图的分析和使用 4.3.1 其他类型的二元相图 1、 其他类型的恒温转变相图 (1)熔晶转变相图 定义:一个固相在恒温下转变成一个液相和另一个固相的转 变。 (2)偏晶转变相图 定义:一个液相在恒温下分解为一个固相和另一个液相的转 变。 (3)共析转变相图 定义:一定成分的固相在恒温下生成另外两个一定成分的固 相的转变。 (4)包析转变相图 定义:两个一定成分的固相,在恒温下,转变为一个新的固 相的转变。
陶瓷物化第四章陶瓷相图详解.ppt

力基本不影响凝聚态系统的平衡状态,n=1。 相律: F=C-P+1
第二节 单元系统
单元系统只有一个组分,即独立组分C=1。 根据相律: F = C-P + 2 =1-P+2 F=3-P
Pmax= 3-0 = 3,单元系统中平衡共存的最多相。三相共存点为无 变量点,系统为无变量状态。系统相数最少为1,单元系统最大自由 度为2。温度和压力是单元相图中两个独立变量,用温度和压力的二 维图表示单元系统的相平衡与二者的关系。
p=3 f=0
E(液相消失)[O , A+C]
1
b
T
M
a
L
L+A E A+C
P D
L+C
L+B
J
F
B+C
L C
B
A
C
B
• 同理可分析组成1的冷却过程。在转熔点P处,
L+BC时,L先消失,固相组 成点为D和F,其含量 由D、J、 F三点相对位置求出。P点是回吸点又是析晶终点。
4 低共熔点温度以下有化合物生成与分解的二元相图
α-石英 870α℃-鳞石英 1470℃α-方石英
573℃
163℃
180~270℃
β-石英
β-鳞石英 117℃
β-方石英
γ-鳞石英
二、 相律:
平衡体系中,自由度F、组分C和相数p的规律。
Gibbs提出,系统平衡时:
F C-P+n F : 自由度数,温度、压力、组分浓度等可能影响系统平衡
状态的变量,在一定数量内任意变化而不引起旧相消失 或新相产生的独立变量的数目。 C:独立组分数,构成平衡物系所有各相所需最少组分数。 P :相数。 n :影响系统平衡的外界因素,如温度、压力、电场等。 通常,外界因素主要是温度和压力,一般相律表示为:
第四章 相图

合金是指由两个或两个以上元素或组元组成的, 具有金属特性的物质。
纯金属结晶时,相状态只与温度有关,且有固定 的凝固点。
在合金凝固过程中,除了温度变量以外,还有成 分变量,为了描述合金状态与温度与成分的关系, 需要借助于相图来表示。
相图是用来表示合金系中各合金结晶过程的 简明图解。又称平衡状态图。
在杠杆定律中,杠杆的支点是合金的成分,杠杆的端 点是所求的两平衡相(或两组织组成物)的成分。
杠杆定律只适用于两相区。
例(如图)
Q
0.53 0.45 100% 61.5% 0.58 0.45
QL
0.58 0.58
0.53 0.45
100%
38.5%
杠杆定律应用条件:
1 必须是在两相区; 2 必须是平衡转变。
1
2
⑵ 确定两平衡相的相对重量
设合金的重量为1,液相重量为QL,固相重量为Q。
则 QL + Q =1
液相重量 + 固相重量 = 合金重量
QL x1 + Q x2 =x 液相中B组元含量 + 固相中B组元含量
解方程组得:
= 合金中B组元含量
QL
x2 x x2 x1
Qα
x x1 x2 x1
式中的x2-x、x2-x1、x-x1即为相图中线段xx2 (ob)、
二、二元共晶相图
当两组元在液态下 完全互溶,在固态 下有限互溶,并发 生共晶反应时所构 成的相图称作共晶 相图。
以Pb-Sn相图为例进 行分析。
Pb-Sn合金相图
1、相图分析
⑴ 相:相图中有 L、、三种相, A
是溶质Sn在 Pb
B
中的固溶体,
是溶质Pb 在Sn中
第四章:二元相图

2.杠杆定律: 问题提出: ①当二元合金(成分已知)由两相组成时两相的相对重量是多少?
例:45钢(含C=0.45%),铁素体(F)和Fe3C两相各占多少? ②当二元合金两相相对重量已知时,合金成分是多少?
例:金相观察:F:95%; Fe3C:5%;求钢的含碳量? 杠杆定律可以解决此类问题。
纯金属结晶:在负的温度梯度下---------树枝晶。 在正的温度梯度下------平滑界面(平面长大)
固溶体合金,即使在正的温度梯度下,也会形成树枝晶-------是由于 成分过冷造成的。 (1)成分过冷概念:固溶体合金结晶时,由于液固界面前沿存在溶质 浓度梯度而改变了过冷情况,称为成分过冷。
(2) 产生原因: 以K0<1为例(图示说明) 过冷度:界面前沿液相实际温度<液相平衡结晶温 度 (3) 产生成分过冷的条件: (讨论成分过冷的影响)
④具有共晶转变的二元合金: Pb-Sn Pb-Sb Fe-C(C>2.11%) Al-Si Al-Cu Ag-Cu
第四章:二元相图
4.2.2共晶相图
1.相图分析
以Pb-Sn二元合金相图为例:
三个单相区:L、α、β α:Sn溶入Pb中固溶体 β: Pb溶入Sn中固溶体
AEB-液相线 E点:共晶合金 AMNB-固相线 ME之间:亚共晶 ; EN之间:过共晶合金 MF-Sn在Pb中溶解度曲线,随T↓,溶解度↓ NG- Pb在Sn中溶解度曲线
第四章:二元相图
4.2.2共晶相图
2.典型合金平衡结晶及组织
(2)共晶合金结晶过程(61.9%Sn) 在183℃,由61.9%Sn的液相,同时结 晶出α(19%Sn)和β(97.5%Sn)两 种固溶体。
第四章_二元相图
⒊ 相区
⑴ 五个单相区: L、、、、Fe3C
⑵ 七个两相区: L+、 L+、L+Fe3C、 +、
+Fe3C、+ 、 +Fe3C
⑶ 三个三相区:即HJB (L++)、ECF(L++ Fe3C)、 PSK(++ Fe3C)三条水平线
13
二、包晶转变(HJB)
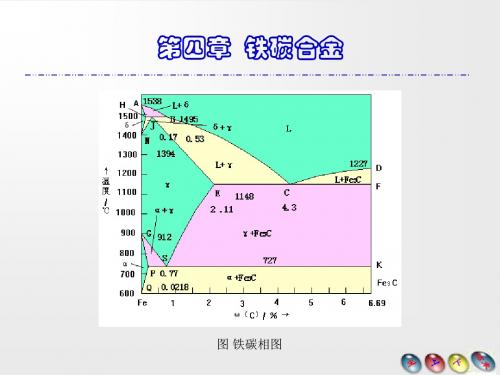
第四章 铁碳合金
图 铁碳相图
铁碳相图
铁碳相图是研究钢和铸铁的基础,对于钢铁材料的应用 以及热加工和热处理工艺的制订也具有重要的指导意义。 铁和碳可以形成一系列化合物,如Fe3C、Fe2C、FeC等, 有实用意义并被深入研究的只是Fe- Fe3C部分,通常称其为 Fe-Fe3C相图, 此时相图的组元为Fe和Fe3C。
S P Fe3C
珠光体是铁素体和渗碳体 两相的混合物,是共析反应 的产物,用符号“P”表示。 珠光体是一种双相组织。 一般情况下,两相呈层片状 分布,强度较高、硬度适中、 有一定塑性。
7270 C
图 共析钢的室温组织
五、三条重要的特征线——ES、PQ、GS线
ES线是碳在奥氏体中的溶解度曲线。含碳量大于0.77% 的合金,从1148℃冷到727℃的过程中,将自奥氏体中析出 渗碳体,这种渗碳体称为二次渗碳体(Fe3CII)。
Q
1 2
3
4
9
25
2. 亚共析钢的结晶过程
Ⅲ
0.09~0.53%C亚共析钢
A
H J
B
冷却时发生包晶反应.
以0.45%C的钢为例
G S P
相图

结晶过程:包晶线以下,L, α对β过饱和- 界面生成β-三相间存在浓度梯度-扩散-β 长大-全部转变为β。
室温组织: β或β+αⅡ。
64
2 成分在C-D之间合金的结晶 结晶过程:α剩余; 室温组织:α+β+αⅡ+βⅡ。
65
3 其他平衡结晶过程及其组织
66
三、不平衡结晶及其组织 异常α相导致包晶偏析〔包晶转变要经β扩
③ 室温组织(α+βⅡ) 其中βⅡ一般分布于相界面上,有时也在晶内 析出,呈细小颗粒状。
相对量计算:
4g
f
100 % fg
II
4f fg
100 %
35
2共晶合金的结晶过程 ① 凝固过程(冷却曲线、相变、组织示意图)。
36
② 组织: 共晶转变刚好结束后的组织:(αm+βn) 室温组织:(α+β+αⅡ+βⅡ)(二次相为脱熔 转变产物) (因为二次相依附共晶体中的 同类相析出,因此难以辨别) 通常室温组织:
共晶组织:共晶转变产物。(是两相混合物)
26
一、 相图分析(相图三要素) 1 点:纯组元熔点;最大溶解度点;共晶点 (是亚共晶、过共晶合金成分分界点)等。 2 线:液相线(结晶开始)、固相线(结晶结 束线);溶解度变化曲线。
Pb-Sn相图 27
3 区: 3个单相区(L、α、β) ; 3个两相区(L+α、L+β、α+β) ; 1个三相线(区)。
(α+β)共晶体
37
③共晶合金结晶过程中的相的相对量计算。
恰好要发生共晶反应时:L相,相对量:100 %;
共晶反应过程中:三相(L+α+β),不适用 杠杆定律;
共晶反应刚好结束:两相(αm+βn)
m
en 100% mn
第四章 铁碳合金相图(全)

第四章 铁碳合金相图
主讲人: 刘 怿 凡
§4.1 固态合金的相结构
几个重要概念
1.合金
两种或两种以上的金属,或金属与非金属元素组成 的具有金属特性的物质
2.组元
组成合金的最基本的独立物质称为组元,可以是组 成合金的元素,也可以是化合物,有二元、三元等。
3.相
在合金中,凡成分相同、结构相同并以明显界面相 互分开的均匀组成部分,是合金中最基本的组成部分。
●白口铸铁硬度高、脆性大,不能切削加工,也不能锻造,但其耐 磨性好,铸造性能优良,适用于作要求耐磨、不受冲击、形状复杂 的铸件,例如拔丝模、冷轧辊、货车轮、犁铧、球磨机的磨球等。
§4.4 铁碳合金相图的应用
2.在铸造工艺方面的应用
根据Fe—Fe3C相图可以确定合金的浇注温度。浇注温度一般在 液相线以上50~100℃。
§4.1 固态合金的相结构
4.组织
用肉眼或显微镜观察到的金属材料的内部情景,包 括晶粒的大小、形状、相对数量和相对分布。“特殊形 态的微观形貌”
5.合金系
由相同组元配制的一系列成分不同的合金,组成一 个合金系统。
合金组织中的相结构决定合金的性能
§4.1 固态合金的相结构
合金的相结构
晶体结构、原子结构不同、组元相互作用不同——不同相结构
4.在热处理工艺方面的应用
Fe—Fe3C相图对于制订热处理工艺有着特别重要的意义。一些 热处理工艺如退火、正火、淬火的加热温度都是依据Fe—Fe3C相图 确定的。
§4.4 铁碳合金相图的应用
在运用Fe—Fe3C相图时应注意以下两点:
①Fe—Fe3C相图只反映铁碳二元合金中相的平衡状态,如含有其 它元素,相图将发生变化,与实际情况有较大差异。
4 第四章 相图(二元)

配制合金系中几种不同成分合金 熔化后,测试其冷却曲线 根据曲线上的转折点,确定各合金的凝固温度 将上述数据引入以温度为纵轴,成分为横轴的坐标
平面中 连接意义相同的点,作出相应的曲线 曲线将图面分成若干区域----相区。经过金相组织分 析,测出各相区所含的相,将相的名称标注其中, 相图工作就完成
4,过共晶合金
★ E点以右,D点以左,为过共晶合金,与亚 共晶合金类似,白色卵形为初晶β,黑色为共 晶体(α+β)。 ★α,β,αⅡ,βⅡ,(α+β)称组织组成物 ★α,αⅡ为一个相。(α+β)两相混合物,称共晶 体。 ★求组织组成物的相对量,同样可用杠杆定理 标明各区的组织---组织分区图
四、共晶组织和初晶形貌 1,共晶组织的形貌
测试时要求合金的成分准确,纯度高,冷却
速度要慢0.5~1.5℃/min
下面是Ni-Cu合金相图,是最简单的相图之一
Ni 1500 1400 1300 1200 1100 1000 900 20% 40% Cu Cu
80% Cu 60% Cu
Cu
Ni 20 40 60 80 Cu Cu%
2.2. 使用二元合金相图的基本方法
2 > 2 ;此时 2 -2 <0
dG<0
当α相与β相彼此平衡时,在dG=0, 同理 :------------------------------
= =
1
2
2
1
1.3. 相律
相律是分析和使用相图的重要依据。凝集态
受压力影响很小,在恒压下:相平衡条件的 数学表达式:f=c-p+1 (在物理化学中也指出) 式中C为组元数,P为共存的平衡相数,f为自 由度数。 单元系(纯金属) f=1-2+1=0,自由度为1,表 明恒温下平衡熔化或凝固。 二元系C=2,当f=0,p=3,在恒定温度下处于三 相平衡;两相共存时,自由度数目为1,表明 平衡凝固或熔化就在一定温度范围
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章
1.在Al-Mg合金中,X
Mg 为0.15,计算该合金中镁的W
Mg
为多少。
2.根据图4-117所示二元共晶相图,试完成:
(1)分析合金Ⅰ,Ⅱ的结晶过程,并画出冷却曲线.
(2)说明室温下合金Ⅰ,Ⅱ的相和组织是什么?并计算出相和组织组成物的相对量.
(3)如果希望得到共晶组织加上相对量为5%的β初的合金,求该合金的成分.
(4)合金Ⅰ,Ⅱ在快冷不平衡状态下结晶,组织有何不同.
3.分析图4-118所示Ti-W合金相图中,合金Ⅰ(ww=0.40)和(ww=0.93)在平衡冷却和快冷时组织的变化.
4.含W
Cu
为0.0565的Al-Cu合金(见图4-119)圆棒,置于水平钢模中加热熔化,然后采用一端顺序结晶方式冷却,试求合金圆棒内组织组成物的分布,各组成物所占圆棒的百分数及沿圆棒长度上Cu浓度的分布曲线(假设液相内熔质完全混合,固相内无扩散,界面平直移动,液相线与固相线呈垂直)。
5.参看图4-45所示的Cu-Zn相图,指出图中有多少三相平衡,写出它们的反应式.并分析含wZn为0.4的铜锌合金平衡结晶过程中的冷却曲线,主要转变反映式及室温相组成物与组织组成物.
6.根据下列数据绘制Au-V二元相图.已知金和钒的熔点分别为1064℃和1920℃.金与钒可形成中间相β(AuV3),钒在金中的固熔体为α,其室温下的熔解度为wV=0.19,金在钒中的固熔体为γ, 其室温下的熔解度为wAu=0.25.合金系中的两个包晶转变,即
(1) β(wV=0.4)+L(wV=0.25)== α(wV=0.27)
(2) γ(wV=0.52)+ L(wV=0.345)== β(wV=0.45)
7.计算含wC为0.04的铁碳合金按压稳态冷却到室温后组织中的珠光体`、二次渗碳体和莱氏体的相对量,并计算组成物珠光体中渗碳体和铁素体及莱氏体中二次渗碳体、共晶渗碳体与共析渗碳体的相对量.
8.根据显微组织分析,一灰口铁内含有12%的石墨和88%的铁素体.试求其wC.
9.汽车挡泥板应选用高碳钢还是低碳钢制造?
10.当800℃时, 试求:
(1)含wC =0.002的钢内存在哪些相.
(2)写出这些相的成分.
(3)各相所占的相对量是多少.
11.根据Fe-Fe3C相图,试完成:
(1)比较wC =0.004的合金在铸态和平横状态下结晶过程和室温组织有何不同.
(2)比较wC =0.019合金在慢冷和铸态下结晶过程和室温组织的不同.
(3)说明不同成分区铁碳合金的工艺性(铸造性、冷热变形性).
12.图4-120为Pb-Sn-Zn三元合金相图液相面投影图.
(1)在图上标出合金X(wPb =0.75,wSn=0.15,wZn=0.10)的位置 ,合金Y(wPb =0.50, wSn=0.30, wZn=0.20)的位置及合金Z(wPb =0.10, wSn=0.10, wZn=0.80)的位置.
(2)若将2Kg X,4Kg Y及6Kg Z混熔成合金W,指出W的成分点位置.
(3)若有3Kg合金X,问需要配多少何种成分的合金才能混合成6Kg的合金Y?
13.有合金R由α, β, γ三相组成,合金R及三相中的组元A的含量依次为AR,A α,Aβ,Aγ,组元B的含量依次为BR,Bα,Bβ,Bγ,组元C的含量依次为CR,Cα,C β,Cγ.试利用代数方法求合金R中的三相的质量分数.
14.试分析图4-96中所示①,②,③,④和⑤区内合金的结晶过程,冷却曲线及组织
组成物.
15.试分析图4-102所示中Ⅰ,Ⅱ,Ⅲ,Ⅳ和Ⅴ区内合金的结晶过程,冷却曲线及组织组成物.
16.请在图4-113所示中指出合金X(wCu=0.15,wMg=0.05)及合金Y(wCu= wMg =0.20)的成分点、初生相及开始凝固温度;并根据液相单变量线的走向判断所有四相平衡转变的类型.
17.wCr=0.18,wC=0.01的不锈钢,其成分点在1150℃截面图(见图4-112)中p点处,合金在1150℃时各平衡相质量分数应如何计算?
18.利用图4-111分析2Cr13不锈钢(wCr=0.13,wC=0.0002),4Cr13不锈钢(wCr=0.13,wC=0.0004)和Cr12型模具钢(wCr=0.13,wC=0.02)的凝固过程及组织组成物;并说明它们的组织特点.
19根据图4-121分析陶瓷(wSiO2=0.57,wCaO=0.38,wAl2O3=0.05)的凝固顺序及试问室温下各相的质量分数.
20.指出下列各题错误之错,并更正.
(1)固熔体晶粒内存在枝晶偏析,主轴与枝间成分不同,所以整个晶粒不是一个相。
(2)尽管固熔体合金的结晶速度很快,但是在凝固的某一个瞬间,A,B组元在液相和固相内的化学位都是相等的。
(3)固熔体合金无论平衡和非平衡结晶过程中,液-固界面上液相成分沿着液相平均成分线变化;固相成分沿着固相成分线变化。
(4)在共晶线上利用杠杆定律可以计算出共晶体的相对量.而共晶线属于三相区,所以杠杆定律不仅适用于两相区,也适用于三相区。
(5)固熔体合金棒顺序结晶过程中,液-固界面推进速度越快,则棒中宏观偏析越严重。
(6)将固熔体合金棒反复多次"熔化-凝固"并采用定向快速凝固的方法,可以有效的提纯金属。
(7)从产生成分过冷的条件G/R<mc0(1-ko)/Dk0可见,合金中溶质浓度越高,成分过冷区域小,越易形成胞状组织。
(8)厚薄不均匀的Ni-Cu合金铸件,结晶后薄处易形成树状组织,而厚处易形成胞状组织。
(9)不平衡结晶条件下,靠近共晶线端点内侧的合金比外侧的合金易于形成离异共晶组织。
(10)具有包晶转变的合金,室温的相组成物为α+β,其中β相均是包晶转变产物。
(11)用循环水冷却金属模,有利于获得柱状晶区,以提高铸件的致密性。
(12)铁素体与奥氏体的根本区别在于熔碳量不同,前者少而后者多。
(13)727℃是铁素体与奥氏体的同素异构转变温度。
(14)在Fe-Fe3C系合金中,只有过共析钢的平衡结晶组织中才有二次渗碳体存在。
(15)凡是碳钢的平衡结晶过程都具有共析转变,而没有共晶转变;相反,对于铸铁则只有共晶转变而没有共析转变。
(16)无论何种成分碳钢,随着含碳质量分数的增加,组织中铁素体相对量减少,而珠光体相对量增加。
(17)含Wc=0.043的共晶白口铸铁的显微组织中,白色的基体为Fe3C,其中包括FeC1,FeCⅡ,FeCⅢ,Fe3C共析,Fe3C共晶。
(18)图4-55所示为含Wc=0.0077C的珠光体组织,图中显示渗碳体片密集程度不同,凡是片层密集处则Wc偏多,而疏稀处则Wc偏少。
(19)试说明三元相图垂直截面的两相区内杠杆定律不适用的原因。
(20)只有单析熔解度曲面或双析熔解度曲面投影内的三元合金,才有一个次生相或两个次生相析出。
(21)在三元相图中,液相面投影图十分重要,根据它就可以判断该合金系凝固过程中所有相平衡的关系。
